随着我国电力事业的快速推进,人们对电力资源的需求日益增大. 双平臂抱杆作为一种起重类桅杆结构,杆身长,横截面小,长细比大,结构非常柔,是典型的风敏感结构,在施工期间比钢管塔本身更易发生风致破坏. 一旦在施工期间发生倒塌破坏会造成非常严重的后果.
抱杆结构的抗风安全性与稳定性是大跨越输电钢管塔施工过程的瓶颈问题,影响着整个舟山跨海特高压输电工程的顺利实施. 周焕林等[1]对舟山大跨越高塔抱杆进行现场试验,为此类高塔抱杆的设计制造和安全使用提供参考. 抱杆结构除受到自重和吊重荷载,其主要的设计控制因素是强风条件下的水平风荷载及其风振效应. 抱杆结构通过设置腰环和拉索与主塔相连,为其提供侧向约束. 在动力风荷载作用下,抱杆的风致响应与其独特的类似拉索桅杆结构紧密相关. 文献调查表明直接针对抱杆结构风振响应的研究很少,而与抱杆结构类似的桅杆结构及塔架结构动力风荷载问题得到广泛关注,相关的研究较多. 潘峰等[2]推导钢管构架结构的风致响应和风振系数计算公式. 马晋等[3]基于风速时程模拟技术进行典型塔式起重机塔架结构风致动力响应分析和疲劳计算分析. 高松等[4]研究单柱拉线塔的风振系数,发现主柱上存在横隔材的位置风振系数会发生突变. 邓洪洲等[5-6]分析规范中桅杆结构风振系数计算公式在实际工程运用中存在的一些问题,考虑桅杆结构前四阶振型的贡献,提出杆身的风振系数简化计算公式. 赵爽等[7]基于风洞试验计算苏通大跨越输电塔在0°~ 90°的惯性力风振系数、位移风振系数和有效荷载风振系数,并分析3种风振系数沿高度的分布规律. 史国富等[8]基于谐波合成法模拟得到脉动风荷载,并对比高柔结构时程分析和基于规范计算的风振响应结果,验证规范方法在实际工程设计中的适用性. 柯世堂等[9]采用瞬态时域动力计算,探讨钢烟囱高柔结构在4种典型等效目标下的风振系数分布和取值,给出该结构分层和整体的风振系数取值建议.
由于抱杆腰环拉索的几何非线性及杆身大位移产生的二阶矩效应,抱杆结构在风荷载作用下表现出较强的非线性. 这点与拉索桅杆柔性结构类似,需要开展柔性结构风振响应的非线性分析[10-11]. Hamada等[12-14]研究多跨拉线式输电塔线体系的气动特性和动力响应,结果表明多跨拉线式输电塔线体系的风致动力响应更多表现为风振背景分量占主导的准静态特性. Ladubec等[15]对拉线式输电塔的研究发现,考虑抱杆几何非线性的轴力最大值比线性分析计算得到的轴力值大34%. Lorenzo等[16]研究飓风袭击下的自立式输电塔风振响应,与时程分析法相比,采用欧洲规范中的静态等效法计算时输电塔构件受力和位移增加20%~25%.
本文基于高频天平测力试验,获得双平臂抱杆结构的体型系数与风力系数;结合风洞高频天平试验得到的风荷载数据和谐波叠加法,生成不同姿态下抱杆结构在不同高度处的风荷载时程样本;建立各典型施工工况下抱杆结构有限元模型,在时域内开展抱杆结构的风振响应时程分析,得到抱杆结构在各施工工况强风条件下的风振系数,为大跨越钢管塔施工过程的抗风安全性能评估提供可靠依据,确保舟山连岛输电工程在台风期的顺利实施.
1. 双平臂抱杆风洞试验
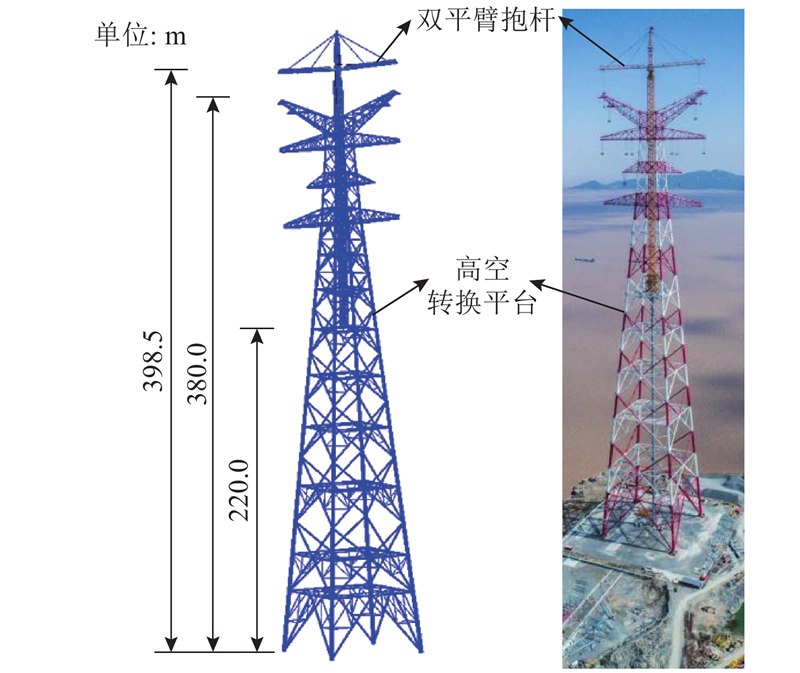
位于舟山的380 m西堠门大跨越钢管塔创造了钢管输电塔高度、总重等多项世界纪录,钢管塔在组立过程中采用的特制施工装备T2T1260双平臂抱杆,如图1所示.
图 1
图 1 输电塔和双平臂抱杆施工现场
Fig.1 Construction of transmission tower and crane structure with double flat arms
本文以该项目施工过程中采用的双平臂抱杆结构作为研究对象,开展针对双平臂抱杆结构的风洞试验,试验在浙江大学ZJU-1单回流闭口型边界层风洞中进行. 根据文献[17]的规定,抱杆所在地区为A类地貌,地面粗糙度系数为0.12,大气边界层梯度风高度为300 m. 双平臂抱杆主要由标准节、支座、塔顶和平臂等部分组成. 试验采用高频底座测力天平测量不同风向角、不同平臂姿态下的抱杆标准节以及抱杆整体结构在来流风作用下的风荷载时程数据,采样频率为300 Hz.
1.1. 标准节节段模型测力试验
抱杆标准节为平面尺寸4 m×4 m、高度为6 m的正方形截面格构式塔架. 按照几何相似要求,采用ABS工程塑料制作缩尺比为1∶20的抱杆标准节节段模型,包含3节标准节,模型高约0.9 m,如图2(a)所示. 空气密度取1.25 kg/m3,试验中参考点设置于风洞内0.71 m高度处,测试风速为8 m/s,流场为均匀湍流,湍流强度为8%.
图 2
图 2 双平臂抱杆风洞试验模型
Fig.2 Wind tunnel model of crane structure with double flat arms
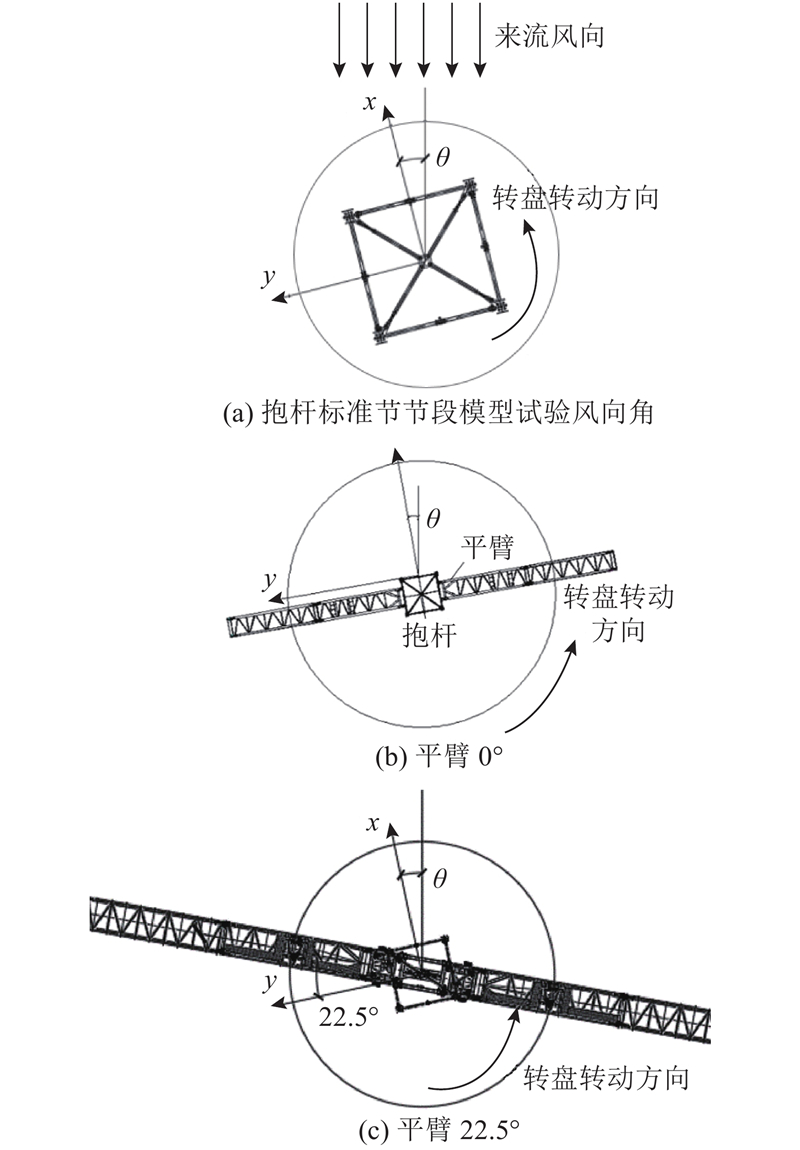
风洞试验中根据标准节和平臂的相对位置关系,标准节节段模型按逆时针设置0°、15°、22.5°、30°、37.5°、45°、52.5°、60°、67.5°、75°、82.5°、90°、105°、112.5°、120°和135°共16个风向角试验工况,采样时间长度为165 s,试验中风向角设定见图3(a).
图 3
图 3 风洞试验风向角和平臂姿态
Fig.3 Wind direction angle and position of double flat arms for wind tunnel test
1.2. 抱杆平臂主体模型测力试验
表 1 风洞试验风向角
Tab.1
| 平臂姿态 | |
| 0° | 0°、15°、30°、45°、60°、75°、90°; |
| 22.5° | 22.5°、37.5°、52.5°、67.5°、82.5°、97.5°、112.5°; |
| 45° | 45°、60°、75°、90°、105°、120°、135° |
1.3. 试验数据处理和结果
风洞试验中抱杆标准节的体型系数计算公式为
式中:μx、μy分别为抱杆标准节的x方向和y方向的体型系数,
式中:
式中:Cx、Cy分别为抱杆结构整体x向和y向的风力系数;Fx、Fy分别为抱杆沿x向和y向的总风荷载,即各部分构件风荷载之和;AT为平臂在0°位置时抱杆x向迎风面净投影总面积.
图 4
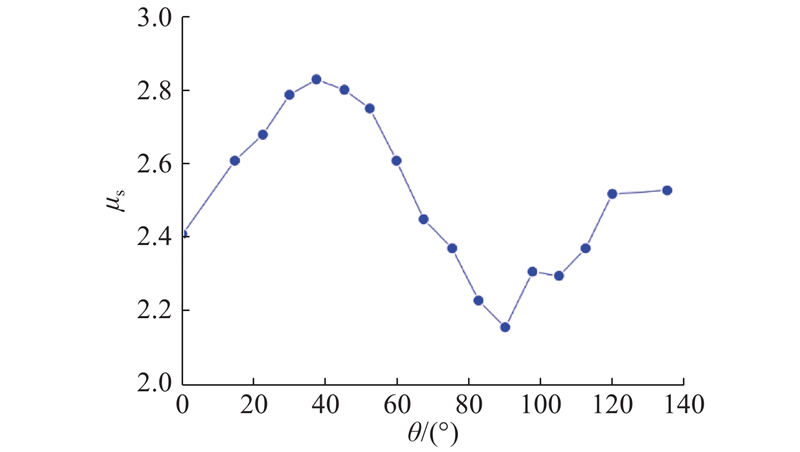
图 4 抱杆标准节合力体型系数
Fig.4 Aerodynamic force coefficients of standard section of crane structure
表 2 抱杆标准节整体体型系数对比
Tab.2
| | μ s | 误差/% | |
| 风洞试验 | 文献[18] | ||
| 0 | 2.41 | 2.31 | −4.15 |
| 45 | 2.80 | 2.81 | 0.36 |
| 90 | 2.16 | 2.31 | 6.94 |
表 3 双平臂抱杆结构整体风力系数对比
Tab.3
| 平臂姿态 | | Cx | 误差/% | Cy | 误差/% | ||
| 文献[18] | 风洞试验 | 文献[18] | 风洞试验 | ||||
| 0° | 0 | 2.23 | 2.26 | −1.33 | 0 | −0.03 | |
| 0° | 45.0 | 1.71 | 1.89 | −9.52 | 1.56 | 1.68 | −7.14 |
| 0° | 90.0 | 0 | 0.23 | 1.90 | 1.72 | 10.47 | |
| 22.5° | 22.5 | 2.07 | 2.13 | −2.82 | 0.92 | 1.04 | −11.54 |
| 22.5° | 67.5 | 0.93 | 1.02 | −8.82 | 1.83 | 2.26 | −19.03 |
| 22.5° | 112.5 | −0.79 | −0.53 | 49.06 | 1.76 | 1.81 | 2.76 |
| 45° | 45.0 | 1.79 | 1.58 | 13.29 | 1.79 | 1.90 | −5.79 |
| 45° | 90.0 | 0.11 | 0.17 | −35.29 | 2.02 | 2.24 | −9.82 |
| 45° | 135.0 | −1.55 | −1.14 | 35.96 | 1.55 | 1.41 | 9.93 |
本文的2个风洞试验是为了分别获取标准节节段和双平臂抱杆的风荷载体型系数或风力系数,故风洞试验只采用了均匀湍流场. 风致抱杆动力响应分析所需要的风荷载时程数据由数值模拟形成的脉动风荷载和按A类地貌的平均风荷载叠加得到.
2. 抱杆动力风荷载
2.1. 抱杆计算工况
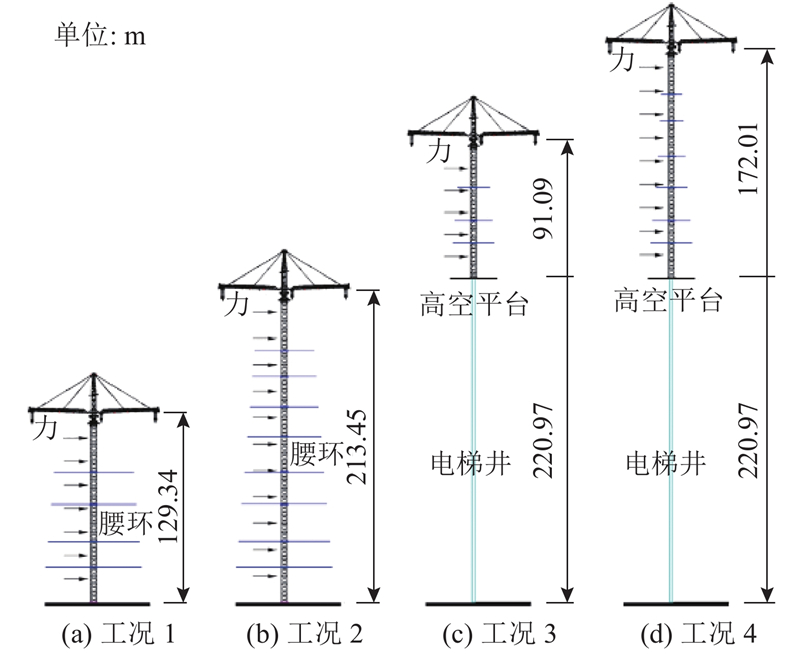
施工进度不同,抱杆结构高度和横向约束和受力情况也不同. 综合考虑钢管塔施工方案与数值计算精度,选取施工过程中4种典型工况进行研究,如图5所示. 图中,工况1、2的抱杆从地面开始组立,工况3、4的从220.97 m高空平台开始组立,220.97 m以下为电梯井. 4种工况下的平臂姿态为0°,风向角取0°和45°.
图 5
图 5 抱杆施工全过程典型工况示意图
Fig.5 Typical working conditions of crane structure during tower construction
2.2. 动力风荷载确定
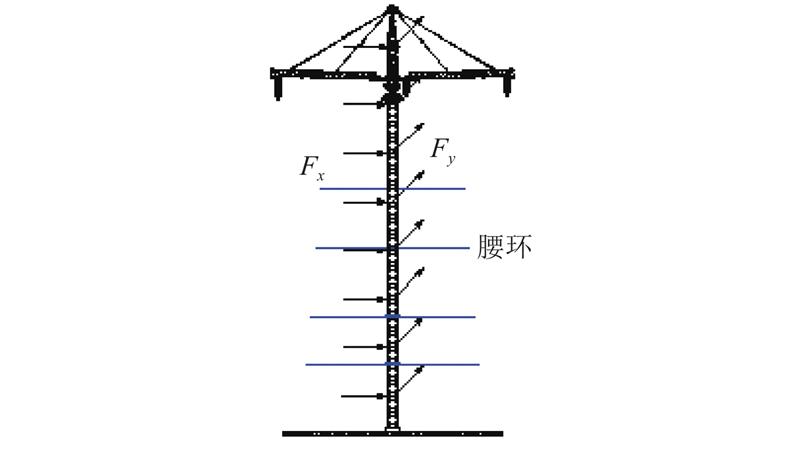
双平臂抱杆结构竖向尺寸远大于水平尺寸,在进行风振分析时,可将其视作高耸结构. 以工况1为例,如图6所示,平臂及以上部分简化为1个加载点;抱杆杆身部分,每3个标准节简化为1个加载点,风荷载考虑2个平动方向的水平风力,即Fx和Fy.
图 6
若不考虑x向和y向风荷载的相关性,可分别模拟x向和y向随机风荷载. 对于x向风荷载,随机风荷载功率谱密度矩阵
根据脉动风速均方根与风力功率谱密度的积分关系,以抱杆最顶部标准节风力功率谱密度
式中:
式中:n为脉动风的频率;Cuz为相干函数的衰减指数,本文中取7;
式中:CL=60. 按式(7)~(9)可依次计算出风荷载的自谱与互谱,由此可得到随机风荷载谱矩阵
式中:H(ω)为下三角矩阵。采用逆快速傅里叶变换(inverse fast Fourier transform,IFFT)技术,可计算得到第i节段处的脉动风荷载时程样本:
式中:
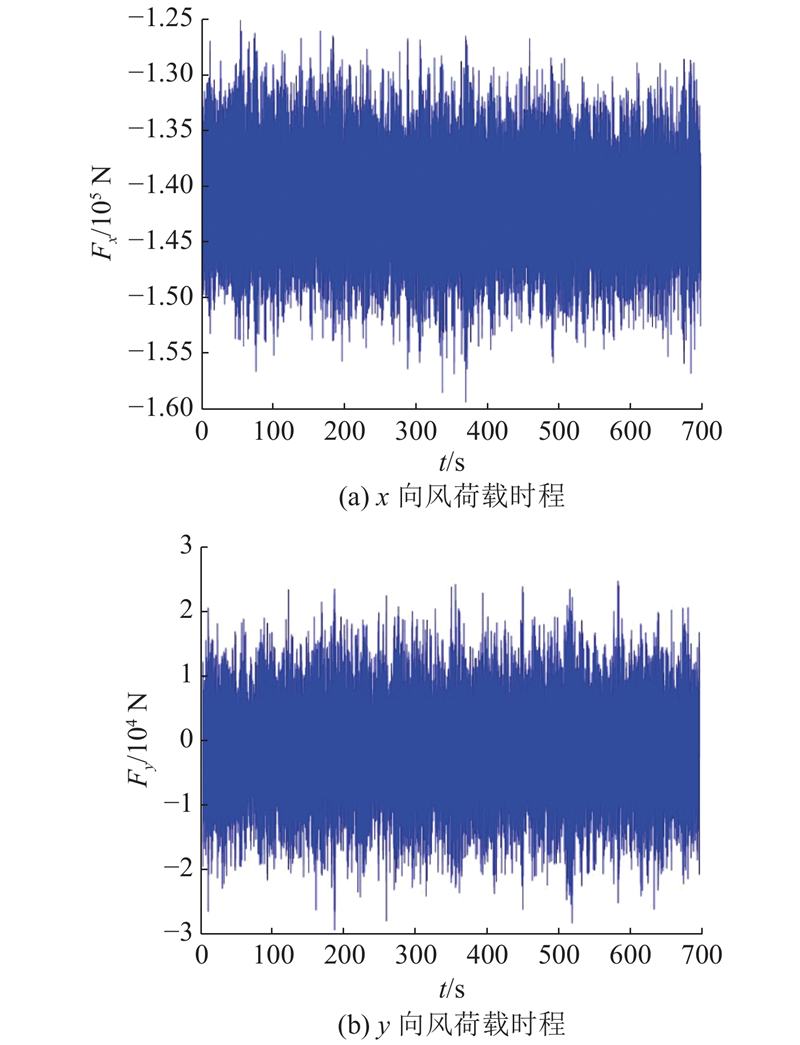
图 7
图 7 0°风向角下抱杆顶部标准节风荷载时程
Fig.7 Time histories of wind force at top standard section of crane structure under zero degree wind
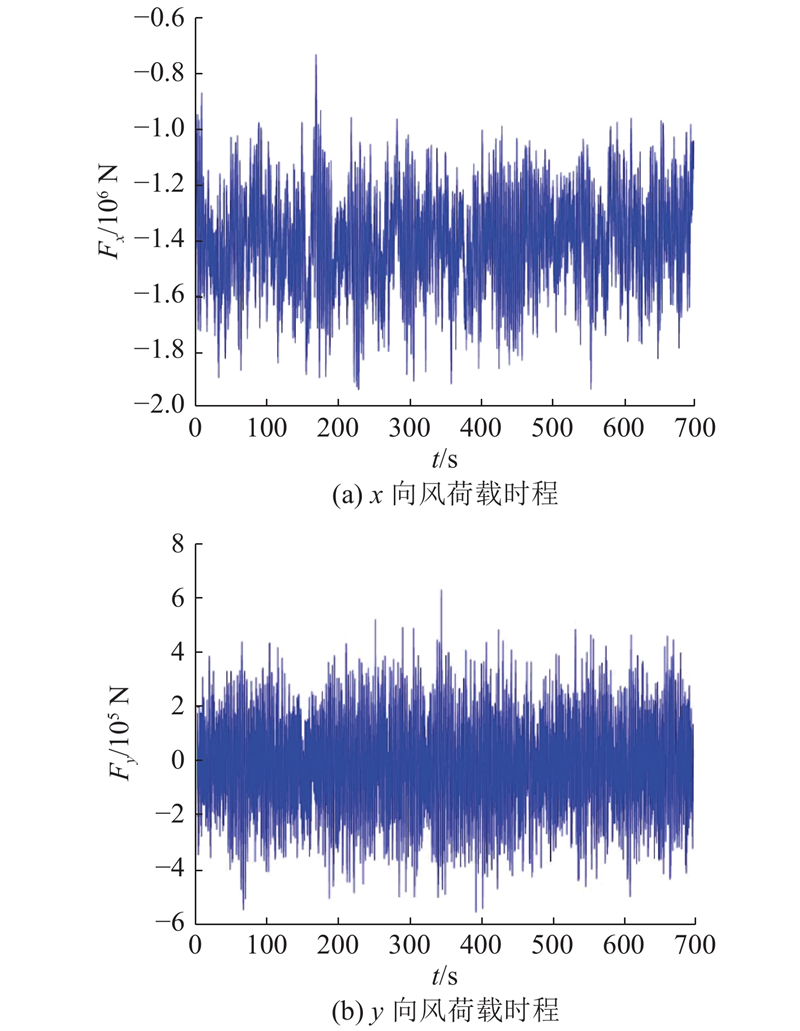
图 8
图 8 0°风向角下抱杆平臂及以上结构风荷载时程
Fig.8 Time histories of wind force on double flat arms and top part of crane structure under zero degree wind
3. 组塔过程风致抱杆动力响应分析
3.1. 抱杆整体结构有限元模型
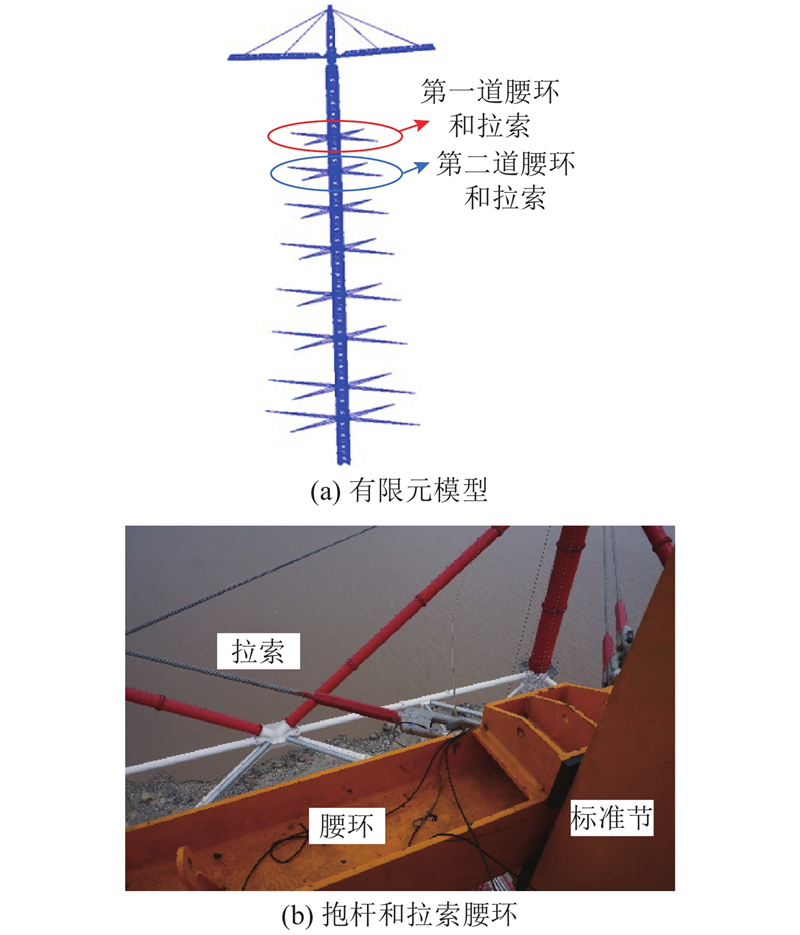
利用ANSYS软件,建立施工过程中典型工况下的抱杆有限元模型,其中抱杆标准节及平臂主材部分采用BEAM188单元模拟;回转塔身部分采用SHELL181单元和SOLID185单元模拟平臂及以上部分的旋转;采用LINK180单元模拟腰环拉索,并设定该单元只受拉力不受压力. 腰环套在标准节四周,在腰环上设置拉索拉到周边的主塔上,沿高度每隔3个标准节(18 m左右)设置一道腰环及拉索,保证整个抱杆结构的侧向稳定. 工况2下双平臂抱杆结构及其拉索腰环的有限元模型和实物照片如图9所示.
图 9
图 9 双平臂抱杆带腰环拉索有限元模型
Fig.9 Finite element model of guyed crane structure with double flat arms
3.2. 抱杆动力特性
图 10
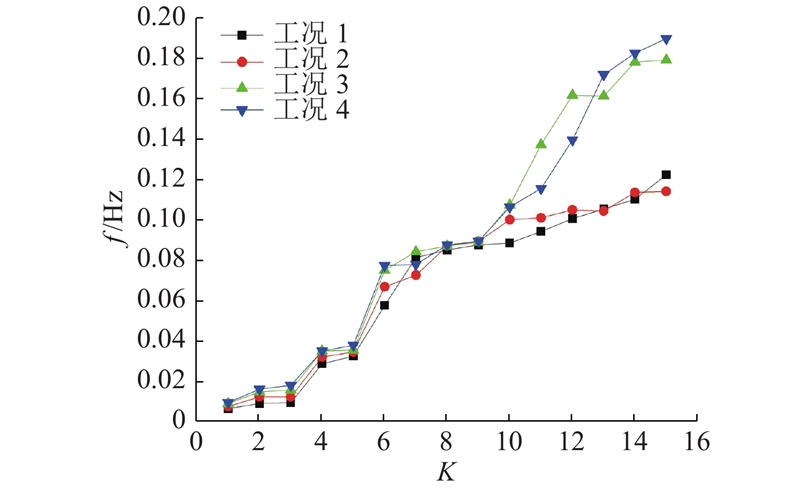
图 10 双平臂抱杆4个工况下的自振频率
Fig.10 Natural vibration frequency of four working conditions of guyed crane structure with double flat arms
图 11
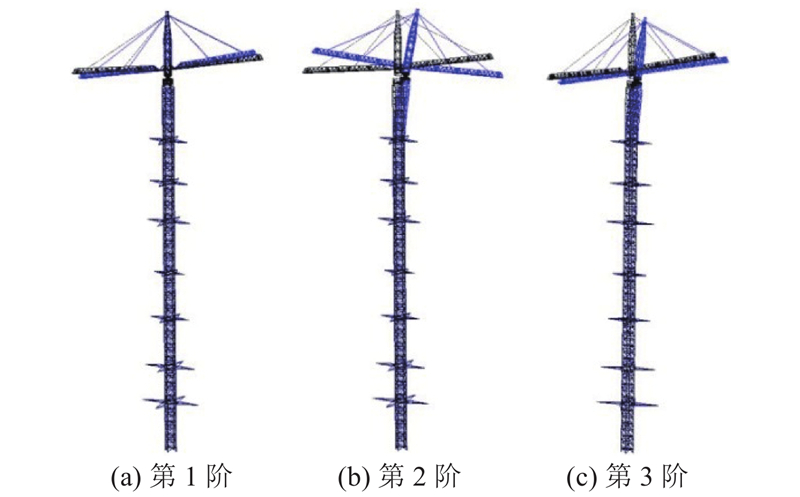
图 11 双平臂抱杆工况4的前3阶振型示意图
Fig.11 First three vibration formation of fourth working condition of guyed crane structure with double flat arms
3.3. 抱杆动力响应
采用非线性时程动力分析方法对抱杆整体结构有限元模型进行分析,抱杆结构的阻尼比
图 12
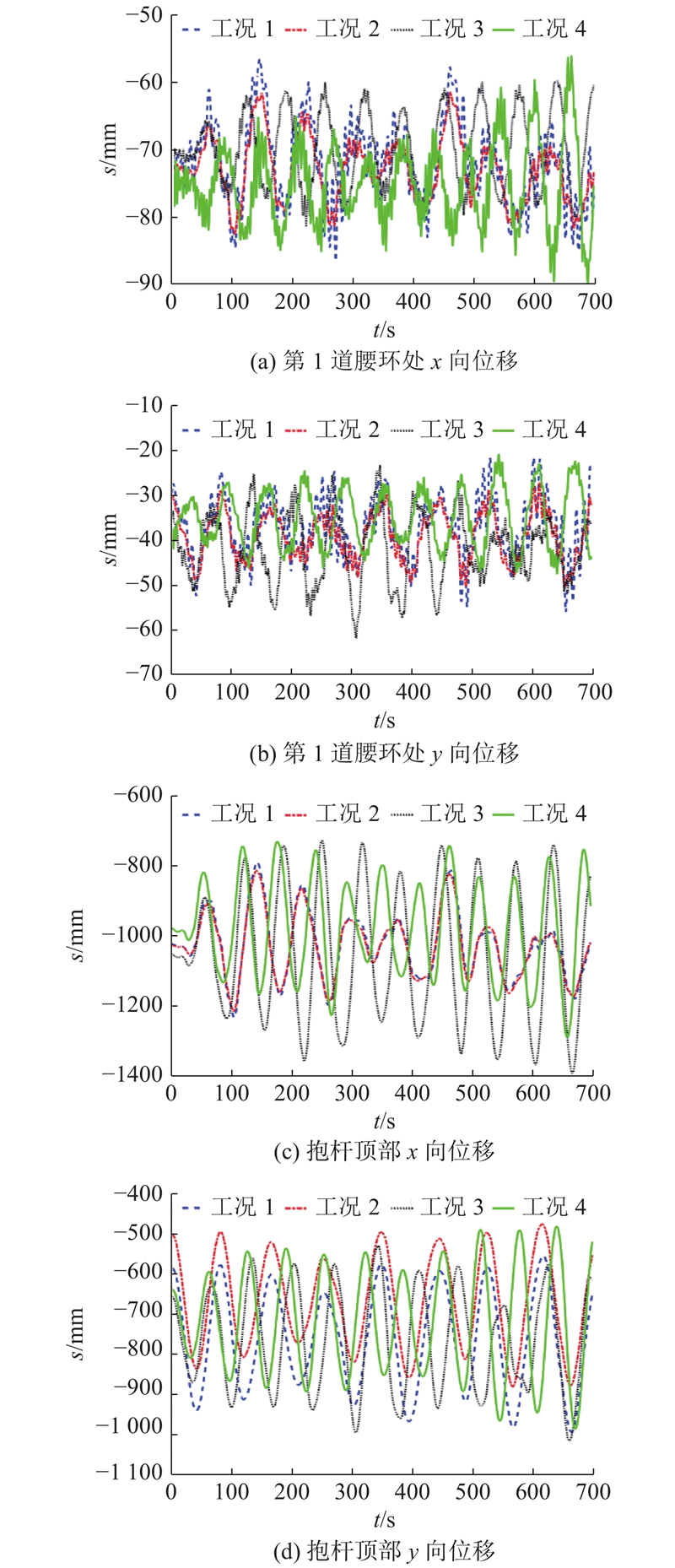
图 12 45°风向角4种工况下抱杆关键部位位移
Fig.12 Time history displacements at key location of crane structure under 45° wind angle
4. 基于时程分析方法的风振系数
4.1. 高耸结构设计规范风振系数
抱杆结构某高度Z处所受风荷载P由静、动2部分风荷载组成,定义风振系数为静动力风荷载P与静力风荷载Pc的比值,其表达式为
式中:Pd为动力风荷载. 文献[18]采用惯性风荷载法计算风振系数,为了简化计算,用高耸结构设计规范定义参数
式中:
4.2. 典型工况下抱杆结构的时程风振系数
基于典型工况下抱杆结构的风致时程分析结果可以直接获得风振系数. 为了便于和规范方法比较,采用基于惯性荷载法原理得到各竖向高度处的时程风振系数[21]:
式中:
根据公式(14)、(18),分别计算得到各高度处的规范风振系数和时程风振系数. 表4给出了工况4在0°、45°风向角下第1道腰环以上抱杆悬臂部分的风振系数计算结果. 在0°风向角下,规范计算的风振系数与时程风振系数结果基本接近,2种计算结果整体趋势较为一致. 在45°风向角下,x方向和y方向的风振系数较为接近,规范计算的风振系数大于时程风振结果. 在抱杆顶端(432.2 m)处,0°、45°风向角下的时程风振系数分别为3.05、2.24(x向)和2.28(y向),小于相应的规范风振系数3.17、2.62和2.67.
表 4 双平臂抱杆结构工况4风振系数对比
Tab.4
| Z/m | β1 | β2 | |||||
| 0° | 45°x向 | 45°y向 | 0° | 45°x向 | 45°y向 | ||
| 364.7 | 1.41 | 1.36 | 1.32 | 1.37 | 1.01 | 1.02 | |
| 370.8 | 1.51 | 1.46 | 1.47 | 1.21 | 1.06 | 1.02 | |
| 376.9 | 1.74 | 1.60 | 1.60 | 1.71 | 1.13 | 1.14 | |
| 383 | 2.20 | 1.82 | 1.80 | 2.02 | 1.37 | 1.34 | |
| 389 | 2.42 | 2.03 | 2.00 | 2.29 | 1.61 | 1.69 | |
| 396.2 | 2.62 | 2.23 | 2.26 | 2.62 | 1.81 | 1.82 | |
| 403.4 | 2.85 | 2.35 | 2.36 | 2.84 | 2.15 | 2.01 | |
| 410.5 | 2.92 | 2.46 | 2.50 | 2.89 | 2.18 | 2.05 | |
| 417.8 | 2.99 | 2.51 | 2.52 | 2.92 | 2.18 | 2.11 | |
| 424.8 | 3.08 | 2.56 | 2.60 | 2.95 | 2.20 | 2.21 | |
| 432.2 | 3.17 | 2.62 | 2.67 | 3.05 | 2.24 | 2.28 | |
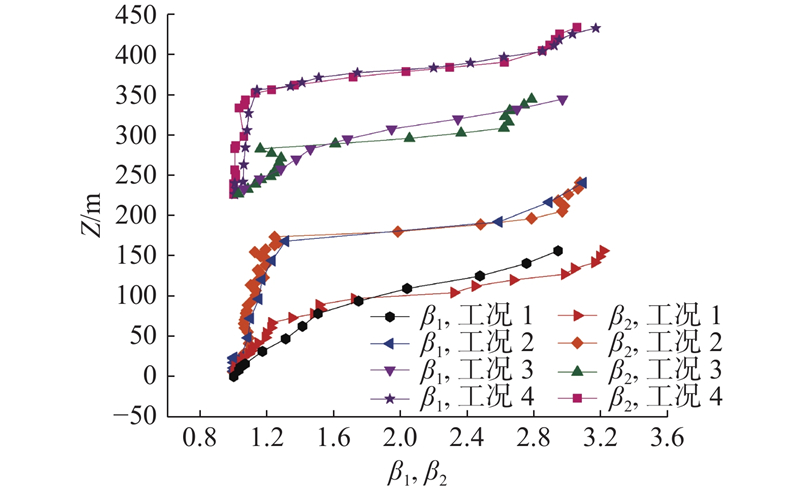
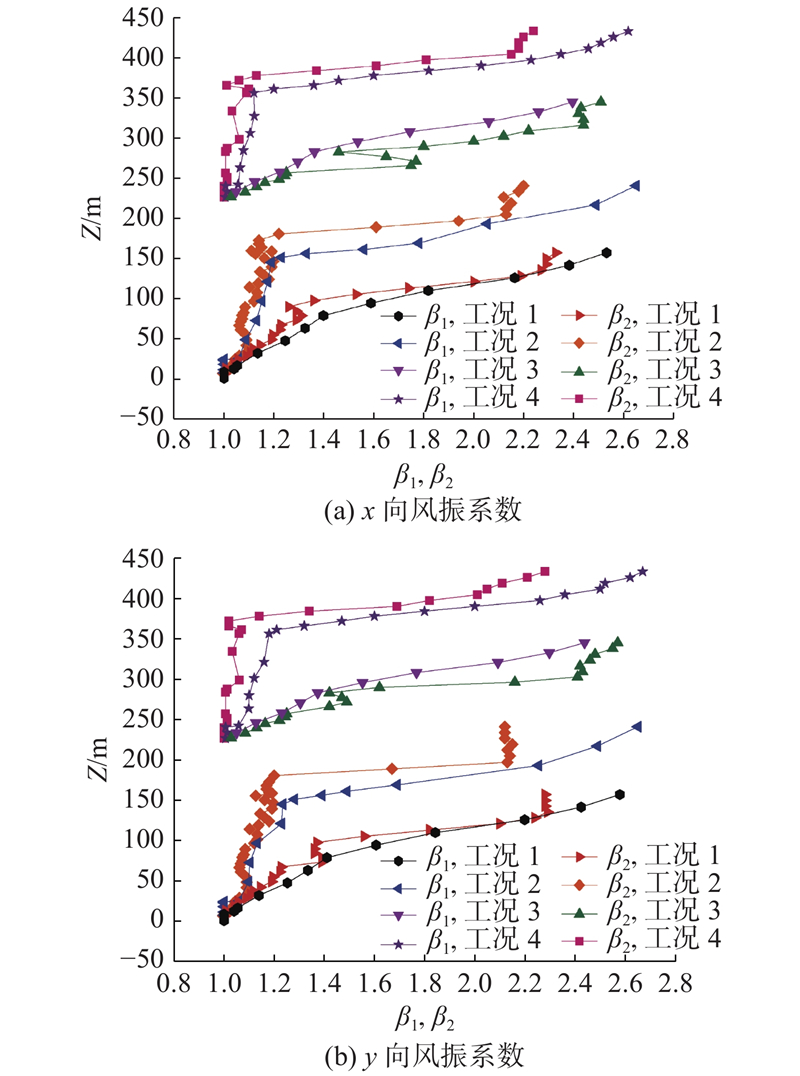
4种典型工况在0°风向角下抱杆结构沿高度的顺风向风振系数如图13所示. 4种典型工况在45°风向角下抱杆结构沿高度的x向和y向风振系数如图14所示. 由图可以看出:1)时程风振系数与规范风振系数随高度整体变化规律较为一致,但在抱杆悬臂部分,即第一道腰环以上部分两者存在显著差异。2)规范风振系数随高度增加保持单调增加,而时程风振系数沿高度的变化规律更加复杂. 规范只考虑了前几阶振型的影响,动力时程综合考虑了多阶振型的影响,因此时程风振系数能更加准确地反映出拉索式结构风振响应沿高度变化情况. 3)相比于0°风向角的顺风向风振系数,45°风向角的x向和y向时程风振系数和规范风振系数相差更大. 在45°风向角下,对于抱杆杆身部分,时程风振系数变化更加复杂;对于抱杆悬臂部分,规范风振系数随高度继续线性增加,显著大于时程方法风振系数,偏保守. 可见对于抱杆结构在大跨越钢管塔施工过程的抗风安全性能,基于规范的风振系数取值难以准确描述抱杆结构的实际风致动力效应,需要通过风洞试验和精细化有限元分析加以安全可靠评估.
图 13
图 13 4种施工工况在0°风向角下抱杆风振系数对比
Fig.13 Comparisons of gust response factors of crane structure under four working conditions and 0° wind angle
图 14
图 14 4种施工工况在45°风向角下抱杆风振系数对比
Fig.14 Comparisons of gust response factors of crane structure under four working conditions and 45° wind angle
由于抱杆结构为施工装备,抱杆设计验算风速确定为11级风力即32.6 m/s,大于舟山地区10年一遇的设计风速28.3 m/s. 对于抱杆所在的舟山地区A类地貌,台风风场和普通风场从平均风剖指数来看并无很大的区别[22],本文的研究结果能为抱杆的抗台风评估提供依据. 基于本文研究,施工单位编制了西堠门大跨越钢管塔的施工防台风预案,如果施工期遭遇大于10年一遇设计风速的强台风,需要采取停止作业、降低抱杆.
5. 结 论
(1)平臂在0°位置时抱杆结构风力系数试验值与规范值差别不大;但抱杆在22.5°平臂位置时,试验得到的最大风力系数达2.26,比规范值高23%,应在抱杆的抗风验算中予以重视.
(2)对于抱杆杆身第一道腰环以下部分,由于连接腰环的拉索提供额外的横向约束,在32.6 m/s的施工工况验算风速下抱杆风致位移较小,根据规范得到的风振系数与动力时程计算结果相近;对于抱杆悬臂部分,由于双平臂的存在导致抱杆整体质量和刚度分布发生突变,抱杆风致位移急剧增大,抱杆顶部x向位移有1 m 以上.
(3)时程风振系数与规范风振系数随高度整体变化规律较为一致,但在抱杆悬臂部分即第一道腰环以上部分,两者存在显著差异. 相比于0°风向角下的顺风向风振系数,45°风向角下的x向和y向时程风振系数和规范风振系数相差更大. 由于规范风振系数只考虑前几阶振型,难以准确描述抱杆结构的实际动力风效应,需要采用本文研究结果开展抱杆结构抗风强度验算.
(4)本文中4个工况条件的抱杆结构风振系数取用建议:考虑抱杆顶部出现11级风力即32.6 m/s的验算风速,在0°风向角下,抱杆顶部在四种工况下的顺风向风振系数建议统一取为3.05;在45°风向角下,需要考虑x和y 2个方向的风振系数,对于抗风最不利的工况4,抱杆顶部(432.2 m)的时程风振系数分别为2.24(x向)和2.28(y向).
参考文献
舟山大跨越高塔抱杆现场试验
[J].DOI:10.3969/j.issn.1000-7229.2009.08.016 [本文引用: 1]
Site test of holding poles used in Zhoushan large high crossing tower
[J].DOI:10.3969/j.issn.1000-7229.2009.08.016 [本文引用: 1]
1 000 kV大型薄壁钢管变电构架风致振动响应研究
[J].
Wind-induced dynamic response of large thin-walled steel tube frame for 1 000 kV substation
[J].
典型塔式起重机塔架结构风致动力响应与疲劳分析
[J].
Analysis of Wind-Induced vibration and fatigue effects of a typical tower crane
[J].
特高压单柱拉线塔风振系数研究
[J].
Analysis on wind-induced vibration coefficient of UHV single-mast guyed tower
[J].
桅杆结构风振系数研究
[J].
Wind-vibration coefficient of guyed masts
[J].
桅杆结构风振系数计算方法研究
[J].
Study on the calculation method for wind vibration coefficient of guyed masts
[J].
基于风洞试验的苏通大跨越输电塔风振系数研究
[J].
Investigation on wind-induced vibration coefficients of Sutong long span transmission tower based on wind tunnel tests
[J].
一体化通信基站风振响应及风振计算研究
[J].
Calculation and analysis on wind-induced vibration response of integrated communication base station
[J].
特高压单柱拉线塔塔线体系风振响应时程分析
[J].
Time history analysis on wind-induced response of UHV guyed single-mast transmission tower-line system
[J].
Dynamic response of transmission lines guyed towers under wind loading
[J].
Behavior of guyed transmission line structures under tornado wind loading
[J].DOI:10.1016/j.compstruc.2011.01.015 [本文引用: 1]
Failure analysis of guyed transmission lines during F2 tornado event
[J].DOI:10.1016/j.engstruct.2014.11.045
The response of a guyed transmission line system to boundary layer wind
[J].DOI:10.1016/j.engstruct.2017.01.047 [本文引用: 1]
Effect of geometric nonlinear behavior of a guyed transmission tower under downburst loading
[J].DOI:10.4028/www.scientific.net/AMM.226-228.1240 [本文引用: 1]
Dynamic analysis of self-supported tower under hurricane wind conditions
[J].DOI:10.1016/j.jweia.2019.104078 [本文引用: 1]
Experimental and computational simulation for wind effects on the Zhoushan transmission towers
[J].DOI:10.1080/15732479.2010.497540 [本文引用: 1]
基于HFFB试验的特高压输电塔风振响应分析
[J].
Wind-induced vibration analysis of UHV transmission tower based on the HFFB tests
[J].
大跨干煤棚网壳风振时程分析和等效静风荷载研究
[J].
Wind-induced vibration time history analysis and equivalent static wind loads for long-span lattice shells
[J].
Examination of typhoon-wind profiles reaching 1 000 m height over the Southeast China Sea based on reanalysis data set and mesoscale simulation
[J].DOI:10.1061/(ASCE)ST.1943-541X.0002744 [本文引用: 1]