微电网(microgrid,MG)能够高效地集成各种分布式电源,提高可再生能源(renewable energy source,RES)的渗透率,具有孤岛和并网2种运行模式[1-3]. 逆变器作为RES与MG的接口,当采用下垂控制和虚拟同步发电机(virtual synchronous generator,VSG)控制时,对外近似为电压源,具有在孤岛和并网模式间无缝切换、“即插即用”的优点,因而被广泛使用[4-5]. 处于孤岛模式时由于缺乏电网电压支撑,在下垂控制和VSG控制功能层下还需要加入底层电压控制,以维持MG电压稳定,保证供电质量. 受死区时间、控制和采样延迟、参数摄动等因素的影响,逆变器表现为多变量、强耦合的非线性系统. 除传统双闭环比例积分(proportional integral,PI)控制外,有学者还提出了多种逆变器控制方法. 这些控制方法各有优缺点,如重复控制可以抑制谐波但响应较慢[6]、滑模控制鲁棒性较强但存在抖振问题[7].
自抗扰控制(active disturbance rejection control,ADRC)是韩京清[8]提出的通用控制器,因其不依赖被控对象的精确模型、简单结构、强抗干扰能力而被广泛研究和应用. 但作为非线性控制方法,ADRC包含过多控制参数,其参数整定和应用较为困难. 为此,Gao[9]利用线性化和带宽的概念推广出线性自抗扰控制(linear active disturbance rejection control,LADRC),将参数调节过程简化为控制器和观测器带宽选择问题,简化了参数调节过程,促进了自抗扰控制的工程化应用. 近年来ADRC在逆变器控制方面取得了较大的进展,如VSG功率控制[10-11]、并网逆变器电流控制[12-14]、微电网内无功支撑[15]等. 在逆变器电压控制方面,曹永锋等[16]在LADRC基础上加入微分前馈和部分已知模型补偿,但这与ADRC无模型设计的初衷相悖,而且加入模型补偿后,扩张状态观测器(extended state observer,ESO)的参数设计变得复杂. 杨林等[17]在ESO中引入输出电压误差微分项,提高ESO抗扰动能力,但是参数增加不利于工程化应用. 袁晓冬等[18]将LADRC应用于电压控制器的电压环,以抑制并网逆变器从并网切换至孤岛时的暂态振荡,但是为了简化设计流程,直接忽略了电流内环动态特性,且缺乏实验验证. 由文献[19]分析可知,观测器带宽越大,系统抗扰动能力越强. 在LADRC中,观测器带宽越大对传感器性能的要求就越高,同时系统对高频噪声更加敏感,过大的观测器带宽会引发系统振荡,导致系统不稳定,因此观测器带宽通常受限制. 当带宽受限时,如何提高LADRC的控制性能是重要的技术问题[20].
针对以上问题,本文将LADRC应用于微电网逆变器电压外环,将补偿因子作为可调参数,用以改善系统抗负载扰动性能. 设计以 dq 同步旋转坐标系下逆变器输出电压为状态变量的二阶LADRC;在忽略采样和控制延迟前提下,对系统控制增益进行推导;利用根轨迹分析补偿因子对系统稳定性、动态性能的影响,利用在干扰下闭环传递函数频域特性分析补偿因子对系统抗干扰能力的影响,为补偿因子的调节提供理论依据;对不同补偿因子下电压控制器的电压跟踪性能和抗负载扰动能力进行对比仿真和实验.
1. 微电网逆变器建模
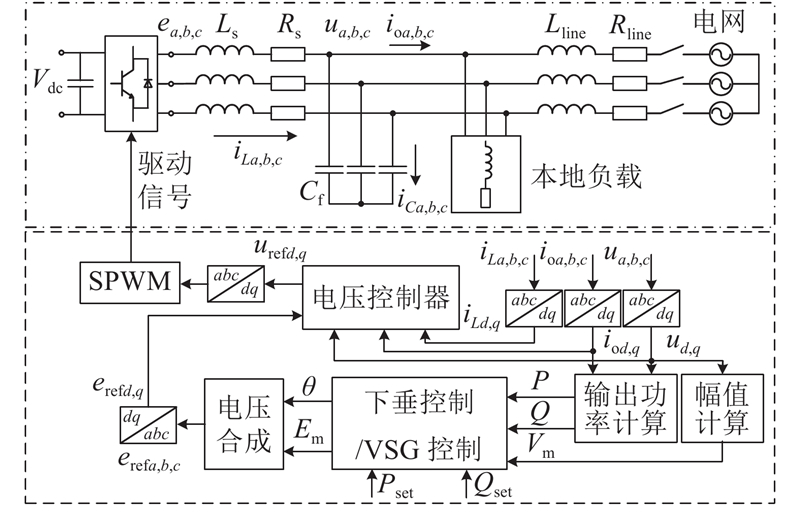
如图1所示为MG逆变器的整体结构,包括分布式电源、三相逆变桥、LC滤波器,以及相应的控制算法. 图中,直流侧电压为
图 1
逆变器在dq同步旋转坐标系下的数学模型为
式中:
式中:s为拉氏变换算子;
2. 基于LADRC电压外环设计
2.1. 被控对象建模及系统控制增益推导
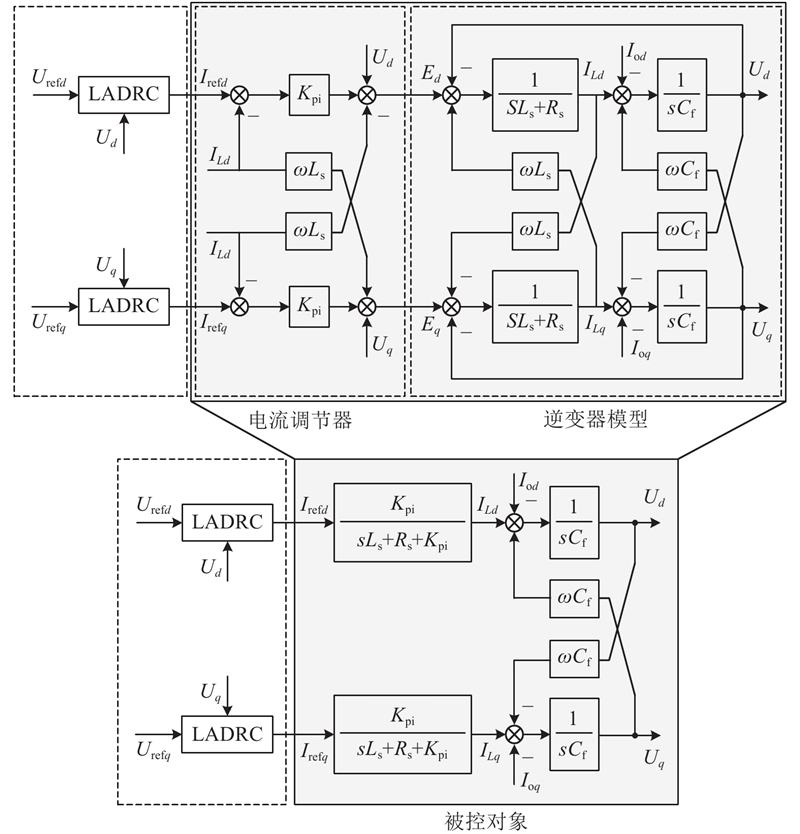
采用双闭环电压控制器,为了提高响应速度,电流环采用比例调节器,比例系数为
图 2
为了简化分析过程,忽略采样和开关引入的延迟,SPWM中载波幅值为
结合式(2)、(3),忽略滤波电感等效电阻
式中:
将式(4)、(5)进行反拉氏变换
仅以d轴为例进行控制器设计. 令
得到系统控制增益
在得到被控对象的状态空间模型后,进行电压外环的LADRC设计,包括线性扩张状态观测器(linear extended state observer,LESO)设计、扰动前馈补偿和线性状态误差反馈(linear state error feedback,LSEF)设计3部分. 其核心思想是通过LESO将系统内、外扰动总和观测出来,再通过扰动补偿,将系统转换为积分串联标准型,最后通过LSEF配置系统极点,保证系统稳定. 通过将极点配置成特殊形式,在一定程度上解决超调和快速性的矛盾.
2.2. LESO设计
LESO是LADRC的核心部分,可以实时估计系统的总扰动,并进行前馈补偿. 式(8)等效为
式中:b为LADRC中补偿因子,一般有
式中:h表示
式中:
2.3. LSEF和扰动补偿设计
在忽略
式中:
式中:r为参考输入,
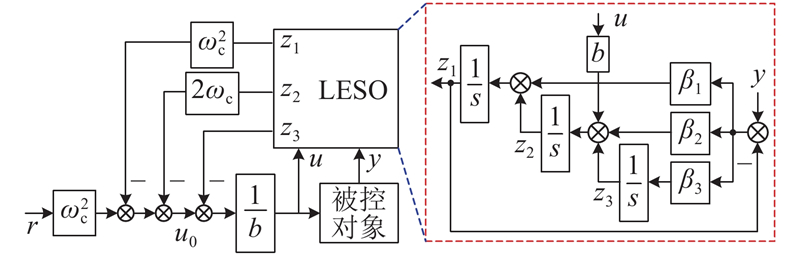
式(10)、(12)、(13)构成基于LADRC的d轴电压外环控制器,控制结构如图3所示. 从式(11)、(14)可以看出,LADRC中参数配置问题可以转换为
图 3
3. 补偿因子对系统性能的影响
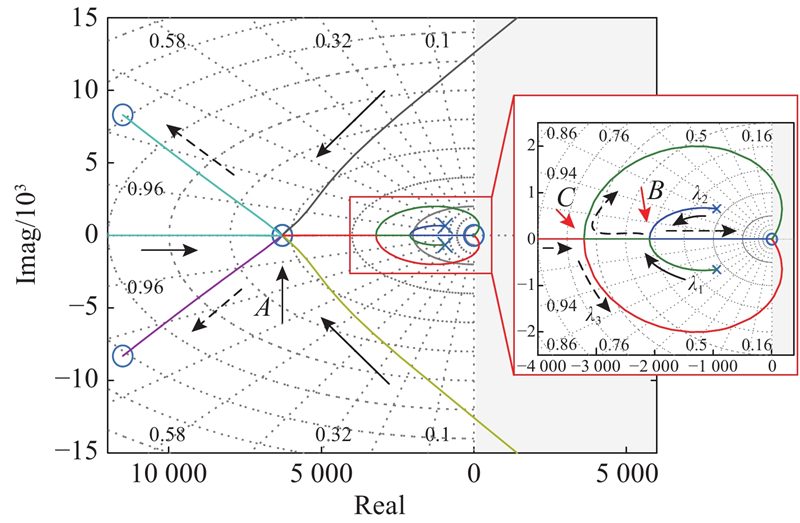
文献[19]中仅考虑补偿因子不确定的情况,利用李纳德−戚帕特稳定性判据分析补偿因子对系统稳定性的影响,并未将补偿因子视为可调参数. 本文利用根轨迹分析补偿因子对系统稳定性和动态性能的影响,利用干扰下闭环传递函数频域特性分析补偿因子对系统抗干扰能力的影响,为可调参数b的调节提供理论依据.
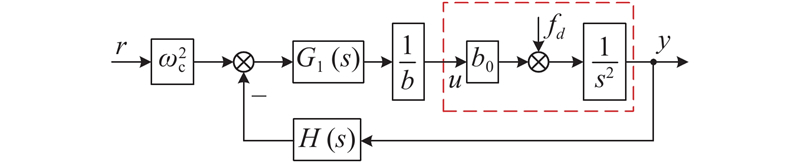
根据式(11)、(12),推导LESO输出表达式为
图 4
式中:
3.1. 补偿因子对稳定性和动态性能的影响
根据式(17)得到参考作用下闭环传递函数为
由式(18)、(19)可以看出,
图 5
表 1 不同ωc和ωo对应ρ取值范围
Tab.1
| ωc/(rad·s−1) | ωo/ωc | ωo/(rad·s−1) | ρ |
| 2094 | 2 | 4188 | 0.247~4.10 |
| 2094 | 5 | 10470 | 0.195~5.87 |
| 2094 | 8 | 16752 | 0.171~7.87 |
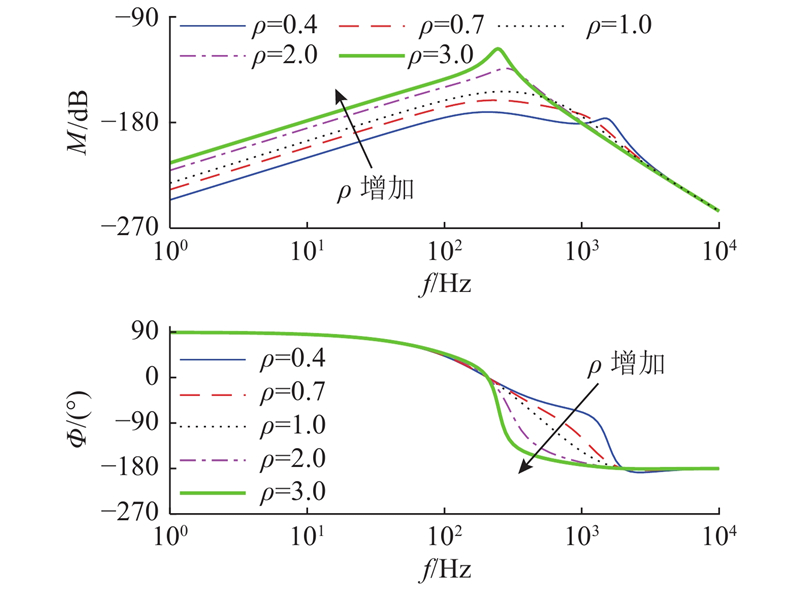
3.2. 补偿因子对抗干扰能力的影响
由式(8)可知,扰动项
LADRC中当
图 6
图 6 干扰作用下闭环传递函数频域特性曲线
Fig.6 Frequency domain characteristics of transfer function under disturbance
4. 控制参数配置方法
根据前述分析,结合仿真和实验情况,仿真和实验中电压控制器的参数设计过程:1)初步确定b. 对系统进行建模,根据系统控制增益初步确定补偿因子,见式(7). 2)确定比例系数
5. 仿真和实验
为了验证本文方案的有效性,搭建微电网逆变器带载系统仿真和实验平台,分别对不同补偿因子下电压控制器跟踪性能和抗负载扰动能力进行对比实验. 仿真和实验模型参数相同,如表2所示.
表 2 仿真和实验中系统模型参数
Tab.2
| 参数 | 符号 | 数值 | 单位 |
| 直流电压 | Vdc | 300 | V |
| 滤波电感 | Ls | 3 | mH |
| 等效串联电阻 | Rs | 0.16 | Ω |
| 开关频率 | fsw | 10 | kHz |
| 死区时间 | Td | 2.6 | μs |
| 滤波电容 | Cf | 4.7 | μF |
| 线电压有效值 | Vrms | 154.3 | V |
| 额定频率 | fn | 50 | Hz |
| 采样频率 | fs | 10 | kHz |
| 电流环系数 | Kpi | 18.85 | |
| 控制器带宽 | ωc | 2 094 | rad/s |
| 观测器带宽 | ωo | 6 283 | rad/s |
5.1. 仿真结果
仿真的控制部分采用触发模式,触发频率与开关频率一致,控制和滤波算法均采用离散形式. 仿真的LADRC中
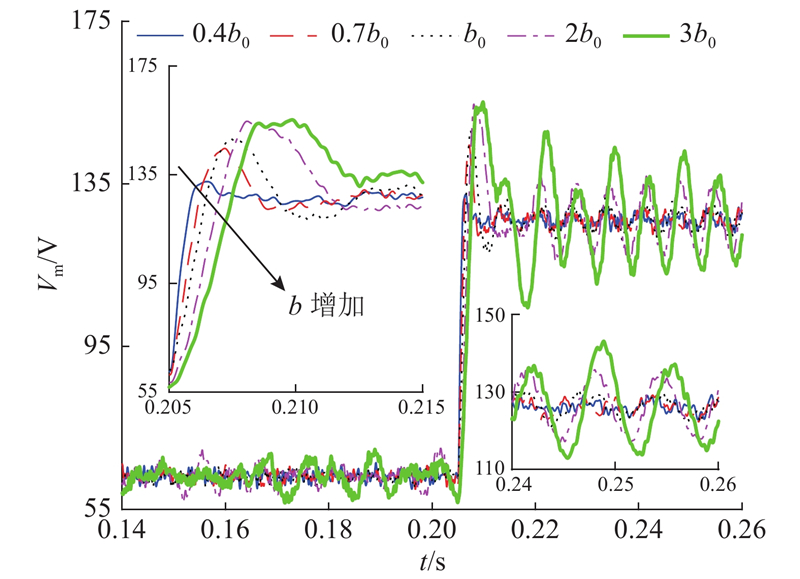
如图7所示为在不同补偿因子下参考电压幅值变化时,逆变器输出电压幅值的仿真结果. 三相电压幅值
图 7
图 7 不同补偿因子下的电压跟踪仿真结果
Fig.7 Simulation results of voltage tracking under different compensation factors
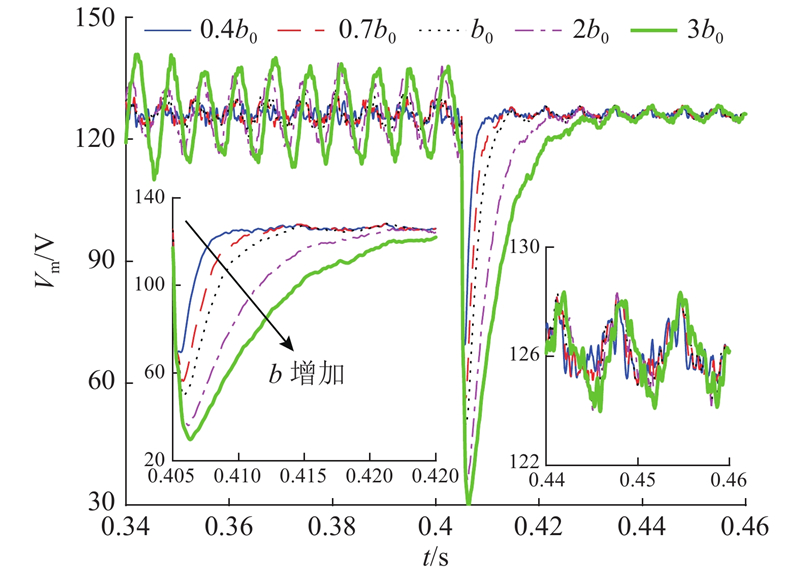
如图8所示为在不同补偿因子下逆变器负载切换时,输出电压幅值的仿真结果. 图中,当b取0.4b0、0.7b0、b0、2b0、3b0时,突加负载均会导致电压跌落,分别跌落至67.9 V、54.8 V、48.2 V、35.6 V、28.6 V. 可以看出,b取值越大,突加负载的电压跌落越严重,且恢复时间越长,无明显超调. 另外,带载的输出电压波动明显小于空载.
图 8
图 8 不同补偿因子下负载扰动仿真结果
Fig.8 Simulation results of load disturbance under different compensation factors
5.2. 实验结果
图 9
实验中各系统参数取值见表1,LADRC控制器和观测器带宽与仿真相同,补偿因子稳定范围也与仿真相同,为(0.226~4.65)b0. 为了验证仿真结果的有效性,实验内容与仿真中基本一致,补偿因子b分别取0.4b0、0.7b0、b0、2b0、3b0进行对比实验.
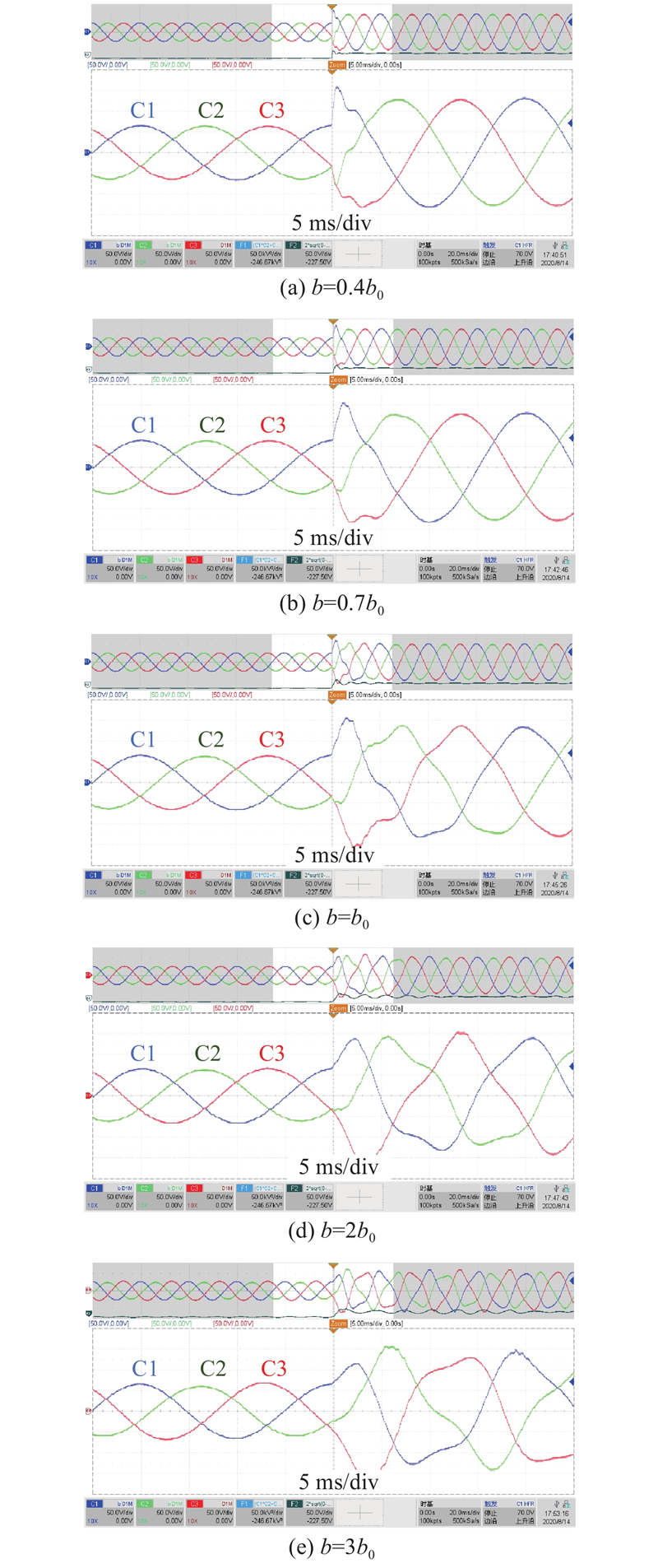
在A相电压最大时,触发参考变化程序,对应t = 0 s时,参考电压幅值从63 V变为126 V,频率保持不变,实验结果如图10所示. 图10(a)、(b)、(c)、(d)、(e)分别对应不同补偿因子下参考变化后逆变器输出电压变化情况,图中:C1、C2、C3分别表示A、B、C相输出电压. 由图可以看出,LADRC控制算法对补偿因子的选择具有较好的包容性,在偏离系统控制增益较大范围内均能保证系统稳定,与根轨迹分析和仿真结果吻合. 当b取0.4b0、0.7b0时,电压可以在半个周期内稳定;当b取b0、2b0时,电压经过2~3个周期稳定;当b取3b0时,通过根轨迹分析可知,此时闭环极点靠近虚轴,阻尼较弱,同时对干扰衰减作用降低,在参考变化时,电压振荡较为剧烈.
图 10
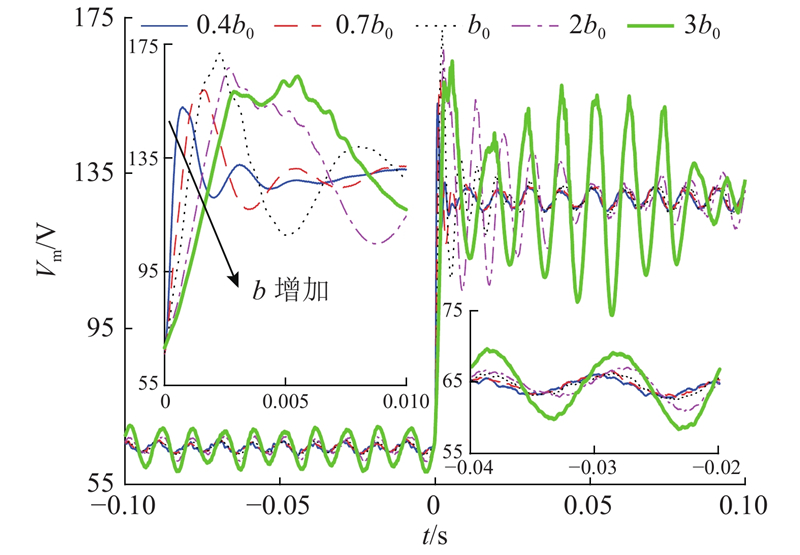
为了对比不同补偿因子下,输出电压幅值变化情况,将示波器数据导出、计算后得到三相电压幅值,如图11所示. 为了减小噪声影响,保留变化趋势,计算结果经过低通滤波处理,截止频率与仿真中一致,均为1 kHz. 由图可以看出,当b越大,参考变化时,电压响应越慢,这是由于b越大,
图 11
图 11 参考变化时输出电压幅值变化情况
Fig.11 Changes of output voltage amplitude after reference changed
图 12
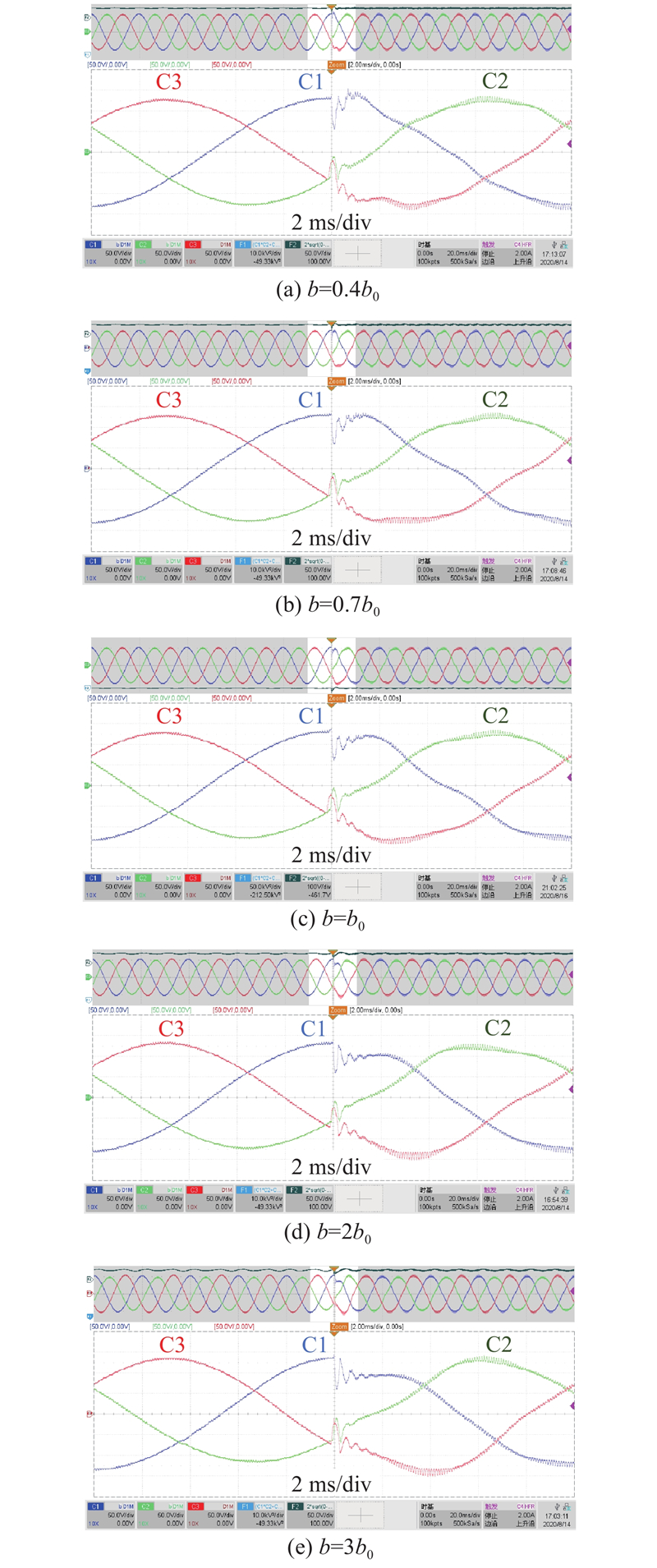
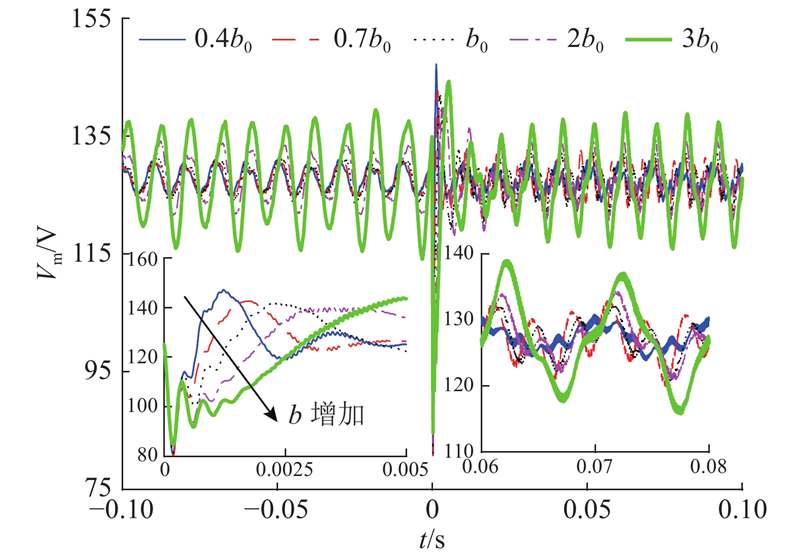
如图13所示为在不同补偿因子下负载切换前后逆变器输出电压幅值变化情况. 由图可以看出,b越小,系统响应越快,电压跌落后恢复时间越短,抗负载扰动能力越强. 与仿真结果不同的是,不同补偿因子下,突加负载后跌落深度相差不大,且恢复过程存在明显超调,b越小,超调越大. 另外,受传感器误差、电感、负载参数摄动等影响,实验中增加负载后,输出电压波动变大,与仿真结果相差较大,特别对于电感、电容等参数摄动直接影响到系统控制增益的大小,对系统性能的影响较大.
图 13
图 13 负载切换时输出电压幅值变化情况
Fig.13 Changes of output voltage amplitude after load switching
6. 结 论
(1)基于LADRC设计的电压控制器对补偿因子的选择具有较强的鲁棒性,在适当偏离系统控制增益时均能保持系统稳定,特别在仿真和实验中,受控制和采样延迟、死区等因素影响,理论推导系统控制增益会偏离实际值的情况下,仍能保持稳定.
(2)在保证系统稳定前提下,适当减小补偿因子可以提高系统响应速度,在保证系统稳定性和动态性能的同时,有效提高系统抗负载扰动能力. 当补偿因子过大时,阻尼小,抗干扰能力差,容易导致电压振荡和畸变,当补偿因子过小时,系统响应过快,容易导致控制量饱和,造成系统不稳定.
(3)文中仅对补偿因子在提高抗干扰能力和动态性能之间折中进行了定性分析,未提供最优参数的计算方法。本文设计电压控制器采用的是二阶LADRC,在受限的观测器带宽下,观测效果欠佳,从而影响系统抗扰动能力,下一步计划通过模型补偿或扰动补偿的方式来进一步提高系统稳态性能和抗扰动能力。
参考文献
微电网技术在主动配电网中的应用
[J].
Application of microgrid technology in active distribution network
[J].
Trends in microgrid control
[J].
Overview of AC microgrid controls with inverter-interfaced generations
[J].DOI:10.3390/en10091300 [本文引用: 1]
虚拟同步机技术在电力系统中的应用与挑战
[J].
Application and challenge of virtual synchronous machine technology in power system
[J].
基于自适应旋转惯量的虚拟同步发电机控制策略
[J].
Control strategy of virtual synchronous generator based on adaptive rotational inertia
[J].
基于改进型重复控制算法的多功能并网逆变器设计
[J].DOI:10.7500/AEPS20161223006 [本文引用: 1]
Design of multi-functional grid-connected inverter based on modified repetitive control algorithm
[J].DOI:10.7500/AEPS20161223006 [本文引用: 1]
带LCL滤波的单相逆变器滑模控制
[J].
Sliding mode control method of single-phase inverter with LCL filter
[J].
Active disturbance rejection control strategy for grid-connected photovoltaic inverter based on virtual synchronous generator
[J].DOI:10.1109/ACCESS.2019.2894786 [本文引用: 1]
A control strategy for smooth power tracking of a grid-connected virtual synchronous generator based on linear active disturbance rejection control
[J].DOI:10.3390/en12153024 [本文引用: 1]
Active disturbance rejection control of LCL filtered grid-connected inverter using Padé approximation
[J].DOI:10.1109/TIA.2018.2855128 [本文引用: 1]
Linear ADRC direct current control of grid-connected inverter with LCL filter for both active damping and grid voltage induced current distortion suppression
[J].
线性自抗扰技术在LCL逆变器并网电流控制及有源阻尼中的应用
[J].
Application of linear active disturbance rejection technique in grid-connected current control and active damping of LCL type inverter
[J].
基于自抗扰控制技术的光储微电网无功支撑策略
[J].
Reactive power support strategy of photovoltaic/battery microgrid based on ADRC
[J].
基于微分前馈自抗扰的逆变器控制策略
[J].
Active disturbance rejection control strategy with differential feedforward for inverters
[J].
基于改进二阶线性自抗扰技术的微网逆变器电压控制
[J].DOI:10.7500/AEPS20180419002 [本文引用: 4]
Voltage control of microgrid inverter based on improved second-order linear active disturbance rejection control
[J].DOI:10.7500/AEPS20180419002 [本文引用: 4]
基于线性自抗扰的微电网平滑切换控制策略
[J].
Control strategy for microgrid seamless switching via linear active disturbance rejection
[J].
二阶系统线性自抗扰控制器频带特性与参数配置研究
[J].DOI:10.7641/CTA.2013.30424 [本文引用: 3]
Research on frequency-band characteristics and parameters configuration of linear active disturbance rejection control for second-order systems
[J].DOI:10.7641/CTA.2013.30424 [本文引用: 3]
线性自抗扰控制理论及工程应用的若干进展
[J].
Surveys on theory and engineering applications for linear active disturbance rejection control
[J].
基于线性自抗扰控制的微网逆变器时−频电压控制策略
[J].DOI:10.7500/AEPS20190824003 [本文引用: 1]
Time-frequency voltage control strategy of microgrid inverter based on linear active disturbance rejection control
[J].DOI:10.7500/AEPS20190824003 [本文引用: 1]