随着我国整体医疗水平的提高，医院应对各种危重疾病的能力也不断增强. 但三甲医院仍然存在拥堵问题，而病人盲目追求高水平医疗服务不仅使问题更加严重，还导致部分亟须治疗的危重病人得不到及时有效的护理. 为了解决这个问题，有三甲医院采取与其他社区医院组成医联体的方式，给病人提供更优质的医疗服务. 部分社区医院存在医疗质量问题，部分病人会返回三级医院治疗，造成资源浪费和病人满意度下降，因此医院针对不同疾病的转诊决策非常重要.

目前研究医疗系统的文献其研究对象是单个医院系统. 例如Gorunescu等^[1]通过建立排队模型研究单个医院内部各部门的病人流转移问题，并计算出相关的系统评价指标；Osorio等^[2]解析具有服务后堵塞特点的排队系统；Lee等^[3]分析包含多个科室的排队网络模型，并利用迭代算法求解稳态参数. 近年来，学者对多家医院组成的系统进行的大多是定性研究. 例如雷祎等^[4]用统计学的方法探究了北京某社区居民对于双向转诊的行为影响因素；匡莉^[5]通过调研分析目前转诊系统存在的问题，提出包括十大要素在内的“社区双诊责任制”政策框架；张莹^[6]介绍日本医疗机构之间的整合经验，为我国构建整合型医疗转诊体系提供参考. 采用排队模型研究转诊系统的文献较少. 例如Li等^[7-10]通过医联体排队网络系统求解系统稳态参数，提出用阈值控制策略指导三级医院转诊. 另有学者采用博弈论方法进行医院效益优化研究，例如李忠萍等^[11]运用M/M/1排队模型和博弈理论构建转诊期望效益函数模型，得到均衡下转率及均衡效益；张悦等^[12]建立综合医院与社区医院间的转诊博弈模型，分别对非竞争型和竞争型的系统建模，求得最优合同契约方案. 对于多类病人共享资源的问题，只有少数文献采用解析公式求解系统稳态参数，且模型较简单，例如Kella等^[13]求解单个服务节点多类具有优先权的病人的等待时间. 对于更复杂的情况，目前大多数是利用仿真方式进行研究的文献，例如Chen等^[14]利用仿真优化方法研究不同的转诊机制对多种疾病类型的病人的等待时长的影响.

随着学者对于医疗系统的研究越来越深入，定性和宏观系统研究已经不能够满足医院管理的需要；同时，三级医院在对多类疾病的转诊决策过程中很少考虑疾病的差异性，在与社区医院合作时只关注床位资源，忽略了医疗质量水平的影响. 本文对上海某三甲医院骨科进行调查研究，针对其与一家社区医院建立的转诊合作机制，利用模型求解和优化的方式，得到最优转诊策略，并分析医疗质量水平对转诊合作造成的影响.

疾病的治疗分成多个连续的过程，以心脏病为例，心脏病发作时需要立刻送往医院进行紧急治疗，即阶段1−紧急治疗阶段（emergency cure process），例如血管成形术和冠状动脉旁路移植手术. 阶段1的治疗完成后，病人需要进行心脏康复治疗，主要通过药物辅助以恢复心脏机能，即阶段2−术后康复阶段（recovery process）. 在我国，阶段1对医院设备的配置水平要求比较高，手术治疗必须在三级医院进行，阶段2治疗可在三级医院病房或社区医院病房进行治疗.

为了减缓三级医院的拥堵，提高资源的使用效率，本文通过优化三级医院收益指导三级医院进行转诊决策. 在病人的多阶段治疗过程中，不同的疾病有不同的特点，由于阶段1的治疗费用比阶段2高，三级医院在发生拥堵时想让病人尽可能转诊到社区医院进行阶段2治疗，以便空出床位收治更多的病人，实现其效率和收益的最大化，但是转诊病人过多将导致候诊时间变长，造成转诊堵塞从而影响三级医院的整体效率；社区医院的病人存在一定概率返回三级医院治疗，影响三级医院的收益. 三级医院针对多样化的疾病类型如何进行差异化的转诊决策实现收益最大化，是本文要探究的主要问题.

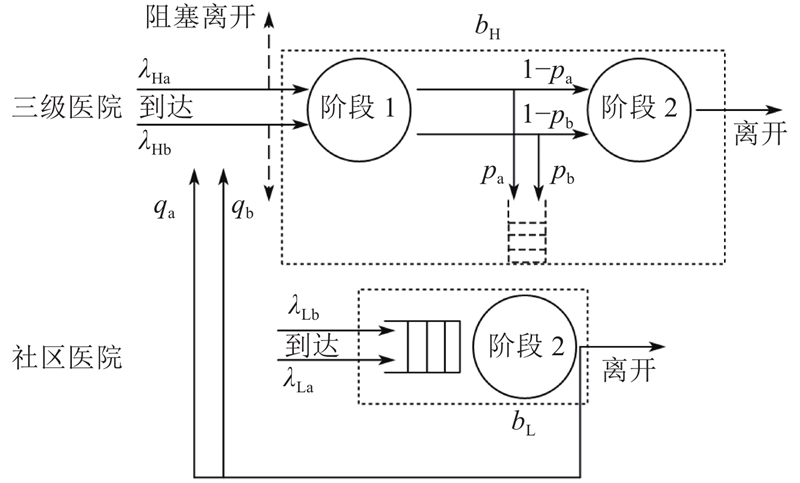
如图1所示为2类病人的排队网络模型. 图中，三级医院和社区医院组成的排队网络包含了3个服务节点，其中三级医院的阶段1和阶段2是共享床位资源的. $ t\in \{\mathrm{a},\mathrm{b}\} $表示病人种类； $ {b}_{\mathrm{H}} $、 ${b}_{\mathrm{L}} $分别表示三级医院和社区医院的病床数量； $ {\mathrm{\lambda }}_{\mathrm{H}t} $、 $ {\mathrm{\lambda }}_{\mathrm{L}t} $分别表示三级医院和社区医院病房入口2类病人的初始到达率； $ \;{\mu }_{1t} $、 $\;{\mu }_{2t} $分别表示阶段1和阶段2的服务速率. 虚线箭头表示病人由于没有多余床位而离开. 社区医院也会接收病情较轻的病人，在这里将其视为阶段2病人. 病人进入三级医院后在三级医院病房接受阶段1的相关治疗，结束后病人可以在三级医院的病房内进行康复，也可以转诊到居住地附近的社区医院进行阶段2的治疗，2类病人的转诊比例分别为 $ {p}_{\mathrm{a}}$、 ${p}_{\mathrm{b}} $. 有时候病人不能立即转诊到社区医院，会在三级医院病房等待，堵塞时长为 $ {T}_{\mathrm{B}} $，社区医院住院病人可能会病情恶化，需要转移到三级医院再次治疗，概率为 $ {q}_{t} $. 该类病人视作阶段1病人， $ {q}_{t} $与社区医院的医疗水平有关. 在完成所有的治疗后，病人从三级医院或者社区医院病房离开.

在上述治疗流程中，三级医院的最优决策受到多个因素的影响. 例如社区医院的床位资源数量、社区医院医疗质量水平和三级医院的床位资源利用率等. 考虑到这些因素，本文建立三级医院的收益函数

式中： $ {\lambda }_{\mathrm{H}t}^{'} $为三级医院2类病人的稳态到达率； $ {Y}_{1t}{\text{、}}{Y}_{2t} $分别为三级医院第1阶段和第2阶段每天治疗2类病人的数量； $ {P}^{\mathrm{H}} $为三级医院满空间的概率； $ {T}_{\mathrm{B}} $是三级医院和社区医院由于转诊存在的堵塞时间； $ {\;\rho }_{\mathrm{H}} $为三级医院的床位资源利用率； $ {R}_{1t}{\text{、}} $ $ {R}_{2t} $分别为三级医院2类病人在阶段1和阶段2的治疗费用； $ {C}_{1t} $为三级医院病房拒绝病人进入导致的服务满意度成本，与病人类别t有关； $ {C}_{2} $为在三级医院转诊堵塞导致的病人等待和转诊效率成本； $ {C}_{3} $为与三级医院资源消耗有关的成本.

在式（1）中，与排队系统相关的参数 $ {Y}_{1t} $、 $ {Y}_{2t} $、 $ {\lambda }_{\mathrm{H}t}^{'} $、 $ {P}^{\mathrm{H}} $、 $ {T}_{\mathrm{B}} $和 $ {\rho }_{\mathrm{H}} $都是未知的，这些参数由 $ {p}_{\mathrm{a}}$、 ${p}_{\mathrm{b}} $唯一确定. 由于医疗合作系统的参数多，多类病人转诊过程的交互作用复杂，社区医院反馈影响未知，进行整个系统的性能分析比较困难，目前很少有进行全面研究的相关文献. 本文设计基于马尔可夫链的迭代算法，可以求解系统在某一转诊决策下的稳态参数，并通过仿真验证其准确性.

通过大量的数值分析研究，发现 ${W_{\rm{H}}}$具有凸函数的性质，可以用内点法^[15]进行精确数值求解. 为了求得最优转诊比例，建立优化模型

在本文的排队系统中，三级医院和社区医院有2个方面的交互影响. 1）三级医院的下转病人将导致社区医院的病房入口到达人数增加；另外，当病人在三级医院病房完成阶段1治疗，但下一节点的社区医院病房空闲资源较少时，将出现转诊堵塞，病人将继续滞留在三级医院病房并占用床位资源，直到社区医院病房有空闲床位资源方可下转. 2）当社区医院里的病人病情加重转移到三级医院急症入口处，造成三级医院入口到达率增加时，又会造成三级医院的拥堵，甚至部分病人不能够进入病房. 在上述的系统交互影响中，到达率、服务率、堵塞时间等系统参数起纽带作用，也是算法设计中的关键参数.

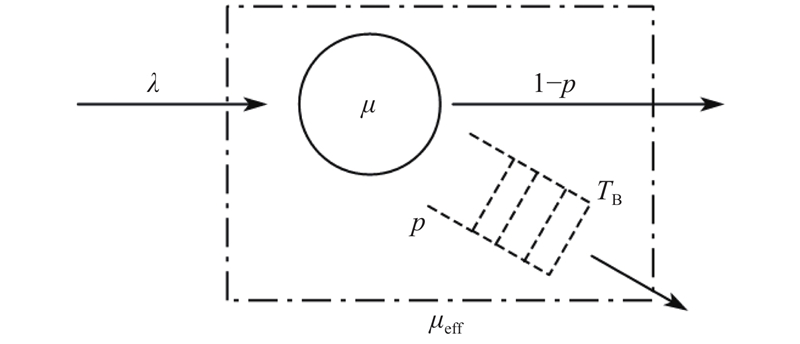
如图2所示，发生在病房内的转诊堵塞为服务后堵塞现象，会导致该服务节点的服务速率变慢，此时的服务速率称为有效服务速率 $ {\;\mu }_{\mathrm{e}\mathrm{f}\mathrm{f}} $. 图中的堵塞时间 $ {T}_{\mathrm{B}} $是社区医院病房入口处的等待时间，假设存在堵塞的转移病人流的比例为 $ p $，则有效服务速率的计算公式为

迭代算法具体步骤如下：1）初始化. 对参数进行初始化 $ {T}_{\mathrm{B}}\left(0\right)=0,{\lambda }_{\mathrm{H}t}\left(0\right)={\lambda }_{\mathrm{H}t},{\lambda }_{\mathrm{L}t}\left(0\right)={\lambda }_{\mathrm{L}t} $， $ {\mu }_{1t}\left(0\right)= $ $ {\mu }_{1t} $. 2）更新迭代. 更新三级医院的2类病人到达率 $ {\lambda }_{\mathrm{H}t}\left(k+1\right)={\lambda }_{\mathrm{H}t}+{\lambda }_{\mathrm{L}t}\left(k\right){q}_{t} $和阶段1的治疗服务速率 $ {\mu }_{1t}^{-1}\left(k+1\right)={\mu }_{1t}^{-1}+{T}_{\mathrm{B}}\left(k\right){p}_{t} $；依据三级医院病房的排队系统求得稳态概率，求得 $ {\;\rho }_{\mathrm{H}}\left(k+1\right){\text{、}} {P}^{\mathrm{H}}\left(k+1\right){\text{、}} $ $ {Y}_{1t}(k+ 1){\text{、}} {Y}_{2t}(k+1) $等三级医院的系统参数；更新社区医院的到达率 $ {\lambda }_{\mathrm{L}t}\left(k+1\right)={\lambda }_{\mathrm{L}t}+{Y}_{1t}\left(k\right){p}_{t} $；根据社区医院的马尔可夫转移过程，求得系统稳态概率，计算等待队长 $ {L}_{q}\left(k+1\right) $和利用率 $ {\;\rho }_{\mathrm{L}}\left(k+1\right) $. $ {T}_{\mathrm{B}} $的计算公式为

3）收敛性判别. 通过计算前后2次迭代产生的差判别，当误差小于 $ {10}^{-6} $时，停止迭代，将最后一次的结果作为系统的稳态输出. 如果其模长大于 $ {10}^{-6} $，转至步骤2）.

须对三级医院和社区医院的子系统求解才能执行步骤2）.

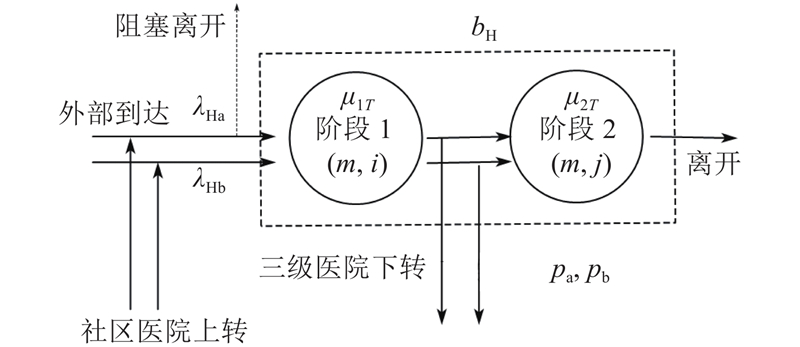
如图3所示为三级医院的排队子系统，进入三级医院病房的病人包含了自主到达的病人和社区医院上转的病人，到达之和记为 $ {\lambda }_{\mathrm{H}t} $. 离开病房的病人包括完成概率 $ {p}_{t} $下转的病人和在三级医院完成2阶段治疗的病人，2阶段的服务速率分别为 $ {\;\mu }_{1t} $和 $ \;{\mu }_{2t} $，2阶段的总床位资源数为 $ {b}_{\mathrm{H}} $.

依据马尔可夫相关理论，定义t′时刻系统的状态 $ {{X}}(t')=\left\{\right(m(t'),i(t'),n(t'),j(t')\left)\right\} $.其中 $ m(t'){\text{、}}n(t') $为 $ t' $时刻在阶段1和阶段2的a类病人数， $ i(t') $、 $ j(t') $为 $ t' $时刻在阶段1和阶段2的b类病人数. 为了方便表述，后文中省略 $ t' $. 根据实际病人治疗流程共有8种状态转移的路径，不同状态之间的状态转移概率可以表示为1） a类病人到达阶段1， $(m,n,i,j) \to (m+1, n,i,j)$. 2）b类病人到达阶段1， $ (m,n,i,j)\to (m,n, $ $ i+1,j)= {\lambda }_{\mathrm{H}\mathrm{b}}, \;0\leqslant i+j+m+n\leqslant {b}_{\mathrm{H}}-1 $. 3）a类病人在三级医院由阶段1转入阶段2， $(m,n,i,j)\to (m-1, n+1,i,j)$= $ m(1-{p}_{\mathrm{a}}){\mu }_{1\mathrm{a}},\; 0\leqslant i+ j+ m+ $ $ n\leqslant {b}_{\mathrm{H}} $. 4）b类病人在三级医院内由阶段1转入阶段2， $(m,n,i,j)\to (m,n, i-1, j+1)= i(1-{p}_{\mathrm{b}}){\mu }_{1\mathrm{b}},\; 0\leqslant $ $ i+j+ m+n\leqslant {b}_{\mathrm{H}}$. 5）a类病人在三级医院阶段1完成治疗后转诊至社区医院， $ (m,n,i,j)\to (m-1, $ $ n,i,j)=m{p}_{\mathrm{a}}{\mu }_{1\mathrm{a}},1\leqslant i+j+m+n\leqslant {b}_{\mathrm{H}}, m\geqslant 1 $. 6）b类病人在三级医院阶段1完成治疗后转诊至社区医院， $ (m,n,i,j)\to (m,n,i-1,j)= i{p}_{\mathrm{b}}{\mu }_{1\mathrm{b}},1\leqslant i+j+m+ n\leqslant $ $ {b}_{\mathrm{H}}, i\geqslant 1 $. 7）a类病人在三级医院完成阶段2治疗后离开， $ (m,n,i,j)\to (m, n-1, i,j)=n{\mu }_{2\mathrm{a}},\; 1\leqslant i+j+m+ n\leqslant $ $ {b}_{\mathrm{H}},n\geqslant 1 $. 8）b类病人在三级医院完成阶段2治疗后离开， $ (m,n,i,j)\to (m, n,i, j-1)=j{\mu }_{2\mathrm{b}} $， $ 1\leqslant i+j+m+ $ $ n\leqslant {b}_{\mathrm{H}},\;j\geqslant 1 $.

由图3定义的排队系统及马尔可夫状态转移的概率可以求出三级医院系统状态 $ \left(m,n,i, j\right), $ $ (0\leqslant i+j+m+n\leqslant {b}_{\mathrm{H}}) $的稳态概率为

证明：在非边界条件下，即当 $ 1\leqslant m,n,i, j\leqslant {b}_{\mathrm{H}}-1 $并且 $ m+n+i+j\leqslant {b}_{\mathrm{H}}-1 $时，平衡方程为

边界条件下，即当 $ 1\leqslant n,i,j\leqslant {b}_{\mathrm{H}}-1,m=0 $并且 $ n+i+ $ $ j< {b}_{\mathrm{H}} $时，平衡方程为

当 $ 1\leqslant m,n,i,j\leqslant {b}_{\mathrm{H}}-1 $并且 $ m+n+i+j={b}_{\mathrm{H}} $时，平衡方程为

根据平衡方程的特点猜想2类病人的稳态概率满足相关性质：

可以证明式（10）满足式（7）~（9），根据系统稳态解的唯一性，联立归一化条件即可得到式（6）. 可以验证当疾病种类多于2类时也有相似形式的稳态概率公式.

通过计算三级医院的状态稳态概率，可以得出下列相关性能评价参数

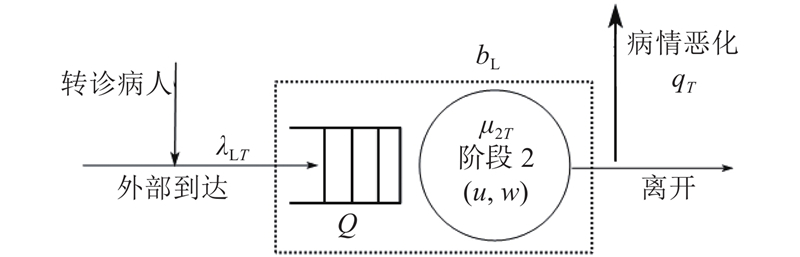
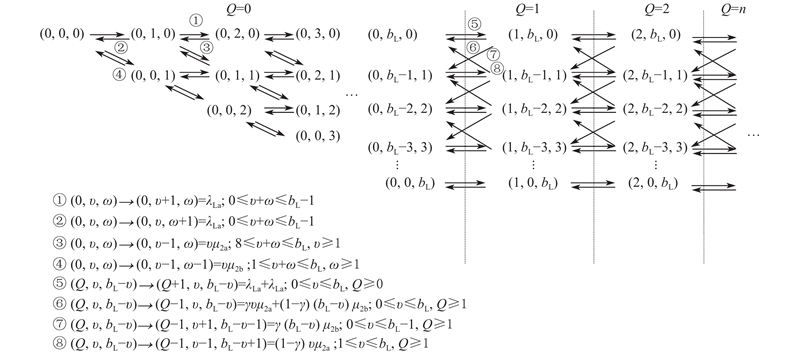
如图4所示为社区医院排队子系统，社区医院的病床数量为 $ {b}_{\mathrm{L}} $，到达社区医院病房的病人包括自主到达和三级医院下转的部分病人，总到达记为 $ {\lambda }_{\mathrm{L}t} $. 如果没有空闲床位，病人会在病房外形成等待的队列（包括转诊等待的虚拟队列），队列人数记为 $ Q $. 大部分病人经过阶段2治疗后会康复离开，部分病人会病情恶化需要返回三级医院进行阶段1的治疗，服务速率为 $ {\mu }_{2t} $，病情恶化概率为 $ {q}_{t} $.

根据图4定义马尔可夫状态空间 $ Y\left(t\right)= \{(Q(t), $ $ v\left(t\right),w\left(t\right)\left)\right|0\leqslant v\left(t\right)+w\left(t\right)\leqslant {b}_{\mathrm{L}}\} $. 其中 $ v\left(t\right) $和 $ w\left(t\right) $表示社区医院病房内部2类病人的数量，为了方便表述，后文中省略 $ t $. 在外部队列中a类病人所占比例为

其中 $\gamma $是后文进行稳态求解的队列状态参数. 如图5所示，根据病人流的转移情况建立马尔科夫状态转移图. 共有8种状态转移概率，如图中①~⑧所示，数字标号均对应最近的箭头.

由于状态空间和转移概率过于复杂，运用矩阵理论对马尔可夫链进行分解计算^[16]. 矩阵 $ {\boldsymbol{M}} $是系统的转移概率矩阵，它可以按照队列中的人数进行分解

式中： $ {\boldsymbol{B}}_{00} $、 $ {\boldsymbol{B}}_{01} $、 $ {\boldsymbol{B}}_{10} $为边界矩阵，即外部没有排队等待的情形； $ {\boldsymbol{A}}_{0} $、 $ {\boldsymbol{A}}_{1} $、 $ {\boldsymbol{A}}_{2} $分别为队列人数减少1、队列人数不变、队列人数增加1的转移概率

式中： $ {\boldsymbol{A}}_{0} $主对角线为概率转移路径⑥，主对角线上方的对角线为路径⑧，主对角线下方的对角线为路径⑦，其余元素均为0. ${{\boldsymbol{A}}_{\rm{2}}} = ({\lambda _{{\rm{La}}}} + {\lambda _{{\rm{Lb}}}}) {{\boldsymbol{I}}_{({b_{\rm{L}}} + 1) ({b_{\rm{L}}} + 1)}}.$ $ {\boldsymbol{A}}_{2} $为路径⑤，即外部队列增加1人的概率. $ {\boldsymbol{A}}_{1} $的主对角线满足概率转移矩阵每行元素之和为零的要求，可以根据 $ {\boldsymbol{A}}_{2} $和 $ {\boldsymbol{A}}_{0} $求出. 当 $ Q=0 $时，系统共有 ${({b}_{\mathrm{L}}+1)({b}_{\mathrm{L}}+2)}/{2}$种状态，因此 $ {\boldsymbol{B}}_{00} $是维度为 ${({b}_{\mathrm{L}}+1)} $ $ {({b}_{\mathrm{L}}+2)}/{2}$的方阵，比较复杂，再次将其分解：按照b类病人数量由0增加至 $ {b}_{\mathrm{L}} $分成 $ {b}_{\mathrm{L}}+1 $层， $ {\boldsymbol{C}}_{i,j} $为对应的子矩阵.

式中： $ {\boldsymbol{C}}_{i,i-1} $对角线表示状态由 $ (0,k,i) $转移到 $ (0,k, $ $ i-1) $的概率，为转移路径④； $ {\boldsymbol{C}}_{i,i+1} $对角线表示系统状态由 $ (0,k,i) $转移到 $ (0,k,i+1) $的概率，为转移路径②； $ {\boldsymbol{C}}_{i,i} $主对角线上下方表示 $ (0,k,i) $转移至 $ (0,k+1,i) $和 $ (0,k-1,i) $的概率，为转移路径①和③，主对角线是同一行其他转移概率之和的相反数. $ {\boldsymbol{B}}_{01} $是维度为 $ {({b}_{\mathrm{L}}+1)({b}_{\mathrm{L}}+2)}({b}_{\mathrm{L}}+1) /{2}$的矩阵， $ {\boldsymbol{B}}_{10} $的维度为 $ ({b}_{\mathrm{L}}+1){({b}_{\mathrm{L}}+1)({b}_{\mathrm{L}}+2)}/{2} $，同理可以对 $ {\boldsymbol{B}}_{01} $和 $ {\boldsymbol{B}}_{10} $进行分解，它们表示 $ Q=0 $与 $ Q=1 $之间的概率转移矩阵.

上述拟生灭过程的稳态概率矩阵满足： $ {\boldsymbol{\varPi }}_{i}={\boldsymbol{\varPi }}_{1}{\boldsymbol{R}}^{i-1},\;i={2,3,}\cdots $；其中 $ {\boldsymbol{\varPi }}_{Q} $是长度为 $ {b}_{\mathrm{L}}+1 $的向量，表示当队列长度为 $ Q $时，系统的稳态概率向量. 令 $ {\boldsymbol{R}}_{0}={\boldsymbol{0}} $， $ {\boldsymbol{R}}_{t{+1}}=-{\boldsymbol{A}}_{2}{\boldsymbol{A}}_{1}^{-1}-{\boldsymbol{R}}_{t}^{2}{\boldsymbol{A}}_{{\boldsymbol{0}}}{\boldsymbol{A}}_{1}^{-1} $，可以通过有限次迭代求得 $ {\boldsymbol{R}} $矩阵的数值解. 根据边界条件和归一化条件可以求得稳态概率 $ {\pi }_{(Q,v,w)}^{\mathrm{L}} $

通过计算社区医院的稳态概率，可以得到社区医院床位利用率 $ {\;\rho }_{\mathrm{L}} $、队列长度 $ {L}_{\mathrm{q}} $以及等待时长 $ {T}_{\mathrm{B}} $

当 ${\;\rho _{\rm{L}}} < 1$时，

式中： $ {\boldsymbol{I}} $为 $ {b}_{\mathrm{L}}+1 $维单位矩阵； $ {\boldsymbol{e}} $为向量，其长度为 $ {b}_{\mathrm{L}}+1 $，分量全为1.

利用实际数据处理后的参数，床位数量 $ {b}_{\mathrm{H}}=46 $， ${b}_{\mathrm{L}}=20 $；a类病人平均外部到达率 $ {\lambda }_{\mathrm{H}\mathrm{a}}=2$， $ {\lambda }_{\mathrm{L}\mathrm{a}}=0. $6人/d；b类病人平均外部到达率 $ {\lambda }_{\mathrm{H}\mathrm{b}}=1 $， $ {\lambda }_{\mathrm{L}\mathrm{b}}=0.2 $. a类病人住院时长阶段1为6 d，阶段2为11 d；b类病人住院时长阶段1为5 d，阶段2为12 d. 另外设置三级医院对于2类病人下转的比率 $ {p}_{\mathrm{a}}=10 {\text{%}}, {p}_{\mathrm{b}}=10{\text{%}} $，社区医院由于医疗质量问题上转的概率 $ {q}_{\mathrm{a}}=0.05,{q}_{\mathrm{b}}=0.05 $. 将仿真结果近似为真实结果，则

本文使用Arena软件建立相应的仿真模型，以“天（d）”为基本时间单位，为了确保系统达到稳态，分别设置预热时间为10000 d和运行时间为500000 d，在不同的随机数状态下重复10次的得到相关的系统参数值. 迭代算法一般经过6~9次即收敛，利用式（23）计算相对误差. 以实验参数为基准，利用控制变量的方式分别对三级医院和社区医院的各项参数，包括床位数、到达速率、服务速率等进行变化以验证算法的普适性，部分参数以及系统评价指标的仿真和算法对比结果如表1所示. 由表可以看出，参数误差都在3%以内，相比文献[3]中使用过多近似公式造成部分参数迭代算法误差达17%，本文算法对医院子系统解析求解更具有效性.

上海市某医疗系统下一家三级医院的骨科科室为国家临床重点专科，其检验、诊疗设施完备，医疗力量雄厚，能够应对各种重大疾病和突发情况，年手术量达2.37万台，床位资源非常紧张，存在堵塞和不得不拒绝部分危重病人的情况. 社区医院骨科床位为康复性床位，病人主要在该床位接受术后治疗和护理^[17]. 本文通过调研采集2013年至2015年病人在三级医院骨科病房内部进行治疗的多种疾病数据. 根据疾病的特点，共有24种疾病适合转诊合作，部分疾病的名称与参数如表2所示.

在适合转诊的疾病中很多具有相似性，将这24种疾病聚成2类，其中a类疾病10种，b类14种，疾病相关参数在2个阶段的服务速率 ${\mu _{{\rm{1a}}}}$、 ${\mu _{{\rm{1b}}}}$、 ${\mu _{{\rm{2a}}}}$、 ${\mu _{{\rm{2b}}}}$分别为1/6、1/5、1/11、1/12人/d，2类疾病在2个阶段的治疗费用 ${R_{{\rm{1a}}}}$、 ${R_{{\rm{2a}}}}$、 ${R_{{\rm{1b}}}}$、 ${R_{{\rm{2b}}}}$分别为31 093.2、12 996.8、51 753.2、13 449.3元. 为了便于本文模型的理论研究，将科室的床位数和到达率都降低为实际数据的十分之一进行分析，即 $ {b}_{\mathrm{H}} $、 ${b}_{\mathrm{L}} $分别为46、20张；2类病人的总到达参数 ${\lambda _{{\rm{H}}a}}$、 ${\lambda _{{\rm{H}}b}}$、 ${\lambda _{{\rm{L}}a}}$、 ${\lambda _{{\rm{L}}b}}$分别为2.0、1.0、0.6、0.2人/d.

根据调研医院成本数据设置成本参数 $ {C}_{1t}= $ $ 0.75{R}_{1t} $， $ {C}_{2} $为5 000元/d，C₃为500元/张. 由于社区医院医疗质量水平不确定，医疗质量较低的社区医院病情恶化概率较大，对于三级医院来说，这部分病人也会造成医疗资源的负担. 以不同医疗质量水平的社区医院为例，探究三级医院在与之转诊合作时的最优转诊决策变化. 1）理想的社区医院：床位资源无限，医疗质量极高（ $ {b}_{\mathrm{L}}=\infty , $ $ {q}_{t}=0,{T}_{{\rm{B}}}=0 $），上述情形可以单独使用三级医院子模型求解. 2）实际的社区医院：床位资源有限，医疗质量水平不同（ $ {b}_{\mathrm{L}}=20 $， $ {q}_{{\rm{a}}}={q}_{{\rm{b}}} $，并且分别取值 $ \mathrm{0,1}{\text{%}},,3 {\text{%}},5 {\text{%}},10 {\text{%}} $），采用转诊合作的模型求解. 根据 $ {b}_{\mathrm{L}} $、 $ {q}_{{\rm{a}}} $、 $ {q}_{{\rm{b}}} $求得最优解 $ {p}_{{\rm{a}}}$、 ${p}_{{\rm{b}}} $和最优收益 $ {W}_{\mathrm{H}} $，如表3所示. 表中，序号1 三级医院最优决策是将所有b类病人转移，再转移部分a类病人，这是因为b类病人的康复阶段耗时较长，并且病人康复阶段的收益较治疗阶段低，a类病人阶段2的时间更短，相对于b类病人三级医院选择少转. 所以三级医院的最终决策是将b类病人全转，保留大部分的a类病人以保证整个医院的利用率在较高水平，最优收益为115 221.72元/d. 序号2~6受社区医院的资源瓶颈限制，三级医院只转移部分b类病人，并且随着社区医院上转率增加，三级医院的下转率呈减小的趋势，另外随着合作伙伴医疗质量水平变低，三级医院的最优收益先些许增加，然后急剧减少. 原因是当少量社区医院自有病人因病情恶化上转三级医院病房进行阶段1护理时，由于存在转诊合作，三级医院利用率如果有部分空余，便能够接受这些病人，实现最优收益的提高，但是当合作伙伴医院的质量水平太差时，病人上转数量太多，导致三级医院内部资源紧缺，部分危重病人便不能够进入病房治疗，惩罚成本将导致医院最优收益迅速降低. 因此在实际情况下，为了提高服务满意度三级医院应该与医疗质量水平较好的伙伴进行合作.

根据实际情况，不同类别疾病的病情恶化概率不同，该骨科所选择的社区医院的质量参数为 $ {q}_{\mathrm{a}}=8 {\text{%}},q_{\mathrm{b}}=3 {\text{%}} $. 计算所得该三级医院能够实现的最大收益是102 205.89元/d，对应的最优决策是转诊56.08%的b类病人.

考虑不同疾病的不同特点，分别从疾病的2阶段治疗需要的住院时长以及疾病的治疗费用探究三级医院转诊决策的变化.

研究发现，阶段1的住院时长不影响三级医院转诊病人的种类，当住院时长增加时，医院转诊另一类疾病的比例会增加，最优收益也会减少. 但是如果阶段2的住院时长增加，那么三级医院转诊的病人类型就会发生改变，会转移阶段2住院时长较长的病人，从而能够接受治疗更多阶段1的病人. 如表4所示，疾病的治疗费用对三级医院的转诊决策影响很大，当a类疾病阶段1费用变大时，三级医院会由转移b类病人变成转移a类病人，这是因为当 $ {R}_{1\mathrm{a}} $增加时， $ {R}_{2\mathrm{a}} $与其差距变大，在三级医院进行阶段2治疗的时间-费用效率变低，所以三级医院更愿意转移该类病人提高效率. 同理当 $ {R}_{2\mathrm{a}} $变大时，相当于2个阶段的收益差距变小，三级医院会更愿意转诊另一类病人.

本文以上海市某三甲医院与社区医院的转诊合作为背景，考虑三级医院内部多类病人多阶段治疗、转诊病人资源占用型堵塞以及社区医院质量水平差异的实际情况，为该三级医院在转诊决策时提供了实际有效的决策建议和完整的理论方法. 研究结果表明疾病的治疗时长、治疗费用的差异、下级医院的诊疗质量差异是影响最优转诊选择的重要因素，在疾病社区医院诊疗质量无差异的情况下，优先转诊低收益高时长的病人. 在疾病社区医院诊疗质量有差异的情况下，其最优的转诊决策较为复杂，常常呈现出综合效应，需要通过算法才能进行最优决策. 未来的研究方向可以针对多家医院中多种疾病类型的动态转诊策略进行设计.