滑带或滑面是坡体内部岩土体受到揉皱及剪切逐渐形成的软弱带或剪切面,影响滑坡的演化过程与变形稳定性. Jiang等[1-2]研究不同部位滑带土的颗粒级配、矿物组成和化学成分的空间差异特征. Lu等[3]探究滑带土颗粒级配的分形维数对黄土坡滑坡微观结构和抗剪强度参数空间变异性的影响. 以上研究表明,在滑带的形成过程中,不同位置岩土体的物质成分、颗粒级配与微观结构是空间变化的,抗剪强度参数存在空间变异性. 目前,滑带力学参数的获取可以通过工程地质类比法、室内外力学试验与强度参数反演等手段. 由于测量误差、岩土体固有变异与转换模型误差等因素的存在[4-5]以及取样数量与取样位置的限制,通过试验手段获取的抗剪强度参数存在误差,不能代表整个研究区域. 对于强度参数反演方法,通常结合力学试验数据,利用滑坡的位移监测数据[6-7]和滑坡实际稳定性状况[8-9]等,对输入强度参数进行反演. 为了建立精确的滑带或滑面抗剪强度参数模型,既需要考虑滑带土力学强度参数的空间变异性与不确定性,也需要利用滑坡的后验信息.
对于土性参数的空间变异性与不确定性,利用随机场理论、地统计学理论与可靠度理论可以研究计算模型的不确定性[10-16]. 这些理论方法依赖于参数的基本统计特征,这些参数信息的获取较困难. 为了解决参数先验信息获取困难或不准确的问题,贝叶斯方法被应用到岩土工程的不确定性建模中,Wang等[12]介绍了岩土体参数表征过程中多种不确定性影响的贝叶斯反分析框架. Zhang等[13]采用马尔可夫链蒙特卡洛(MCMC)的贝叶斯方法,利用边坡的失稳观测信息对边坡的多个参数进行随机反演. Wang等[14]利用MCMC和最大似然的贝叶斯方法,对公路边坡的摩擦角和锚固力进行随机反演. Gong等[15]结合随机场理论与MCMC贝叶斯方法,利用测点信息对场地的岩土参数特征进行表征. 蒋水华等[16]以简单边坡模型为例,基于可靠度的贝叶斯方法利用试验数据对随机场参数进行反演. 以上研究表明,贝叶斯方法可以有效地利用外源信息对参数先验信息进行反演修正,在随机变量反演方面有较多的应用.
综上所述,本文构建基于随机场-贝叶斯方法的滑面抗剪强度参数反演框架,研究更新前、后各滑面抗剪强度参数统计特征的变化规律. 基于PAWN方法,研究不同位置条块滑面抗剪强度参数变量对稳定性的敏感度. 在获取更新前、后滑面强度参数样本的基础上,探究库水位下降工况下滑面抗剪强度参数空间变异性对滑坡变形的影响规律.
1. 计算原理及方法
1.1. 贝叶斯理论
式中:
式中:
式中:
式中:
式中:
采用子集模拟的方法产生属于破坏区域中的样本,定义
式中:中间事件
子集模拟的简要步骤如下.
1)基于随机变量
2)在第1)步产生
3)不断重复步骤2),若模拟进行到第
1.2. 自适应条件抽样算法
自适应条件抽样方法通过构建候选样本与抽取样本的联合分布函数,抽取符合破坏区域的样本[20]. 该方法的优势如下:基于每次模拟过程中接受率参数
在第k+1层子集模拟中,将k层模拟中的样本
第
式中:
1.3. 随机场模型
根据
由于斜坡的稳定性通常由滑面上的平均强度决定,而不是某一点的强度,采用二维局部平均法[21]进行随机场的离散. 局部平均法通过局部平均过程将点强度离散到一定的区域,具有更好的适应性. 为了建立滑面黏聚力
式中:
自相关矩阵
式中:
图 1
图 1
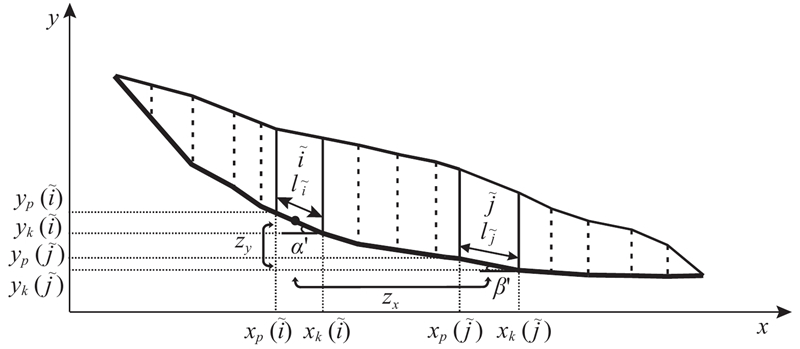
滑坡任意2个条块
Fig.1
Sketch of arbitrarily two slices
1.4. 基于PAWN方法的参数全局敏感性分析
不同于基于方差的全局敏感性分析方法,PAWN通过计算输出变量
将每一个输入变量
式中:stat 表示取均值、最大值或中位数,由用户自定义[22],结合实例对各种状态的结果进行比较;
基于式(22)计算得到敏感性指标具有一定的近似误差,尤其是当样本容量较小时,评估输入变量敏感性指标的可靠性是很重要的. 伪参数
2. 白水河滑坡
2.1. 滑坡概况
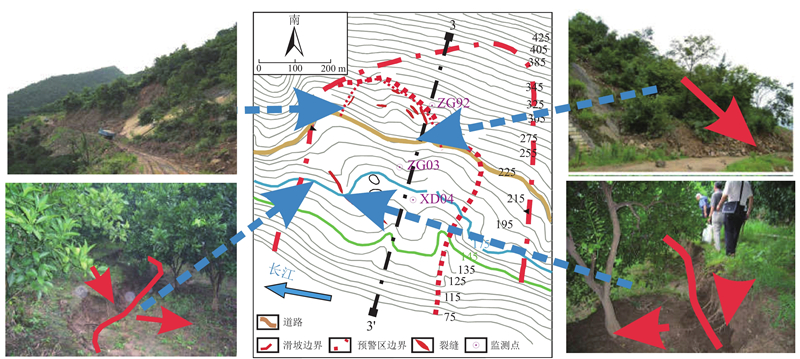
白水河滑坡位于长江主干道的南岸,距三峡大坝坝址56 km,滑坡前缘临空面较陡(高度为30~50 m,坡度为20°~30°),滑面平均倾角为25°. 白水河滑坡划分为预警区和非预警区两部分(见图2). 滑坡地质勘察和滑坡监测信息表明,变形破坏区域主要分布在预警区内,后缘和边界处出现剧烈变形,预警区外没有明显的宏观变形迹象,钻孔取出的岩芯没有明显的滑带.
图 2
图 2 白水河滑坡平面图与变形破坏现场图片
Fig.2 Plane picture and deformation picture of Baishuihe landslide
自三峡水库蓄水到135 m后,滑坡内出现强烈的宏观变形. 2003年6月到2006年9月,库水位在135 m到138 m间波动,坡体变形稳定. 2006年9月到2007年2月,库水位逐步升到155 m;到2007年6月,库水位首次下降至145 m,伴随着季节性强降雨(每年6月~9月),滑坡产生了较大的一次阶跃变形,具有加速滑动的迹象,位于3-3′剖面处发现多处裂缝[24-25]. 如图2所示,滑坡后缘沿江公路南侧(山上方向)约104 m3的岩土体发生塌滑,滑坡东侧和后缘边界基本贯通,西侧边界裂缝呈羽状断续展布. 卢书强等[24]根据专业监测成果与勘查报告分析认为,白水河滑坡在库水位快速下降和强降雨共同作用下是不稳定的. 根据滑坡不同发育阶段的稳定系数评估方法[9-10]可知,滑坡3-3′剖面在当时自重、强降雨与库水位首次下降的工况下处于不稳定状态[25],稳定系数为0.95~1.00,为该工况下的反演分析提供了条件.
2.2. 物质组成与岩土参数
滑坡体物质由碎石、块石、角砾和粉质黏土、黏土组成,厚度为7.75~38.50 m,总体趋势是滑坡后部滑体厚度小,前缘滑体厚度大. 滑带以含碎石或者含角砾粉质黏土为主,部分滑带岩土的物质成分为角砾土和黏土,滑面可见明显的磨光面和擦痕. 滑带厚度为0.20~1.30 m,平均厚度为0.7 m.
滑坡稳定系数计算和滑坡渗流变形模拟所需的参数有容重
表 1 岩土体的物理力学参数
Tab.1
| 材料 | | E /MPa | c /kPa | | | |
| 滑体 | 20.7 | 36.5 | 32.4 | 18 | 0.32 | 0.35 |
| 滑带 | 22.0 | 1.88 | — | — | 0.33 | 0.22 |
3. 计算流程
3.1. 参数反演框架
基于自适应条件抽样算法的贝叶斯方法的具体步骤如下.
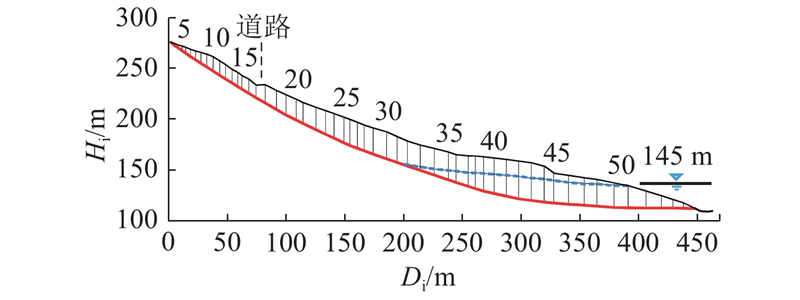
1)建立白水河滑坡3-3′剖面的二维地质模型,条块划分见图3,共划分了55个条块,导出所有条块的滑面位置坐标信息. 图中,Hi为高程,Di为距离.
图 3
2)基于黏聚力与摩擦角的先验统计信息特征值,如均值、变异系数、波动范围与变量间的相关系数等,建立滑面的初始随机场模型,生成随机变量样本
3)采用剩余推力法计算白水河滑坡3-3′剖面的稳定系数,其中地下水位由有限元软件通过施加相应的时间段的工况而获取.
4)基于白水河滑坡3-3′剖面的实际稳定性状况(欠稳定),评估该剖面的实际稳定系数为0.95~1.00. 结合正态分布95%的置信区间,确定
5)在结构可靠度的贝叶斯更新框架下,利用白水河滑坡3-3′剖面的实际稳定性状况与预测状况的差异,对滑面随机场模型的变量样本进行筛选,获得更新后的变量.
6)基于更新后的变量,采用非侵入式随机有限元法[11]开展白水河滑坡3-3′剖面的渗流变形分析,探究滑面抗剪强度参数空间变异下的滑坡变形以及反演更新前、后样本下的变形差异.
3.2. 渗流变形模拟
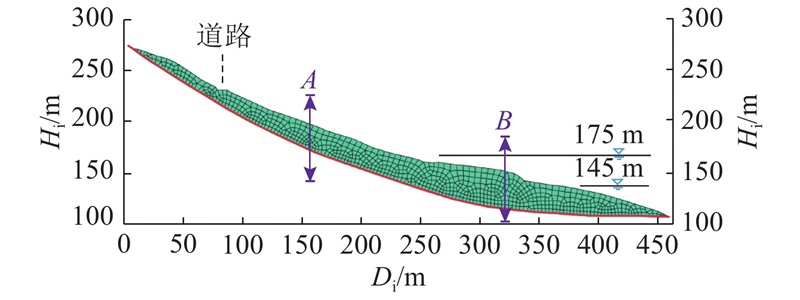
依据3-3′剖面的地质模型,建立如图4所示的有限元模型,滑带厚度为0.5 m. 模型采用孔压/位移耦合的CPE4RP平面应变四边形单元,该减缩积分单元在满足位移精度要求的条件下计算代价相对较低. 坡体共划分747个四边形单元、884个节点,滑带共划分170个四边形单元、342个节点. 采用理想弹塑性本构和摩尔库仑破坏准则,模型底部约束竖直位移和水平位移,滑坡前缘库水位以下部分为水头边界,水位以上部分为降雨边界.
图 4
图 4 白水河滑坡3-3′剖面有限元模型
Fig.4 Finite element model of Baishuihe landslide 3-3′ profile
参数反演工况为2007年2月1日到2007年7月1日,库水位从155 m降到145 m,期间并施加强降雨[25]. 为了探究库水位下降条件下滑面抗剪强度参数空间变异对滑坡变形的影响,分析反演更新前、后样本下的滑坡变形差异,采用的研究工况为库水位从175 m下降到145 m.
4. 计算结果
4.1. 滑面抗剪强度参数敏感性分析
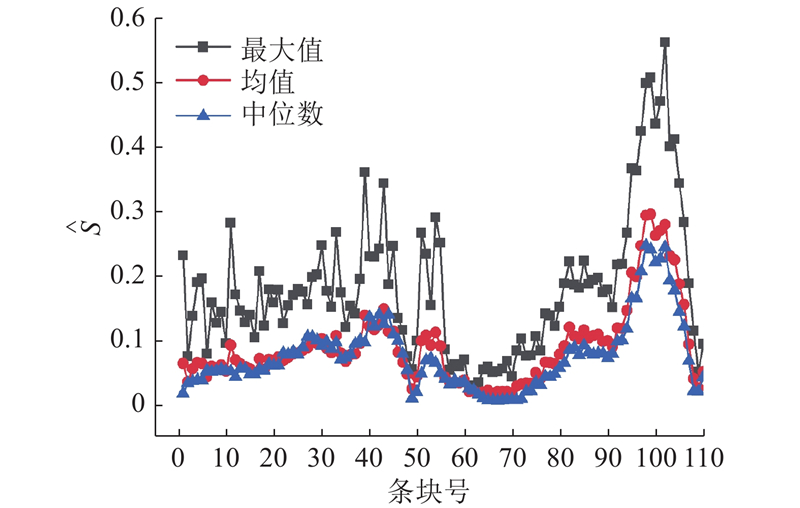
为了研究式(22)中stat 取不同状态(均值、最大值或中位数)对敏感性结果的影响,结合PAWN方法,分别计算不同状态下55个条块的黏聚力与摩擦角共110个变量对稳定系数的敏感度指标,如图5所示. 图中,1~55号为对应条块号的黏聚力变量,56~110号为对应条块号的摩擦角变量. 从图5可以看出,stat 取均值和中位数的敏感度指标结果基本相同,stat 取最大值的敏感度指标略大于其他2种结果,且变量间敏感度指标的波动幅度相对较大,但从整体来看,3种状态的敏感度指标变化趋势较相似,均能够反映出不同条块敏感度指标的变化趋势. 总之,由于最大值为数据出现的极端情况,不能有效地反映数据的整体性,建议stat 取均值和中位数来进行分析.
图 5
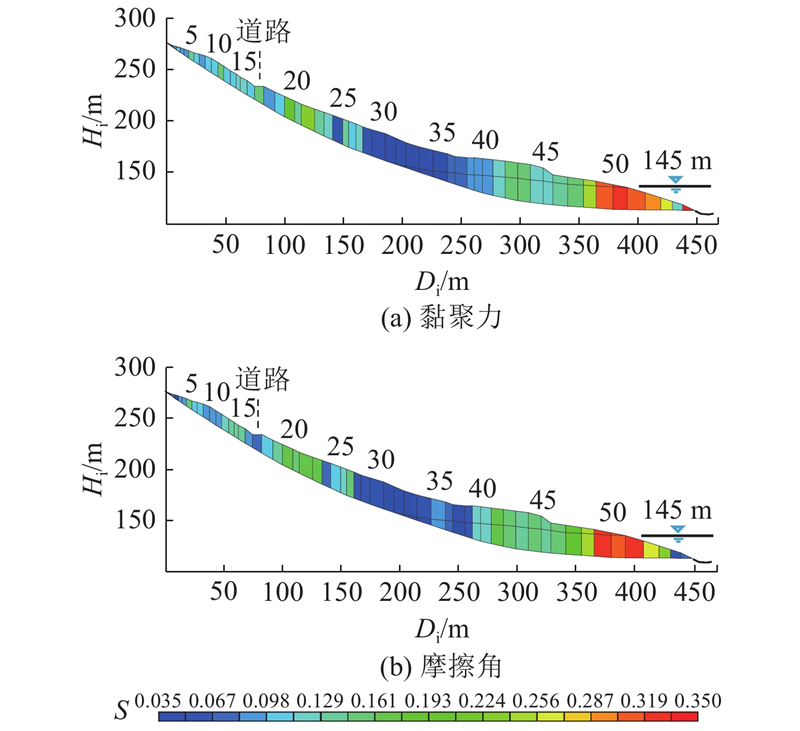
基于stat 取均值的敏感度计算结果进行分析. 结果表明,
图 6
图 6 条块滑面抗剪强度参数对稳定系数的敏感度
Fig.6 Sorting sensitivity index about shear strength parameters over factor of safety
4.2. 滑面抗剪强度参数反演
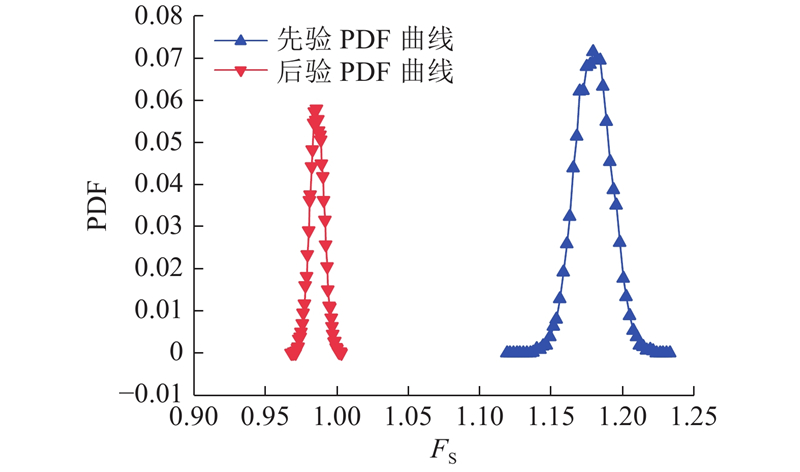
基于结构可靠度的贝叶斯自适应反演流程,共更新10 000组抗剪强度参数随机场样本. 在该过程中,共经历了17层子集模拟. 如图7所示为10 000组稳定系数FS的先验与后验概率密度函数(PDF)分布曲线. 可见,更新前的稳定系数为1.119~1.233,稳定系数的均值和标准差分别为1.176和0.034;更新后的稳定系数为0.95~1.00,均值和标准差分别为0.986和0.011. 可见,更新后的稳定系数区间与预定区间吻合,说明该方法的有效性.
图 7
图 7 稳定系数的先、后验PDF曲线
Fig.7 Prior PDF and posterior PDF curves of factor of safety
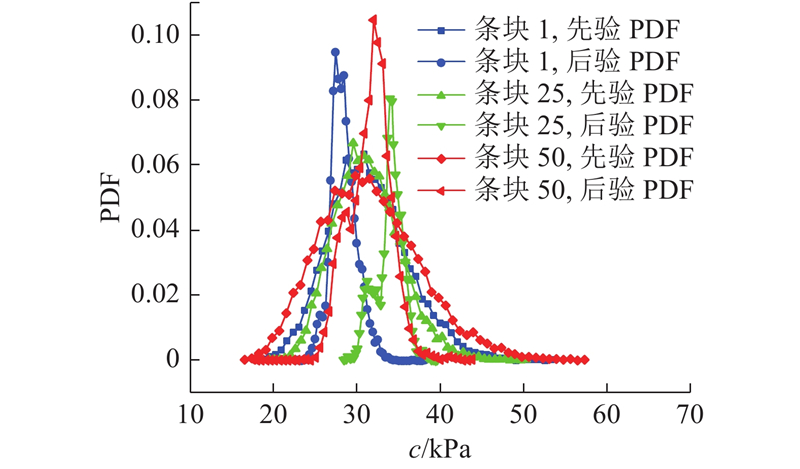
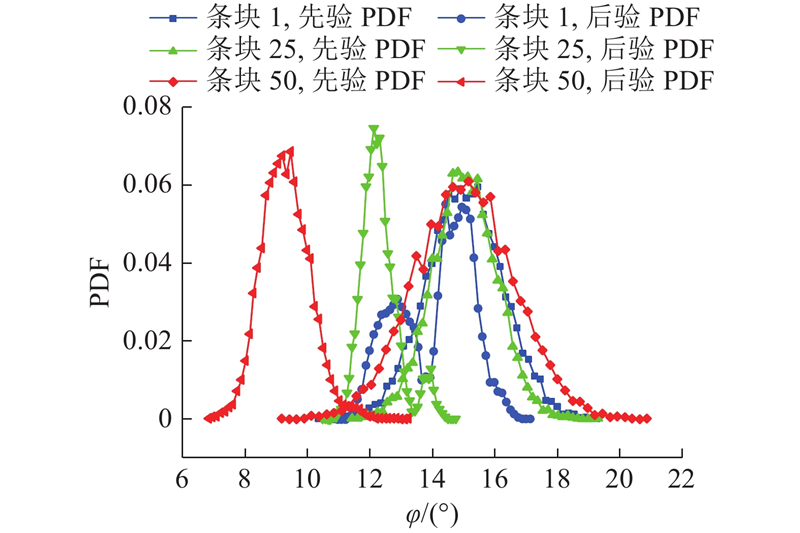
图 8
图 8 不同位置条块的黏聚力先、后验PDF曲线
Fig.8 Prior PDF and posterior PDF curves of cohesion in different slices
图 9
图 9 不同位置条块的摩擦角先、后验PDF曲线
Fig.9 Prior PDF and posterior PDF curves of friction angle in different slices
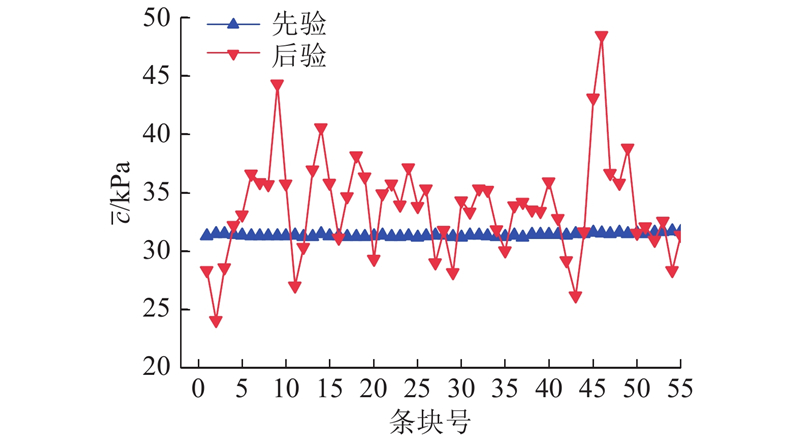
如图10、11所示分别为反演前、后各条块黏聚力与内摩擦角的均值
图 10
图 10 反演前、后的各条块黏聚力均值
Fig.10 Cohesion mean of any slices before and after data inversion
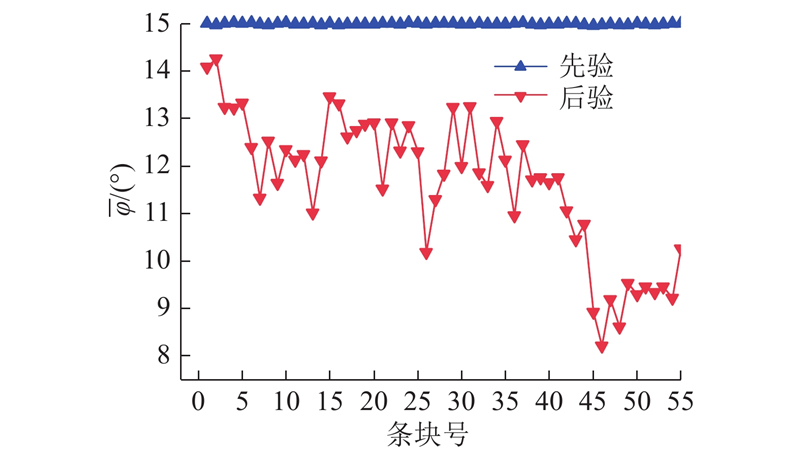
图 11
图 11 反演前、后的各条块摩擦角均值
Fig.11 Friction angle mean of any slices before and after data inversion
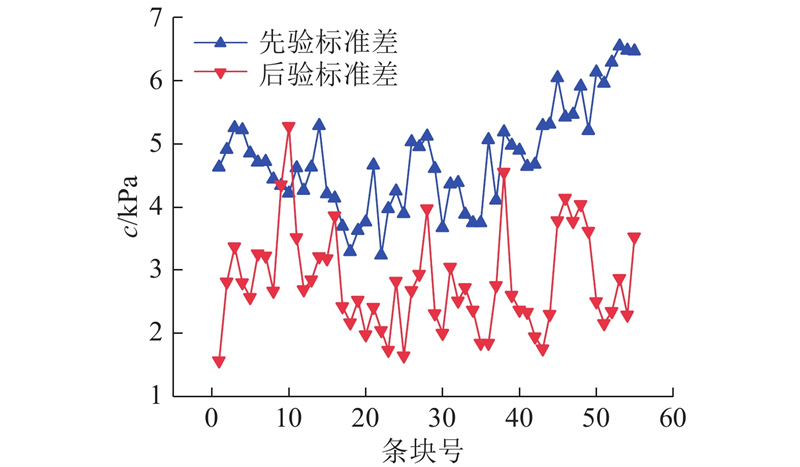
图 12
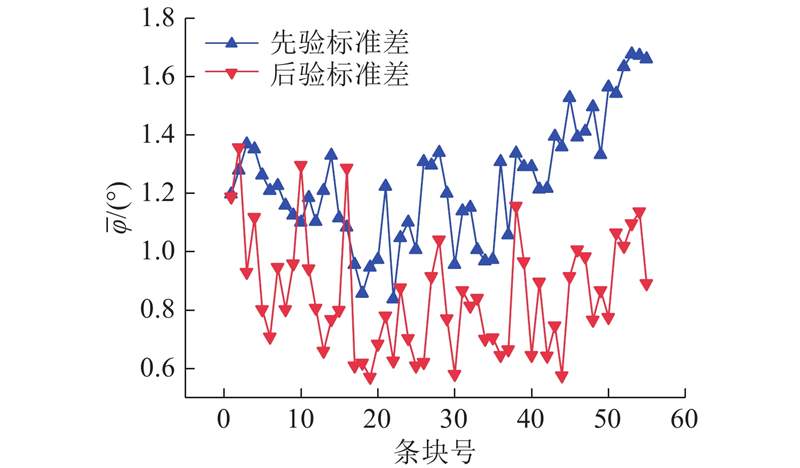
图 12 反演前、后的各条块黏聚力标准差
Fig.12 Cohesion standard deviation of any slices before and after data inversion
图 13
图 13 反演前、后的各条块摩擦角标准差
Fig.13 Friction angle standard deviation of any slices before and after data inversion
4.3. 基于反演参数的滑坡变形分析
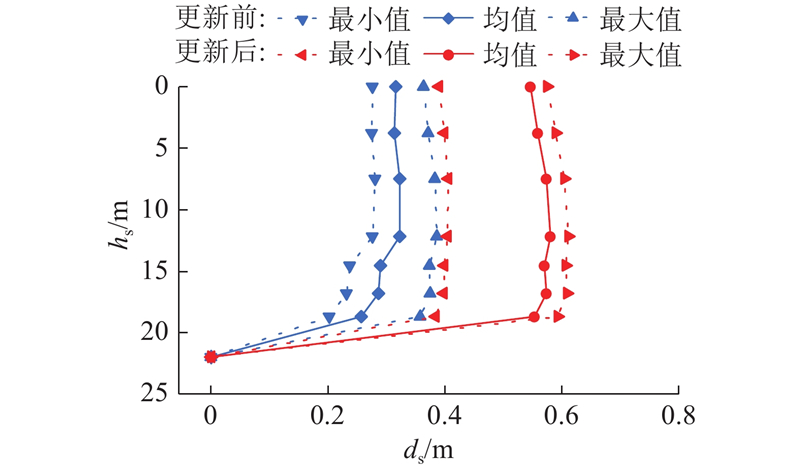
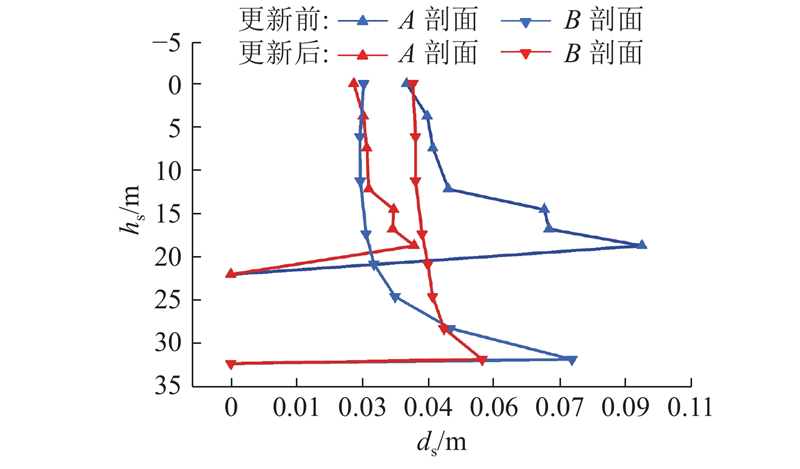
为了探究更新前、后随机场参数变化对滑坡变形的影响,对库水位从175 m下降到145 m时的滑坡位移进行分析. 如图14~16所示为参数更新前、后滑坡在A、B剖面处的位移曲线,其中图16为位移变异系数曲线. 图中,hs为剖面深度,ds为剖面位移. 可以看出,反演前、后位移沿深度的变化趋势一致,但反演后A、B剖面处各深度位移的最值、均值与变化范围均比反演前的大,这符合反演后滑坡稳定性较差的状况. 从图16可知,滑面附近的位移变异系数较其他深度部位的大,说明抗剪强度参数的变化对滑面的位移影响相对较大. 对于A剖面,更新后全部深度范围的变异系数比更新前小;对于B剖面,0~27 m深度处的变异系数比更新前大,大于27 m深度处的变异系数比更新前小. 这由于B剖面位于滑坡前缘,该部位受库水波动的作用明显,位移变形容易出现极端的情况. 比较A、B剖面的位移可知,A剖面的位移最值与均值大于B剖面,说明滑坡在A剖面处变形更明显,位移变化特征符合白水河滑坡的变形规律.
图 14
图 14 反演前、后A剖面处的位移
Fig.14 Displacement of A section before and after data inversion
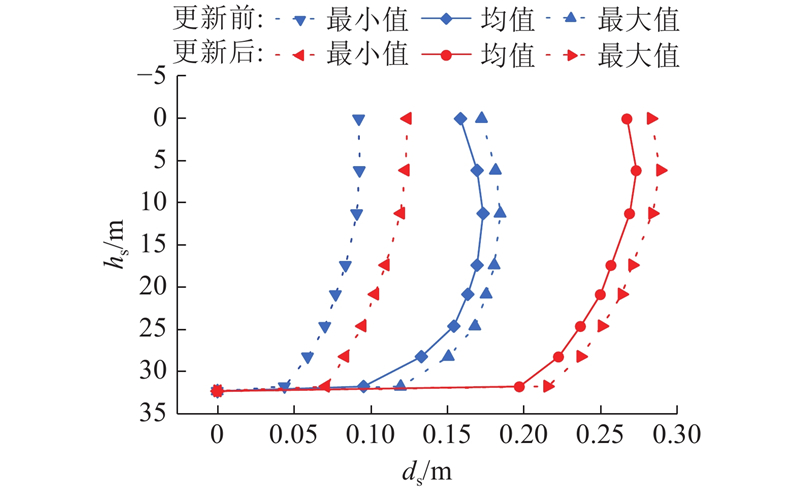
图 15
图 15 反演前、后B剖面处的位移
Fig.15 Displacement of B section before and after data inversion
图 16
图 16 反演前、后A、B剖面处位移的变异系数
Fig.16 Displacement coefficient of variation of A and B section before and after data inversion
5. 结 论
(1)参数反演结果表明,反演前建立的平稳随机场经过更新后变为非平稳随机场,尤其是反演后的摩擦角均值变化趋势更明显. 结合滑带的形成环境分析可知,非平稳随机场的模拟相对适合于滑带. 对于条块滑面参数的标准差,反演后多数条块的抗剪强度参数标准差减小,变化幅度受到影响.
(2)对于白水河滑坡3-3′剖面,全局敏感性分析表明,各条块滑面的抗剪强度参数变量对滑坡稳定系数的影响不可忽略,变量对滑坡稳定系数影响较大的区域分布在滑坡前缘和滑坡后缘道路附近,滑坡防治工程应优选这些影响较大的区域.
(3)经过贝叶斯反演后,抗剪强度参数的不确定性减小,滑坡的位移变形增大,滑坡前缘坡表的位移波动变化较大,能够为滑坡分析与防治提供较危险的工况. 与传统的确定性分析相比,本文既考虑了滑带抗剪强度参数的空间变异性,也考虑了滑坡的后验稳定性,可以获得滑坡变形的极端情况及位移主要分布区间.
参考文献
Research on water–rock (soil) interaction by dynamic tracing method for Huangtupo landslide, Three Gorges Reservoir, PR China
[J].DOI:10.1007/s12665-015-4068-5 [本文引用: 1]
Microstructural study of a natural slip zone: quantification and deformation history
[J].
Effects of the particle-size distribution on the micro and macro behavior of soils: fractal dimension as an indicator of the spatial variability of a slip zone in a landslide
[J].DOI:10.1007/s10064-017-1028-1 [本文引用: 2]
Quantification of prior knowledge in geotechnical site characterization
[J].
基于位移监测的岩质滑带参数拟合反演研究
[J].
Study on fitting inversion for the parameters of rock slip zone based on displacement monitoring
[J].
反算法中滑坡稳定系数的取值问题
[J].
Selection of landslide stability factor in inverse calculation
[J].
争岗滑坡堆积体滑面强度参数反演分析
[J].
Back analysis of strength parameters of sliding surface of Zhenggang landslide deposit body
[J].
库水升降条件下考虑饱和渗透系数空间变异性的白水河滑坡渗流变形分析
[J].
Seepage and deformation analysis of Baishuihe landslide considering spatial variability of saturated hydraulic conductivity under reservoir water level fluctuation
[J].
Bayesian perspective on geotechnical variability and site characterization
[J].
Back analysis of slope failure with Markov chain Monte Carlo simulation
[J].
Probabilistic back analysis of slope failure-a case study in Taiwan
[J].
Optimization of site investigation program for improved statistical characterization of geotechnical property based on random field theory
[J].DOI:10.1007/s10064-016-0869-3 [本文引用: 1]
基于多源试验数据空间变异土体参数概率反演及边坡可靠度更新
[J].
Probabilistic back analysis of spatially varying soil properties and reliability updating of slopes with multiple sources of test data
[J].
Using conditioned random field to characterize the variability of geologic profiles
[J].DOI:10.1061/(ASCE)GT.1943-5606.0001428
岩土参数转换模型的贝叶斯校准方法
[J].
Transformation model for geotechnical parameters calibration based on Bayesian approach
[J].
Bayesian updating with structural reliability methods
[J].DOI:10.1061/(ASCE)EM.1943-7889.0000839 [本文引用: 2]
MCMC algorithms for subset simulation
[J].
Probabilistic assessment of slope stability that considers the spatial variability of soil properties
[J].
Distribution-based sensitivity analysis from a generic input-output sample
[J].
A simple and efficient method for global sensitivity analysis based on cumulative distribution functions
[J].
库水下降作用下滑坡动态变形机理分析--以三峡库区白水河滑坡为例
[J].
Study on dynamic deformation mechanism of landslide in drawdown of reservoir water level: take Baishuihe landslide in three gorges reservoir area for example
[J].
三峡库区滑带土抗剪强度参数的统计规律研究
[J].
Study on statistical rule of shear strength parameters of soil in landslide zone in Three Gorges Reservoir Area
[J].
一种新的边坡稳定性因素敏感性分析方法: 可靠度分析方法
[J].
A new sensitivity analysis approach slope stability: reliability ananlysis method
[J].