在对各类结构模型进行荷载试验时,研究者关注的重点问题包括变形特征和变形能力.
分解梁剪切变形的传统方法是测量目标梁段长度范围对角线的长度变化,据此推算剪切变形. 该传统方法的缺陷是对角线的长度变化包含了弯曲变形的影响. Hiraishi[1]在研究弯曲型剪力墙恢复力模型时,提出采用实测剪力墙顶部两侧水平位移和竖向位移来推算剪切变形,结果发现必须要引入给定弯矩分布下的转角分布. 剪切变形是在总变形中扣除依据假定模型计算的弯曲变形后获得的,通过试验获得的剪切变形与弯曲变形不独立,损害了实测剪切变形的客观性.
Debernardi等[13]通过试验方法分解混凝土梁局部区段的弯曲变形和剪切变形. 在梁的局部区段布置一个矩形框,测量矩形框4条边变形量和角节点的竖向位移. 通过上、下2条边的变形量推算弯曲变形,再从总变形中减去弯曲变形获得剪切变形.
上述获得剪切变形的方法存在以下弊端. 1)在总变形中减去弯曲变形以获得剪切变形,导致剪切变形、弯曲变形和总变形之间互不独立,试验层面上无法直接验证分解方法的正确性. 2)采用实测对角线的变形推算剪切变形,忽略了弯曲变形实际上会引起对角线长度变化的事实. 3)取剪切变形为上述2种方法获得的剪切变形的平均值,使得剪切变形的物理意义变得模糊不清,如Hansapinyo等[11]采用的方法.
鉴于以上情况,本文寻求能够客观、独立、准确分解梁的弯曲变形、剪切变形的试验方法.
1. 梁变形分解试验方法推导
推导针对等截面直梁,认为梁的材料变形只包含弯曲变形和剪切变形. 任意截面的挠度由梁的弯曲变形、剪切变形和该截面的刚体转动构成.
1.1. 弯曲变形引起的挠度
等截面直梁受弯后在截面上会形成明确的拉应力区和压应力区. 对于简支梁而言,梁上部纵向纤维会缩短,梁下部纵向纤维会伸长,对于给定的梁和荷载分布,梁的弯曲挠度是唯一确定的. 由弯曲变形构成的挠度可以用最大弯矩截面至支座之间梁段上部纵向纤维的压缩变形量和下部纵向纤维的拉伸变形量进行表征.
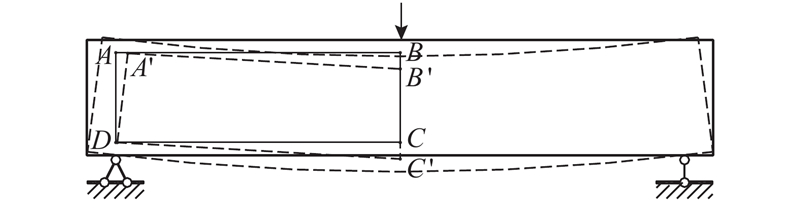
为了便于推导,研究对称加载的情况. 如图1所示,简支梁承担跨度中点集中荷载,在荷载弯矩作用下梁发生挠曲变形. 在剪跨长度范围内,选定梁体上部纵向纤维AB和下部纵向纤维DC,则纤维AB的缩短量和纤维DC的伸长量与荷载点截面的弯曲挠度存在确定的关联性. 为此,作出如下假定. 1)所有变形量均为小变形量. 2)弯曲变形后,纵向纤维AB的缩短量可以由A、B两点之间实测的相对位移
图 1
图 1 对称加载条件下梁的弯曲变形特征
Fig.1 Flexural deformation characteristics of beam under symmetrical loading condition
在弯曲变形后,
图 2
先假定变形后线段
由于
可知
在图2中,过
在
过
由三角形
借助图2中
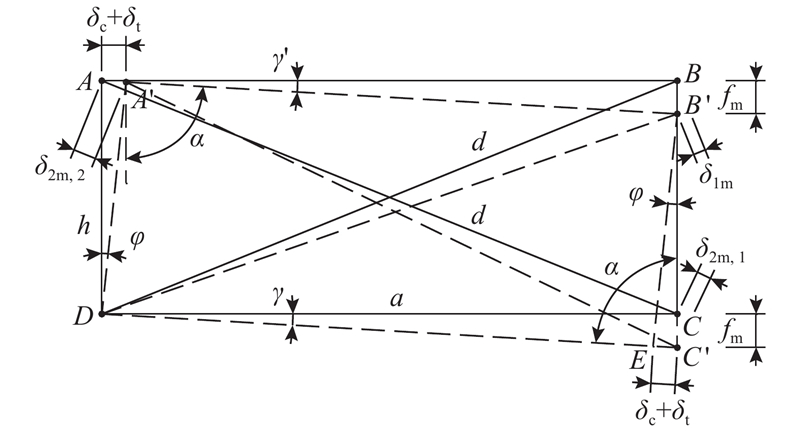
从图2可见,弯曲变形会引起对角线长度的变化. 对角线DB由弯曲变形引起的缩短量(以缩短为正)为
弯曲变形后对角线AC的变形量
由于存在弯曲挠度
当A点到
因此,对角线AC的伸长量为
1.2. 剪切变形引起的挠度
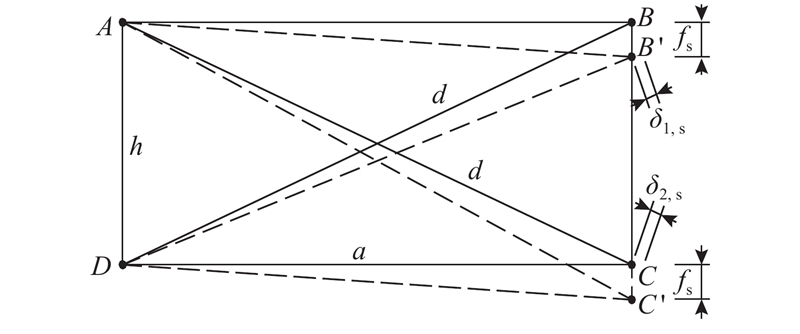
剪切变形的特征是矩形ABCD各条边的长度不发生改变,但ABCD对角线的长度会发生改变,其中对角线BD会缩短,对角线AC会伸长. 理论上讲,2条对角线的增长量和缩短量绝对值相等,即
图 3
实测对角线BD的缩短量
剪切变形引起的对角线BD实测缩短量为
剪切变形引起的对角线AC实测伸长量为
取
1.3. 荷载点截面转动引起的挠度 $ {{f}}_{{\theta }} $
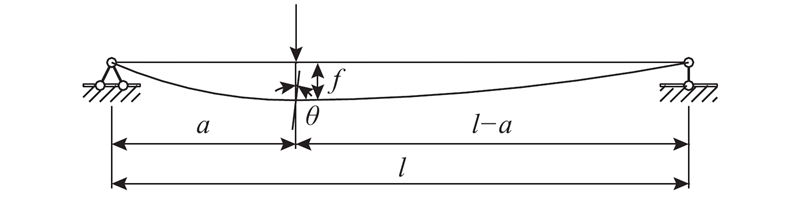
利用前述试验方法获得的弯曲变形和剪切变形是构件的材料变形. 在对称加载条件下,弯曲变形与剪切变形之和构成跨度中点的挠度;在非对称加载条件下,最大挠度截面会发生转动,需要考虑截面转动对挠度的影响,如图4所示. 截面实测转角
图 4
对于弹性梁而言,式(11)是很容易验证的. 以图4中承担集中荷载的简支梁为例,荷载点的理论计算挠度为
式中:
采用广义单位力法,可以获得荷载点截面转角为
若取
在式(12a)、(12b)中剪力
式(12d)验证了式(11)的正确性.
通过测量剪跨范围上部和下部2条纵向纤维的变形、上、下纵向纤维端点之间对角线的长度变化以及目标截面转角,可以获得
独立获得的挠度推算值可以与荷载点的实测挠度进行比较,以验证本文方法的有效性.
2. 验证性试验设计
为了验证提出的试验方法分解梁弯曲变形和剪切变形的有效性,设计4根混凝土简支梁的剪切试验. 表1列出各试件的基本参数. 表中,d为箍筋直径,s为箍筋间距,a为剪跨,fyv为箍筋屈服强度,fs为箍筋抗拉强度,Fu为实测极限剪力. 试验区段编号中字母A表示试验区段;试件用箍筋和抗弯纵筋均为HRB400级钢筋,混凝土强度设计等级为C30. 试验序列包含2个水平的剪跨比取值,分别约为1.0和2.0. 在每个剪跨比取值水平下,箍筋直径分为6 mm和8 mm两个水平,抗弯纵筋用量相应改变,以满足发生剪切破坏的设计要求.
表 1 钢筋混凝土梁试件的参数
Tab.1
| 试验区段 | 截面尺寸 | d /mm | s /mm | a /mm | fyv /MPa | fs /MPa | Fu /kN | 破坏形态 |
| SP-1A | 260 mm×500 mm | 6 | 100 | 500 | 536.4 | 664.9 | 544.8 | 剪切破坏 |
| SP-2A | 260 mm×500 mm | 8 | 100 | 500 | 474.8 | 634.0 | 690.0 | 弯剪破坏 |
| SP-3A | 260 mm×500 mm | 6 | 100 | 900 | 536.4 | 664.9 | 540.0 | 剪切破坏 |
| SP-4A | 260 mm×500 mm | 8 | 100 | 900 | 474.8 | 634.0 | 540.0 | 剪切破坏 |
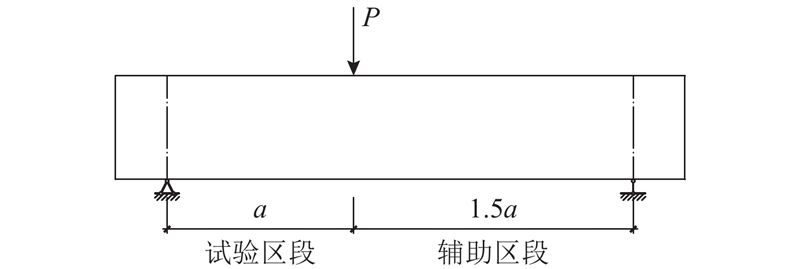
试件采用单点加载方式,如图5所示. 图中,P为荷载. 以荷载点为参考,梁跨度全长划分为试验区段和辅助区段2部分,其中辅助区段的长度为试验区段长度的1.5倍,以确保剪切破坏发生在试验区段.
图 5
在试验过程中,数据采集系统获得的荷载和对应荷载点的挠度在监控屏幕上实时显示,作为加载控制的依据. 在曲线稳定上升段,采用荷载控制;刚度明显退化后改为变形控制.
3. 变形与挠度测试方法
3.1. 百分表和倾角仪组成的测试系统
在试件支座处和荷载点处布置百分表,可以分别测量支座沉降和荷载点挠度,扣除支座沉降后可以获得荷载点的真实挠度. 在试验区段的一个侧面,分别在上缘和下缘布置百分表,可以获得上缘纵向纤维的压缩量和下缘纵向纤维的伸长量. 在上、下纵向纤维端点对角线方向交叉布置百分表,可以获得对角线的长度变化. 荷载点截面转角通过安装在截面高度中点的电子倾角仪测量,如图6所示.
图 6
图 6 百分表和倾角仪组成的测试系统
Fig.6 Measuring system composed of LVDTs and electric inclinometer
3.2. 基于DIC技术的测试系统
数字图像相关(digital image correlation,DIC)技术能够高精度测试目标位移,完成应变测试. 当需要掌握应变场整体变形情况时,DIC技术具有远胜于百分表测试技术的优势.
采用DIC技术时,需要在测试区域布置散斑点. 在该试验序列中,散斑点布置在与百分表测试系统相对的另一侧面,散斑点布置的长度范围超过支座中心线及荷载线外30~50 mm. DIC方法需要利用高清晰度的数码照片,该试验采用Gazelle GZL-CL-41C6M工业相机实时监测试件的变形过程. 分辨率预设为2 048×2 048像素,以拍摄高质量的图像. 2个与该工业相机配套提供的LED灯置于试件截面高度中部,保持水平状态为试验区段构件侧面均衡提供充足的照明,确保相机可以有效地识别散斑点,如图7所示. 采用商业软件Vic-Snap8分析构件表面位移场,获取与试验区段另一侧面上、下纵向纤维对应位置的长度变形和对角线对应位置的长度变化.
图 7
DIC技术按下述方法获得荷载点截面的转角.
1)沿荷载点截面高度设置若干个观测点,观测点的分布高度取为与百分表方法中上、下纵向纤维端点距离.
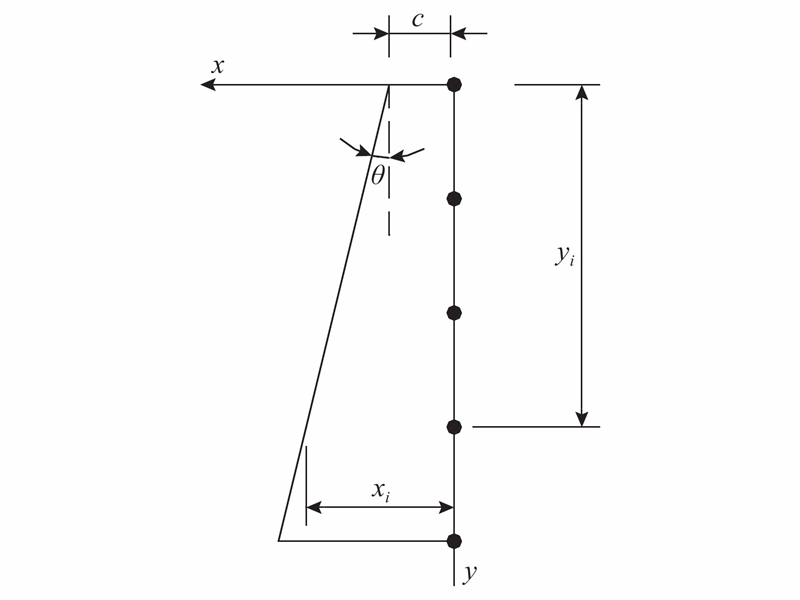
2)在平截面假定条件下,不同高度处的观测点移位后的位置处于同一条直线上,该直线的偏转角为截面转角. 参考图8可知,该直线方程可以表达为
图 8
3)利用配套分析软件Vic-Snap8,获取各级荷载下各观测点
式中:n为观测点数.
4)荷载点截面转角按下式计算:
4. 挠度推算值与实测挠度的比较
按顺序完成4个混凝土简支梁的荷载试验,除了试验段SP-2A外,其余均发生剪切破坏. 试验段SP-2A几乎同时发生弯曲破坏和剪切破坏,弯曲裂缝和斜裂缝都有明显开展,其中荷载点截面处弯曲裂缝宽度达到0.85 mm,剪切斜裂缝宽度达到0.8 mm.
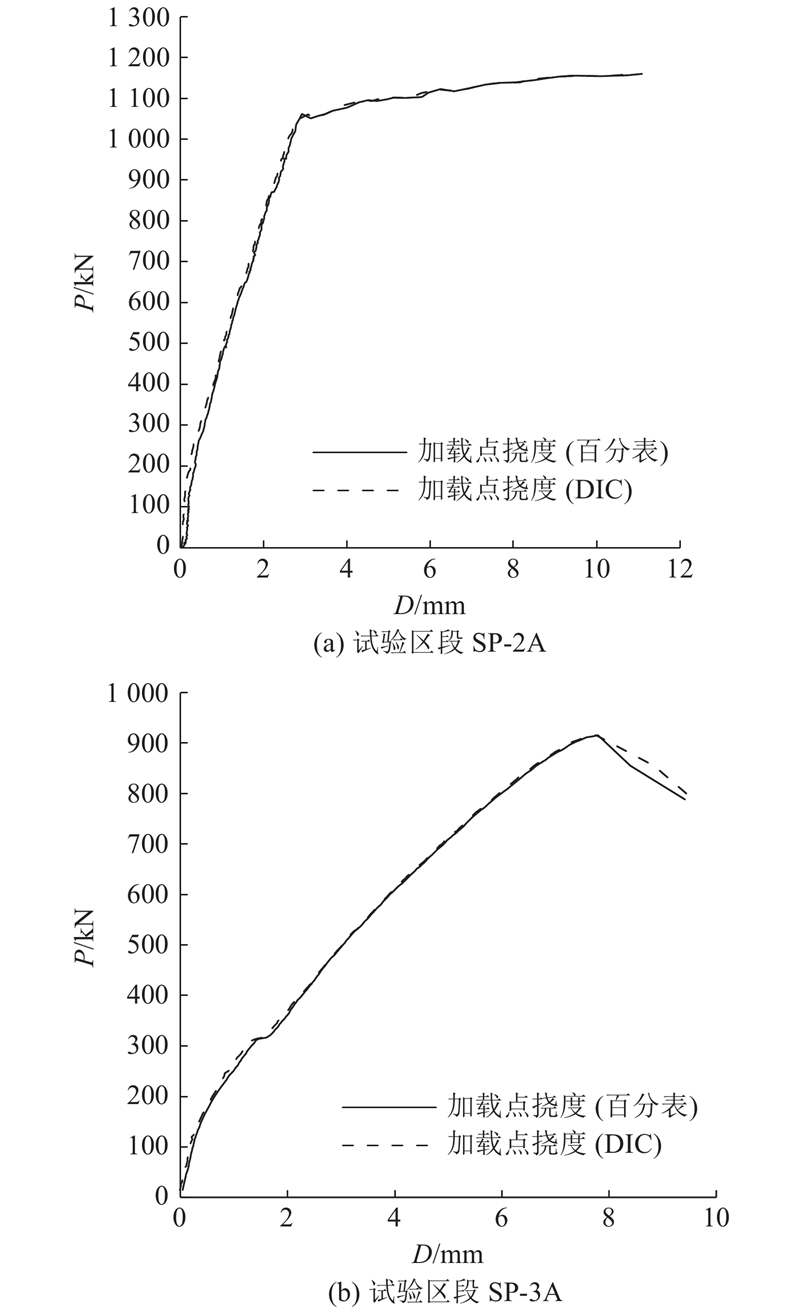
图 9
图 9 基于百分表和DIC的实测荷载-挠度曲线比较
Fig.9 Comparison of measured load-deflection curves from LVDTs and DIC approaches
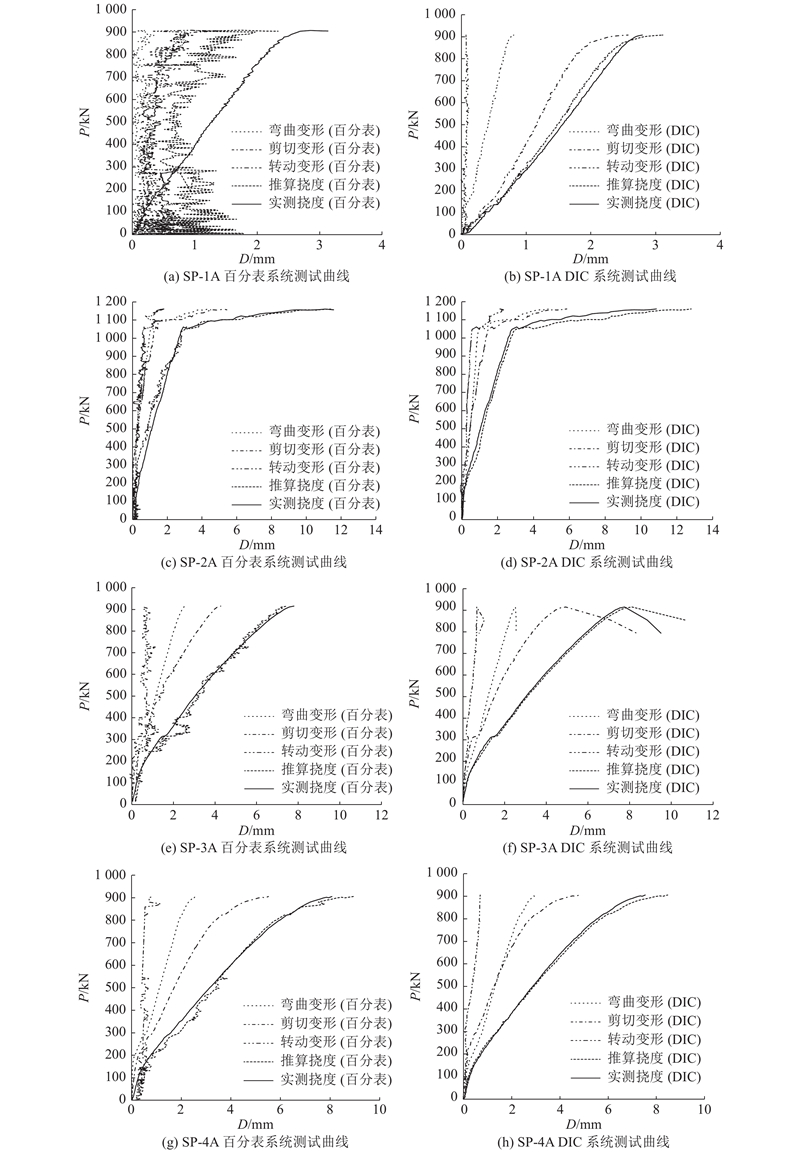
图 10
图 10 各试件推算挠度与实测挠度比较
Fig.10 Comparison between estimated deflection and measured deflection of each specimen
5. 结果讨论
如图10所示的荷载点推算挠度曲线与实测挠度曲线吻合良好,但以下问题值得讨论.
1)实测数据获得弯曲变形时的第2)条假定规定,梁段上部、下部纵向纤维的纵向变形由纤维端点的实测相对位移代替,该假定会随着剪跨比的增大而逐渐偏离. 结合本文的试验结果可知,至少在剪跨比不大于2的条件下,该假定是合理的.
2)实测数据获得弯曲变形时的第4)条假定规定,荷载点截面高度保持不变,该规定在对称荷载条件下的跨度中点截面是真实的. 在非对称荷载条件下,最大挠度截面通常不会出现斜裂缝,因此该规定是真实的. 当目标截面不是最大挠度截面,且存在发育的斜裂缝穿过该截面时,本条假定不成立.
3)在通过实测数据推算各分解挠度的过程中,未对材料种类、本构关系、荷载形式和受力阶段等作出限制,因此本文的变形分解方法适用于各类材料等截面直梁的变形分解.
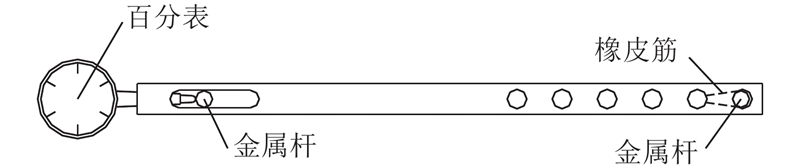
4)当采用百分表测量纵向纤维长度变化和纵向纤维端点对角线长度变化时,测量装置安装质量至关重要. SP-1A的百分表系统几乎未能获得有用数据,如图10(a)所示. 如图11所示为百分表通过导杆安装的情形,每根导杆安装在后植于混凝土内的2根金属杆上,其中一端通过橡皮筋的张力使得安装孔壁与金属杆侧面接触;另一端为条形孔,当试件变形时导杆相对于金属杆滑动,固定于导杆端头的百分表能够测出2根金属杆之间的相对变形,这代表了纵向纤维的长度变化或对角线的长度变化. 如果2根金属杆不平行,可能导致条形孔壁与金属杆卡死,另一端橡皮筋约束力不足以使导杆孔壁与金属杆保持接触状态,使得百分表获得的变形量不真实. 为了避免这种缺陷,应提高弹性约束的刚度.
图 11
6. 结 语
在等截面直梁的弯曲变形可以由受拉一侧和受压一侧纵向纤维变形量予以表征的假定条件下,采用几何方法推导了利用目标截面至相邻支座间梁段范围上部、下部纵向纤维长度变化获得弯曲变形的计算方法. 在考虑梁上部、下部纵向纤维变形影响后,利用上部、下部纵向纤维端点间2条对角线的变形实测值,推导了剪切变形的计算方法. 合并考虑目标截面实测转角对挠度的影响后,获得由弯曲变形、剪切变形和截面刚体转动影响3个分量构成的推算挠度. 通过4根钢筋混凝土梁的荷载试验,实测了荷载点的荷载-挠度曲线,根据提出的方法获得各级荷载水平下荷载点截面的推算挠度,推算挠度曲线与实测荷载-挠度曲线吻合良好. 鉴于推算挠度是在试验区段弯曲变形、剪切变形和目标截面转动引起挠度的基础上独立获得的,且推导过程未引入材料种类、本构关系、荷载形式和受力阶段等限制条件,良好的吻合性证明了该变形分解方法的可靠性.
参考文献
Evaluation of shear and flexural deformations of flexural type shear walls
[J].DOI:10.5459/bnzsee.17.2.135-144 [本文引用: 2]
Shear ductility of reinforced lightweight concrete beams of normal strength and high strength concrete
[J].DOI:10.1016/0958-9465(94)00029-X [本文引用: 1]
Shear characteristics of high-strength concrete deep beams without shear reinforcements
[J].DOI:10.1016/S0141-0296(03)00110-X [本文引用: 1]
HRB500级钢筋配箍的混凝土梁受剪性能试验研究
[J].
Experimental study on the shear failure of reinforced concrete beams with grade HRB500 steel stirrups
[J].
高强钢筋活性粉末混凝土简支梁受剪性能试验研究
[J].DOI:10.3963/j.issn.1671-4431.2013.08.022
Experimental study on shear behavior of high strength reinforced reactive poweder concrete beam
[J].DOI:10.3963/j.issn.1671-4431.2013.08.022
集中荷载作用下预应力钢骨超高强混凝土梁受剪性能试验研究
[J].
Experimental study on shear performance of prestressed steel ultra-high reinforced concrete beam under concentrated load
[J].
Shear strengthening of fire-damaged reinforced concrete beams using bolted-side plating
[J].DOI:10.1016/j.proeng.2017.11.065
活性粉末混凝土梁抗剪性能试验研究
[J].
Experimental study on shear performance of reactive powder concrete beam
[J].
Shear performance of bolted side-plated reinforced concrete beams
[J].DOI:10.1016/j.engstruct.2017.04.043
内嵌FRP筋加固混凝土梁的抗剪性能研究
[J].
Study on shear behavior of RC beams strengthened with NSM FRP bars
[J].
Proposed model of shear deformation of reinforced concrete beam after diagonal cracking
[J].
Experimental study on high-strength concrete beams failing in shear
[J].DOI:10.1016/j.engstruct.2005.04.010 [本文引用: 2]
Shear deformation in reinforced concrete beams with thin web
[J].DOI:10.1680/macr.2006.58.3.157 [本文引用: 1]