随着国家倡导大数据公开政策的逐步落地以及无人驾驶技术的逐步成熟,使未来出行前发布出行计划以及获取出行计划数据成为可能. 不同于以往利用历史数据进行行程时间的预测,利用用户实时出行计划数据,提前获得路网中不同起讫点之间各路段将要承载的交通量,能让求得的行程时间更具时效性和准确性.
准确的行程时间计算值对整个路网至关重要,其中,计算行程时间的2个重要方法包括运用神经网络进行预测和运用路阻函数进行计算. 在神经网络预测方面,Zhao等[1]提出利用2D-ODC-LSTM网络的时空相关性进行建模. Duan等[2]研究用于行程时间预测的长短期记忆(long short-term memory, LSTM)神经网络模型. Siripanpornchana等[3]基于不同的神经网络算法对车辆的行程时间预测做了大量的研究分析. Li 等[4]提出新的数据驱动的车速预测方法,基于长期传播的短期记忆(BP-LSTM)算法,可对计划路线上的长期单个车速进行预测. Ma等[5]提出新颖的卷积LSTM神经网络架构,用于多车道短期交通量预测. Xu等[6-7]基于海量用户出行计划数据,构建交通流时间序列动态模型对道路上未来的交通流量进行预测. 在路阻函数计算方面,专家和学者们更偏向于改进路阻函数模型. Davidson[8]基于排队论方法提出具有渐进性的阻抗函数. Spiess[9]通过改进阻抗函数模型,解决模型中待定参数
本文基于LSTM神经网络进行路阻函数模型的改进研究,对经典的BPR函数进行改进,引入LSTM神经网络预测改进函数中待定系数的正负,以获得更加准确的行程时间计算结果.
1. 经典BPR函数模型改进
基于LSTM的路阻函数模型的改进过程包括1)改进经典BPR函数;2)重新标定待定系数
1.1. 经典BPR函数模型
1964年,美国联邦公路局调查了大量的路段,并对获取的数据进行回归分析,得到BPR函数模型. 经典BPR阻抗函数的表达式为
式中:
1.2. BPR函数模型改进
经典BPR函数模型具有简单易行的优点,也存在不足之处. 1)该函数通过回归分析美国大量低饱和流量的道路得到,因此当城市交通状况处在饱和或过饱和状态时,其拟合精度较差. 例如当实时的交通量大于设计交通量时,道路开始拥堵,但是随着实时交通量的逐渐增加,车辆的行程车速下降的速度却越来越不符合实际状况. 2)该函数为单调增函数,不能反映出随着速度的增大,交通量先逐渐增加后逐渐减少的状况. 3)以往建立的阻抗函数,或将
式中:
其中
与以往的计算行程时间的方法相比,基于LSTM神经网络改进后的BPR函数具有以下特点. 1)保留了BPR函数结构简单的优点,所需的输入参数量少. 2)引入
2. 参数标定
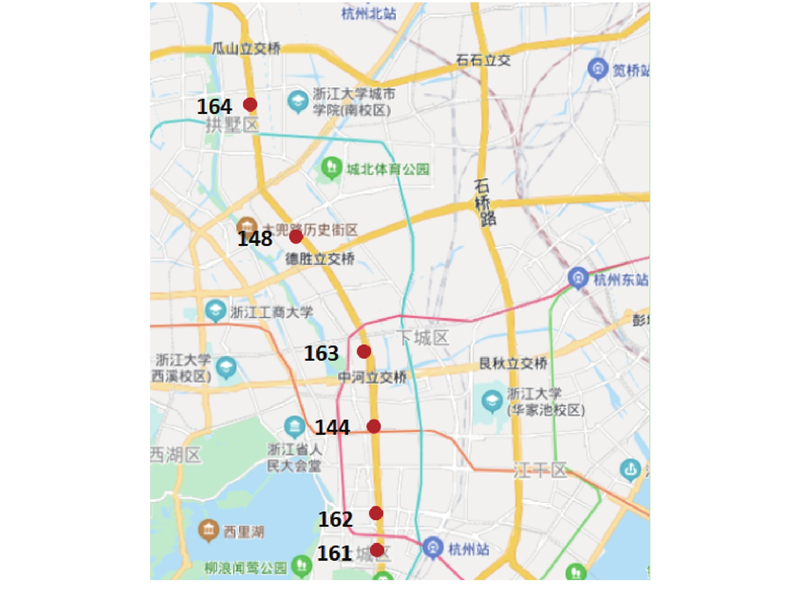
选取2015年8月25日到9月21日,杭州市上塘高架至中河高架路段上6个远程交通微波检测器连续4周采集的交通数据进行参数标定,微波检测器的位置如图1所示,其编号从北到南依次为164、148、163、144、162、161.
图 1
数据集包括微波检测器检测路段的流量、速度、车道占有率、时间、车道编号以及检测器编号数据。选取采集点7:00—22:00的数据进行参数标定,包含高峰时间段和平峰时间段,每个点位448组数据,6个采集点共计2 688组数据. 参数标定以及验证所需的数据包括平峰时段的交通量和高峰时段的交通量,部分时间段的部分路段存在拥堵现象,但是不存在大范围或长时间的拥堵状况,也不存在因拥堵而产生的车辆停滞情况.
2.1. $\alpha $
由式(2)可以看出,当通过该路段的交通量
式中:
通过筛选数据
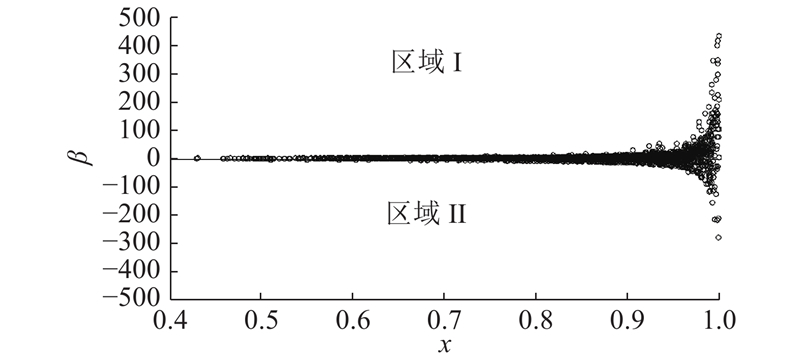
2.2. $\;\beta $
两边取对数
求得
式中:
图 2
图 2
引入
Fig.2
Scatter distribution of value
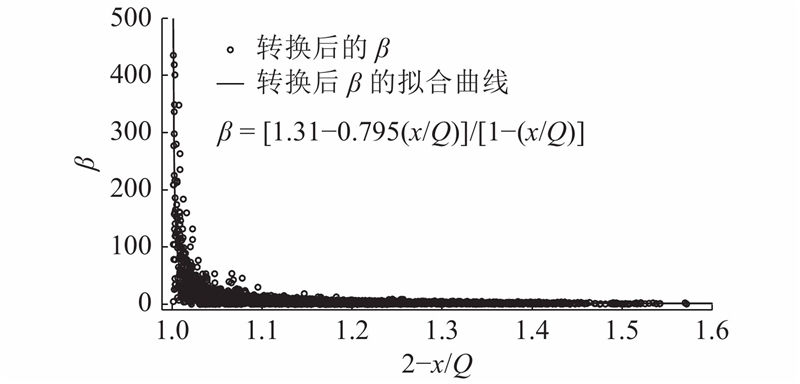
图 3
用确定系数R-square判断模型拟合结果的优劣,系数R-square的取值为[0,1.0]. 拟合结果越接近1.0,说明模型的拟合精度越高,计算公式为
式中:
此时拟合得出的
3. LSTM神经网络的引入
LSTM神经网络是特殊的循环神经网络(recursive neural network,RNN),能够较好地解决梯度消失问题,被专家、学者普遍应用于行程时间预测. LSTM神经网络在预测路阻大小这种较长时间依赖性的时间序列问题上具有较大优势.
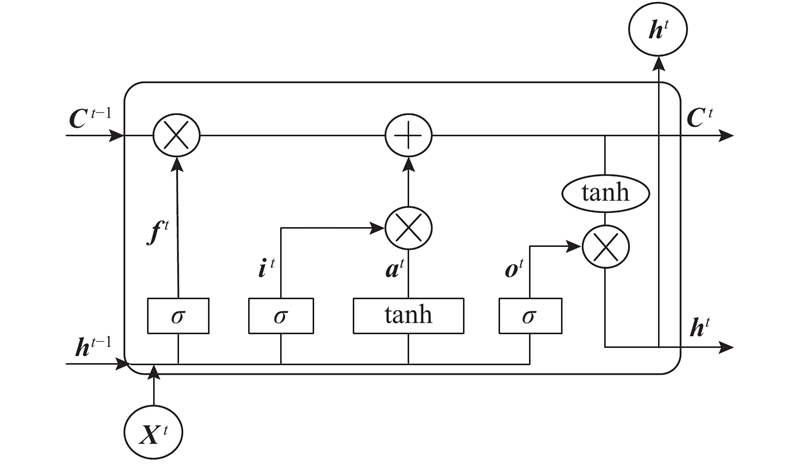
3.1. LSTM单个模型结构
如图4所示为LSTM神经网络的单个模型结构. 图中,上一时间段的单元状态
图 4
输入门:
当前输入单元的状态:
状态单元:
输出门:
LSTM最终结果:
激活函数
激活函数
式中:
3.2. 构建LSTM神经网络结构与训练
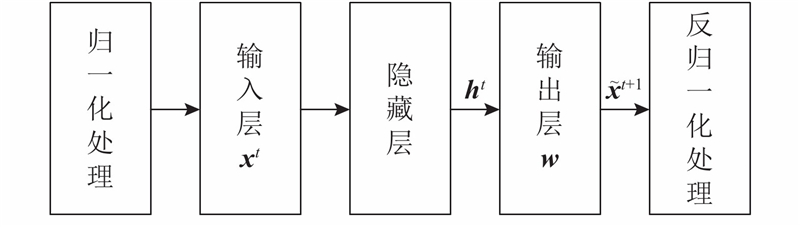
本文构建的LSTM神经网络如图5所示. 实验发现,
图 5
式中:w为输出层矩阵.
LSTM神经网络的神经元个数同样影响着神经网络预测结果的准确性. 神经元较少影响网络的联想能力,神经元较多不但会降低运算速度,还会使计算结果发散或者陷入局部最小值. 因此合理的神经元数量对于LSTM神经网络模型至关重要. 实验发现,在本研究中当神经元的数量为10时,计算的结果较好.
LSTM神经网络的损失函数为
式中:
选取远程交通微波检测器采集28天数据中的前90%的数据用于训练,后10%的数据用于LSTM神经网络建模合理性验证. 拟合准确度计算公式为
式中:
3.3. 基于LSTM神经网络改进的路阻函数模型
根据调查已知该路段两车道的通行能力为2 500 pcu/h,自由流速度为80 km/h,结合标定过程得到行程时间
4. 模型的计算与验证
为了检验改进的BPR函数具有较好的拟合精度,选取2015年9月22日到2015年9月28日杭州市上塘高架至中河高架路段上6个远程交通微波检测器采集的7:00—22:00共672 h的交通数据进行计算与验证. 将前2周和前1个小时的流量和
图 6
图 6
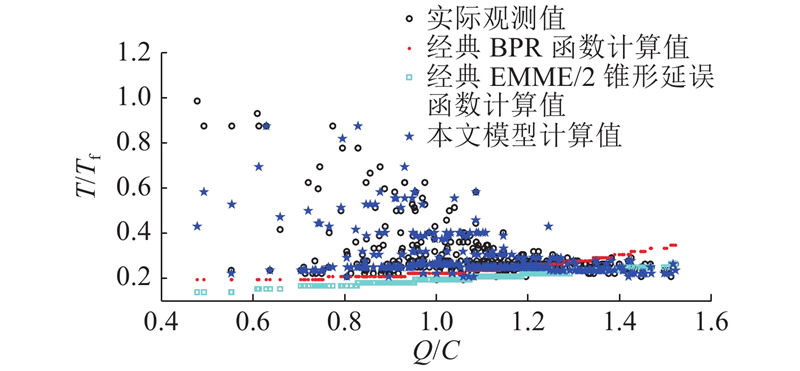
本文模型与经典路阻模型的
Fig.6
Comparison chart of value
图 7
图 7
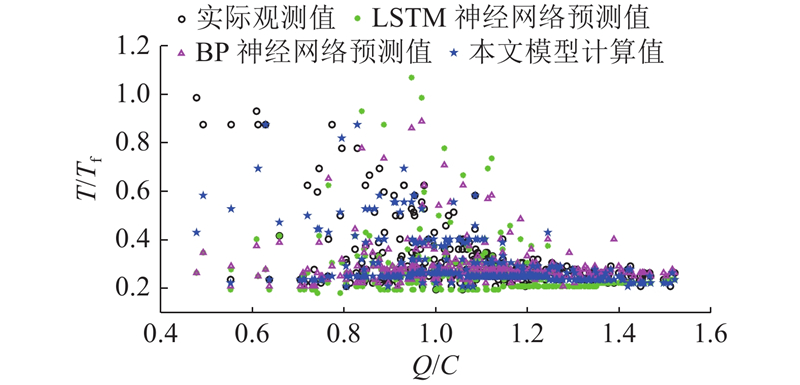
本文模型与神经网络的
Fig.7
Comparison chart of value
图 8
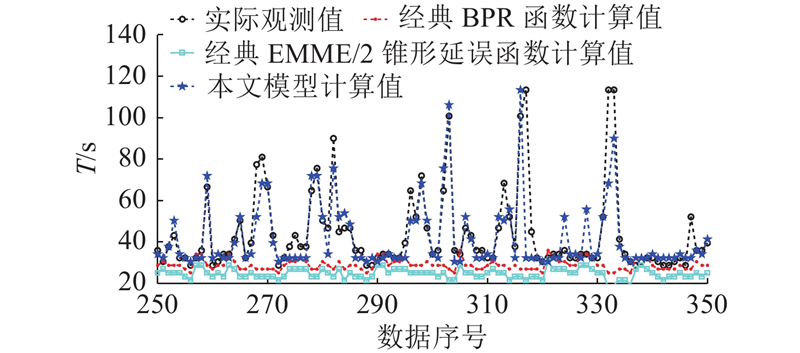
图 8 本文模型与经典路阻模型的行程时间计算结果对比
Fig.8 Comparison of travel time calculation results between improved model and classic road resistance model
图 9
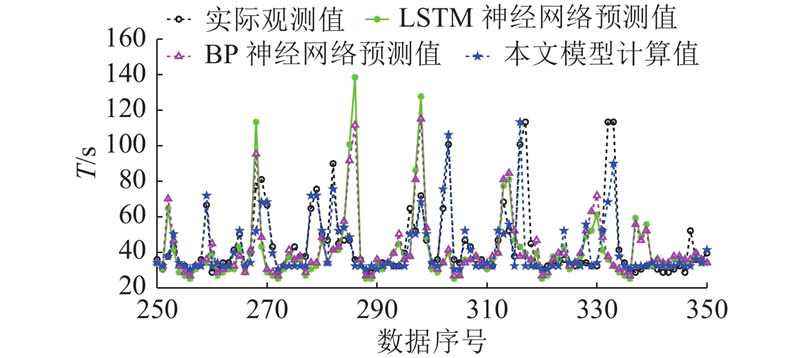
图 9 本文模型与神经网络的行程时间计算结果对比
Fig.9 Comparison of travel time calculation results between improved model and neural network
误差分析如表1所示,误差的计算公式如下. 平均绝对误差为
表 1 本文模型与经典模型拟合结果误差对比
Tab.1
| 模型 | MAE | MAPE | RMSE |
| 经典BPR | 6.34 | 0.22 | 11.06 |
| 经典EMME/2 锥形延误函数 | 7.78 | 0.29 | 12.31 |
| BP神经网络 | 18.29 | 0.69 | 136.44 |
| LSTM神经网络 | 5.87 | 0.21 | 10.86 |
| 本文方法 | 2.54 | 0.09 | 4.91 |
平均绝对百分比误差为
平均均方根误差为
式中:
由表1可以看出,本文模型计算的结果具有更小的误差以及更高的拟合精度,说明该模型能较准确地计算调查区域内路段的行程时间.
5. 结 语
针对经典BPR函数存在的诸多问题,建立基于LSTM神经网络改进的路阻函数模型. 结合实际采集数据,将改进模型计算结果分别与2种经典路阻函数模型、2种经典的神经网络预测结果进行对比. 结果表明:1)利用改进后的模型能够较好地解决经典路阻函数模型单调递增、求解结果值偏小的问题;2)利用改进后的模型能够较好地解决经典的神经网络在预测行程时间时拟合结果偏大且较分散的问题. 利用本文模型能够较精确地计算调查区域内路段的行程时间.
由于数据获取难度较大,本研究仅结合杭州市上塘高架至中河高架部分快速路路段,未来将考虑研究不同等级的道路交通阻抗,以扩大本文模型的适用范围.
参考文献
LSTM network: a deep learning approach for short-term traffic forecast
[J].DOI:10.1049/iet-its.2016.0208 [本文引用: 1]
Investigating long-term vehicle speed prediction based on BP-LSTM algorithms
[J].DOI:10.1049/iet-its.2018.5593 [本文引用: 1]
Multi-lane short-term traffic forecasting with convolutional LSTM network
[J].
The theoretical basis of a flow-travel time relationship for use in transportation planning
[J].
Conical volume-delay functions
[J].DOI:10.1287/trsc.24.2.153 [本文引用: 1]
交通网络费用函数的标定与分析
[J].DOI:10.3969/j.issn.1009-6744.2003.04.010 [本文引用: 1]
Traffic network costs analysis and validation
[J].DOI:10.3969/j.issn.1009-6744.2003.04.010 [本文引用: 1]
路阻函数关系式推导及其拟合分析研究
[J].DOI:10.3969/j.issn.1002-0268.2006.04.026 [本文引用: 1]
Deduction of link performance function and its regression analysis
[J].DOI:10.3969/j.issn.1002-0268.2006.04.026 [本文引用: 1]
城市混合交通条件下路段阻抗函数的研究
[J].DOI:10.3969/j.issn.1009-6744.2008.01.011 [本文引用: 1]
A link resistance function of urban mixed traffic network
[J].DOI:10.3969/j.issn.1009-6744.2008.01.011 [本文引用: 1]
BPR路阻函数的改进研究
[J].DOI:10.3963/j.issn.1006-2823.2009.03.011 [本文引用: 1]
Improvement study on BPR link performance function
[J].DOI:10.3963/j.issn.1006-2823.2009.03.011 [本文引用: 1]
基于BPR函数的路阻函数研究
[J].DOI:10.3963/j.issn.2095-3844.2013.03.023 [本文引用: 1]
Further study of impedance function based on BPR function
[J].DOI:10.3963/j.issn.2095-3844.2013.03.023 [本文引用: 1]
城市道路路段行程时间计算模型研究
[J].DOI:10.3969/j.issn.1674-0610.2016.03.040 [本文引用: 1]
Research on the calculation models of vehicle travel time on urban road segments
[J].DOI:10.3969/j.issn.1674-0610.2016.03.040 [本文引用: 1]
基于路段与节点的城市道路阻抗函数改进
[J].
Improvement of urban road impedance function based on section impedance and node impedance
[J].
基于模糊神经网络的混合交通流路阻测算模型
[J].
Calculation model of road resistance in mixed traffic flow based on fuzzy neural network
[J].
Development and validation of improved impedance functions for roads with mixed traffic using taxi GPS trajectory data and simulation
[J].