浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(4): 648-657 doi: 10.3785/j.issn.1008-973X.2021.04.006

计算机技术、电信技术

基于GWO-SVM的下肢假肢穿戴者骑行相位识别

高新智,, 刘作军,, 张燕, 陈玲玲

河北工业大学 智能康复装置与检测技术教育部工程研究中心，天津 300130

Bicycle riding phase recognition of lower limb amputees based on GWO-SVM

GAO Xin-zhi,, LIU Zuo-jun,, ZHANG Yan, CHEN Ling-ling

Engineering Research Center of Intelligent Rehabilitation and Detecting Technology, Ministry of Education, Hebei University of Technology, Tianjin 300130, China

通讯作者: 刘作军，男，教授，博导. orcid.org/0000-0001-7671-4665. E-mail： liuzuojun@hebut.edu.cn

收稿日期: 2020-07-2  

基金资助: 国家自然科学基金资助项目（61703135，61773151）；河北省青年自然科学基金资助项目（F2018202279）

Received: 2020-07-2  

Fund supported: 国家自然科学基金资助项目（61703135，61773151）；河北省青年自然科学基金资助项目（F2018202279）

作者简介 About authors

高新智（1993—），男，博士生，从事智能假肢、模式识别的研究.orcid.org/0000-0001-7644-7667.E-mail：982570895@qq.com , E-mail：982570895@qq.com

摘要

针对下肢假肢穿戴者骑行相位识别的问题，提出基于灰狼算法优化的支持向量机(GWO-SVM)分类模型. 建立下肢多源信息系统，采集膝关节、踝关节的加速度信号以及膝关节角度信号. 应用奇异值分解，对采集到的信号进行降噪处理. 在对信号进行降噪处理之后，为了避免单一信号不确定的影响，从数据冗余角度，选取各信号的特征点，开展归一化处理，组成多维特征向量，作为SVM分类模型的输入. 为了能够进一步提高分类精度，加强全局优化能力，利用GWO算法对核参数进行优化. 通过与PSO-SVM分类模型、GA-SVM分类模型对比表明，基于GWO优化的SVM分类模型对骑行相位的识别率为94%，高于其他方法优化的SVM分类模型.

关键词： 下肢假肢 ; 骑行运动 ; 相位识别 ; 灰狼优化(GWO) ; 支持向量机(SVM)

Abstract

An approach based on gray wolf algorithm optimization and support vector machine was proposed aiming at the problem of identifying the riding phases of lower limb prosthetic wearers. A multi-sensor system was constructed for the motion data collection. Then the acceleration signals of the knee joint, ankle joint and the angle signals of the knee joint on the prosthetic side were collected. Singular value noise reduction was used to reduce the noise of the collected signal. Then feature points of each signal were selected and normalized from the perspective of data redundancy. These motion feature point signals formed a multi-dimensional feature vector as the input of SVM classification model, which solved the problem of the uncertain influence of a single signal. The gray wolf algorithm optimized support vector machine kernel parameters, which not only improved the classification accuracy of the recognition, but also enhanced the global optimization ability. The support vector machine model optimized by the gray wolf algorithm has an accuracy rate of 94% for bicycle riding phase recognition, which is higher than the support vector machine model based on particle swarm optimization and the support vector machine model optimized based on genetic optimization algorithm.

Keywords： lower prosthesis ; bicycle riding ; phase recognition ; grey wolf optimization (GWO) ; support vector machine (SVM)

PDF (1222KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高新智, 刘作军, 张燕, 陈玲玲. 基于GWO-SVM的下肢假肢穿戴者骑行相位识别. 浙江大学学报(工学版)[J], 2021, 55(4): 648-657 doi:10.3785/j.issn.1008-973X.2021.04.006

GAO Xin-zhi, LIU Zuo-jun, ZHANG Yan, CHEN Ling-ling. Bicycle riding phase recognition of lower limb amputees based on GWO-SVM. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(4): 648-657 doi:10.3785/j.issn.1008-973X.2021.04.006

近年来，由于车祸、灾害、疾病等原因导致的下肢截者数量不断增加[1-2]. 假肢作为能够帮助截肢者恢复运动的唯一辅具，是截肢者恢复正常运动的重要工具. 从早期的被动型假肢[3-4]、半主动型假肢[5]到现在的智能动力型假肢[6-8]，截肢者对运动时的安全性、流畅性以及运动方式的多元化需求日益增强. 调研表明，骑行运动在截肢者恢复期具有很好的避免残肢端萎缩的效果，对于训练截肢者平衡性的效果更突出，会使截肢者日常出行更便利.

国外关于智能假肢骑行的研究相对较早. Lawson等[9]利用递归最小二乘算法研制1种电动股骨假肢四连杆控制器，达到了使假肢穿戴者更加省力骑行的目的. Kim等[10]利用无模型PID控制器实现了机器人骑行运动，在反馈中增加了脚蹬曲柄速度，使得机器人骑行时更加平衡、稳定，所用的方法对于假肢控制具有很好的借鉴价值.

在智能假肢样机方面，冰岛Ossur公司的仿生磁控膝关节、美国YOBAND公司的3K180型假肢、德国Otto Bock公司的C-LEG假肢[9]在假肢穿戴者骑行的流畅性和稳定性方面均取得了一定的成果.

国内对于下肢假肢的研究主要集中在行走、跑动方面，刘作军等[6, 11]利用隐马尔可夫模型及PSO-SVM分类模型实现对于假肢穿戴者行走、跑动运动的相位识别. 王永雄等[12]通过高斯混合模型结合隐马尔可夫模型，实现了对假肢穿戴者骑行状态及不同路况下行走状态的区分. 虽然国内已经展开了对假肢穿戴者行走、跑动相位及不同运动状态识别的研究，但是未提及假肢穿戴者骑行时的相位识别.

骑行相对于其他运动而言，运动方式有很大的不同. 当假肢穿戴者骑行时，双脚均与脚蹬持续接触，下肢运动频率相较于其他运动方式更快；相较于正常人而言，当假肢侧处于放松区时，若假肢不能与健肢侧协调运动，则会导致健肢脚蹬曲柄支撑假肢向上运动，极大地消耗假肢穿戴者骑行时的体力，且会影响截肢者骑行时的平衡性和安全性.

下肢假肢穿戴者骑行相位识别作为骑行控制的基础，识别准确率在假肢控制方面起到了至关重要的作用. 为了保证对截肢者相位识别的准确率，本文选取膝关节、踝关节加速度信号以及膝关节角度信号组成多维特征向量，作为假肢穿戴者骑行相位识别模型的输入，分别使用支持向量机（support vector machines，SVM）分类模型及BP神经网络分类模型对骑行相位进行识别. 通过对比发现SVM分类模型的识别效果更好，为了进一步提高识别准确率，将灰狼优化算法（grey wolf optimization，GWO）与SVM进行融合，并与粒子群优化算法（particle swarm optimization，PSO）[6]、遗传优化算法（genetic algorithm，GA）[13]优化后的SVM分类模型进行对比. 实验结果表明，灰狼优化算法的优化效果更优.

1. 骑行相位分析

下肢假肢穿戴者骑行运动的循环模式，与行走运动有明显的区别. 行走运动是支撑相和摆动相的交替循环过程. 在支撑相，假肢会与地面接触；在摆动相，假肢脚底会出现与地面不接触的腾空状态. 骑行运动是用力区和放松区的交替循环过程，假肢脚底与脚蹬间持续接触. 相较于行走而言，骑行的周期性更明显，运动频率更高. 假肢穿戴者的骑行相位识别对将来的假肢穿戴者骑行控制研究具有重要的作用.

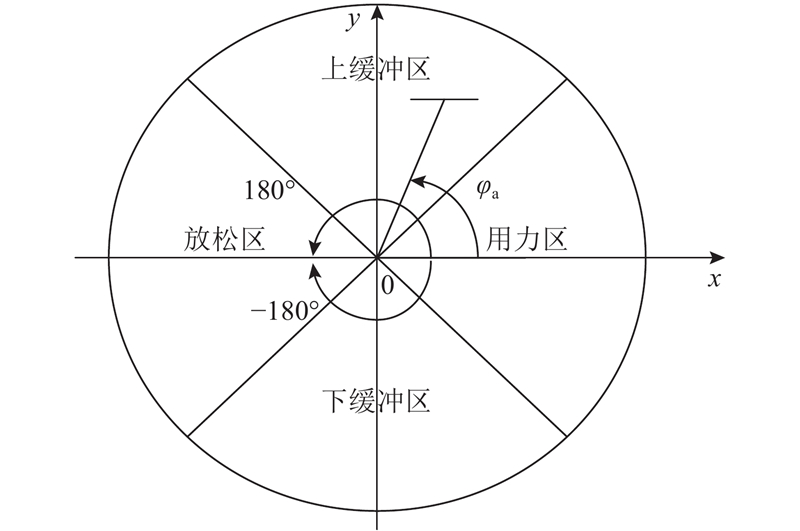
在对假肢穿戴者骑行相位的研究中，根据假肢穿戴者骑行周期中的用力以及能量效率情况，将骑行周期分为4个阶段[9]，如图1所示. 以圆心为原点，过原点的水平面为x轴，其中原点右侧为正半轴，右侧为负半轴，垂直于x轴且过原点为y轴，其中上侧为正半轴，下侧为负半轴. 定义从x轴正半轴开始向y轴正半轴旋转，角度为正，当到达x负半轴时，角度达到最大值180°. 从x轴正半轴开始向y轴负半轴旋转，角度为负，当到达x轴负半轴时角度达到最小为−180°.φa为脚蹬曲柄与水平面所成角度，在用力区（−45°<φa <45°）的能量利用率最高. 在下缓冲区（−135°< φa <−45°）能量利用率不高，所以减少关节用力达到放松区（−180°< φa <−135°，135°< φa <180°）. 在放松区，假肢膝关节不能同步收缩，所以导致脚蹬会支撑假肢向上运动至上缓冲区. 在上缓冲区（45°< φa <135°），逐渐用力，当到达用力区临界时，关节用力达到最大. 在实际应用中，由于 φa无法通过在假肢上安装传感器直接测得，需要在各个相位起始点静态条件下，采集脚蹬角度与各传感器信号的数据样本，利用样本分类方法来判断假肢穿戴者的骑行相位.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   骑行相位划分

Fig.1   Bicycle riding phase partition


2. 数据处理及特征信号提取

2.1. 信号采集

在人体下肢运动的相位识别中，通常采取生物电学信号和生物力学信号2类方法[14-15]. 不同信号对识别系统的稳定性及可靠性会有很大的影响. 生物电学信号能够预测假肢穿戴者的运动意图，但是具有采集困难、人体差异性大的不足[16]，所以采用重复度高、稳定性好的生物力学信号进行假肢穿戴者骑行相位的识别[17-18]. 采集膝关节水平和竖直方向加速度、踝关节水平和竖直方向加速度、膝关节角速度信号，作为相位识别判断的依据.

为了避免给假肢穿戴者带来不便，均采用无线传感器仪器实现对骑行数据的采集. 利用维特智能公司生产的MPU9250陀螺仪无线姿态传感器，放置在假肢膝关节部位，采集膝关节角度信号，如图2（a）所示. 把高轻度的Trigno无线采集器分别放置在膝关节、踝关节部位，采集膝关节、踝关节的水平和竖直方向的加速度信号，如图2（b）所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   加速度、角度测量仪器

Fig.2   Acceleration and angle measuring apparatus


选择3名假肢穿戴者（A1、A2、A3）作为受试者，为了保证假肢穿戴者骑行时的安全，将自行车架在自行车架子上，使假肢穿戴者以40~50 r/min的速度骑行3 min后，开始采集数据. 如图3所示，将MPU9250陀螺仪传感器1放置在假肢膝关节上部，采集大腿姿态信号. 将MPU9250陀螺仪传感器2放置在膝关节下部，采集小腿姿态信号. 对采集到的大腿姿态信号和小腿姿态信号处理之后，可以得到膝关节角度信号. 将加速度传感器放置于假肢膝关节内侧3位置，采集膝关节在水平、竖直方向加速度信号. 将加速度传感器4放置于踝关节，采集踝关节在水平、竖直方向的加速度信号. 3名受试者的基本信息如表1所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   假肢穿戴者骑行图片

Fig.3   Bicycle riding of prosthetic wearers


表 1   受试者情况

Tab.1  Subject physical condition

受试者编号 性别 年龄/岁 身高/cm
A1 男 42 173
A2 男 27 175
A3 女 25 162

新窗口打开| 下载CSV


2.2. 信号降噪处理

在信号采集中，由于自行车架振动以及假肢穿戴者自身平衡感较差的原因，会导致采集到的信号中包含噪声信号. 特别是在放松区，受试者均为气缸型被动假肢，膝关节无法主动收缩，所以会由脚蹬曲柄支撑假肢膝关节收缩，导致采集数据中掺入大量的噪声信号. 为了保留原始信号的特征，采用奇异值分解（singular value decomposition，SVD）对采集到的信号进行降噪处理[19-21]，SVD降噪将采集到的原始信号矩阵分解为一系列的奇异值和正交子空间. 选取有效的奇异值和有效的阶次进行信号重构，达到信号降噪的目的.

以W信号为例，离散时间序列为W=[w1，w2，··· ，wK]，对信号W的长度i进行分段，按照下式构造新的特征矩阵：

${{G}} = \left[ {\begin{array}{*{20}{c}} {{w_1}}&{{w_2}}& \cdots &{{w_i}}\\ {{w_{i + 1}}}&{{w_{i + 2}}}& \cdots &{{w_{2i}}}\\ \cdot & \cdot & &{}\cdot\\ \cdot & \cdot & &{}\cdot\\ \cdot & \cdot & &{}\cdot\\ {{w_{\left( {j - 1} \right)i + 1}}}&{{w_{\left( {j - 1} \right)i + 2}}}& \cdots &{{w_{ji}}} \end{array}} \right].$

式中：K为矩阵G的采样点数量，K=ji. 对矩阵G进行奇异值分解计算：

${{G}} = {{UZV^{\rm{T}}}}.$

式中：U为左奇异矩阵，U为j×j的方阵，满足UUT=I；V为右奇异矩阵，V为i×i的方阵，满足VV T=I；Z为j×i的对角矩阵，对角元素为z1，z2，··· ，zq，q=min （j，i），z1≥z2≥··· ≥zq，其中z1，z2，··· ，zq为矩阵G的奇异值，矩阵G的奇异值可以反映原始信号及噪声信号的情况，如果奇异值中p个占据优势，即

$\displaystyle\sum\limits_{i = 1}^p {s_i^2} \Bigg/\displaystyle\sum\limits_{i = 1}^q {s_i^2} \approx 1.$

其中前p个奇异值反映的是原始信号中的有用信号，其余较小的奇异值反映的是噪声信号. 将反映噪声的奇异值置0，即可完成对原始信号的降噪处理. 利用式（2）实现对原始信号的重建，将有用信号的奇异值对应项相加，取均值，可以完成对原始信号的降噪处理.

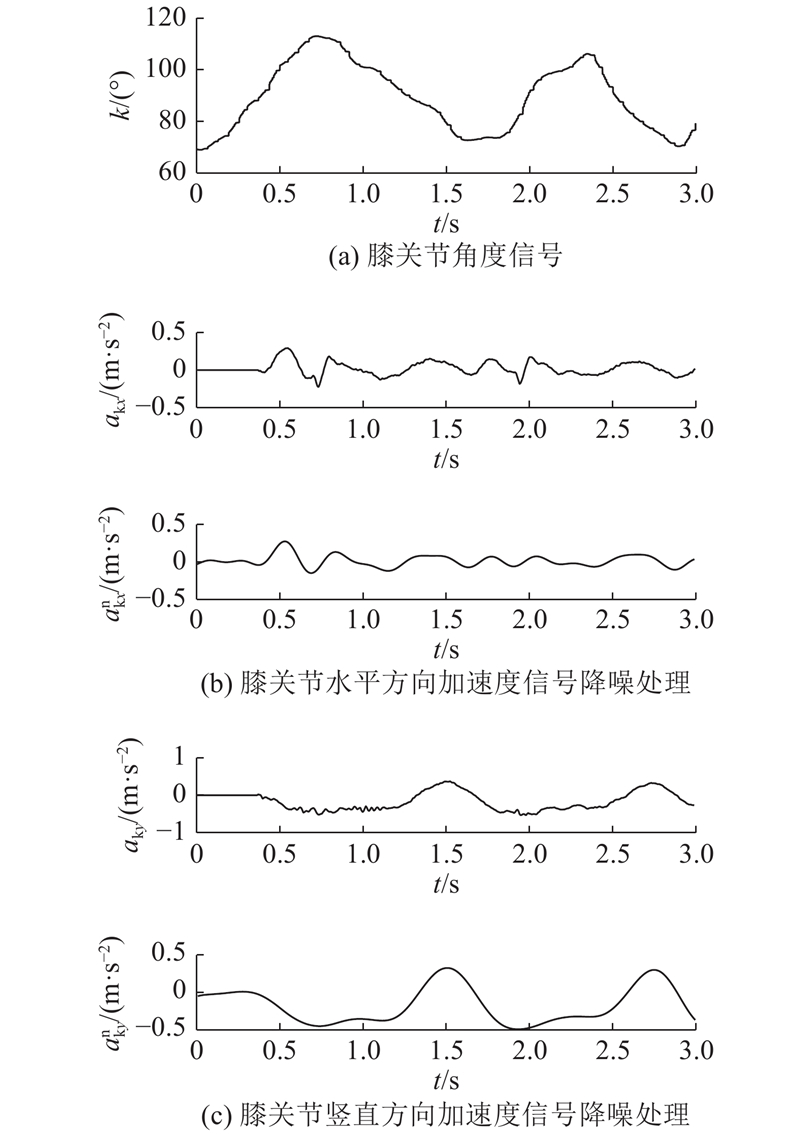
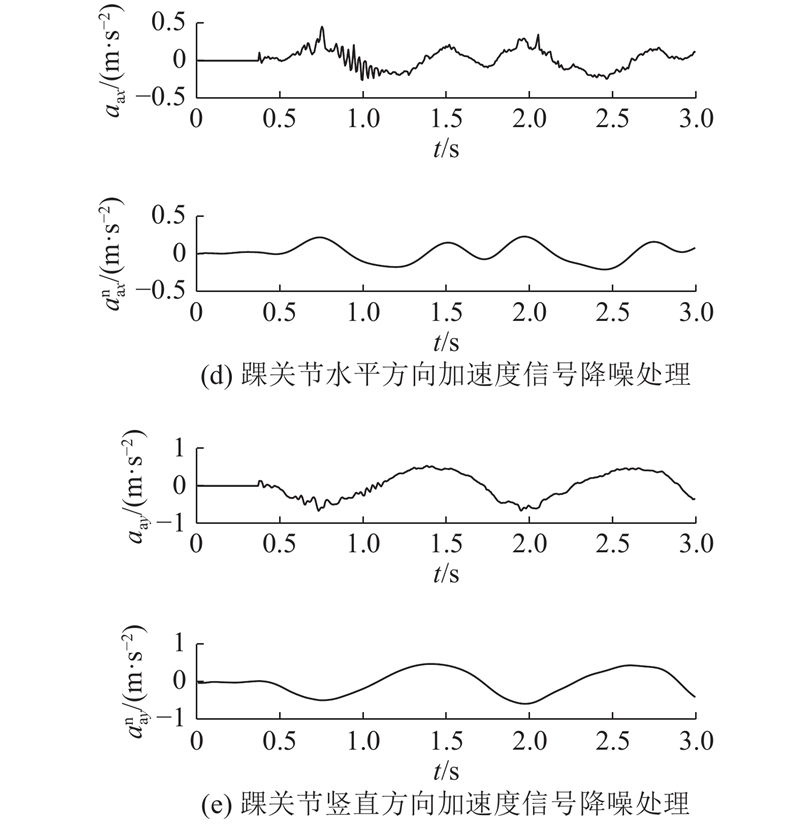
如图4所示为A2受试者在稳定骑行状态下，同一时段的膝关节水平、竖直方向原始信号以及踝关节水平、竖直方向的原始信号和经过奇异值降噪后的信号对比图. 图中，k为膝关节角度，akx、 $a_{{\rm{k}}x}^{\rm{n}} $分别为膝关节水平方向加速度原始信号和奇异值降噪信号，aky、 $a_{{\rm{k}}y}^{\rm{n}} $分别为膝关节竖直方向加速度原始信号和奇异值降噪信号，aax、 $a_{{\rm{a}}x}^{\rm{n}} $分别为踝关节水平方向加速度原始信号和奇异值降噪信号，aay、 $a_{{\rm{a}}y}^{\rm{n}} $分别为踝关节竖直方向加速度原始信号和奇异值降噪信号. 其中MPU9250陀螺仪带有卡尔曼滤波降噪功能，所以不需要进行降噪处理.

图 4-1

新窗口打开| 下载原图ZIP| 生成PPT

图 4-1  

Fig.4-1  


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   运动信号预处理

Fig.4   Motion signal preprocessing


2.3. 信号特征提取

为了能够对假肢穿戴者骑行的4个相位进行有效的识别，需要确定膝关节在各个相位对应的角度. 设定如下：在用力区起点时，假肢膝关节角度为θp；在下缓冲区起点时，假肢膝关节角度为θl；在放松区起点时，假肢膝关节角度为θr，在上缓冲区起点时，假肢膝关节角度为θu. 3位受试者对应的角度如表2所示. 在实验中发现，在1个完整的骑行周期中，假肢膝关节会张开、收缩各1次，所以上述的膝关节角度会出现在2个区域，例如θp还可能出现在放松区，θr还可能出现在用力区.

表 2   受试者各相位对应角度

Tab.2  Subject angle corresponding to each phase

受试者 θp /（°） θl /（°） θr /（°） θu /（°）
A1 89.27 113.72 100.51 80.39
A2 86.75 108.26 96.86 75.24
A3 85.73 103.62 96.83 78.57

新窗口打开| 下载CSV


为了提高骑行相位识别的准确性，避免单一信号的不确定影响，从数据冗余的角度，以假肢穿戴者骑行时各个相位的膝关节特征点θp、θl、θr、θu，提取经过奇异值降噪后的膝关节、踝关节的水平和竖直方向加速度信号. 对膝关节角度信号进行归一化处理，对膝关节、踝关节水平方向的加速度分别提取平均值，对竖直方向的信号提取偏度，组成多维特征向量作为分类模型的输入. 其中平均值m（mean）表示加速度信号的平均强度，偏度s表示运动时的倾斜方向及倾斜角度：

${k_i} = ({k_i} - {k_{\min }})/({k_{\max }} - {k_{\min }}),$

$m = {{\sum\limits_{i = 1}^n {{X_i}^2} } / M},$

$s = {M\sum\limits_{{{i}} = 1}^n {{{({Y_i} - \overline Y )}^3}} } \Big/ \left[ {{(M - 1)(M - 2){\sigma ^3}}} \right].$

式中：ki为第i个相位的膝关节角度采样值；kmin为膝关节角度中的最小值；kmax为膝关节角度中的最大值；M为采样点数；Xi为水平方向上的加速度采样值；Yi为竖直方向上的加速度采样值. 将4个相位的信号特征点组成特征向量 ${{{\lambda}} _i} $= $\left[ {a_{{{\rm{k}}x},i}^{\rm{n}},a_{{{\rm{k}}y},i}^{\rm{n}},a_{{{\rm{a}}x},i}^{\rm{n}},a_{{{\rm{a}}y},i}^{\rm{n}},{{k}_i}} \right]$进行相位识别.

3. 骑行相位识别方法

骑行过程中的振动颠簸，即使经过滤波降噪，单个传感器信号也无法保证相位识别的准确度，因此需要应用SVM、BP神经网络等方法对多路传感器信号组成的多维向量进行分类，实现4个骑行相位的准确识别.

3.1. 支持向量机

SVM是适于处理高维数据的算法. SVM根据结构风险最小化原理，构造最优超平面，实现对数据的分类，具有良好的分类精度[22-26]. 以分类样本集N=（xi，yi）（i=1，2，3，···，n）为例，其中xi=[xi1，xi2，···，xid]为特征向量，yi∈{±1}为类别号. SVM分类模型的决策函数为

$f\left( {{x}} \right) = {\rm{sgn}}\left( {\left( {{{{w}}^{{\rm{T}}}} \cdot {{x}}} \right) + {b}} \right) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^n {{y_i}{{\chi}} _i^{\rm{T}}T\left( {{{{x}}_i},{{x}}} \right) + {b}} } \right).$

式中：T（xi，x）为核函数，w、b分别为最优的权值向量和阈值.

SVM分类算法根据决策函数在高维空间中构造最优分类面，实现对二维数据的分类. 由于加速度信号及角度信号属于线性不可分的情况，为了实现对骑行4个相位的划分，需要把信号映射到高维空间中，构造多个决策分类函数，在高维空间中解决线性不可分的问题.

以多维特征向量作为SVM分类模型的输入，实现x从低维空间Rn到高维空间G的转换，即x→λ（x）=[λ1（x），λ2（x），···，λn（x）]T. 将输入向量变为多维特征向量λ（x），可得最优分类函数为

$f\left( {{x}} \right) = \operatorname{sgn}\; \left( {\sum\limits_{i = 1}^l {{y_i}{{\chi}} _i^{{\rm{T}}}T\left( {({\lambda _i}({{x}}),\lambda ({{x}})} \right) + {b}} } \right).$

以 ${{{\lambda}} _i} $为特征向量，构造新的特征子空间，用于SVM分类模型的训练与识别.

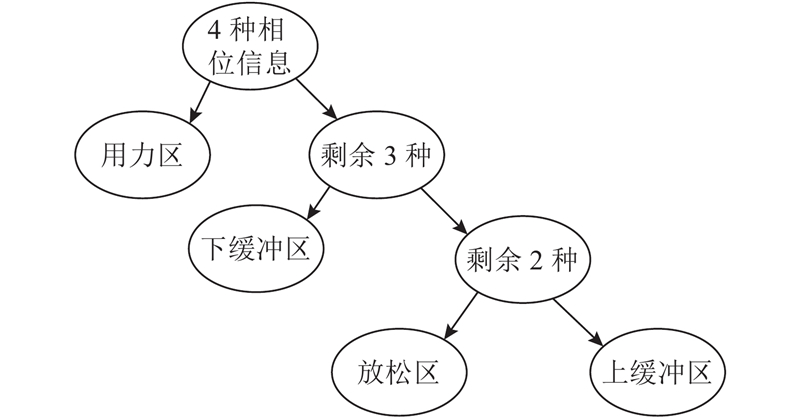
3.2. 二分类法

利用从假肢穿戴者骑行信号特征中提取的特征信号构成多维特征向量 ${{{\lambda}} _i} $，构建支持向量机二叉树的多分类模型. 如图5所示，开展假肢穿戴者骑行的相位识别. 采用SVM1对用力区数据进行分离，用SVM2分离出下缓冲区的数据. 利用SVM3将放松区的数据进行分离，由于整个系统中只包含骑行4个相位的信息，最终剩下的为上缓冲区的数据.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   二分类法示意图

Fig.5   Schematic diagram of binary classification


3.3. SVM核函数

SVM分类模型通过核函数将低维空间中的数据映射到高维空间中，在高维空间中建立最优决策面，实现对数据的分类. 在假肢穿戴者骑行相位识别过程中，SVM核函数的选择对识别准确率有重要的影响. SVM常用核函数主要有多项式核函数（polynomial）、Sigmoid核函数（sigmoid）、线性核函数（linear）、径向基核函数（RBF）4种. 核函数内的参数会对结果产生重要的影响，其中核函数宽度γ会影响支持向量机模型的复杂度和分类精度；惩罚因子C可以调节模型的复杂度，有效地提高模型的泛化性能.

为了确定最优的核函数，选取50组骑行数据样本，从其中4个不同的运行阶段共提取200组数据，进行归一化处理. 选取100组数据，每个阶段25组作为分类模型的训练集. 剩下的100组数据作为模型的测试集. 不同核函数的试验结果如表3所示.

表 3   不同核函数的测试结果

Tab.3  Different kernel function test results

核函数 C=2，γ=1 C=1，γ=1 C=2，γ=0.5 C=3，γ=2
polynomial 75% 73% 48% 83%
sigmoid 31% 28% 82% 3%
linear 77% 83% 80% 85%
RBF 79% 85% 85% 83%

新窗口打开| 下载CSV


经过对比可以看出，高斯核函数（RBF）在识别过程中比较稳定且具有较高的准确率，所以选择RBF核函数作为SVM分类模型中的核函数.

3.4. 与BP神经网络对比

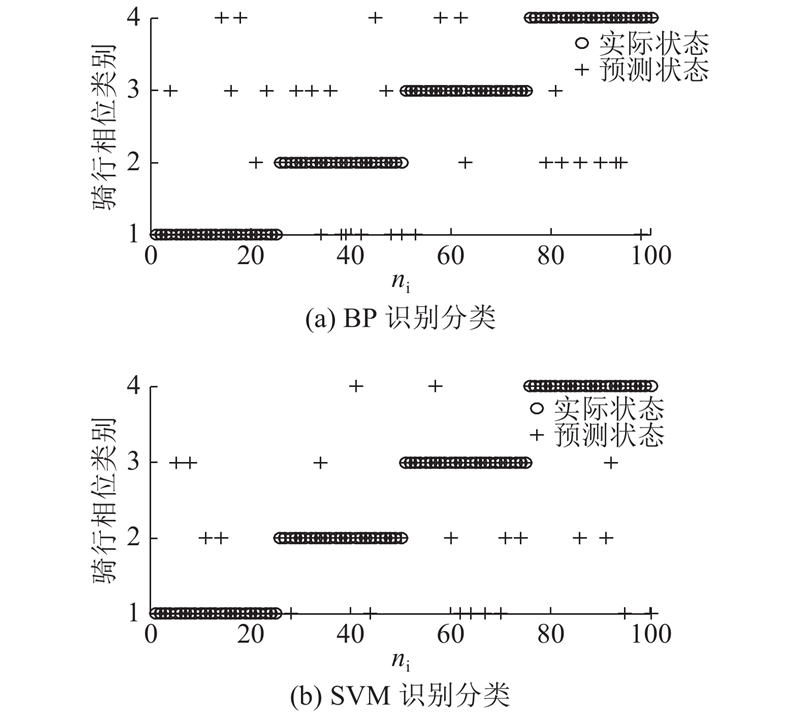
为了验证SVM方法较其他算法在假肢穿戴者骑行相位识别中的准确性，开展基于BP神经网络的骑行相位识别实验. 根据预测误差和期望输出，调整神经网络连接权值和节点阈值，通过迭代将预测误差函数沿负梯度方向降到最小，使得网络对未知类别特征集具有辨识能力[27-28].

在对骑行各个相位的识别中，采集4个相位的信号各50组，共200组. 其中100组作为训练集，训练分类模型，剩余100组作为测试集. 在BP神经网络分类模型中，每组信号为5维，待识别的信号有4类，所以BP神经网络的节点数为5--6--4，即输入层有5个节点，隐含层有6个节点，输出层有4个节点. 如图6所示分别为 BP方法、SVM方法的相位识别结果图. 图中，ni为测试样本数量，1为用力区，2为下缓冲区，3为放松区，4为上缓冲区，空心圆表示实际相位，+表示预测相位，若两者重合则表示预测准确，若不重合则表示预测错误. 在100组预测数据中，BP分类模型的总体识别率为72%，SVM分类模型的总体识别率为79%. 通过对比可知，SVM分类模型相对于BP神经网络分类模型的准确率更高.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   骑行相位分类结果

Fig.6   Bicycle riding phases classification result


3.5. 灰狼优化算法

虽然SVM分类模型相较于BP神经网络分类模型的识别率较高，但是在假肢穿戴者进行骑行时，由于骑行周期短，频率快，需要识别分类模型拥有较高的识别率. 利用灰狼优化算法（GWO）对支持向量机分类模型进行优化. 灰狼优化算法是Mirjalili等提出的模拟灰狼群体捕食行动的新型智能优化算法[29-32]. 灰狼算法具有较强的收敛性、全局优化能力，提高分类效率，且容易实现，在参数优化，图像分类等领域应用十分广泛. 灰狼优化算法的基本思想是模拟狼群捕食实物活动. 灰狼算法的基本原理如下. 在搜索空间中随机创建1组灰狼，通过计算适应度构建等级层次，将适应能力最强的设置为α狼，将适应度稍弱于α狼的设置为β狼，剩下的适应度最弱的设置为δ狼. GWO优化算法的优化过程主要通过每代种群中的α狼、β狼、δ狼，对猎物进行定位计算，通过自身优化缩短与猎物之间的距离，捕杀猎物. GWO算法主要包括以下3个定义.

定义1 　在进行灰狼算法优化之前，需要确定猎物的位置，计算出猎物距离灰狼的距离：

$D = \left| {C{{{S}}_{\rm{p}}}(t) - {{{S}}{(t)}}} \right|.$

式中：S（t）、Sp（t）分别为第t代时灰狼以及猎物的位置向量；C为系数，

$C = {2{{r_1}}},$

其中r1为0~1.0的随机数.

定义2 　确定第t+1代灰狼的位置：

${{S}}(t + 1) = {{{S}}_{\rm{p}}} - {{\mu}} D,$

${{\mu}} = 2{{a}}{r_2} - {{a}}.$

式中：μ、r2分别为收敛向量和a的随机数，其中|a|会随着迭代次数的增多由2减小至0；S（t+1）为经过t+1次迭代后灰狼的位置向量.

定义3 　确定猎物的位置，在每次迭代过程中α狼距离猎物的距离均是最近的，可以通过S（t+1）代中的α狼来计算猎物的方向，从而求出α狼、β狼以及δ狼和猎物之间的距离：

${D_k} = \left| {{C_i}{{{S}}_k}(t) - {{S}}(t)} \right|,$

${{{S}}_i} = {{{S}}_k} - {{{\mu}} _i}{D_k}.$

根据下式确定寻优方向：

${{{S}}_{\rm{p}}}(t + 1) =({{{{{S}}_1} + {{{S}}_2} + {{{S}}_3}}})/{3}.$

式中：k=α，β，γ；i=1，2，3；Sp（t+1）为第t+1迭代时猎物的位置向量.

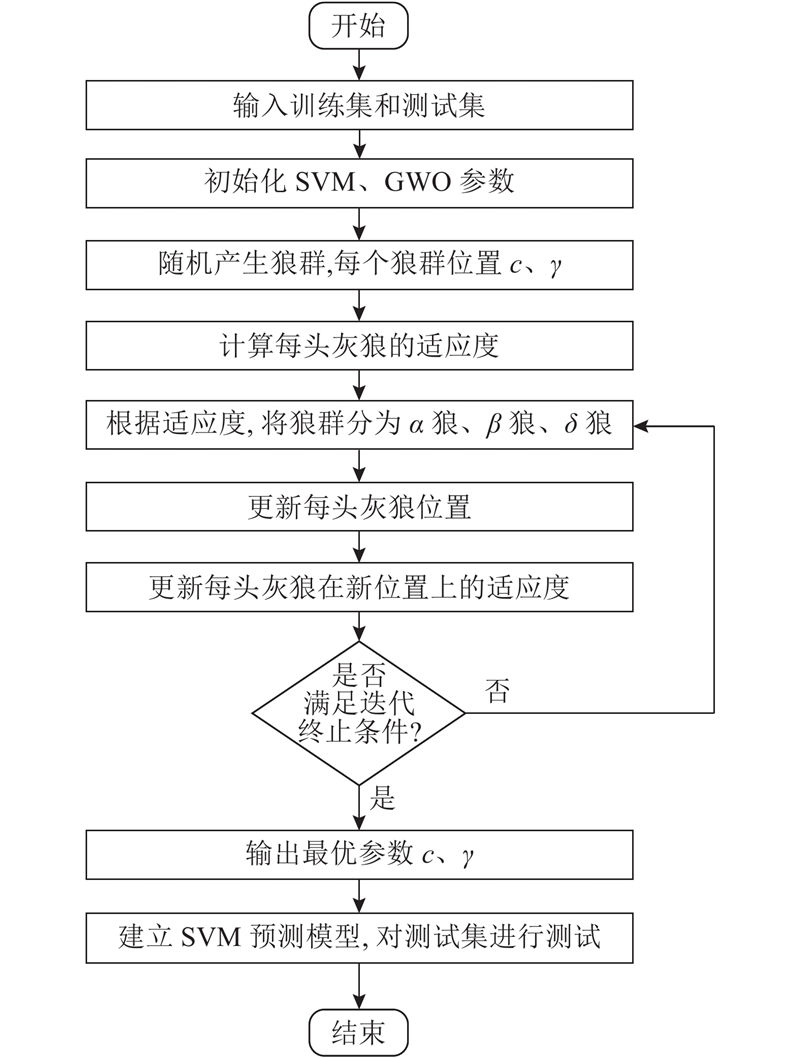
在SVM分类模型中，C及γ影响模型的复杂度，提高泛化性能，对分类结果有着重要的影响. 为了提高分类准确率，利用灰狼算法（GWO）用于优化和驯服参数C和γ. 利用SVM分类模型，预测假肢穿戴者的骑行相位. 灰狼优化支持向量机分类模型的流程如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   GWO优化SVM分类模型算法流程

Fig.7   GWO optimized SVM classification model flow


4. 实验结果

通过对比SVM分类模型和BP神经网络分类模型对于假肢穿戴者骑行相位识别的准确率，确定使用识别准确率更高的SVM分类模型. 为了进一步提高分类识别的准确率，使用灰狼优化（GWO）算法对SVM分类模型进行核参数优化. 为了验证将GWO与SVM分类模型相融合算法的有效性及可行性，将粒子群优化算法（PSO）、遗传算法（GA）优化后的SVM分类模型进行对比.

优化模型对比试验所采用的假肢穿戴者骑行数据与之前的相同，共200组. 其中100组作为训练集，训练分类模型；剩余100组作为测试集，检验模型识别的准确率. SVM的核函数均采用RBF核函数. GWO优化参数设置为：狼群数量为20，迭代次数为50次. PSO优化参数设置为：粒子群数为20，进化代数为50，c1、c2分别设置为1.5和1.7. GA优化参数设置为：种群数量为20，进化代数为50，交叉概率为0.9，变异概率为0.01.

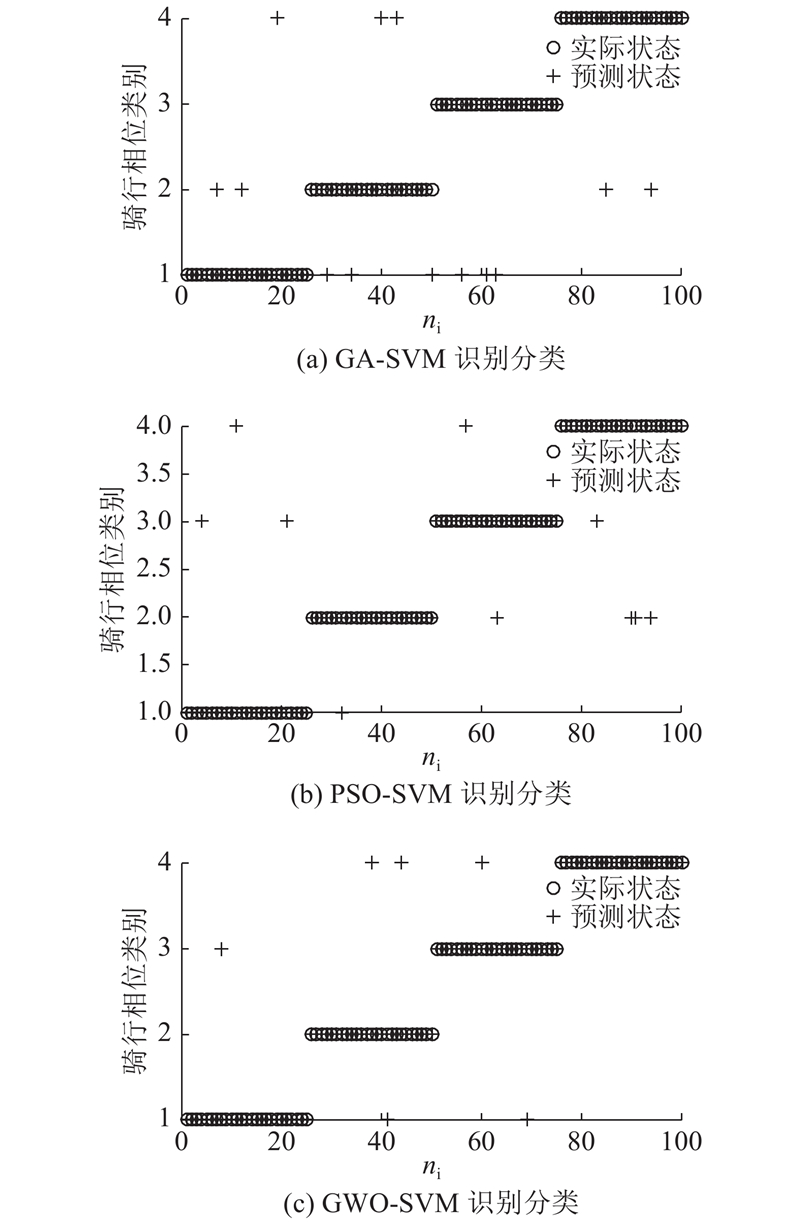
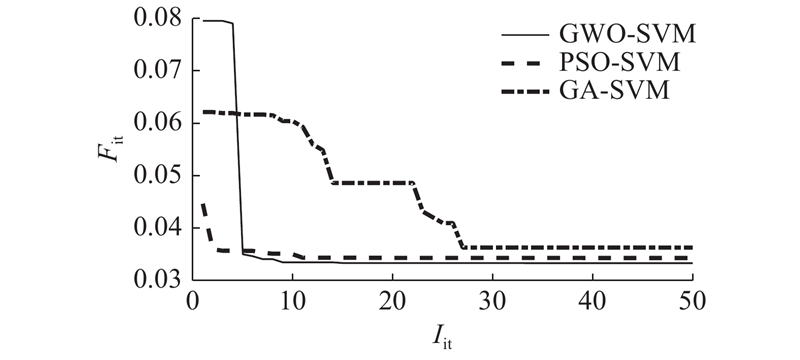
如图8所示为GA-SVM分类模型、PSO-SVM分类模型及GWO-SVM分类模型对骑行相位识别的结果图. 图中，1为用力区，2为下缓冲区，3为放松区，4为上缓冲区，空心圆表示实际相位，+表示预测相位，若两者重合则表示预测准确，若不重合则表示预测错误. 对比实验结果中，GA-SVM分类模型在100组测试数据中共识别出87组，总体识别率为87%. PSO-SVM分类模型在100组测试数据中共识别出90组，总体识别率为90%. 经过GWO优化后的SVM分类模型在100组骑行测试数据中共识别出94组，总体识别率为94%，优化后的核函数参数值如表4所示. 表中，np为种群数量，PC为交叉概率，Pm为变异概率，npar为粒子群数，nw为狼群数量，A为准确率. 如表5所示为所有分类模型对100组假肢穿戴者骑行相位的具体识别结果. 表中，nr为识别样本数量，pr为识别率. 通过适应度来进一步对比3种优化算法对SVM分类模型的优化程度. 如图9所示为3种优化算法的适应度收敛曲线. 图中，Fit为适应度，Iit为迭代次数.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   优化SVM识别结果

Fig.8   Recognition results of optimizing SVM


表 4   优化SVM的识别结果

Tab.4  Recognition results of optimizing SVM

优化方法 参数设置 寻优结果 A /%
GA-SVM np = 20，
PC = 0.9，
Pm = 0.01 		C = 44.602 7
γ = 25.110 6 		87
PSO-SVM npar = 20，
c1 = 1.5，
c2 = 1.7 		C = 53.835 4
γ = 22.018 6 		90
GWO-SVM nw = 20 C = 20.246 2
γ = 35.184 2 		94

新窗口打开| 下载CSV


表 5   各分类模型的识别结果

Tab.5  Recognition results of each classification model

算法 nr pr /%
用力区 下缓冲区 放松区 上缓冲区 总和
BP 19 15 21 17 72 72
SVM 21 22 17 19 79 79
GA-SVM 22 20 22 23 87 87
PSO-SVM 22 24 23 21 90 90
GWO-SVM 24 22 23 25 94 94

新窗口打开| 下载CSV


图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   3种优化算法的适应度

Fig.9   Fitness values of three optimization algorithm


在适应度曲线方面，从图9可以看出，GWO的适应度最小，说明优化效果最好. 在收敛效果方面，GA优化算法在24代左右得到最优结果，较PSO优化算法及GWO优化算法而言，收敛速度较缓慢. 对比PSO优化算法及GWO优化算法可以看出，虽然PSO在迭代前期收敛速度较快，但是不能迅速地达到最低适应度，需要1个较长的过程，在第13次迭代时才能够完全收敛；GWO优化算法能够较快地完成收敛，在第10次迭代时能够达到最佳的适应度. 综上所述，GWO-SVM分类模型无论是在识别准确度、适应度还是在收敛速度上均优于其他2种分类模型.

从表5可以看出, GWO-SVM分类模型对于假肢穿戴者骑行各个相位识别的准确率大于其他分类模型. 骑行相较于行走运动而言，骑行运动的频率更快，所以对于骑行相位识别的准确率越高，假肢穿戴者骑行时的流畅性越高. 在基本的分类模型中，选择传统的SVM分类模型和BP神经网络分类模型，但BP神经网络需要基于经验最小化原则，因此可能引起连接权重陷入局部最小化，影响系统的输出误差，导致BP神经网络分类模型处于学习不足或过度学习的状态. SVM分类模型是以结构风险最小化为基础，所以在稳定性和泛化性能上相较于BP神经网络更优. 利用GWO算法对SVM核参数进行寻优处理，使得GWO-SVM分类模型在假肢穿戴者骑行相位识别中无论是在识别的准确率上还是在收敛的速度上都有很大的提升.

对于所采集提取的假肢穿戴者骑行各相位数据，通过GWO优化后的SVM分类模型对于识别骑行相位的方法是可行的，且识别精度高. 利用该分类模型得到的识别结果对于之后的假肢穿戴者骑行时的膝关节控制提供了基础作用.

5. 结　语

通过在假肢膝关节上配置陀螺仪，在膝关节、踝关节上配置加速度传感器，采集假肢穿戴者的运动特征. 应用GWO-SVM优化模型的方法，将骑行相位识别的准确率提高到了94%，明显优于BP神经网络、PSO-SVM、GA-SVM分类模型等方法. 骑行相位的准确识别是实现假肢膝关节高效率、准确控制的基础. 对于被动型假肢，可以根据不同的骑行相位阶段，调节气缸阻尼，以配合残肢髋关节的施力、过渡调节和放松回收；对于主动型假肢，可以在不同骑行相位控制关节驱动电机的正反转和加减速，缓解假肢穿戴者的疲劳程度，提升关节驱动电机的能量效率.

参考文献

ZIEGLER-GRAHAM K, MACKENZIE E J, EPHRAIM P L, et al

Estimating the prevalence of limb loss in the United States: 2005 to 2050

[J]. Archives of Physical Medicine and Rehabilitation, 2008, 89 (3): 422- 429

DOI:10.1016/j.apmr.2007.11.005      [本文引用: 1]

DAVIES B, DATTA D

Mobility outcome following unilateral lower limb amputation

[J]. Prosthetics and Orthotics International, 2003, 27 (3): 186- 190

DOI:10.1080/03093640308726681      [本文引用: 1]

MASSALIN Y, ABDRAKHMANOVA M, VAROL H A

User-independent intent recognition for lower-limb prostheses using depth sensing

[J]. IEEE Transactions on Biomedical Engineering, 2017, 65 (8): 1759- 1770

URL     [本文引用: 1]

宣伯凯, 刘作军, 陈玲玲, 等

膝上型假肢的运动意图识别与控制

[J]. 东南大学学报: 自然科学版, 2017, 47 (6): 1107- 1116

URL     [本文引用: 1]

XUAN Bo-kai, LIU Zuo-jun, CHEN Ling-ling, et al

Motion intention recognition and control of above knee prosthesis

[J]. Journal of Southeast University: Natural Science Edition, 2017, 47 (6): 1107- 1116

URL     [本文引用: 1]

CHEN Bao-jun, WANG Qin-ning, WANG Long

Adaptive slope walking with a robotic transtibial prosthesis based on volitional EMG control

[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20 (5): 2146- 2157

DOI:10.1109/TMECH.2014.2365877      [本文引用: 1]

赵晓东, 刘作军, 陈玲玲, 等

下肢假肢穿戴者跑动步态识别方法

[J]. 浙江大学学报: 工学版, 2018, 52 (10): 1980- 1988

DOI:10.3785/j.issn.1008-973X.2018.10.018      [本文引用: 3]

ZHAO Xiao-dong, LIU Zuo-jun, CHEN Ling-ling, et al

Approach of running gait recognition for lower limb amputees

[J]. Journal of Zhejiang University: Engineering Science, 2018, 52 (10): 1980- 1988

DOI:10.3785/j.issn.1008-973X.2018.10.018      [本文引用: 3]

赵晓东, 刘作军, 苟斌, 等

下肢假肢斜坡路况运动控制策略分析

[J]. 控制与决策, 2019, 34 (6): 1160- 1168

URL    

ZHAO Xiao-dong, LIU Zuo-jun, GOU Bin, et al

Analysis of slope motion control strategy of lower limb prostheses

[J]. Control and Decision, 2019, 34 (6): 1160- 1168

URL    

CHAICHAOWARAT R, GRANADOS D F P, KINUGAWA J, et al. Passive knee exoskeleton using torsion spring for cycling assistance [C]// IEEE International Conference on Intelligent Robots and Systems. Vancouver: IEEE, 2017: 3069-3074.

[本文引用: 1]

LAWSON B E, LEDOUX E D, GOLDFARB M

A robotic lower limb prosthesis for efficient bicycling

[J]. IEEE Transactions on Robotics, 2017, 33 (2): 432- 445

DOI:10.1109/TRO.2016.2636844      [本文引用: 3]

KIM H W, AN J W, YOO H D, et al. Balancing control of bicycle robot using PID control [C]// International Conference on Control, Automation and Systems. Gwangju: IEEE, 2013: 145-147.

[本文引用: 1]

赵丽娜, 刘作军, 苟斌, 等

基于隐马尔可夫模型的动力型下肢假肢步态预识别

[J]. 机器人, 2014, 36 (3): 337- 341

URL     [本文引用: 1]

ZHAO Li-na, LIU Zuo-jun, GOU Bin, et al

Gait pre-recognition of dynamic lower limb prosthesis based on hidden Markov model

[J]. Robot, 2014, 36 (3): 337- 341

URL     [本文引用: 1]

王永雄, 陈晗, 尹钟, 等

基于惯导信息的人体动作和路况识别

[J]. 生物医学工程学杂志, 2018, 35 (4): 621- 630

URL     [本文引用: 1]

WANG Yong-xiong, CHEN Han, YIN Zhong, et al

Human action and road condition recognition based on the inertial information

[J]. Journal of Biomedical Engineering, 2018, 35 (4): 621- 630

URL     [本文引用: 1]

GHAMISI P, BENEDIKTSSON J A

Feature selection based on hybridization of genetic algorithm and particle swarm optimization

[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12 (2): 309- 313

DOI:10.1109/LGRS.2014.2337320      [本文引用: 1]

彭亮, 侯增广, 王晨, 等

康复辅助机器人及其物理人机交互方法

[J]. 自动化学报, 2018, 44 (11): 2000- 2010

URL     [本文引用: 1]

PENG Liang, HOU Zeng-guang, WANG Chen, et al

Physical interaction methods for rehabilitation and assistive robots

[J]. Acta Automatica Sinica, 2018, 44 (11): 2000- 2010

URL     [本文引用: 1]

王启宁, 郑恩昊, 陈保君, 等

面向人机融合的智能动力下肢假肢研究现状与挑战

[J]. 自动化学报, 2016, 42 (12): 1780- 1793

URL     [本文引用: 1]

WANG Qi-ning, ZHENG En-hao, CHENG Bao-jun, et al

Recent progress and challenges of robotic lower-limb prostheses for human robot integration

[J]. Acta Automatica Sinica, 2016, 42 (12): 1780- 1793

URL     [本文引用: 1]

YOUNG A J, HARGROVE L J, KUIKEN T A

The effects of electrode size and orientation on the sensitivity of myoelectric pattern recognition systems to electrode shift

[J]. IEEE Transactions on Biomedical Engineering, 2011, 58 (9): 2537- 2544

DOI:10.1109/TBME.2011.2159216      [本文引用: 1]

CHEN Bao-jun, WANG Xue-gang, HUANG Yan, et al

A foot-wearable interface for locomotion mode recognition based on discrete contact force distribution

[J]. Mechatronics, 2015, 12 (32): 12- 21

[本文引用: 1]

JURI T, EDUARDO P, STEFANO R, et al

Gait partitioning methods: a systematic review

[J]. Sensors, 2016, 16 (1): 66- 82

DOI:10.3390/s16010066      [本文引用: 1]

YANG Bin, YU Chun-yang, DONG Yong-gui

Capacitively-coupled electrocardiogram measuring system and noise reduction by singular spectrum analysis

[J]. IEEE Sensors Journal, 2016, 10 (16): 3802- 3810

URL     [本文引用: 1]

MONDAL A, SAXENA I, TANG Hong, et al

A noise reduction technique based on nonlinear kernel function for heart sound analysis

[J]. IEEE Journal of Biomedical and Health Informatics, 2017, 22 (3): 775- 784

URL    

张晓涛, 李伟光

基于奇异值和奇异向量的振动信号降噪方法

[J]. 振动. 测试与诊断, 2018, 38 (3): 553- 558

URL     [本文引用: 1]

ZHANG Xiao-tao, LI Wei-guang

Noise reduction method of vibration signal based on singular value and singular vector

[J]. Journal of Vibration, Measurement and Diagnosis, 2018, 38 (3): 553- 558

URL     [本文引用: 1]

WEI Qiang, WU Bin, XU De-wei, et al

Natural sampling SVM-based common-mode voltage reduction in medium-voltage current source rectifier

[J]. IEEE Transactions on Power Electronics, 2017, 32 (10): 7553- 7560

DOI:10.1109/TPEL.2016.2632442      [本文引用: 1]

WU Jian-xin, YANG Hao

Linear regression-based efficient SVM learning for large-scale classification

[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 26 (10): 2357- 2369

URL    

YIN Ying-jie, XU De, WANG Xin-gang, et al

Online state-based structured SVM combined with incremental PCA for robust visual tracking

[J]. IEEE Transactions on Cybernetics, 2015, 45 (9): 1988- 2000

DOI:10.1109/TCYB.2014.2363078     

严秀权, 吴洪涛, 李耀, 等

压电作动器的支持向量机迟滞模型

[J]. 仪器仪表学报, 2018, 39 (9): 228- 235

URL    

YAN Xiu-quan, WU Hong-tao, LI Yao, et al

Support vector machine-based hysteresis model of piezoelectric actuator

[J]. Chinese Journal of Scientific Instrument, 2018, 39 (9): 228- 235

URL    

刘忠宝, 秦振涛, 罗学刚, 等

利用融合数据分布特征的模糊双支持向量机对恒星光谱分类

[J]. 光谱学与光谱分析, 2019, 39 (4): 1307- 1311

URL     [本文引用: 1]

LIU Zhong-bao, QIN Zhen-tao, LUO Xue-gang, et al

Stellar spectra classification by support vector machine with spectral distribution properties

[J]. Spectroscopy and Spectral Analysis, 2019, 39 (4): 1307- 1311

URL     [本文引用: 1]

LIANG Gao-bo, HONG Hui-chao, XIE Wei-fang, et al

Combining convolutional neural network with recursive neural network for blood cell image classification

[J]. IEEE Access, 2018, 7 (6): 36188- 36197

URL     [本文引用: 1]

李镇, 樊炳辉, 王鑫, 等

基于BP神经网络的仿生眼定位追踪算法

[J]. 机器人, 2017, 39 (1): 63- 69

URL     [本文引用: 1]

LI Zhen, FAN Bing-hui, WANG Xin, et al

Locating and tracking algorithm of biomimetic eye based on backpropagation neural network

[J]. Robot, 2017, 39 (1): 63- 69

URL     [本文引用: 1]

焦晓璇, 景博, 李娟, 等

基于ADEGWO-SVM的机载燃油泵寿命预测研究

[J]. 仪器仪表学报, 2018, 39 (8): 43- 52

URL     [本文引用: 1]

JIAO Xiao-xuan, JIN Bo, LI Juan, et al

Research on remaining useful life prediction of fuel pump based on adaptive differential evaluation grey wolf optimizer-support vector machine

[J]. Chinese Journal of Scientific Instrument, 2018, 39 (8): 43- 52

URL     [本文引用: 1]

戚晓利, 王振亚, 吴保林, 等

基于ACMPE、ISSL-Isomap和GWO-SVM的行星齿轮箱故障诊断

[J]. 航空动力学报, 2019, 34 (4): 744- 755

URL    

QI Xiao-li, WANG Zhen-ya, WU Bao-lin, et al

Planetary gearbox fault diagnosis based on ACMPE, ISSL-Isomap and GWO-SVM

[J]. Journal of Aerospace Power, 2019, 34 (4): 744- 755

URL    

李麟玮, 吴益平, 苗发盛

基于灰狼支持向量机的非等时距滑坡位移预测

[J]. 浙江大学学报: 工学版, 2018, 52 (10): 1998- 2006

DOI:10.3785/j.issn.1008-973X.2018.10.020     

LI Lin-wei, WU Yi-ping, MIAO Fa-sheng

Prediction of non-equidistant landslide displacement time series based on grey wolf support vector machine

[J]. Journal of Zhejiang University: Engineering Science, 2018, 52 (10): 1998- 2006

DOI:10.3785/j.issn.1008-973X.2018.10.020     

LI Ke, CHENG Guo-yu, SUN Xiao-dong, et al

A nonlinear flux linkage model for bearingless induction motor based on GWO-LSSVM

[J]. IEEE Access, 2019, 3 (7): 36558- 36567

URL     [本文引用: 1]

/

〈 〉