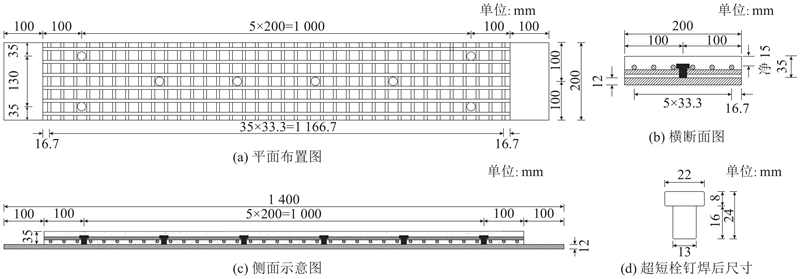
由于超薄体系中UHPC层厚度仅有35 mm,栓钉规范[11]规定的最短栓钉长度为40 mm,焊接熔融后长度为35 mm. 若采用此种规格栓钉作为连接件,则UHPC的保护层厚度为零,无法满足构造要求. 本文提出采用超短栓钉作为连接件的钢-超薄UHPC轻型组合桥面结构. 超短栓钉的长径比仅为1.8,远小于常规栓钉(
1. 试验概况
1.1. 构件设计及材料特性
参考常规钢-UHPC轻型组合桥面板的受弯试验方法[13-15],选取200 mm宽的横向条带进行负弯矩受弯试验. 各构件的外观尺寸一致,总长为1 200 mm,净跨为1 000 mm,宽度为200 mm,主要设计参数如表1所示. 表中,
表 1 钢-超薄UHPC组合板设计参数
Tab.1
| 构件编号 | | | | |
| S12-33-6 | 12 | 6 | 33 | 2.4 |
| S12-33-8 | 12 | 8 | 33 | 4.3 |
| S12-50-8 | 12 | 8 | 50 | 2.9 |
| S12-50-10 | 12 | 10 | 50 | 4.5 |
| S20-33-6 | 20 | 6 | 33 | 2.4 |
| S20-33-8 | 20 | 8 | 33 | 4.3 |
| S20-50-8 | 20 | 8 | 50 | 2.9 |
图 1
UHPC中钢纤维采用混合纤维,体积分数为3.5%,采用长度不同的平直型钢纤维. 其中,直径为0.12 mm、长8 mm的纤维体积分数为1.5%,直径为0.2 mm、长13 mm的纤维体积分数为2%. 钢筋采用等级为HRB400的带肋钢筋,钢板采用Q345qD钢材,超短栓钉选用ML15材料,力学性能指标满足规范要求.
1.2. 试验加载和量测方案
试验采用MTS加载设备进行负弯矩四点加载,纯弯段长度为400 mm. 在试验过程中,主要关注组合板的钢筋应变、跨中和端部支座位移及UHPC顶面的裂缝发展情况. 使用静态数据采集仪(TDS-530)采集钢筋应变数据,钢筋应变片布置如图2所示. 跨中和端部支座位移由布置在支座处以及跨中位置的千分表测量,精度为0.001 mm.
图 2
试验现场加载装置如图3所示. 在线弹性阶段,采用力控制加载,在构件即将进入非线性阶段时,转为位移控制加载.
图 3
1.3. 材性试验结果
浇筑构件时,制作6个100 mm×100 mm×100 mm的立方体试块、6个100 mm×100 mm×400 mm、6个100 mm×100 mm×300 mm的棱柱体试块,与构件在同条件下养护. 按照标准试验程序测得UHPC的抗压强度为170 MPa,弹性模量为49 GPa,抗折强度为33 MPa. 根据法国UHPC规范[16]中的计算方法,得到UHPC轴拉强度标准值为8 MPa.
2. 试验结果及分析
2.1. 荷载-挠度曲线
钢-超薄UHPC组合板的挠度由千分表
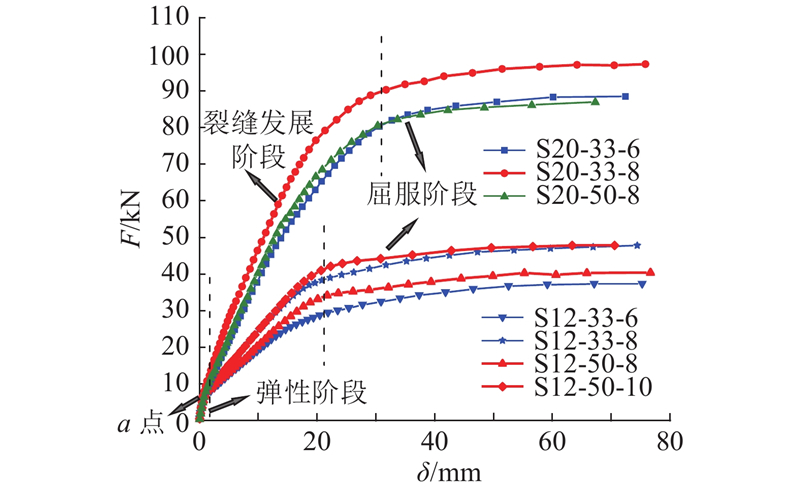
图 4
从图4可以看出,各组合板的荷载-挠度曲线形状相似,可以分成3个阶段:弹性阶段、裂缝发展阶段和屈服阶段. 在弹性阶段,荷载-挠度曲线大致呈直线;继续增大荷载,组合板的UHPC层顶面出现裂缝,构件刚度发生变化,荷载-挠度曲线出现拐点(a点),构件进入裂缝发展阶段. 在裂缝发展阶段,荷载-挠度曲线的斜率逐渐减小,钢筋应力不断增大直至受拉屈服. 在屈服阶段,钢纤维从UHPC中逐步被拔出,裂缝宽度和构件挠度迅速增大,但承载力基本保持不变,构件表现出良好的延性. 观察全过程的荷载-挠度曲线可以发现,组合板的钢板厚度越大,配筋率越高,构件弹性阶段和裂缝发展阶段的刚度越大,屈服承载力越高.
表 2 组合板受弯试验结果
Tab.2
| 构件编号 | | | |
| S12-33-6 | 7.3 | 16.1 | 37.7 |
| S12-33-8 | 7.8 | 19.4 | 47.9 |
| S12-50-8 | 7.6 | 16.1 | 39.0 |
| S12-50-10 | 8.3 | 17.2 | 47.2 |
| S20-33-6 | 8.0 | 23.5 | 88.0 |
| S20-33-8 | 9.4 | 29.1 | 97.8 |
| S20-50-8 | 8.7 | 23.4 | 88.8 |
2.2. 裂缝发展及分布规律
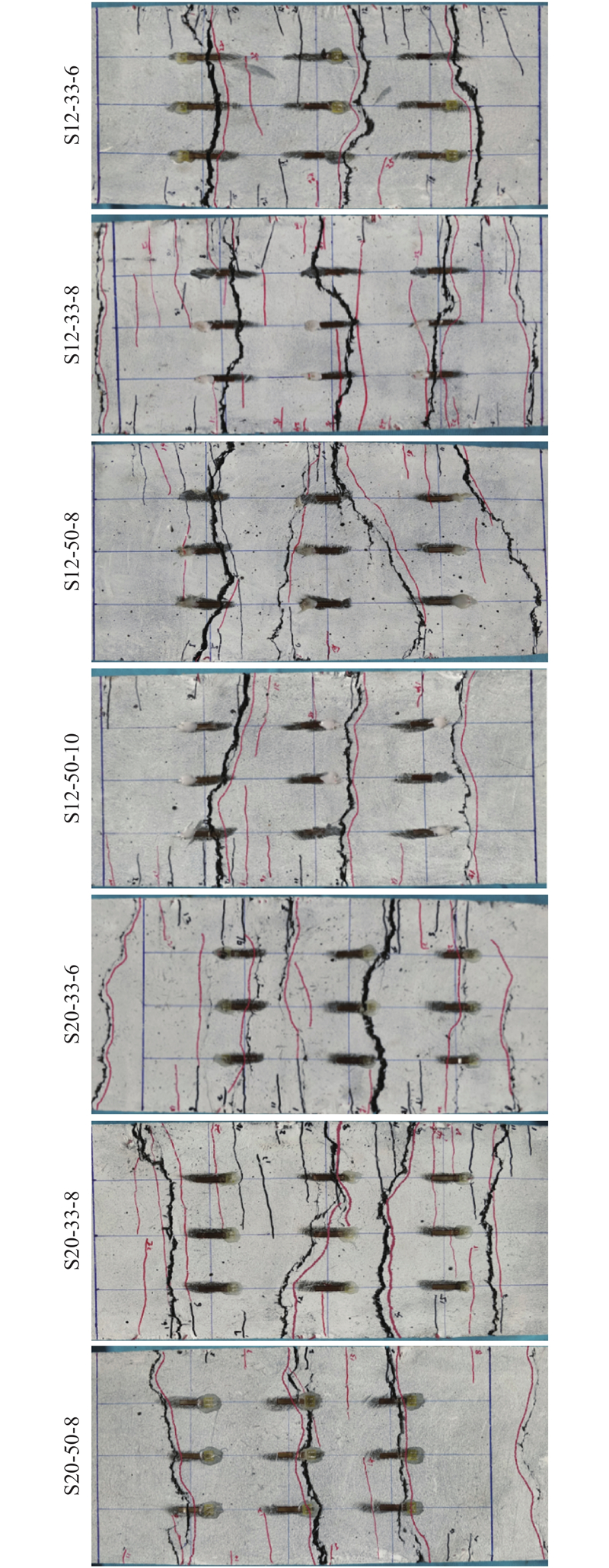
对于不同参数的构件,裂缝的发展具有相似的规律特征. 在弹性阶段,UHPC层未开裂,表面无裂缝;当荷载增大到弹性极限时,UHPC层顶面开始出现长度和宽度均较小的裂缝,构件进入裂缝扩展阶段. 随着荷载的增加,裂缝长度和宽度不断增大,且竖向发展逐渐变深,同时纯弯段继续出现新的裂缝,使得裂缝间距减小. 在钢筋屈服,构件进入屈服阶段后,纯弯段UHPC顶面逐渐形成3、4条主裂缝,裂缝宽度迅速增大. 由于支座位置受力比较复杂,最终破坏时,部分构件在支座附近的纯弯段以外出现了1、2条较宽的裂缝. 组合板UHPC顶面的最终裂缝形态如图5所示.
图 5
从图5可以看出,对于钢板厚度相同的构件,当截面配筋率增大时,构件的裂缝数量增多,裂缝的平均间距减小,裂缝分布更加密集,主裂缝的数量有增多的趋势(3、4条);对于采用同种类型钢筋的构件(S33-8和S50-8),钢筋间距减小,裂缝间距随之减小;对于配筋率比较接近的构件(S33-6和S50-8,S33-8和S50-10),当采用较细钢筋作为受拉钢筋时,构件的裂缝分布有更加密集的趋势. 主要原因是当构件的配筋率增大时,采用较细钢筋,可以减小钢筋间距,钢筋与UHPC之间的握裹更加均匀可靠,钢筋与UHPC之间的应变差值减小,传递长度减小,使得裂缝间距变小.
对于采用相同配筋形式的构件,当钢板厚度由12 mm增大至20 mm时,裂缝的分布形态和数量没有特别大的变化. 这主要是因为钢板厚度的增加,没有增强钢板与UHPC之间的黏结联系,且钢板主要处于受压状态,钢板对受拉UHPC的约束没有增强,因此钢板厚度无法对UHPC的裂缝分布产生影响.
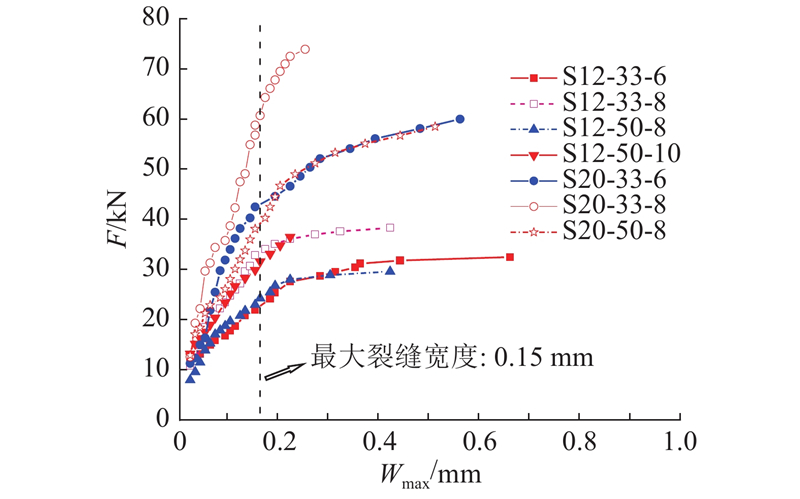
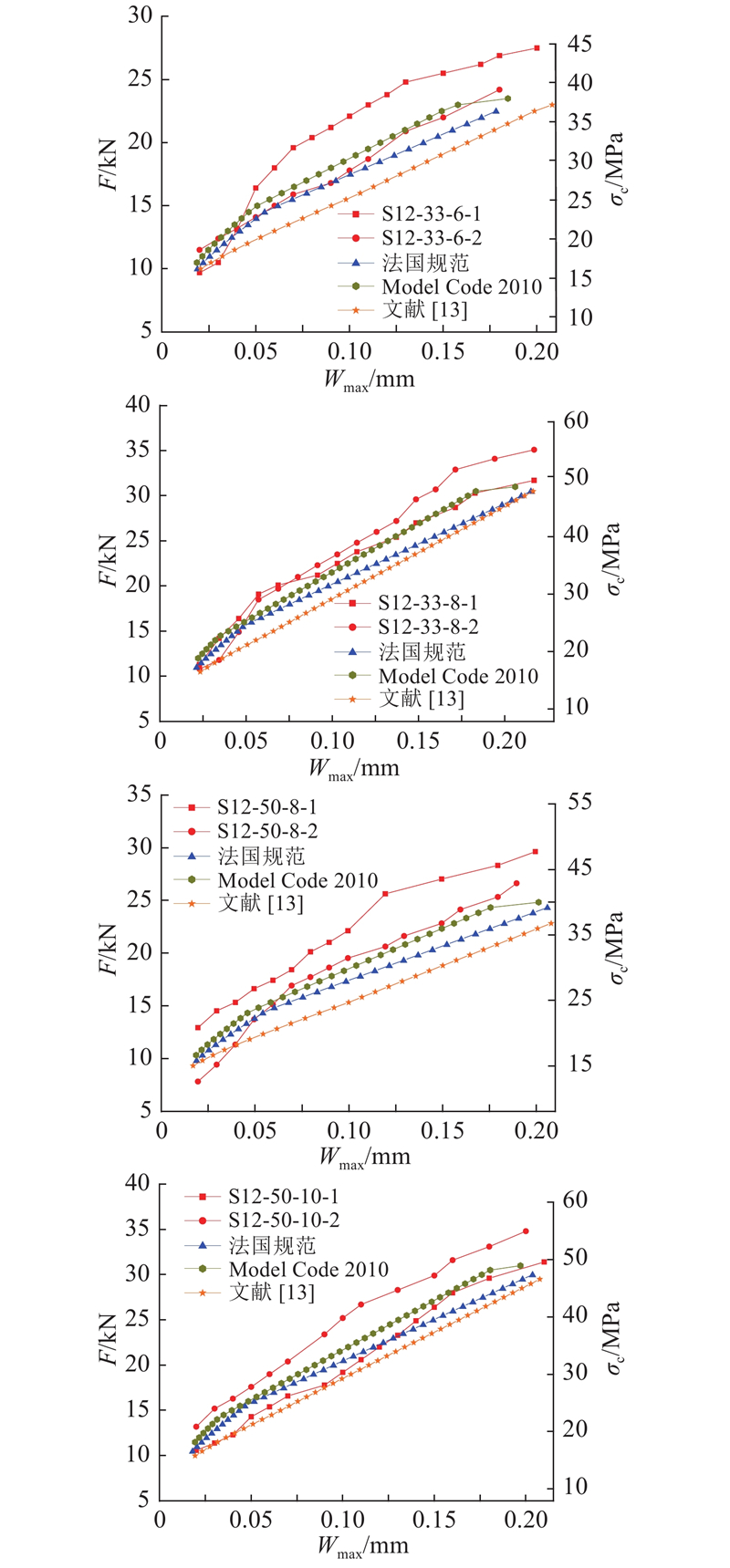
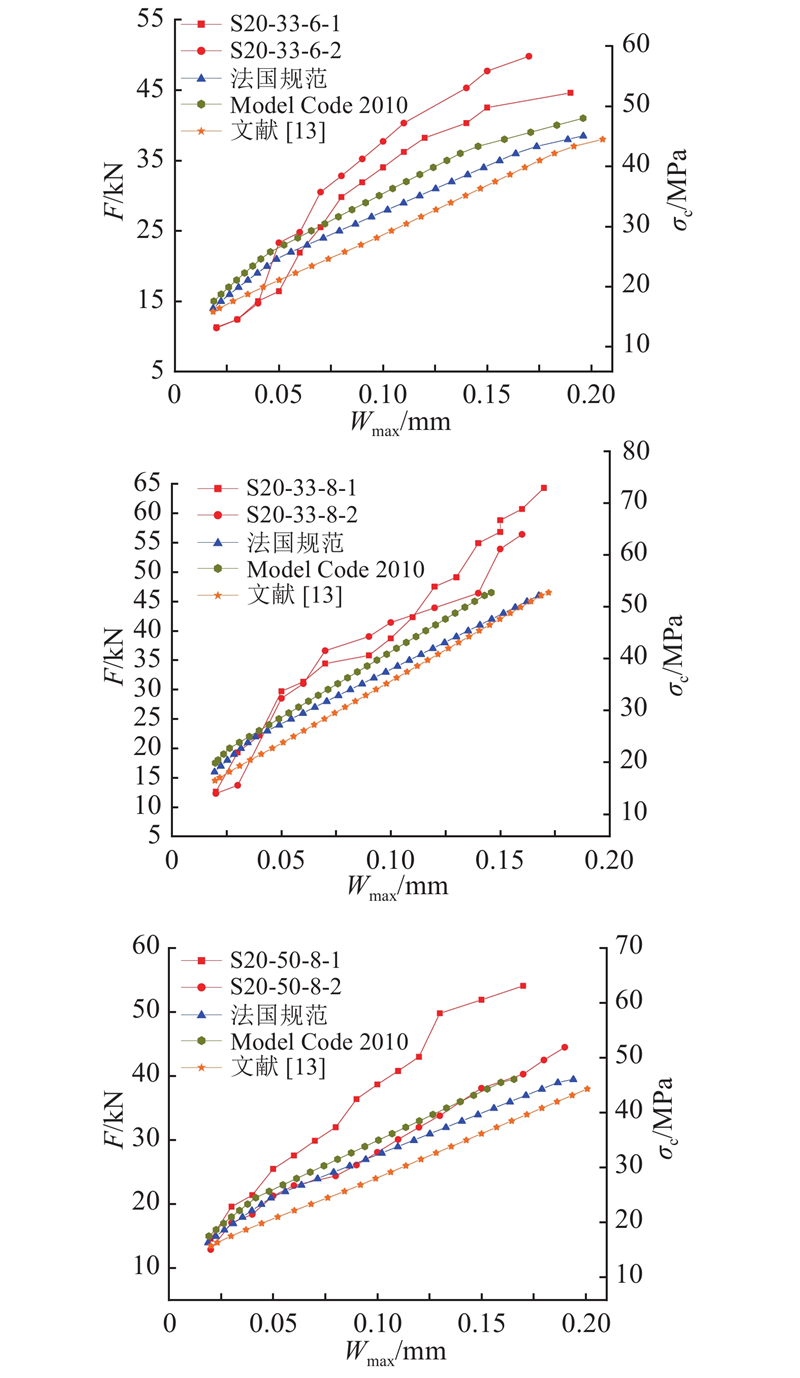
每组参数选取一个构件,绘制荷载与UHPC层顶面最大裂缝宽度曲线,如图6所示.
图 6
从图6可以看出,不同参数构件最大裂缝宽度曲线的发展规律基本一致:在裂缝萌生前期,裂缝宽度发展较缓慢;当最大裂缝宽度小于0.15 mm时,荷载与最大裂缝宽度近似呈线性关系;在最大裂缝宽度达到0.2 mm或钢筋屈服之后,最大裂缝宽度迅速增加. 对于钢板厚度为20 mm的构件,当最大裂缝宽度未达到0.2 mm时,受拉钢筋应力达到屈服强度,这与12 mm厚钢板构件是不同的.
通过以上的分析可知,增大配筋率,减小钢筋间距,可以有效地减小裂缝的平均间距并有效地约束裂缝的发展;钢板厚度不会对裂缝的分布产生影响,但当钢板厚度增大时,构件刚度提高,所以构件裂缝的出现和发展速度可以得到有效抑制.
2.3. 名义开裂应力计算及分析
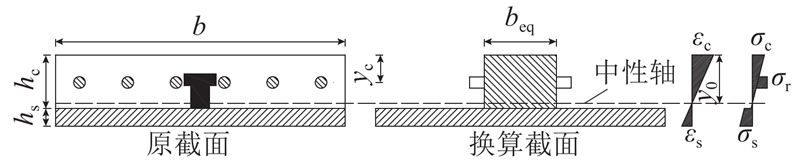
图 7
经截面换算后,按材料力学方法可得名义开裂应力
式中:
利用式(1)~(3)计算得到的名义开裂应力如表3所示. 由表可知,钢-超薄UHPC层组合板的名义开裂应力为25.3~33.0 MPa. 对表3数据进行设计参数的变量分析可知:对于配筋相同的组合板,当钢板厚度由12 mm增大到20 mm时,名义开裂应力提高5.4%~8.7%,表明增大钢板厚度可以提高名义开裂应力,但提高幅度有限;对于采用同种类型钢筋的构件(S33-8和S50-8),当钢筋间距由50 mm减小至33 mm时,名义开裂应力提高了17.7%~20.8%;对于采用相同钢筋间距的构件(S33-6和S33-8、S50-8和S50-10),当钢筋直径增大时,名义开裂应力提高了5.0%~20.8%,原因如下:减小钢筋间距或增大钢筋直径均可以增大配筋率,表明增大配筋率可以显著提高名义开裂应力. 当配筋率由2.4%提高到4.3%时,钢板厚12和20 mm构件的名义开裂应力分别增加了20.6%和20.0%,提升幅度接近,因此配筋率对名义开裂应力的影响与钢板厚度基本无关.
表 3 名义开裂应力计算结果
Tab.3
| 试件编号 | | |
| S12-33-6 | 16.1 | 25.3 |
| S12-33-8 | 19.4 | 30.5 |
| S12-50-8 | 16.1 | 25.9 |
| S12-50-10 | 17.2 | 27.2 |
| S20-33-6 | 23.5 | 27.5 |
| S20-33-8 | 29.1 | 33.0 |
| S20-50-8 | 23.4 | 27.3 |
对于配筋率相近的构件,当配筋形式采用S33-6和S50-8时,构件的名义开裂应力处于同一水平;当配筋形式采用S33-8和S50-10时,虽然S50-10构件的配筋率略高于S33-8构件,但名义开裂应力下降了12.1%. 原因如下:相比于常规的钢-UHPC层组合板,超薄体系的UHPC层的厚度仅为35 mm,当采用
通过以上的分析可知,配筋率和钢筋直径对名义开裂应力的影响较大,增大钢板厚度可以提高名义开裂应力,但提升幅度有限. 对于UHPC层厚度为35 mm的超薄体系,建议采用直径为8 mm的带肋钢筋作为配筋.
3. 最大裂缝宽度计算
目前对于UHPC裂缝宽度的计算,国内外的规范和规程尚无统一的计算方法. 在世界各国的规范中,UHPC裂缝宽度计算公式主要以综合分析理论和数理统计法为基础,考虑裂缝宽度的主要影响参数,得到裂缝宽度的计算公式.
法国规范[16]以综合分析理论为基础,考虑纤维长度、配筋率、保护层厚度及钢筋类型等的影响,根据不同的结构性质(配筋情况),计算公式不同. 规范中,假定UHPC层开裂后,截面应变分布满足平截面假定,考虑UHPC开裂后的强度.
欧洲模型规范(Model Code 2010)[18]是以普通混凝土的裂缝宽度计算方法为基础,考虑钢纤维阻裂增韧的作用,引入裂缝修正系数,对传递长度和裂缝形成阶段中裂缝处的最大钢筋应力进行修正,得到配筋钢纤维混凝土的裂缝宽度计算公式.
通过对40个常规钢-UHPC组合板的正交试验,参照《混凝土结构设计规范》(GB 50010−2010),邵旭东等[13]提出常规钢-UHPC组合板最大裂缝宽度的计算方法,给出计算公式:
式中:
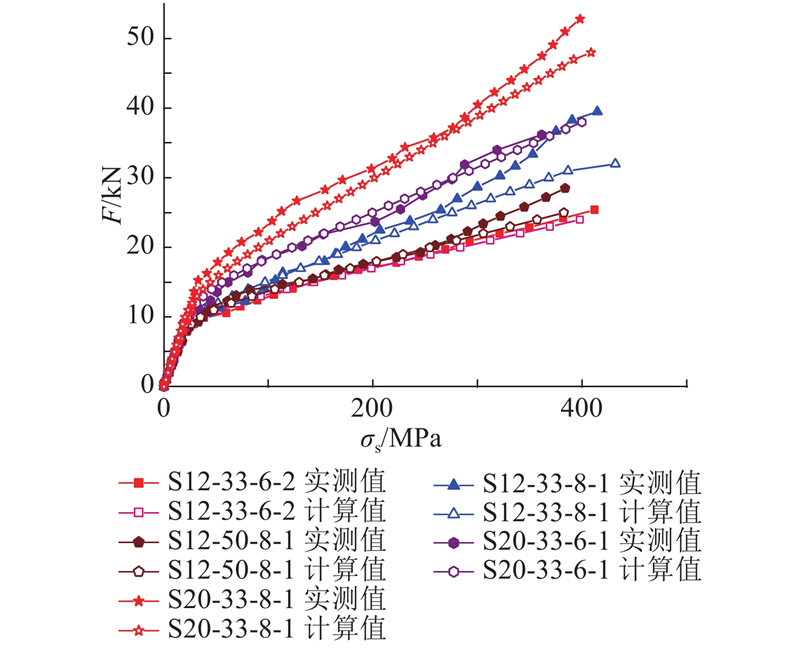
图 8
图 9
图 9
图 9 实测与计算裂缝宽度对比图
Fig.9 Contrast diagram of measured and calculated crack width
整体而言,对于基于超短栓钉的钢-超薄UHPC组合桥面结构的最大裂缝宽度计算,建议采用邵旭东等[13]提出的计算公式.
4. 有限元计算
为了进一步验证提出的超薄体系的可行性,采用有限元分析方法,建立整桥和局部梁段有限元模型,研究主梁和桥面体系的性能.
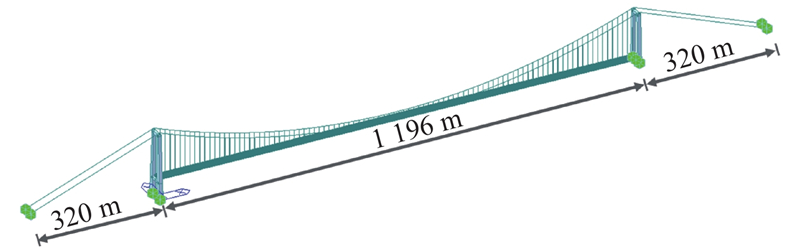
以某特大跨径悬索桥为工程背景,该大桥的主要设计参数如下:主跨跨径为1 196 m,矢跨比为1/10.5,吊索标准间距为12.4 m. 加劲梁采用扁平流线形钢箱梁,梁高3.0 m,宽30.5 m,横隔板间距为3.1 m. 桥面系为正交异性钢桥面:顶板厚16 mm,U肋厚8 mm,高280 mm,上口宽300 mm,下口宽170 mm,标准间距为600 mm.
4.1. 整体受力分析
采用Midas Civil有限元分析软件,建立不同铺装方案的全桥空间整体模型,计算桥梁第一体系的内力,铺装方案如表4所示. 表中,γc为材料重度.
表 4 整体计算铺装方案
Tab.4
| 铺装方案 | 铺装结构 | |
| 方案1(原铺装) | 60 mm 环氧沥青铺装层 | 环氧沥青:24 |
| 方案2-1 | 35 mm UHPC+15 mm TPO | TPO:20 |
| 方案2-2 | 35 mm UHPC+30 mm SMA | SMA:24 |
| 方案3 | 45 mm UHPC+30 mm SMA | UHPC:27 |
模型中,主缆和吊索采用索单元模拟,钢箱梁和桥塔采用梁单元模拟,铺装层以二期恒载的形式考虑. 计算模型如图10所示,计算结果重点关注主缆和吊索内力.
图 10
整体有限元计算结果如表5所示. 表中,
表 5 Midas整体计算结果
Tab.5
| 铺装方案 | | | | |
| 方案1 | 187696.6 | − | 1030.7 | − |
| 方案2-1 | 184338.7 | −1.8 | 1003.5 | −2.6 |
| 方案2-2 | 191561.9 | 2.1 | 1062.1 | 3.0 |
| 方案3 | 196179.7 | 4.5 | 1099.7 | 6.7 |
4.2. 局部有限元分析
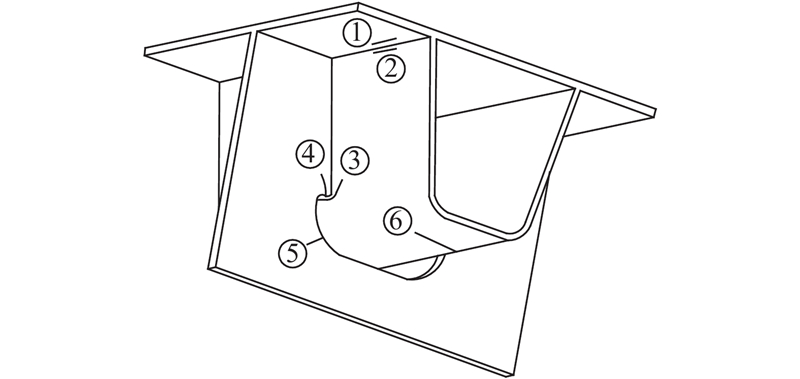
4.2.1. 钢桥面疲劳验算细节
图 11
4.2.2. 钢桥面疲劳验算方法及疲劳强度
《公路钢结构桥梁设计规范》(JTG D64−2015)中,给出正交异性钢桥面各典型疲劳验算细节的S-N曲线及疲劳强度取值. 依据该规范可知,各典型疲劳细节的疲劳强度和应力评定方法如表6所示. 表中,Δσc为疲劳强度(200万次).
表 6 钢桥面连接细节疲劳强度
Tab.6
| 细节编号 | | 评定方法 |
| 注:1)表中的疲劳强度已考虑疲劳抗力分项系数. | ||
| 细节① | 60.9 | 名义应力法 |
| 细节② | 60.9 | 名义应力法 |
| 细节③ | 69.6 | 名义应力法 |
| 细节④ | 69.6 | 名义应力法 |
| 细节⑤ | 60.9 | 名义应力法 |
| 细节⑥ | 95.7 | 名义应力法 |
4.2.3. 局部有限元模型
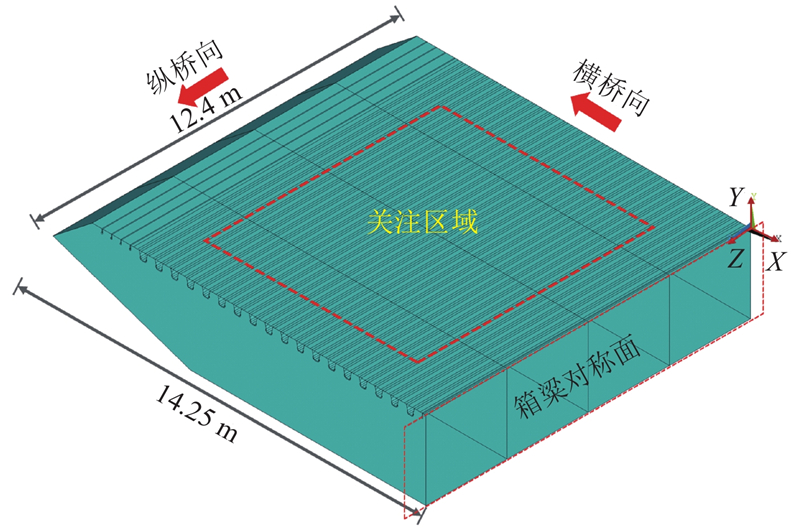
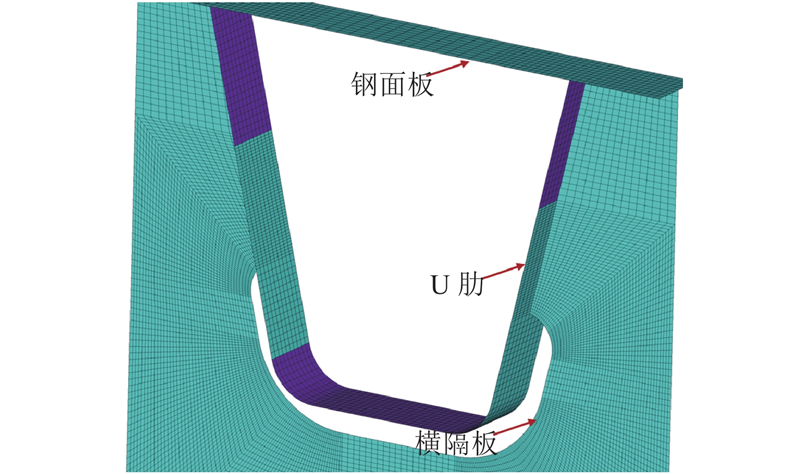
利用有限元分析软件ANSYS建立加劲梁标准梁段的节段模型,进行局部轮载分析. 为了节省计算时间和成本,局部有限元模型中忽略附属构造,选取半幅桥宽进行建模,模型宽14.25 m,长12.4 m. 疲劳和静力分析采用相同的有限元模型,局部有限元模型如图12所示.
图 12
图 13
图 13 有限元模型关键位置网格细化
Fig.13 Key location mesh refinement in finite element model
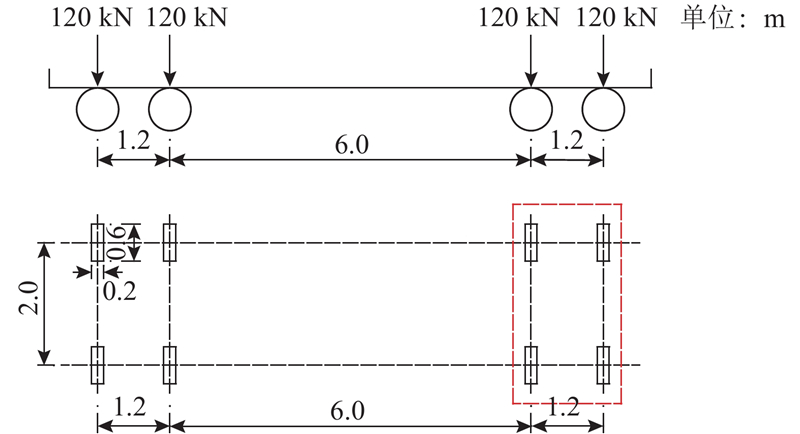
疲劳荷载采用《公路钢结构桥梁设计规范》(JTG D64−2015)中的标准疲劳车型III,如图14所示. 由于标准疲劳车的前、后轴轴距较大(相距6 m),且钢桥面板应力分布的局部性较强,可以忽略前、后车轴之间的叠加效应,只采用标准疲劳车的后轴(120 kN+120 kN)进行加载.
图 14
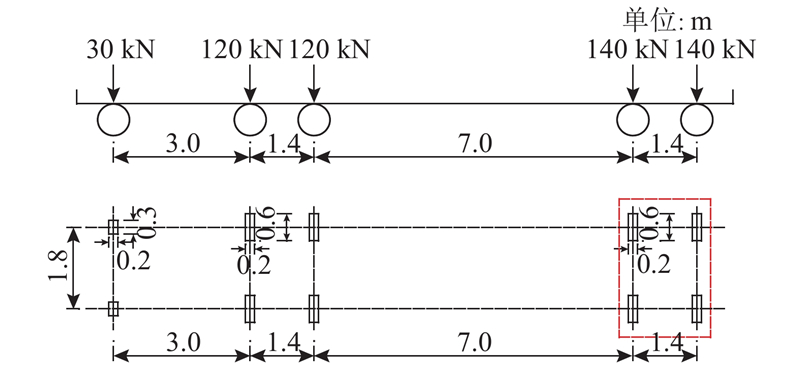
静力荷载采用《公路桥涵设计通用规范》(JTG D60−2015)中的标准车辆荷载,只考虑后轴(140 kN+140 kN)进行加载,如图15所示.
图 15
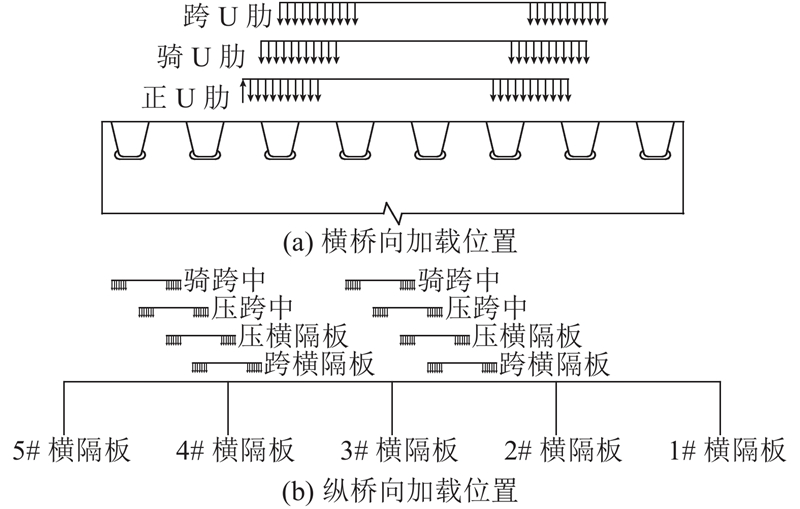
疲劳分析与静力分析采用相同的加载工况. 根据加载车辆以及正交异性钢桥面板的几何尺寸,在横桥向选取正U肋、骑U肋、跨U肋3种加载方式,在纵桥向分别移动双联轴加载位置,选取骑横隔板、压横隔板、压跨中、骑跨中4种加载方式,在2#横隔板和5#横隔板之间进行加载,共有24个加载工况,结合各细节应力历程,通过泄水法获得各细节最大应力幅,如图16所示.
图 16
表 7 钢结构各疲劳细节应力幅
Tab.7
| 细节编号 | | MPa | % | |
| 纯钢梁 | 超薄体系 | |||
| 细节① | 65.2 | 31.3 | 60.9 | 52.0 |
| 细节② | 62.0 | 40.8 | 60.9 | 34.2 |
| 细节③ | 83.3 | 64.7 | 69.6 | 22.3 |
| 细节④ | 49.0 | 38.81 | 69.6 | 20.8 |
| 细节⑤ | 43.7 | 39.3 | 60.9 | 10.1 |
| 细节⑥ | 43.4 | 36.7 | 95.7 | 15.4 |
静力荷载的计算结果表明,超薄UHPC层表面横桥向最大拉应力为8.4 MPa,顺桥向最大拉应力为6.6 MPa.
4.2.4. 超薄UHPC层最大应力
大跨径悬索桥属于柔性结构,使得UHPC层的顺桥向应力受第一体系的影响较大. 在前文的整桥有限元模型中,考虑恒载+四车道汽车荷载,可得超薄UHPC层的顺桥向最大应力
表 8 UHPC层应力计算结果
Tab.8
| 应力方向 | | | |
| 顺桥向 | 2.8 | 6.6 | 9.4 |
| 横桥向 | − | 8.4 | 8.4 |
5. 结 论
(1)组合板的裂缝分布呈现“多而密”的特点,且随着配筋率的增大,组合板的裂缝分布更加密集,最终破坏时的主裂缝有增多的趋势. 当UHPC表面最大裂缝宽度小于0.15 mm时,最大裂缝宽度的增长近似呈线性;在最大裂缝宽度达到0.2 mm或钢筋屈服以后,裂缝宽度迅速增大,但裂缝数量基本不再增加.
(2)配筋率和钢筋直径对名义开裂应力的影响较大,且当采用较小直径的钢筋时,提高配筋率可以最大幅度提高名义开裂应力;当钢板厚度从12 mm增加到20 mm时,名义开裂应力仅提高5.4%~8.7%,提升幅度有限,表明钢板厚度对超薄体系名义应力的影响不大.
(4)有限元分析结果表明:当采用超薄体系替换常规钢桥面铺装时,主缆和吊索内力的变化小于3.0%,桥梁结构的整体受力状态基本无变化,可以保证特大跨径桥梁的整体安全性;超薄体系可以显著改善正交异性钢桥面板的受力性能,钢桥面各典型疲劳细节应力降幅为10.1%~52.0%,且降幅后的最大应力幅均小于200万次疲劳强度;试验得到超薄体系的开裂强度是实桥UHPC层最大弯拉应力的3.0~3.9倍,具有足够的安全储备,方案应用于实际工程是完全可行的.
(5)本文建议UHPC层厚为35 mm的超薄体系采用直径为8 mm的带肋钢筋作为配筋,钢筋间距为33~50 mm,保护层厚度为15 mm,超短栓钉间距与常规钢-UHPC轻型组合桥面保持一致,取150~200 mm.
参考文献
正交异性钢桥面板的疲劳研究综述
[J].DOI:10.3969/j.issn.1007-9963.2009.09.003 [本文引用: 2]
Review of fatigue research for orthotropic steel bridge decks
[J].DOI:10.3969/j.issn.1007-9963.2009.09.003 [本文引用: 2]
Evaluation of cracking in the rib-to-deck welds of the Bronx-Whitestone Bridge
[J].
Empirical design rules for effective utilization of orthotropic decks
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000462 [本文引用: 1]
Retrofit of an orthotropic steel deck with compact reinforced reactive powder concrete
[J].
Basic performance of the composite deck system composed of orthotropic steel deck and ultra-thin RPC layer
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000348 [本文引用: 1]
大跨径钢桥面铺装设计理论与方法研究
[J].DOI:10.3321/j.issn:1000-131X.2005.01.007 [本文引用: 1]
Research on theory and method of long-span steel bridges deck surfacing design
[J].DOI:10.3321/j.issn:1000-131X.2005.01.007 [本文引用: 1]
Static and fatigue properties of the Steel-UHPC lightweight composite bridge deck with large U ribs
[J].DOI:10.1016/j.jcsr.2018.05.011 [本文引用: 1]
钢-超薄UHPC层轻型组合桥面性能研究
[J].
Performance of light-type composite bridge dec-k system with steel and ultra-thin UHPC layer
[J].
钢-UHPC轻型组合桥面结构试验及裂缝宽度计算研究
[J].
Experimental study and crack width calculation of steel-UHPC lightweight composite deck structure
[J].
钢-超高性能混凝土组合板开裂荷载正交试验及计算方法
[J].
Orthogonal test and calculation method of cracking load of steel-ultra-high performance concrete composite specimen
[J].
钢-UHPC组合板受弯性能的试验研究
[J].
Experimental study on flexural behavior of steel-UHPC composite slabs
[J].
带大U肋的轻型组合桥面板基本力学性能
[J].DOI:10.3969/j.issn.1001-7372.2018.08.010 [本文引用: 1]
Fundamental mechanical performance of lightweight composite bridge deck with large U-ribs
[J].DOI:10.3969/j.issn.1001-7372.2018.08.010 [本文引用: 1]
钢-STC轻型组合桥面结构多参数分析
[J].
Multi-parametric analysis on steel-STC lightweight composite bridge deck
[J].