浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(10): 2009-2017 doi: 10.3785/j.issn.1008-973X.2020.10.019

能源工程、机械工程

基于空间动力学优化的机床结构件质量匹配设计

黄华,, 邓文强, 李源, 郭润兰

Mass matching design of machine tool parts based on spatial dynamics optimization

HUANG Hua,, DENG Wen-qiang, LI Yuan, GUO Run-lan

收稿日期: 2019-11-12  

Received: 2019-11-12  

作者简介 About authors

黄华（1978—），男，副教授，博士，从事数控技术及装备的研究.orcid.org/0000-0002-4945-5888.E-mail：hh318872@126.com , E-mail：hh318872@126.com

摘要

提出基于整机空间动力学预测模型、以移动结构件质量为设计变量的多目标匹配设计方法. 基于机床移动件的工作行程构建整机工作空间，运用正交试验法进行空间位姿试验设计，建立整机空间固有频率预测模型；在工作空间内对机床进行动力学性能的灵敏度分析，识别动力学的最优位姿和最差位姿；以最差位姿机床固有频率为优化目标，采用多目标质量匹配法对移动部件的质量进行最佳分布设计；重新计算优化后机床的固有频率，通过频率响应分析，比较优化前、后机床在最差和最优位姿下的动力学性能. 结果表明，经过多目标质量匹配优化后，机床的固有频率得到了提高，刀尖节点的最大频响振幅明显降低，机床的整机动力学性能有了较大程度的改善.

关键词： 空间位姿 ; 预测模型 ; 动态特性 ; 多目标优化 ; 质量匹配

Abstract

A multi-objective matching design method based on the whole machine space dynamics prediction model was proposed by taking the moving structure mass as design variables. The whole machine workspace was constructed based on the working stroke of the moving parts of the machine tool. Then the orthogonal test method was used to design the spatial pose, and the prediction model of the spatial natural frequency was established. The sensitivity analysis of the machining path was conducted in the workspace. The best and worst position was identified. Then the optimal distribution of the mass of moving parts was designed by multi-objective mass matching method by taking the natural frequency of the machine tool with the worst position as the optimization objective. The natural frequency of the optimized machine tool was calculated. The dynamic characteristics of the best and worst position before and after optimization were analyzed and compared. Results show that the natural frequency of the machine tool was improved with the optimization of multi-objective mass matching, and the maximum frequency response amplitude of the tool tip was significantly reduced. The dynamic performance of the machine tool was greatly improved.

Keywords： spatial pose ; prediction model ; dynamic characteristics ; multi-objective optimization ; mass matching

PDF (1203KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

黄华, 邓文强, 李源, 郭润兰. 基于空间动力学优化的机床结构件质量匹配设计. 浙江大学学报(工学版)[J], 2020, 54(10): 2009-2017 doi:10.3785/j.issn.1008-973X.2020.10.019

HUANG Hua, DENG Wen-qiang, LI Yuan, GUO Run-lan. Mass matching design of machine tool parts based on spatial dynamics optimization. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(10): 2009-2017 doi:10.3785/j.issn.1008-973X.2020.10.019

机床动态性能对加工精度有重要影响[1-2]，然而传统的机床动态特性研究往往局限于某一固定位姿，忽略了整个工作空间内动态特性随着各移动件质量分布和位姿改变而发生变化的趋势[3-5]，难以获得机床的最优性能. 在研究机床空间动态特性的基础上，有必要对整机运动空间内的性能进行优化.

目前，已有学者对机床工作空间的动力学性能进行了研究. 刘海涛等[6]提出广义模态和广义刚度场的概念，研究广义加工空间内机床的动态特性变化，以三轴龙门机床和四轴立式机床为例进行了验证. 王磊等[7]以超重型卧式镗床为例，分析广义加工空间内的模态和刚度场特性. 刘响求[8]运用多轴联合自激励方法，获取工作空间内的全模态参数，通过空间划分分析数控机床在工作空间的动态特性. 笔者等[9]运用响应面模型研究机床在广义空间内的切削稳定性，以最小临界切削深度为评判，说明了立柱位置对切削稳定性的重要影响. 李天箭等[10]采用空间统计学方法，建立机床工作空间内的动力学性能预测Kriging模型，与其他模型进行比较，证明了该模型的精确性. 于长亮等[11]通过对机床整机的动刚度分析，辨识出立柱是整机x向和z向动刚度的最薄弱环节，利用灵敏度分析法和拓扑优化方法对立柱进行优化. 邓聪颖等[12]通过响应面模型，揭示了机床动态特性在工作空间内的变化规律，定义影响因子识别不同位姿对x、y、z轴的影响程度，为工艺路线规划提供指导.

上述研究虽然对机床广义工作空间内的动态特性进行了分析和优化，但未识别出机床在工作空间内的最差位姿和最优位姿，忽略了各移动部件质量分布和位姿变化对机床动力学性能的影响规律. 本文基于响应面分析法，获取较高精度的机床空间固有频率预测模型；采用灵敏度分析法，确定各移动部件对整机空间固有频率的影响大小和次序；通过遗传算法识别出机床在工作空间内的最差位姿和最优位姿，进行多目标质量匹配优化设计，从而提高机床的动态性能.

1. 机床空间动态特性定义

基于动力学知识可知，机床在某一位姿下的动态特性本构方程为

${{M\ddot q}} + {{C\dot q}} + {{K}}{{q}} = {{0}}.$

式中：M为机床的质量矩阵，C为机床的阻尼矩阵，K为机床的刚度矩阵，q=[x, y, z]T.

当机床处于工作状态时，各移动件的位置不断变动，导致机床整体结构发生改变，使得机床的

M、C和K发生改变，因此机床的动态特性会随着移动件位置的变化而改变. 在加工空间内，M、C和K均可以视为各移动件空间位姿(x，y，z)的函数，故机床空间动态特性的本构方程可以描述为

$ {{M}}(x,y,z){\ddot{ q}} + {{C}}(x,y,z){{\dot q}} + {{K}}(x,y,z){{q}} = {{0}}. $

式中：x、y、z为工作台、立柱、主轴箱相对于原始位置的线位移，指机床x轴、y轴、z轴的线位移.

当结构件质量发生改变时，机床空间动态特性的本构方程可以描述为

$ \left( {{{M}}(x,y,z) + \Delta {{m}}(x,y,z)} \right){\ddot{ q}} + {{C}}(x,y,z){{\dot q}} + {{K}}(x,y,z){{q}} = {{0}}. $

式中： $\Delta { m} $为机床结构件的质量变化矩阵.

根据上述运动微分方程，采用模态分析法求解，得到结构件质量变化后机床的第r阶固有频率：

${\omega _{ir}} ={({{1 + {\phi}_r^{\rm T}\Delta m(x,y,z){\phi} _{r}}}}) ^{-1/2} {\omega _{0r}}.$

式中：i为机床结构模型的自由度编号，ω0r为结构件质量变化前机床的第r阶固有频率， ${\phi}_r $为结构件质量变化后机床的第r阶模态振型. 由式(4)可知，对于机床空间动态特性而言，机床固有频率是空间位姿(x, y, z)的函数. 作为机床动态特性的重要指标，固有频率的精确性严重影响机床动态特性的预测精度. 为了研究机床在工作空间内的动态特性，应着重分析固有频率的变化规律[13-14].

2. 机床空间固有频率预测模型的建立

机床的动态特性会随着各坐标轴线位移的改变而发生变化. 为了获得机床空间的固有频率预测模型，须对机床的不同位姿进行模态测试分析. 由于机床的空间位姿可以离散为无数组空间坐标组合，模态试验时研究不同位姿变化对机床固有频率的影响. 为了提高计算效率，引入正交试验法，利用有限元模态分析获得机床各空间位姿的前5阶固有频率，通过响应面分析法得到机床的空间固有频率预测模型.

2.1. 机床空间位姿正交试验设计

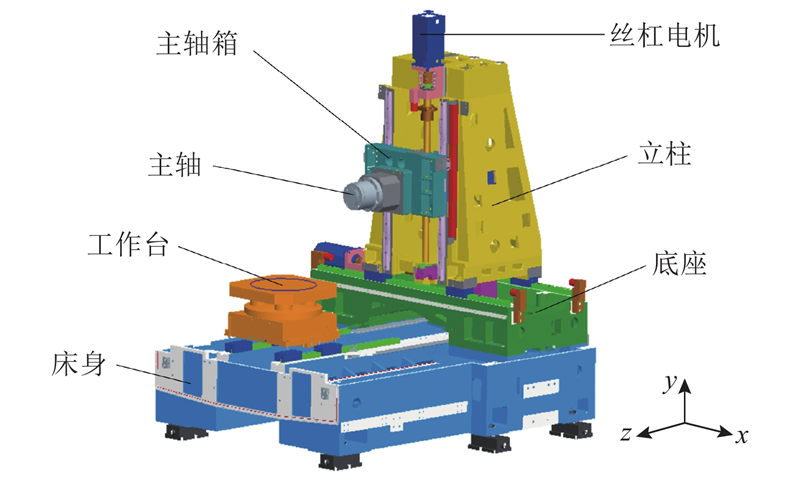
选用HMC630卧式加工中心作为研究对象，如图1所示. 工作台、立柱和主轴箱分别沿着x、y、z方向移动，各向行程分别如下：x方向为800 mm，y方向为700 mm，z方向为550 mm.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   HMC630卧式加工中心

Fig.1   HMC630 Horizontal Machining Center


为了建立机床空间的固有频率预测模型，根据移动件行程构建工作空间，将移动件在工作空间内的位姿坐标离散化，分为x、y、z 3个因素，每个因素内均匀设置5个水平，如表1所示. 采用正交试验法，对机床移动件在工作空间内的位姿坐标进行试验设计，共得到25组试验，如表2所示.

表 1   正交试验因素与水平

Tab.1  Orthogonal experimental factors and levels

水平 因素
x/m y/m z/m
1 0.02 0.02 0.02
2 0.2 0.175 0.1375
3 0.4 0.35 0.275
4 0.6 0.525 0.4125
5 0.78 0.68 0.53

新窗口打开| 下载CSV


表 2   位姿正交试验表

Tab.2  Orthogonal experiment of position

试验号 位姿坐标
x/m y/m z/m
1 0.02 0.02 0.02
2 0.02 0.175 0.1375
3 0.02 0.35 0.275
4 0.02 0.525 0.4125
5 0.02 0.68 0.53
6 0.2 0.02 0.1375
7 0.2 0.175 0.275
8 0.2 0.35 0.4125
9 0.2 0.525 0.53
10 0.2 0.68 0.02
11 0.4 0.02 0.275
12 0.4 0.175 0.4125
13 0.4 0.35 0.53
14 0.4 0.525 0.02
15 0.4 0.68 0.1375
16 0.6 0.02 0.4125
17 0.6 0.175 0.53
18 0.6 0.35 0.02
19 0.6 0.525 0.1375
20 0.6 0.68 0.275
21 0.78 0.02 0.53
22 0.78 0.175 0.02
23 0.78 0.35 0.1375
24 0.78 0.525 0.275
25 0.78 0.68 0.4125

新窗口打开| 下载CSV


2.2. 整机有限元建模及结合面的处理

根据表2提供的机床移动件位姿坐标，重新建立不同空间位姿下机床的CAD模型，导入有限元软件中进行固有频率的分析计算. 分析时，设置主轴的材料为钢，其他结构件的材料均为铸铁，钢和铸铁的主要参数如表3所示. 表中，ρ为密度，E为弹性模量，μ为泊松比，ξ为阻尼比.

表 3   钢和铸铁的材料参数

Tab.3  Material parameters for steel and cast iron

材料 ρ/(kg·m−3) E/GPa μ ξ
钢 7850 200 0.30 0.28
铸铁 7200 110 0.28 0.006

新窗口打开| 下载CSV


导轨、螺栓及旋转结合面的存在对机床的动态特性影响很大[15-16]. Burdekin等[17-18]的研究表明：机床结合部的接触刚度占机床总刚度的60%~80%,结合部的接触阻尼占机床全部阻尼的90%以上，结合部引起的变形量占机床总变形量的40%~60%, 因此结合面的处理对机床有限元建模的准确性至关重要. 为了提高计算结果的准确性，将整机模型中的导轨滑块结合部、丝杠螺母结合部及螺栓结合部用参数已知的等效弹簧阻尼系统代替，其他结合部简化为固定结合. 查阅通用数据库和文献[19~21]，采用吉村允孝法和模态试验方法，获取机床主要结合部的等效刚度和阻尼参数，结果如表4所示. 表中，k为刚度系数，ζ为阻尼系数.

表 4   主要结合部的等效刚度和阻尼参数

Tab.4  Equivalent stiffness and damping parameters of joints

结合部类型 k / (N·m−1) ζ / (N·s·m−1)
导轨滑块法向 4.9×106 3150
导轨滑块切向 4.2×106 1400
丝杆螺母轴向 1.7×106 3200
螺栓法向 9.0×106 6860
螺栓切向 7.8×106 5500

新窗口打开| 下载CSV


有关所建立有限元模型的准确性问题，笔者等[9]的实验研究结果表明：通过对关键结合部的有效处理，采用有限元建模方法获得的机床固有频率与模态实验获得的相比，误差基本都小于3%. 本文采用的有限元建模方法与文献[9]方法基本相同，因此准确性有保证，不作详细论述.

按照建立的有限元模型对机床不同空间位姿的前5阶固有频率进行计算，结果如表5所示. 表中，f1~f5为机床1~5阶固有频率.

表 5   正交试验结果

Tab.5  Results of orthogonal experiment

试验号 f1/Hz f2/Hz f3/Hz f4/Hz f5/Hz
1 64.215 71.125 148.50 199.19 212.03
2 65.631 72.928 147.55 205.56 217.52
3 65.630 73.673 145.08 211.32 221.69
4 63.995 71.216 139.55 210.05 224.00
5 69.530 80.051 139.90 239.68 243.26
6 64.211 70.475 146.21 201.19 215.28
7 65.098 71.842 143.10 206.99 220.27
8 64.254 72.413 140.08 211.84 224.32
9 62.146 70.023 135.10 209.57 224.63
10 64.607 71.649 150.37 201.22 213.29
11 63.682 69.430 141.86 202.19 218.09
12 64.573 71.680 139.53 210.28 225.33
13 70.307 85.978 140.70 238.65 252.55
14 65.857 74.416 151.69 206.07 215.94
15 64.571 70.841 147.78 203.02 216.33
16 62.404 68.259 137.13 202.42 220.20
17 61.911 69.460 133.94 207.20 223.36
18 66.171 75.681 152.24 206.73 216.89
19 65.849 73.548 149.12 208.59 218.43
20 64.069 69.794 143.28 203.77 219.17
21 60.671 67.130 132.92 202.07 220.87
22 65.646 73.803 150.05 203.48 214.90
23 66.163 74.787 149.68 209.48 219.10
24 65.322 72.449 144.50 209.89 221.29
25 62.833 68.567 138.40 203.60 221.10

新窗口打开| 下载CSV


2.3. 求解整机空间固有频率预测模型

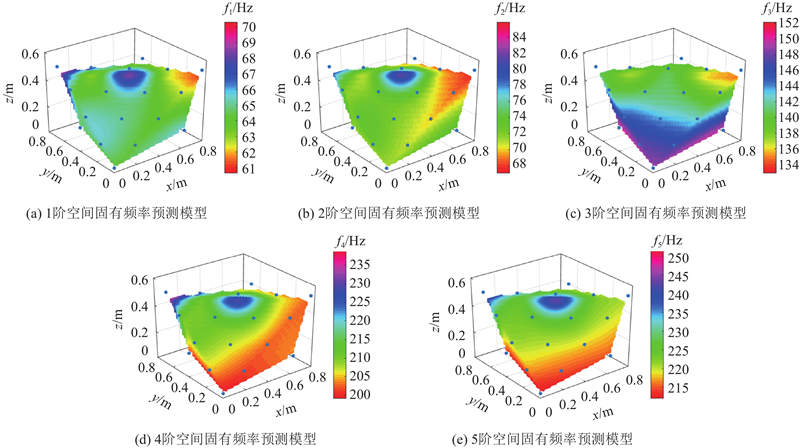
以机床各空间位姿前5阶固有频率，采用响应面分析法在Matlab软件中建立机床的空间固有频率的预测模型:

${{\omega }}{\rm{ = }}\left[ {{\omega _{\rm{1}},}\;\;{\omega _{\rm{2}},}\;\;{\omega _{\rm{3}},}\;\;{\omega _{\rm{4}},}\;\;{\omega _{\rm{5}}}} \right] = {{X\beta }}.$

式中：ω1~ω5分别为机床的前5阶固有频率；β为基函数待定系数矩阵；X为基函数，X=[1, x4, y4, z4, x3, y3, z3, x2, y2, z2, x3y, x3z, xy3, y3z, xz3, yz3, x2y2, y2z2, x2z2, x2yz, xy2z, xyz2].

为了检验空间固有频率预测模型的可靠性，采用决定系数 ${R^2}$对该模型进行评估. 一般该数值越接近1表明预测模型精度越高，预测值越准确.

${R^2} = 1 - \frac{{{S_{\rm{SE}}}}}{{{S_{\rm{ST}}}}},$

${S_{{\rm{SE}}}} = \sum\limits_{i = 1}^N {({Y_i} - {y_i}} {)^2},$

${S_{{\rm{ST}}}} = \sum\limits_{i = 1}^N {{Y_i}^2 - } {{{{\left(\sum\limits_{i = 1}^N {{y_i}} \right)}^2}} \bigg/ N}.$

式中： $N$为试验点的个数， ${Y_i}$为试验样本点的响应值， ${y_i}$为预测模型的近似值.

通过计算得到机床前5阶空间固有频率预测模型的决定系数，如表6所示. 结果表明，建立的机床空间固有频率预测模型满足精度要求.

表 6   预测模型精度检验

Tab.6  Accuracy test of prediction model

ω R2 ω R2
ω1 0.996 5 ω4 0.998 4
ω2 0.998 6 ω5 0.998 7
ω3 0.999 2 − −

新窗口打开| 下载CSV


如图2所示为机床空间固有频率预测模型，通过颜色变化表示机床移动件在工作空间内运动对机床固有频率的影响. 由图2可知，除第3阶空间固有频率预测模型以外，机床移动件位姿变化对其余4阶空间固有频率的影响基本相同. 对于第3阶空间固有频率而言，当主轴箱沿z向坐标越低时，机床的动态性能越好；对于其余4阶空间固有频率而言，当工作台和立柱处于坐标轴中心位置而主轴箱z向坐标越大时，机床的动态性能较好.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   机床空间固有频率预测模型

Fig.2   Spatial inherent frequency prediction model of machine tools


3. 坐标轴灵敏度分析及机床位姿识别

由机床空间固有频率预测模型可知，当移动件在加工过程中不断改变位置时，机床的动态特性会随之变化. 为了保证机床在加工过程中的稳定性，针对空间固有频率对加工路径进行灵敏度分析，确认关键加工路径，完成对加工工艺的路径规划.

根据建立的预测模型，通过DOE分析，获得空间固有频率对各坐标轴的全局效应α，确定各坐标轴对固有频率的影响，结果如图3所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   固有频率对坐标轴的全局效应

Fig.3   Global effect of inherent frequency on coordinate axis


由图3可知，空间固有频率对z轴的全局效应最大，即z轴对机床空间固有频率的影响最大；x轴和y轴对固有频率的影响相差无几. 当规划加工路径时，应优先移动x轴和y轴，最后移动z轴.

坐标轴灵敏度分析结果可以用于解释图2中的现象. 对于第1、2、4、5阶空间固有频率而言，x、y、z轴对机床固有频率的影响系数基本相等，当x、y、z取中间值时，工作台、立柱和主轴箱位于机床的左右中轴线上，主轴箱位于立柱的中部，机床整机的质量分布较均匀，结构上较稳定，此时整机的固有频率较大，动态性能较好. 对于第3阶空间固有频率而言，z轴对机床固有频率的影响系数远大于x轴和y轴，当z轴移动距离较大时，立柱在外部激励的作用下容易产生摆动，此时整机的固有频率较小，动态性能较差.

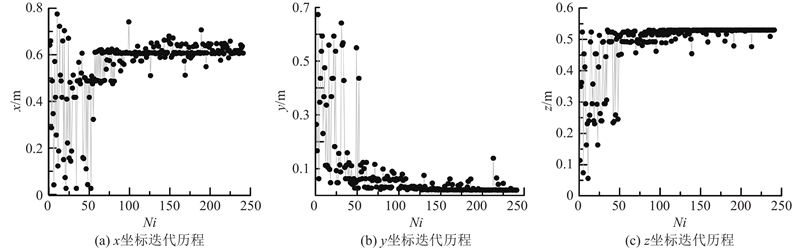
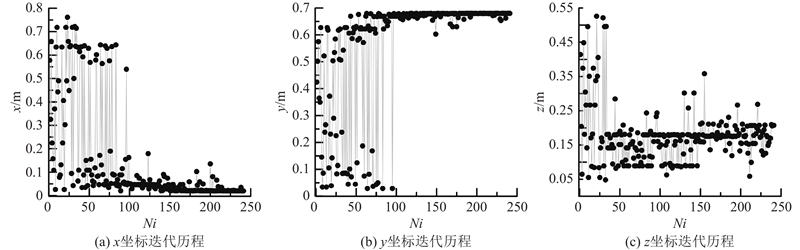
为了获得机床工作空间内的最差位姿和最优位姿，运用遗传算法在工作空间内识别出机床固有频率的最差位姿坐标和最优位姿坐标. 当机床处于加工状态时，各移动件应避免最差位姿坐标，保证机床具有较高的固有频率，以减少机床发生共振的几率，从而提高机床的加工稳定性和被加工件的表面质量.

如图4、5所示分别为最差位姿和最优位姿的坐标迭代历程图. 图中, Ni为迭代次数.由图4可知，工作空间内机床动态特性最差位姿的x坐标随着迭代次数的增加而逐渐稳定于0.607 4 m附近, y坐标随着迭代次数的增加而逐渐稳定在0.020 1 m处, z坐标逐渐稳定于0.53 m. 由图5可知，机床动态特性最优位姿的x坐标随着迭代次数的增加而逐渐稳定于0.02 m，y坐标逐渐稳定在0.68 m，z坐标逐渐稳定在0.207 4 m. 综上所述，机床工作空间内的最差位姿如下：x=0.607 4 m，y=0.020 1 m，z=0.53 m；最优位姿如下：x=0.02 m，y=0.68 m，z=0.207 4 m.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   最差位姿坐标迭代历程图

Fig.4   Iterative history diagram of worst position coordinates


图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   最优位姿坐标迭代历程图

Fig.5   Iterative history diagram of best position coordinates


4. 移动件多目标质量匹配优化

质量匹配设计可以将机床各移动件质量与整机动态特性相结合，从全局的角度指导工作台、立柱和主轴箱的质量分布，减少因结构件质量分布不均造成的加工速度和能量的损耗. 选取机床最差位姿，针对工作台、立柱和主轴箱等移动件，以整机前5阶模态固有频率最大为目标，开展质量匹配优化. 优化时，固定各移动件的空间位置，以保证优化结果的准确性. 将工作台、立柱和主轴箱质量划分为−1、0和1共3个水平，以各移动件初始设计质量作为0水平，将初始质量的80%和120%分别作为−1水平和1水平，详细数据如表7所示.表中，m1为工作台质量，m2为立柱质量，m3为主轴箱质量.

表 7   移动件质量试验设计水平表

Tab.7  Levels for mass test of moving parts

kg
水平 m1 m2 m3
−1 1209.115 2245.745 293.764
0 1511.400 2807.200 367.200
1 1813.672 3368.618 440.646

新窗口打开| 下载CSV


基于三因素三水平，选择Box-Behnken方法对移动件质量分布进行方案设计. Box-Behnken方法是响应曲面设计方法的一种，适合于5因素以下且每个因素只有3个水平的响应面设计，可以在因素数相同时减少试验次数，从而提高计算效率. 可得各移动件质量分布试验表，如表8所示.

表 8   移动件质量分布试验表

Tab.8  Test table for mass distribution of moving parts

kg
试验号 移动件质量
m1 m2 m3
1 1209.115 2245.745 293.764
2 1209.115 3368.618 367.200
3 1813.672 2245.745 367.200
4 1813.672 3368.618 367.200
5 1209.115 2807.200 293.764
6 1209.115 2807.200 440.646
7 1813.672 2807.200 293.764
8 1813.672 2807.200 440.646
9 1511.400 2245.745 293.764
10 1511.400 2245.745 440.646
11 1511.400 3368.618 293.764
12 1511.400 3368.618 440.646
13 1511.400 2807.200 367.200

新窗口打开| 下载CSV


根据表8可知，对每一组试验进行响应值计算，求出机床前5阶模态固有频率，通过最小二乘法建立m1、m2及m3与机床前5阶模态固有频率的回归方程模型.

如图6所示为各移动件质量对机床各阶固有频率的主效应. 可知，各移动件质量对机床动态特性的影响不同. 由图6(a)可知，m1与机床前5阶固有频率的关系表现为：近似平行的直线，故m1对机床动态特性的影响较小；由图6(b)可知，m2对机床动态特性的影响较大；由图6(c)可知，m3对机床1、2阶固有频率的影响较小，对3~5阶固有频率的影响较大. 综上所述，m2对机床动态特性的影响最大，m3次之，m1最小. 为了提高机床的动态特性，应依次调整各移动件的质量.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

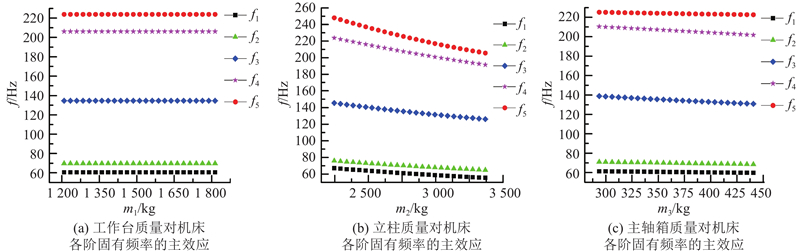
图 6   移动件质量对机床各阶固有频率的主效应

Fig.6   Main effect of moving parts mass on natural frequencies of machine tools


根据移动件质量与机床前5阶固有频率之间的回归方程模型，将机床各阶固有频率的最高值设置为优化目标. 利用Box-Behnken方法设计13组试验方案，事实上全部的试验参数组合有17种，有4种是归因实验. 为了避免丢失重要的试验结果，同时为了提高计算效率，选用NSGA-II多目标遗传算法进行移动件的质量匹配优化，获得m1、m2和m3的最优分布设计.

如表9所示为质量匹配优化前、后机床移动件的质量变化对比. 与优化前相比，工作台、立柱和主轴箱的质量均发生不同程度的改变，其中工作台质量增加了8.5%，立柱和主轴箱质量均减少了20%. 总体来讲，机床移动件的总质量减少了约10.8%，降低了机床移动件在加工过程中的能量消耗，节省了制造成本.

表 9   优化前、后各移动件质量变化对比

Tab.9  Comparison of mass changes of moving parts before and after optimization

kg
状态 m1 m2 m3
优化前 1511.400 2807.200 367.200
优化后 1639.916 2245.745 293.801

新窗口打开| 下载CSV


5. 优化结果分析

将机床移动件按照匹配优化后的质量分布进行重新设计，运用有限元软件重新计算机床的动态特性. 如表10所示为机床在最差位姿状态下优化前、后的前5阶固有频率对比，如表11所示为机床在最优位姿状态下优化前、后的前5阶固有频率对比.

表 10   优化前、后机床最差位姿前5阶固有频率

Tab.10  First five natural frequencies of worst position of machine tools before and after optimization

状态 f1/Hz f2/Hz f3/Hz f4/Hz f5/Hz
优化前 59.534 65.709 133.986 197.342 220.331
优化后 68.056 77.534 150.375 229.642 249.632

新窗口打开| 下载CSV


表 11   优化前、后机床最优位姿前5阶固有频率

Tab.11  First five natural frequencies of best position of machine tools before and after optimization

状态 f1/Hz f2/Hz f3/Hz f4/Hz f5/Hz
优化前 64.397 70.327 145.61 203.57 217.91
优化后 71.946 78.541 162.53 226.94 243.00

新窗口打开| 下载CSV


由表10、11可知，经过重新设计后的机床无论是在最差位姿还是在最优位姿状态下，整机前5阶固有频率均有不同程度的提高. 在最差位姿状态下，机床前5阶固有频率分别提高了14.3%、18.0%、12.2%、16.4%和13.3%；在最优位姿状态下，前5阶固有频率分别提高了11.7%、11.7%、11.5%、11.5%和10.3%.

由于刀尖的振动特性对机床加工精度的影响非常大，以机床刀尖节点为研究对象，对质量匹配优化后的机床进行频率响应分析，激励范围设置为10~250 Hz，共设40个激励点. 如图7、8所示分别为机床刀尖节点在最差位姿和最优位姿状态下的频率响应曲线.图中，A为响应振幅.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   最差位姿频率响应曲线

Fig.7   Frequency response curve of worst position


图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   最优位姿频率响应曲线

Fig.8   Frequency response curve of best position


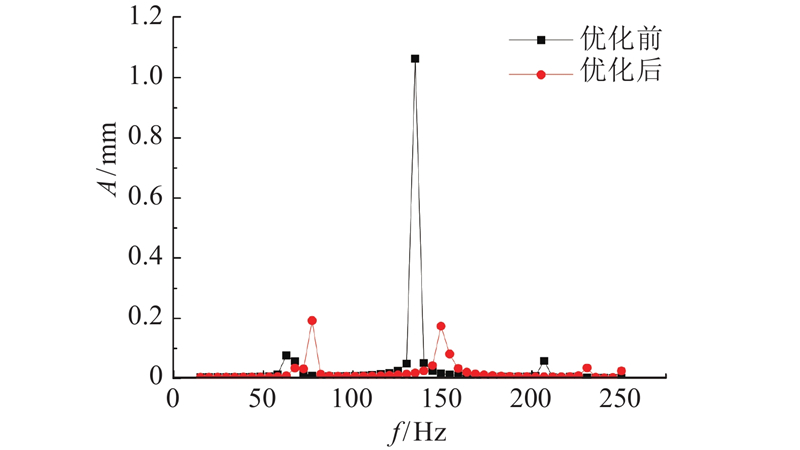
由图7可知，在最差位姿状态下，机床优化前的最大响应振幅为1.063 1 mm，发生在134.8 Hz处，与机床的第3阶固有频率基本重合. 经过质量匹配优化后，机床的最大响应振幅发生在第2阶固有频率处，为0.192 7 mm，比优化前降低了81.9%.

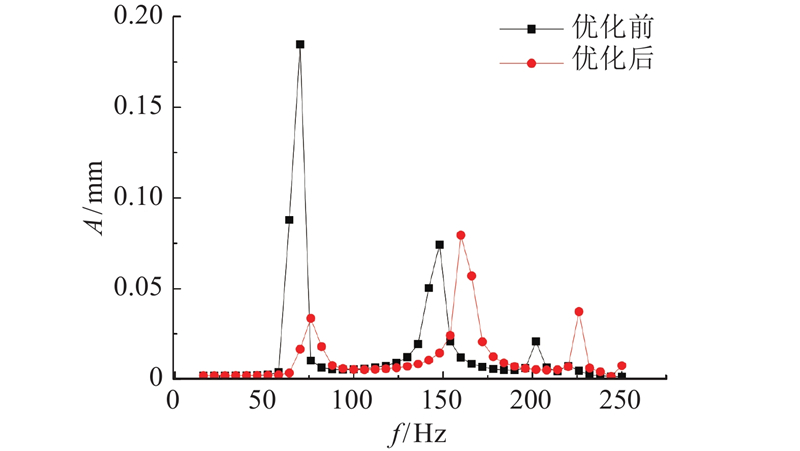
由图8可知，与最差位姿状态下相比，机床最优位姿状态下的响应振幅较小. 优化前为0.184 6 mm，发生在70 Hz处，与机床的第2阶固有频率基本重合. 移动件质量经重新分布设计后，最大响应振幅降低为0.079 5 mm，发生在机床的第3阶固有频率处，最大振幅比优化前降低了56.9%.

综合分析可知，各移动件质量经过匹配优化后，机床的前5阶固有频率都得到了不同程度的提高，刀尖节点的频率响应振幅明显降低，机床的动力学性能得到了改善.

6. 结　论

(1) 采用正交试验法将机床的工作空间进行离散化，得到各移动件位姿正交试验表；运用有限元分析软件计算各试验的响应值，通过最小二乘法建立机床的空间固有频率预测模型. 对机床沿x、y、z方向的工作路径进行灵敏度分析，获得机床加工过程中的最佳工艺路线；采用遗传算法，识别出机床工作空间内的最差和最优位姿.

(2) 以机床最差位姿的固有频率为优化目标，采用Box-Behnken方法对工作台、立柱和主轴箱的质量进行试验设计，建立机床固有频率与移动件质量间的响应面模型，基于NSGA-II算法进行匹配优化. 结果表明：优化后移动件的总质量减少了约10.8%，在最差位姿状态下，机床前5阶固有频率分别提高了14.3%、18.0%、12.2%、16.4%和13.3%；在最优位姿状态下，前5阶固有频率分别提高了11.7%、11.7%、11.5%、11.5%和10.3%.

(3) 以机床刀尖为研究对象，对优化后的机床进行频率响应分析. 结果表明：在最差位姿状态下，刀尖节点的最大响应振幅降低了81.9%；在最优位姿状态下，刀尖节点的最大响应振幅降低了56.9%. 机床工作空间内的动力学性能得到了有效提高，为后续面向平稳加工的工艺路径规划提供了保证.

参考文献

TOH C K

Vibration analysis in high speed rough and finish milling hardened steel

[J]. Journal of Sound and Vibration, 2004, 278 (1/2): 101- 115

[本文引用: 1]

ZAGHBAN I, SONGMENE V

Estimation of machine-tool dynamic parameters during machining operation through operational modal analysis

[J]. International Journal of Machine Tools and Manufacture, 2009, 49 (12): 947- 957

[本文引用: 1]

李天箭, 吴晨帆, 沈磊, 等

基于模态预测及敏度分析的机床动特性设计方法

[J]. 机械工程学报, 2019, 55 (7): 178- 186

DOI:10.3901/JME.2019.07.178      [本文引用: 1]

LI Tian-jian, WU Chen-fan, SHEN Lei, et al

Improving machine tool dynamic performance using modal prediction and sensitivity analysis method

[J]. Journal of Mechanical Engineering, 2019, 55 (7): 178- 186

DOI:10.3901/JME.2019.07.178      [本文引用: 1]

ZAGHBANI I, SONGMENE V

Estimation of machine-tool dynamic parameters during machining operation through operational modal analysis

[J]. International Journal of Machine Tools and Manufacture, 2009, 49 (12/13): 947- 957

DOI:10.1016/j.ijmachtools.2009.06.010     

LAW M, ALTINTAS Y, PHANI A S

Rapid evaluation and optimization of machine tools with position-dependent stability

[J]. International Journal of Machine Tools and Manufacture, 2013, 68 (3): 81- 90

[本文引用: 1]

刘海涛, 赵万华

基于广义加工空间概念的机床动态特性分析

[J]. 机械工程学报, 2010, 45 (21): 54- 60

[本文引用: 1]

LIU Hai-tao, ZHAO Wan-hua

Dynamic characteristic analysis for machine tools based on concept of generalized manufacturing space

[J]. Journal of Mechanical Engineering, 2010, 45 (21): 54- 60

[本文引用: 1]

王磊, 金涛, 陈卫星, 等

基于广义加工空间及工件效应的超重型机床动态特性分析

[J]. 机械设计, 2012, 29 (1): 69- 73

[本文引用: 1]

WANG Lei, JIN Tao, CHEN Wei-xing, et al

Dynamic characteristic analysis of super heavy machine tool based on generalized manufacturing space and workpiece effect

[J]. Journal of Machine Design, 2012, 29 (1): 69- 73

[本文引用: 1]

刘响求. 基于多轴联合自激励的数控机床工作空间内结构动态特性分析[D]. 武汉: 华中科技大学, 2015.

[本文引用: 1]

LIU Xiang-qiu. Analysis of dynamic characteristics of CNC machine tool structure during working space based on multi-axis excitation technology [D]. Wuhai: Huazhong University of Science and Technology, 2015.

[本文引用: 1]

黄华, 张树有, 刘晓健, 等

基于响应面模型的广义空间切削稳定性研究

[J]. 浙江大学学报: 工学版, 2015, 49 (7): 1215- 1223

[本文引用: 3]

HUANG Hua, ZHANG Shu-you, LIU Xiao-jian, et al

Research on cutting stability of generalized manufacturing space based on response surface model

[J]. Journal of Zhejiang University: Engineering Science, 2015, 49 (7): 1215- 1223

[本文引用: 3]

李天箭, 丁晓红, 程凯

基于空间统计学的机床动力学特性

[J]. 机械工程学报, 2015, 51 (21): 87- 94

DOI:10.3901/JME.2015.21.087      [本文引用: 1]

LI Tian-jian, DING Xiao-hong, CHENG Kai

Machine tool dynamics based on spatial statistics

[J]. Journal of Mechanical Engineering, 2015, 51 (21): 87- 94

DOI:10.3901/JME.2015.21.087      [本文引用: 1]

于长亮, 张辉, 王仁彻, 等

机床整机动刚度薄弱环节辨识与优化方法研究

[J]. 机械工程学报, 2013, 49 (21): 11- 17

DOI:10.3901/JME.2013.21.011      [本文引用: 1]

YU Chang-liang, ZHANG Hui, WANG Ren-che, et al

Research on identification and optimization method of weakness of machine tool's whole maneuvering stiffness

[J]. Journal of Mechanical Engineering, 2013, 49 (21): 11- 17

DOI:10.3901/JME.2013.21.011      [本文引用: 1]

邓聪颖, 刘蕴, 殷国富, 等

基于响应面方法的数控机床空间动态特性研究

[J]. 工程科学与技术, 2017, 49 (4): 211- 218

[本文引用: 1]

DENG Cong-ying, LIU Yun, YIN Guo-fu, et al

Research on machine tool spatial dynamic characteristics based on response surface method

[J]. Advanced Engineering Sciences, 2017, 49 (4): 211- 218

[本文引用: 1]

杨闪闪, 王玲, 廖启豪, 等

基于径向基函数法的五轴数控机床空间动态性能研究

[J]. 机械工程学报, 2019, 55 (9): 144- 153

DOI:10.3901/JME.2019.09.144      [本文引用: 1]

YANG Shan-shan, WANG Ling, LIAO Qi-hao, et al

Study on the spatial dynamic performance of five-axis CNC machine tools based on radial basis function method

[J]. Journal of Mechanical Engineering, 2019, 55 (9): 144- 153

DOI:10.3901/JME.2019.09.144      [本文引用: 1]

LUO B, PAN D W, CAI H, et al

A method to predict position-dependent structural natural frequencies of machine tool

[J]. International Journal of Machine Tools and Manufacture, 2015, 92: 72- 84

DOI:10.1016/j.ijmachtools.2015.02.009      [本文引用: 1]

ZHANG G P, HUANG Y M, SHI W H, et al

Predicting dynamic behaviors of a whole machine tool structure based on computer-aided engineering

[J]. International Journal of Machine Tools and Manufacture, 2003, 43 (7): 699- 760

DOI:10.1016/S0890-6955(03)00026-9      [本文引用: 1]

武友德, 伍晓亮, 朱超

机床典型结合部参数优化识别

[J]. 机械设计与研究, 2015, 31 (2): 147- 150

[本文引用: 1]

WU You-de, WU Xiao-liang, ZHU Chao

Parameter optimization identification of typical joints of machine tools

[J]. Machinery Design and Research, 2015, 31 (2): 147- 150

[本文引用: 1]

BURDEKIN M, BAEK N, COWLEY A

Analysis of the local deformation in machine joints

[J]. Journal Mechanical Engineering Science, 1979, 21 (1): 25- 32

DOI:10.1243/JMES_JOUR_1979_021_006_02      [本文引用: 1]

VAFAEI S, RAHNEJAT H, AINI R

Vibration monitoring of high speed spindles using spectral analysis techniques

[J]. International Journal of Machine Tools and Manufacture, 2002, 42 (11): 1223- 1234

DOI:10.1016/S0890-6955(02)00049-4      [本文引用: 1]

邓聪颖, 殷国富, 方辉, 等

基于正交试验的机床结合部动刚度优化配置

[J]. 机械工程学报, 2015, 51 (19): 146- 153

[本文引用: 1]

DENG Cong-ying, YIN Guo-fu, FANG Hui, et al

Optimal configuration of dynamic stiffness of machine tool joints based on orthrogonal experiment

[J]. Journal of Mechanical Engineering, 2015, 51 (19): 146- 153

[本文引用: 1]

米良, 殷国富, 孙明楠, 等

基于结合部动力学特性的立柱-主轴系统动力学模型研究

[J]. 农业机械学报, 2011, 42 (12): 202- 207

MI Liang, YIN Guo-fu, SUN Ming-nan, et al

Study on dynamics model of column-spindle system based on dynamic characteristics of joints

[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42 (12): 202- 207

廖伯瑜, 周新民, 尹志宏, 等. 现代机械动力学及其工程应用[M]. 北京: 机械工业出版社, 2003.

[本文引用: 1]

/

〈 〉