随着训练强度的不断提升，舰载机的出动愈加频繁，这使得狭小的甲板空间与保障资源及保障效率之间的矛盾日益突出. 舰载机在甲板上调运作业的效率和安全性，直接决定着舰载机的出动效率，因此，研发一种合适的路径规划与控制模型以及求解方法，是确保舰载机在甲板上安全、高效地进行调运作业的基础. 目前，在舰载机的路径规划问题上，相关研究主要还是借鉴机器人、无人车等领域的理论，其中，路径规划方法主要包括基于节点的搜索类算法、人工势场法、智能算法、最优控制方法这4类.

基于节点的搜索类算法主要通过将地图离散化，在离散区域内搜索若干节点，并将搜索到的节点连接以生成可行路径，主要可分为基于图论的节点搜索算法和单元分解法这两大类^[1-5]. 该类算法具有效率高、计算速度较快的优点，但其往往没有考虑非完整运动约束问题^[6-9]，且容易忽略初始和终点位置的姿态约束^[10-13].

人工势场法将环境表示成物理势场，终点提供引力场，障碍物提供斥力场，通过计算运动体受到的合力来生成路径^[14-16]. 需要指出的是，这类方法将运动体视作质点，忽略了物体最小转弯半径等机械约束.

机器学习算法根据已有的路径规划数据，采用人工智能方法对路径规划模型进行训练，目前主要有强化学习、SVM等. 这类算法的自学习能力较强，智能程度较高，但对数据的依赖较大，需要科学、合理地进行大量训练^[17-18]. 通过这类算法得到的轨迹难以严格满足各类约束，因此难以确保安全性.

以上3种方法各具特点，均考虑了如何避障并以尽量短的距离得出次优路径，但未考虑最优路径的控制问题，且所得路径很难严格满足终端位置的约束. 在实际调运需求中，舰载机需要以固定的姿态准确地滑行或被牵引至预定位置，即舰载机调运对飞机的终端位置和姿态具有严格的要求. 此外，在调运过程中还需要考虑运动学约束、各类机械约束以及控制输入饱和等若干因素.

最优控制技术将路径规划问题和约束描述成数学模型，得到满足约束条件下的最优轨迹和相应的控制输入，在性能指标中综合考虑调运时间和调运过程的能量消耗. 相比于前述3类方法，该类方法具有2点明显的优势：1）基于系统的运动学方程在获得最优轨迹的同时，可以获得相应的控制输入；2）能够全面考虑各类约束条件，且可以在统一框架下对各类约束进行求解. 但是，该类方法的问题同样突出，即其需要解决一个复杂的非线性动态优化问题. 在实际战争中，战机稍纵即逝，采用高效、高精度的数值算法对该问题进行求解，是该类方法能够被广泛应用的先决条件.

目前，最优控制问题的数值算法主要分为间接法和直接法. 间接法是基于变分法、Pontryagin极大值原理等将原问题转化为Hamilton边值问题进行求解，其优点是所得解的精度高且为局部最优解，缺点是对协态变量的初值比较敏感，因此一般难以被用于工程实际中^[19-23]. 直接法是通过对状态变量和控制变量进行离散化处理，从而将连续时间的最优化问题转换成非线性规划问题进行求解. 随着计算科学的发展，直接法（如：伪谱法）已逐步成为求解最优化控制问题的主流方法，但随着配点数目的增加，很容易出现“维数灾难”的现象^[24-26].

由于大部分路径规划方法只考虑如何得到距离最短的路径，且没有将控制问题考虑在内，很难保证距离最短路径等价于耗时最短路径，从而很可能无法据其设计出满足约束的控制律并实现工程应用. 舰载机路径规划问题的关键是在确保安全的条件下使舰载机尽可能快地到达预定位置，即时间-能量最优问题，因此本研究首先建立舰载机轨迹规划的时间-能量最优控制模型；为实现高效求解，在间接法的框架下，基于第三类生成函数，对最优控制问题的一阶必要条件使用高精度的伪谱插值，构造保辛伪谱方法^[27-29]，并结合牛顿迭代方法提出牛顿迭代保辛伪谱算法.

动力学模型可以更准确地表示系统行为，其允许轮胎发生滑动，且可将惯性力等考虑在内. 但是，该模型一般较为复杂，且需要结合参数识别及多体建模技术才能获得系统的精确模型，基于该类模型进行数值计算耗时较长.

运动学模型是一种基本的“无褶边”模型，在低速运动条件下可以准确地描述系统的运动特性. 相比于动力学模型，运动学模型的主要优点是模型结构简单，在计算耗时较少的情况下仍可以对系统进行精确求解. 运动学模型的缺点主要是其假定地面完全水平且轮胎没有滑动，因此忽略了惯性和侧向力，但如果系统地球表面上低速运行，该假设并不会显著影响结果的准确性.

考虑到舰载机在甲板上的滑行（或被牵引）速度较小，本研究采用运动学模型对舰载机的路径规划问题进行研究，下文将分别对3类调运方式进行建模.

当舰载机在甲板上运动时，其运动机制可概括如下：由发动机以及刹车提供加速度从而使舰载机向前运动，通过前轮的转向角来实现方向控制. 假设舰载机在甲板上的运动只产生滚动摩擦，而不发生滑动，则无须分析其水平推力、摩擦力或惯性特性即可对其运动进行分析，其运动约束为一个非完整的运动约束^[30]，则其运动学方程可表示为

(1) $\dot {{X}} = {\left[ {{v_1}\cos \theta_1 ,}\;{{v_1}\sin \theta_1 ,}\;{{{{v_1}{u_1}} / {{L_1}}},}\;{{u_2}} \right]^{\rm{T}}}.$

式中： ${L_1}$为沿舰载机轴线方向上前轮与后轮之间的垂直距离；方位角 ${\theta _1}$为舰载机轴线与横坐标的夹角； $\left( {{x_1},{y_1}} \right)$为飞机后轮中间点位置坐标； ${v_1}$为飞机的速度大小；系统状态变量为 ${{X}} = {\left( {{x_1},{y_1},{\theta _1},{v_1}} \right)^{\rm{T}}}$，系统控制变量为U = $ {\left( {\tan \;{\beta _1},{a_1}} \right)^{\rm{T}}}$，其中， ${\beta _1}$为飞机前轮的转向角， ${a_1}$为飞机的加速度. 关于状态变量和控制变量的约束为

(2) $\left. \begin{array}{l} 0 \leqslant {v_1} \leqslant {v_1}_{\max },\\ \left| {{u_1}} \right| \leqslant \tan\; {\beta _{1\max} },\\ {a_1}_{{\rm{min}}} \leqslant {u_2} \leqslant {a_1}_{\max }. \end{array} \right\}$

根据文献[31]的结论，当系统的速度较小（< 4.5 m/s）时，运动学模型可以较好地描述带拖车系统的运动. 由于无牵引车的舰载机系统与带拖车系统的结构类似，该无杆牵引系统也可被视为一个带拖车系统. 在不考虑系统的横向推力、摩擦或者惯性等因素的前提下，可将其运动关系进行简化. 设 $\theta_2 $为牵引车的轴向与横坐标之间的夹角，（ $x_2 $， $y_2 $）为牵引车后轮中心位置，该点的平动速度为 $v_2 $； $\beta_1=\theta_2-\theta_1 $，为牵引车与舰载机之间的夹角（飞机的转向角）， $\beta_2 $为牵引车的转向角， $L_2 $为牵引车的前、后轮距， $M_0 $为飞机和牵引车的铰接点与牵引车后轮之间的距离. 根据牵引系统的结构特点，舰载机的平动速度 ${v_1}$与牵引车之间平动速度 ${v_2}$关系为

(3) ${v_1} = {v_2}\left( {\cos \;{\beta _1} + {{{L_2}\sin\; {\beta _1}{u_1}} / {{M_0}}}} \right).$

根据系统的结构关系以及运动关系，可得到其运动学方程：

(4) $\begin{split}\dot {{X}} =& \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{x_1}},& {{y_1}},& {{\theta _1}},& {{\theta _2}},& {{v_2}} \end{array}} \right]^{\rm T} =\\ &\left[ {\begin{array}{*{20}{c}} {{{\left( {{L_2}{v_2}\cos\; {\beta _1} + {M_0}{v_2}{u_1}\sin\; {\beta _1}} \right)\cos\; {\theta _1}} / {{L_2}}}} \\ {{{\left( {{L_2}{v_2}\cos\; {\beta _1} + {M_0}{v_2}{u_1}\sin\; {\beta _1}} \right)\sin\; {\theta _1}} / {{L_2}}}} \\ {{{\left( {{L_2}{v_2}\sin\; {\beta _1} - {M_0}{v_2}{u_1}\cos\; {\beta _1}} \right)} / {{L_1}{L_2}}}} \\ {{{{v_2}{u_1}} / {{L_2}}}} \\ {{u_2}} \end{array}} \right].\end{split}$

式中：系统状态变量为 ${{X}} = {\left( {{x_1},{y_1},{\theta _1},{\theta _2},{v_2}} \right)^{\rm{T}}}$，系统控制变量为 ${{U}} = {\left( {{u_1},{u_2}} \right)^{\rm{T}}}$， ${u_1} = \tan\; {\beta _2}$. 该模型中关于状态变量和控制变量的约束为

(5) $\left. \begin{array}{l} {v_{{\rm{1min}}}} \leqslant {v_1} \leqslant {v_1}_{\max },\;\;\left| {{\beta _1}} \right| \leqslant {\beta _1}_{\max },\\ \left| {{u_1}} \right| \leqslant \tan \;{\beta _{2\max }},\;\;\;\;\left| {{u_2}} \right| \leqslant {a^2_{\max }}. \end{array} \right\}$

目前，在航母上使用的有杆牵引系统一般均为离轴系统. 设 $\theta {}_1$、 ${\theta _2}$以及 ${\theta _3}$分别为舰载机、牵引杆以及牵引车的方向角， $\left( {{x_1},{y_1}} \right)$、 $\left( {{x_2},{y_2}} \right)$、 $\left( {{x_3},{y_3}} \right)$以及 $\left( {{x_4},{y_4}} \right)$分别为舰载机、舰载机与牵引杆的铰接点、牵引杆与牵引车的铰接点以及牵引车的位置坐标. 设 ${\alpha _1}$为牵引车的转向角， ${L_2}$为牵引杆的长度， $M$为牵引杆与牵引车铰接点到牵引车后轮的垂直距离， ${L_3}$为牵引车前、后轮的距离. 飞机和牵引车的速度分别为 ${v_1}$和 ${v_3}$. 根据系统的结构设计和使用规定，飞机和牵引车的速度、转向角均应被约束在一定范围内.

与无杆牵引系统类似，牵引系统最终的目标是将飞机调运到指定位置，为此将表征飞机姿态的变量视为状态变量，以便更好地满足起始位置和终端位置处的约束. 根据系统的自由度，当飞机的姿态已知时，只需要唯一确定 ${\beta _1}$和 ${\beta _2}$即可确定飞机与牵引杆的铰接点、牵引杆与牵引的车铰接点以及牵引车的位置坐标. 因此，选取系统的状态变量为 ${{X}} = {\left( {{x_1},{y_1},{\theta _1},{\beta _1},{\beta _2}} \right)^{\rm{T}}}$. 考虑到舰载机与牵引车的速度可以表示为

(6) ${v_1} = {{{v_3}\cos \;{\beta _1}\cos\; {\beta _2}\left( {{L_3} + M\tan\; {\beta _2}\tan\; \alpha } \right)} / {{L_3}}}.$

则控制变量可以表示为飞机的速度以及牵引车的转向角，即 ${{U}} = {\left( {{u_1},{u_2}} \right)^{\rm{T}}}$，其中 ${u_1} = \tan \;\alpha$. 因此，系统的运动学方程可表示为

(7) $\begin{split}\dot {{X}} =& \dfrac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{x_1}}, & {{y_1}} ,& {{\theta _1}} ,& {{\beta _1}} ,& {{\beta _2}} \end{array}} \right]^{\rm T} =\\ &\left[ {\begin{array}{*{20}{c}} {{u_2}\cos \;{\theta _1}} \\ {{u_2}\sin \;{\theta _1}} \\ {{{{u_2}\tan \;{\beta _1}} / {{L_1}}}} \\ {{u_2}\left( {\dfrac{{{L_3}\tan\; {\beta _2} - M{u_1}}}{{{L_2}\cos\; {\beta _1}\left( {{L_3} + M{u_1}\tan\; {\beta _2}} \right)}} - \dfrac{{\tan\; {\beta _1}}}{{{L_1}}}} \right)} \\ {{u_2}\left( {\dfrac{{{L_2}{u_1} - {L_3}\sin \;{\beta _2} + M{u_1}\cos\; {\beta _2}}}{{{L_2}\cos \;{\beta _1}\cos \;{\beta _2}\left( {{L_3} + M{u_1}\tan \;{\beta _2}} \right)}}} \right)} \end{array}} \right].\end{split}$

式（7）成立的前提条件是所有转向角均小于53°，且 $M \!\leqslant\! 0.5{L_3}$，使得 $\cos\; {\beta _1}\cos\; {\beta _2}\left( {{L_3} + M{u_1}\tan \;{\beta _2}} \right) \ne 0$，且 $\cos \;{\beta _1} \ne 0$， $\cos \;{\beta _2} \ne 0$，该假设可适用于大部分拖-拉系统.

本研究所提舰载机路径规划是指在满足舰载机的运动约束和边界约束下，使得舰载机以最安全、最快的方式从起始位置运动到终点位置. 为此，分别对单架舰载机滑行、无杆牵引系统以及有杆牵引系统的路径规划模型进行描述.

由于甲板区域狭小，舰载机在甲板上运动的过程中，往往会遇到各种障碍物，而连接起点和终点的路径需要落在不包含障碍物的可行解构成的空间内. 因此，利用数学模型合理地描述边界约束（障碍物约束），使得边界约束模型所表示的空间尽可能地包含实际障碍物却又不浪费理论上的可行空间，是进行路径规划的重要环节.

为了不失一般性，采用下述公式来表示待规划舰载机和第 $i$个障碍物之间没有发生碰撞：

(8) $1 - {\left| {\frac{{{x_1} - {x_{{\rm{o}}i}}}}{{{a_i} + {{d}_{\rm{s}}}}}} \right|^{p_i}} - {\left| {\frac{{{y_1} - {y_{{\rm{o}}i}}}}{{{b_i} + {{d}_{\rm {s}}}}}} \right|^{p_i}} \leqslant 0.$

式中： $1 \leqslant i \leqslant n$，（ ${x_{{\rm{o}}i}}$， ${y_{{\rm{o}}i}}$）分别为第 $i$个障碍物的中心位置坐标， ${a_i}$和 ${b_i}$分别为其宽和高， ${d_{\rm{s}}}$为根据安全要求和飞机外形结构所设置的安全距离， ${p_i}$为图形的形状参数. 当 ${p_i} = 1$时，式（8）描述的为菱形；当 ${p_i} = 2$时，所描述的为圆或者椭圆；当 ${p_i} \to \infty $时，所描述的为矩形.

由于障碍物约束和平动速度、控制变量等约束均为不等式约束，可将这两部分放在一起考虑，以构成一个统一形式的不等式约束关系，则可将式（2）和式（8）的不等式约束统一表示为

(9) ${{h}} \leqslant {\bf{0}}.$

对于舰载机的路径规划问题，通常要寻求以最短时间从起点到达终点的可行路径. 然而，考虑到还需要尽可能地避免由速度、角度的急剧变化所带来的控制不稳定及安全隐患，需要尽可能地使舰载机匀速走直线，即使转向角尽可能地小. 因此，可将目标函数视为一个时间-能量最优的Bolza型代价目标函数，具体为

(10) $J = {w_{\rm k}}\left( {{t_{\rm f}} - {t_0}} \right) + \frac{1}{2}\int\limits_{{t_0}}^{{t_{\rm f}}} {\left( {{{{U}}^{\rm{T}}}{{RU}}} \right){\rm{d}}t} .$

式中： ${t_{\rm f}}$为到达终点的时刻， ${t_0}$为出发时刻， ${w_{\rm k}}$为权重调节因子， $J$为目标函数. 因此，单架舰载机滑行路径规划的最优控制模型可以描述为

(11) $ {\rm{min}}\;\;J; \quad {\rm{s}}{\rm{.t}}{\rm{.}}\;\;{\dot{ X}} = {{f}}\left( {{{X}}\left( \cdot \right),{{U}}\left( \cdot \right),t} \right),\;\;{{h}} \leqslant {\bf{0}}.$

式中： ${\dot{ X}} = {{f}}\left( {{{X}}\left( \cdot \right),{{U}}\left( \cdot \right),t} \right)$对应于式（1）所描述的运动学方程.

与舰载机自主滑行类似，可将障碍物约束（式（8））、关于状态变量和控制变量的约束（式（5））统一表示为不等式向量（式（9）），则无杆牵引系统路径规划可以描述为与式（11）类似的最优控制模型，其中， ${\dot{ X}} = {{f}}\left( {{{X}}\left( \cdot \right),{{U}}\left( \cdot \right),t} \right)$对应于式（4）所描述的运动学方程.

式（7）所描述的模型较现有拖-拉系统的运动学模型更加简单，但仍然是一个复杂的非线性强耦合系统. 虽然该模型可以直接被用于轨迹规划和控制设计，但其强非线性易造成求解过程中优化算法的发散，不利于工程应用. 为了解决这一问题，将轨迹规划与控制设计问题转化为2个子问题：1）系统轨迹规划问题；2）牵引车的控制设计.

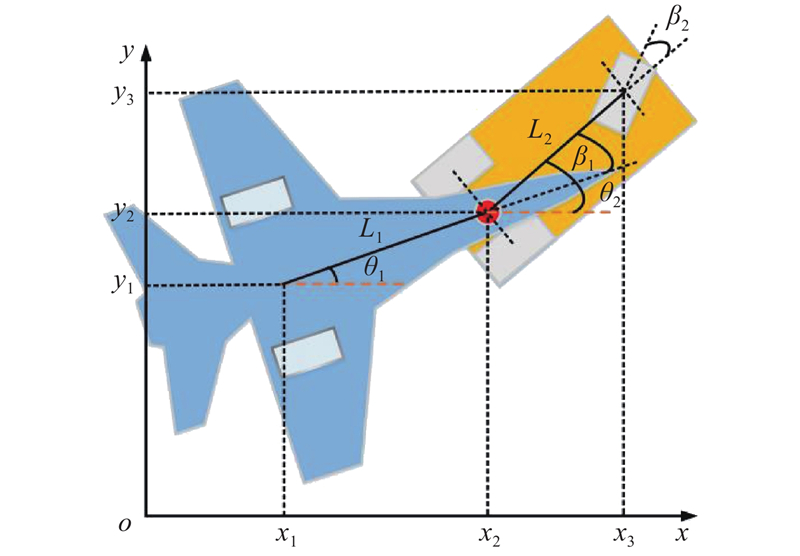
为了找到一个有效的方法来解决有杆牵引系统的轨迹规划问题，将原系统转化成一个在轴的虚拟无杆牵引系统，具体如图1所示. 该系统由飞机和牵引杆组成，而牵引杆又被视为一个虚拟的牵引车，虚拟牵引车的前、后轮距等于牵引杆的长度. 通常牵引杆可以被看作一个具有两轮（前轮和后轮）的设备，方向由前轮控制，驱动力由后轮控制，但考虑到虚拟牵引车的平衡性，本研究将其虚拟为一个三轮的牵引车，这并不会改变其功能和运动学特性. 然而，在这个系统中，系统的驱动权限从真实牵引车转移到了虚拟牵引车（牵引杆）. 上述虚拟系统的运动学方程为

(12) $ \begin{split}&\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{x_1}},&{{y_1}},&{{\theta _1}},&{{\theta _2}},&{{v_2}} \end{array}} \right]^{\rm T} =\\& {\left[ {{v_2}\cos\; {\beta _1}\cos\; {\theta _1},\;{v_2}\cos\; {\beta _1}\sin\; {\theta _1},\;\frac{{{v_2}\sin\; {\beta _1}}}{{{L_1}}},\;\frac{{{v_2}{u_1}}}{{{L_2}}},\;{u_2}} \right]^{\rm{T}}}.\end{split}$

其中，控制变量由虚拟牵引车的加速度以及转向角（ ${u_1} = \tan \;{\beta _2}$）组成. 该系统的运动学方程较原系统更加简单，因此，可采用该系统来代替原系统进行路径规划. 考虑到真实牵引车的存在，在采用上述虚拟系统进行路径规划时，需要合理设计安全半径，以确保不会发生碰撞.

根据该虚拟系统，可得到 ${x_1}$、 ${y_1}$、 ${\theta _1}$、 ${\theta _2}$、 ${\beta _2}$的值，而根据系统的结构特点，牵引车的位置和姿态可以表示为

(13) $\left. \begin{array}{l} {x_4} = {x_1} + {L_1}\cos\; {\theta _1} + {L_2}\cos\; {\theta _2} + M\cos\; {\theta _3}, \\ {y_4} = {y_1} + {L_1}\sin\; {\theta _1} + {L_2}\sin\; {\theta _2} + M\sin\; {\theta _3} ,\\ {\theta _3} = {\theta _2} + {\beta _2} .\\ \end{array} \right\}$

牵引车的路径也可由此得到，进而可以得到整个系统各个部分（牵引车、牵引杆以及飞机）的路径以及姿态信息. 此外，飞机的转向角 $\ {\beta _1}$和速度 ${v_1}$应该满足：

(14) $\left| {{v_2}\cos \;{\beta _1}} \right| \leqslant {v_{1\max }},\;\;\left|\ {{\beta _1}} \right| \leqslant {\beta _{1\max }}.$

与无杆牵引系统类似，虚拟系统的控制变量还应满足：

(15) $\left| {{u_1}} \right| \leqslant {u_{1\max }},\;\;\;\left| {{u_2}} \right| \leqslant {u_{2\max }}.$

其中，平移速度和平移加速度的上、下限根据具体的安全规范要求来给定，转向角一般是根据舰载机和牵引车的转弯半径进行计算.

与单架舰载机类似，可将障碍物约束（式（8））和平移速度、控制变量等约束统一表示为式（9）的形式，则虚拟系统路径规划的最优控制模型可以描述为式（11），其中，运动学模型为式（12）. 结合虚拟系统的结果以及式（13），即可得出有杆牵引系统中飞机、牵引杆以及牵引车的路径数据，进而实现对有杆牵引系统的路径规划. 采用这种处理方式可以得到飞机和真实牵引车的轨迹，但仍然无法得到真实牵引车的控制律. 为了解决这一问题，可采用轨迹跟踪的方法来确定牵引车的实际控制规律，本研究只考虑其路径规划问题.

基于牛顿迭代法、第三类生成函数的保辛伪谱算法的牛顿迭代保辛伪谱算法（Newton symplectic pseudospectral method, NSP），对终端时间 ${t_{\rm f}}$以及对应的最优轨迹进行求解，可得最优轨迹对应的最优解，具体的计算步骤如下.

1）初始化式（11）中的末端时间 ${t_{\rm f}} = t_{\rm f}^0$，初始化牛顿迭代法的迭代精度 $\rho $；采用拟线性化技术，将式（11）中带约束的时间-能量最优控制问题转化为一个带约束且末端状态、末端时间固定的能量最优控制问题，具体可描述为

(16) $\left. \begin{split} {\rm{Min }}\;\;{{{J}}^{\left[ {{{k}} + 1} \right]}} =& \frac{1}{2}\int\limits_{{{{t}}_0}}^{{{{t}}_{\rm f}}} {\left( {{{\left( {{{{U}}^{\left[ {{{k}} + 1} \right]}}} \right)}^{\rm{T}}}{{{R}}^{\left[ {{{k}} + 1} \right]}}{{{U}}^{\left[ {{{k}} + 1} \right]}}} \right){\rm{d}}t}\, ; \\& {\rm{s}}{\rm{.t}}{\rm{.}} \\& {{\dot {{X}}}^{\left[ {{{k}} + 1} \right]}} = {{{A}}^{\left[ {{k}} \right]}}{{{X}}^{\left[ {{{k}} + 1} \right]}} + {{{B}}^{\left[ {{k}} \right]}}{{{U}}^{\left[ {{{k}} + 1} \right]}} + {{{w}}^{\left[ {{k}} \right]}} ,\\& {{{C}}^{\left[ {{k}} \right]}}{{{X}}^{\left[ {{{k}} + 1} \right]}} + {{{D}}^{\left[ {{k}} \right]}}{{{U}}^{\left[ {{{k}} + 1} \right]}} + {{{V}}^{\left[ {{k}} \right]}} + {{{a}}^{\left[ {{k }}\right]}} = {{0}} .\\ \end{split} \right\}$

式中： ${{\alpha }}$为非负补偿向量，状态变量的个数记为 ${n_{\rm s}}$， $k = 0,1,2, \cdots$， ${\left( \cdot \right)^{\left[ k \right]}}$表示变量 $\left( \cdot \right)$在第 $k$次迭代中得到的计算结果. 为了表示方便，下文省略表示迭代次数的上标符.

对于上述最优控制模型，通过引入Lagrange算子 ${{\lambda }}$以及参数乘子向量 ${{\beta }}$，使得原问题变为无约束问题，且参数乘子向量满足 ${{{\alpha }}^{\rm{T}}}{{\beta}} = 0$， ${{\beta}} \geqslant {{0}}$，则目标函数可表示为

(17) $J = \int\limits_{{t_0}}^{{t_{\rm f}}} {\left( {{ H} - {{{\lambda }}^{\rm{T}}}{\dot{ X}}} \right)} {\rm d}t.$

其中，Hamiltonian函数为

$\begin{split} H = & \frac{1}{2}{{{U}}^{\rm{T}}}{{RU}} + {{{\lambda }}^{\rm{T}}}\left( {{{AX}} + {{BU}} + {{W}}} \right) + \\ & {{{\beta }}^{\rm{T}}}\left( {{{CX}} + {{DU}} + {{V}} + {{\alpha }}} \right) .\\ \end{split} $

若要使目标函数 $J$的值最小，需要使系统同时满足控制方程和Hamiltonian正则方程，则控制方程为

(18) $\frac{{\partial { H}}}{{\partial {{U}}}} = {{UR}} + {{{B}}^{\rm{T}}}{{\lambda }} + {{{D}}^{\rm{T}}}{{\beta }} = {{0}}.$

Hamiltonian正则方程为

(19) ${\dot{ X}} = \frac{{\partial { H}}}{{\partial {{\lambda }}}},\;{\dot{ \lambda }} = - \frac{{\partial { H}}}{{\partial {{X}}}}.$

由于Hamiltonian函数是关于状态变量、控制变量、拉格朗日乘子向量、参数乘子向量和补偿向量的函数，而根据式（18）可将控制变量用拉格朗日乘子向量和参数乘子向量来表示，则Hamiltonian函数为状态变量、拉格朗日乘子向量、参数乘子向量和补偿向量这4个自变量的函数.

2）初始化迭代参数 $k = 0$，设置控制变量、控制变量和协变量的初始猜测解分别为 ${{{X}}^{\left[ 0 \right]}}$、 ${{{U}}^{\left[ 0 \right]}}$和 ${{{\lambda }}^{\left[ 0 \right]}}$.

3）结合 ${{{X}}^{\left[ k \right]}}$、 ${{{U}}^{\left[ k \right]}}$和 ${{{\lambda }}^{\left[ k \right]}}$，采用基于第三类的保辛伪谱算法计算出式（16）的解： ${{{X}}^{\left[ {k + 1} \right]}}$、 ${{{U}}^{\left[ {k + 1} \right]}}$和 ${{{\lambda }}^{\left[ {k + 1} \right]}}$，具体计算步骤如下.

将时间区间 $T = \left[ {{t_0},{t_{\rm f}}} \right]$离散化处理成 $P$个区间，第 $j$个区间为 ${T^j} = \left[ {{t_{j - 1}},{t_j}} \right]$， $j = 1,2,\cdots,P$，并将第 $j$个区间采用 ${N^j}$维的Legendre多项式 ${L^j}\left( \tau \right)$进行插值，即LGL配点个数为 ${N^j}$，则 ${{X}}$、 ${{\lambda }}$、 ${{\beta }}$和 ${{\alpha }}$可统一表示为如下形式：

(20) ${{{\upsilon }}^j}\left( \tau \right) = \sum\limits_{l = 0}^{{N^j}} {{{\upsilon }}_l^j\frac{{\left( {{\tau ^2} - 1} \right){{\dot L}^j}\left( \tau \right)}}{{{N^j}\left( {{N^j} + 1} \right)\left( {\tau - \tau _l^j} \right)L_l^j}}} .$

式中： ${{\upsilon }}$代表 ${{X}}$、 ${{\lambda }}$、 ${{\beta }}$和 ${{\alpha }}$中的任意变量.

通过对状态表达式进行微分求解，可得到

(21) $\frac{{d{{X}}_k^j\left( \tau \right)}}{{{\rm d}\tau }} = \sum\limits_{l = 0}^{{N^j}} {{{X}}_l^j} {{D}}_{kl}^j.$

式中： ${{D}}_{kl}^j = \dot L_l^j\left( {\tau _k^j} \right)$为 $j$区间的伪谱微分矩阵.

由于第三类生成函数只是关于 ${{\lambda }}_0^j$和 ${{X}}_{{N^j}}^j$的函数^[32-34]，可将其视为独立变量，而在其他插值点处均可取驻值得到

(22) $\left. \begin{split} & \frac{{\partial S_0^j}}{{\partial {{\lambda }}_{^0}^j}} = {{X}}_{^0}^j\,; \\ & {\dfrac{{\partial S_m^j}}{{\partial {{\lambda }}_{^m}^j}} = {{0}},}\quad{m = 1,2, \cdots ,{N^j}} \,;\\ & {\dfrac{{\partial S_m^j}}{{\partial {{X}}_{^m}^j}} = {{0}},}\quad{m = 0,1, \cdots ,{N^j} - 1} \,; \\ & \dfrac{{\partial S_{{N^j}}^j}}{{\partial {{X}}_{{N^j}}^j}} = {{\lambda }}_{{N^j}}^j\,. \end{split} \right\}$

进一步可得

(23) ${{{K}}^j}{{{\sigma }}^j} + {{{\xi }}^j}{{{\beta }}^j} + {{{\gamma }}^j} = {{{r}}^j}.$

由控制方程可得 ${{U}} = {{g}}\left( {{{X}},{{\lambda }},{{\beta }}} \right)$，则可将边界约束等式进行进一步整理为

(24) ${{{C}}^j}{{{X}}^j} - {{{H}}^j}{{{\lambda }}^j} - {{{M}}^j}{{{\beta }}^j} + {{{V}}^j} + {{{\alpha }}^j} = {{0}}.$

进一步整理可得到单个区间内的形式为

(25) $\left. \begin{aligned} & {{{K}}^j}{{{\sigma }}^j} + {{{\xi }}^j}{{{\beta }}^j} + {{{\gamma }}^j} = {{{r}}^j} ;\\& {{{\varGamma }}^j}{{{\sigma }}^j} - {{{M}}^j}{{{\beta }}^j} + {{{{\hat V}}}^j} + {{{\alpha }}^j} = {{0}} ;\\& {{{\left( {{{{\alpha }}^j}} \right)}^{\rm{T}}}{{{\beta }}^j} = 0,}\;{{{{\alpha }}^j} \geqslant {{0}},}\;{{{{\beta }}^j} \geqslant {{0}}} . \end{aligned} \right\}$

其中， ${{{\varGamma }}^j} = [ { - {{{H}}^j},}{{{{C}}^j}} ]$.

将单个区间得到的结果进行组装，以得到整个区间的求解形式为

(26) $\left. \begin{split} & {{K\sigma }} + {{\xi \beta }} + {{\gamma }} = {{r}} \,;\\ & {{\varGamma \sigma }} - {{M\beta }} + {{V}} + {{\alpha }} = {{0}} \,;\\ & {{{{{\alpha }} }^{\rm{T}}}{{\beta }} = 0{{,}}}\;{{{\alpha }} \geqslant {{0,}}}\;{{{\beta }} \geqslant {{0}}} \,. \end{split} \right\}$

式中：系数矩阵K为对称的稀疏矩阵.

进一步可得状态变量和协变量为

(27) ${{\sigma }} = - {{{K}}^{ - {\rm{1}}}}{{\xi \beta }} - {{{K}}^{ - {\rm{1}}}}\left( {{{\gamma }} - {{r}}} \right).$

从而可得到最优控制下的解，并将其代入到边界约束等式中，可得到如下关系：

(28) $ {{Y\beta }} + {{q}} = {{\alpha }} ,\; {{{{{\alpha }} }^{\rm{T}}}{{\beta }} = 0};\; {{{\alpha }} \geqslant {{0,}}}\; {{{\beta }} \geqslant {{0}}} . $

${{Y}} = {{\varGamma }}{{{K}}^{ - {\rm{1}}}}{{\xi }} + {{M}}$， ${{q}} = {{\varGamma }}{{{K}}^{ - {\rm{1}}}}\left( {{{\gamma }} - {{r}}} \right) - {{V}}$，由于该方程变量 ${{\beta }}$和方程右端 ${{\alpha }}$的值均为未知，且两者满足正交关系，可以视其为一个标准的线性互补问题，采用Lemke方法对其进行求解，即可得到 ${{\beta }}$和 ${{\alpha }}$的值，进一步得到在该次迭代中的解： ${{{X}}^{\left[ {k + 1} \right]}}$、 ${{{U}}^{\left[ {k + 1} \right]}}$和 ${{{\lambda }}^{\left[ {k + 1} \right]}}$.

4）判断是否满足收敛条件 $\left| {{{\left( {{{{X}}^{\left[ {k + 1} \right]}} - {{{X}}^{\left[ k \right]}}} \right)} / {{{{X}}^{\left[ {k + 1} \right]}}}}} \right| \leqslant $ $\varepsilon $（其中， $\varepsilon $为计算精度），若满足该收敛条件，则停止迭代，并将本次迭代所得到的解作为在 ${t_{\rm f}} = t_{\rm f}^0$时能量最优控制问题的最优解；反之，令 $k = k + 1$，返回步骤3）；

5）根据在 ${t_{\rm f}} = t_{\rm f}^0$条件下的能量最优控制问题对应的最优解，得出在最优轨迹末端的Hamiltonian函数 $H\left( {{t_{\rm f}}} \right)$，若满足 $\left| {H\left( {{t_{\rm f}}} \right) + {w_{\rm k}}} \right| \leqslant \rho$，则步骤4）中最优轨迹对应的状态变量、控制变量以及末端时间即为式（11）的最优解；反之，需要根据末端的横截条件 $H\left( {{t_{\rm f}}} \right) + {w_{\rm k}} = 0$，采用牛顿迭代法进行迭代，以得出新的末端时间 $t_{\rm f}^0 = t_{\rm f}^{\rm{new}}$，返回步骤1）.

为了验证上述算法的效率和准确性，本文结合具体算例进行实验分析，同时结合算例将所提出的方法与伪谱法进行对比. 具体的计算环境如下：Win7 64 bit，RAM 4.00 GB，Matlab. 飞机最大速度为1 m/s，最大加速度为3 m/s²，最大转向角（ ${\beta _1}$、 ${\beta _2}$、 ${\beta _3}$及 $\alpha $）为0.9 rad. 无杆牵引系统为在轴牵引系统，飞机的前、后轮距为7 m，牵引车的前、后轮距为4 m；有杆牵引系统为离轴系统，牵引车的前、后轮距为2 m，牵引车与牵引杆的铰接点距离牵引车后轮1 m.

算法的收敛指标 $\varepsilon \!=\! {10^{ - 4}}$， $\rho \!=\! {10^{ - 3}}$， ${{R}} \!=\! {\rm{diag}}\left( {1,1} \right) .$将整个区间分为20段，在每段内采用5维Legendre多项式进行插值，从而将整个时间区间分为100段，共101个离散点. 为了更加公平地对比2类方法的性能，将本文算法和伪谱法的区间段数、每个区间的插值阶数、收敛指标等参数均设为相同.

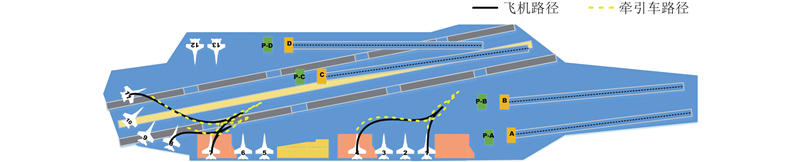
为了更加贴近舰载机的实际使用环境，以“尼米兹”航母为实验平台，选取3架飞机进行研究，具体的甲板环境如图2所示.

通过实验分析可知，最优解（或者次优解）所对应的时间部分（Mayer项）的数值远大于能量部分（Lagrange项），为了平衡两者之间的关系，以同时体现出两者的重要性， ${w_{\rm k}}$的取值不能太大，本实验中取 ${w_{\rm k}} = 0.1$（也可根据实际需要赋值）.

采用本文算法得到的舰载机调运路径如图2所示. 分析图2可知，舰载机在整个滑行过程中均为正向行驶，所得出的路径均非常平滑，且均满足起点和终点的姿态约束. 对于舰载机3和5，由本文算法所得的路径长度明显要短于由伪谱法得到的路径长度，而由这2种算法所得的舰载机11的路径基本重合. 为了进一步分析，给出控制变量的变化规律，具体如图3所示.

如图3（a）、（b）和（c）所示分别为舰载机3、5和11滑行时的控制变量随时间的变化规律. 其中，U为控制变量. 分析图3可知，最优路径对应的控制变量变化比较平缓，其中转向角控制变量 ${u_1}$处于 $\left[ { - 0.6,\;0.6} \right]$，即转向角处于 $\left[ { - 30.96^{\rm{o}}},\;30.96^{\rm{o}} \right]$，这说明在整个调运过程中没有出现急转弯的现象；舰载机的加速度 ${u_2}$均处于 $\left[ { -0.4,\;0.4} \right]\;{\rm{m/}}{{\rm{s}}^{\rm{2}}}$，其中舰载机的加速度只有在起点和终点附近不为0，即除了开始的加速阶段和末端的减速阶段之外，均是以匀速进行滑行. 为了进一步分析舰载机的运动过程，根据控制变量得到舰载机的转角和速度变化规律，具体如图4所示.

如图4（a）、（b）和（c）所示分别为舰载机3、5和11在滑行过程中的速度变化和角度变化. 结合图4和3可知：在大部分运动阶段，舰载机均是以最大速度1 m/s保持匀速运动，直到终点处速度减为0，且舰载机在运动过程中没有出现急刹车或者其他大幅加速的情况. 舰载机在沿最优路径运动过程中，其转角的变化曲线均比较平滑，没有出现较大幅度的转弯现象，这在一定程度上降低了转弯产生的事故风险.

为了验证算法的精度和效率，在相同的参数设置下，选取比较典型的伪谱法进行对比分析，具体的对比结果如表1所示. 其中，t_c为CPU计算耗时. 分析表1可知，采用这2种方法所得到的目标函数值基本接近，但是本文算法的计算效率更高，对于舰载机3，NSP的计算时间为伪谱法的17.70%，对于舰载机5和11，NSP的计算时间分别为伪谱法的14.22%和16.68%；较伪谱法而言，采用本文方法所得到的最优末端时间更少. 这说明本文算法所需的计算时间明显小于伪谱法，在计算效率上较伪谱法具有更大的优势，且NSP所得到的结果更有利于缩短舰载机的滑行时间（得到的末端时间更小）、提高出动效率.

实验选取3架飞机进行研究，舰载机10、12均是从同一升降机的同一位置（位置7）被牵引至预定位置（位置10、12），舰载机11是从位置4被牵引至位置11. 由于本研究的关注重点是飞机的状态，牵引车的终端角度可设置为自由，其余4项状态变量均是固定终端状态.

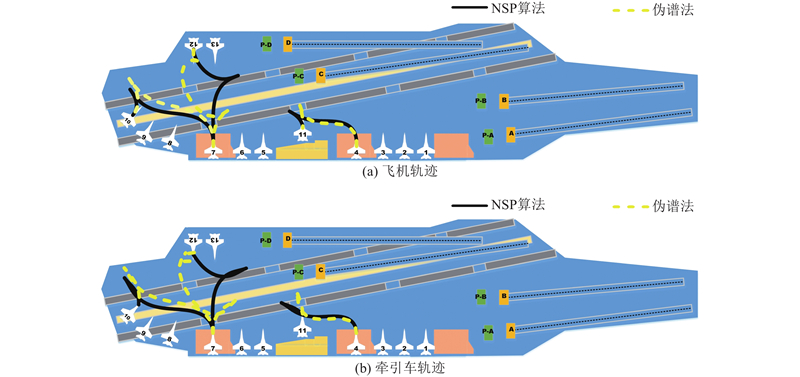
本实验中取 ${w_k} = 0.1$，根据提出的路径规划算法以及伪谱法，可得出3架飞机和无杆牵引车的路径如图5所示. 图5（a）表示的是无杆牵引系统中的飞机轨迹；图5（b）表示的是无杆牵引系统中的牵引车轨迹；实线表示的是采用NSP算法得到的路径曲线，虚线表示的是采用伪谱法得到的路径曲线. 由图5可得，采用2种方法得到的路径均满足起点和终点的姿态约束，这说明得到的路径可满足终端约束条件. 此外，由本文方法所得出的舰载机和牵引车的路径均非常平滑，而在采用伪谱法所得到的路径中，舰载机10和11以及对应的牵引车路径均较为平滑，但是舰载机12以及对应牵引车在末端时的牵引过程比较紊乱.

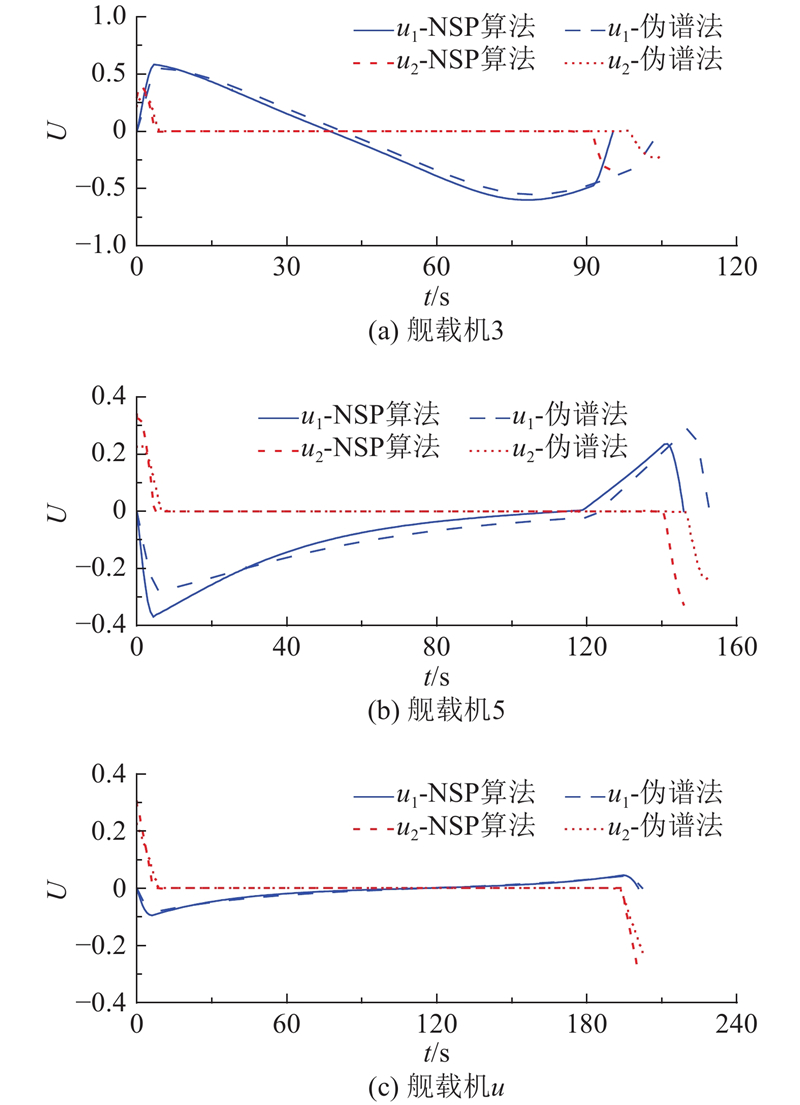
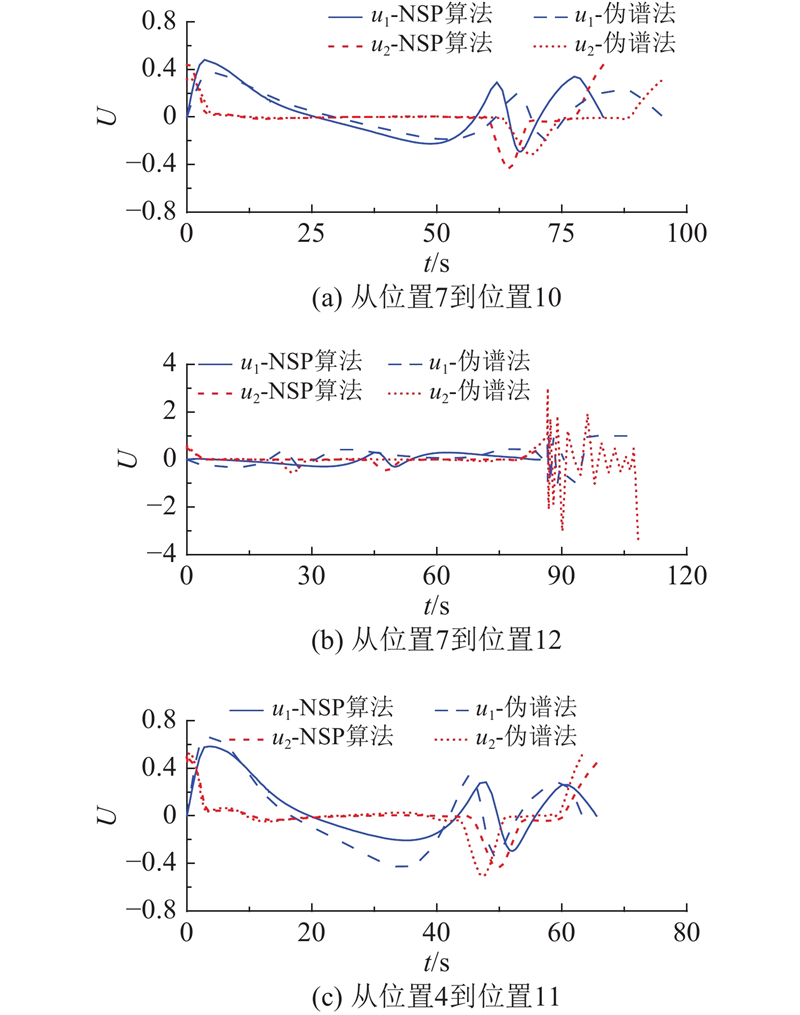
为了进一步分析所提方法的有效性，本文给出无杆牵引系统的控制变量变化规律. 如图6（a）、（b）和（c）所示分别为从位置7到位置10、位置7到位置12和位置4到位置11的无杆牵引系统控制变量随时间的变化规律. 分析图6可知，采用本文算法得到的最优路径所对应的控制变量变化均比较平缓，其中，转向角控制变量 ${u_1}$ 处于 $\left[ { - 0.8,\;0.8} \right]$，即无杆牵引车的转向角均处于 $\left[ - 38.66^{\rm{o}},\;38.66^{\rm{o}} \right]$，这说明在整个调运过程中没有出现急转弯的现象；无杆牵引车的加速度 ${u_2}$均处于 $\left[ { - 0.5,\;0.5} \right]\;{\rm{m/}}{{\rm{s}}^{{2}}}$，系统的减速以及加速过程均比较平缓，在大部分过程的加速度均为0，即在整个阶段未出现急刹车现象. 以上结果可证明最优路径对应的控制律均满足平稳性要求，符合工程实际. 在采用伪谱法得到的路径中，从位置7到位置12的路径对应的控制变量在末端时发生了严重的震荡，且 ${u_2}$超出了约束范围，其所得到的解为非可行解.

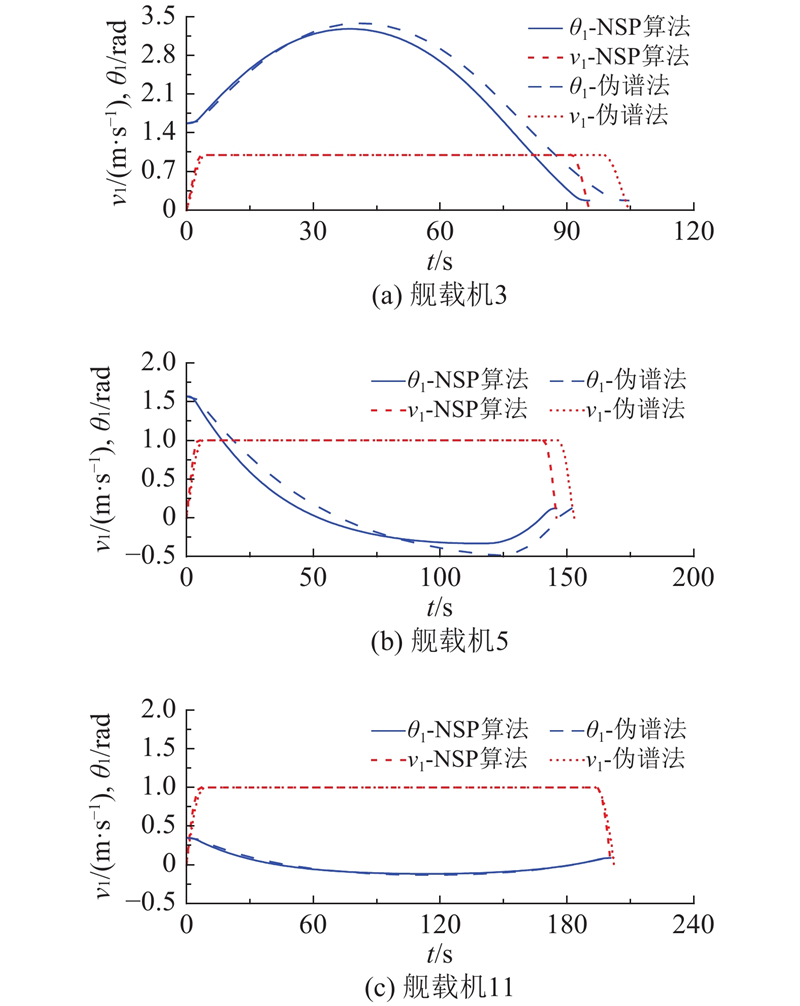
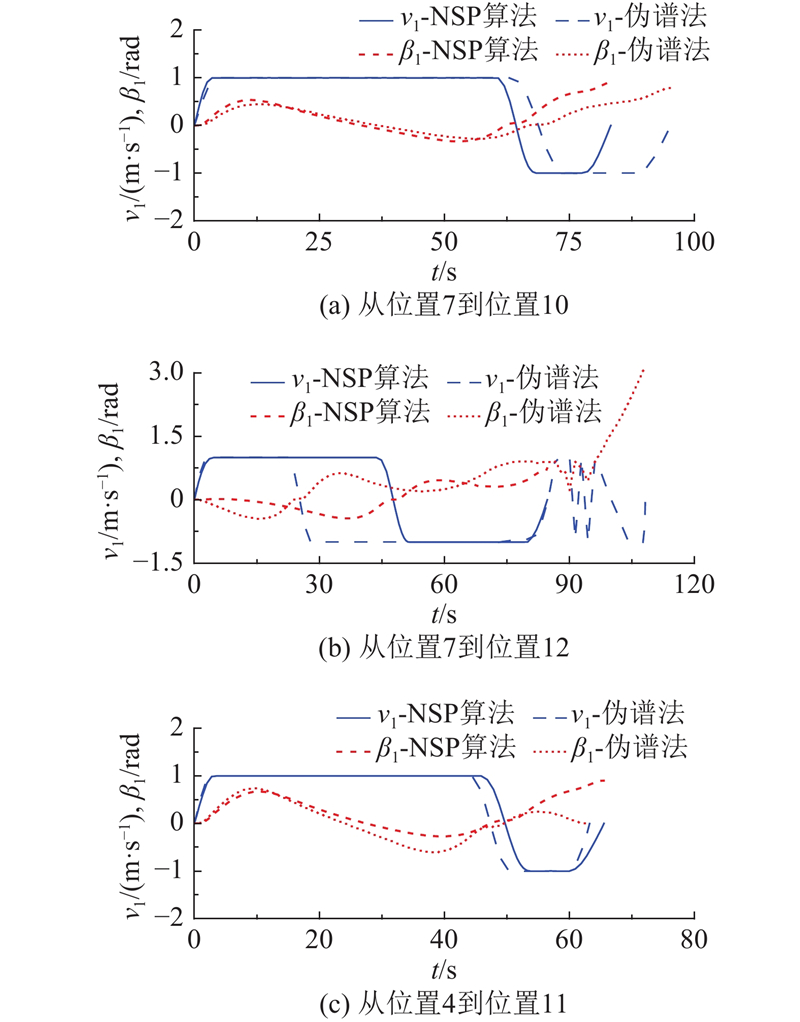
为了进一步分析牵引系统中舰载机的运动情况，根据求得的状态变量得到舰载机速度和转向角的变化规律. 如图7（a）、（b）和（c）所示分别为从位置7到位置10、位置7到位置12和位置4到位置11的舰载机速度和转向角随时间的变化规律. 结合图6和7可知，根据本文算法得到的结果，在大部分的运动阶段内，舰载机均是以最大速度1 m/s或者最小速度−1 m/s保持匀速运动，终点处速度为0，且舰载机在运动过程中没有出现急刹车或者其他大幅加速的情况；舰载机在沿最优路径运动的过程中，其转向角曲线的变化均比较平滑，且控制变量 ${u_1}$保持在 $\left[ { - 0.9,\;0.9} \right]$，没有出现较大幅度的转弯现象，在一定程度上了降低了转弯产生的事故风险. 当采用伪谱法时，从位置7到位置10和从位置4到位置11的飞机速度、转向角也较为平滑，但是从位置7到位置12的飞机转向角明显超出了约束范围.

为了验证NSP算法的精度和效率，在相同的参数设置下，本文选取比较典型的伪谱法进行对比分析，具体的对比结果如表2所示. 由表2可分析出：采用这2种方法所得到的目标函数值基本接近，但是NSP可在更短的时间内得到最优解，对于从位置7到位置10、位置7到位置12，所需的计算时间分别为伪谱法的11.78%和6.97%；对于从位置4到位置1，所需的计算时间为伪谱法的11.03%；在从位置7到位置10和从位置7到位置12中，采用提出的方法所得到的末端时间明显小于伪谱法；在从位置4到位置11中，采用提出的方法所得到的末端时间略大于伪谱法，但差别较小. 这说明本文算法的计算效率明显要优于伪谱法，所得的结果均能够满足相应的约束，没有出现非可行解，可靠性更高.

实验选取3架飞机进行研究，舰载机8、11均是从同一升降机的同一位置（位置7）被牵引至预定位置（位置8、11），舰载机1是从位置4牵引至预定位置1.

本实验中取 ${w_k} = 0.1$，根据NSP算法可得出3架飞机和有杆牵引车的路径如图8所示. 图8中，实线表示的是采用本文算法得到的路径曲线，虚线表示的是牵引车的路径曲线. 由图8分析可知，得到的路径满足末端约束，且由NSP所得出的舰载机和牵引车的路径均非常平滑.

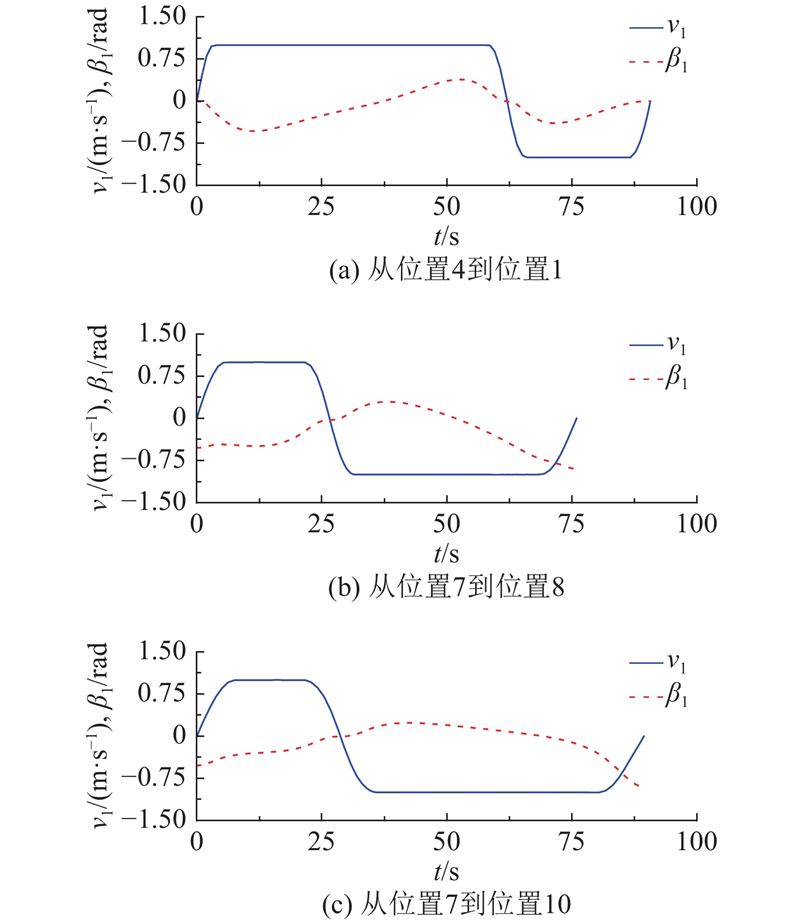
NSP算法对在轴无杆虚拟系统进行路径规划的可行性在第4.3节已进行了研究和验证，本节不再赘述，只给出飞机速度和转向角的变化规律. 如图9（a）、（b）和（c）所示分别为从位置4到位置1、从位置7到位置8和从位置7到位置10的舰载机速度和转向角随时间的变化规律. 分析图9可知，采用本文算法得到的舰载机速度和转向角变化均比较平缓，其中飞机的速度均处于 $\left[ { -1.0,\;1.0} \right]\;{\rm{m/s}}$，即控制变量 ${u_1}$均处于 $\left[ { - 0.9,\;0.9} \right]$，这说明飞机速度和转向角均满足相应的约束，且变化均比较平稳，满足工程实际需求.

在末端时间优化方面，使用有杆牵引方式，将飞机从位置4牵引至位置1需要90.701 1 s，将飞机从位置7牵引至位置8需要60.767 7 s，将飞机从位置7牵引至位置11需要107.295 6 s.

实验验证结果表明：本文提出的算法能够以较高的精度和效率对舰载机路径规划最优控制问题进行求解，可得出最优的调运时间，对应的调运路径也很平滑，相应的控制变量变化均较为平稳，且该算法对协变量和控制变量的初始值要求均较低，具有很强的可操作性和适用性，便于实际应用. 本文研究内容及方法的主要优势如下.

1）本研究提出了舰载机单机滑行、离轴无杆牵引系统、离轴有杆牵引系统的运动学模型. 其中，无杆牵引系统的路径规划目前鲜有研究，所建立的运动学模型可以为后续无杆牵引系统的控制等问题提供参考. 提出的有杆牵引系统的运动学模型较现有的模型更加简洁，提出的模型可为有杆牵引系统的研究提供参考. 此外，由于有杆牵引系统最为复杂，所建立的有杆牵引系统运动学模型仍为一个强非线性系统，对初始猜测解以及参数均较为敏感，容易发散. 为此，将复杂的有杆牵引系统转化为一个更加简单的虚拟在轴无杆牵引系统，以实现对舰载机和牵引车的轨迹进行求解，这可为后续的相关研究提供新的思路.

（2）建立了路径规划的最优控制模型，采用最优控制方法进行路径规划，较其他方法而言，该算法所得到的结果不仅可以严格满足终端约束条件，还可以满足最优控制条件，以确保所得到的结果最优.

（3）NSP算法可以以较高的精度和稳定性求解末端时间不定的最优控制问题，对初始猜测解敏感度低、计算效率高、收敛速度快. 此外，本文算法还可以解决时间-能量最优的控制问题，在确保控制平稳的前提下得到使舰载机从起点到终点耗时最短的路径，有利于提高出动和调运效率.

在所提算法中，初始猜测解的设置会影响算法的收敛性，如何提高初始猜测解的质量，以进一步提高算法的收敛速度，是实现其工程应用的基础，也是后续的研究方向. 此外，还需要对算法进一步优化，以提高其计算效率.