浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(9): 1785-1794 doi: 10.3785/j.issn.1008-973X.2020.09.015

机械与能源工程

基于缝隙射流原理的离心泵空化控制研究

赵伟国,, 路佳佳, 赵富荣

Cavitation control of centrifugal pump based on gap jet principle

ZHAO Wei-guo,, LU Jia-jia, ZHAO Fu-rong

收稿日期: 2019-08-14  

Received: 2019-08-14  

作者简介 About authors

赵伟国（1979—），男，教授，从事水力机械流动理论及空化多相流研究.orcid.org/：000-0002-3550-604X.E-mail：zhaowg@zju.edu.cn , E-mail：zhaowg@zju.edu.cn

摘要

为了改善低比转速离心泵内的空化流动状态，提出一种在叶片上设置缝隙的被动控制方法，探究该结构对空化的抑制效果及其控制机理. 采用数值模拟方法探讨结构对空化的抑制. 采用修正的SST k-ω湍流模型和Kubota空化模型，对原始叶轮和改型叶轮分别进行定常及非定常数值计算，获得设计工况下2种叶轮形式在各个空化阶段的流场结构及压力脉动特性. 计算结果表明：改型叶轮中经缝隙流向叶片背面的高压流体提高了叶片背面的压力，对空化初生、空化发展及空化剧烈阶段均产生了抑制作用，特别是空化剧烈阶段，与原始叶轮相比，其空泡体积分数减少了60.6%；与原始叶轮相比，改型叶轮内液相区的压力脉动主频幅值在各个空化阶段均有所下降.

关键词： 低比转速离心泵 ; 空化抑制 ; 缝隙射流 ; 数值模拟

Abstract

A passive control method with slot on the blade was proposed, and the cavitation suppression effect and control mechanism of the structure were explored, in order to improve the cavitation flow state in low specific speed centrifugal pump. The restraining effect of the structure on cavitation was explored by numerical simulation method. The modified SST k-ω turbulence model and Kubota cavitation model were used to calculate the steady and unsteady flow on the original impeller and the modified impeller, respectively, to obtain the flow field structure and pressure pulsation characteristic of two impeller forms in each cavitation stage under the design conditions. The calculation results show that the high-pressure fluid flowing to the back of the blade through the gap in the modified impeller increases the pressure on the back of the blade, which has inhibitory effect on initial cavitation, the development of cavitation and the intense stage of cavitation. Especially for the intense stage of cavitation, the cavity volume fraction decreased by 60.6% compared with the original model. the main frequency amplitude of the pressure pulsation in the liquid region of the modified impeller decreased at each cavitation stage, compared with that of the original impeller.

Keywords： low specific speed centrifugal pump ; cavitation suppression ; gap jet ; numerical simulation

PDF (2238KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

赵伟国, 路佳佳, 赵富荣. 基于缝隙射流原理的离心泵空化控制研究. 浙江大学学报(工学版)[J], 2020, 54(9): 1785-1794 doi:10.3785/j.issn.1008-973X.2020.09.015

ZHAO Wei-guo, LU Jia-jia, ZHAO Fu-rong. Cavitation control of centrifugal pump based on gap jet principle. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(9): 1785-1794 doi:10.3785/j.issn.1008-973X.2020.09.015

空化是液体流场的低压区域形成蒸汽空泡的过程，伴随着空泡的产生、发展及溃灭. 空化的发生会引发水力机械产生不同程度的振动、冲击与噪声[1-2]，从而诱发水力机械运行过程中的非定常特性及动态响应特性[3-6]. 尤其是在空化发生后，空化泡随流体运动到高压区，因受高压流体的挤压作用而大量溃灭，溃灭过程所产生的微射流[7-8]会导致材料表面空蚀，致使水力机械提前发生疲劳破坏. 因此，多年来延缓空化的发生和抑制空泡的发展一直是水力机械行业研究的重点和难点.

国内外学者在空化控制方面作了大量的科学研究. Timoshevskiy等[9]通过可视化方法探究了壁面切向喷射对空化的抑制效果，研究表明：低速喷射源可以有效地抑制空化效应；高速喷射源使得能量损失降低，流体流动的水动力品质提高；同时证明某些条件下实施流量调控能够很好地控制空化流场. 刘汉儒等[10]分析了串列叶栅缝隙流对分离流动的影响，研究表明：缝隙流影响了前叶尾迹流和后叶附面层的流动，同时提高了串列叶栅的气动性能. 孙涛等[11]采用实验设计方法（design of experiments，DOE）和序列二次规划法（sequential quadratic programming，SQP）组合策略对低比转速离心泵缝隙引流叶轮的水力性能进行了优化设计，研究表明：中部缝隙可以减少流道内的堵塞，提高扬程和效率. 张文著等[12]对缝隙引流叶片式叶轮内的压力脉动特性及振动特性进行了研究，证明缝隙引流叶片对离心泵内的压力脉动、振动及二次流输送都有很好的优化作用. 王洋等[13]采用数值方法研究了低比转速离心泵叶片进口边开缝对空化性能的影响，研究表明：叶片进口边开缝能够提高泵的空化性能，降低空蚀对材料结构的影响. 韩伟等[14]提出了在高速离心叶轮叶片吸力面尾部进行开缝抽吸的方法，此方法可以减少叶片表面流动分离，提高离心叶轮效率. 胡赞熬等[15]对叶片进口边进行了开孔研究，结果表明：开孔会造成能量损失，损失大小与孔的几何参数有关；同时证明了开孔能够提高叶轮的水力性能，其主要原因是开孔降低了叶轮进口环量，使得离心泵的扬程和效率都有所提高. 笔者等[16]通过实验和数值仿真的方法研究了在低比转速离心泵叶片工作面布置障碍物对空化性能的抑制作用，研究表明：在叶片表面布置障碍物对离心泵各个阶段的空化都有所抑制，主要原因在于布置障碍物可以有效阻挡回射流.

基于上述空化抑制研究结论，本文提出一种基于缝隙射流原理的新型叶片，采用数值模拟手段对原始叶轮和改型叶轮内的定常及非定常工况分别进行计算，研究此方法对低比转速离心泵内空化现象的抑制作用及其控制机理.

1. 数值方法

1.1. 湍流模型

采用1984年Menter[17]提出的SST k-ω湍流模型对两相流场进行计算，其主要方法是在近壁面区域采用k-ω模型，在远场区域采用k-ε模型，相关方程如下：

$\frac{{\partial \rho k}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = {\tilde p_k} - {\beta ^*}k\omega + \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + {\sigma _k}{\mu _{\rm{t}}}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right],$

$\begin{split} \frac{{\partial (\rho \omega )}}{{\partial t}} + & \frac{{\partial (\rho {u_i}\omega )}}{{\partial {x_i}}} = \alpha \rho {S^2} + \frac{\partial }{{\partial {x_i}}}\left[ {(\mu + {\sigma _\omega }\,{\mu _{\rm{t}}})\frac{{\partial \omega }}{{\partial {x_i}}}} \right] - \\ &\qquad\quad\;\; \beta \rho {\omega ^2} - 2(1 - {F_1})\rho {\sigma _{\omega {\rm{2}}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_i}}}\frac{{\partial \omega }}{{\partial {x_i}}}, \end{split}$

${\mu _{\rm{t}}} = \rho \frac{k}{\omega }.$

式中：ρ为流体密度； ${\tilde p_k} $为由于平均速度梯度产生的湍动能；ω为湍流耗散率；ui为流体速度分量；xi为坐标轴分量；t为时间；i=1，2，3；k为湍动能；μ为湍动黏度；μt为湍流黏性系数；α、β、β*、σk、σω均为经验常数；S为应变速度的不变量；F1为壁面距离的调配函数，在壁面处取值为1，在自由流区取值为0.

SST k-ω湍流模型兼具了近壁面处黏性流动可靠性及远场自由流精准性的优点，能够较为准确地计算单相条件下的流体流动状况. 但是在空化流计算过程中存在对空泡溃灭区域湍流黏度过度预测的问题，因此需要对SST k-ω模型的湍流黏度进行修正，使得模型能更好地捕捉离心泵内空化泡的流动状态. 计算湍流黏度的方式为

$ {\mu _{\rm{t}}} = f(\rho )\frac{k}{\omega }; $

$ f(\rho ) = {\rho _{\rm{v}}} + \frac{{{{({\rho _{\rm{m}}}{\rm{ - }}{\rho _{\rm{v}}})}^n}}}{{{{({\rho _{\rm{l}}}{\rm{ - }}{\rho _{\rm{v}}})}^{n - 1}}}},\;n > 1. $

式中：n为常数，ρm为混合相密度，ρl为液相密度，ρv为汽相密度.

根据上述公式对空泡的湍流黏度进行修正，当n取不同值时，密度变化曲线如图1所示. 根据前人的的研究结果[18]，当n取10时得到的结果与试验结果更为接近，因此本研究中取n=10. 对密度进行修正，修正后的模型能更好地捕捉空化泡，因此在计算过程中采用修正后的SST k-ω湍流模型.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   湍流黏度修正函数

Fig.1   Modified function of turbulent viscosity


1.2. 空化模型

本研究采用Kubota空化模型[19]，该模型又被称为Zwart Gerber Belamri（ZGB）空化模型[20]. 该空化模型是由描述流体内气泡增长的Rayleigh-Plesset方程简化而来：

${R_{\rm{B}}}\frac{{{{\rm d}^2}{R_{\rm{B}}}}}{{{\rm d}{t^2}}} + \frac{3}{2}{\left( {\frac{{{\rm d}{R_{\rm{B}}}}}{{{\rm d}t}}} \right)^2} + \frac{{2\sigma }}{{{R_{\rm{B}}}}} = \frac{{{p_{\rm{v}}} - p}}{{{\rho _{\rm{l}}}}}.$

忽略二阶项和表面张力得到如下方程：

$\frac{{{\rm d}{R_{\rm{B}}}}}{{{\rm d}t}} = \sqrt {\frac{2}{3}\frac{{{p_{\rm{v}}} - p}}{{{\rho _{\rm{l}}}}}} .$

式中：RB为空泡半径，σ为表面张力系数，pv为气泡内部压力（一般认为是液体某一温度下的汽化压力）.

单位体积的质量变化率Re表示如下：

1）当p < pv时，

${R_{\rm e}} = {F_{{\rm{vap}}}}\frac{{3{r_{{\rm{nuc}}}}(1 - {r_{\rm{v}}})\;{\rho _{\rm{v}}}}}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3}\frac{{{p_{\rm{v}}} - p}}{{{\rho _{\rm{l}}}}}} ;$

2）当p > pv时，

${R_{\rm e}} = {F_{{\rm{cond}}}}\frac{{3{r_{\rm{v}}}\;{\rho _{\rm{v}}}}}{{{R_{\rm{B}}}}}\sqrt {\frac{2}{3}\frac{{p - {p_{\rm{v}}}}}{{{\rho _{\rm{l}}}}}} .$

式中：Fvap为蒸发系数，取50；Fcond为凝结系数，取0.01；RB=10−6 m；rnuc=5×10−4.

2. 物理模型及数值求解

2.1. 物理模型及计算网格

本研究所采用的模型为单级单吸离心泵，其主要技术参数如表1所示. 采用Croe 5.0对模型泵水体进行三维造型，所得模型如图2（a）所示.

表 1   单级单吸模型泵几何参数

Tab.1  Geometric parameters of single stage single suction model pump

参数 符号 数值 单位
设计流量 Q0 8.6 m3/h
额定转速 n 500 r/min
叶轮出口直径 D2 310 mm
叶轮进口直径 D1 85 mm
设计扬程 H 4.5 m
叶片数 Z 6 -
叶轮出口宽度 b2 12 mm
叶片通过频率 BPF 50 Hz

新窗口打开| 下载CSV


图 2

新窗口打开| 下载原图ZIP| 生成PPT

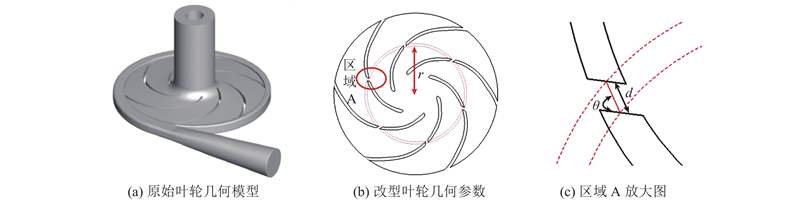
图 2   原始模型的几何模型及射流孔几何参数示意图

Fig.2   Diagram for geometric model of original model and location parameters of jet hole


离心泵是用来提高液体压力的水力机械. 流体从进口流到出口，压力不断增加，且工作面压力高于背面；由于受到叶片进口扰流的影响，叶轮内低压区出现在叶片背面进口靠后的位置，故在此位置容易发生空化现象. 为了有效控制离心泵内空化的发展，通过在叶片上设计合理的缝隙结构，将叶片工作面的高压流体引向叶片背面的低压区，从而控制叶片背面低压区的扩张，抑制空化泡的发展. 在叶片中部设置缝隙结构的主要原因如下：叶片前部工作面压力虽高于背面，但叶片前部的整体压力低于中部和后部，压差效应对压力的补偿作用较弱，空化控制效果不明显；叶片后部的压力虽高，但高压流体很难流到进口边空化发生的位置，本研究将缝隙设置在叶片中部，促使缝隙角度向进口背面位置偏转，使得高压流体能更好地流向空化发生区域.

缝隙几何参数的定义方法如图2（b）、（c）所示，r为仿生射流孔在叶轮上的径向位置，即射流孔前缘径向宽度中点到叶轮圆心的距离；d为射流孔宽度；θ为偏转角，定义为射流孔前缘径向位置与径向宽度中点连线的夹角. 在本研究中取r = 0.5 D2，d = 3 mm，θ = 60°

采用ANSYS ICEM对三维水体模型进行网格划分，全局网格如图3（a）所示，改型叶轮网格如图3（b）所示. 为保证近壁面区域有足够的节点以准确捕捉边界层的流动状况，对叶轮的边界层区域网格进行加密，保证y+值在100以内，叶片表面的y+ 值云图如图3（c）所示.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

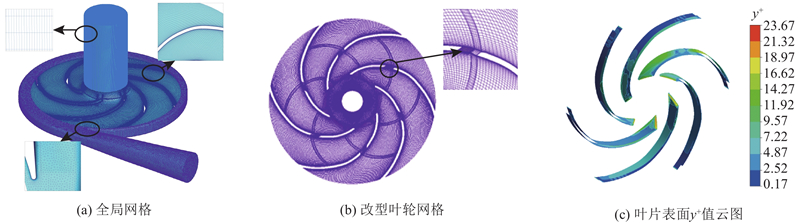
图 3   计算域网格及叶片表面的y+值云图

Fig.3   Grid of calculation domains and y+ of blade surface


y+ 值定义为与壁面最近的网格节点到壁面距离的无量纲参数，方程式为

${y^ + } = \frac{{\sqrt {{{{\tau _{\rm{w}} }} / \rho }} }}{\upsilon }\Delta n. $

式中：τw为壁面切应力， $\upsilon $为运动黏度，Δn为距离固体壁面最近的2个网格节点之间的距离差.

为了在计算过程中兼顾精度和经济性，进行网格无关性检验. 验证方法将三维流体域划分为3种不同数量的网格，对3种不同数量的流域进行外特性模拟计算，结果如表2所示。对比相应的3个扬程的变化幅度可知，随着网格数量的增加，方案2和方案3的扬程效率模拟值逐渐趋于稳定，由于方案2的网格数量低于方案3，为了方便计算，本研究取方案2进行计算。

表 2   计算域网格无关性检验

Tab.2  Grid independence check of calculation domains

方案 网格节点数 总网格数 H/m
进口段 叶轮 蜗壳
方案1 393 576 815 610 302 852 1 512 038 4.42
方案2 721 868 984 378 370 910 2 077 156 4.58
方案3 721 868 1 317 600 370 910 2 410 378 4.58

新窗口打开| 下载CSV


2.2. 边界条件设置

采用全隐式耦合算法对模型中的方程组进行求解；数值仿真过程中进口采用总压进口，出口采用质量流量出口，壁面采用无滑移边界，近壁面采用标准壁面函数处理.

空化计算过程中临界压力取常温下纯水的饱和蒸汽压力（3 169 Pa），采用不断降低进口压力的方法，使泵发生空化. 在计算非定常条件下的空化流流场结构时，将定常计算的收敛结果作为非定常计算的初始值，以加速非定常计算的收敛速度. 在非定常计算过程中，叶轮旋转一周所用的时间为0.12 s，取叶轮旋转3°为一个计算周期，即时间步长为0.001 s，计算总时长为1.2 s，即叶轮旋转10圈. 采用第10圈最后时刻（即第1.2 s）时的计算结果，对叶轮内的压力、空泡体积分数、速度和湍动能进行定常研究，取第10圈的计算结果进行非定常研究. 探究缝隙的存在对叶轮内部流动的影响，分析其对空化的抑制效果及其内在机理.

2.3. 数值模型验证

离心泵的性能试验及空化试验在兰州理工大学水泵实验室可视化试验平台进行，试验平台如图4所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   离心泵可视化实验平台示意图

Fig.4   Diagram of centrifugal pump visualization experiment platform


如图5（a）所示为不同流量下试验值与模拟值的对比，图中，Q为流量值，Q0为额定工况点的流量值. 结果显示：扬程H及效率 $\eta $的最大误差值出现在Q/Q0=1.4处，扬程试验值与模拟值的最大相对误差为3.0%，效率试验值与模拟值的最大相对误差为2.5%，相对误差在可容许的范围内（一般规定误差小于5%即可达到要求）. 如图5（b）所示为不同空化数σ下的试验值与模拟值对比，当σ≥0.82时，两者的相对误差为1.5%；当σ<0.82时，最大相对误差出现在σ = 0.12时，误差值为4.8%，满足误差要求.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

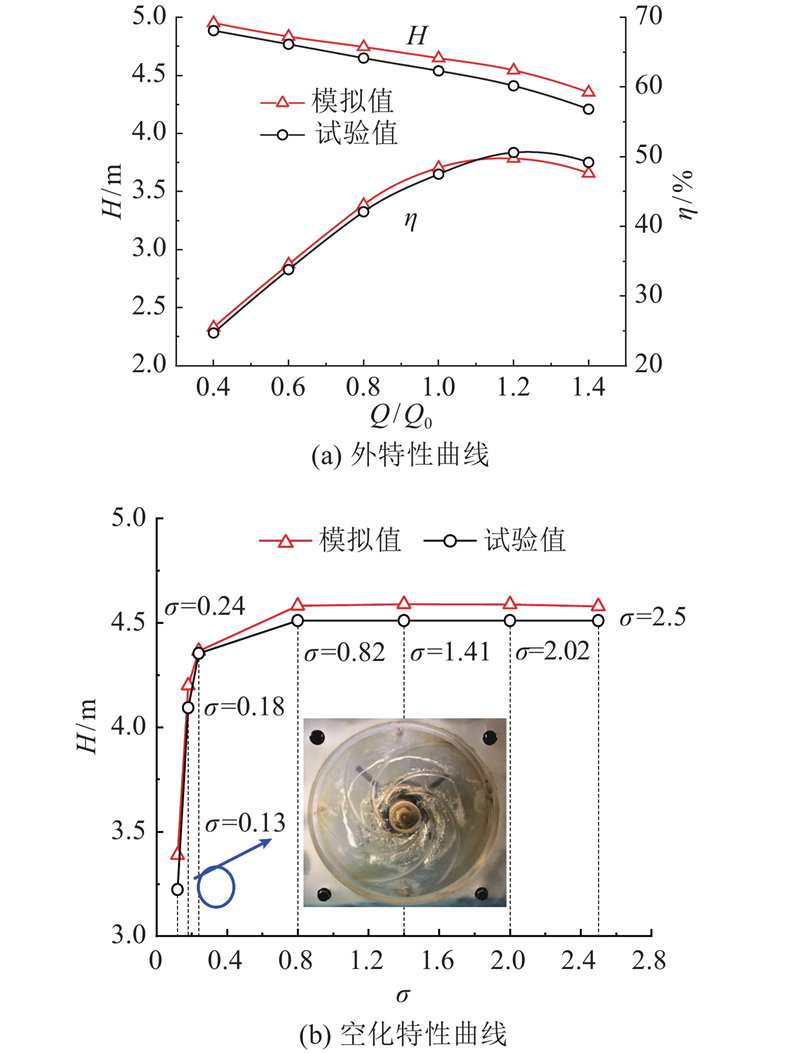
图 5   原始叶轮的模拟值与试验值对比

Fig.5   Comparisons between simulated results and experimental results of original impeller


3. 计算结果对比分析

3.1. 外特性分析

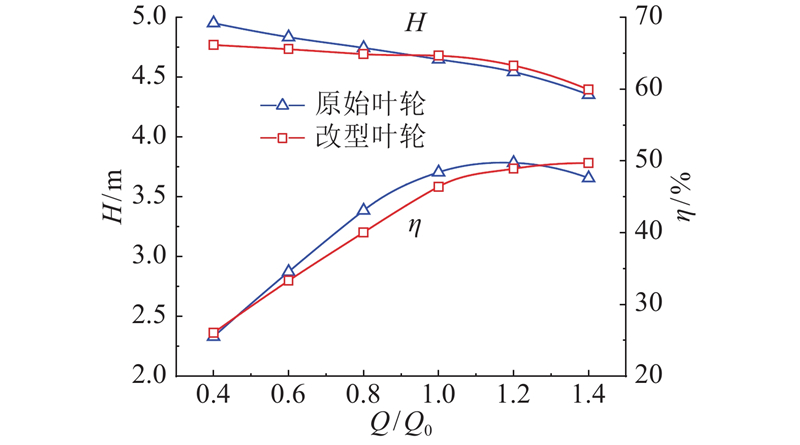
采用相同的计算条件，计算2种模型在不同流量点处的流场结构，主要以计算所得的扬程、效率结果为评价标准，最终结果如图6所示. 与原始叶轮相比，在小流量点处，改型叶轮的扬程降低；在额定流量及大流量点处，扬程增加；当Q/Q0=0.4时，改型叶轮的效率与原始叶轮基本相同；当Q/Q0=1.4时，改型叶轮的效率明显大于原始叶轮；在其他流量点，改型叶轮的效率均低于原始叶轮.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   原始叶轮与改型叶轮的外特性对比

Fig.6   Comparison of external characteristics between original impeller and modified impeller


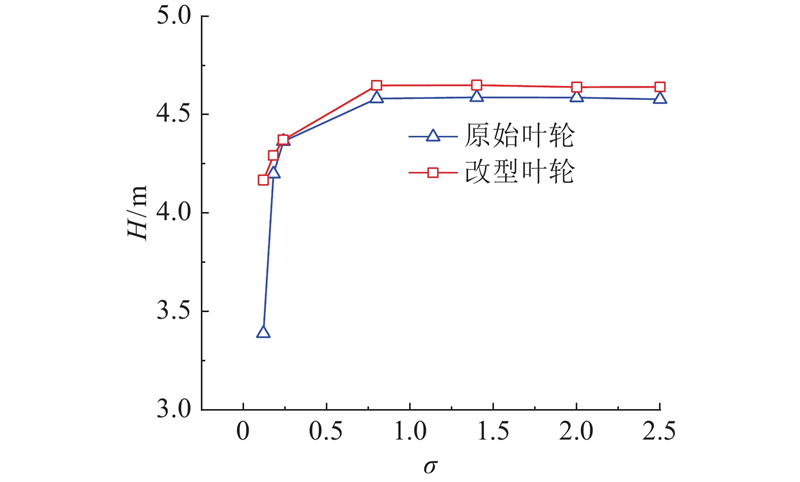
如图7所示为2种不同叶轮形式的空化特性曲线. 当σ > 0.82时，扬程无明显差别；当 σ < 0.82时，两者的扬程差别较大，特别是当 σ = 0.13时，与原始叶轮相比，改型叶轮的扬程提升了23.0%.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   原始叶轮与改型叶轮的空化特性对比

Fig.7   Comparison of cavitation performance between original impeller and modified impeller


3.2. 空泡时域分析

叶轮内空泡体积分数的定义为

${\alpha _{\rm{cav}}} = \frac{{\rm{1}}}{{{V_{{\rm{imp}}}}}}\sum\limits_{i = 1}^N {{\alpha _{{\rm{v}}.i}}{V_i}} .$

式中：N为叶轮内总控制单元的数目，αv.i为每个控制单元内的汽相体积分数，Vi为每个控制单元的体积，Vimp为叶轮体积.

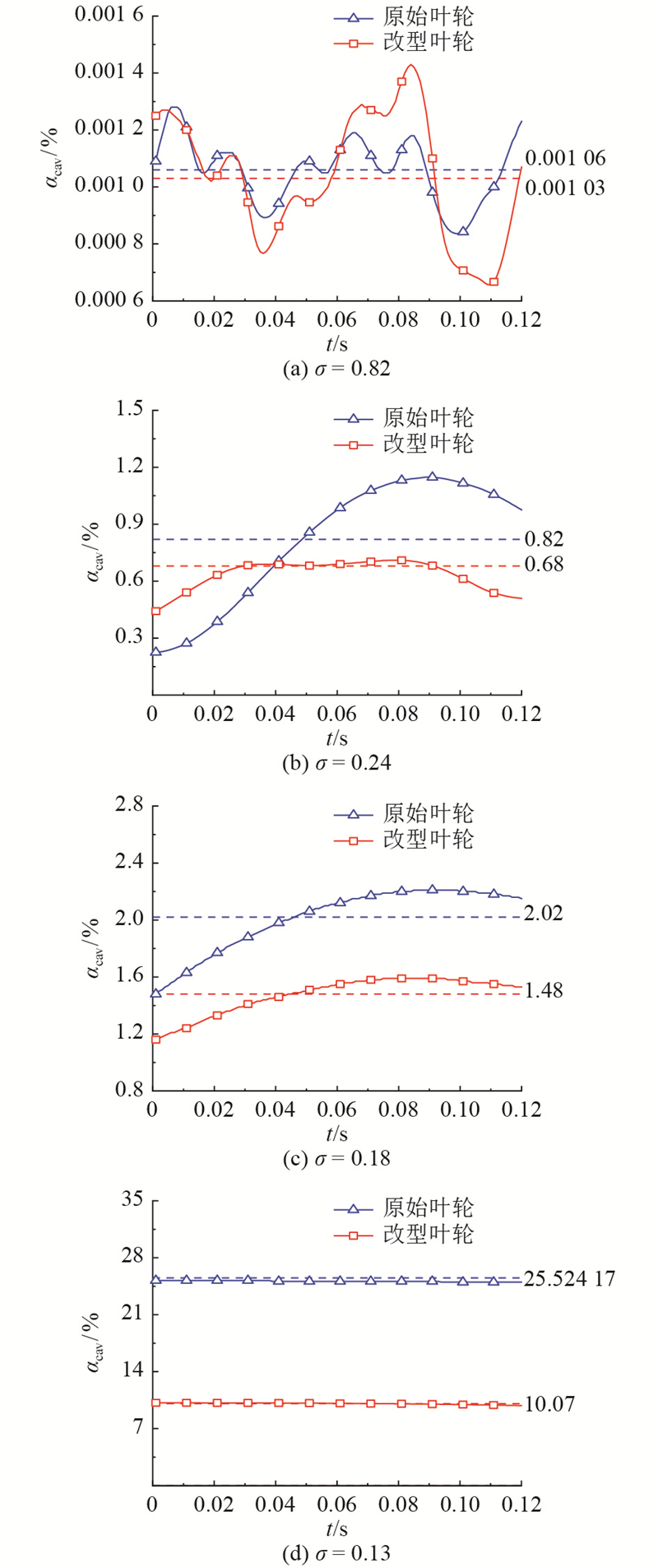
在叶轮的一个旋转周期内，不同空化数下的空泡体积分数随时间的变化趋势如图8所示. 其中，实线代表空泡体积分数随时间的变化，虚线代表最后一个旋转周期内空泡体积分数的均值.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   一个叶轮旋转周期内原始叶轮与改型叶轮的空泡体积分数对比

Fig.8   Comparison of cavitation volume fraction between original impeller and modified impeller in one impeller rotation cycle


在4种不同空化数下，改型叶轮内的平均空泡体积分数αcav与原始叶轮相比均下降；且空泡体积分数随时间的变化趋势基本保持一致. 当σ = 0.82时，如图8（a）所示，空泡体积分数减少了2.8%；在空泡发展及溃灭过程中，即当σ=0.24、0.18时，如图8（b）、（c）所示，空泡体积分数分别减少了17.1%和26.7%；在空化剧烈阶段，如图8（d）所示，空泡体积分数减少了60.6%，空化抑制效果最为明显.

3.3. 叶轮内部绝对压力分析

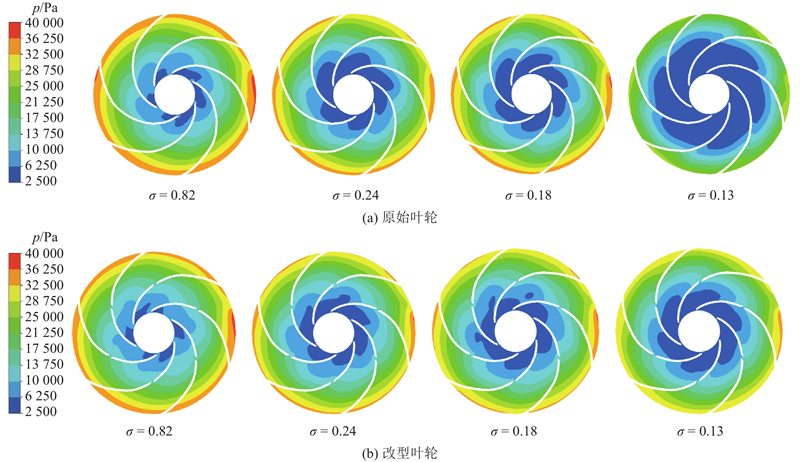
在流体流动过程中，当液体压力低于流体工作温度下的饱和蒸汽压力时，叶轮进口处产生空泡，因此，控制低压区域的产生和扩张是抑制空化的主要方法. 如图9所示，p为叶轮内的绝对压力，改型叶轮叶片结构的改变使得流体流经叶片缝隙区域时的面积发生突变，进而诱发颈缩效应，使得叶片背面压力提高；同时高压流体经缝隙流向叶片背面. 在这2种效应的作用下，叶片背面的低压区域与之前相比明显减少，最终影响了流体域中空化泡的产生、发展及溃灭. 尤其是在空化剧烈阶段，即当σ = 0.13时，缝隙结构有效地将低压区限制在缝隙前，使其不能向叶轮出口扩展，从而对空化泡的发展产生了明显的抑制效果.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   原始叶轮与改型叶轮中的截面绝对压力分布

Fig.9   Absolute pressure distribution in cross section of original impeller and modified impeller


3.4. 叶轮内部流线及空泡体积分数分析

如图10所示，在离心泵空化的不同阶段，改型叶轮叶片工作面的高压流体流向叶片背面，有效削弱了叶片背面的漩涡强度，使得流场结构更具有流线型；限制了前缘空化所形成的空化泡向叶轮出口发展，降低了叶轮流道内的空泡体积分数. 在空化剧烈阶段，缝隙处的高压射流增加了空泡区域的扰动，阻碍了大空穴的形成；原始叶轮内的空泡已经扩展至叶片下游，但对于改型叶轮而言，高压射流有效地将空化区域限制在缝隙结构前的叶轮流域内，限制了空泡向叶轮出口方向的发展.

图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   原始叶轮与改型叶轮的截面空泡体积分数及流线分布

Fig.10   Volume fraction and streamline distribution of cross section of original impeller and modified impeller


3.5. 叶轮内部速度矢量分析

Eckardt[21-22]采用实验和内部流场分析的方法对一高速径向离心叶轮流场进行研究，明确指出：在科式力与离心叶轮曲率的共同作用下，叶片背面的附面层不断加厚，将主流挤压向工作面，导致叶轮出口流场非常不均匀，从而形成射流-尾迹结构，这种流场结构导致叶轮内部的流动及后续元件内部流场产生强烈的非定常性，从而使得损失增加、效率下降[23-24]. 如图11所示，v为截面速度，改型叶轮的缝隙处流过的高速流体产生了由叶片背面指向工作面的力，明显改变了叶轮流道内的二次流图谱，改善了流道内的二次流积聚效应，进而使得叶轮出口的射流-尾迹结构及回流漩涡明显减弱. 同时，从图12中可以看出，在叶片工作面的高速流体经缝隙流向叶片背面的同时，叶片背面的能量增加，这降低了叶片背面附面层加厚的速度，减弱了边界层分离现象.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   当空化数为0.13时原始叶轮与改型叶轮的截面速度矢量图分布

Fig.11   Cross section velocity vectorgraph distribution of original impeller and modified impeller with cavitation number of 0.13


图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   当空化数为0.13时原始叶轮与改型叶轮的截面速度云图分布

Fig.12   Cross section velocity contour distribution of original impeller and modified impeller with cavitation number of 0.13


3.6. 叶轮内部湍动能分析

王振东[25]曾提到陆士嘉教授关于涡的言论：“流体的本质就是涡，因为流体经不住搓，一搓就有涡”，这里的“搓”意指剪切力. 朱兵[26]指出，湍流剪切力的增强会引发速度脉动和湍动能增强，这说明在湍动能大的区域对应的剪切力较大. 这种现象表现在离心泵上便是湍流损失的增强，水力性能的下降.

如图13所示，κ为截面湍动能，2种叶轮形式在空化初生阶段的湍动能无明显的差别；在空化发展及剧烈阶段，湍动能明显减小. 值得注意的是，在空化剧烈阶段，即当σ = 0.13时，原始叶轮几乎完全被空化泡填充，空化泡内的湍动能基本为0，在剩余液相区域，其湍动能均高于改型叶轮. 总的来说，在各个空化阶段，改型叶轮非空泡区域的湍动能均小于原始叶轮，缝隙的存在使得离心泵内的湍动能降低，湍流损失减小，水力性能提高.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   原始叶轮与改型叶轮的截面湍动能分布

Fig.13   Turbulence kinetic energy distribution of cross section of original impeller and modified impeller


3.7. 压力脉动主频幅值分析

为了分析离心泵内部的瞬态空化特性，在流道中间依次布置监测点P1、P2、P3、P4、P5，监测点的位置如图14所示；各监测点的压力脉动主频幅值如图15所示，A为监测点压力脉动主频幅值. 总体来看，除σ = 0.13外，与原始叶轮相比，其他情况下改型叶轮的压力脉动主频幅值均有下降趋势，叶轮内流动状态更加稳定. 当σ = 0.24时，压力脉动主频幅值的下降趋势最为明显，最大下降量出现在σ = 0.24对应的监测点P3；监测点P4次之.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

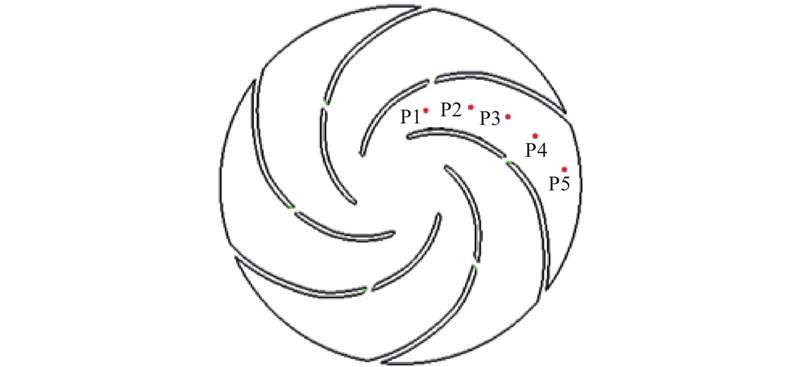
图 14   叶轮流道中的截面监测点布置

Fig.14   Layout of section monitoring points in cross section of impeller


图 15

新窗口打开| 下载原图ZIP| 生成PPT

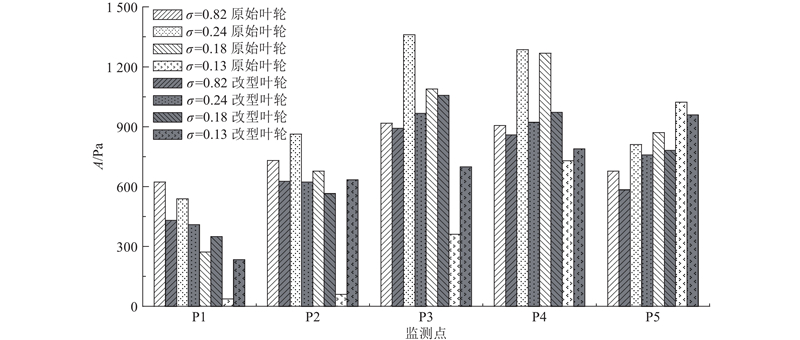
图 15   原始叶轮与改型叶轮的监测点压力脉动主频幅值分布

Fig.15   Main frequency amplitude distribution of pressure fluctuation at monitoring points in original impeller and modified impeller


当σ = 0.13时，对于原始叶轮而言，空化泡已经发展到监测点P4附近，监测点P1~P4处于稳定的云空化内部，其压力脉动主频幅值与其他工况点相比显著下降；而对于改型叶轮，缝隙限制了空化泡向叶轮出口发展，监测点P1~P4处于液相区，因此原始叶轮内监测点P1~P4的压力脉动主频幅值均低于改型叶轮，这一变化趋势与图13中的湍动能变化趋势基本一致. 然而在叶轮出口区域，从图13中可以看出，原始叶轮的湍动能明显高于改型叶轮，而原始叶轮与改型叶轮监测点P5的压力脉动主频幅值相比相差较小. 出现这一现象的主要原因在于：在叶轮出口靠近叶片工作面的流道区域，原始叶轮内的湍动能明显高于改型叶轮；而在流道中部和靠近背面的区域，湍动能变化不大；监测点P5处于流道中部位置，因此改型叶轮湍动能虽下降明显，但所监测到的压力脉动主频幅值与原始叶轮相比下降较少.

4. 结　论

（1）在叶轮的一个旋转周期内，缝隙射流对各个空化阶段空化泡的产生均有抑制作用，对空化初生阶段的影响较小，改型叶轮内的空泡体积分数与原始叶轮相比无明显差别；而对空化剧烈阶段的影响非常显著，与原始叶轮相比，改型叶轮内的空泡体积分数减少了60.6%.

（2）对叶轮内的压力脉动进行了监测，发现在各个空化阶段，与原始叶轮相比，改型叶轮液相区的压力脉动主频幅值都有所下降，与湍动能的变化趋势基本保持一致.

（3）叶轮内缝隙的存在限制了低压区向叶轮出口扩张，降低了流道内的湍动能，优化了流场结构，从而提高了离心泵的水力性能.

参考文献

王勇, 刘厚林, 袁寿其, 等

离心泵非设计工况空化振动噪声的试验测试

[J]. 农业工程学报, 2012, 28 (2): 35- 38

DOI:10.3969/j.issn.1002-6819.2012.02.007      [本文引用: 1]

WANG Yong, LIU Hou-lin, YUAN Shou-qi, et al

Experimental testing on cavitation vibration and noise of centrifugal pumps under off-design conditions

[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28 (2): 35- 38

DOI:10.3969/j.issn.1002-6819.2012.02.007      [本文引用: 1]

WEI Y S, SHEN Y, JIN S B

Scattering effect of submarine hull on propeller non-cavitation noise

[J]. Journal of Sound and Vibration, 2016, 370: 319- 335

DOI:10.1016/j.jsv.2016.01.027      [本文引用: 1]

王松林, 谭磊, 王玉川

离心泵瞬态空化流动及压力脉动特性

[J]. 振动与冲击, 2013, 32 (22): 168- 173

DOI:10.3969/j.issn.1000-3835.2013.22.031      [本文引用: 1]

WANG Song-lin, TAN Lei, WANG Yu-chuan

Characteristics of transient cavitation flow and pressure fluctuation for centrifugal pump

[J]. Journal of Vibration and Shock, 2013, 32 (22): 168- 173

DOI:10.3969/j.issn.1000-3835.2013.22.031      [本文引用: 1]

潘中永. 泵空化基础[M]. 镇江: 江苏大学, 2010.

LIU H L, LIU D X, WANG Y, et al

Experimental investigation and numerical analysis of unsteady attached sheet cavitating flows in a centrifugal pump

[J]. Journal of Hydrodynamics, 2013, 25 (3): 370- 378

DOI:10.1016/S1001-6058(11)60375-3     

黎慧青. 离心泵汽蚀磨损失效分析对策措施研究[D]. 广州: 华南理工大学, 2011.

[本文引用: 1]

LI Hui-qing. Studies on cavitation and fretting wear of centrifugal pump and counter measures [D]. Guangzhou: South China University of Technology, 2011.

[本文引用: 1]

PLESSET M S, CHAPMAN R B

Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary

[J]. Journal of Fluid Mechanics, 1971, 47 (2): 283- 290

DOI:10.1017/S0022112071001058      [本文引用: 1]

魏梦举, 陈力, 伍涛, 等

微尺度空泡溃灭驱使微球运动的机理研究

[J]. 物理学报, 2017, 66 (16): 167- 175

[本文引用: 1]

WEI Meng-ju, CHEN Li, WU Tao, et al

Study on the mechanism of micro-sphere motion driven by micro-cavity collapse

[J]. Acta Physica Sinica, 2017, 66 (16): 167- 175

[本文引用: 1]

TIMOSHEVSKIY M V, ZAPRYAGAEV I I, PERVUNIN K S, et al

Manipulating cavitation by a wall jet: experiments on a 2D hydrofoil

[J]. International Journal of Multiphase Flow, 2018, 99: 312- 328

DOI:10.1016/j.ijmultiphaseflow.2017.11.002      [本文引用: 1]

刘汉儒, 岳少原, 王掩刚, 等

串列叶栅缝隙射流对分离流动及叶栅性能影响的研究

[J]. 推进技术, 2018, 39 (12): 2728- 2736

[本文引用: 1]

LIU Han-ru, YUE Shao-yuan, WANG Pu-gang, et al

Study on the effect of cascade slot jet on separation flow and cascade performance

[J]. Journal of Propulsion Technology, 2018, 39 (12): 2728- 2736

[本文引用: 1]

孙涛, 陈红勋, 朱兵, 等

缝隙引流叶轮的优化设计

[J]. 上海大学学报: 自然科学版, 2014, 20 (2): 207- 213

[本文引用: 1]

SUN Tao, CHEN Hong-xun, ZHU Bing, et al

Optimal design of centrifugal pumps with gap drainage blades

[J]. Journal of Shanghai University: Natural Science Edition, 2014, 20 (2): 207- 213

[本文引用: 1]

张文著, 魏群, 陈红勋, 等

缝隙引流叶轮离心泵的压力脉动及振动特性

[J]. 上海大学学报: 自然科学版, 2018, 24 (2): 236- 248

[本文引用: 1]

ZHANG Wen-zhu, WEI Qun, CHEN Hong-xun, et al

Pressure fluctuation and vibration performance of centrifugal pump with gap drainage impeller

[J]. Journal of Shanghai University: Natural Science Edition, 2018, 24 (2): 236- 248

[本文引用: 1]

王洋, 谢山峰, 王维军

开缝叶片低比转数离心泵空化性能的数值模拟

[J]. 排灌机械工程学报, 2016, 34 (3): 210- 215

DOI:10.3969/j.issn.1674-8530.15.0114      [本文引用: 1]

WANG Yang, XIE Shan-feng, WANG Wei-jun

Numerical simulation of cavitation performance of low specific speed centrifugal pump with slotted blades

[J]. Journal of Drainage and Irrigation Machinery Engineering, 2016, 34 (3): 210- 215

DOI:10.3969/j.issn.1674-8530.15.0114      [本文引用: 1]

韩伟, 高丽敏, 白莹, 等

高速离心叶轮叶片开缝的数值研究

[J]. 流体机械, 2011, 39 (11): 17- 21

DOI:10.3969/j.issn.1005-0329.2011.11.004      [本文引用: 1]

HAN Wei, GAO Li-min, BAI Ying, et al

Numerical study of centrifugal compressor with slots in blade Surface

[J]. Fluid Machinery, 2011, 39 (11): 17- 21

DOI:10.3969/j.issn.1005-0329.2011.11.004      [本文引用: 1]

胡赞熬, 王俊雄, 祝宝山, 等

离心泵叶轮穿孔对空化性能的影响

[J]. 热能动力工程, 2018, 33 (10): 44- 51

[本文引用: 1]

HU Zan-ao, WANG Jun-xiong, ZHU Bao-shan, et al

Effect of blade perforation on centrifugal pump cavitation characteristics

[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33 (10): 44- 51

[本文引用: 1]

赵伟国, 赵国寿, 咸丽霞, 等

离心泵叶片表面布置障碍物抑制空化的数值模拟与实验

[J]. 农业机械学报, 2017, 48 (9): 111- 120

DOI:10.6041/j.issn.1000-1298.2017.09.014      [本文引用: 1]

ZHAO Wei-guo, ZHAO Guo-shou, XIAN Li-xia, et al

Effect of surface-fitted obstacle in centrifugal pump on cavitation suppression

[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48 (9): 111- 120

DOI:10.6041/j.issn.1000-1298.2017.09.014      [本文引用: 1]

MENTER F R

Two-equation eddy-viscosity turbulence models for engineering applications

[J]. AIAA Journal, 1994, 32 (8): 1598- 1605

DOI:10.2514/3.12149      [本文引用: 1]

REBOUD J L, STUTZ B, COUTIER O. Two phase flow structure of cavitation experiment and modeling of unsteady effects [C]// Proceedings of the 3rd International Symposium on Cavitation. Grenoble: PISC, 1998.

[本文引用: 1]

KUBOTA A, KATO H, YAMAGUCHI H, et al

Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling technique

[J]. Journal of Fluids Engineering, 1980, 111 (2): 204- 210

[本文引用: 1]

ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics [C] // Proceedings of the Fifth International Conference on Multiphase Flow. Yokohama: ICMF, 2004.

[本文引用: 1]

ECKARDT D

Instantaneous measurements in the jet-wake discharge flow of a centrifugal compressor impeller

[J]. Journal of Engineering for Power, 1975, 97 (3): 337- 345

DOI:10.1115/1.3445999      [本文引用: 1]

ECKARDT D

Detailed flow investigations within a high-speed centrifugal compressor impeller

[J]. ASME Journal of Fluids Engineering, 1976, 98 (3): 390- 402

DOI:10.1115/1.3448334      [本文引用: 1]

李景银, 梁亚勋, 田华

不同型线离心风机叶轮的性能对比研究

[J]. 工程热物理学报, 2008, 29 (6): 963- 966

DOI:10.3321/j.issn:0253-231X.2008.06.016      [本文引用: 1]

LI Jing-yin, LIANG Ya-xun, TIAN Hua

Flow field comparison between two centrifugal impellers with different blade curves

[J]. Journal of Engineering Thermophysics, 2008, 29 (6): 963- 966

DOI:10.3321/j.issn:0253-231X.2008.06.016      [本文引用: 1]

关醒凡. 现代泵理论与技术[M]. 北京: 中国宇航出版社, 2010.

[本文引用: 1]

王振东

流体涡旋漫谈

[J]. 现代物理知识, 2012, 24 (2): 9- 16

[本文引用: 1]

WANG Zhen-dong

A random talk on fluid vortex

[J]. Modern Physics, 2012, 24 (2): 9- 16

[本文引用: 1]

朱兵. 缝隙引流叶片提高低比转速离心泵性能的机理研究[D]. 上海大学, 2014.

[本文引用: 1]

ZHU Bing. Research on the mechanism of performance improving in low specific speed centrifugal pump with gap drainage blades [D]. Shanghai University, 2014.

[本文引用: 1]

/

〈 〉