喷动气固流化床颗粒混合规律的实验研究
1
2008
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
喷动气固流化床颗粒混合规律的实验研究
1
2008
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
喷动流化床颗粒混合特性的三维直接数值模拟
2
2008
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... [2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
喷动流化床颗粒混合特性的三维直接数值模拟
2
2008
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... [2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Fluid mechanical description of fluidized beds
1
1967
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Discrete particle simulation of two-dimensional fluidized bed
1
1993
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics
0
1997
A discrete numerical model for granular assemblies
1
1979
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
离散单元法及其在流态化领域的应用
1
2014
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
离散单元法及其在流态化领域的应用
1
2014
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Discrete particle simulation of particulate systems: a review of major applications and findings
1
2008
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Discrete element models for non-spherical particle systems: from theoretical developments to applications
2
2015
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... 式中:m与I分别为颗粒的质量和惯性张量,v和ω分别为颗粒的线速度和角速度,Fc为法向与切向接触力的矢量和,Fd为曳力,Fb为浮力,g为重力加速度,Tc为由切向接触力引起的接触力矩. 关于非球形颗粒DEM模型的更多细节,之前的研究已作了较详细的论述[9, 32-35],本文不再赘述. ...
DEM/CFD-DEM modelling of non-spherical particulate systems: theoretical developments and applications
2
2016
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... -10]. ...
Discrete element simulation of cylindrical particles using super-ellipsoids
3
2019
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... 针对上述情况,本文以喷动流化床为研究对象,采用CFD-DEM方法,对具有不同长径比的杆状颗粒在喷动流化床中的流动及混合行为进行数值模拟. 杆状颗粒采用超椭球模型进行描述,因为这种颗粒模型具有较高的精度和计算效率[11-12]. 根据模拟结果,对杆状颗粒的流动与混合特性进行较深入的分析,以期为实际应用中相关喷动床反应器的设计、优化、控制提供参考. ...
... 采用超椭球模型描述杆状颗粒,考虑到Zhao等[11, 26, 31]的研究对超椭球模型进行了较详细的论述,本文仅对其作简要的介绍. 超椭球标准方程[12]为 ...
CFD-DEM simulation of fluidization of rod-like particles in a fluidized bed
6
2017
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
... 针对上述情况,本文以喷动流化床为研究对象,采用CFD-DEM方法,对具有不同长径比的杆状颗粒在喷动流化床中的流动及混合行为进行数值模拟. 杆状颗粒采用超椭球模型进行描述,因为这种颗粒模型具有较高的精度和计算效率[11-12]. 根据模拟结果,对杆状颗粒的流动与混合特性进行较深入的分析,以期为实际应用中相关喷动床反应器的设计、优化、控制提供参考. ...
... 采用超椭球模型描述杆状颗粒,考虑到Zhao等[11, 26, 31]的研究对超椭球模型进行了较详细的论述,本文仅对其作简要的介绍. 超椭球标准方程[12]为 ...
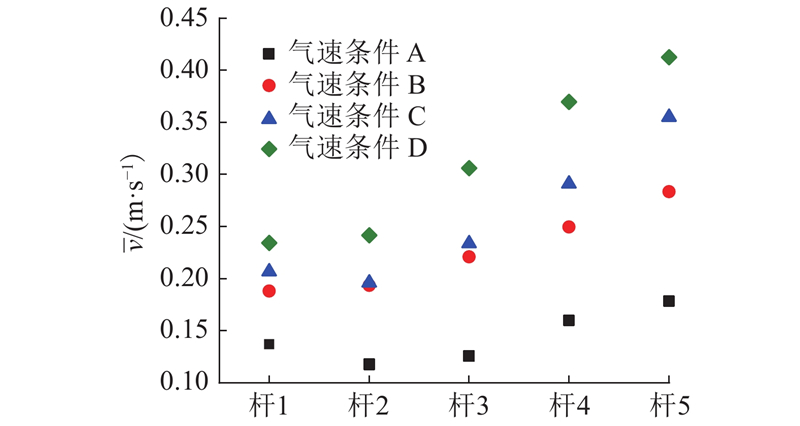
... 对于杆状颗粒而言,颗粒间的互锁会阻碍颗粒的运动,且该现象随着颗粒长径比的增加而更加明显[12, 31]. 若颗粒间的互锁起主导作用,则随着长径比的增加,颗粒的运动应受到抑制. 该现象与图6中颗粒速度的变化趋势不符,这表明颗粒的运动应受到别的因素的影响. 除颗粒间的互锁现象外,杆状颗粒在运动过程中,长轴取向会趋向一致,该现象可以削弱颗粒互锁带来的影响,从而有助于颗粒的运动[31]. 推测图6、7所示的变化规律是颗粒互锁与颗粒长轴取向一致性这2个因素共同作用的结果. ...
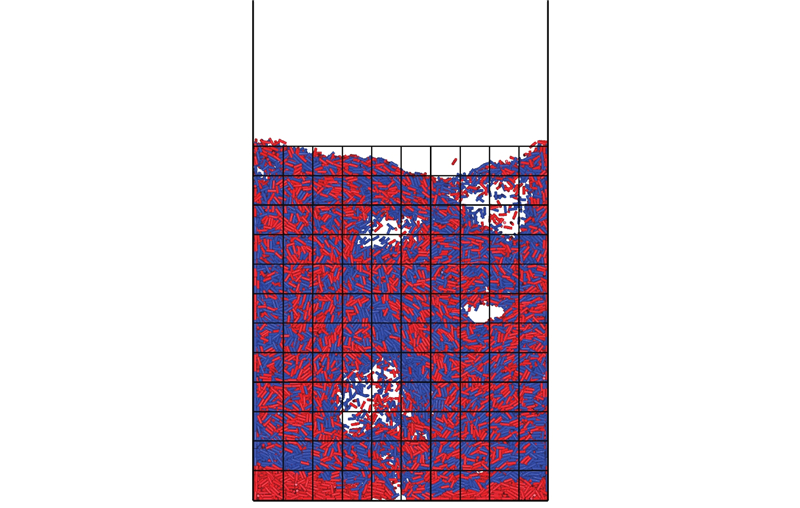
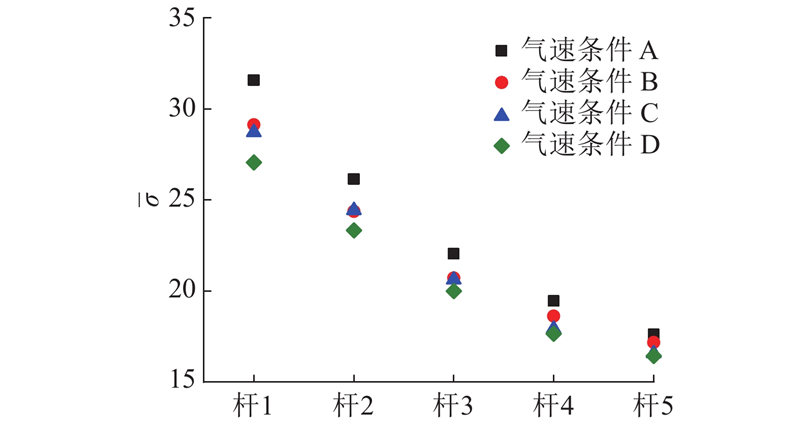
... 为了验证上述推测的合理性,对颗粒长轴取向一致性进行量化. 对于杆状颗粒在流化床中的流动,长轴取向在流化床的不同位置存在不同的倾向性[12],故将流化床区域划分成一定数量的子单元,如图8所示. 通过DEM可以直接获取颗粒的取向,计算每个颗粒的长轴与任意固定方向的夹角(0~90°)以及每个子单元内上述夹角的方差. 子单元内的颗粒取向越趋于一致,求得的方差越小. 将所有子单元对应的方差进行平均,用以量化颗粒取向的一致性. 基于上述思路,将轴向方向1(0,0,1)设为固定方向,对上述平均方差的时均值 $\bar \sigma $(2~10 s) 进行统计,如图9所示. 可以看出,随着长径比的增加,方差逐渐减小,表明颗粒取向一致性越好. 这证明前述推测是合理的,即当杆状颗粒长径比较小时,颗粒取向一致性的影响不足以抵消颗粒间互锁的影响,颗粒长径比的增加使得颗粒运动强度降低,导致混合变差;当颗粒长径比较大时,颗粒取向一致性的影响逐渐增强并超过颗粒互锁所带来的影响,使得颗粒长径比的增加可以促进颗粒运动与混合. ...
Polyhedra faster than spheres?
1
2014
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Distinct element simulation of impact breakage of lactose agglomerates
1
1997
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Cylindrical object contact detection for use in discrete element method simulations. Part I: contact detection algorithms
1
2010
... 在气固流化床中,颗粒的混合过程实质上反映了床层内颗粒的径向与轴向的运动及传递特性,是了解与认识流化床内传热传质过程的关键[1-2]. 研究颗粒的混合特性对于设计和优化气固流化床反应器的结构具有十分重要的现实意义. 对于气固两相体系中颗粒的流动与混合特性,可以通过实验手段进行研究,但是气固两相流动往往表现出多态性与复杂性. 全面了解与获取颗粒的运动与混合特性通常会受到实验手段的限制,尤其是对于比较稠密的气固两相系统[2]. 近年来,随着数值模拟和计算机技术的快速发展,人们建立了各种数值模型用以模拟气固两相系统,如双流体模型[3](two fluid model,TFM)、CFD-DEM模型[4-6](computational fluid dynamics/discrete element method,即计算流体力学/离散单元法)等. 与其他数值模拟方法相比,CFD-DEM模型所需的经验参数较少,可以比较容易获取较丰富的颗粒尺度的微观信息,这对于研究气固两相流动的微观机理十分重要. CFD-DEM现已被广泛用于对气固两相系统的研究[7-10]. 由于非球形颗粒的建模难度较大,CFD-DEM模型过去多用于对球形颗粒的研究[8]. 在实际应用中,颗粒形状多为非球形. 针对这种情况,人们提出多种模型用于描述非球形颗粒,包括超椭球模型[11-12]、多面体模型[13]、组合球模型[14]、真实形状模型[15]等. 借助于这些颗粒模型,近年来对非球形颗粒系统的CFD-DEM数值模拟研究取得了较大的进展[9-10]. ...
Orientation of cylindrical particles in gas-solid circulating fluidized bed
1
2012
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Numerical investigation of the mixing of non-spherical particles in fluidized beds and during pneumatic conveying
2
2015
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
... , 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Numerical simulation of spouting of cylindroid particles in a spouted bed
2
2014
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
... [18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed
1
2009
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Numerical analysis on the fluidization dynamics of rodlike particles
0
2016
Pressure drop investigations in packings of arbitrary shaped particles
0
2015
Experimental and numerical study of fluidization and pressure drop of spherical and non-spherical particles in a model scale fluidized bed
0
2016
Numerical investigation of mixing and orientation of non-spherical particles in a model type fluidized bed
0
2014
Non-spherical particles in a pseudo-2D fluidised bed: modelling study
0
2018
CFD-DEM investigation of the fluidization of binary mixtures containing rod-like particles and spherical particles in a fluidized bed
0
2018
CFD-DEM modeling of rod-like particles in a fluidized bed with complex geometry
2
2019
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
... 采用超椭球模型描述杆状颗粒,考虑到Zhao等[11, 26, 31]的研究对超椭球模型进行了较详细的论述,本文仅对其作简要的介绍. 超椭球标准方程[12]为 ...
Spouting of biomass particles: a review
1
2008
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Spouting behaviors of binary mixtures of cylindroid and spherical particles
1
2015
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Mixing behaviors in an industrial-scale spout-fluid mixer by 3D CFD-TFM
0
2017
Experimental investigation on the translational and rotational motion of biomass particle in a spout-fluid bed
1
2013
... 作为一种比较常见的非球形颗粒,杆状颗粒广泛存在于能源、化工、制药等工业生产过程中,比如生物质燃烧和气化、塑料颗粒加工、化肥及农药颗粒制备等过程. 其中的许多工业过程均涉及到气固两相流动,为了更好地了解杆状颗粒的流动与混合特性以达到控制和优化相关工业过程的目的,研究人员已把CFD-DEM方法应用到与杆状颗粒相关的过程中,如提升管[16]、气力输送[17]、喷动床[18]、鼓泡流化床[12, 17, 19-26]等. 对于涉及到杆状颗粒的气固两相体系,目前的研究存在一些不足. 例如,喷动床作为处理生物质颗粒(杆状颗粒)的重要设备[27],包括钟文琪教授团队在内的众多研究人员通过数值模拟、实验等手段研究生物质颗粒在喷动床中的流动[18, 28-30],但目前对其混合特性的了解较缺乏,如颗粒长径比的影响. ...
Investigating the flow of rod-like particles in a horizontal rotating drum using DEM simulation
3
2018
... 采用超椭球模型描述杆状颗粒,考虑到Zhao等[11, 26, 31]的研究对超椭球模型进行了较详细的论述,本文仅对其作简要的介绍. 超椭球标准方程[12]为 ...
... 对于杆状颗粒而言,颗粒间的互锁会阻碍颗粒的运动,且该现象随着颗粒长径比的增加而更加明显[12, 31]. 若颗粒间的互锁起主导作用,则随着长径比的增加,颗粒的运动应受到抑制. 该现象与图6中颗粒速度的变化趋势不符,这表明颗粒的运动应受到别的因素的影响. 除颗粒间的互锁现象外,杆状颗粒在运动过程中,长轴取向会趋向一致,该现象可以削弱颗粒互锁带来的影响,从而有助于颗粒的运动[31]. 推测图6、7所示的变化规律是颗粒互锁与颗粒长轴取向一致性这2个因素共同作用的结果. ...
... [31]. 推测图6、7所示的变化规律是颗粒互锁与颗粒长轴取向一致性这2个因素共同作用的结果. ...
Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube
2
2009
... 式中:m与I分别为颗粒的质量和惯性张量,v和ω分别为颗粒的线速度和角速度,Fc为法向与切向接触力的矢量和,Fd为曳力,Fb为浮力,g为重力加速度,Tc为由切向接触力引起的接触力矩. 关于非球形颗粒DEM模型的更多细节,之前的研究已作了较详细的论述[9, 32-35],本文不再赘述. ...
... 对于连续相,采用SIMPLEC算法进行求解,流体方程对流项的差分采用QUICK差分格式,流体的运动通过基于压力的隐式积分法进行求解. 对于颗粒相,采用笔者等开发的DEM代码进行求解,其中颗粒的运动通过显式时间积分法进行求解. 对于CFD与DEM间的耦合,之前的研究进行了较详细的论述[32-33, 40],本文不再赘述. ...
Numerical prediction of erosion in elbow based on CFD-DEM simulation
1
2016
... 对于连续相,采用SIMPLEC算法进行求解,流体方程对流项的差分采用QUICK差分格式,流体的运动通过基于压力的隐式积分法进行求解. 对于颗粒相,采用笔者等开发的DEM代码进行求解,其中颗粒的运动通过显式时间积分法进行求解. 对于CFD与DEM间的耦合,之前的研究进行了较详细的论述[32-33, 40],本文不再赘述. ...
CFD-DEM simulation of tube erosion in a fluidized bed
0
2017
Investigation of the vibration sorting of non-spherical particles based on DEM simulation
1
2018
... 式中:m与I分别为颗粒的质量和惯性张量,v和ω分别为颗粒的线速度和角速度,Fc为法向与切向接触力的矢量和,Fd为曳力,Fb为浮力,g为重力加速度,Tc为由切向接触力引起的接触力矩. 关于非球形颗粒DEM模型的更多细节,之前的研究已作了较详细的论述[9, 32-35],本文不再赘述. ...
Discrete particle simulation of particulate systems: theoretical developments
1
2007
... 在气固两相系统中,颗粒与流体间的作用力包括曳力、浮力、Saffman力和Magnus力等[36]. 因为颗粒的运动速度较低,仅考虑曳力与浮力的作用. 对于单颗粒,曳力计算公式[37]为 ...
Numerical simulation of the gas-solid flow in a bed with lateral gas blasting
1
2000
... 在气固两相系统中,颗粒与流体间的作用力包括曳力、浮力、Saffman力和Magnus力等[36]. 因为颗粒的运动速度较低,仅考虑曳力与浮力的作用. 对于单颗粒,曳力计算公式[37]为 ...
The voidage function for fluid-particle interaction systems
1
1994
... 考虑到周围颗粒对曳力的影响,Di Felice[38]对式(7)进行了修正: ...
New simple correlation formula for the drag coefficient of non-spherical particles
1
2008
... 采用Hölzer/Sommerfeld模型[39]计算曳力系数: ...
Numerical simulation of hydrodynamics in downers using a CFD-DEM coupled approach
1
2010
... 对于连续相,采用SIMPLEC算法进行求解,流体方程对流项的差分采用QUICK差分格式,流体的运动通过基于压力的隐式积分法进行求解. 对于颗粒相,采用笔者等开发的DEM代码进行求解,其中颗粒的运动通过显式时间积分法进行求解. 对于CFD与DEM间的耦合,之前的研究进行了较详细的论述[32-33, 40],本文不再赘述. ...
Nonspherical particles in a pseudo-2D fluidized bed: experimental study
1
2018
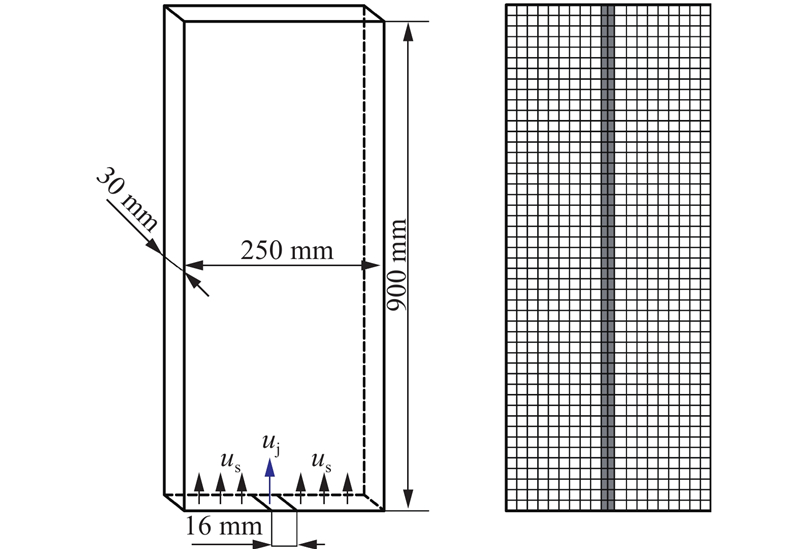
... 通过实验验证CFD-DEM模型的精度. 喷动流化床尺寸与图1所示的模拟装置相同,壁面材料为透明亚克力玻璃,流化床前方放置一台高速相机用于拍摄颗粒的流动状态. 实验中所使用的颗粒为木质杆状颗粒,尺寸为2.5 mm × 7 mm(直径×长度),颗粒数量为28 000. 颗粒及气体的物理性质与表2所列参数相同,如密度、黏度等. 实验及与实验相对应的CFD-DEM模拟结果均表明,此时床层的最小流化速度约为0.7 m/s. 设置uj=5 m/s,us为0.7和1.0 m/s,开展相应的实验和模拟. 如图3所示为在不同气速条件下实验与模拟中颗粒流动状态的对比. 表4列出实验与模拟中的时均床层高度及标准差(2~10 s),床层高度H的计算方法与Mahajan等[41]的方法相同. 从图3和表4可以看出,模拟结果与实验结果吻合良好. 建立的CFD-DEM模型对于模拟杆状颗粒在喷动流化床中的流动具有较高的精度. ...
Developments in the theory of particle mixing
2
1954
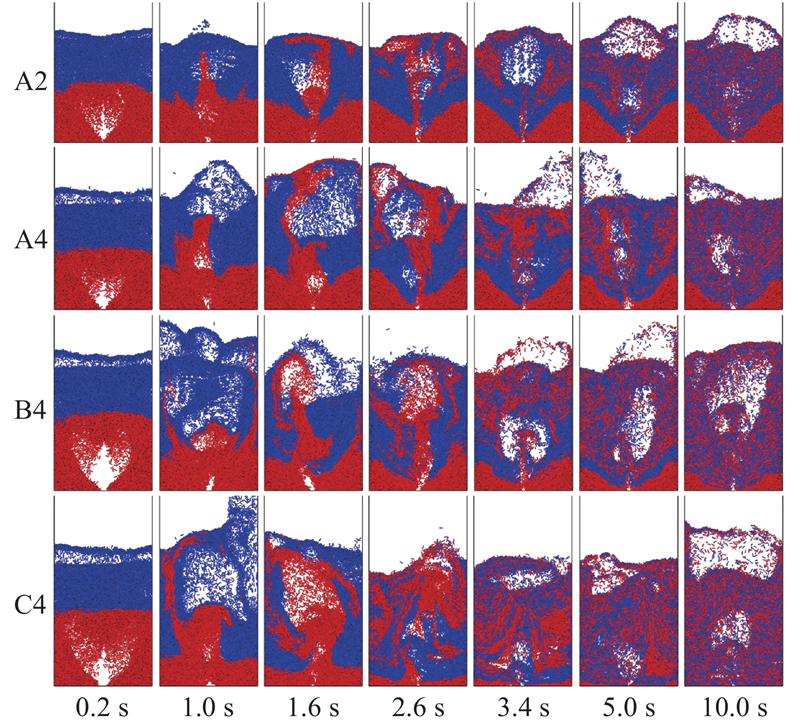
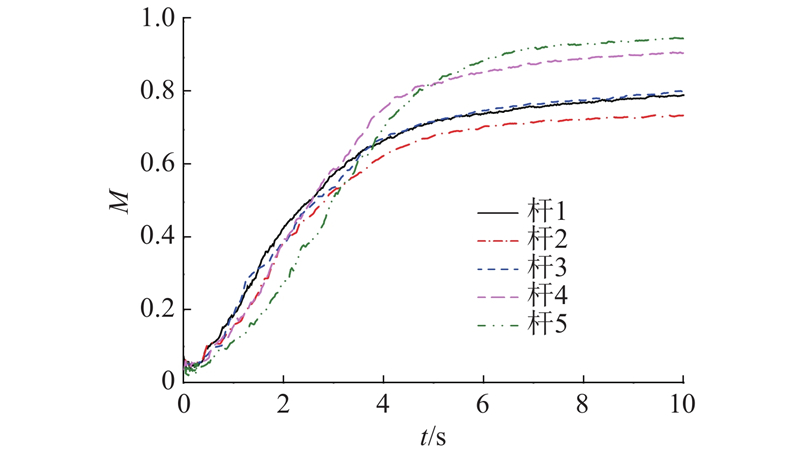
... 从图4可以看出颗粒形状及气速条件对颗粒混合的影响. 例如,对比算例A2与A4可以发现,在相同气速的条件下,杆4的混合质量优于杆2,即增加杆状颗粒长径比有利于混合;对于同一种颗粒,对比算例A4、B4和C4可以看出,提高us和uj均有利于混合. 为了了解颗粒形状及气速条件对杆状颗粒混合的影响,对更多的算例进行更全面的对比,引入Lacey混合指数[42]量化颗粒混合程度. ...
... Lacey混合指数[42]的表达式为 ...
滚筒内非等粒径二元颗粒体系增混机理研究
1
2009
... 式中: $S_0^2 = pq$为2种颗粒完全分离时的方差; $S_{\rm{r}}^2 = pq/n$为完全混合时的方差,其中p和q为2种颗粒所占的体积分数,n为取样样本中的平均颗粒数量;S2为实际混合方差. 在计算Lacey混合指数时,将计算区域划分成一定数量的样本. 由于颗粒的流动特性,每个样本中的颗粒数量可能相差较大. 针对这种情况,采用加权方法解决该问题,即样本内颗粒的数量越多,该样本所占的权重越大. 据该原则可知,颗粒的实际混合方差[43]为 ...
滚筒内非等粒径二元颗粒体系增混机理研究
1
2009
... 式中: $S_0^2 = pq$为2种颗粒完全分离时的方差; $S_{\rm{r}}^2 = pq/n$为完全混合时的方差,其中p和q为2种颗粒所占的体积分数,n为取样样本中的平均颗粒数量;S2为实际混合方差. 在计算Lacey混合指数时,将计算区域划分成一定数量的样本. 由于颗粒的流动特性,每个样本中的颗粒数量可能相差较大. 针对这种情况,采用加权方法解决该问题,即样本内颗粒的数量越多,该样本所占的权重越大. 据该原则可知,颗粒的实际混合方差[43]为 ...
矩形喷动床混合特性的三维数值研究
1
2010
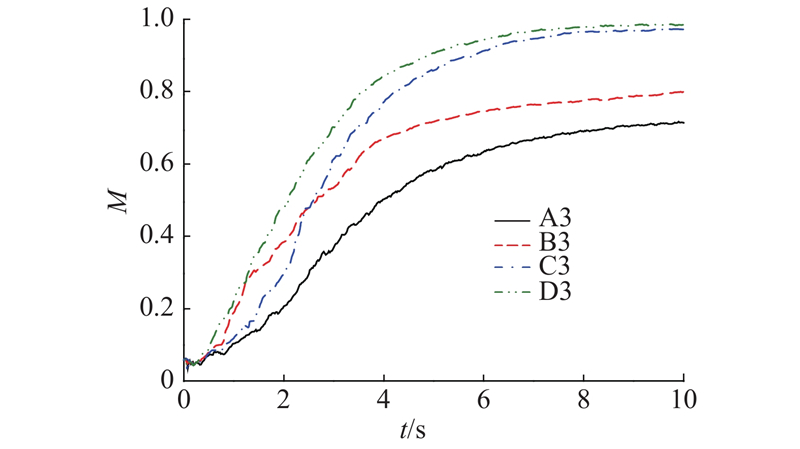
... 从图5、6可以看出,us对混合的影响大于uj,即相较于提高uj,提高us更有助于颗粒混合. 喷动流化床中杆状颗粒的流动具有典型喷动床的喷动特性. 朱润孺等[44]的研究表明,喷动床中密相区的混合控制着全床的混合. 在喷动流化床中,流化气可以直接作用于密相区,对密相区内颗粒的影响更大,故us对混合的影响大于uj. ...
矩形喷动床混合特性的三维数值研究
1
2010
... 从图5、6可以看出,us对混合的影响大于uj,即相较于提高uj,提高us更有助于颗粒混合. 喷动流化床中杆状颗粒的流动具有典型喷动床的喷动特性. 朱润孺等[44]的研究表明,喷动床中密相区的混合控制着全床的混合. 在喷动流化床中,流化气可以直接作用于密相区,对密相区内颗粒的影响更大,故us对混合的影响大于uj. ...