热电材料是利用热电效应直接实现电能与热能相互转化的半导体新能源材料. 热电材料以载流子（空穴和电子）输运的方式转换能量，因此，以热电材料为核心技术的热电器件具有结构简单、可靠性高、寿命长、不排放污染物质等特点，在运行时无须机械传动，不存在磨损、振动和噪声等问题，具有广阔的应用前景和商业价值^[1-2]. 热电器件的应用受到热电材料性能的限制，其最高能量转换效率约为10%.

热电材料的能量转换效率由热电优值来描述，定义为Z=α²σ/λ，α、σ、λ分别为塞贝克系数、电导率和热导率^[3]. 理想的热电材料须具有较大的塞贝克系数和电导率，以保证有明显的热电效应和较小的焦耳热，同时，还要求热导率较小，以维持热电材料两端较大的温差. 热电发电器的性能不仅取决于热电材料的热电优值，还取决于热电偶的几何形状^[4-5]，比如在高度方向采用梯形或曲线形热电偶可以显著提高热电发电器的能量转换效率^[6-7]，热电偶臂的不同截面形状也会改变其表面的对流效应，继而影响热电器件的输出性能^[8-10]. 对于实际热电发电器件而言，通常在导流片上加一层热导率较高但电绝缘的陶瓷板. 热电偶和导流片之间的接触电阻，以及在各界面上接触热阻的存在，会产生一定量的热损失，从而使实际热电发电器的效率和输出功率低于理想情形^[3,11]. 通常在理论分析计算时，认为两电偶臂在结构设计上具有相同的构型尺寸，但实际上这种设计只适合于两热电偶臂的电导率和热导率分别相等的情形。对于一般情况，器件的热电优值与热电偶臂的尺寸有关，因而当构成热电发电器的两热电偶臂具有不同的电导率和热导率时，要求两热电臂的几何尺寸也不相同，才能获得最佳的器件热电优值.

当热电发电器用于在圆柱形热源表面进行能量采集时，如利用汽车余热发电的情况^[12-14]，为了减少热电发电器与热源间的接触热阻，可以将热电发电器设计成环形^[15]. Shen等^[16]针对环形热电发电器建立理论模型，并计算环形电偶臂长度对输出功率和能量转换效率的影响. Zhang等^[17]研究接触电阻和接触热阻对环形热电发电器性能的影响，发现当考虑界面接触阻力的影响时，输出功率随着热电偶臂的减小，先增大后逐渐减小至零，总是存在一个最优长度；当热电偶长度较小时，须计入接触阻力的影响，才能正确估算器件的输出功率. 目前针对热电偶臂构型尺寸对平板型热电器件性能的影响已有大量文献研究^[18-20]，但关于环形热电器件的材料参数与热电偶臂之间的影响关系研究还未见报道。环形热电发电器的构型尺寸参数主要为热电偶臂的圆周角，而平板形热电器件主要利用热电偶臂的长度和截面积比反映其构型特征，无法直接应用平板形热电器件的分析结果指导环形热电发电器的构型设计。本研究探讨当两热电偶臂具有不同热电性质时，环形热电器件热电偶臂构型尺寸与材料性质之间的关系，从而为环形热电器件的深入研究和设计应用提供理论基础.

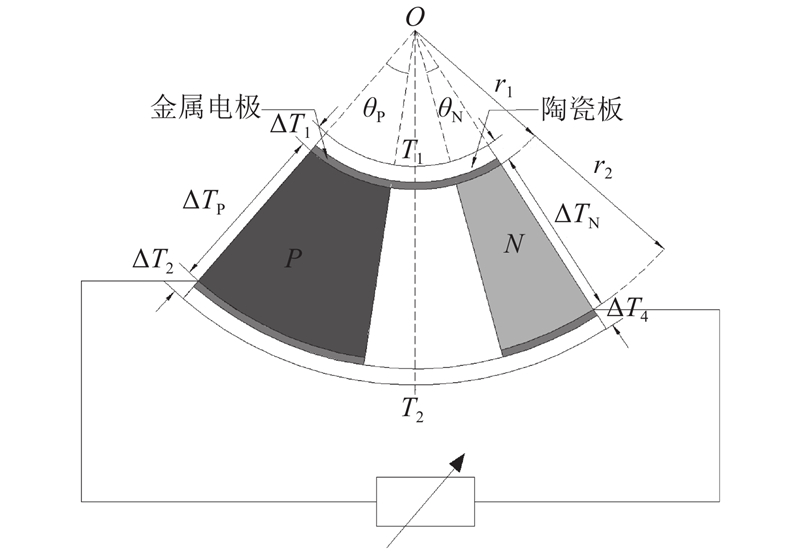
环形热电发电器的P型和N型热电偶臂由金属导流片连接，夹在热导通而电绝缘的陶瓷板之间，如图1所示. 图中，r₁、r₂分别为器件热源端和冷源端半径，θ_P、θ_N分别为P型和N型热电偶臂的圆周方向角度，T₁、T₂分别为热源和冷源温度， $\Delta {T_1}$、 $\Delta {T_{\rm{2}}}$分别为P型热电偶臂热源端和冷源端陶瓷板两侧温差， $\Delta {T_3}$、 $\Delta {T_4}$分别为N型热电偶臂热源端和冷源端陶瓷板两侧温差， $\Delta {T_{\rm{P}}}$、 $\Delta {T_{\rm{N}}}$分别为实际作用于P型、N型热电偶臂两端的温差. 环形热电发电器从高温端吸收热量，一部分传递给低温冷源，另一部分转化为电能. 为了简化理论模型的复杂程度，进行以下几方面的合理假设：1）模型主要针对低温热电发电器开展研究，假设材料的热电性质与温度变化无关，无须考虑汤姆逊效应；2）热源端和冷源端温度分别为T₁、T₂，不随时间变化；3）忽略热电偶间的热对流和热辐射的影响；4）模型为沿半径方向的一维热传导问题.

环形热电发电器的热电输运方程^[11]可以表示为

(1) $\lambda A\;(r)\frac{{{{\rm d}^2}T(r)}}{{{\rm d}{r^2}}} + \lambda \frac{{{\rm d}A\;(r)}}{{{\rm d}r}}\frac{{{\rm d}T(r)}}{{{\rm d}r}} + \frac{{{I^2}}}{{\sigma A\;(r)}} = 0.$

式中：T为温度，r为径向坐标，I为回路中产生的电流，A为热电偶臂的截面积.

热电偶臂半径方向的热流可以表示为

(2) $Q\left( r \right) = - \lambda A\left( r \right){{{\rm d}T(r)} / {{\rm d}r}} + \alpha IT(r).$

式中：右侧第1、2项分别为傅立叶热传导和塞贝克效应的影响. 对于金属导流片或陶瓷板而言，塞贝克系数等于零，式(2)可以简化为

(3) $Q\left( r \right) = - \lambda A\left( r \right){{{\rm d}T(r)} / {{\rm d}r}}.$

不考虑接触阻力的影响，热电偶热端和冷端分别有温度边界条件T(r₁)=T₁、T(r₂)=T₂，结合控制方程（式(1)），可以得到P型和N型热电偶臂温度场的分布：

(4) $\begin{split} {T_{\rm{P}}} = & - \frac{{{I^2}}}{{2{\sigma _{\rm{P}}}{\lambda _{\rm{P}}}{{({l_{\rm r}} \; {\theta _{\rm{P}}})}^2}}}{(\ln r)^2} + \left[ {\frac{{{I^2}(\ln {r_1} + \ln {r_2})}}{{2{\sigma _{\rm{P}}}{\lambda _{\rm{P}}}{{({l_{\rm r}} \; {\theta _{\rm{P}}})}^2}}} + } \right. \\ & \left. { \frac{{{T_1} - {T_2}}}{{\ln {r_1} - \ln {r_2}}}} \right]\ln r + \frac{{{T_2}\ln {r_1} - {T_1}\ln {r_2}}}{{\ln {r_1} - \ln {r_2}}} -\\ & \frac{{{I^2}\ln {r_1}\ln {r_2}}}{{2{\lambda _{\rm{P}}}{\sigma _{\rm{P}}}{{({l_{\rm r}} \; {\theta _{\rm{P}}})}^2}}} , \end{split} $

(5) $\begin{split} {T_{\rm{N}}} = & - \frac{{{I^2}}}{{2{\sigma _{\rm{N}}}{\lambda _{\rm{N}}}{{({l_{\rm r}} \; {\theta _{\rm{N}}})}^2}}}(\ln r)^2 + \left[ {\frac{{{I^2}(\ln {r_1} + \ln {r_2})}}{{2{\sigma _{\rm{N}}}{\lambda _{\rm{N}}}{{({l_{\rm r}} \; {\theta _{\rm{N}}})}^2}}} + } \right. \\ & \left. {\frac{{{T_1} - {T_2}}}{{\ln {r_1} - \ln {r_2}}}} \right]\ln r + \frac{{{T_2}\ln {r_1} - {T_1}\ln {r_2}}}{{\ln {r_1} - \ln {r_2}}} -\\ & \frac{{{I^2}\ln {r_1}\ln {r_2}}}{{2{\lambda _{\rm{N}}}{\sigma _{\rm{N}}}{{({l_{\rm r}} \; {\theta _{\rm{N}}})}^2}}} . \end{split} $

式中：l_r为热电偶厚度，σ_P、λ_P为P型热电偶臂的电导率、热导率，σ_N、λ_N为N型热电偶臂的电导率、热导率. 将式(4)、(5)代入式(2)，并令r=r₁、r=r₂，可以得到P型、N型热电偶臂的热流：

(6) ${Q_{\rm{P}}}\left( {{r_1}} \right) = {G_{\rm{P}}}\left( {{T_1} - {T_2}} \right) - {{{I^2}{R_{\rm{P}}}} / 2} + {\alpha _{\rm{P}}}I{T_1},$

(7) ${Q_{\rm{P}}}\left( {{r_2}} \right) = {G_{\rm{P}}}\left( {{T_1} - {T_2}} \right) + {{{I^2}{R_{\rm{P}}}} / 2} + {\alpha _{\rm{P}}}I{T_2},$

(8) ${Q_{\rm{N}}}\left( {{r_1}} \right) = {G_{\rm{N}}}\left( {{T_1} - {T_2}} \right) - {{{I^2}{R_{\rm{N}}}} / 2} - {\alpha _{\rm{N}}}I{T_1},$

(9) ${Q_{\rm{N}}}\left( {{r_2}} \right) = {G_{\rm{N}}}\left( {{T_1} - {T_2}} \right) + {{{I^2}{R_{\rm{N}}}} / 2} - {\alpha _{\rm{N}}}I{T_2}.$

式中：α_P、α_N分别为P型、N型热电偶臂的塞贝克系数；G_P、R_P为P型热电偶臂的热导和电阻，G_N、R_N为N型热电偶臂的热导和电阻，表达式为

$ {G_{\rm{P}}} = \frac{{{\lambda _{\rm{P}}} \; {\theta _{\rm{P}}} \; {l_{\rm{r}}}}}{{\ln {r_2} - \ln {r_1}}},\;{G_{\rm{N}}} = \frac{{{\lambda _{\rm{N}}} \; {\theta _{\rm{N}}} \; {l_{\rm{r}}}}}{{\ln {r_2} - \ln {r_1}}}, $

$ {R_{\rm{P}}} = \frac{{\ln {r_2} - \ln {r_1}}}{{{\sigma _{\rm{P}}} \; {\theta _{\rm{P}}} \; {l_{\rm r}}}},\;{R_{\rm{N}}} = \frac{{\ln {r_2} - \ln {r_1}}}{{{\sigma _{\rm{N}}} \; {\theta _{\rm{N}}} \; {l_{\rm r}}}}. $

热电偶在热端吸收的热量Q_h(r₁)和在冷端放出的热量Q_c(r₂)分别为

(10) ${Q_{\rm{h}}}\left( {{r_1}} \right) = {G_{{\rm{PN}}}}\left( {{T_1} - {T_2}} \right) - {{{I^2}{R_{{\rm{PN}}}}} / 2} + {\alpha _{{\rm{PN}}}}I{T_1},$

(11) ${Q_{\rm{c}}}\left( {{r_2}} \right) = {G_{{\rm{PN}}}}\left( {{T_1} - {T_2}} \right) + {{{I^2}{R_{{\rm{PN}}}}} / 2} + {\alpha _{{\rm{PN}}}}I{T_2}.$

式中：G_PN=G_P+G_N，R_PN=R_P+R_N，α_PN=α_P−α_N.

环形热电发电器中的电流为

(12) $I = {{{\alpha _{{\rm{PN}}}}({T_1} - {T_2})} / {\left( {{R_{{\rm{PN}}}} + {R_{\rm{L}}}} \right)}}.$

式中：R_L为外加负载电阻.

器件的输出功率和能量转换效率可以分别表示为

(13) ${P_{{\rm{out}}}} = {I^2}{R_{\rm{L}}} = \frac{{\alpha _{{\rm{PN}}}^2{{({T_1} - {T_2})}^2}{R_{\rm{L}}}}}{{{{\left( {{R_{{\rm{PN}}}} + {R_{\rm{L}}}} \right)}^2}}},$

(14) $ \eta = \frac{{{P_{{\rm{out}}}}}}{{{Q_{\rm{h}}}\left( {{r_1}} \right)}} = \frac{{{I^2}{R_{\rm{L}}}}}{{{G_{{\rm{PN}}}}\left( {{T_1} - {T_2}} \right) - {I^2}{R_{{\rm{PN}}}}/2 + {\alpha _{{\rm{PN}}}}I{T_1}}}. $

基于1.1节建立的环形热电发电器理想模型分析热电偶臂构型尺寸对其输出性能的影响. 令S=R_L/R_PN，式(14)可以简化为

(15) $\begin{split} \eta = & \frac{{{T_1} - {T_2}}}{{{T_1}}} \times \\ & \frac{S}{{(1 + S) - {{({T_1} - {T_2})} / {\left( {2{T_1}} \right)}} + {{{{(1 + S)}^2}} / {Z{T_1}}}}}. \end{split}$

式中： $Z = {{\alpha _{{\rm{PN}}}^2} / {\left( {{G_{{\rm{PN}}}}{R_{{\rm{PN}}}}} \right)}}$，与传统平板形热电发电器的热电优值形式相同. 显然，对于给定温差和热电材料的热电参数，环形热电发电器的效率与比值S有关. 令dη/dS=0，可以求得，若器件内阻R_PN和负载电阻R_L满足

(16) $S = {{{R_{\rm{L}}}} / {{R_{{\rm{PN}}}}}} = \sqrt {1 + Z\bar T}, $

环形热电发电器具有最大效率：

(17) ${\eta _{\max }} = \frac{{{T_1} - {T_2}}}{{{T_1}}} \; \frac{{\sqrt {1 + Z\bar T} - 1}}{{\sqrt {1 + Z\bar T} + {{{T_2}} / {{T_1}}}}}.$

式中：右边第1项为卡诺效率；第2项与器件的材料性质有关，且数值小于1； $\overline T $为平均温度. 可以看出，最大效率是热电优值Z的单调递增函数，即Z越大，η_max越大. 将热电优值Z展开，有

(18) $Z = \frac{{\alpha _{{\rm{PN}}}^2}}{{\left[ {1/\left( {{\theta _{\rm{P}}}{\sigma _{\rm{P}}}} \right) + 1/\left( {{\theta _{\rm{N}}}{\sigma _{\rm{N}}}} \right)} \right]\left( {{\lambda _{\rm{P}}}{\theta _{\rm{P}}} + {\lambda _{\rm{N}}}{\theta _{\rm{N}}}} \right)}}.$

若P型和N型环形热电偶臂满足

(19) ${{{\theta _{\rm{N}}}} / {{\theta _{\rm{P}}}}} = \sqrt {{{{\lambda _{\rm{P}}}{\sigma _{\rm{P}}}} / {\left( {{\lambda _{\rm{N}}}{\sigma _{\rm{N}}}} \right)}}} ,$

热电优值达到最大：

(20) ${Z_{\max }} = \alpha _{{\rm{PN}}}^2{\left( {\sqrt {{\lambda _{\rm{P}}}/{\sigma _{\rm{P}}}} + \sqrt {{\lambda _{\rm{N}}}/{\sigma _{\rm{N}}}} } \right)^{{\rm{ - }}2}}.$

可以看出，根据两电偶臂的电导率和热导率间的相互关系，环形热电发电器P型和N型热电偶臂的构型尺寸有以下3种情况：1）两热电偶臂的电导率和热导率分别相等，即σ_P=σ_N和λ_P=λ_N，则有θ_P=θ_N，即两热电偶臂具有相同的圆周角度；2）两热电偶臂的电导率和热导率分别不相等，但满足λ_Pσ_P/(λ_Nσ_N)=1，则两热电偶臂也具有相同的圆周角度；3）两热电偶臂的电导率和热导率均不相等，且不满足λ_Pσ_P/(λ_Nσ_N)=1，此时，须采用两热电偶臂圆周角不相等的热电偶结构，才能满足式(19)，从而获得最大的热电优值和能量转换效率.

上述关于环形热电发电器的性能计算是在理想模型基础上给出的，忽略器件的接触热阻和接触电阻. 采用上述模型对环形热电发电器性能进行计算和设计的前提是要求热电偶臂的长度较大，以保证热电偶的电阻（热阻）远远大于接触电阻（热阻），此时接触效应可以忽略不计。当利用低温余热发电时，环形热电发电器长度须较小，须考虑接触阻力对器件性能的影响.

由于陶瓷板的存在，实际作用于P型、N型热电偶臂两端的温差分别为 $\Delta {T_{\rm{P}}}$、 $\Delta {T_{\rm{N}}}$，由式(2)、(3)可知：

(21) $\left. \begin{array}{c} \Delta {T_1} = {{{Q_{\rm{P}}}({r_1})} / {G_{\rm C1}}}, \\ {G_{\rm C1}} = {\lambda _{\rm C}} \; {\theta _{\rm P}} \; {l_{\rm r}}/\ln \; \left[ {{r_1}/\left( {{r_1} - {h_{\rm C}}} \right)} \right], \end{array} \right\}$

(22) ${Q_{\rm{P}}}({r_1}) = {G_{\rm{P}}}\Delta {T_{\rm{P}}} - {{{I^2}{R_{\rm{P}}}} / 2} + {\alpha _{\rm{P}}}I({T_1} - \Delta {T_1}),$

(23) ${Q_{\rm{P}}}({r_2}) = {G_{\rm{P}}}\Delta {T_{\rm{P}}} + {{{I^2}{R_{\rm{P}}}} / 2} + {\alpha _{\rm{P}}}I({T_2} + \Delta {T_2}),$

(24) $\left. \begin{array}{c} \Delta {T_2} = {{{Q_{\rm{P}}}({r_2})} / {{G_{{\rm C}2}}}},\\ {G_{{\rm C}2}} = {\lambda _{\rm C}} \; {\theta _{\rm P}} \; {l_{\rm r}}/\ln \; \left[ {\left( {{r_2} + {h_{\rm C}}} \right)/{r_2}} \right], \end{array} \right\}$

(25) $\left. \begin{array}{c} \Delta {T_3} = {{{Q_{\rm{N}}}({r_1})} / {{G_{{\rm C}3}}}}, \\ {G_{{\rm C}3}} = {\lambda _{\rm C}} \; {\theta _{\rm N}} \; {l_{\rm r}}/\ln \; \left[ {{r_1}/\left( {{r_1} - {h_{\rm C}}} \right)} \right], \end{array} \right\}$

(26) ${Q_{\rm{N}}}({r_1}) = {G_{\rm{N}}}\Delta {T_{\rm{N}}} - {{{I^2}{R_{\rm{N}}}} / 2} - {\alpha _{\rm{N}}}I({T_1} - \Delta {T_3}),$

(27) ${Q_{\rm{N}}}({r_2}) = {G_{\rm{N}}}\Delta {T_{\rm{N}}} + {{{I^2}{R_{\rm{N}}}}/ 2} - {\alpha _{\rm{N}}}I({T_2} + \Delta {T_4}),$

(28) $\left. \begin{array}{c} \Delta {T_4} = {{{Q_{\rm{N}}}({r_2})} / {{G_{{\rm C}4}}}},\\ {G_{{\rm C}4}} = {\lambda _{\rm C}} \; {\theta _{\rm N}} \; {l_{\rm r}}/\ln \; \left[ {\left( {{r_2} + {h_{\rm C}}} \right)/{r_2}} \right]. \end{array} \right\}$

式中：h_C、λ_C分别为陶瓷板的高度和热导率.

联立式(21)~（28)，可以得到

(29) $\begin{aligned} & \Delta {T_{\rm{P}}} = \\& \frac{{{G_{{\rm C}1}}{G_{{\rm C}2}}\Delta T \!-\! {\alpha _{\rm{P}}}I({G_{{\rm C}1}}{T_1} \!+\! {G_{{\rm C}2}}{T_2}) \!+\! {{{I^2}{R_{\rm{P}}}({G_{{\rm C}2}} \!-\! {G_{{\rm C}1}})} / 2} \!-\! {\alpha _{\rm{P}}}{R_{\rm{P}}}{I^3}}}{{{G_{\rm{P}}}({G_{{\rm C}2}} + {G_{{\rm C}1}}) + ({G_{{\rm C}1}} + {\alpha _{\rm{P}}}I)({G_{{\rm C}2}} - {\alpha _{\rm{P}}}I)}}, \end{aligned}$

(30) $\begin{aligned} & \Delta {T_{\rm{N}}} = \\& \frac{{{G_{{\rm C}3}}{G_{{\rm C}4}}\Delta T \!+\! {\alpha _{\rm{N}}}I({G_{{\rm C}3}}{T_1} \!+\! {G_{{\rm C}4}}{T_2}) \!+\! {{{I^2}{R_{\rm{N}}}({G_{{\rm C}4}} \!-\! {G_{{\rm C}3}})} / 2} \!+\! {\alpha _{\rm{N}}}{R_{\rm{N}}}{I^3}}}{{{G_{\rm{N}}}({G_{{\rm C}4}} + {G_{{\rm C}3}}) + ({G_{{\rm C}3}} - {\alpha _{\rm{N}}}I)({G_{{\rm C}4}} + {\alpha _{\rm{N}}}I)}}.\end{aligned}$

考虑电接触阻力对器件的影响，环形热电发电器中的电流表达式如下：

(31) $\left. \begin{array}{c} I = {{\left( {{\alpha _{\rm{P}}}\Delta {T_{\rm{P}}} - {\alpha _{\rm{N}}}\Delta {T_{\rm{N}}}} \right)} / {{R_{\rm{T}}}}},\\ {R_{\rm{T}}} = {R_{\rm{P}}} + {R_{\rm{N}}} + {R_{{\rm C}1}} + {R_{{\rm C}2}} + {R_{{\rm C}3}} + {R_{{\rm C}4}} + {R_{\rm{L}}},\\ {R_{{\rm C}1}} = 1/({\sigma _{\rm C}} \; {l_{\rm r}} \; {\theta _{\rm{P}}} \; {r_1}),\\ {R_{{\rm C}2}} = 1/({\sigma _{\rm C}} \; {l_{\rm r}} \; {\theta _{\rm{P}}} \; {r_2}),\\ {R_{{\rm C}3}} = 1/({\sigma _{\rm C}} \; {l_{\rm r}} \; {\theta _{\rm{N}}} \; {r_1}),\\ {R_{{\rm C}4}} = 1/({\sigma _{\rm C}} \; {l_{\rm r}} \; {\theta _{\rm{N}}} \; {r_2}). \end{array} \right\}$

式中：R_C1、R_C2、R_C3、R_C4为界面接触电阻，σ_C为接触层的电导率.

结合式(29)~(31)，可以得到关于电流I的一元五次方程：

(32) $\left.\!\!\!\!\begin{array}{c} {m_5}{I^5} + {m_4}{I^4} + {m_3}{I^3} + {m_2}{I^2} + {m_1}I + {m_0} = 0,\\ {m_0} = {a_1}{e_2} - {a_2}{e_1},\\ {m_1} = {a_1}{f_2} - {e_2}{b_1} - {a_2}{f_1} + {e_1}{b_2} - {R_{\rm T}}{e_1}{e_2},\\ {m_2} = {a_2}{g_1} + {b_2}{f_1} - {a_1}{g_2} - {b_1}{f_2} + {d_1}{e_2}- \\ {d_2}{e_1} - {R_{\rm T}}({e_1}{f_2} + {e_2}{f_1}),\\ {m_3} = {b_1}{g_2} - {c_1}{e_2} + {d_1}{f_2} - {b_2}{g_1} + {c_2}{e_1} - {d_2}{f_1} - \\ {R_{\rm T}}({f_1}{f_2} - {e_1}{g_2} - {e_2}{g_1}) ,\\ {m_4} = {c_2}{f_1} + {d_2}{g_1} - {c_1}{f_2} - {d_1}{g_2} - {R_{\rm{T}}}({f_1}{g_2} + {f_2}{g_1}),\\ {m_5} = {c_1}{g_2} - {c_2}{g_1} - {R_{\rm{T}}}{g_1}{g_2}.\end{array}\!\!\!\right\}$

式中：

$ {a_1} = {\alpha _{\rm{P}}}{G_{{\rm C}1}}{G_{{\rm C}2}}\Delta T,\;{a_2} = {\alpha _{\rm{N}}}{G_{{\rm C}3}}{G_{{\rm C}4}}\Delta T, $

$ {b_1} = \alpha _{\rm{P}}^{\rm{2}}({G_{{\rm C}1}}{T_1} + {G_{{\rm C}2}}{T_2}),\;{b_2} = - \alpha _{\rm{N}}^2({G_{{\rm C}3}}{T_1} + {G_{{\rm C}4}}{T_2}), $

$ {c_1} = \alpha _{\rm{P}}^{\rm{2}}{R_{\rm{P}}},\;{c_2} = - \alpha _{\rm{N}}^2{R_{\rm{N}}}, $

$ {d_1} = \frac{1}{2}{\alpha _{\rm{P}}}{R_{\rm{P}}}({G_{{\rm C}2}} - {G_{{\rm C}1}}),\;{d_2} = \frac{1}{2}{\alpha _{\rm{N}}}{R_{\rm{N}}}({G_{{\rm C}4}} - {G_{{\rm C}3}}), $

$ {e_1} = {G_{\rm{P}}}({G_{{\rm C}1}} + {G_{{\rm C}2}}) + {G_{{\rm C}1}}{G_{{\rm C}2}},\;{e_2} = {G_{\rm{N}}}({G_{{\rm C}3}} + {G_{{\rm C}4}}) + {G_{{\rm C}3}}{G_{{\rm C}4}}, $

$ {f_1} = {\alpha _{\rm{P}}}({G_{{\rm C}2}} - {G_{{\rm C}1}}),\;{f_2} = - {\alpha _{\rm{N}}}({G_{{\rm C}4}} - {G_{{\rm C}3}}), $

$ {g_1} = \alpha _{\rm{P}}^2,\;{g_2} = \alpha _{\rm{N}}^{\rm{2}}. $

如果考虑λ_C→∞和σ_C→∞，式(29)、(30)将退化为 $\Delta {T_{\rm{P}}} = \Delta {T_{\rm{N}}} = {T_1} - {T_2}$，电流方程（式 (32)）将变为式(12)，结果与理想模型一致.

电流方程（式(32)）的封闭解形式较复杂，即使得到也难以应用。文献[11]研究发现，对于一般的环形热电发电器件，式(32)中m₅I⁵、m₄I⁴、m₃I³、m₂I²项均远远小于m₁I项，故在电流I求解时，可以将式（32）简化成关于电流I的线性方程直接求解，即有 $I = - {m_0}/{m_1}$. 此时环形热电发电器的输出功率和效率仍可以表示为P_out=I²R_L、η=P_out/Q_h(r₁). 为了验证上述简化求解的正确性，如表1所示为关于I的5次方程精确解与忽略非线性系数项线性解的对比. 表中，s_r=r₂/r₁，I_e为电流精确解，I_l为线性解，e为误差. 在计算中采用P型热电材料Bi₂Te₃和N型热电材料Bi_0.5Sb_1.5Te₃（情况1），材料参数如表2所示. 取接触阻力参数λ₀=λ_P/λ_C=0.4、σ₀=σ_P/σ_C=0.1 mm，T₁=400 K，T₂=300 K，l_r=1 mm，θ_P=π/6，r₁=1 mm，h_C=0.1 mm. 结果显示电流方程的线性简化解与精确解的误差较小，即使当环形热电偶长度比取较小值s_r=1.05时，精确解与线性解也只相差0.129 4%. 另一方面，当环形热电发电器的总内电阻近似等于外接电阻时，即R_L=R_P+R_N+R_C1+R_C2+R_C3+R_C4，器件的输出功率达到最大^[3,11]. 一般说来，热电发电器的最大能量转换效率与最大输出功率对应的最优外接电阻不一致，但最大输出功率对应的效率相比于最大效率减少较小^[3,17]. 故本研究后续讨论均基于电流的线性简化方程和最大输出功率的最优外接电阻进行.

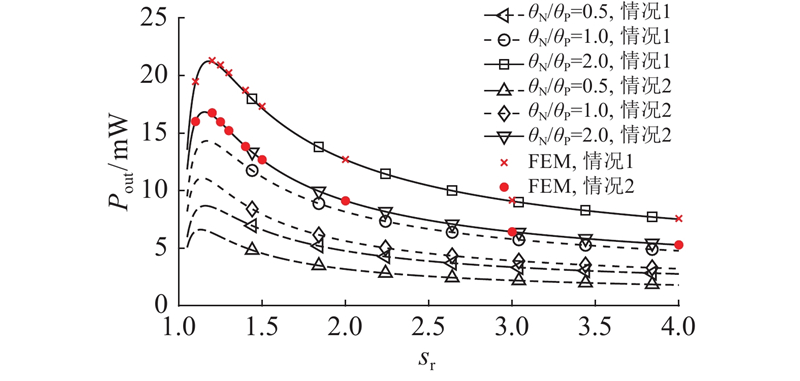
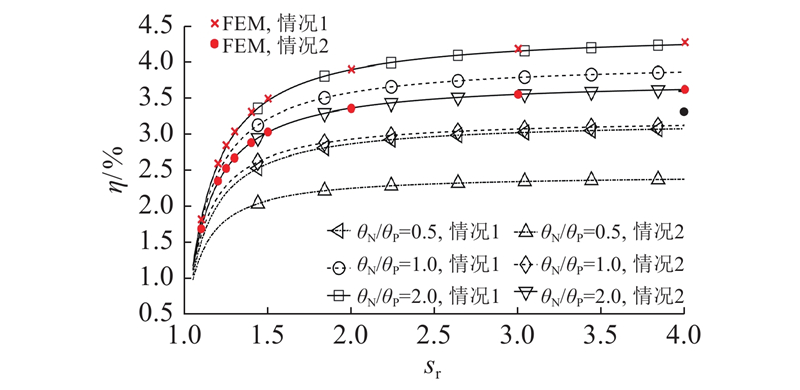
如图2、3所示分别为环形热电发电器输出功率和能量转换效率与器件长度之间的关系. 情况2代表的材料组合为：P型热电材料Bi₂Te₃和N型热电材料BiSbTe. 为了验证算例结果的正确性，分别针对s_r=1.10、1.20、1.25、1.30、1.40、1.50、2.00、3.00、4.00等情况，给出θ_N/θ_P=2.0、λ₀ = 0.4、σ₀ = 0.1 mm时环形热电发电器输出功率和能量转换效率的有限元（finite element method，FEM）分析结果。由图2、3可知，2种方法的计算结果一致，说明本研究的计算结果是可靠的. 如图2所示，考虑接触效应时总存在最优长度使得输出功率达到最大. 由于P型和N型热电材料参数的不对称性，对于情况1、情况2，均有θ_N/θ_P=2.0（即θ_N=2θ_P=π/3）时输出功率最大，初步体现了不同热电偶臂组合与器件构型尺寸的影响关系. 如图3所示，当环形热电发电器长度较小时，接触阻力对器件的能量转换效率影响较大，但是随着器件长度的增加其影响逐渐减小，最终趋近于不考虑接触阻力的理想情况. 如表3所示，当取λ₀ = 0.4，σ₀ = 0.1 mm时，s_r=2.00、3.00、4.00对应的效率分别为4.29%、4.42%、4.46%，即当器件长度比s_r≥2.00时，考虑接触效应时的能量转换效率与利用理想模型（式(17)）计算得到的效率之间的误差总小于4.24%，此时接触效应对能量转换效率的影响可以忽略.

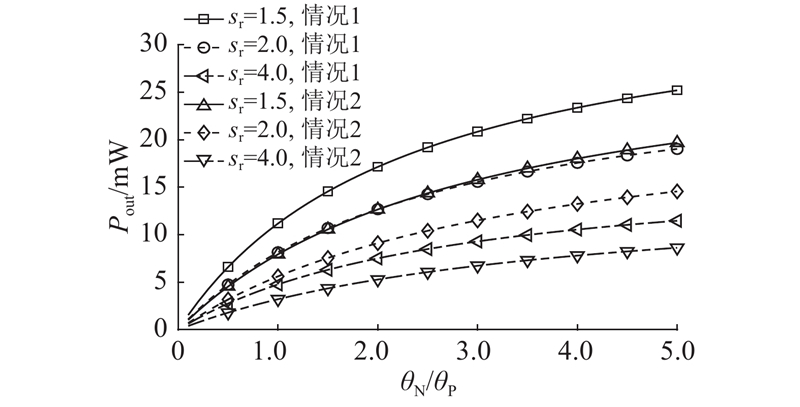
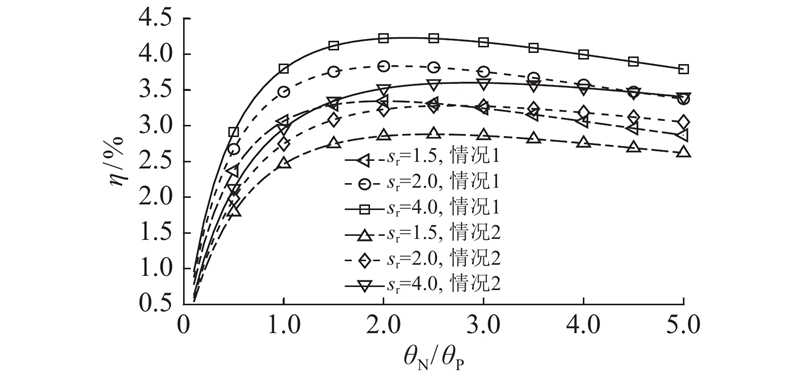
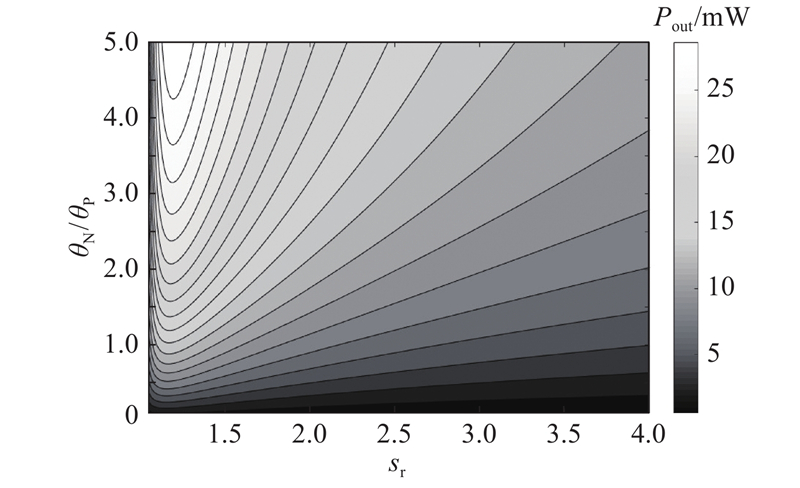
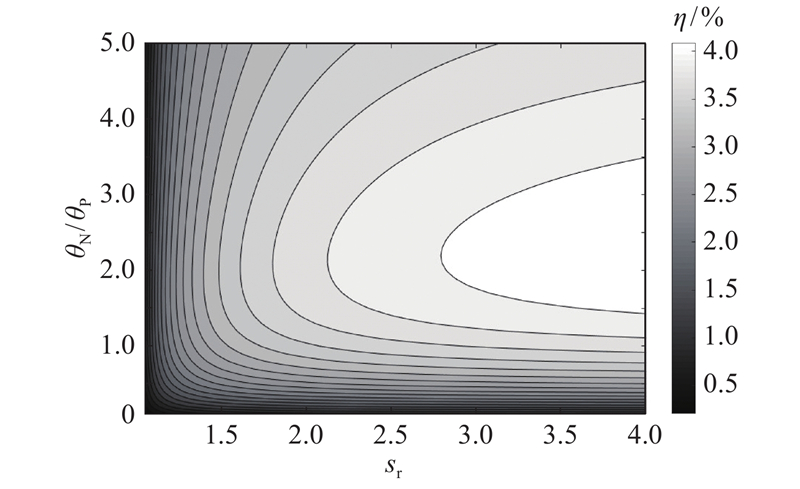
如图4、5所示分别为环形热电发电器输出功率和能量转换效率与热电偶臂圆周角度比之间的关系。可以看出，热电偶臂圆周角度比对器件输出性能的影响较大. 当θ_P=π/6时，θ_N越大，器件的输出功率越大，因为当θ_N增大时，N型热电偶臂电阻、热阻和相应接触电阻均减小，导致器件内部的电流增大，输出功率增大. 由图5可知，当P型和N型热电偶臂热电性质非对称时，存在使能量转换效率最大的最优圆周角度比θ_N/θ_P. 在不考虑接触阻力的理想情况下，由式（19）可以确定情况1的最优圆周角度比θ_N/θ_P=2.330；对于实际环形热电发电器，当s_r较小时，接触阻力对最优θ_N/θ_P影响较大，随着s_r继续增大，最优θ_N/θ_P逐渐趋近于理想模型的结果. 由表3可以看出，当s_r=2.00、3.00、4.00时，对应的最优θ_N/θ_P分别等于2.273、2.316、2.321. 当s_r≥2.00时，利用理想模型（式(19)）计算得到的最优角度比θ_N/θ_P的误差总小于2.5%. 如图6、7所示为情况1下（λ₀ = 0.4、σ₀ = 0.1 mm）的输出功率、能量转换效率与器件长度和热电偶臂圆周角度比的关系，从中可以更直观的观察到上述结论.

（1）给出理想环形热电器件最大能量转换效率下的构型尺寸与P型、N型热电偶臂热电参数之间的定量关系，即 ${{{\theta _{\rm{N}}}} / {{\theta _{\rm{P}}}}} = \sqrt {{{{\lambda _{\rm{P}}}{\sigma _{\rm{P}}}} / {\left( {{\lambda _{\rm{N}}}{\sigma _{\rm{N}}}} \right)}}} $.

（2）对于实际小尺寸热电发电器而言，考虑界面接触阻力，给出关于器件电流的线性简化解，在此基础上得到最大输出功率和最大能量转换效率下的热电偶臂圆周角度比θ_N/θ_P. 发现当器件长度s_r较小时，接触效应对最优θ_N/θ_P影响明显，但随着s_r继续增大，最优θ_N/θ_P逐渐趋近于理想模型的预测结果.

（3）当接触阻力参数取λ₀ = 0.4和σ₀ = 0.1 mm，热电发电器的尺寸参数s_r≥2时，利用理想模型计算的能量转换效率和最优角度比与考虑接触阻力效应得到的结果误差分别小于4.24%、2.50%，即此时接触效应可以忽略，可以基于理想模型指导环形热电发电器的设计计算.

接下来将进一步考虑Thomson效应、热电偶臂与周围环境热对流和热辐射对环形热电发电器输出性能的影响，可以为其结构优化设计和性能评价提供更坚实的理论基础.