上述文献中,Fan等[7]使用关系探索算法评价稳定裕度与电网特征之间的关系,并选取关联性最强的特征进行非线性拟合,从而得出电压稳定裕度的评估模型. Devaraj等[8-9]分别使用互信息法和Kohonen SOM算法对输入特征进行精简,使用优化后的特征分别训练RBF神经网络和模糊神经网络,并进行电压稳定的评估. 刘昇等[10]首先使用SIPSS方法评估电网运行状态的相似度,从而剔除冗余样本,之后使用Lasso方法进行特征降维,并训练神经网络对电压稳定性进行拟合. Zhou等[11]使用多层神经网络进行电压稳定评估,考虑了同步相量量测单元(phasor measurement unit,PMU)可能的测量错误对评估结果的影响,并使用特征选择方法对PMU的经济配置进行了讨论. Fan等[12]使用最大相关-最小冗余算法挖掘电压稳定裕度与电网运行特征之间的关系,并使用筛选出的特征集拟合非线性方程,评估电压稳定性. Malbasa等[13]使用主动学习方法进行电压稳定评估,该方法可以在模型出现评估错误后,自动控制仿真数据的进一步积累,从而进行模型的在线更新.
基于机器学习的电压稳定评估方法的以下几个方面可以进一步研究:第一,随着机器学习技术的进步,使用最新模型进行电压稳定裕度的预测,有望获得更高的精度和更快的计算速度. 第二,在实际使用环节,PMU测量的电网运行特征,有时会发生数值错误和数值缺失,因此模型如何适应这2种情况,在数据异常时也能给出相对准确的评估结果,是一个有待解决的问题. 第三,机器学习模型的预测结果不可避免地会有一些偏差,针对一些样本,其预测偏差可能显著高于其他样本. 在这种情况下,模型更新就十分重要. 针对误差较大的样本,采取何种方式使得模型能够从中学习到更多信息,使其在后续应用中不再出现类似问题,使模型表现更稳定,也是需要解决的问题.
极限梯度提升树(extreme gradient boosting,XGBoost)算法[14]是最新开源的机器学习算法,算法效果经过了各类算法竞赛以及各领域学者的充分检验. 本文使用XGBoost算法进行电压稳定裕度评估,使用电压稳定样本集训练XGBoost算法的回归模型,并将其用于在线评估. 研究模型的预测准确性和计算速度问题,并针对实际应用环节PMU测量特征可能出现的2类错误,考察算法的容错性. 针对模型预测偏差较大的样本,研究模型更新问题.
1. 基于机器学习的电压稳定评估问题
1.1. 电力系统电压稳定裕度
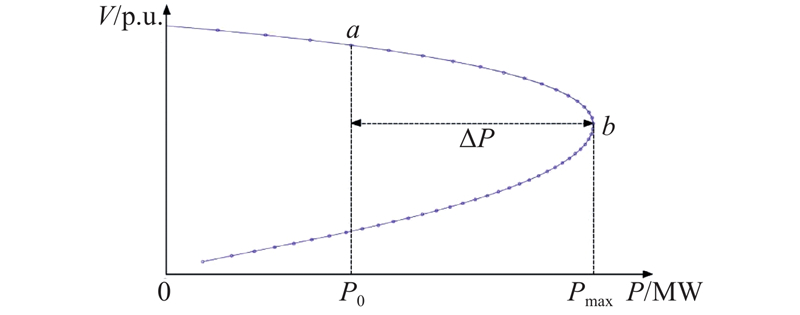
图 1
由于∆P本身的分布是连续的,当利用机器学习方法进行建模时,电压稳定裕度VSM作为映射目标,电压稳定评估问题转化为机器学习中的回归问题.
1.2. 电力系统的稳态特征集
当电力系统运行在某种运行方式时,根据CPF方法,所对应的电压稳定裕度是唯一的,因此可以建立由当前运行方式特征到VSM之间的映射. 选取此运行方式下的电气量作为描述此种运行方式的特征,一些常见的稳态电气量特征如表1所示. 这些物理量中,发电机出力PGi、QGi和负荷需求PLi、QLi反映系统的整体供需关系,在同一系统中,是随运行方式变化的. 其他电气量,包括节点电压情况V i和θ i、线路功率传输情况PBi–j和QBi–j,均是在供需确定之后,由电网的物理结构和参数确定. 这些特征共同反映一个电力网络在稳态运行时的特征.
表 1 电网稳态特征
Tab.1
| 特征符号 | 特征含义 |
| V i、θ i | 节点i 的电压幅值、相角 |
| PGi、QGi | 发电机节点i 的有功、无功出力 |
| PLi、QLi | 负荷节点i 的有功、无功负荷需求 |
| PBi–j、QBi–j | 线路i–j传输的有功、无功功率 |
1.3. 样本的获取方法
针对电压稳定评估问题,电压稳定裕度值是电网在一种运行方式之下的属性. 当系统的运行方式发生变化时,系统的电压稳定裕度也会相应不同. 采用文献[15]介绍的方法,在系统的某个基准运行方式之下,在一定范围内随机改变系统各发电机的出力和各负荷的需求情况,模拟系统的各类运行方式. 通过求解稳态潮流获取各运行方式对应的电气量特征;在模拟出的各运行方式之下,进一步采用CPF,获取各运行方式对应的电压稳定裕度. 在进行CPF计算时,本文按照固定变化方向逐渐增加系统负荷和出力,从产生的各运行方式出发,按照同一比例增加负荷需求和发电机出力,进行连续潮流计算.
2. 电压稳定裕度的XGBoost算法建模
2.1. 针对回归问题的基本原理
XGBoost算法是一种集成学习算法,其训练结果是一个集成模型,由多个CART决策树[14]函数相加得到:
式中:K为决策树函数的个数,
针对电压稳定裕度问题,由于评估目标VSM是连续的,需要采用XGBoost算法的回归模式,即在训练误差环节使用回归类的损失函数. 相比于其他基于树的模型,如随机森林、梯度提升回归树(gradient boosted regression trees, GBRT)等,XGBoost模型的损失函数不仅考虑了训练误差,还定义了模型复杂度,用于防止过拟合,其回归模式的损失函数如下所示:
式中:N为样本数量,第一项为平方误差函数形式的训练误差,用于衡量预测值yi*与标签值yi之间的偏差,在电压稳定裕度预测应用中,预测结果与实际VSM之间的偏差越大,该项的值越大.
式(3)中第二项Ω为正则项,用于衡量树模型的复杂度,当树模型的复杂程度越高时(反映为叶子节点的个数较多,权重向量出现较大值),该项的值越大. 因此在进行模型训练时,为了使得整体损失函数
式中:正则项的第一项用于控制树模型中叶子节点的个数,使其不会过多,第二项用于控制权重向量w,避免其出现过大值;参数γ和λ用于调节正则项中两部分之间的相对比例[14],是模型中的超参数.
2.2. 数据异常处理
对于电压稳定裕度评估问题,在实际应用时,电网的实时电气量特征通过PMU测量、传输,才能被机器学习模型使用. 尽管PMU是高精度的测量工具,但仍然会出现数据异常. 常见的数据异常包括数值错误和数值缺失2种. 数值错误指由于测量元件的误差等原因,测量值与真实值之间存在一定的偏差. 数值缺失指由于元件失效或传输失败等原因,一些特征的具体数值在某一时刻无法得到. 对于数值错误问题,需要考察机器学习模型的容错性,针对XGBoost算法,由于损失函数
在机器学习中,数值缺失可分为训练样本数值缺失和测试样本数值缺失2种. 对于电压稳定评估问题,算法的整体框架是使用积累起的仿真数据训练模型,再将训练好的模型在线使用. 因此,数值缺失问题仅仅会出现在“测试样本环节”. 针对XGBoost算法,当预测环节出现样本中的一些特征存在缺失值时,其CART决策树在进行样本划分时会将这类样本划分到右子树上. 在此逻辑下,即使测试样本存在缺失值,XGBoost算法依然可以给出评估结果,并且评估结果被证明是相对合理的[14].
3. 算例分析
3.1. 数据准备
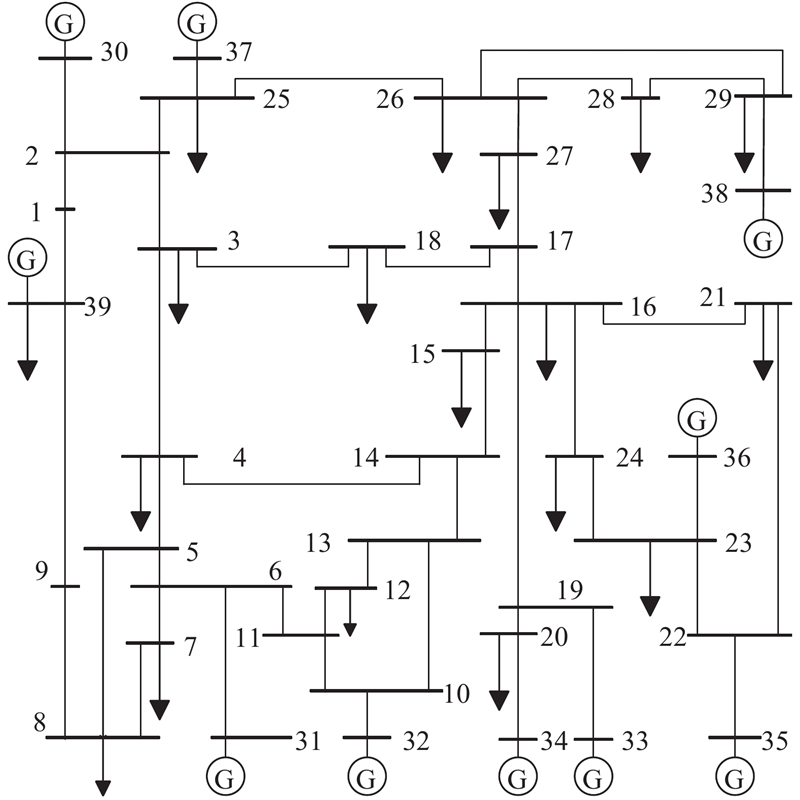
图 2
3.2. XGBoost算法与各类机器学习算法效果对比
将3 000个样本按照0.8∶0.2的比例分为训练集和测试集,使用训练集训练模型,使用测试集验证分析模型效果,选择如下几种机器学习算法[17]与XGBoost算法进行对比:随机森林算法(random Forest,RF)、梯度提升树回归算法(gradient boosting regression tree,GBRT)、支持向量回归算法(support vector regression,SVR)、K近邻回归算法(k-nearest neighbors regressor,KNNRegressor),并使用R2和MAPE指标度量模型效果,结果如表2所示. 需要说明的是,所有机器学习模型在训练过程中,均使用交叉验证法[18]进行超参数调优,以保证表2给出的结果是各类模型在此数据集上所能达到的最优效果. 与此同时,特征选择是机器学习建模的一个重要问题,由于树模型(RF、GBRT、XGBoost)均已包含特征选择的功能,在此规模的数据集上无须单独考虑特征选择;而针对SVR模型和KNNRegressor模型,需要讨论特征选择对结果的影响,针对这2类模型,本文考虑了3种情况:不进行特征选择、互信息法特征选择(保留90%特征)、PCA降维法(降维至原特征数的90%),并取3种方式(配合模型层面的交叉验证)中效果最优的情况作为该模型的最优表现.
表 2 不同机器学习模型的预测表现对比
Tab.2
| 模型 | R2 | MAPE |
| KNNRegressor | 0.946 | 4.869 |
| SVR | 0.961 | 4.152 |
| RF | 0.977 | 2.960 |
| GBRT | 0.987 | 2.140 |
| XGBoost | 0.992 | 1.621 |
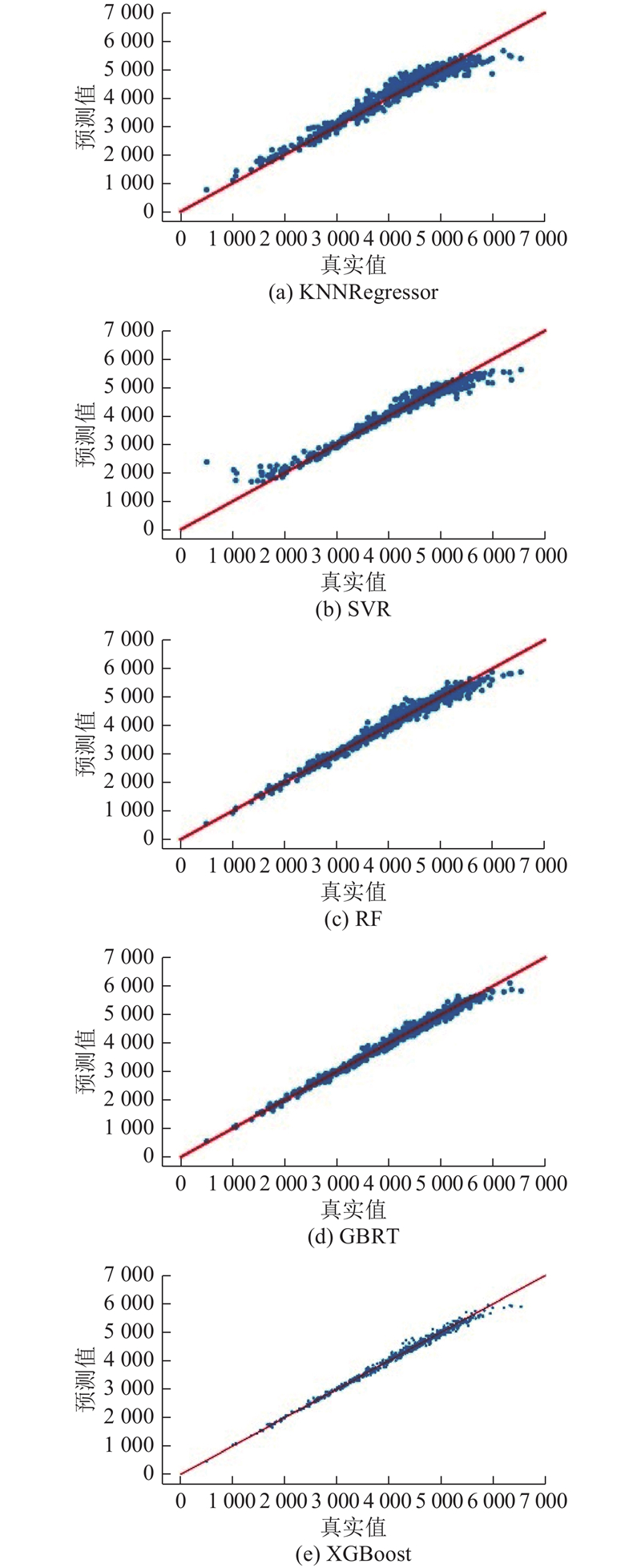
上述模型给出的测试集样本预测值与真实值之间的对照图如图3所示. 图中,横轴和纵轴分别表示样本的真实值和模型给出的预测值,直线为y=x,一个点表示一个样本. 当所有样本越靠近直线时,模型效果越好.
图 3
图 3 不同机器学习算法的预测效果
Fig.3 Prediction results of different machine learning algorithms
在上述结果中,KNNRegressor模型在不进行特征选择时表现最优,SVR模型在使用PCA降维时表现最优,具体性能如表2所示. RF、GBRT和XGBoost算法均是基于树的机器学习模型,其效果优于基于最大化分类间隔的SVR以及基于距离度量的KNNRegressor;在这3类基于树的机器学习模型中,RF为基于bagging思想的集成学习方法,而GBRT与XGBoost均为基于boosting的集成学习方法,可见在此问题上boosting的效果优于bagging. 相比于GBRT,XGBoost算法在boosting环节使用了梯度的二阶导数,相比于只使用梯度一阶导数的GBRT算法,能够更加准确地找到使模型损失下降最快的方向,从而使模型能够快速学习样本中包含的信息,并作出有效拟合.
在正则项的设计上,XGBoost算法考虑了树模型的复杂度,即单个树模型的叶子节点个数不至于过多,权重不至于过大,在追求训练样本拟合效果的同时,使得训练出的模型不至于过拟合,因此效果比GBRT算法更优. 在具体表现上,损失函数正则项限制了单个树模型的复杂度,避免模型在拟合时由于追求精度而将单个树模型的深度学得很深,造成过拟合,因此,XGBoost模型在达到最优训练效果时,相比于GBRT这类一般树模型,往往深度更少,而树的个数更多. 在本实验中,当达到最优效果时,GBRT中树模型的个数是79,而树模型的最大深度是8;而XGBoost模型的树个数为89,树模型的最大深度是5. 由于更好地避免了过拟合,模型精度得到提高,计算速度得到提升,计算速度的具体分析见第3.3节.
3.3. 模型计算速度
模型计算速度分析在一台使用windows10操作系统的个人计算机上进行,处理器主频为3.3 GHz,内存为8 GB. 使用Matpower对IEEE-39节点系统进行连续潮流计算仿真,随系统运行方式的不同,一次仿真的时间在0.8~1.9 s. 若对600种运行方式均进行仿真,时间消耗在480~1 140 s. 第3.2节几种机器学习算法的模型训练时间Tt和对测试集的整体预测时间Tp分别如表3所示.
表 3 不同模型训练、预测的消耗时间对比
Tab.3
| 模型 | Tt /s | Tp /s |
| KNNRegressor | 0.022 0 | 0.480 6 |
| SVR | 1.753 2 | 0.405 5 |
| RF | 9.060 5 | 0.006 0 |
| GBRT | 7.285 5 | 0.003 2 |
| XGBoost | 4.609 0 | 0.000 1 |
相比于仿真方法,使用机器学习方法进行电压稳定裕度预测在时间上明显有优势. 在如表3所示的机器学习模型中,KNNRegressor为惰性模型,基于测试样本与训练样本之间的向量相似度给出预测,因此不需要在模型训练上消耗过多时间;而在预测环节,需要比较测试样本与训练集的相似情况,因此预测时间较长. 除此之外,其他机器学习模型均在模型训练环节消耗较多的时间;而在预测环节消耗的时间很少,预测时间明显少于训练时间. 3种基于树的模型复杂度较高,因此在训练时间上高于SVR,而在预测时间上均很少,给出600个测试样本的预测值的时间均少于0.01 s. 特别地,XGBoost模型不仅精确度较高,并且训练速度比其他树模型更快,预测时间更是达到了0.000 1 s. XGBoost算法的高效性由本身原理和工程实现两方面决定. 在算法原理上,如第3.2节所述,正则项的设计使得树的深度更低,而树的个数更多;在预测计算时,由于多个树可以并行计算,树的深度越少,计算速度越快(最深的一棵树限制计算速度). 这是预测环节速度较快的原因. 在工程实现上,训练环节加入了一些算法实现上的优化. 在训练时,树模型最为耗时的操作是寻找最优分叉点(包括分叉点处所用特征和分叉点的数值选取),在XGBoost算法的训练过程中,采用并行计算的方式计算每个特征和每个分叉点数值,这使得模型的训练时间相比于其他树模型大大压缩. XGBoost算法的高效性使其完全可以满足在线应用的需要.
3.4. PMU测量错误对模型预测结果的影响
对于PMU可能发生的2类数据异常,分别考察XGBoost模型的容错性.
针对数值错误问题,研究如下:对于测试集样本,每个样本的所有特征,均叠加一个随机误差,误差范围分别设置为0.5%、1%、2%、5%时,使用XGBoost算法进行预测,得到的结果如表4所示.
表 4 样本存在数值错误时的XGBoost模型预测效果
Tab.4
| 误差范围 | R2 | MAPE | 误差范围 | R2 | MAPE | |
| 5% | 0.972 | 3.096 | 1% | 0.988 | 2.002 | |
| 2% | 0.980 | 2.478 | 0.5% | 0.991 | 1.789 |
针对数值缺失问题,研究如下:对于测试集样本,每个样本随机选取一定比例的特征,设置为空值. 当缺失特征个数分别为1%和2%时,XGBoost算法的评估结果如表5所示.
表 5 样本存在数值缺失时XGBoost模型效果
Tab.5
| 缺失比例 | R2 | MAPE |
| 1% | 0.987 | 1.905 |
| 2% | 0.976 | 2.356 |
由上述结果可见,针对PMU可能发生的数值错误和数值缺失2类数据异常,XGBoost算法均可以给出相对稳定的预测结果,预测精度均不会发生大幅度下降,具有一定的容错性;同时说明了特征的准确度对于XGBoost的预测精度有一定的影响.
3.5. 模型更新
机器学习模型的预测结果不可避免地会有一些偏差. 针对一些样本,其预测偏差可能显著高于其他样本. 为此,针对误差较大的样本,继续补充运行方式相近的样本进入训练集,对模型进行更新,从而使得模型在后续的使用中能减小偏差.
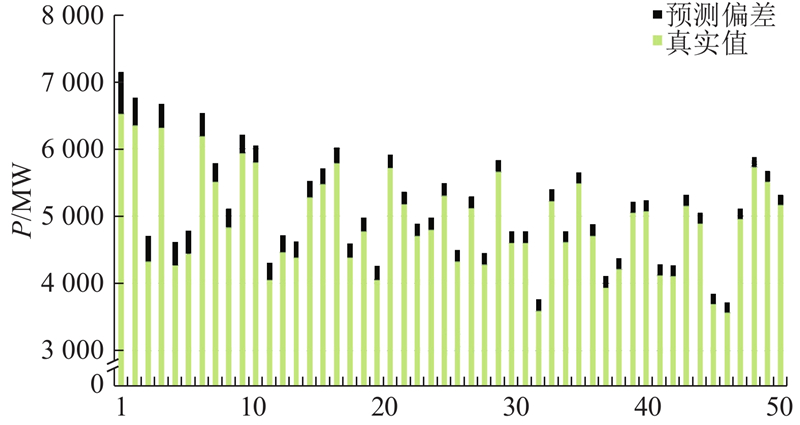
图 4
图 4 测试集误差最大的50个样本的真实值和预测偏差
Fig.4 Real value and prediction error of fifty samples with largest errors in test set
表 6 XGBoost模型更新前、后效果对比
Tab.6
| XGBoost模型 | 样本集 | 测试集 | |||
| MAE | MRE% | R2 | MAPE | ||
| 更新前 | 219 | 4.460 | 0.992 | 1.621 | |
| 更新后 | 2.49 | 0.017 | 0.996 | 1.313 | |
由表6可见,上述50个样本的预测误差均明显减小,平均绝对误差为2.49,平均相对误差为0.017%. 测试集整体的R2指标上升为0.996,MAPE下降为1.313. 可见,当模型对一些样本的预测结果存在一定偏差时,针对此类样本再次积累一定的样本,重新训练模型对其进行更新,可以降低新模型对此类样本的误差. 由此也可以说明,训练样本的合理分布是影响模型性能的重要因素.
4. 结 论
(1)XGBoost算法有更高的准确度,R2指标和MAPE指标都优于其他算法;
(2)XGBoost模型在训练时间上短于其他基于树的模型,在预测时间上大幅短于其他机器学习模型,可以满足在线计算的要求;
(3)针对实际应用中PMU测量电气量特征可能存在的数值错误和数值缺失2类问题,XGBoost算法都有较好的容错性.
(4)针对预测偏差较大的样本,可以有针对性地补充一部分类似样本进入训练集,重新训练模型,可以有效减少此类误差.
本研究是在各负荷和发电机出力按照同一比例增长的建模方式下进行,这是连续潮流计算中一种具有代表性的建模方式. 然而,针对不同电力系统的需求,探究不同负荷按照不同比例增长的方式对电力系统电压稳定性判别的影响,是后续一个值得探索的方向.
参考文献
Voltage stability probabilistic assessment in composite systems: modeling unsolvability and controllability loss
[J].DOI:10.1109/TPWRS.2009.2039234 [本文引用: 1]
The continuation power flow: a tool for steady state voltage stability analysis
[J].DOI:10.1109/59.141737 [本文引用: 1]
基于PSS/E的浙江电网静态电压稳定性分析
[J].DOI:10.3969/j.issn.1007-1881.2009.06.003 [本文引用: 1]
Analysis of static voltage stability of Zhejiang electric grid based on PSS/E
[J].DOI:10.3969/j.issn.1007-1881.2009.06.003 [本文引用: 1]
基于模糊神经网络决策树的电压稳定性评估
[J].
Evaluation of power system voltage stability based on fuzzy neural network decision tree
[J].
基于混合互信息的特征选择方法及其在静态电压稳定评估中的应用
[J].DOI:10.3321/j.issn:0258-8013.2006.07.015 [本文引用: 1]
Hybrid mutual information based feature selection method as appied to static voltage stability assessment in power systems
[J].DOI:10.3321/j.issn:0258-8013.2006.07.015 [本文引用: 1]
A novel online estimation scheme for static voltage stability margin based on relationships exploration in a large data set
[J].DOI:10.1109/TPWRS.2014.2349531 [本文引用: 2]
On-line voltage stability assessment using radial basis function network model with reduced input features
[J].
基于模糊神经网络的电力系统电压稳定评估
[J].DOI:10.3969/j.issn.1674-3415.2009.11.010 [本文引用: 1]
Fuzzy neural network based voltage stability evaluation of power systems
[J].DOI:10.3969/j.issn.1674-3415.2009.11.010 [本文引用: 1]
用于在线预测静态电压稳定性的SIPSS-Lasso-BP网络
[J].
A SIPSS-Lasso-BP network for online forecasting static voltage stability
[J].
Online monitoring of voltage stability margin using an artificial neural network
[J].DOI:10.1109/TPWRS.2009.2038059 [本文引用: 1]
Real-time static voltage stability assessment in large-scale power systems based on maximum-relevance minimum-redundancy ensemble approach
[J].DOI:10.1109/ACCESS.2017.2758819 [本文引用: 1]
Voltage stability prediction using active machine learning
[J].DOI:10.1109/TSG.2017.2693394 [本文引用: 2]
An artificial intelligence-based method for evaluating power grid node importance using network embedding and support vector regression
[J].DOI:10.1631/FITEE.1800146 [本文引用: 1]
Matpower: steady-state operations, planning, and analysis tools for power systems research and education
[J].DOI:10.1109/TPWRS.2010.2051168 [本文引用: 1]
Scikit-learn: machine learning in python
[J].
Cross-validation methods
[J].DOI:10.1006/jmps.1999.1279 [本文引用: 1]