研究表明,机械振动信号作为典型的非线性、非平稳信号,在一定的尺度范围内具有分形特征[9],这一特征能精确刻画信号的内在几何结构特点. Lin等[10]利用多分形去趋势波动分析(multi-fractal detrended fluctuation analysis,MF-DFA)方法量化轴承数据的多分形性,并提取5个多分形特征用于表征轴承故障状态. Xiong等[11]利用核主成分分析方法将5个MF-DFA特征与5个稳态分布特征进行特征融合,以提取滚动轴承故障特征. 在MF-DFA方法中,须经复杂的Legendre变换才能得到多分形特征值,计算量较大;在Wavelet leader方法中,采用Chhabra算法替代复杂的Legendre变换,计算简便. 因此,本研究利用Wavelet leader方法提取回转支承振动信号的高维多分形特征. 高维特征包含大量重复冗余信息,导致信息利用率较低且计算量较大. 等距映射(isometric mapping,ISOMAP)算法作为新型非线性数据压缩算法,在去除冗余信息的同时能较好地保持数据空间结构不变. 因此,为了提取回转支承振动信号的有效特征信息,本研究提出基于Wavelet leader和融合参数优化算法的ISOMAP算法的多分形自适应特征提取方法.
本研究通过Wavelet leader方法计算正常状态、螺栓破坏和外圈破坏3种状态下的多分形特征,挖掘数据几何结构信息,由此构造出高维多分形特征矩阵,并通过优化的ISOMAP方法对高维矩阵进行有效特征的自适应筛选. 为了定量分析特征提取效果,利用经遗传算法优化的最小二乘支持向量机(genetic algorithm-least squares support vector machine,GA-LSSVM)方法对筛选后的特征进行建模分析,并通过某型号回转支承的全寿命加速实验进行验证.
1. 基于Wavelet leader多分形特征提取理论
1.1. Wavelet leader多分形理论
设所需处理的信号为
定义二元区间
1.2. Wavelet leader多分形特征提取
定义Wavelet leader的结构函数为
式中:
为了简化计算,采用Chhabra算法获得直接计算多重分形特征的经验公式[14]:
式中:D(q)为多分形谱;h(q)为奇异指数;
2. 优化ISOMAP自适应特征筛选理论
2.1. 等距映射算法
ISOMAP算法[15]在多维尺度分析(multidimensional scaling,MDS)算法基础上加以改进,并基于两点间降维前后距离保持不变的准则,以测地线距离替代欧氏距离,较好地保留高维数据的空间特征,避免有效信息的流失. 具体实现过程如下.
1)设高维集
2)选取k个距离xi最近的点作为近邻点,记为
3)以采样点xi为节点,欧氏距离d(i,l)为边,构造采样点间邻域关系图G;
4)利用Dijkstra算法[16]计算邻域图G中任意两点间的最短距离dG(i,j),以逼近高维空间上测地线距离DG,测地线距离矩阵D={dG(i,j)};
5)应用MDS算法[17]对高维数据集X进行降维处理,过程如下.
设高维矩阵D对应的低维空间距离矩阵为
对Z进行中心化可以得到
式中:m为距离矩阵D的维数;tr (∙)表示矩阵的迹,且
联立式(9)、(10),可以得到:
根据式(11),可通过D求出B. 对B进行特征值分解:
2.2. ISOMAP参数寻优
由2.1节可知,低维空间集合Y能否有效表征高维空间X的结构特征,取决于近邻参数k的取值,且由残差e作为评价指标[18],e=1−Corr2 (D,Z). Corr (·)为标准线性相关系数. e越趋于0,表明数据嵌入效果越好. 为了获取最优参数kopt,提出混合灰狼算法(hybrid grey wolf optimization algorithm,HGWO)进行ISOMAP参数寻优.
灰狼算法(GWO)[19]是模拟狼群捕食的仿生智能算法. 随机产生一个狼群位置P={P1,P2,
式中:Dd为灰狼与猎物之间的距离;Pp为猎物位置;P为灰狼位置;t为当前迭代次数;A、C为参数向量.
狼群狩猎(优化)行为主要由α狼(最优解)、β狼(次优解)和δ狼(第3优解)主导. 在狩猎时个体位置因猎物位置改变而发生变化,因此狼群根据(α,β,δ)更新后的位置重新确定猎物(最优解)位置,更新公式如下:
式中:Dα、Dβ、Dδ分别为α、β、δ狼到狼群的距离,Pα、Pβ、Pδ分别为α、β、δ狼的位置,A1、A2、A3、C1、C2、C3分别为参数向量.
GWO在寻找最优位置时依赖参数A,当1<|A|<2时,狼群会偏离猎物,导致GWO陷入局部最优解. 差分进化(differential evolutionary,DE)算法[20]具备全局搜索能力和鲁棒性强的特点,因此可将DE算法与GWO算法相结合,构造混合灰狼优化算法HGWO,以获取ISOMAP算法的最优参数. 在DE算法中,通过变异、交叉和选择实现对(α,β,δ)的位置更新,避免GWO陷入局部最优,实现过程如下:
式中:Hi=[hi1,hi2,
选择的适应度函数表达式为
ISOMAP的参数优化实现过程如下.
1)初始化灰狼参数(N,d,t).
2)For i=1,2,···,t
根据式(14)计算狼群与α狼、β狼、δ狼的距离,并根据式(15)、(16)更新α狼、β狼、δ狼与猎物的位置.
根据式(20)计算父代灰狼的个体适应度,将前3个最优解标记为(Pα,Pβ,Pδ),并将适应度最优值记为父代狼群最优解.
根据式(17)、(18)对父代狼群变异、交叉操作,获得子代狼群Ui.
根据式(20)计算每个子代灰狼的个体适应度,并将最优值记为子代狼群最优解.
根据式(19)筛选出子代和父代狼群中的优秀个体位置,由此确定猎物位置(最优解).
END
3)求出狼群最优解,确定最优参数kopt.
2.3. 回转支承自适应特征提取方法流程图
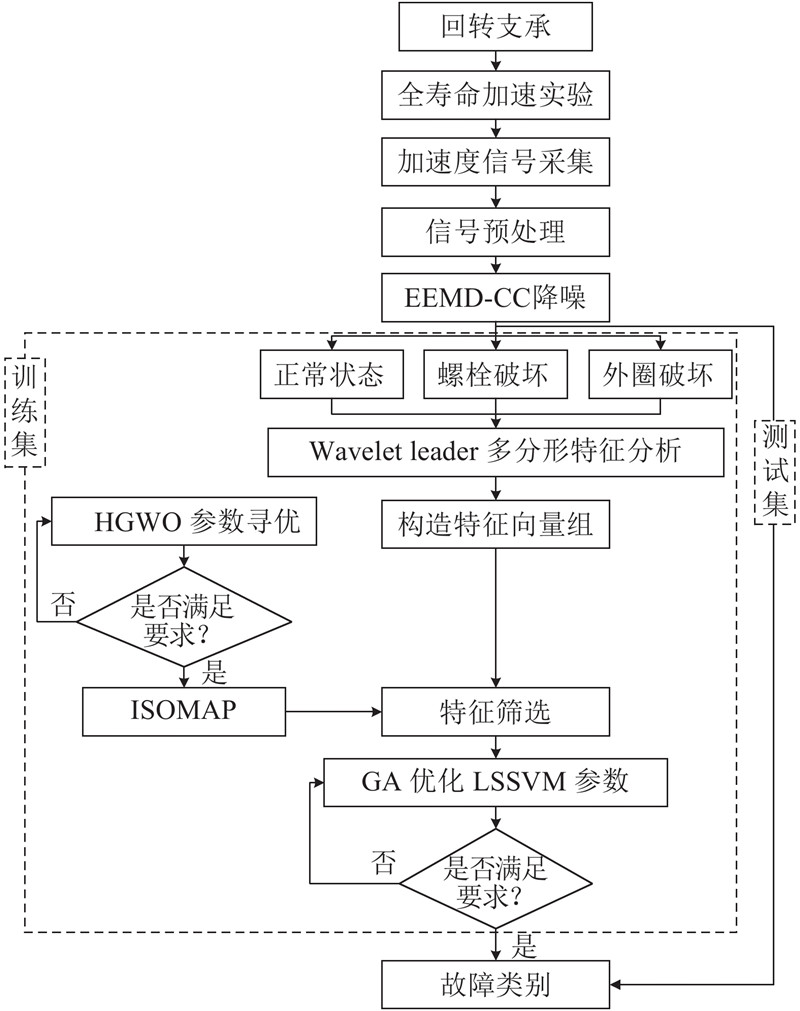
如图1所示为回转支承自适应特征提取方法的流程图,实施步骤如下. 1)从全寿命加速试验的回转支承振动信号中采集数据信息,确定能有效表征回转支承运行状态的数据,对数据进行集合经验模态分解-相关系数(ensemble empirical mode decomposition- correlation coefficient,EEMD-CC)[21-22]降噪处理. 2)对实验过程中采集到的正常状态、螺栓破坏状态以及外圈破坏状态的数据进行Wavelet leader多分形分析,分别计算出3种状态下的多分形谱值D(q)、奇异指数h(q)以及尺度指数
图 1
图 1 回转支承自适应特征提取方法流程图
Fig.1 Flow chart of adaptive feature extraction method of slewing bearing
3. 回转支承全寿命加速试验
为了验证所提方法的可行性,通过课题组自主研发的回转支承综合性能试验台模拟实际工况,实现振动信号采集. 为了加速试验,对待测设备施加100%极限载荷:轴向力为171.758 kN,倾覆力矩为482.618 kN∙m,径向力影响较小,忽略不计.
3.1. 回转支承试验台
图 2
图 3
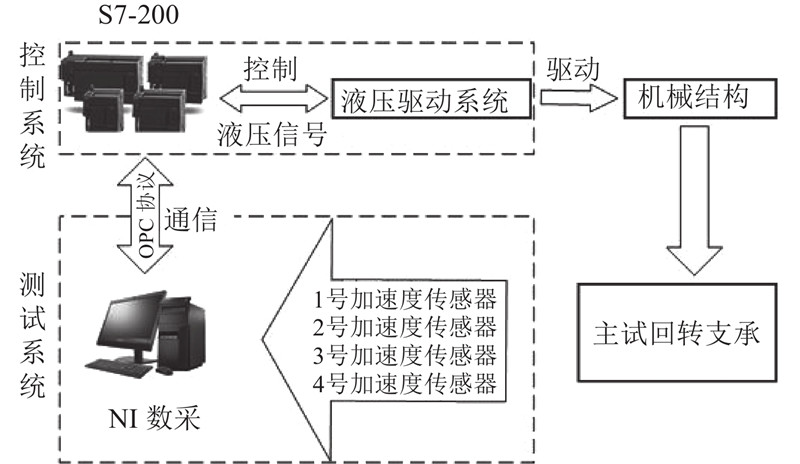
图 3 回转支承试验台系统结构流程图
Fig.3 System structure flow chart of slewing bearing test rig
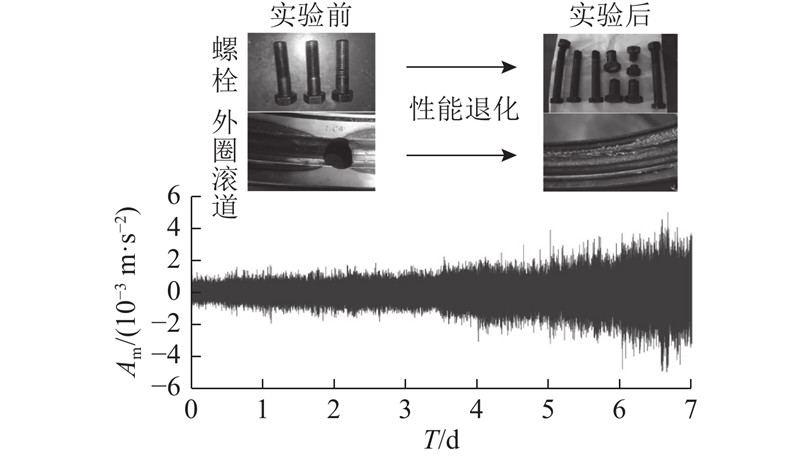
针对某型号回转支承进行全寿命加速试验,回转支承结构参数如表1所示. 回转支承在工作时,承受轴向载荷、径向载荷以及倾覆力矩,回转支承不同部位的受力情况有所不同,因此,在回转支承上沿周向间隔90°均匀布置传感器. 传感器编号分别为1、2、3、4,设置采样频率为2 048 Hz. 完成为期7 d的回转支承全寿命加速试验,借助测试系统完成信息的采集. 为了反映回转支承不同时刻的运行状况,每隔2 h取一次样本,取样时间为20 s. 对4组加速度传感器采集的数据进行观察分析,发现4号传感器采集的信号变化最为明显,因此对4号传感器采集的信息进行分析. 回转支承全寿命振动信号(部分数据)如图4所示. 图中,Am为加速度幅值,T为测试时间. 在实验结束后拆机检查,发现回转支承外圈滚道及螺栓出现严重破坏.
表 1 某型号回转支承的结构参数
Tab.1
| 参数 | 数值 | 参数 | 数值 | |
| 滚道中心直径/mm | 1 000 | 滚珠数目 | 71 | |
| 齿数 | 96 | 螺栓个数 | 36 | |
| 滚珠直径/mm | 40 | 轴/径向间隙/mm | 0.05~0.20 | |
| 外圈外径/mm | 1 185.6 | 内圈内径/mm | 878 | |
| 钢球材料 | GCr15 | 内/外圈材料 | 42GMo |
图 4
3.2. 实验数据处理与分析
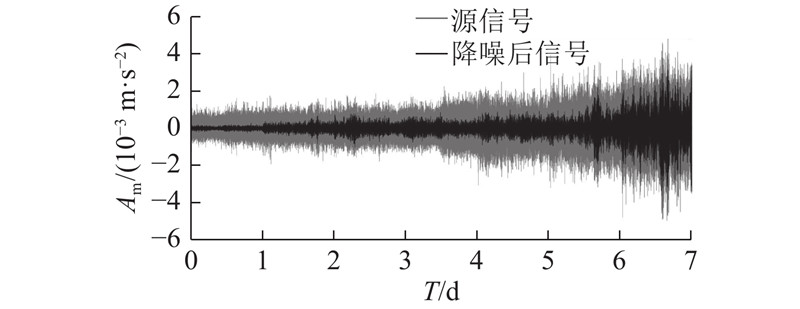
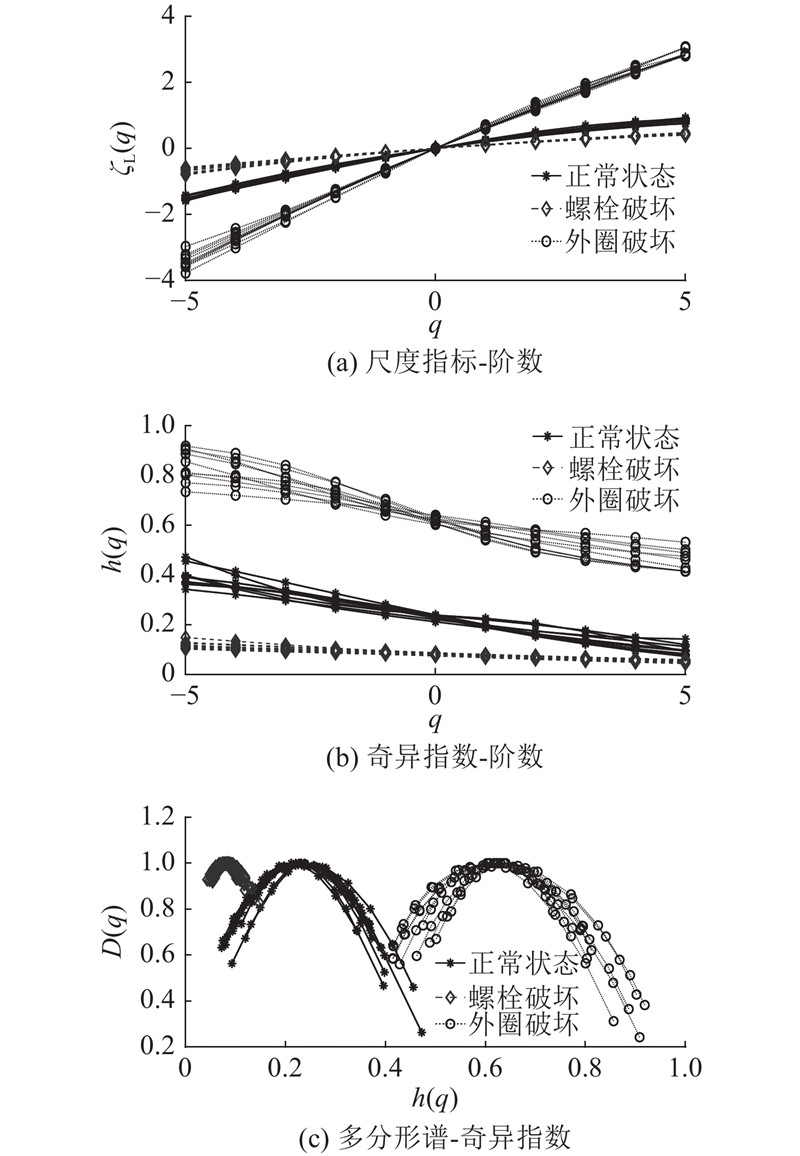
1)对采集的信号进行EEMD-CC降噪处理. 振动信号降噪前后的对比结果如图5所示. 可以看出,降噪能初步去除干扰信号,保留有用信息. 2)对降噪后的振动信号进行多分形分析. 通过Wavelet leader方法分别计算出正常状态、螺栓破坏以及外圈破坏3种状态下振动信号的尺度指数、奇异指数以及多分形谱值,计算结果如图6所示(以10个样本为例). 如图6(a)所示,在同一状态下尺度指标与阶数存在线性递增关系,且不同阶数对应的尺度指标均聚集在同一数值附近;在不同状态下,同一阶数对应的尺度指标的聚集点有明显的差别((0,0)点除外). 如图6(b)所示,在同一状态下奇异指数随阶数线性递减,不同阶数对应的奇异指数聚集在同一数值附近,不同状态下的奇异指数的分布范围具有明显的差异性. 如图6(c)所示,多分形谱与奇异指数呈现凸形曲线关系,同一状态下的D (q)-h (q)图集聚在同一范围内,不同状态下的D (q)-h (q)图分布较分散.
图 5
图 5 振动信号降噪前后对比图
Fig.5 Comparison of vibration signal before and after noise reduction
图 6
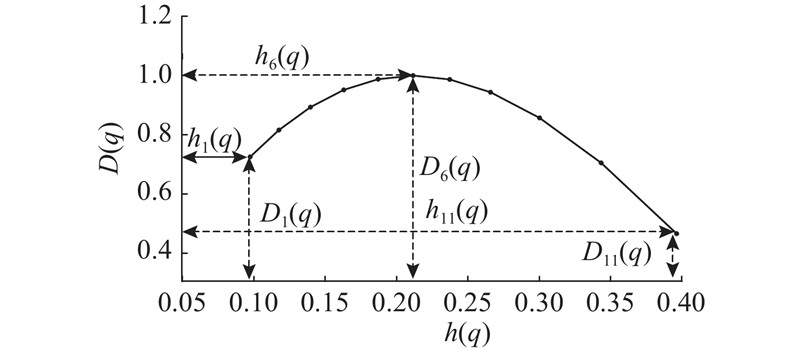
如图7所示为正常状态下某一样本的D (q)-h (q)图. 可以看出,回转支承振动信号的多分形谱与奇异指数具有凸曲线关系,结合图6(c)可知,图7中11个点均分布在一定的范围内,并且不同状态下的分布范围具有明显的区别. 为了定量说明3种状态下各点的分布情况,对3种状态的样本计算结果进行统计. 统计结果如图8所示(以初始点、最高点及终止点3个特殊点为例). 图中,Nu为频数,Ra为分布区间. 可以看出,在正常状态下初始点、最高点、终止点的主要分布范围分别为0.05~0.15、0.22~0.29、0.32~0.40. 在螺栓破坏状态下初始点、最高点、终止点的主要分布范围分别为0.04~0.07、0.07~0.10、0.12~0.20. 在外圈破坏状态下初始点、最高点、终止点的主要分布范围分别为0.35~0.54、0.57~0.65、0.72~0.88,如表2所示.
图 7
图 7 单个样本的多分形谱-奇异指数图
Fig.7 Multifractal spectrum-singular exponential graph of a single sample
图 8
图 8 3种状态下的特殊点分布统计结果
Fig.8 Statistical results of special point distribution in three states
表 2 特殊点分布区间统计结果
Tab.2
| 状态 | 初始点范围 | 最高点范围 | 终止点范围 |
| 正常状态 | 0.05~0.15 | 0.22~0.29 | 0.32~0.40 |
| 螺栓破坏 | 0.04~0.07 | 0.07~0.10 | 0.12~0.20 |
| 外圈破坏 | 0.35~0.54 | 0.57~0.65 | 0.72~0.88 |
奇异指数反映不同测度回转支承振动信号的随机性,奇异指数越大,表明振动信号越不规则,随机性越强. 多分形谱表征奇异指数所在测度的差别(见图7). 计算回转支承振动信号在3种状态下的多分形谱、奇异指数和尺度指数,构造1×33维特征矩阵Tj=[hi(q),Di(q),
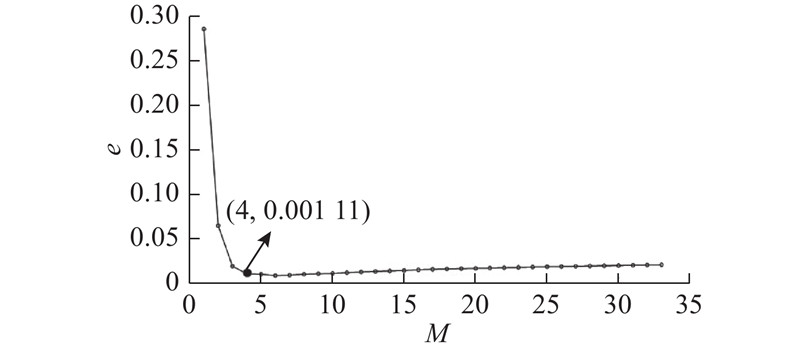
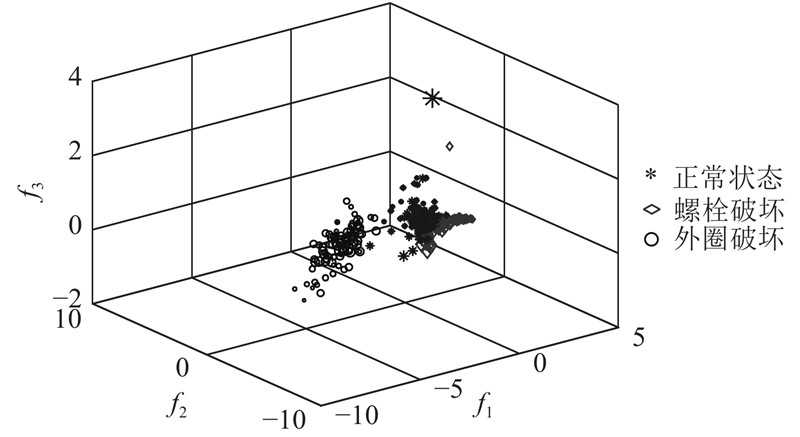
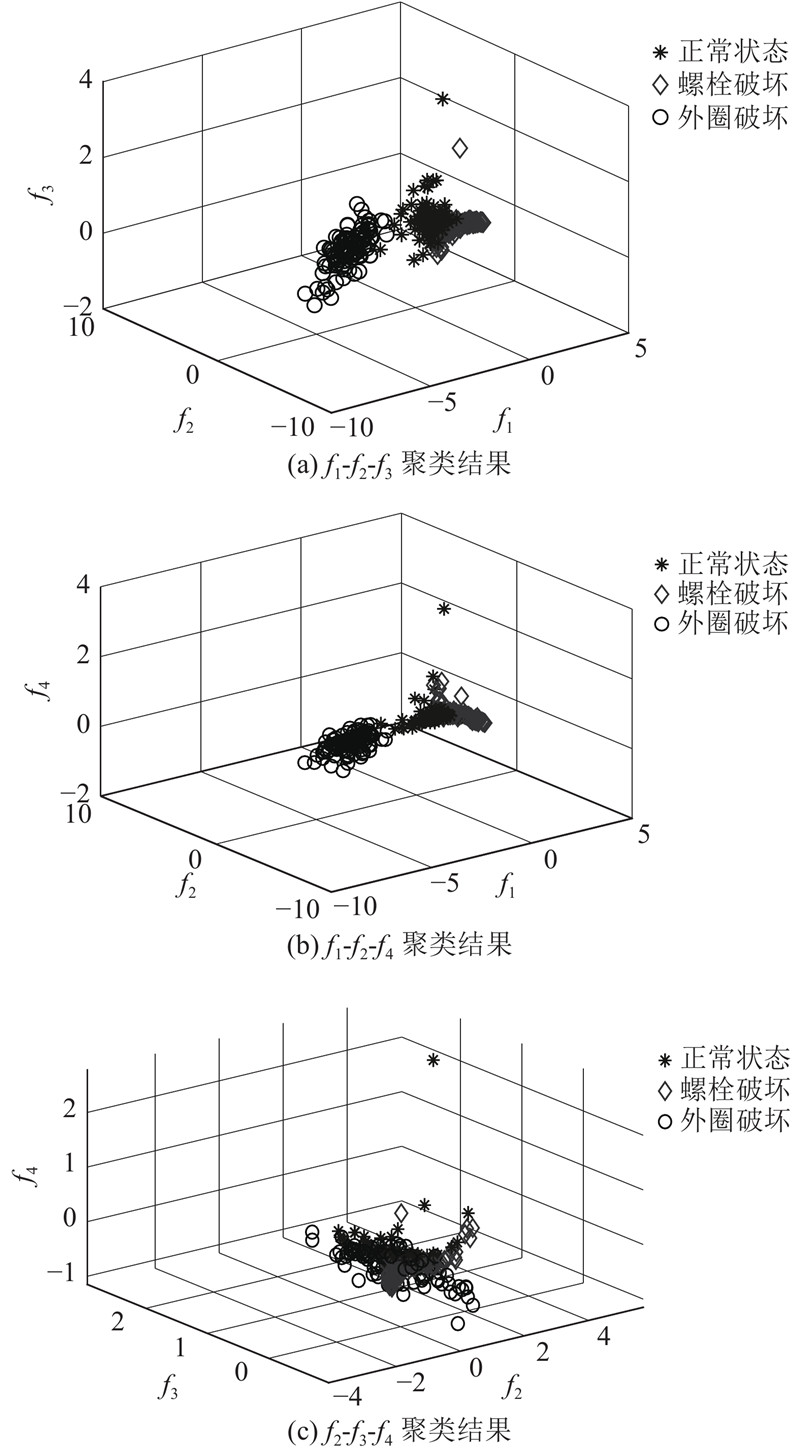
高维特征能全面包含信号信息,但信息重叠问题必然存在. 为了去除冗余信息,降低特征维数,以解决数据处理工作量大、耗时长的问题,利用所提出的降维方法对高维向量特征进行筛选. 经HGWO优化后得到的ISOMAP近邻参数k=96,ISOMAP自适应筛选特征结果如图9所示. 由图可知,当特征维数M=4时,剩余方差e达到最小值,且随着维数的增加,剩余方差趋于稳定,由此可知,当特征维数降到4时,所得数据能基本包含原特征矩阵的全部信息. 对降维后的数据进行可视化处理,结果如图10所示. 图中,f1为降维后第1维数据,f2为降维后第2维数据,f3为降维后第3维数据,通过标记大小表示降维后第4维数据f4. 可以看出,3类状态的区分度较大,其中外圈故障状态与其他状态间的区分最为明显. 正常状态与螺栓破坏状态下的数据虽有部分重合,但整体区分度仍较大. 为了进一步分析降维后得到的4维数据的聚类效果,选取4维数据中任意3维数据进行分析,绘制聚类图,如图11所示. 结果表明,f1-f2-f3和f1-f2-f4聚类效果显著,类间的区分度大;f2-f3-f4类间区分度较小,类间存在严重的重叠现象.
图 9
图 9 HGWO-ISOMAP方法的降维结果
Fig.9 Dimension reduction results of HGWO-ISOMAP method
图 10
图 11
图 11 降维后任选三维数据的可视化
Fig.11 Optional three-dimensional data visualization after dimensionality reduction
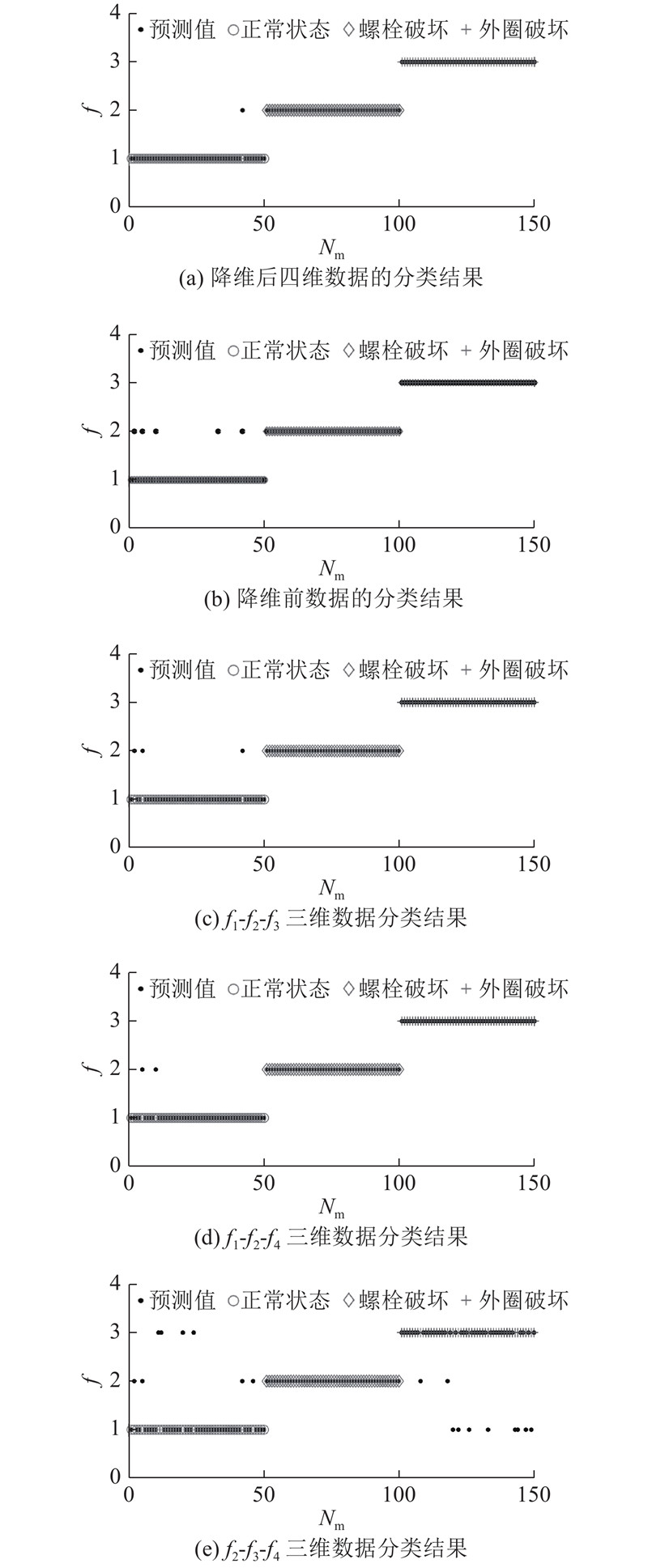
为了定量分析HGWO-ISOMAP的特征筛选效果,将降维后的特征矩阵分成训练样本和测试样本两部分,训练样本的输入为某状态降维后的特征矩阵,输出为该状态对应的状态函数值f,定义f={1,2,3}(f=1、2、3分别表示正常状态、螺栓破坏状态、外圈破坏状态),测试样本的输入为某一降维后的特征矩阵. 由此,总共形成了300组训练样本和150组测试样本. 通过训练样本对LSSVM进行训练建模,将测试样本输入训练好的LSSVM模型中,以实现定量评价特征筛选效果的目的. 为了提高模型的识别精度,采用遗传算法对LSSVM模型进行参数优化,初始种群大小为80,最大迭代次数为100,最终获得的最优参数
图 12
表 3 本研究所提方法的识别结果
Tab.3
| 分类器 | 方法 | Rc/% | t/s |
| LSSVM | HGWO-ISOMAP-Wavelet leader | 99.33 | 361.453 |
| 降维前-Wavelet leader | 96.67 | 560.643 | |
| f1-f2-f3 | 98.00 | 374.419 | |
| f1-f2-f4 | 98.67 | 360.888 | |
| f2-f3-f4 | 88.00 | 366.519 |
表 4 其他方法的识别结果
Tab.4
| 分类器 | 方法 | Rc/% | t /s |
| LSSVM | 时域特征 | 85.33 | 377.801 |
| 频域特征 | 88.00 | 366.634 | |
| 时频域特征 | 89.33 | 352.214 | |
| 时域-频域-时频域混合特征 | 92.00 | 417.547 | |
| BP神经网络 | HGWO-ISOMAP-Wavelet leader | 88.67 | 30.158 |
| 降维前-Wavelet leader | 82.67 | 217.013 | |
| f1-f2-f3 | 86.00 | 28.765 | |
| f1-f2-f4 | 88.45 | 29.127 | |
| f2-f3-f4 | 67.33 | 29.333 | |
| 时域特征 | 66.00 | 17.497 | |
| 频域特征 | 66.67 | 21.377 | |
| 时频域特征 | 68.67 | 20.046 | |
| 时域-频域-时频域混合特征 | 75.33 | 23.223 |
4. 结 论
(1)基于Wavelet leader方法挖掘的回转支承振动信号具有显著的多分形特征,在3种状态下,多分形谱-奇异指数关系图具有较大的区分度,可以作为回转支承故障状态识别的可靠特征指标.
(2)HGWO-ISOMAP方法能自适应性筛选出多分形特征矩阵中的有效信息,在保留原特征矩阵中全部有效信息的同时,剔除干扰信息,降低特征维数,显著提高计算效率和识别准确率.
(3)对本研究所提出的特征提取方法进行GA-LSSVM模型定量分析,进一步证明了所提方法的优越性. 所提方法为回转支承振动信号特征提取的新型有效分析方法. 这对回转支承运行状态在线监测和故障诊断具有一定的工程意义.
参考文献
大型回转支承故障信号处理方法综述
[J].DOI:10.3969/j.issn.1001-3997.2012.03.080 [本文引用: 1]
Research on signal processing method of large slewing bearing
[J].DOI:10.3969/j.issn.1001-3997.2012.03.080 [本文引用: 1]
Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals
[J].
A roller bearing fault diagnosis method based on EMD energy entropy and ANN
[J].
基于EEMD和SVM的滚动轴承退化状态识别
[J].
Degradation state recognition of rolling bearing based on EEMD and SVM
[J].
采用概率主成分分析的回转支承寿命状态识别
[J].DOI:10.7652/xjtuxb201510015 [本文引用: 1]
Recognition of life state for slewing bearings using probabilistic component analysis
[J].DOI:10.7652/xjtuxb201510015 [本文引用: 1]
Degradation trend estimation of slewing bearing based on LSSVM model
[J].DOI:10.1016/j.ymssp.2016.02.031 [本文引用: 1]
多重分形近似熵与减法FCM聚类的研究及应用
[J].
Application of multifractal approximate entropy and subtractive FCM clustering in gearbox fault diagnosis
[J].
基于多重分形去趋势波动分析的齿轮箱故障特征提取方法
[J].DOI:10.3969/j.issn.1000-3835.2013.02.019 [本文引用: 1]
Fault feature extraction of gearboxes based on multifractal detrended fluctuation analysis
[J].DOI:10.3969/j.issn.1000-3835.2013.02.019 [本文引用: 1]
Fault diagnosis of rolling bearings based on multifractal detrended fluctuation analysis and Mahalanobis distance criterion
[J].DOI:10.1016/j.ymssp.2012.12.014 [本文引用: 1]
A fault diagnosis method for rolling bearings based on feature fusion of multifractal detrended fluctuation analysis and alpha stable distribution
[J].
基于等距映射与加权KNN的旋转机械故障诊断
[J].DOI:10.3969/j.issn.0254-3087.2013.01.031 [本文引用: 1]
Rotating machinery fault diagnosis based on isometric mapping and weighted KNN
[J].DOI:10.3969/j.issn.0254-3087.2013.01.031 [本文引用: 1]
Dijkstra算法的设计与实现
[J].
Design and implementation of Dijkstra algorithm
[J].
基于自适应近邻参数的局部线性嵌入
[J].DOI:10.3969/j.issn.1003-6059.2010.06.015 [本文引用: 1]
Self-regulation of neighborhood parameter for locally linear embedding
[J].DOI:10.3969/j.issn.1003-6059.2010.06.015 [本文引用: 1]
Grey wolf optimizer
[J].
一种带有随机变异的动态差分进化算法
[J].
Dynamic differential evolution algorithm with random mutation
[J].
基于相关系数的EEMD转子振动信号降噪方法
[J].DOI:10.3969/j.issn.1004-6801.2012.04.004 [本文引用: 1]
Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system
[J].DOI:10.3969/j.issn.1004-6801.2012.04.004 [本文引用: 1]
基于EEMD降噪与PNN的齿轮箱齿轮故障诊断
[J].
Fault diagnosis of gearbox gear based on EEMD de-noising and PNN
[J].
基于深度学习特征提取和粒子群支持向量机状态识别的齿轮智能故障诊断
[J].DOI:10.3969/j.issn.1004-132X.2017.09.009 [本文引用: 1]
Intelligent fault diagnosis for gears based on deep learning feature extraction and particle swarm optimization SVM state identification
[J].DOI:10.3969/j.issn.1004-132X.2017.09.009 [本文引用: 1]