柔性结构件被广泛应用于汽车和飞机制造行业. 由于柔性结构件通常为弱刚性薄板零件，不仅在加工成型过程中难以保证较高的尺寸精度，而且在装配过程中会引起装配体的回弹变形. 初始零件制造误差以及装配回弹变形等因素使得实际装配体偏离其设计模型，从而产生装配偏差. 在飞机生产过程中，误差不可避免地出现在制造和装配等各个环节，并伴随产品生产过程沿制造和装配尺寸链不断传播和累积，最终体现为产品的装配偏差，装配偏差的大小直接影响所生产的飞机产品乃至整机的性能、质量和寿命. 航空工业具有严格的制造准确度和协调准确度要求，因此对柔性航空结构件装配偏差的准确分析和预测十分重要.

装配偏差预测的准确性取决于建立的装配偏差模型的有效性，以及对装配偏差源实际信息表达的准确性. 其中，装配偏差模型旨在建立零件尺寸和形状偏差等偏差源与装配体关键特征偏差之间的关联关系模型. 对于柔性装配偏差建模与分析研究，Liu等^[1]基于影响系数法（method of influence coefficients，MIC）和蒙特卡洛模拟（Monte Carlo simulation，MCS）进行的装配偏差建模和分析，显著提升了装配偏差预测的计算效率. 在此研究基础上，Saadat等^[2]运用有限元分析（finite element analysis，FEA）模拟肋脚与蒙皮的连接过程，可以有效地预测肋脚的实际位置，从而通过连接前调整肋脚，以控制肋脚和蒙皮之间的间隙，最终实现对翼盒整体变形的控制. Liu等^[3]考虑铆接变形，基于有限元分析、影响系数法和蒙特卡洛模拟等，分析和预测了飞机机身壁板装配偏差. Cai等^[4-5]提出了综合考虑刚性和柔性2种影响因素的壁板装配偏差分析方法. 除装配偏差模型以外，研究人员对柔性装配偏差源的类型以及偏差源之间的相关性也进行了研究. 例如，考虑弹性材料耦合和曲面连续变化问题，Merkley等^[6]基于统计协方差法分析了材料协方差和几何协方差对柔性件装配偏差的影响，预测了装配体的装配应力和装配变形. Tan等^[7]提出了一种基于混合多项式近似和频谱分析的几何协方差建模方法，准确地表征了零件表面变化的幅度和相关关系. 偏差源信息的正确表征直接影响装配偏差预测结果的准确性. Wang等^[8]对偏差源的概率分布进行修正，与把偏差源近似为正态分布相比，得到的翼盒装配偏差预测结果更为准确. 在进行装配偏差分析时，通常假设偏差源为已知概率分布的随机变量，根据偏差源的统计特征计算装配偏差的统计特征，所得到的装配偏差预测结果的置信度为99.73%. 但是，对于高成本、小批量生产的航空制造业，特别是在飞机样机生产阶段，通常难以获得偏差源的大样本数据抑或其准确的概率统计分布，在此情况下，基于概率统计方法难以有效地表征装配偏差源的实际信息.

针对概率统计方法在偏差源信息匮乏条件下表征偏差源的局限性，近年来，区间分析和区间数学被引入机械工程领域. Rao等^[9]将不确定参数表示为区间数，将静态结构分析问题转化为线性区间方程组，显示了区间法在不确定性系统分析设计中的实用性. Lee等^[10]将连杆长度和扭转角等参数用区间数表示，采用区间分析解决了串联机器人的几何设计问题. Merlet等^[11-13]运用区间分析解决了Gough类型并联机器人的正则运动和多准则优化设计问题. 鉴于区间范围已知的偏差源可以用区间数进行表达，Wu等^[14]基于区间分析对公差和间隙进行建模. Mei等^[15]使用区间数表示翼肋的翘曲和扭转变形角度，预测了翼盒骨架试验件装配偏差的波动范围. 使用区间分析可使装配偏差预测结果的置信水平达到100%，但由于区间数的运算总是对区间的上限和下限进行操作，预测的范围会随着区间数个数和区间数出现次数的增大而增大^[16]，即产生区间扩张问题. 同时，采用区间分析方法所获得的装配偏差预测结果仅是一个有界区间，无法得到装配偏差的分布情况.

本文提出一种基于模糊区间分析的柔性装配偏差分析和预测方法，通过模拟翼盒骨架装配试验验证建立的装配偏差模型以及提出的装配偏差分析方法的有效性. 该方法采用支集元素扩展为区间数的离散模糊数表征偏差源的实际信息，离散模糊数^[17]能给出不确定参数在不同置信水平下的取值信息，可以更好地描述偏差源的实际分布，结合建立的装配偏差模型，使用模糊区间分析方法可以得到装配偏差的模糊分布.

在进行装配偏差分析时，必须先建立装配体的装配偏差模型，即装配偏差与偏差源之间的关联函数：

(1) $u=f\left( {{v_1},{v_2},\cdots,{v_n}} \right).$

式中： $u$为装配偏差， ${v_i}$为第 $i$个偏差源，函数 $f\left( * \right)$为装配偏差的数学模型.

为了获得仅知偏差源区间范围条件下的装配偏差分布情况，采用离散模糊数对偏差源进行描述. 离散模糊数是支集为有限个离散点的特殊模糊数，相关定义和运算法则可参考文献[17]~[19]. 离散模糊数A的Zadeh表示方法为

(2) $A=\sum\limits_{i=1}^k {\frac{{A\left( {{x_i}} \right)}}{{{x_i}}}} =\frac{{A\left( {{x_1}} \right)}}{{{x_1}}} + \frac{{A\left( {{x_2}} \right)}}{{{x_2}}} + \cdots + \frac{{A\left( {{x_k}} \right)}}{{{x_k}}}.$

式中：论域X为有限集 $\left\{ {{x_1},{x_2},\cdots,x{}_k} \right\}$，其中各支集元素满足 ${x_1},{x_2},\cdots,x{}_k \in {\bf{R}}$且 ${x_1} \leqslant {x_2} \leqslant \cdots \leqslant x{}_k$， ${{A\left( {{x_i}} \right)} / {{x_i}}}$为论域X中的支集元素 ${x_i}$ 与集合A的隶属程度.

当离散模糊数A的支集元素 ${x_i}$ 扩展为区间 $\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]$时，离散模糊数 $\hat A$的Zadeh表示方法如下：

(3) $\begin{split} \hat A=& \sum\limits_{i=1}^k {\left\{ {{{A\left( {\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]} \right)} \Big/ {\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]}}} \right\}}= \\ & \frac{{A\left( {\left[ {\overline {{x_1}} ,\underline {{x_1}} } \right]} \right)}}{{\left[ {\overline {{x_1}} ,\underline {{x_1}} } \right]}} + \frac{{A\left( {\left[ {\overline {{x_2}} ,\underline {{x_2}} } \right]} \right)}}{{\left[ {\overline {{x_2}} ,\underline {{x_2}} } \right]}} + \cdots + \frac{{A\left( {\left[ {\overline {{x_k}} ,\underline {{x_k}} } \right]} \right)}}{{\left[ {\overline {{x_k}} ,\underline {{x_k}} } \right]}}. \end{split} $

式中： ${{A\left( {\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]} \right)} \Big/ {\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]}}$为支集元素区间 $\left[ {\overline {{x_i}} ,\underline {{x_i}} } \right]$与集合 $\hat A$的隶属程度， $k$为该离散模糊数的项数.

假设装配过程中的偏差源由支集元素扩展为区间的离散模糊数 ${V_i}\left( {i=1,2,\cdots,k} \right)$表征，且通过装配过程分析已经建立了装配偏差和偏差源之间的关联函数，可以基于模糊运算计算得到装配偏差. 因此，基于模糊区间分析的装配偏差模型为

(4) $\hat U=f\left( {{{\hat V}_1},{{\hat V}_2},\cdots,{{\hat V}_n}} \right).$

式中： ${\hat V_1}$， ${\hat V_2}$，···， ${\hat V_n}$分别为偏差源 ${v_1}$， ${v_2}$，···， ${v_n}$对应的离散模糊数， $\hat U$为支集元素扩展为区间的离散模糊数表示的装配偏差.

可以根据模糊分析计算得到的装配偏差的模糊分布：

(5) $\begin{split} \hat U=& \sum\limits_{i=1}^t {\left\{ {{{U\left( {\left[ {\overline {{u_i}} ,\underline {{u_i}} } \right]} \right)} \Big/ {\left[ {\overline {{u_i}} ,\underline {{u_i}} } \right]}}} \right\}} = \\ & \frac{{U\left( {\left[ {\overline {{u_1}} ,\underline {{u_1}} } \right]} \right)}}{{\left[ {\overline {{u_1}} ,\underline {{u_1}} } \right]}} + \frac{{U\left( {\left[ {\overline {{u_2}} ,\underline {{u_2}} } \right]} \right)}}{{\left[ {\overline {{u_2}} ,\underline {{u_2}} } \right]}} + \cdots + \frac{{U\left( {\left[ {\overline {{u_t}} ,\underline {{u_t}} } \right]} \right)}}{{\left[ {\overline {{u_t}} ,\underline {{u_t}} } \right]}}. \end{split} $

式中： ${{U\left( {\left[ {\overline {{u_i}} ,\underline {{u_i}} } \right]} \right)} \Big/ {\left[ {\overline {{u_i}} ,\underline {{u_i}} } \right]}}$为区间 $\left[ {\overline {{u_i}} ,\underline {{u_i}} } \right]$在装配偏差模糊集 $U$中的隶属程度， $t$为该离散模糊数的项数.

基于模糊分析并将离散模糊数的支集元素扩展到区间数的装配偏差模型可以得到不同置信水平下装配偏差的分布区间范围，可以更好地描述装配偏差分布. 当存在多个相同类型的偏差源时，采用支集元素扩展为区间数的离散模糊数构成的向量表示装配偏差源. 该模型既可用于刚性装配偏差计算，也适用于柔性装配偏差预测.

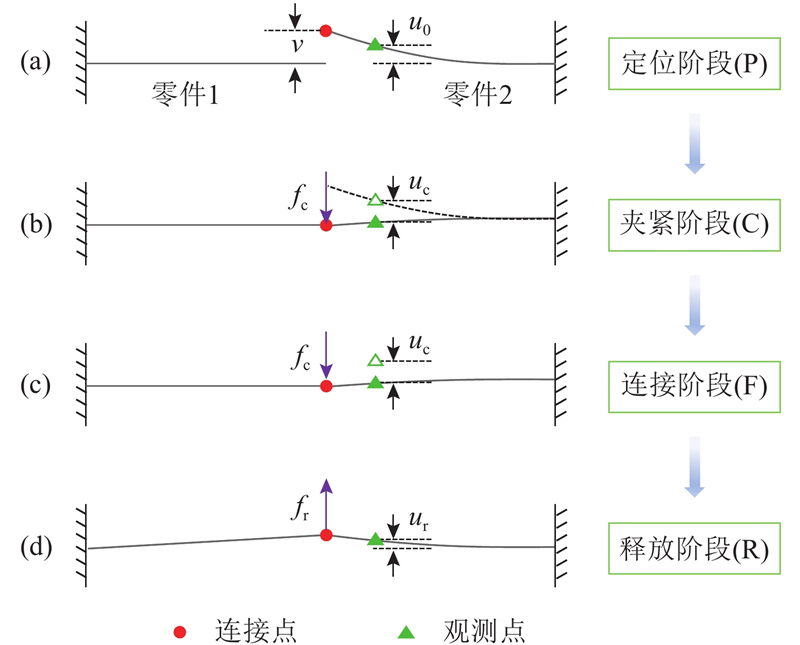
柔性航空结构件的装配过程通常可简化为定位（position，P）、夹紧（clamping，C）、连接（fastening，F）和释放（releasing，R）4个基本阶段，如图1所示，详细过程如下所述.

1）在定位阶段，零件被装夹到各自的夹具上，由于存在制造误差，零件在连接点处存在初始间隙 ${{v}}$；

2）在夹紧阶段，通过施加夹紧力 ${{{f}}_{\rm{c}}}$将零件连接点夹持到理想位置，此时会引起观测点位移 ${{{u}}_{\rm{c}}}$；

3）在连接阶段，通过铆钉或螺栓等紧固件对2个零件进行连接；

4）在释放阶段，移除夹具，释放夹紧力，零件变形回弹引起观测点位移 ${{{u}}_{\rm{r}}}$.

综合步骤1）~4），考虑观测点处存在初始制造误差 ${{{u}}_{\rm{0}}}$，因此，装配完成后观测点的总位移 ${{u}}$为

(6) ${{u}}={{{u}}_0} - {{{u}}_{\rm{c}}} + {{{u}}_{\rm{r}}}.$

对基于影响系数法的机械装配偏差模型进行分析^[1]. 消除连接点处初始偏差引起的观测点处位移为

(7) ${{{u}}_{\rm{c}}}={{{S}}_{\rm{c}}}{{v}}.$

式中： ${{{S}}_{\rm{c}}}$为观测点位移和连接点初始偏差之间的敏感度矩阵，可由有限元分析计算得到.

装配完成后，夹紧力释放，由零件变形回弹引起的观测点位移为

(8) ${{{u}}_{\rm{r}}}={{{S}}_{\rm{r}}}{{v}}.$

式中： ${{{S}}_{\rm{r}}}$为观测点变形回弹和连接点初始偏差间的敏感度矩阵，可由有限元分析计算得到.

因此，考虑观测点处制造误差以及零件变形、回弹引起的观测点位移的总装配偏差为

(9) ${{u}}={{{u}}_0} - {{{S}}_{\rm{c}}}{{v}}+ {{{S}}_{\rm{r}}}{{v}}={{{u}}_0} + \left( {{{{S}}_{\rm{r}}} - {{{S}}_{\rm{c}}}} \right){{v}}={{{u}}_0} + {{S}}v.$

式中： ${{S}}$为观测点装配偏差和连接点初始偏差间的敏感度矩阵.

在大型飞机结构装配中，除了零件制造误差和装配回弹变形，装配偏差可能还受定位协调误差、温度、重力和接触作用等因素的影响. 根据叠加原理，各因素对装配偏差的影响可以线性叠加，因此大型柔性航空结构件的装配偏差模型为

(10) ${{u}}={{{u}}_0} + {{S}}{{v}} + {{{u}}_{\rm{P}}} + {{{u}}_{\rm{T}}} + {{{u}}_{\rm{g}}}.$

式中： ${{{u}}_{\rm{P}}}$为定位协调误差引起的装配偏差，可以通过零件之间的位姿协调计算得到， ${{S}}{{v}}$为装配变形引起的装配偏差， ${{{u}}_{\rm{T}}}$和 ${{{u}}_{\rm{g}}}$分别为由温度和重力因素引起的装配偏差，可以通过有限元分析计算得到.

当存在 $m$个观测点和 $n$个相同类型的偏差源时，柔性航空结构件装配偏差模型的完整表达式为

(11) $ \begin{split} \left[ {\begin{array}{*{20}{c}} \!\!\! {{u_1}} \!\!\! \\ \!\!\! {{u_2}} \!\!\! \\ \!\!\! \vdots \!\!\! \\ \!\!\! {{u_m}} \!\!\! \end{array}} \right]= & \left[ {\begin{array}{*{20}{c}} \!\!\! {{u_{01}}}\!\!\! \\ \!\!\! {{u_{02}}}\!\!\! \\ \!\!\! \vdots\!\!\! \\ \!\!\!{{u_{0m}}} \!\!\! \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \!\!\! {{s_{11}}}&{{s_{12}}}& \cdots &{{s_{1n}}} \!\!\! \\ \!\!\! {{s_{21}}}&{{s_{22}}}& \cdots &{{s_{2n}}}\!\!\! \\ \!\!\! \vdots & \vdots & {\rm{}} & \vdots \!\!\! \\ \!\!\! {{s_{m1}}}&{{s_{m2}}}& \cdots &{{s_{mn}}}\!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!\! {{v_1}}\!\!\! \\ \!\!\!{{v_2}}\!\!\! \\ \!\!\! \vdots\!\!\! \\ \!\!\! {{v_n}} \!\!\! \end{array}} \right] + \\ & \left[ {\begin{array}{*{20}{c}} \!\!\! {{u_{{\rm{P}}1}}}\!\!\! \\ \!\!\! {{u_{{\rm{P}}2}}}\!\!\! \\ \!\!\! \vdots \!\!\! \\ \!\!\! {{u_{{\rm{P}}m}}} \!\!\! \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \!\!\! {{u_{{\rm{T}}1}}}\!\!\! \\ \!\!\! {{u_{{\rm{T}}2}}}\!\!\! \\ \!\!\! \vdots \!\!\! \\ \!\!\! {{u_{{\rm{T}}m}}}\!\!\! \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \!\!\! {{u_{{\rm{g}}1}}} \!\!\!\\ \!\!\! {{u_{{\rm{g}}2}}} \!\!\!\\ \!\!\! \vdots \!\!\! \\ \!\!\! {{u_{{\rm{g}}m}}} \!\!\! \end{array}} \right]. \end{split} $

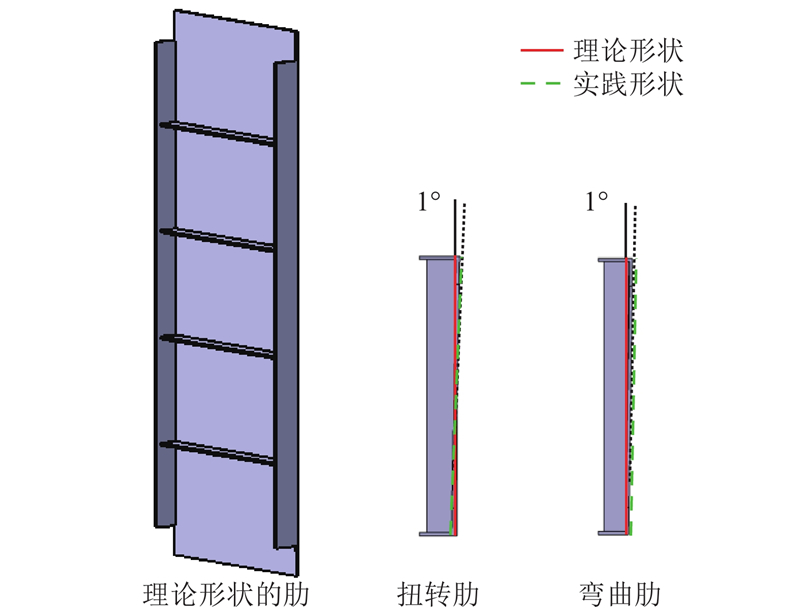
在柔性装配偏差分析中，通过关键点位移等效零件变形的方法不能完整、准确地描述零件的翘曲变形和扭转变形，因此采用翘曲和扭转角分别描述肋的翘曲变形和扭转变形，如图2所示.

当飞机处于样机制造阶段时，仅知偏差源的可能区间范围，基于第2.1节建立柔性航空结构件装配偏差与偏差源之间的关联函数，同时将偏差源表征为支集元素为区间的离散模糊数，柔性航空结构件装配偏差模型可改写为

(12) $\hat {{U}}={\hat {{U}}_0} + {{S}}\hat {{V}} + {\hat {{U}}_{\rm{P}}} + {\hat {{U}}_{\rm{T}}} + {\hat {{U}}_{\rm{g}}}.$

若仅考虑装配体的零件制造误差和变形回弹对装配偏差的影响，则装配偏差模型可以简化为

(13) $\hat {{U}}={\hat {{U}}_0} + {{S}}\hat {{V}}.$

式中： $\hat {{U}}$为观测点的装配偏差， ${\hat {{U}}_0}$为观测点的制造误差， ${{S}}$为由零件变形引起的装配偏差和偏差源之间的敏感度矩阵，由有限元分析计算得到.

式（13）是考虑单个偏差源的情形，若存在 $n$个相同类型的偏差源，则柔性航空结构件装配偏差模型的完整表达为

(14) $\left[ {\begin{array}{*{20}{c}} \!\!\!{{{\hat U}_1}}\!\!\! \\ \!\!\! {{{\hat U}_2}}\!\!\! \\ \!\!\! \vdots \!\!\! \\ \!\!\!{{{\hat U}_m}} \!\!\! \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} \!\!\! {{{\hat U}_{01}}} \!\!\! \\ \!\!\! {{{\hat U}_{02}}} \!\!\! \\ \!\!\! \vdots \!\!\! \\ \!\!\! {{{\hat U}_{0m}}} \!\!\! \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} \!\!\! {{s_{11}}}&{{s_{12}}}& \cdots &{{s_{1n}}}\!\!\! \\ \!\!\! {{s_{21}}}&{{s_{22}}}& \cdots &{{s_{2n}}}\!\!\! \\ \!\!\! \vdots & \vdots & {\rm{}} & \vdots\!\!\! \\ \!\!\! {{s_{m1}}}&{{s_{m2}}}& \cdots &{{s_{mn}}}\!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \!\!\! {{{\hat V}_1}}\!\!\! \\ \!\!\! {{{\hat V}_2}}\!\!\! \\ \!\!\! \vdots\!\!\! \\ \!\!\! {{{\hat V}_n}} \!\!\! \end{array}} \right].$

根据模糊数学理论，由模糊分析得到的装配偏差结果为模糊分布，可以表征出不同置信水平下装配偏差的区间范围，因此能够更准确地刻画预测出的装配偏差的分布情况.

通过模拟翼盒骨架装配验证所提出的装配偏差预测方法的可行性和有效性. 飞机翼盒骨架主要由前梁、后梁和翼肋等构成，简化的模拟翼盒骨架模型如图3所示. 鉴于机翼翼盒由骨架和蒙皮连接装配而成，前、后梁上与蒙皮内型面配合的配合面上的装配偏差应该得到有效控制，图中圆点表示该配合面上用于检测骨架装配质量的观测点，如图3所示共设20个观测点. 翼盒骨架模型的几何尺寸为850 mm×600 mm×200 mm，翼肋之间的间距为200 mm，前、后梁和翼肋的厚度分别为5.0和2.5 mm，材料为Al 2A12. 模拟翼盒骨架的3D模型在CATIA中设计完成.

机翼翼盒的装配过程如下所述. 后梁在夹具上定位固定，前梁根据后梁位姿定位协调并固定，最后按照一定顺序依次连接各肋与梁. 肋和梁的连接过程包括定位、夹紧、连接和释放4个阶段：1)使用固定装置将肋的后梁端固定在后梁的肋定位柱上；2)使用夹具将变形肋的前梁端夹紧到前梁的肋定位柱上；3)进行肋和肋定位柱叠层结构制孔并连接；4)移除固定装置和夹具，肋倾向于恢复到其原来的变形形状，因而在装配体内部会累积内应力，最终造成装配体变形.

在翼盒骨架装配过程中，很多因素会引起装配偏差，由于模拟翼盒骨架结构尺寸小，不考虑温度和重力因素对装配偏差的影响，仅考虑零件制造误差和肋变形引起的装配偏差. 为了降低影响系数法中敏感度矩阵的维数，减少计算时间，本文使用角度代替关键点的位置偏差表征肋的翘曲和扭转变形2种类型的偏差源，如图2所示. 因此与肋变形相关的基于支集扩展为区间的离散模糊数描述的偏差源共10个，本文假设肋的翘曲角和扭转角的范围为 $\left[ { - 0.6^{\circ} ,0.6^{\circ} } \right]$，前、后梁观测点的制造误差区间是 $\left[ { - 0.5,\;0.5} \right]$ mm. 通过模糊分析运算可以得到20个观测点处不同置信水平下装配偏差的区间范围.

使用2.2部分提出的装配偏差模型计算装配偏差. 本文考虑的偏差源包括20个观测点处的制造误差，区间范围为 $\left[ { - 0.5,\;0.5} \right]$ mm；肋的5个翘曲角和5个扭转角的区间范围为 $\left[ { - 0.6^{\circ} ,0.6^{\circ} } \right]$.

首先将偏差源用支集元素扩展为区间数的离散模糊数表示，显然，偏差源的支集区间元素划分越精细，计算所得到的装配偏差分布更准确. 考虑到离散模糊数运算的不封闭性，装配偏差的支集元素会随着偏差源支集元素和运算次数的增加而增加. 为了验算提出的基于模糊区间分析的装配偏差预测方法的有效性，这里的装配偏差源仅考虑置信水平分别为0.2、0.4、0.6、0.8和1.0的5种情况（当置信水平为0时，对应的区间范围为0，离散模糊数的Zadeh表示方法通常省略支集元素为0的项）. 因此描述肋翘曲变形和扭转变形的翘曲角和扭转角可以表示为（省略角度单位（°）以简化表达形式）：

$\begin{split} {{\hat V}_i}= & \frac{{0.2}}{{\left[ { - 0.12,0.12} \right]}} + \frac{{0.4}}{{\left[ { - 0.24,0.24} \right]}} + \frac{{0.6}}{{\left[ { - 0.36,0.36} \right]}} + \\ & \frac{{0.8}}{{\left[ { - 0.48,0.48} \right]}} + \frac{{1.0}}{{\left[ { - 0.60,0.60} \right]}}. \end{split} $

式中： $i=1,2,\cdots,10$，表示与肋变形相关偏差源的编号. 基于离散模糊数表征的前、后梁观测点处的制造误差可以表示为

$\begin{split} {{\hat U}_{0j}}= & \frac{{0.2}}{{\left[ { - 0.10,0.10} \right]}} + \frac{{0.4}}{{\left[ { - 0.20,0.20} \right]}} + \frac{{0.6}}{{\left[ { - 0.30,0.30} \right]}} + \\ & \frac{{0.8}}{{\left[ { - 0.40,0.40} \right]}} + \frac{{1.0}}{{\left[ { - 0.50,0.50} \right]}}. \end{split} $

式中： $j=1,2, \cdots,20$，表示观测点的编号.

有限元分析和影响系数法常用来获取柔性装配中的敏感度矩阵S. 模拟翼盒骨架有限元建模在Abaqus6.14中完成，其中，采用C3D8R单元进行网格划分，模型中的材料属性与截面属性设置与实际模拟翼盒骨架保持一致. 肋和梁之间的连接严格遵循柔性航空结构件定位、夹紧、连接和释放（PCFR）的装配步骤. 在进行有限元分析时，PCFR过程分为2个阶段：在定位-夹紧（PC）阶段，考虑肋和梁的实际作用情况，将连接面之间的接触设置为滑动摩擦接触；在连接-释放（FR）阶段，将肋和梁之间的接触设置为绑定接触. 以上的接触设置考虑到了接触引起的非线性因素，更加符合实际装配情况，因此所获得的敏感度矩阵较为精确. 模拟翼盒骨架模型的有限元仿真过程如图4所示.

将基于支集元素扩展为区间数的离散模糊数表示的偏差源与敏感度矩阵代入式（14）所描述的装配偏差模型中. 由于离散模糊数运算具有不封闭性，相同置信水平可能对应不同的支集元素区间. 因此，取相同置信水平下的最大区间范围作为该置信水平的装配偏差预测结果. 当置信水平分别为0、0.2、0.4、0.6、0.8和1.0时，对应着偏差源不同的区间范围，由此可以求出不同置信水平下的装配偏差区间范围.

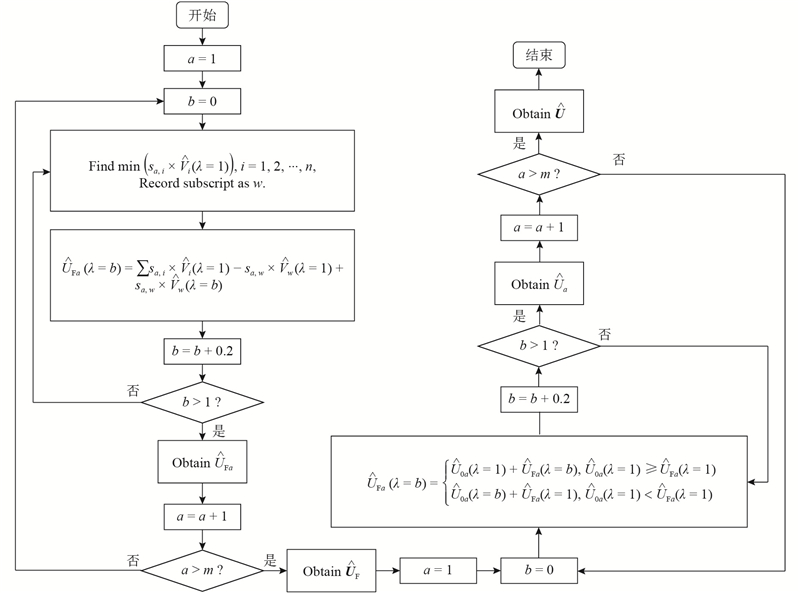
如图5所示为模拟翼盒骨架观测点装配偏差模糊分布的计算过程. 图中， $n$为与肋变形相关偏差源的个数， $m$为模拟翼盒骨架观测点的个数，此案例中 $n=10$、 $m=20$， ${\hat V_i}\left( {\lambda =b} \right)$表示第 $i$ 个与肋变形相关的偏差源在置信水平为 $b$下的区间范围， ${s_{a,i}}$表示第 $i$ 个与肋变形相关的偏差源与第 $a$ 个装配偏差之间的敏感度系数， ${\hat U_{{\rm{F}}a}}\left( {\lambda =b} \right)$表示第 $a$ 个观测点由肋变形引起的装配偏差在置信水平为 $b$下的区间范围， ${\hat U_{{\rm{F}}a}}$表示第 $a$ 个观测点由肋变形引起的装配偏差. ${{\hat{ U}}_{\rm{F}}}$表示观测点由肋变形引起的装配偏差矩阵， ${\hat U_{0a}}\left( {\lambda =b} \right)$表示第 $a$ 个观测点的制造误差在置信水平为 $b$下的区间范围， ${\hat U_a}\left( {\lambda =b} \right)$表示第 $a$ 个观测点的总装配偏差在置信水平为 $b$下的区间范围， ${\hat U_a}$为第 $a$ 个观测点的总装配偏差， ${\hat{ U}}$为观测点的总装配偏差矩阵.

此外，本研究实际制造了肋和梁等零件，装配模拟翼盒骨架，并利用三坐标测量机（coordinate measuring machine，CMM）测量模拟翼盒骨架的装配偏差数据. 如表1所示为模拟翼盒骨架装配偏差的试验测量数据 ${U_{{\rm{mea}}}}$，基于区间分析方法^[24]预测的装配偏差数据 ${U_{{\rm{int}}}}$，以及基于模糊区间分析方法预测的装配偏差数据 ${U_{{\rm{fuz}}}}$. 如图6所示为模拟翼盒骨架装配试验件和测量平台.

通过表1模拟翼盒骨架装配试验实测数据与2种装配偏差预测方法所预测的装配偏差的对比发现，在基于模糊区间分析的装配偏差预测方法得到的装配偏差中，当置信水平为1.0时，所得到的区间范围与基于区间分析方法的装配偏差分析方法所预测结果相同，这是因为区间数是文中模糊数的一种特殊情况，基于区间分析的装配偏差预测方法的预测结果包含于基于模糊区间分析的装配偏差分析方法的预测结果；当置信水平分别为0.8、0.6、0.4、0.2和0时，采用基于模糊区间分析的装配偏差分析方法可得到更为严格的装配偏差区间范围；实测装配偏差结果在文中提出的装配偏差分析方法预测的装配偏差区间范围内. 由此可见，表1数据验证了所提出的基于模糊区间分析的装配偏差预测方法的有效性，同时，由于该装配偏差预测方法可以得到不同置信水平下的装配偏差区间范围，对装配偏差信息的描述更加全面.

本文提出了一种基于模糊区间分析的柔性航空结构件装配偏差预测方法. 将偏差源描述为支集元素扩展为区间数的离散模糊数，通过模糊运算得到装配偏差的模糊分布. 为了降低敏感度矩阵的维数和有限元分析时间，采用翘曲和扭转角表示肋的翘曲和扭转变形. 通过与基于区间分析的装配偏差预测方法的装配偏差预测结果以及模拟翼盒骨架装配偏差实测数据对比，验证了提出的基于模糊区间分析的柔性航空件装配偏差预测方法的有效性. 基于区间分析的装配偏差预测方法的预测结果是基于模糊区间分析方法所预测结果中置信水平为1.0时的特例，实测装配偏差包含于预测结果区间中. 基于模糊区间分析的装配偏差预测方法能有效预测仅知偏差源区间条件下的装配偏差，同时能得到不同置信水平下的装配偏差区间范围，可以给出更为全面的装配偏差信息. 本文提出的基于模糊区间的柔性航空结构件装配偏差分析方法不仅适用于航空结构件装配偏差的预测，也适用于汽车等其他领域柔性装配偏差的分析，是传统基于蒙特卡洛模拟的装配偏差分析方法的一种补充.