浅水数值模拟备受关注[1-9]. 基于Godunov思想的有限体积法能够自动捕捉激波/间断,在浅水模拟方面得到了长足的发展[10-13],从一维到平面二维;从清水定床到泥沙运动;从均匀到非均匀沙;从明渠流到水下异重流[14-21]. 这类方法的时间步长受到CFL(Courant-Friedrichs-Lewy)稳定性条件的限制. 以往数学模型普遍采用整体时间步长(global-time-step, GTS)理念,取所有单元最小的
1. 水沙耦合数学模型
1.1. 水沙耦合的控制方程
式中:
1.2. 经验公式
阻力坡度采用曼宁公式估算:
式中:
式中:
式中:
1.3. 数值计算方法
1.3.1. 基于非结构网格的有限体积离散
采用非结构三角网格离散计算区域,将控制方程组(1)在编号为i的三角形单元积分,可得
式中:
式中:
式中:上标
1.3.2. 局部分级时间步长技术
动床水沙耦合数学模型的局部时间步长技术的实现分为以下2步.
1)重构每个单元的局部时间步长
式中:
式中:
式中:
2)更新单元水沙变量. 每个单元在一个
根据
将式(15)、(16)循环
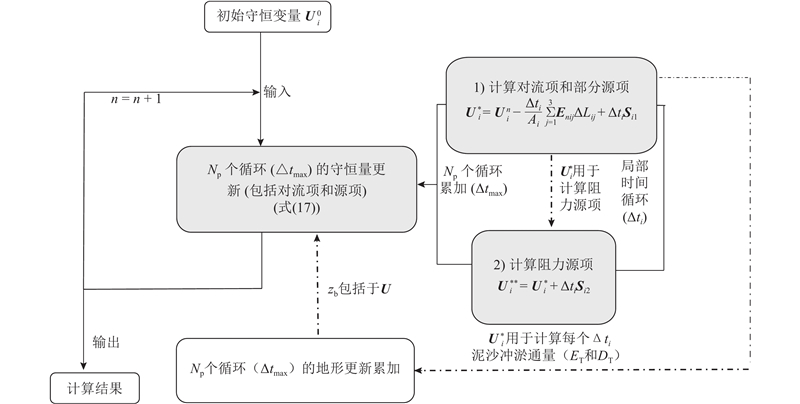
式(17)实现了式(11)的动床局部时间步长计算方法. 如图1所示为局部时间步长技术的实现流程示意图.
图 1
2. 算例验证
为了检验局部时间步长算法的计算精度和计算效率,采用2组算例验证. 第1组算例(2.1节)复演Sanders[22]针对清水定床模型的局部时间步长算法的结果;第2组算例(2.2节)采用UCL大学动床溃坝水流实验. 为了对比局部时间步长与整体时间步长给计算结果带来的差异,采用两者的均方根误差作为定量指标,定义如下:
式中:
式中:
2.1. 溃坝定床算例验证
溃坝定床算例采用理想的溃坝过程. 采用1 000 m× 100 m的矩形计算区域,共计3 802个计算单元,平均三角单元网格边长为7.8 m.
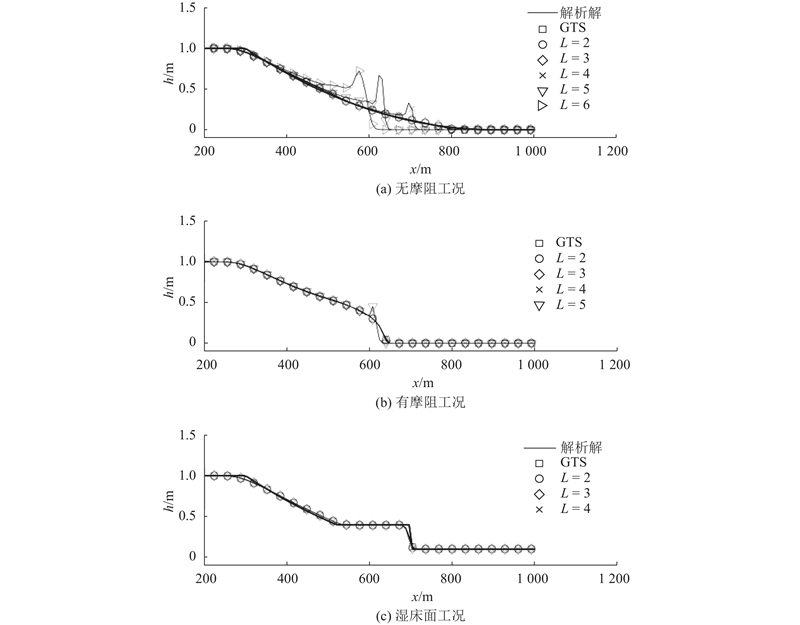
计算结果如图2所示. 如图2(a)所示为无摩阻工况. 可以看出,当
图 2
图 2 清水定床溃坝算例沿程水深在64 s时的分布图
Fig.2 Water depth profiles at 64 s for simulating dam-break flow over fixed bed
表 1 局部时间步长技术模拟定床溃坝水流的成本和精度
Tab.1
| 工况 | L | Tr | L2(h) | L2(u) |
| 无摩阻工况 | 1(GTS) | 1.0 | 0 | 0 |
| 2 | 0.59 | 9.5×10−4 | 0.14 | |
| 3 | 0.39 | 10−2 | 1.40 | |
| 4 | 0.31 | 4.8×10−2 | 1.91 | |
| 5 | 0.26 | 1.1×10−1 | 2.21 | |
| 6 | 0.26 | 9.3×10−2 | 2.78 | |
| 有摩阻工况 | 1(GTS) | 1.0 | 0 | 0 |
| 2 | 0.57 | 1.3×10−3 | 10−2 | |
| 3 | 0.36 | 2.8×10−3 | 1.8×10−2 | |
| 4 | 0.27 | 5.2×10−3 | 2.3×10−1 | |
| 5 | 0.24 | 4.3×10−2 | 7.4×10−1 | |
| 湿床面工况 | 1(GTS) | 1.0 | 0 | 0 |
| 2 | 0.58 | 2.4×10−3 | 2.1×10−2 | |
| 3 | 0.36 | 5.7×10−3 | 5.0×10−2 | |
| 4 | 0.36 | 5.7×10−3 | 5.0×10−2 |
2.2. 溃坝动床算例验证
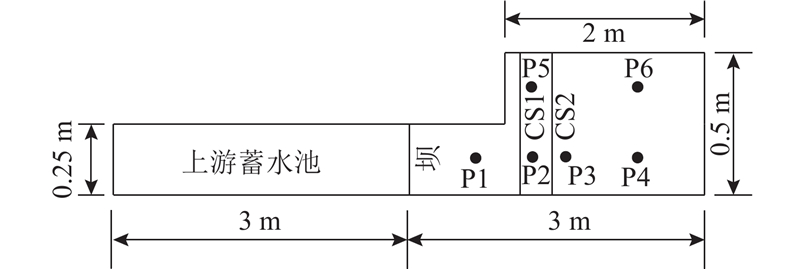
溃坝动床算例采用比利时UCL大学实验数据[35-36]. 水槽平面如图3所示,水槽长6 m,宽度在距离左边界4 m的地方展宽,离左侧3 m位置设置水闸;床面铺厚度为0.1 m的泥沙,中值粒径
图 3
图 3 UCL动床溃坝洪水实验水槽的平面布置示意图
Fig.3 Plan view of UCL dam-break experimental configuration
图 4
图 4 UCL算例6个测点的计算(采用不同L)和实测水位
Fig.4 Computed (using different L) and measured water level hydrographs against time at six gauges for UCL case
图 5
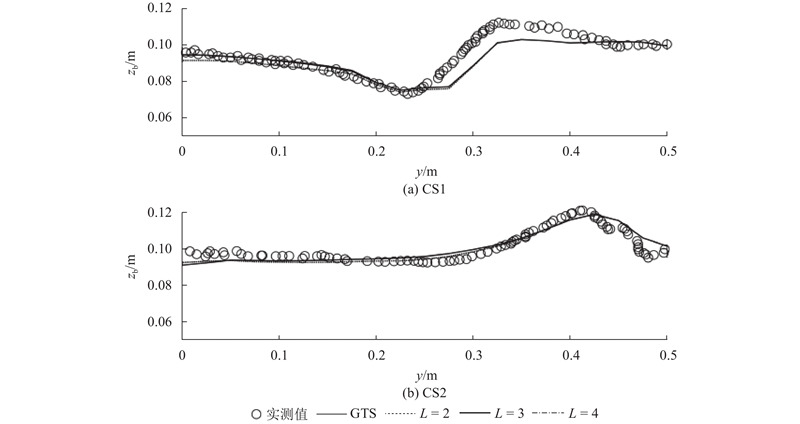
图 5 UCL算例2个断面冲淤分布的计算(采用不同L)和实测值
Fig.5 Computed (using different L) and measured bed profiles at CS1 and CS2 for UCL case
表 2 局部时间步长技术模拟动床溃坝水流的成本和精度
Tab.2
| L | Tr | L2(z)/10−4 | L2(Δzb)/10−5 |
| 1(GTS) | 1.0 | 0 | 0 |
| 2 | 0.53 | 1.8 | 2.8 |
| 3 | 0.32 | 3.5 | 7.7 |
| 4 | 0.25 | 2.3 | 48 |
3. 模型应用与讨论
图 6
图 7
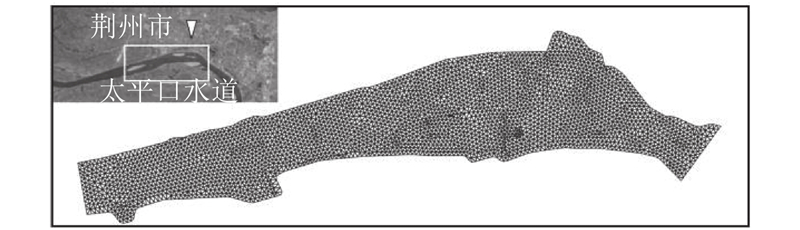
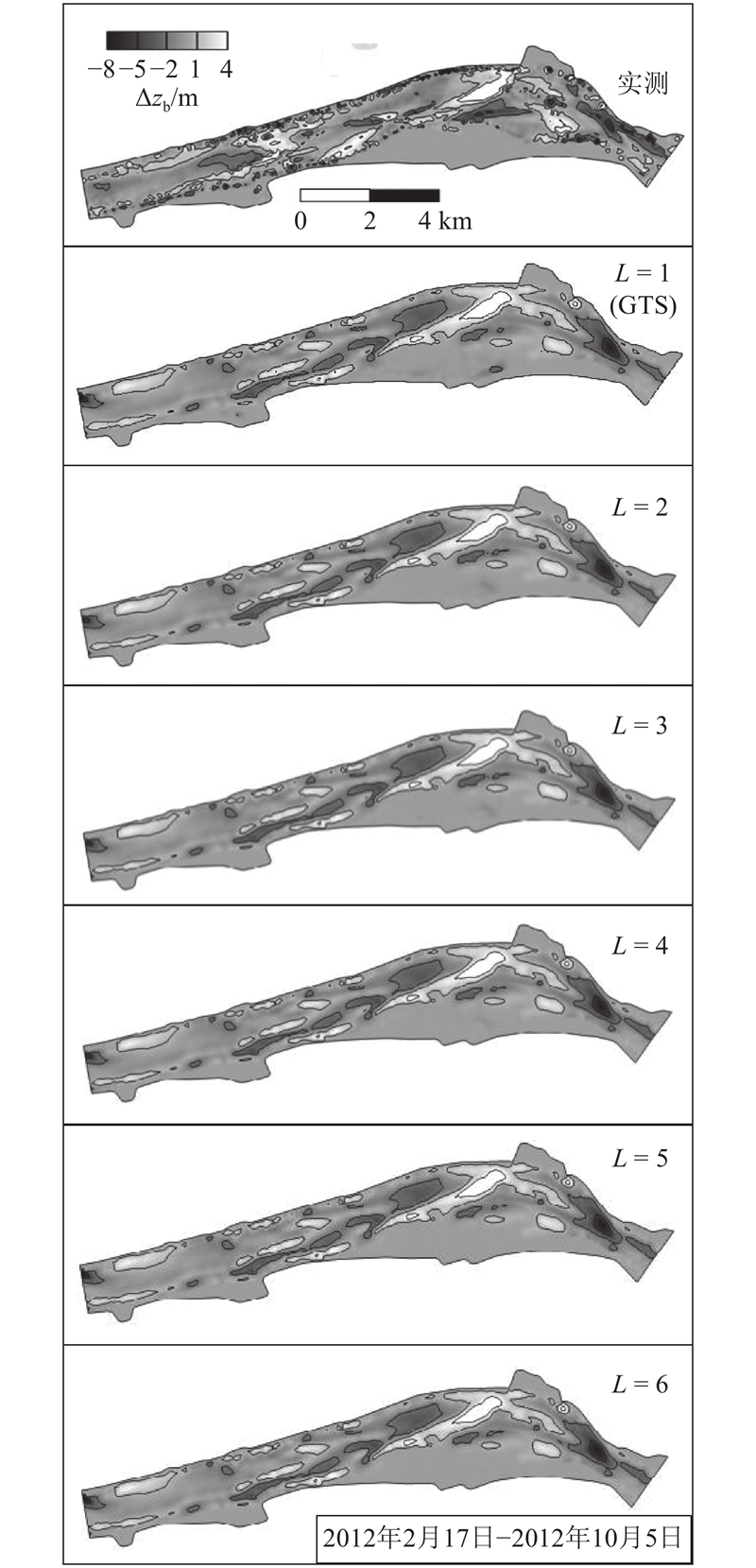
如图8所示为不同级数下2012年10月5日计算水深分布对比图. 可以看出,在不同级数下,水深分布基本一致. 如图9所示为不同L下2012年2月17日—2012年10月5日计算地形冲淤分布对比图. 对比GTS与实测值计算结果可以看出,该算例复演了太平口水道2012年经历洪峰过程下的地形冲淤演变,实测冲刷和淤积位置与计算保持一致,且从冲淤的量级上来看吻合很好. 对比不同级数条件下的计算结果与GTS的结果可以看出,该模型在不同局部时间步长级数下,地形冲淤的结果图像对比上几乎完全一致. 对于实际河道(如本文太平口水道)冲淤的水沙模拟,存在较大的不确定性. 在没有大规模调整参数的情况下,该模型较好地复演了2012年2月—10月太平口水道的实际冲淤过程.
图 8
图 8 计算(用不同级数L)所得太平口水道水深分布
Fig.8 Computed (with different L) water depth for Taipingkou waterway
图 9
图 9 计算(用不同级数L)和实测太平口水道冲淤分布
Fig.9 Computed (with different L) and measured bed erosion and deposition patter for Taipingkou waterway
如表3所示为太平口水道算例组在不同
表 3 局部时间步长技术模拟太平口水道冲淤的成本和精度
Tab.3
| L | Tr | L2(h) | L2(Δzb) | L | Tr | L2(h) | L2(Δzb) | |
| 1(GTS) | 1.00 | 0 | 0 | 4 | 0.21 | 0.18 | 0.20 | |
| 2 | 0.39 | 0.17 | 0.19 | 5 | 0.12 | 0.22 | 0.18 | |
| 3 | 0.31 | 0.17 | 0.20 | 6 | 0.08 | 0.22 | 0.19 |
4. 结 论
(1)算例验证表明,现有局部时间步长技术对于无摩阻地形上溃坝水流的模拟要取较小的级数. 这是由于溃坝水流前锋波速大,水流变化剧烈,前锋两侧单元的局部时间步长级数相差较大,导致计算不稳定. 当地形有摩阻时,溃坝前锋遇到阻力,水流变化减弱,可取的局部时间步长级数可以相应增大. 对于UCL大学的溃坝动床算例,该模型在保证精度的前提下,能够节省68%的计算时间. 如何处理水流变化剧烈界面两侧单元的局部时间步长是需要进一步研究的内容.
(2)模型在太平口水道的应用表明,如果水流交替变化不剧烈,较大的局部时间步长级数不会降低计算精度. 本文模拟了太平口水道近7个月的地形冲淤过程,取局部时间步长级数为6,能够节省92%的计算时间(加速12.5倍).
除局部时间步长技术外,还可以通过并行计算技术(如Open MP、MPI、GPU等)进一步提高计算效率. 本文模型已采用适应于个人计算机的Open MP并行技术.
参考文献
二维溃坝问题的高分辨率数值模拟
[J].DOI:10.3321/j.issn:1006-2467.1999.10.006 [本文引用: 1]
High-resolution numerical simulations for two-dimensional dam-break problems
[J].DOI:10.3321/j.issn:1006-2467.1999.10.006 [本文引用: 1]
An efficient unstructured MUSCL scheme for solving the 2D shallow water equations
[J].
A well-balanced and fully coupled noncapacity model for dam-break flooding
[J].
基于GPU并行计算的浅水波运动数值模拟
[J].
Numerical simulation of shallow water motion based on parallel computation using GPU
[J].
台风暴雨影响区域的溃坝洪水演进数值计算
[J].
Numerical simulation for dam-break flood in hurricane-prone regions
[J].
冰湖溃决模式对下游洪水过程的影响
[J].
Impact of glacial lake breach mechanism on downstream flood progress
[J].
基于守恒稳定格式的二维坡面降雨动力波洪水模型
[J].
Well-balanced two-dimensional dynamic wave model for rainfall-included overland flood
[J].
基于二维浅水方程的滑坡体兴波数值模型
[J].
A numerical model for landslide-generated waves based on two-dimensional shallow water equations
[J].
二维风暴潮实时预报模型及其在杭州湾的应用
[J].DOI:10.3969/j.issn1000-4874.2011.06.014 [本文引用: 1]
2-dimesional real time forecasting model for storm tides and its application in Hangzhou Bay
[J].DOI:10.3969/j.issn1000-4874.2011.06.014 [本文引用: 1]
The surface gradient method for the treatment of source terms in the shallow-water equations
[J].
Unstructured grid finite volume algorithm for shallow-water flow and transport with wetting and drying
[J].DOI:10.1061/(ASCE)0733-9429(2006)132:4(371)
Adaptive quadtree simulation of shallow flows with wet dry fronts over complex topography
[J].DOI:10.1016/j.compfluid.2008.02.008 [本文引用: 1]
Shallow water hydrodynamic models for hypercon-centrated sediment-laden floods over erodible bed
[J].DOI:10.1016/j.advwatres.2005.06.011 [本文引用: 1]
Computational dam-break hydraulics over erodible sediment bed
[J].DOI:10.1061/(ASCE)0733-9429(2004)130:7(689)
Well-balanced high-order centred schemes for non-conservative hyperbolic systems. applications to shallow water equations with fixed and mobile bed
[J].DOI:10.1016/j.advwatres.2009.02.006
Modeling overland flow and soil erosion on nonuniform hillslopes: a finite volume scheme
[J].
Morphological modeling using a fully coupled, total variation diminishing upwind-biased centered scheme
[J].
Fully coupled mathematical modeling of turbidity currents over erodible bed
[J].DOI:10.1016/j.advwatres.2008.07.018
Well-balanced two-dimensional coupled modeling of submarine turbidity currents
[J].
Numerical modelling of riverbed grain size stratigraphic evolution
[J].DOI:10.1016/S1001-6279(14)60048-2 [本文引用: 2]
Integration of a shallow water model with a local time step
[J].DOI:10.3826/jhr.2008.3243 [本文引用: 5]
RKDG2 shallow-water solver on non-uniform grids with local time steps: application to 1D and 2D hydrodynamics
[J].
Local time stepping applied to mixed flow modelling
[J].
Numerical approximations to nonlinear conservation laws with locally varying time and space grids
[J].DOI:10.1090/S0025-5718-1983-0717689-8
High resolution schemes for conservation laws with locally varying time steps
[J].
Local time stepping for modeling open channel flows
[J].DOI:10.1061/(ASCE)0733-9429(2003)129:6(455) [本文引用: 1]
Time accurate local time stepping for the unsteady shallow water equations
[J].DOI:10.1002/(ISSN)1097-0363 [本文引用: 2]
浅水方程的并行化求解
[J].DOI:10.3969/j.issn.0254-0053.2013.04.013
Parallel simulation of shallow water flow
[J].DOI:10.3969/j.issn.0254-0053.2013.04.013
A local time stepping algorithm for GPU-accelerated 2D shallow water models
[J].
Well-balanced numerical modelling of non-uniform sediment transport in alluvial rivers
[J].DOI:10.1016/j.ijsrc.2015.03.002 [本文引用: 1]
Small-scale laboratory dam-break waves on movable beds
[J].
Dam-break flow on mobile bed in abruptly widening channel: experimental data
[J].DOI:10.1080/00221686.2010.548969 [本文引用: 1]