浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(5): 1010-1018 doi: 10.3785/j.issn.1008-973X.2021.05.022

土木工程、水利工程

基于多水文模型预报能力分析的洪水预报

刘登嵩,, 葛路, 许月萍, 张善亮, 江衍铭,

1. 浙江大学 建筑工程学院 水文与水资源工程研究所，浙江 杭州 310058

2. 中国电建集团华东勘测设计研究院有限公司，浙江 杭州 310058

Flood prediction by multi-hydrological models with forecasting ability analysis

LIU Deng-song,, GE Lu, XU Yue-ping, ZHANG Shan-liang, CHIANG Yen-ming,

1. Institute of Hydrology and Water Resources, College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China

2. Power China HuaDong Engineering Co. Ltd, Hangzhou 310058, China

通讯作者: 江衍铭，男，副教授. orcid.org/0000-0002-6303-9303. E-mail： chiangym@zju.edu.cn

收稿日期: 2020-07-22  

基金资助: 浙江省重点研发计划择优委托资助项目（2021C03017）；国家重点研发计划政府间/港澳台重点专项资助项目（2016YFE0122100）；浙江省自然基金重点资助项目（LZ20E090001）

Received: 2020-07-22  

Fund supported: 浙江省重点研发计划择优委托资助项目（2021C03017）；国家重点研发计划政府间/港澳台重点专项资助项目（2016YFE0122100）；浙江省自然基金重点资助项目（LZ20E090001）

作者简介 About authors

刘登嵩（1995—），男，硕士，从事水文预报研究.orcid.org/0000-0002-7106-4218.E-mail：liuds@zju.edu.cn , E-mail：liuds@zju.edu.cn

摘要

为了解决概念性和黑箱模型在小时尺度模拟效果对比中预见期选择的问题，提出利用滞后演算法求解概念性模型预报能力. 在两模型共同预报能力条件下，引入集对分析理论对比新安江模型、土壤水核算与演算（SMAR）模型、倒传递（BP）和Elman神经网络模型模拟效果. 概念性模型预报能力与流域面积成正相关且特定流域的预报能力相对固定，其中金华江和龙泉溪流域的预见期可以分别取第7、3 h；在相同预见期条件下，龙泉溪流域表现最好的是BP模型而最差的是Elman模型，金华江流域表现最好的是新安江模型而最差的是SMAR模型；引入集对分析方法可以从单指标转向更多指标进行综合评价，具有较好的适用性和高效性.

关键词： 黑箱模型 ; 概念性模型 ; 滞后演算法 ; 集对分析 ; 洪水预报

Abstract

The forecast ability of the conceptual model was evaluated by the lag and route method to solve the selection problem of appropriate forecast lead time for both black box and conceptual models with hourly time scale. With the same forecast lead time, the flood forecasting was carried out by using the Xin'an jiang model, soil moisture accounting and routing (SMAR) model, back propagation (BP) neural network and Elman neural network and the performance was analyzed according to the set pair analysis method. The forecast ability of the conceptual models was relatively stable in specific watersheds and was corresponding to the size of the watershed. According to the lag and route method, the forecast lead time values for Jinhua and Longquan watersheds were 7 hours and 3 hours, respectively. Results indicated that the BP model and the Elman model produced the best and the worst performance, respectively, for flood forecasting in Longquan basin under the same forecast lead time. Moreover, the Xin'an jiang model and the SMAR model produced the best and the worst performance, respectively, for flood forecasting in Jinhua basin. The set pair analysis method is able to carry out comprehensive evaluation from single criterion to multiple criteria, indicating that the method has better applicability and higher efficiency.

Keywords： black-box model ; conceptual model ; lag and route method ; set pair analysis ; flood forecasting

PDF (1142KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

刘登嵩, 葛路, 许月萍, 张善亮, 江衍铭. 基于多水文模型预报能力分析的洪水预报. 浙江大学学报(工学版)[J], 2021, 55(5): 1010-1018 doi:10.3785/j.issn.1008-973X.2021.05.022

LIU Deng-song, GE Lu, XU Yue-ping, ZHANG Shan-liang, CHIANG Yen-ming. Flood prediction by multi-hydrological models with forecasting ability analysis. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(5): 1010-1018 doi:10.3785/j.issn.1008-973X.2021.05.022

洪水预报的准确度与可靠性一直是国内外水文领域关注度极高的研究课题，探索精度更高、更稳定的水文模型成为趋势. 水文模型的发展历史最早可以追溯到1851年Mulvaney提出的推理公式[1]，纵观已有水文模型，从反映水文循环规律的过程性和复杂度来看，可以分为黑箱模型、概念性模型和物理模型[2].

倒传递（back propagation，BP）神经网络模型[3]和Elman神经网络模型[4]作为黑箱模型，其在水文应用上的目的主要是进行预报，因此构建水文预报模型首先须确定模型的预见期，之后确定模型的输入输出，最后训练模型进行预报；新安江模型（Xin’an jiang model，XAJ）[5]和土壤水核算与演算模型（soil moisture accounting and routing，SMAR）[6]作为概念性模型，其构建的目的是模拟天然径流过程，因此模型输入输出是同时刻实测数据，在率定好模型后进行预报须引入降雨预报、蒸发、气温等数据，模型自身无预见期，取决于降雨预报预见期. 虽然2类模型在机理上有着本质不同，但是关于它们在小时尺度上的对比研究从未停止.

Badrzadeh等[7]在澳大利亚的Richmond流域上对比ANN、ANFIS、WNN和WNF这4个数据驱动智能模型的预报效果时，构建预见期为1、6、12、24、36、48 h的模型；江衍铭等[8]在龙泉溪流域进行基于ANN的集合预报研究时，构建预见期为1、2、3 h的模型；崔巍等[9]在福建延寿溪流域对比LSTM神经网络和BP神经网络模型预报效果时，构建预见期为1~24 h的模型. 可以看出，前人在对比不同黑箱模型预报效果时，不同预见期对模型结果产生的影响是绕不开的研究方向. 概念性模型之间的对比研究方向则不同，Harris等[10]在研究TOPMODEL模型对小时尺度卫星降雨产生洪水的模拟效果时对比NRCS、CN、Green-Ampt和常用类型4种不同模型结构所得到的结果；Bram等[11]在对比HBV模型和PDM模型小时尺度径流模拟效果时聚焦于不同参数率定方法得到结果间的优劣；张漫莉[12]在对比HBV模型和新安江模型小时尺度径流时主要对比不同改进策略下的HBV模型与新安江模型的优劣；Tayyab等[13]在中国金沙江流域对比新安江、Tank和API模型小时尺度模拟效果时侧重于分析模型选择的重要性. 可以看出，前人在对比不同概念性模型模拟效果时，几乎不提预见期这一概念而着重于模型结构或者模型参数的变化带来的影响. 在概念性模型和黑箱模型进行对比时，须克服一些困难，De Vos等[14]在构建小时尺度ANN模型和HBV模型对比时将预见期简单设定为1、6 h，却未说明选取该预见期的原因，而提出采用多目标替代单目标方法以解决因2类模型差异不能进行直接、明确对比的问题；Banihabib等[15]在对比2类模型在洪水预警中的表现时，通过一定方法确定预警提前期作为DANN和HEC-HMS模型的中间桥梁以实现直接、明确的对比. 可以看出，在进行2类模型的对比时，须寻找中间桥梁才可以将两者联系起来进行直接、明确的对比. 虞慧[16]在江西盘溪水库对小时尺度新安江模型参数进行率定时，将滞后演算法中河道演算滞时从1、3 h中寻优选定为1 h，但文中并未在更大范围内寻优并进一步探索河道演算滞时的现实意义. 故本研究通过深入挖掘滞后演算法原理，赋予河道演算滞时概念性模型预报能力的现实意义，以此作为黑箱模型预见期搭建两者桥梁开展对比研究，并利用粒子群优化算法（particle swarm optimization，PSO）[17]对模型参数进行寻优.

本研究涉及4个模型，选择4个评价指标对模型模拟效果进行评价. Zhang等[18]在多模型评价中虽然选择了多个评价指标却按照单个指标进行对比，其他人则选择了模糊数学[19]、信息理论[20]、DS证据理论[21]、信息熵[22]等理论方法将多指标综合成单指标进行评价，在此将集对分析理论从水资源承载力综合评价体系[23]中引入到水文模型的综合评价中.

本研究通过集对分析方法综合评价黑箱模型和概念性模型在两流域的表现，并通过滞后演算法解决两模型进行对比时黑箱模型预见期的选择问题，研究成果可供相关研究参考.

1. 研究方法

1.1. 滞后演算法

流域降水通过地表截留、地表产流、下渗形成地下径流，之后汇流到河道内，在河道内可以利用滞后演算法、马斯京根法、纳须法等进行河道演算直到下游监测断面. 本研究选取的滞后演算法（lag and route method，LRM）是由Clark[24]提出用于流域汇流计算的，之后赵人俊等[25]对滞后演算法在国内的应用进行了深入探讨. 概化原理如图1所示，可以将原理总结为如下公式：

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   滞后演算法原理

Fig.1   Principle of lag and route method


${Q_{{\rm{T}}}}(t) = {Q_{{\rm{S}}}}(t) + {Q_{{\rm{I}}}}(t) + {Q_{{\rm{G}}}}(t),$

$Q(t) = {C_{\rm{r}}} Q(t{\rm{ - 1}}) + (1 - {C_{\rm{r}}}) {Q_{\rm{T}}}(t - L).$

式中：QT（t）为河网总入流（体积流量），QS（t）为地面径流，QI（t）为壤中流，QG（t）为地下径流，Q为演算后河网监测断面体积流量，Cr为河网消退系数，L为河网平均演算滞时，t为时间序列序号.

由图1可知，LRM的主要作用有2个：由Cr产生“坦化”作用；由L产生“平移”作用，即在率定模型时将河网总入流向后平移L时刻来满足实测数据. 在实际预报中，现时刻降雨产生径流会往后平移L时刻，故L的大小决定监测断面可以在上游降水发生后提前多久知晓洪峰的到来，实现预见期的功能.定义L为概念性模型的预报能力，其只反映径流在河道内的演算，故一般小于主降雨峰停止与监测断面洪峰出现的时间差且存在唯一最优值.

1.2. 粒子群优化算法

PSO算法是Kennedy等[17]提出的基于鸟群捕食行为智能模拟的群集优化算法. 其具有原理简单、参数较少、结构稳定的优点，适用于求解大规模非线性、多峰值复杂优化问题. 刘苏宁等[26]发现PSO算法在率定新安江模型参数的效率上较其他传统方法有明显的提高且稳定性较好.

本研究采取PSO算法，基于MATLAB环境，对XAJ模型和SMAR模型分别在龙泉溪和金华江流域进行参数率定. 其中龙泉溪XAJ模型不同初始种群数目no和迭代次数N试验结果如图2所示. 图中，NSE为纳什系数（Nash Sutcliffe efficiency，NSE）. 可以看出，当初始种群数量增加到40个，迭代次数超过130次之后，纳什系数几乎不变，表明无法通过增加初始种群数目或迭代次数改变模型模拟效果. 本研究综合考虑效率和精度将PSO算法中的初始种群数目取为50个，迭代次数取为150次进行模型参数率定.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   龙泉溪新安江模型不同种群数量和迭代次数下的训练结果

Fig.2   Training results of Xin'an jiang model with different population numbers and iterations in Longquan River


1.3. 集对分析法

集对分析是由赵克勤[27]提出用来处理系统确定性和不确定性相互作用的理论，核心思想是将不确定系统中2个有关联的集合A、B组成集对H，对其进行统一性、差异性和对立性的分析，得到N个特征，其中集合A、B的统一特征、差异特征和对立特征个数分别为S、F、P，三者之和为N. 分别称S/N、F/N、P/N为集合A、B的同一度、差异度和对立度，分别记为a、b、c，有a+b+c=1. 则有联系度的表达式[28]为

$\mu = a + bi + cj = \frac{S}{N} + \frac{F}{N}i + \frac{P}{N}j.$

式中：μ为联系度；i为差异度系数，i∈[–1.0，1.0]；j为对立度系数，一般取j=–1.0.

金菊良等[23]基于集对分析基本理论，建立水资源承载力评价体系，将复杂系统中15个评价指标展示的不确定性进行集合得到直观、清晰的评价等级. 基于此建立包含4个指标的水文模型综合评价体系，通过评价等级及对应联系数实现不同模型间的对比.

评价等级采用置信度准则通过模型结果的1、2、3等级联系数[29]得到：

$h = \mathop {\min }\limits_{{g^ * }} \;\left\{ {{g^ * }|\sum\limits_{g = 1}^{{g^ * }} v > \lambda } \right\}.$

式中：h为结果，包含评价等级和联系数；g为评价等级，分为等级1、2、3；v为分属等级1、2、3的联系数，取值范围为[0，1.0]；λ为置信度，一般范围为[0.5，0.7]，λ越大则评价结果越稳妥，本研究取λ=0.7.

1.4. 评价指标

水文模型在训练过程中采用单一目标函数率定，而在测试阶段时若仍然只采用单一指标进行评价会显得片面，故选取水量平衡误差系数Ivf、NSE、洪峰体积流量误差系数Qe和洪峰出现时间误差Te这4个指标从多角度对模型结果进行相对全面的评价.

${I_{{\rm{vf}}}} = \frac{{\left|\displaystyle\sum\nolimits_t {{Q(t)} - \displaystyle\sum\nolimits_t {{Q_{{\rm{o}}}(t)}}}\right| }}{{\displaystyle\sum\nolimits_t {{Q(t)}} }} \times 100{\text{%}}, $

${\rm{NSE = }}1{\rm{ - }}\frac{{\displaystyle\sum\nolimits_t {{{({Q(t)} - {Q_{{\rm{o}}}}(t))}^2}} }}{{\displaystyle\sum\nolimits_t {{{({Q(t)} - \bar Q)}^2}} }},$

${Q_{\rm{e}}} = \frac{{|{Q_{{\rm{o}},{\rm{m}}}} - {Q_{\rm{m}}}|}}{{{Q_{\rm{m}}}}} \times 100{\text{%}} ,$

${T_{\rm{e}}} = |T({Q_{{\rm{o}},{\rm{m}}}}) - T({Q_{\rm{m}}})|.$

式中： $\bar Q $为实时观测体积流量的均值；Qo(t)为模型预报体积流量；Qm为实测洪峰体积流量；Qo,m为模型预报洪峰体积流量；T（Qo,m）为预报洪峰出现时间；T（Qm）为实测洪峰出现时间.

基于以上4个指标，取Qe≤20%洪水所占总场次比例计算洪峰体积流量相对误差合格率Qer，取Te≤2洪水所占总场次比例计算峰现时间合格率Ter，构建模型评价指标三等级标准[19]如表1所示.

表 1   评价指标各等级标准

Tab.1  Standard of evaluation index grade

评价指标 Ivf NSE Qer Ter
1级 ≤5 ≥0.9 ≥80 ≥80
2级 5~10 0.8~0.9 50~80 50~80
3级 10~50 0~0.8 0~50 0~50

新窗口打开| 下载CSV


1.5. 水文模型

1.5.1. XAJ模型

新安江三水源典型模型[5]，坡面汇流采用直接产流，壤中流和地下汇流采用线性水库演算，河网汇流采用LRM. 龙泉溪流域按照雨量站将流域划分为3个子流域，金华江划分为4个子流域.

1.5.2. SMAR模型

SMAR模型[30]，均采用3层土壤张力水蓄量结构，地表径流采用直接产流、地下径流采用线性水库、河网汇流采用LRM，同样进行子流域划分.

1.5.3. 神经网络模型

神经网络模型参数通过试错法得到[31]，学习率取0.01；训练步数取300；隐含层神经元个数龙泉溪取4个，金华江取5个. 输入因子通过按照不同输入变量组合进行未来1 h径流预报寻优得到[31]，输出因子根据预报能力进行调整.

2. 研究区域及数据

选取浙江省金华江流域和龙泉溪流域作为研究对象. 金华江流域面积为6781 km2，介于117.62°E~121.87°E、28.17°N~30.48°N，多年平均降雨量为1458 mm，流域四周多高山，中间为较平缓盆地，流域森林覆盖率约为59.6%，多为常绿针叶林，表层土壤中沙、淤泥、黏土和砾石约占40.08%，地质条件较好. 龙泉溪流域面积为1440 km2，介于118.75°E~119.23°E、27.28°N~28.48°N，多年平均降雨量为1807.8 mm，地处瓯江源头，坡降为6.32‰~0.97‰，流域内流速较快，洪水持续时间较短，土壤条件和金华江流域类似. 两流域均属于亚热带季风气候，降雨主要集中在3~6月季风雨和9~10月台风雨，降雨强度大，持续时间短，使得两流域成为洪水多发区. 其中金华江流域选取安文、佛堂、新建和国湖4个雨量站降水数据以及金华水文站体积流量数据，龙泉溪选取新建、山溪口和石玄湖3个雨量站降水数据以及龙泉水文站体积流量数据，流域研究范围及站点信息如图3所示. 搜集来自浙江省水文局金华江2006~2015年和龙泉溪流域1994~2003年各10 a逐小时降雨、径流、蒸发数据，从金华江和龙泉溪流域中分别各挑出具有代表性洪水27、30场，按照洪水场次7∶3划分率定和测试阶段.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   研究区域龙泉溪、金华江站点及边界情况

Fig.3   Stations and boundary of Longquan and Jinhua study area


3. 研究结果及讨论

3.1. 流域预报能力分析

通过计算流域逐场洪水主降雨峰止时刻到洪峰出现时刻的平均滞时，将龙泉溪流域L范围设为1~6 h，金华江流域L范围设为1~14 h，通过PSO算法对模型所有参数寻优后，得到模型训练和测试阶段纳什系数随L的变化结果，如图4、5所示.可以看出，模型在训练和测试阶段的纳什系数都存在随L的增加而上升到达顶点后再下降的趋势. 这种趋势表明，SMAR模型和XAJ模型的参数L存在相对固定值，取值太小则在实际径流还未到达监测断面时演算已停止，太大则在实际径流达到监测断面时演算仍在继续，只有当L和实际径流到达监测断面时间一致时，模型模拟效果最佳. 龙泉溪流域XAJ模型和SMAR模型的纳什系数最大值点或与最大值接近且纳什系数-河网平均演算滞时曲线开始快速下降所对应的时刻取3 h，而金华江流域取7 h，故龙泉溪流域L=3 h，金华江流域L=7 h，即各模型在龙泉溪流域的预见期定为3 h，金华江流域为7 h.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   龙泉溪流域不同河网演算滞时NSE结果

Fig.4   NSE Results of different lag times for river networks in Longquanxi basin


图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   金华江流域不同河网演算滞时NSE结果

Fig.5   NSE Results of different lag times for river networks in Jinhuajiang basin


3.2. 基于预报能力分析的各模型结果对比

概念性模型通过PSO率定参数，黑箱模型为了避免局部最优采用100组随机初值进行训练选取最优，得到测试阶段各模型输出结果与实测场次洪水体积流量过程线如图6、7所示.

图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   龙泉溪流域BP、Elman、SMAR和XAJ模型体积流量拟合效果比较

Fig.6   Comparison of fitting effects of runoff for BP, Elman, SMAR and XAJ models in Longquanxi basin


图 7

新窗口打开| 下载原图ZIP| 生成PPT

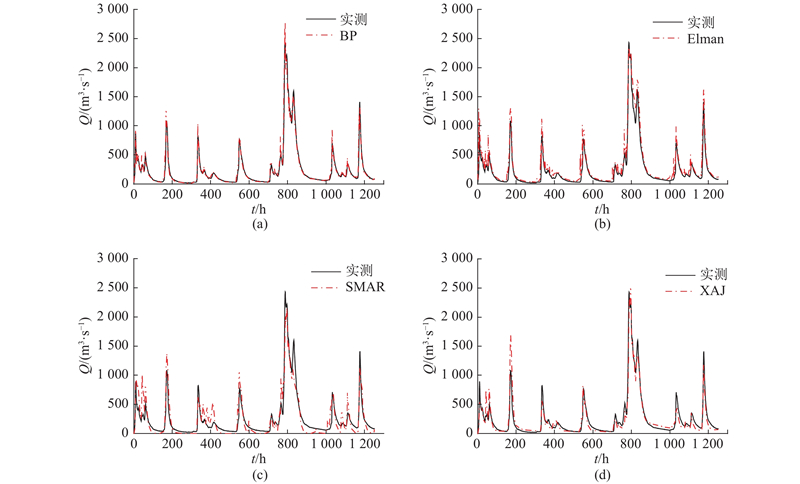
图 7   金华江流域BP、Elman、SMAR和XAJ模型体积流量拟合效果比较

Fig.7   Comparison of fitting effects of runoff for BP, Elman, SMAR and XAJ models in Jinhuajiang basin


由图6（a）、（b）可以看出，BP和Elman神经网络模型对趋势的拟合度均较高，其中后者相对较差且存在整体偏离情况，但是两者都存在过程线“毛边”（相邻数值差别较大）的现象；由图6（c）、（d）可以看出，XAJ和SMAR模型对趋势的整体拟合不如神经网络模型，其中后者还出现几处较大的预报误差，但是两者的过程线较“光滑”（相邻数值差别较小），总体结果较稳定.

由图7（a）、（b）可以看出，相较于龙泉溪流域，BP和Elman神经网络模型的过程线“毛边”现象更严重，影响预报结果准确性；由图7（c）、（d）可以看出，XAJ和SMAR模型继续保持过程线“光滑”的优势并提高了对整体趋势的拟合程度，但是两者对峰值的模拟偏小并且SMAR模型对第1场洪水的模拟误差过大.

3.3. 各模型评价指标结果

各流域不同模型4个评价指标计算结果如表2所示. 表中，Ivf越小表示模型模拟效果越好，其他3个指标都是值越大模型模拟效果越好. 在龙泉溪流域中，只从逐个指标就可以得到各模型从优到次的排名，其中对于NSE、Qe、Te指标，模型表现从优到次分别为BP、XAJ、Elman和SMAR模型，而对于Ivf，从优到次分别为BP、SMAR、XAJ和Elman模型，据此并不能得到完全一致的排名. 在金华江流域中，通过单个指标得到的各模型从优到次的排名更不一致，其中对于Ivf指标，模型排名为Elman、XAJ、BP和SMAR模型；对于NSE指标，模型排名为Elman、BP、XAJ和SMAR模型；对于Qer指标，模型排名为XAJ、Elman、BP和SMAR模型；对于Ter指标，模型排名为XAJ、BP、Elman和SMAR模型. 从上述排名不能较好地综合对比各模型模拟效果. 由以上分析可知，虽然模型模拟效果评价体系从单一指标增加为4个指标可以从不同角度进行评价，但是须通过特定方法将4个指标结果转化成1个指标，才能进行更有效、直观的对比.

表 2   不同流域各模型不同评价指标

Tab.2  Evaluation indexes of varies models in different basins

流域 模型 Ivf NSE Qer Ter
龙泉溪 BP 1.46 0.96 66.67 100.00
Elman 21.46 0.88 44.44 66.67
SMAR 1.86 0.85 33.33 55.56
XAJ 4.58 0.93 55.56 66.67
金华江 BP 3.85 0.88 50.00 50.00
Elman 0.67 0.84 75.00 25.00
SMAR 14.88 0.67 50.00 12.50
XAJ 3.26 0.85 75.00 62.50

新窗口打开| 下载CSV


3.4. 集对分析评价结果

为了解决多指标评价体系在面对相近结果时不能较好地得出综合评价结果的问题引入集对分析理论. 其中等级1、2、3依次表示效果变差；当等级相同时，联系数较大更优；当评价等级为3级时，按照置信度准则联系数应为1，故选取前1、2级累加结果以示区别. 各模型集对分析评价结果如表3所示. 可以看出，龙泉溪流域模型从优到次为BP、XAJ、SAMR、Elman模型，和单指标结果中多数指标排序一致，金华江流域为XAJ、Elman、BP、SMAR模型，可以看出，不同模型在不同流域的适应性不同.

表 3   不同流域各模型集对分析结果

Tab.3  Results of set pair analysis method in different areas

流域 模型 等级 联系数
龙泉溪 BP 1 0.72
Elman 3 0.55
SMAR 2 0.78
XAJ 2 0.86
金华江 BP 2 0.76
Elman 2 0.81
SMAR 3 0.40
XAJ 2 0.87

新窗口打开| 下载CSV


分析黑箱模型，在3 h预见期下，BP模型远优于Elman模型，而在7 h预见期下则正好相反，故推测BP模型适合短预报要求而Elman模型更适合长预报要求. 原因可能是BP神经网络为前馈式网络，隐含层神经元之间无法交流，只有误差反向传播，对较长预报期规律学习效果较差；Elman神经网络则是反馈式网络，隐含层神经元之间可以互相交流，前后输出互有影响，可以更好地学习较长预报期规律.

分析概念性模型，XAJ模型在2个流域均要优于SMAR模型，并且在大流域上优势差距更大；SMAR模型在小流域上表现要远优于大流域，而XAJ模型则在大流域上更优，主要原因可能是两者对流域产汇流物理机制的概化所采取的策略不同. XAJ模型采取蓄满产流而SMAR模型采取超渗产流模式；XAJ模型采用流域蓄水曲线，考虑下垫面不均匀产流面积变化的影响而SMAR模型没有考虑；XAJ模型采用自由水蓄水库划分水源而SMAR模型则采用多蓄水土壤层法划分水源. 因此，对流域产汇流物理机制概化相对完整且准确的XAJ模型比SMAR模型效果更优. 流域面积大则下垫面不均匀性相对减小，故XAJ模型对不均匀性刻画不足的缺点在金华江大流域被削弱反而模拟效果更好，但是对于SMAR模型，更大的体积流量使其物理机制不完整的缺点被放大而模拟效果更差.

对比概念性模型和黑箱模型，在小流域短预报能力条件下，BP神经网络可以占据绝对优势得到更可信的结果；在大流域长预报能力条件下，XAJ模型比BP和Elman神经网络模型表现更好，并且对于XAJ模型，预报能力L稍微延长一点对模型精度降低的影响幅度应该要小于对黑箱模型的，体现了XAJ模型的稳定性.

4. 结　论

为了解决小时尺度下2类模型对比时黑箱模型预见期选择问题，基于河道滞后演算法，采用粒子群优化算法针对不同滞时L进行寻优得到龙泉溪和金华江流域较优滞时，并将其定义为概念性模型在对应流域的预报能力. 在此基础上，构建BP模型、Elman模型、XAJ模型和SMAR模型，采用水量平衡系数、纳什系数、洪峰体积流量合格率和峰现时间合格率4个评价指标，结合集对分析方法对4个模型在2个流域的应用效果展开对比.

（1）通过河道汇流滞后演算法求解的概念性模型预报能力与流域面积成正相关，龙泉溪流域取3 h，金华江流域取7 h. 大流域主降雨峰止到洪峰出现的时间间隔较长，特定流域的预报能力可以因计算方法的不同而适当调整，但在相对固定范围内.

（2）同一模型在不同流域的适用性不同，在龙泉溪流域表现最好的是BP模型，在金华江流域表现最好的是XAJ模型. 黑箱模型中BP和Elman模型因为网络结构的不同而对规律的学习能力不同，其中BP模型适合短预报要求，Elman模型适合较长预报要求；概念性模型中XAJ和SMAR模型因对流域产汇流物理机制的阐述准确性不同表现不一致，XAJ模型比SMAR模型对物理机制的阐述更完整且准确，故能在金华江流域上进行相对准确且稳定地预报.

（3）将集对分析方法从水资源承载力综合评价体系中引入到水文模型模拟效果综合评价体系中，展现了较好的适用性和高效性. 该方法可以帮助研究者将多个不同评价角度指标综合为评价结果，避免单个指标对模型模拟效果评价产生的偶然误差.

从滞后演算法原理出发，提出概念性模型预报能力并将其作为2类模型在特定流域的预报能力，以解决小时尺度下2类模型对比时黑箱模型预见期的选择问题；将集对分析理论引入水文模型多指标综合评价，结果证明其较好的适用性和高效性，为水文预报综合评价提供新理论方法；后续研究在未来还有改进空间，如选择更多类型流域、更高时效和更长时间长度水文相关资料，以提高研究结果的时效性和普适性.

参考文献

MULVANEY T J

On the use of self registering rain and flood gauges

[J]. Proceedings of the Institution of Civil Engineers of Ireland, 1850, 4: 1- 8

URL     [本文引用: 1]

周琦, 朱跃龙, 陆佳民, 等

组合式水文模型建模方法综述

[J]. 国外电子测量技术, 2020, 39 (2): 11- 18

URL     [本文引用: 1]

ZHOU Qi, ZHU Yue-long, LU Jia-min, et al

Overview of combined hydrological modeling methods

[J]. Foreign Electronic Measurement Technology, 2020, 39 (2): 11- 18

URL     [本文引用: 1]

RUMELHART D E, HINTON G E, WILLIAMS R J

Learning representations by back-propagating errors

[J]. Nature, 1986, 323 (9): 533- 536

URL     [本文引用: 1]

CHEN P A, CHANG L C, CHANG F J

Reinforced recurrent neural networks for multi-step-ahead flood forecasts

[J]. Journal of Hydrology, 2013, 497: 71- 79

DOI:10.1016/j.jhydrol.2013.05.038      [本文引用: 1]

赵人俊. 流域水文模拟: 新安江模型与陕北模型[M]. 北京: 水利电力出版社, 1984: 106-130.

[本文引用: 2]

O"CONNELL P E, NASH J E, FARRELL J P

River flow forecasting through conceptual models part II-the Brosna catchment at Ferbane

[J]. Journal of Hydrology, 1970, 10 (4): 317- 329

DOI:10.1016/0022-1694(70)90221-0      [本文引用: 1]

BADRZADEH H, SARUKKALIGE R, JAYAWARDENA A W

Hourly runoff forecasting for flood risk management: application of various computational intelligence models

[J]. Journal of Hydrology, 2015, 3 (529): 1633- 1643

URL     [本文引用: 1]

江衍铭, 张建全, 明焱

集合神经网络的洪水预报

[J]. 浙江大学学报: 工学版, 2016, 50 (8): 1471- 1481

URL     [本文引用: 1]

CHIANG Yen-ming, ZHANG Jian-quan, MING Yan

Flood forecasting by ensemble neural networks

[J]. Journal of Zhejiang University: Engineering Science, 2016, 50 (8): 1471- 1481

URL     [本文引用: 1]

崔巍, 顾冉浩, 陈奔月, 等

BP与LSTM神经网络在福建小流域水文预报中的应用对比

[J]. 人民珠江, 2020, 41 (2): 74- 84

URL     [本文引用: 1]

CUI Wei, GU Ran-hao, CHEN Ben-yue, et al

Comparison of BP and LSTM neural network for hydrologic forecasting of a small watershed in Fujian

[J]. Pearl River, 2020, 41 (2): 74- 84

URL     [本文引用: 1]

HARRIS A, HOSSAIN F

Investigating the optimal configuration of conceptual hydrologic models for satellite-rainfall-based flood prediction

[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5 (3): 532- 536

DOI:10.1109/LGRS.2008.922551      [本文引用: 1]

BRAM V A F, BRUNO S, VALENTIJN R N P

Internal validation of conceptual rainfall-runoff models using baseflow separation

[J]. Journal of Hydrology, 2010, 381 (1/2): 158- 173

URL     [本文引用: 1]

张漫莉

改进的HBV模型与新安江模型在武江流域洪水预报中的应用比较

[J]. 人民珠江, 2014, 35 (1): 34- 37

DOI:10.3969/j.issn.1001-9235.2014.01.009      [本文引用: 1]

ZHANG Man-li

Comparison of improved HBV model and Xin'anjiang model in flood forecasting of Wujiang river basin

[J]. Pearl River, 2014, 35 (1): 34- 37

DOI:10.3969/j.issn.1001-9235.2014.01.009      [本文引用: 1]

TAYYAB M, ZHOU J Z, ZENG X F, et al. Optimal application of conceptual rainfall-runoff hydrological models in the Jinshajiang river basin, China [C]// Proceedings of RSHS and ICGRHWE 2015. Portugal: [s. n], 2015, 368: 227-232.

[本文引用: 1]

DE VOS N J, RIENTJES T H M

Multi-objective performance comparison of an artificial neural network and a conceptual rainfall-runoff model

[J]. Hydrological Sciences Journal, 2007, 52 (3): 397- 413

DOI:10.1623/hysj.52.3.397      [本文引用: 1]

BANIHABIB M E, REVELLI R

Performance of conceptual and black-box models in flood warning systems

[J]. Cogent Engineering, 2016, 3: 1- 13

DOI:10.1080/2331186X.2016.1139438      [本文引用: 1]

虞慧. 新安江模型在中型水库洪水预报中的应用研究[D]. 南昌: 江西师范大学, 2010.

[本文引用: 1]

YU Hui. Study on the application of Xin’anjiang model for forecasting in medium-sized reservoir[D]. Nanchang: Jiangxi Normal University, 2010.

[本文引用: 1]

KENNEDY J, EBERHART R. Particle swarm optimization [C]// 1995 IEEE International Conference on Neural Networks Proceedings. Piscataway: IEEE, 1995: 1942-1948.

[本文引用: 2]

ZHANG L, YANG X Y

Applying a multi-model ensemble method for long-term runoff prediction under climate change scenarios for the Yellow River Basin, China

[J]. Water, 2018, 301: 1- 15

[本文引用: 1]

盖永岗, 熊立华, 万民, 等. 基于模糊数学的水文预报综合评价方法 [C]// 环境变化与水安全——第五届中国水论坛论文集. 南京: 中国水利水电出版社, 2007: 141-144.

[本文引用: 2]

GAI Yong-gang, XIONG Li-hua, WAN Min, et al. Comprehensive evaluation method of hydrological forecast based on fuzzy mathematics [C]// Environmental Change and Water Security: the 5th Chinese Water Forum. Nanjing: China Water and Power Press, 2007: 141-144.

[本文引用: 2]

WEIJS S V, SCHOUP G, GIESEN N

Why hydrological predictions should be evaluated using information theory

[J]. Hydrology and Earth System Sciences, 2010, 14: 2545- 2558

DOI:10.5194/hess-14-2545-2010      [本文引用: 1]

肖洁, 罗军刚, 张晓

基于DS证据理论的多模型洪水预报方案优选

[J]. 西北农林科技大学学报: 自然科学版, 2013, 41 (9): 193- 199

URL     [本文引用: 1]

XIAO Jie, LUO Jun-gang, ZHANG Xiao

DS evidence theory based scheme optimization of multi-model flood forecasting

[J]. Journal of Northwest A and F University: Natural Science Edition, 2013, 41 (9): 193- 199

URL     [本文引用: 1]

石继海, 宋松柏, 李航

中长期径流预报模型优选研究

[J]. 西北农林科技大学学报: 自然科学版, 2019, 47 (7): 174- 154

URL     [本文引用: 1]

SHI Ji-hai, SONG Song-bai, LI Hang

Optimization of mid-long term runoff forecasting models

[J]. Journal of Northwest A and F University: Natural Science Edition, 2019, 47 (7): 174- 154

URL     [本文引用: 1]

金菊良, 陈磊, 陈梦璐, 等

基于集对分析和风险矩阵的水资源承载力评价方法

[J]. 人民长江, 2018, 49 (7): 35- 41

URL     [本文引用: 2]

JIN Ju-liang, CHEN Lei, CHEN Meng-lu, et al

Evaluation method of water resources carrying capacity based on set pair analysis and risk matrix

[J]. Yangtze River, 2018, 49 (7): 35- 41

URL     [本文引用: 2]

CLARK C O

Flood-storage accounting

[J]. Eos, Transactions American Geophysical Union, 1994, 25 (6): 1014- 1030

[本文引用: 1]

赵人俊, 王厥谋

论滞后演算法

[J]. 水文, 1983, (5): 30- 34

URL     [本文引用: 1]

ZHAO Ren-jun, WANG Jue-mou

A discussion of the lag and route method

[J]. Journal of China Hydrology, 1983, (5): 30- 34

URL     [本文引用: 1]

刘苏宁, 甘泓, 魏国孝

粒子群算法在新安江模型参数率定中的应用

[J]. 水利学报, 2010, 41 (5): 537- 544

URL     [本文引用: 1]

LIU Su-ning, GAN Hong, WEI Guo-xiao

Application of PSO algorithm to calibrate the Xin’anjiang hydrological model

[J]. Journal of Hydraulic Engineering, 2010, 41 (5): 537- 544

URL     [本文引用: 1]

赵克勤. 集对分析及其初步应用[M]. 杭州: 浙江科学技术出版社, 2000.

[本文引用: 1]

段新光, 栾芳芳

基于模糊综合评判的新疆水资源承载力评价

[J]. 中国人口·资源与环境, 2014, 24 (Suppl. 1): 119- 122

URL     [本文引用: 1]

DUAN Xin-guang, LUAN Fang-fang

Evaluation of water resources carrying capacity in xinjiang based on fuzzy comprehensive model

[J]. China Population, Resources and Environment, 2014, 24 (Suppl. 1): 119- 122

URL     [本文引用: 1]

XIN G, YOU H E, XIAO Y I

Attribute measure recognition approach and its applications to emitter recognition

[J]. Science China Information Sciences, 2005, 48 (2): 225- 233

DOI:10.1360/122004-82      [本文引用: 1]

王光生, 夏士谆

SMAR模型及其改进

[J]. 水文, 1998, (Suppl. 1): 28- 30

URL     [本文引用: 1]

WANG Guang-sheng, XIA Shi-chun

SMAR model and its improvement

[J]. Journal of China Hydrology, 1998, (Suppl. 1): 28- 30

URL     [本文引用: 1]

张建全. 基于人工神经网络的集合洪水预报研究[D]. 杭州: 浙江大学, 2016.

[本文引用: 2]

ZHANG Jian-quan. Ensemble flood forecasting by artificial neural network[D]. Hangzhou: Zhejiang University, 2016.

[本文引用: 2]

/

〈 〉