浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(5): 991-998 doi: 10.3785/j.issn.1008-973X.2021.05.020

材料与化学工程

Al2O3纳米流体液滴撞击壁面的动力学行为数值研究

胡定华,, 刘诗雨

南京理工大学 能源与动力工程学院，江苏 南京 210094

Numerical study on dynamic behaviors of Al2O3 nanofluid droplet impacting on solid wall

HU Ding-hua,, LIU Shi-yu

School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

收稿日期: 2020-05-12  

基金资助: 国家自然科学基金青年基金资助项目（51706102）；中央高校基本科研业务费专项资金资助项目（30917011325）

Received: 2020-05-12  

Fund supported: 国家自然科学基金青年基金资助项目（51706102）；中央高校基本科研业务费专项资金资助项目（30917011325）

作者简介 About authors

胡定华（1986—），男，讲师，博士，从事微尺度相变散热研究.orcid.org/0000-0002-2725-7389.E-mail：dhhu@njust.edu.cn , E-mail：dhhu@njust.edu.cn

摘要

针对纳米流体液滴撞击固体壁面的动力学行为，建立基于相场方法描述液滴动态过程的二维数值模型，引入Kistler动态接触角模型以模拟铺展过程中液滴动态接触角变化以及三相接触线的迁移. 通过模拟分析液滴铺展因子、无量纲高度的变化研究不同纳米颗粒体积分数、惯性力和液滴直径等因素对水基Al2O3纳米流体液滴撞击壁面的铺展回缩过程的影响机制. 结果表明：超过一定体积分数的纳米颗粒使流体表现出明显的剪切稀化特性，增加液滴的黏性耗散，抑制液滴的铺展回缩过程；液滴撞击速度的增加会增大其撞击壁面时最大铺展直径和达到稳定状态的耗时，直径的增加使液滴振荡周期加长；体积分数为4%的纳米颗粒可以抑制上述两者带来的影响，使液滴更快到达稳定状态.

关键词： 纳米流体 ; 液滴 ; 撞击壁面 ; 体积分数 ; 相场方法

Abstract

The dynamical behavior of nanofluid droplet impacting on the solid wall was numerically studied. A two-dimensional numerical model based on the phase-field method was established, and the Kistler dynamic contact angle model was introduced to describe the evolution of droplet contact angle and three-phase contact line during spreading. The influences of nanoparticle volume fraction, inertia force and droplet diameter on the spreading and retraction behaviors of water-based Al2O3 nanofluid droplets were studied in terms of spreading factor and dimensionless height. Results indicated that the nanoparticles with volume fraction over a certain value made the fluid exhibit obvious shear-thinning characteristics, which can increase the viscous dissipation of droplets and suppress the spreading and retraction process of droplets. The increase of droplet initial velocity would increase the maximum spreading diameter and the time to reach the stable state when it impacts on the solid surface, while the increase of droplet diameter would lengthen the oscillation period of the droplet. It is also found that the nanoparticles of 4% volume fraction can suppress the influence of increase of droplet initial velocity and diameter, and help the droplet faster to reach stable state.

Keywords： nanofluid ; droplet ; surface impingement ; volume fraction ; phase-field method

PDF (1277KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

胡定华, 刘诗雨. Al2O3纳米流体液滴撞击壁面的动力学行为数值研究 . 浙江大学学报(工学版)[J], 2021, 55(5): 991-998 doi:10.3785/j.issn.1008-973X.2021.05.020

HU Ding-hua, LIU Shi-yu. Numerical study on dynamic behaviors of Al2O3 nanofluid droplet impacting on solid wall . Journal of Zhejiang University(Engineering Science)[J], 2021, 55(5): 991-998 doi:10.3785/j.issn.1008-973X.2021.05.020

液滴撞击固体壁面在很多领域有着广泛的应用，如3D打印[1]、喷墨印刷[2]、农药喷洒[3]、质谱分析[4]等. 液滴撞击壁面后其动态行为较复杂，存在沉积铺展、飞溅、回缩破碎、反弹等[5-6]多种形式，是受各种因素[7-8]影响导致的，包括固体壁面的表面特性（温度、润湿性、粗糙度等），液滴的性质（密度、黏度、表面张力作用等）和液滴撞击时的状态（液滴直径大小、撞击速度）. 这些因素使得分析液滴撞击壁面后动态行为的规律更加复杂，也因此吸引了较多学者对此类现象展开研究[9-10].

Šikalo等[11-12]通过改变固体壁面的倾斜角，来研究壁面相对液滴角度对其撞击壁面后动力学行为的影响；李维仲等[13]利用高速摄影装置观察液滴撞击壁面过程，分析固体表面材料、流体物性对撞击过程的影响；An等[14]通过实验，研究非牛顿流体液滴在不同亲疏水性固体表面的冲击动力学，并提出预测液滴最大铺展直径的数学模型. 在数值模拟方面，Gupta等[15]提出三维格子玻尔兹曼方法（lattice Boltzmann method，LMB），以模拟液滴撞击固体表面时的扩散破碎行为；Fujimoto等[16]用流体体积法（volume of fluid，VOF）跟踪自由液滴表面，模拟液滴在低速下撞击固体表面的现象，并与实验结果比较.

纳米颗粒的加入改变流体的物性，如密度、黏度、表面张力等，从而导致纳米流体液滴撞击壁面时的动态行为更加复杂. 刘海龙等[17]通过实验研究碳纳米管流体液滴在不同韦伯数下撞击壁面的动态过程，总结其铺展沉积的规律；Hao等[18]观察研究二氧化硅-乙二醇流体液滴撞击疏水表面后的弹跳现象，认为纳米颗粒抑制液滴在固体表面弹跳的原因可能是其增加了液滴黏性耗散；Shen等[19]用水平集的方法模拟对比纳米石墨粉-环氧树脂流体液滴和多壁纳米管-环氧树脂流体液滴撞击固体壁面的铺展过程.

纳米流体的应用日益广泛，如在喷雾冷却领域[20-21]，纳米颗粒的加入会进一步强化传热，使冷却效率提高，但喷雾液滴撞击壁面的动态过程也会在一定程度上影响冷却效果. 针对纳米流体液滴撞击固体壁面动态过程的分析是具有实际现实意义的. 目前，相较于纯水液滴，关于纳米流体液滴撞击固体壁面的动力学特性研究相对较少，且影响其动态过程的相关条件机理尚不明确，须进一步研究探讨.

本研究基于相场方法对水基氧化铝纳米流体液滴撞击固体壁面的动力学行为特征展开数值模拟研究，通过分析液滴撞击过程中的铺展因子、无量纲高度来研究纳米颗粒体积分数、惯性力和液滴直径对撞击后液滴动力学行为和铺展回缩过程的影响机制.

1. 物理及数学模型

1.1. 物理模型

1.1.1. 几何参数

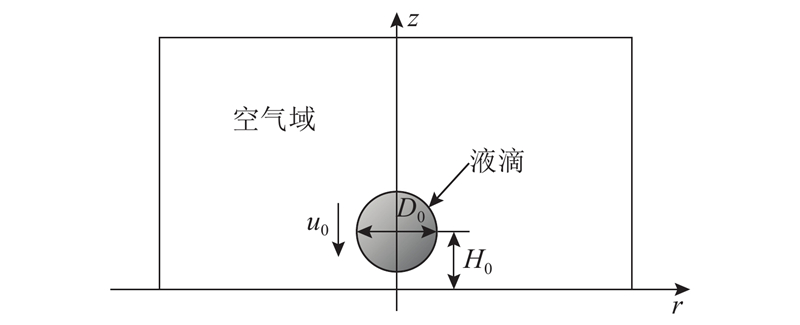
所研究的水基氧化铝纳米流体液滴撞击固体壁面的几何模型如图1所示. 图中， ${D_0}$为纳米流体液滴直径， ${H_0}$为初始时刻液滴距离固体壁面的高度， ${u_0}$为给定的下落初始速度.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   液滴撞击固体表面物理模型

Fig.1   Physical model of liquid droplet impacting solid surface


1.1.2. 物性参数

纳米颗粒的加入会改变流体的密度 $\rho $、黏度 $\mu $与表面张力 $\sigma $，影响程度与纳米颗粒体积分数 ${\varphi _{\rm{p}}}$相关.

水基氧化铝纳米流体的密度可以用近似公式[22]计算：

$\rho = (1 - {\varphi _{\rm{p}}}){\rho _{\rm{f}}} + {\rho _{\rm{p}}}.$

式中： ${\rho _{\rm{f}}}$、 ${\rho _{\rm{p}}}$分别为基液和纳米颗粒的密度.

使用幂律模型表征水基氧化铝纳米流体的流变特性：

$\mu = m{\gamma ^{n - 1}}.$

式中： $m$为稠度系数， $n$为无量纲幂律指数， $\gamma $为剪切速率. 幂律参数值参考文献[23]，如表1所示. 文献中的Al2O3纳米流体虽有Fe的添加，但是其体积分数仅为0.003%，相较于Al2O3纳米颗粒体积分数，相差3个数量级，因此本研究忽略Fe对Al2O3纳米流体整体流变性质的影响.

表 1   纳米流体液滴幂律参数

Tab.1  Power-law parameters of nanodroplet

$\varphi _{\rm{p}} $/% m n
1 0.0060 0.599
2 0.0118 0.614
3 0.0458 0.641
4 0.2562 0.678

新窗口打开| 下载CSV


纳米流体液滴的表面张力可以用近似公式[24-25]计算：

${\sigma }/{{{\sigma _{\rm{f}}}}} = - 1.022\;19{\varphi _{\rm{p}}} + 0.912\;27.$

式中： $\sigma $、 ${\sigma _{\rm{f}}}$分别为纳米流体和基液在指定温度下的表面张力. 在25 ℃时纯水的表面张力为73 mN/m，即为 ${\sigma _{\rm{f}}}$；当纳米颗粒体积分数为1%、2%、3%、4%时，其表面张力分别为65.85、65.10、64.36、63.61 mN/m. 在室温25 ℃，标准大气压条件下，空气的物性参数保持不变，密度为1.146 kg/m3，黏度为1.848×10−5 Pa·s.

1.1.3. 无量纲参数

为了分析纳米流体液滴撞击固体表面的系列过程，引入无量纲参数进行分析讨论，包括韦伯数 $We = \rho u_0^2{D_0}{\rm{/}}\sigma $；无量纲时间 $\tau = $ $ t{u_0}{\rm{/}}{D_0}$；铺展因子 ${D^*} = D(t){\rm{/}}{D_0}$， $D(t)$为液滴在撞击壁面时的瞬时直径；无量纲高度 ${H^*} = H(t){\rm{/}}{D_0}$， $H(t)$为液滴撞击壁面时中心处的液膜高度.

1.2. 数学模型

采用相场方法模拟液滴两相动力学行为，并考虑液滴撞击壁面时的动态接触角变化，使模拟过程更加准确且接近实际.

1.2.1. 相场方法

相场方法[26]使用Cahn-Hilliard方程（包含一个化学势）来表示分隔两相的扩散界面. 界面的轮廓和厚度取决于分子的吸引力和随机分子运动，并由无量纲相场变量 $\phi $控制， $\phi $∈[−1.0，1.0]. 在求解时，Cahn-Hilliard方程一分为二：

$ \frac{{\partial \phi }}{{\partial t}} + {{u}} \cdot \nabla \phi = \nabla \cdot \frac{{\alpha \lambda }}{{{\varepsilon ^2}}}\nabla \psi , $

$ \psi = - \nabla \cdot {\varepsilon ^2}\nabla \phi + ({\phi ^2} - 1)\phi . $

式中： ${{u}}$为流体速度； $\alpha $为迁移速率，决定Cahn-Hilliard扩散的时间尺度； $\lambda $为混合能量密度； $\varepsilon $为界面厚度参数； $\psi $为相场助变量.

将混合能量密度、界面厚度与表面张力系数相关联：

$\sigma = \frac{{2\sqrt 2 }}{3}\frac{\lambda }{\varepsilon }.$

在此模型中，空气和流体的体积分数分数分别为

${\varphi_{\rm{f1}}} = {{(1 - \phi) }}/{2},$

${\varphi_{\rm{f2}}} ={{(1 + \phi) }}/{2}.$

1.2.2. 控制方程

不可压缩纳维-斯托克斯方程（包括表面张力）描述质量和动量传递：

$\nabla \cdot {{u}} = 0,$

$\rho \left( {\frac{{\partial {{u}}}}{{\partial t}}} \right) + \rho ({{u}} \cdot \nabla ){{u}} = \nabla \left[ { - p{{I}} + \mu \left( {\nabla {{u}} + {(\nabla {{u}})^{\rm{T}}}} \right)} \right] + \rho {{g}} + {{{F}}_{{\rm{st}}}}.$

式中： $p$为液滴内部压力， ${{{F}}_{{\rm{st}}}}$为表面张力.

${{{F}}_{{\rm{st}}}} = G\nabla \phi .$

其中， $G$为化学式.

$G = \lambda \left[ { - {\nabla ^2}\phi + \frac{{\left( {{\phi ^2} - 1} \right)\phi }}{{{\varepsilon ^2}}}} \right] = \frac{\lambda }{{{\varepsilon ^2}}}\psi .$

1.2.3. 边界条件

指定模型（见图1）顶端和左右两侧为开放边界以模拟液滴周围无限空间的环境条件：

$\left.\begin{array}{l} [ - p{{I}} + {{K}}]{{n}} = - ({f_0} + {p_{{\rm{hyd}}}}){{n}},\\ {{K}}=\mu(\nabla {{u}}+(\nabla {{u}})^{\rm{T}}). \end{array}\right\}$

式中： ${f_0}$为法向应力， ${p_{{\rm{hyd}}}}$为静水补偿压力， ${{n}}$为法向量.

考虑到液滴撞击壁面过程的对称性，为了减小计算量，采用二维轴对称模型，取r=0为对称轴，取轴对称边界条件.

固体壁面为润湿壁，为了更加准确地模拟液滴撞击固体表面的动态过程，针对液滴的铺展过程采用Kistler动态接触角模型[27]，通过跟踪液滴与壁面接触的三相线，模拟过程中动态接触角的变化. 描述Kistler模型的方程如下：

${\theta _{\rm{d}}} = {f_{\rm{H}}}\left[ {{\rm{Ca}} + f_{\rm{H}}^{ - 1}({\theta _{\rm{e}}})} \right].$

式中： ${\theta _{\rm{e}}}$为静态接触角， ${\rm{Ca}}$为毛细数， ${f_{\rm{H}}}$、 $f_{\rm{H}}^{ - 1}$分别为是霍夫曼函数和其反函数. 纳米颗粒的体积分数对液滴静态接触角的影响相对较小[28-30]，在本研究模型中，取液滴的静态接触角均为60°. ${f_{\rm{H}}}$可以表示为

$ {f_{\rm{H}}}{\rm{ = }}\arccos \;\left\{ {1 - 2\tanh \;\left[ {5.16{{\left( {\frac{x}{{1 + 1.31{x^{0.99}}}}} \right)}^{0.706}}} \right]} \right\}. $

${\rm{Ca}}$与接触线速度 ${U_{\rm{cl}}}$有关，表达式如下：

${\rm{Ca}} = {{\mu {U_{\rm{cl}}}}}/{\sigma }.$

2. 模型求解与验证

2.1. 模型求解

使用基于有限元多物理场数值软件COMSOL Multiphysics5.4的CFD模块完成模型计算，模型计算域宽为22 mm，高为10 mm. 为了提高计算效率，节约计算资源，在液滴界面处自适应网格细化，最大网格尺寸不超过5×10−5 μm，在保证有效性的同时，提高数值模拟的精确性，如图2所示为计算域的网格划分. 在液滴撞击壁面前，适当加大时间步的计算间隔，而在撞击过程中，重新调整时间步，使撞击过程的模拟得到更多的计算资源. 瞬态求解器采用向后差分的方法，自动约束计算时的最大步长，考虑使用全耦合的方法求解非线性方程组，以提高模型的收敛性. 设置阻尼因子为0.9，且在每个时间步更新求解时的雅可比矩阵，同时采用Anderson加速非线性收敛.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   液滴网格细化

Fig.2   Mesh refinement for droplet


2.2. 网格无关性及模型验证

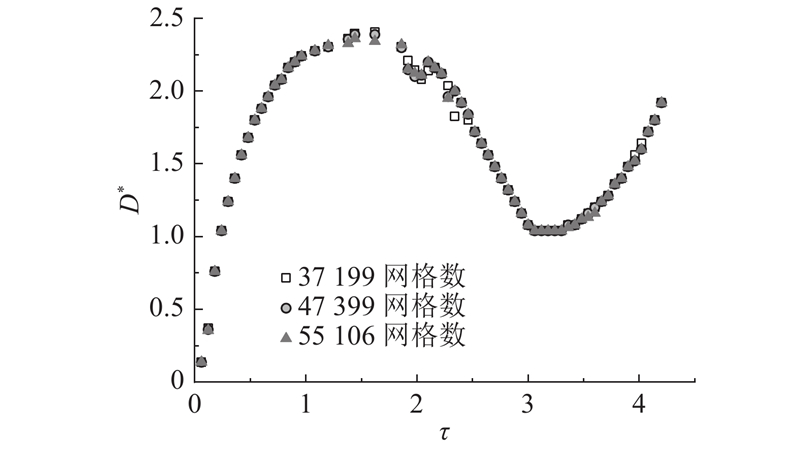
为了验证数值计算结果与网格的无关性，计算网格数分别为37119、47399、55106时的液滴铺展直径变化. 如图3所示为纳米颗粒体积分数为1%的液滴撞击固体壁面时无量纲直径随时间的变化曲线. 可以看出，3种网格数的求解结果基本重合. 考虑到计算效率，选择网格数为47399的网格划分模型进行研究.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   网格无关性验证

Fig.3   Verification of grid independence


为了验证本研究模型计算结果的准确性，分别对相同实验条件下的纯水液滴、符合幂律模型的非牛顿流体液滴和纳米流体液滴这3种液滴[31-33]撞击固体壁面计算结果进行验证，结果如图4所示. 图中，左侧为实验结果，右侧为模拟结果. 如图4（a）所示为纯水液滴撞击疏水壁面的铺展过程，并与相同条件下实验[33]进行对比；如图4（b）所示为选择实验[32]中m=0.208，n=0.4的X025流体液滴进行模拟对比的结果；如图4（c）所示为在实验[31]条件下，模拟纳米颗粒质量分数为2%的水基SiO2纳米流体液滴撞击壁面的铺展行为. 该纳米流体的幂律值分别为m=0.0036、n=0.24，可以参考文献[31]中的剪切度曲线拟合得到. 可以看出，3种液滴的模拟结果与实验结果基本一致，两者在相同时间点的液滴形态高度吻合，说明本研究建立的模型可以较为准确地模拟流变特性符合幂律模型的液滴撞击固体壁面的动力学行为. 水基Al2O3纳米流体的黏度与水基SiO2纳米流体黏度有相似的特征，即均满足幂律模型[23]，因此本研究所建立的模型能够准确模拟水基Al2O3纳米流体液滴动力学行为.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   液滴撞击壁面实验结果[31-33]和本研究所建模型模拟结果的验证对比

Fig.4   Comparison and validation of droplet impingement experiments results[31-33] and simulation results based on proposed model


3. 模拟结果与讨论

通过改变液滴的纳米颗粒体积分数、惯性力和液滴直径，研究这3种因素对撞击后液滴铺展和回缩过程的影响.

3.1. 纳米流体体积分数对液滴撞击过程影响

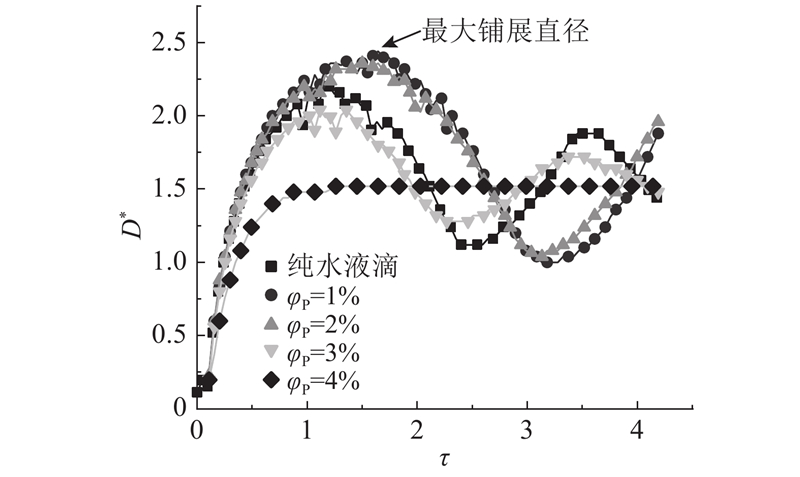
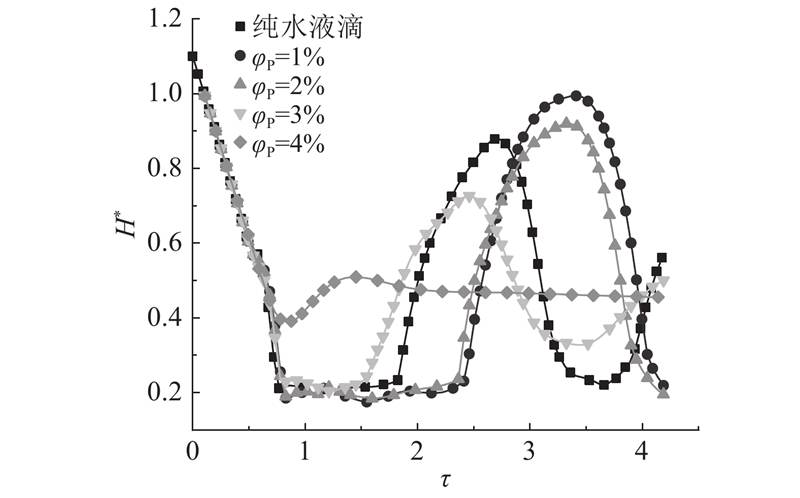
液滴中纳米颗粒的加入会导致其物性发生变化，从而影响液滴撞击固击固体壁面的动态过程. 为了研究纳米颗粒体积分数对纳米流体液滴撞体表面铺展过程的影响，取液滴初始直径D0=2.5 mm，初速度均为0.3 m/s，分别对纳米颗粒体积分数为1%、2%、3%、4%的液滴和纯水液滴的撞击动力学行为进行模拟. 如图5、6所示为相应纳米流体液滴撞击固体壁面时的铺展因子和无量纲高度随时间的变化曲线. 可以看出，纳米颗粒体积分数为1%和2%的纳米流体液滴最大铺展因子大于纯水液滴，且其铺展过程时间也更长，可能是因为此时纳米颗粒体积分数较小，纳米流体液滴基本表现为牛顿流体，而由于纳米颗粒的加入，纳米流体液滴的表面张力减少，更有利于铺展的进行.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   纯水与不同颗粒体积分数的纳米流体液滴铺展因子变化曲线

Fig.5   Variation curves of spreading factor for pure water droplets and nanofluid droplets with different nanoparticle volume fractions


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   纯水与不同颗粒体积分数的纳米流体液滴无量纲高度变化曲线

Fig.6   Variation curves of dimensionless height for pure water droplets and nanofluid droplets with different nanoparticle volume fractions


纳米颗粒的加入除了使得流体表面张力减小外，还会使流体黏性增加，而黏性的增加会抑制其铺展过程，这两方面的影响相互制衡. 由图5、6可以看出，随着纳米颗粒体积分数继续增加到3%、4%，液滴的铺展因子和无量纲高度减小，铺展时间也更短，开始回缩的时间点早于纯水液滴. 同时，纳米流体液滴更不易发生垂直方向上的振荡，特别是当纳米颗粒体积分数为4%时，液滴的铺展和回缩过程几乎被完全抑制，撞击后液滴基本没有出现震荡行为.

从微观角度分析，是由于纳米粒子与水分子的相互作用（包括分子间吸引以及摩擦），随着相对较多纳米颗粒的加入，纳米颗粒增强了纳米流体液滴的内部凝聚力，使得液滴的铺展受到抑制[34]，可以更快到达最大铺展直径状态；从宏观角度来看，纳米颗粒浓度的增加会使流体黏度升高，且流体表现出非牛顿特性，纳米流体黏度随剪切速率变化的这一流变特性也会进一步抑制液滴的铺展回缩过程，增加液滴的黏性耗散[18, 35]. 当纳米粒子体积分数增加到3%后，由于纳米流体的剪切稀化特性增强，液滴铺展过程中速度逐渐减小流体黏度升高，铺展速度能够更快降到最低，铺展时间也相对变更短.

3.2. 纳米流体液滴惯性力对液滴撞击过程影响

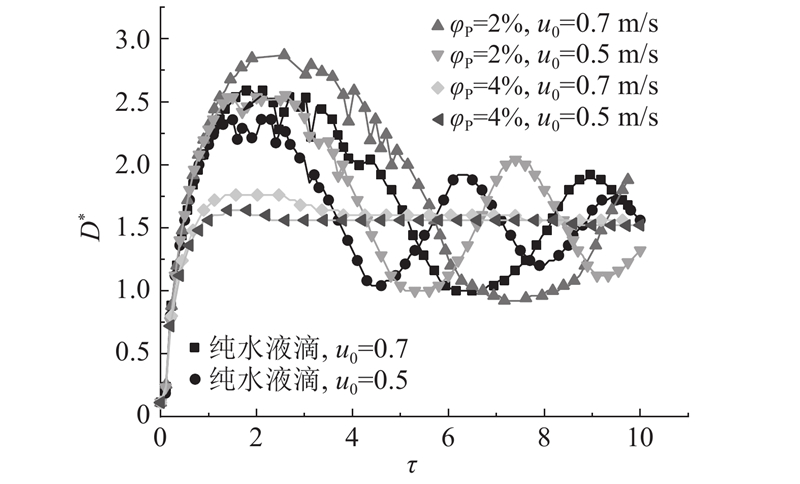
液滴的初始速度也是影响液滴动态过程的重要因素，改变液滴撞击壁面的初速度，使初速度分别为0.5 m/s（We≈3.5）、0.7 m/s（We≈20），保持液滴初始直径不变，均为2.5 mm. 选择纯水液滴、纳米颗粒体积分数分别为2%、4%的液滴作为对象，研究纳米流体液滴的惯性力对撞击固体壁面过程的影响，模拟所得的铺展因子变化曲线，如图7所示.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   纯水与不同颗粒体积分数的纳米流体液滴在不同初速度下的铺展因子变化曲线

Fig.7   Variation curves of spreading factor for pure water droplets and nanofluid droplets with different nanoparticle volume fractions at different initial velocities


较大的初速度为液滴提供了较高的动能，带来更大的铺展直径. 由图7可以看出，随着撞击速度的增加，液滴最大铺展因子变大，且铺展时间也相对较长；2%的纳米流体液滴由于纳米颗粒体积分数较小，纳米颗粒的加入对铺展过程的影响并不大，表现与纯水液滴相近，而纳米颗粒体积为4%的纳米流体液滴相较于其他2种液滴在改变撞击速度的情况下铺展因子变化并不明显，铺展过程所需时间也远小于其他.

如图8所示为纯水液滴和4%纳米颗粒体积分数液滴在We≈20时的模拟结果对比. 可以看出，随着纳米颗粒体积分数的增加，其撞击壁面时的铺展过程相较纯水液滴有较大不同，对铺展和回缩过程的抑制较为明显. 尽管4%体积分数的纳米流体液滴表面张力低于纯水液滴，但是纳米颗粒的加入带来了相对较大的黏度，有效抵消冲击的能量[36]，使其撞击过程更加规则稳定，表明仅靠毛细力并不能阻止液滴在较高速下的铺展和运动，而液滴的黏度对保持液滴形态稳定可能起了更大的作用.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

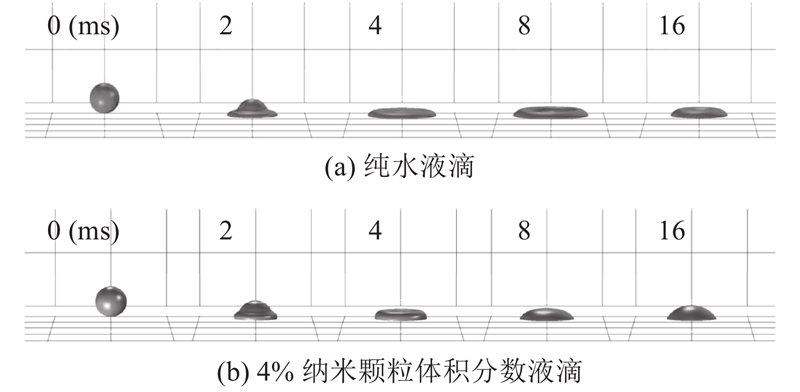
图 8   纯水液滴与4%体积分数的纳米流体液滴在相同时间的模拟结果对比

Fig.8   Simulation results of pure water droplet and 4% volume fraction nano droplet at same time


在液滴铺展的初期，在相同速度下，3种液滴的铺展因子变化趋势几乎相同，而当无量纲时间大于0.5时，液滴的铺展和回缩有了不同的趋势，纯水和低颗粒体积分数的液滴表现出更加明显的铺展回缩过程，而4%的纳米流体液滴铺展因子变化幅度较小，在液滴撞击壁面的初期，惯性力起主导作用，这与Rioboo等[37]的研究结论一致.

3.3. 纳米流体液滴直径对液滴撞击过程影响

分别选择直径为2.5、6.0 mm的液滴作为研究对象，保持液滴初速度一致，均为0.3 m/s. 模拟结果如图9、10所示. 图中，D*max为最大铺展直径. 可以看出，随着液滴直径的增大，液滴撞击后的最大铺展因子变大，此外铺展至最大直径所需时间也增长，且直径较大的液滴振荡周期更长. 因为液滴直径越大，其与壁面的接触面积越大，液滴与壁面间会产生更多的摩擦能量耗散黏性，对振荡的抑制较明显，使得振荡频率减少，周期变长.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

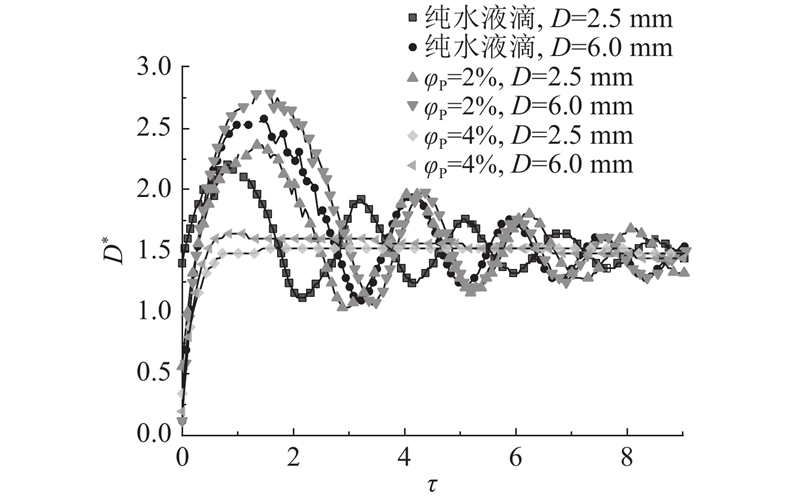
图 9   纯水与不同颗粒体积分数的纳米流体液滴在不同直径下的铺展因子变化曲线

Fig.9   Variation curves of spreading factor for pure water droplets and nanofluid droplets of different nanoparticle volume fractions with different droplet diameters


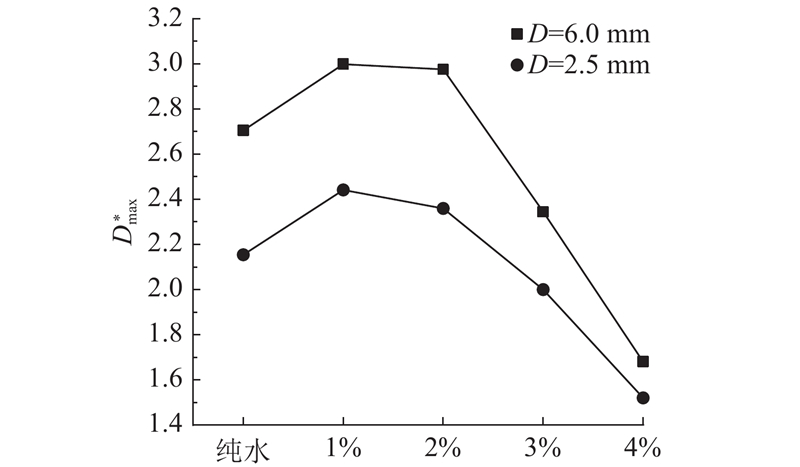
图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   纯水与不同颗粒体积分数的纳米流体液滴在不同直径下的最大铺展因子

Fig.10   Maximum spreading factor of pure water droplets and nanofluid droplets of different nanoparticle volume fractions with different droplet diameters


在后期稳定后，2种不同直径的液滴铺展因子较接近，且变化趋势也较为一致，说明液滴直径对撞击前期有影响作用，对后期的影响效果不大. 由图10可以看出，对于纳米颗粒体积分数为4%的液滴，在改变其直径时，最大铺展因子的增加并不如其他液滴明显，可能是因为较多纳米颗粒的加入进一步增加了三相接触线的有效摩擦[38]，抑制了铺展过程，减少了液滴的不稳定振荡振

Bartolo等[39]提出聚合物的添加会带来较高法向应力，这些法向应力抵消了驱动接触线运动的毛细作用力，进而抑制液滴运动，且Bartolo等[39]强调这种接触线动力学的变化不仅局限于稀释聚合物溶液，对颗粒悬浮液也可能有重要影响. 因此法向应力的作用可能也是解释本研究中纳米流体液滴铺展回缩过程受到抑制的原因之一.

4. 结　论

（1）随着纳米颗粒的加入，流体表面张力降低，液滴黏度增加，且逐渐表现出较明显的非牛顿特性，这些改变使得纳米流体液滴撞击壁面的过程与纯水液滴有较大不同. 模拟研究发现，纳米颗粒体积分数超过3%可以有效抑制液滴铺展回缩过程.

（2）随着撞击固体壁面的惯性力增大，液滴的最大铺展因子变大，且铺展所需时间加长，惯性力对撞击铺展初期起主导作用. 同时较大的纳米颗粒体积分数可以抑制高速下的铺展过程，使液滴的撞击过程更稳定，反复振荡的次数减少.

（3）增大液滴直径，其撞击固体壁面后最大铺展因子也将随之增大，且液滴不稳定振荡的周期加长，但改变液滴直径并不影响液滴最终的铺展因子. 含有4%纳米颗粒体积分数的液滴在大直径的条件下，其最大铺展因子变化不明显，且无明显的振荡过程，能快速到达稳定状态，可以说明较多的纳米颗粒会在一定程度上抑制液滴直径所带来的影响.

（4）通过数值模拟对纳米流体液滴撞击固体壁面的影响机制进行研究，未来须开展实验研究进一步验证，并针对纳米颗粒的加入对液滴表面张力和流体黏性耗散的制衡机制展开相关研究.

参考文献

WANG C H, TSAI H L, WU Y C, et al

Investigation of molten metal droplet deposition and solidification for 3D printing techniques

[J]. Journal of Micromechanics and Microengineering, 2016, 26 (9): 095012

DOI:10.1088/0960-1317/26/9/095012      [本文引用: 1]

PALM L, NILSSON J

Impact on droplet placement on paper by the level of droplet flight stability in a continuous ink jet printer

[J]. Journal of Imaging Science and Technology, 1998, 42 (6): 534- 540

URL     [本文引用: 1]

DORR G J, WANG S, MAYO L C, et al

Impaction of spray droplets on leaves: influence of formulation and leaf character on shatter, bounce and adhesion

[J]. Experiments in Fluids, 2015, 56 (7): 143

DOI:10.1007/s00348-015-2012-9      [本文引用: 1]

ASAKAWA D, CHEN L C, HIRAOKA K

The analysis of industrial synthetic polymers by electrospray droplet impact/secondary ion mass spectrometry

[J]. Journal of Mass Spectrometry, 2009, 44 (6): 945- 951

DOI:10.1002/jms.1569      [本文引用: 1]

YARIN A L

Drop impact dynamics: splashing, spreading, receding, ${\rm{bouncing}}\cdots $

[J]. Annu Rev Fluid Mech, 2006, 38: 159- 192

DOI:10.1146/annurev.fluid.38.050304.092144      [本文引用: 1]

RIOBOO R, TROPEA C, MARENGO M

Outcomes from a drop impact on solid surfaces

[J]. Atomization and sprays, 2001, 11 (2): 155- 165

URL     [本文引用: 1]

杨宝海, 王宏, 朱恂, 等

速度对液滴撞击超疏水壁面行为特性的影响

[J]. 化工学报, 2012, 63 (10): 3027- 3033

DOI:10.3969/j.issn.0438-1157.2012.10.003      [本文引用: 1]

YANG Bao-hai, WANG Hong, ZHU Xun, et al

Effect of velocity on the behavior of droplet impacting superhydrophobic wall

[J]. CIESC Journal, 2012, 63 (10): 3027- 3033

DOI:10.3969/j.issn.0438-1157.2012.10.003      [本文引用: 1]

KANNANGARA D, SHEN W

Roughness effects of cellulose and paper substrates on water drop impact and recoil

[J]. Colloids Surfaces A: Physicochemical and Engineering Aspects, 2008, 330 (2/3): 151- 160

URL     [本文引用: 1]

MAO T, KUHN D C, TRAN H

Spread and rebound of liquid droplets upon impact on flat surfaces

[J]. AIChE Journal, 1997, 43 (9): 2169- 2179

DOI:10.1002/aic.690430903      [本文引用: 1]

MARENGO M, ANTONINI C, ROISMAN I V, et al

Drop collisions with simple and complex surfaces

[J]. Current Opinion in Colloid and Interface Science, 2011, 16 (4): 292- 302

DOI:10.1016/j.cocis.2011.06.009      [本文引用: 1]

ŠIKALO Š, GANIĆ E

Phenomena of droplet: surface interactions

[J]. Experimental Thermal and Fluid Science, 2006, 31 (2): 97- 110

DOI:10.1016/j.expthermflusci.2006.03.028      [本文引用: 1]

ŠIKALO Š, MARENGO M, TROPEA C, et al

Analysis of impact of droplets on horizontal surfaces

[J]. Experimental Thermal and Fluid Science, 2002, 25 (7): 503- 510

DOI:10.1016/S0894-1777(01)00109-1      [本文引用: 1]

李维仲, 朱卫英, 权生林, 等

液滴撞击水平固体表面的可视化实验研究

[J]. 热科学与技术, 2008, 7 (2): 155- 160

URL     [本文引用: 1]

LI Wei-zhong, ZHU Wei-ying, QUAN Sheng-lin, et al

Visual experimental study on droplet impacted onto horizontal solid surface

[J]. Journal of Thermal Science and Technology, 2008, 7 (2): 155- 160

URL     [本文引用: 1]

AN S M, LEE S Y

Observation of the spreading and receding behavior of a shear-thinning liquid drop impacting on dry solid surfaces

[J]. Experimental Thermal and Fluid Science, 2012, 37: 37- 45

DOI:10.1016/j.expthermflusci.2011.09.018      [本文引用: 1]

GUPTA A, KUMAR R

Droplet impingement and breakup on a dry surface

[J]. Computers and Fluids, 2010, 39 (9): 1696- 1703

DOI:10.1016/j.compfluid.2010.06.006      [本文引用: 1]

FUJIMOTO H, SHIOTANI Y, TONG A Y, et al

Three-dimensional numerical analysis of the deformation behavior of droplets impinging onto a solid substrate

[J]. International Journal of Multiphase Flow, 2007, 33 (3): 317- 332

DOI:10.1016/j.ijmultiphaseflow.2006.06.013      [本文引用: 1]

刘海龙, 沈学峰, 王睿, 等

纳米流体液滴撞击壁面铺展动力学特性研究

[J]. 力学学报, 2018, 50 (5): 56- 63

URL     [本文引用: 1]

LIU Hai-long, SHEN Xue-feng, WANG Rui, et al

Research on spreading dynamics characteristics of nanofluid droplets impacting on wall

[J]. Theoretical and Applied Mechanics, 2018, 50 (5): 56- 63

URL     [本文引用: 1]

HAO C, ZHOU Y, ZHOU X, et al

Dynamic control of droplet jumping by tailoring nanoparticle concentrations

[J]. Applied Physics Letters, 2016, 109 (2): 021601

DOI:10.1063/1.4958691      [本文引用: 2]

SHEN X, LIU H, WANG R, et al. Numerical simulation of spreading characteristics for nanofluids droplet impinging on the solid surface [EB/OL]. [2020-05-01]. https://www.comsol.ch/paper/numerical-simulation-of-spreading-characteristics-for-nanofluids-droplet-impingi-53733.

[本文引用: 1]

RAVIKUMAR S V, HALDAR K, JHA J M, et al

Heat transfer enhancement using air-atomized spray cooling with water–Al2O3 nanofluid

[J]. International Journal of Thermal Sciences, 2015, 96: 85- 93

DOI:10.1016/j.ijthermalsci.2015.04.012      [本文引用: 1]

朱冬生, 孙纪远, 宋印玺, 等

喷雾冷却技术综述及纳米流体喷雾应用前景

[J]. 化工进展, 2009, 28 (3): 368- 373

DOI:10.3321/j.issn:1000-6613.2009.03.002      [本文引用: 1]

ZHU Dong-sheng, SUN Ji-yuan, SONG Yin-xi, et al

Overview of spray cooling technology and application prospects of nanofluid spray

[J]. Chemical Industry and Engineering Progress, 2009, 28 (3): 368- 373

DOI:10.3321/j.issn:1000-6613.2009.03.002      [本文引用: 1]

PAK B C, CHO Y I

Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles

[J]. Experimental Heat Transfer and International Journal, 1998, 11 (2): 151- 170

DOI:10.1080/08916159808946559      [本文引用: 1]

ADRIANA M A

Electrical and rheological behavior of stabilized Al2O3 nanofluids

[J]. Current Nanoscience, 2013, 9 (1): 81- 88

URL     [本文引用: 2]

YANG L, DU K

Investigations of surface tension of binary nanofluids

[J]. Advanced Materials Research, 2011, 347−353: 786- 790

DOI:10.4028/www.scientific.net/AMR.347-353.786      [本文引用: 1]

CHINNAM J, DAS D K, VAJJHA R S, et al

Measurements of the surface tension of nanofluids and development of a new correlation

[J]. International Journal of Thermal Sciences, 2015, 98: 68- 80

DOI:10.1016/j.ijthermalsci.2015.07.008      [本文引用: 1]

YUE P, FENG J J, LIU C, et al

A diffuse-interface method for simulating two-phase flows of complex fluids

[J]. Journal of Fluid Mechanics, 2004, 515: 293- 317

DOI:10.1017/S0022112004000370      [本文引用: 1]

KISTLER S F

Hydrodynamics of wetting

[J]. Wettability, 1993, 6: 311- 430

[本文引用: 1]

CIEŚLIŃSKI J T, KRYGIER K A

Sessile droplet contact angle of water-Al2O3, water-TiO2 and water-Cu nanofluids

[J]. Experimental Thermal and Fluid Science, 2014, 59: 258- 263

DOI:10.1016/j.expthermflusci.2014.06.004      [本文引用: 1]

DAS P K, ISLAM N, ZAKARIA K, et al. Measurement of surface tension and contact angle of different nanofluids: an experimental study [C]// Proceedings of the Proceedings of the 24th National and 2nd International ISHMT-ASTFE Heat and Mass Transfer Conference. Kolkata: Begel House Inc, 2017: 2441-2448.

KIM S J, BANG I C, BUONGIORNO J, et al

Surface wettability change during pool boiling of nanofluids and its effect on critical heat flux

[J]. International Journal of Heat and Mass Transfer, 2007, 50 (19/20): 4105- 4116

URL     [本文引用: 1]

ZANG D, WANG X, GENG X, et al

Impact dynamics of droplets with silica nanoparticles and polymer additives

[J]. Soft Matter, 2012, 9 (2): 394- 400

URL     [本文引用: 5]

GERMAN G, BERTOLA V

Impact of shear-thinning and yield-stress drops on solid substrates

[J]. Journal of Physics: Condensed Matter, 2009, 21 (37): 375111

DOI:10.1088/0953-8984/21/37/375111      [本文引用: 1]

杨舒生. 液滴撞击碳纳米管阵列表面动态特性的实验与数值模拟研究[D]. 镇江: 江苏大学, 2018.

[本文引用: 4]

YANG Shu-sheng. Experimental and numerical simulation research on the dynamic characteristics of droplets impacting the surface of carbon nanotube array [D]. Zhenjiang: Jiangsu University, 2018.

[本文引用: 4]

LI Y, WANG F, LIU H, et al

Nanoparticle-tuned spreading behavior of nanofluid droplets on the solid substrate

[J]. Microfluidics and Nanofluidics, 2015, 18 (1): 111- 120

DOI:10.1007/s10404-014-1422-y      [本文引用: 1]

BERGERON V, BONN D, MARTIN J Y, et al

Controlling droplet deposition with polymer additives

[J]. Nature, 2000, 405 (6788): 772- 775

DOI:10.1038/35015525      [本文引用: 1]

DUURSMA G, SEFIANE K, KENNEDY A

Experimental studies of nanofluid droplets in spray cooling

[J]. Heat Transfer Engineering, 2009, 30 (13): 1108- 1120

DOI:10.1080/01457630902922467      [本文引用: 1]

RIOBOO R, MARENGO M, TROPEA C

Time evolution of liquid drop impact onto solid, dry surfaces

[J]. Experiments in Fluids, 2002, 33 (1): 112- 124

DOI:10.1007/s00348-002-0431-x      [本文引用: 1]

SMITH M, BERTOLA V

Effect of polymer additives on the wetting of impacting droplets

[J]. Physical Review Letters, 2010, 104 (15): 154502

DOI:10.1103/PhysRevLett.104.154502      [本文引用: 1]

BARTOLO D, BOUDAOUD A, NARCY G, et al

Dynamics of non-Newtonian droplets

[J]. Physical Review Letters, 2007, 99 (17): 174502

DOI:10.1103/PhysRevLett.99.174502      [本文引用: 2]

/

〈 〉