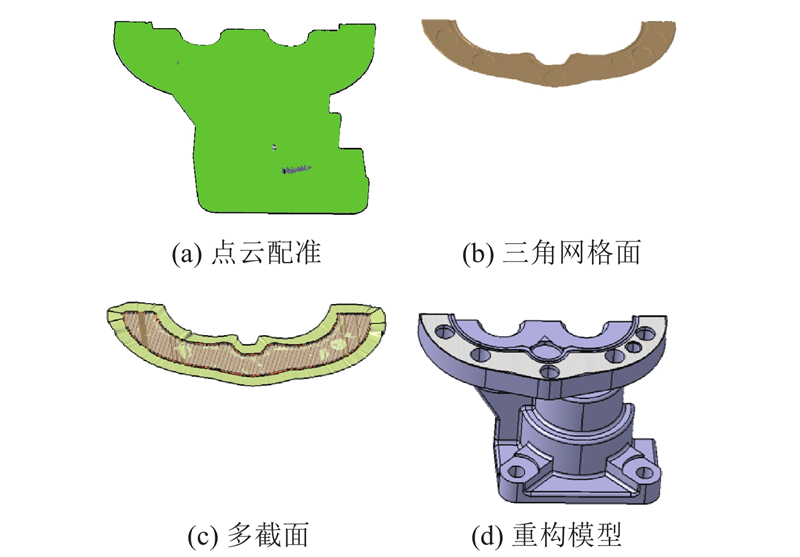
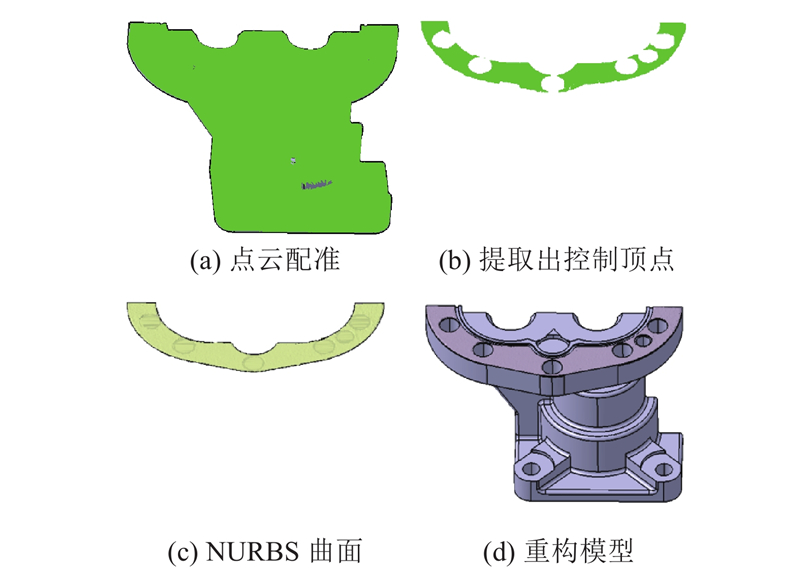
点云重构方法在逆向工程、计算机视觉、文物数字化、制造仿真等领域有着十分重要的意义[1]. 但是目前,点云重构技术在仿真模型重构方面依然不成熟[1]. 仿真模型是建模者为了满足应用需求而建立的,对实体、现象、过程的逻辑、数学或物理的描述,分别对应着概念模型、数学模型以及计算机辅助设计(computer aided design,CAD)模型等计算机实现模型[2]. 点云重构技术的不成熟性,主要表现在零件的实际状态无法精确和快速映射到仿真的CAD模型上,导致仿真试验的精度难以提高[3]. 例如,广泛采用的喷丸成形和复合材料成形工艺引起的装配变形,以及装配现场的误差积累,均加剧了飞机装配中实物产品与设计模型间的差异,为飞机装配仿真的精确度带来了较大的挑战[3].
研究者针对点云重构技术进行了大量研究. 1)基于网格的点云重构. Owen等[4]提出Q-Morph算法,将三角网格转化为质量较高的四边网格,减少网格中畸形单元的数量;王伟杰[5]提出根据区域选择基段的网格转化算法,该算法通过三角网格的平坦性确定不同的基段,改善四边形及邻近单元的质量. 上述方法虽然在一定程度上提高了重构的精度,但是网格面片数量较多、占用内存资源较大、重构精度较低. 2)基于非均匀有理B样条(non-uniform rational B-spline,NURBS)曲面的点云重构. Ma等[6]提出构建NURBS曲面进行三维模型的重建,利用二次函数拟合曲面,提高曲面重构的精度;黄建梅[7]通过累积弦长法构造非均匀节点矢量和对权因子的约束优化,先进行点云的NURBS曲线拟合,接着对NURBS曲线放样处理得到NURBS曲面;张甜田[8]采用逐点斜率求差法将点云压缩,并选用三次B样条曲线和重节点技术实现曲线曲面插值. 上述方法均获得较高精度的曲面,但是重构速度较慢,并且大多数研究局限于面的重构,缺少对三维实体重构的研究. 3)基于特征的点云重构. Dong等[9]为了高效地将轮胎点云转化为三维模型,首先通过相似度的计算,从点云矩阵中提取花纹设计特征参数,最后快速构建花纹的三维模型. 王海舟等[10]提出基于结构特征模板和逆向设计表的快速重构方法,根据毛坯模型的结构特征,创建结构特征模板和逆向设计表,接着根据设计表对曲面进行拟合、延伸、求交、裁剪、桥接等操作,完成模型的重构. 上述方法的重构速度均较快,但是无法在模型上可视化表达零件表面的轮廓度、粗糙度、刀痕等质量信息.
为了满足装配仿真的CAD模型高精度、快速的重构需求,提出基于点云和设计模型的仿真模型快速重构方法. 以点云和设计模型作为数据源,根据零件的定位方式,对齐点云坐标系和设计模型坐标系;以模型的边界作为约束,分割和精简点云,从而提取重构单面所需的控制顶点;根据重构需求,拟合出不同精度的NURBS曲面;结合边界表示法(boundary representation,BREP)和构造实体表示法(constructive solid geometry,CSG),实现对设计模型表面的按需和快速替换;基于数字化预装配的可拓展标记语言(extensible markup language,XML)和特征完全匹配的方法,用重构的高保真度模型替换XML中的理想模型,并对装配体进行精度和干涉检测,以验证所述方法的可行性.
1. 关键算法与基础理论
1.1. 点云配准
点云配准技术是指将不同视角扫描获得的点云统一到同一个坐标系中[11]. 为了实现点云在CAD系统中和模型的精准“重叠”,将数字化建模系统的坐标系作为统一的坐标系. 基本思想是通过匹配点云和模型上对应的特征点,从而求解坐标系转换矩阵,完成坐标系的对齐. 实现该思想的经典算法是Besl[12]提出的迭代最近点(iterative closest point,ICP)算法. 但是,激光扫描仪获取的点云在顶点处易形成光斑[13],导致点云中特征点的选取较为困难. 为了精确且快速地找到点云中的特征点,对ICP的特征点选取方式进行改进. 鉴于零件加工常用一面两孔的定位方式[14],设计了“一面两孔配准”的点云配准方法.
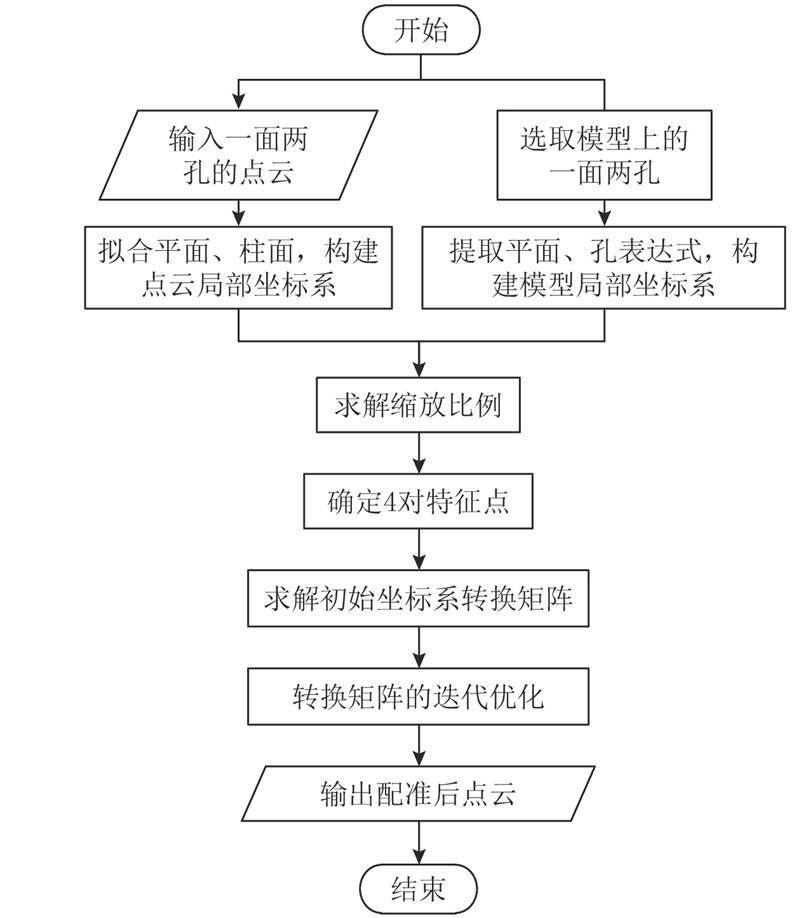
以1对定位面和2对定位孔求解特征点和转换矩阵,从而在CAD模型软件中实现点云和模型的精确“重叠”. 该方法适用于一面两孔定位的零件配准. 具体的“一面两孔配准”流程如图1所示,整个算法主要包括如下步骤.
图 1
图 1 “一面两孔配准”点云配准流程
Fig.1 Point cloud registration flow chart based on one plane and two holes
1)对输入的待拟合点云进行孔和平面的拟合,并构建点云局部坐标系.
(a)拟合平面. 记平面方程为Ax+By+Cz+D=0. 采用最小二乘法拟合平面:
式中:xi、yi、zi为数据点的坐标,n为用于拟合平面的点数量.
(b)拟合柱面. 柱面可以表示为
式中:x0、y0、z0为轴线上点O的坐标分量,m、n、p分别为轴向V的坐标分量,R为柱面半径.
将拟合的平面法线方向作为V的初值,对圆柱面进行最小二乘拟合:
式中:
(c)构建局部坐标系
图 2
2)在模型上,手动选取对应的定位面和孔,并构建模型的局部坐标系.
(a)定位面和孔的数学表达式提取. 借助组件应用架构(component application architecture,CAA)提取交互选中的面、孔的数学表达式.
(b)构建局部坐标系
3)求解缩放因子、四对特征点以及坐标系转换矩阵.
(a)求解缩放因子. 缩放因子
(b)求4对特征点. 第1对特征点为
(c)求解初始坐标系转换矩阵。在齐次空间中,对上述特征点联立矩阵变换方程式:
式中:fi、si为各点的行向量,MF、MS分别为点云上特征点的点集F和模型上与F对应的特征点集S对应的行向量组构成的矩阵,R0为点云配准的坐标系初始旋转矩阵,T0为初始平移矩阵。可以解出R0、T0。
4)转换矩阵的迭代优化.
(a)对步骤1)输入的待拟合点云数据Q中各点的行向量qi进行R0的旋转变换、T0的平移变换和k的比例变换,得到新的行向量
(b)求解
(c)计算
(d)若
(e)求解
(f)则
(g)返回步骤(a),直到配准误差满足条件,从而实现点云的精配准.
5)加载待配准点云的行向量到式(4)的fi中,最后输出和保存已配准点云的行向量si.
1.2. 点云提取
虽然激光扫描可以快捷地获得高精度、高密度的点云数据[15],但是扫描仪无法做到“按需扫描”,即无法只扫描指定的单个面. 因此,提取出单个面重构所需的控制顶点,是模型单个面重构和替换的必要条件. 为了实现点云的高效和精确提取,提出基于设计模型边界的点云分割和精简算法,主要包括如下步骤.
1)交互式选取须被替换的模型表面(简称为原曲面),并借助CAA提取该面的边界信息.
3)点云的精简. 在保证点云几何特征的前提下,去除冗余点,从而提高后续曲面重构效率. 对常用的均匀网格法[18]进行改进,包括如下步骤.
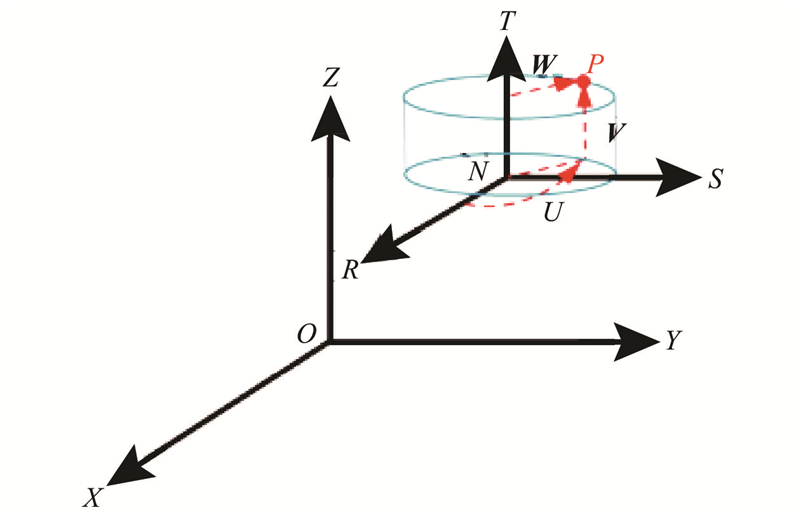
(a)根据原曲面的几何特征创建坐标系NUVW. 例如,若原曲面为圆柱面,则取周向角度变化量为U,取轴线方向为V,垂直于轴线的方向记为W. 如图3是目标点P映射到NUVW过程,则坐标(u,v,w)表达式为
图 3
式中:
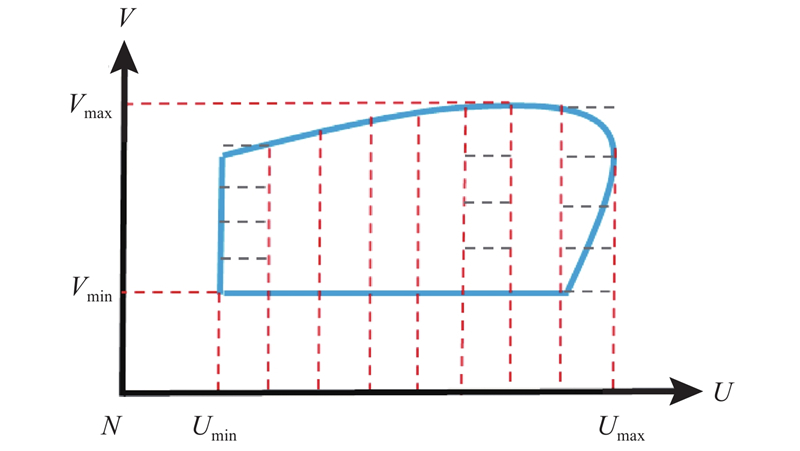
(b)NUV面上构建均匀的网格. 如图4所示,求得点云U和V向的极值:Umin、Umax、Vmin和Vmax;输入U和V向的精简步长Lu、Lv;修正网格V向各列边长为
图 4
式中:
(c)根据数据点的u、v,将点云归入网格框中,再根据w精简点云. w表示点到原曲面的距离,因此设计如下精简过程:若|w|在偏差极值的80%~90%内(可按需修正),则保存该网格框的最大w,并剔除其余的w;否则取框内数据点w的均值作为该框的w,达到保留点云凹凸特征和均匀精简目的.
(d)检查并填补空洞,并保存点云精简结果. 遍历网格框,若框内没有数据点,则将邻近k个网格框的w均值作为该框的w. 最后将各网格框的(u,v,w)映射回原坐标系,实现点云精简.
1.3. NURBS曲面重构和替换
1)NURBS曲面重构. 采用NURBS曲面S(u,v)分式定义[22]进行曲面拟合:
式中:
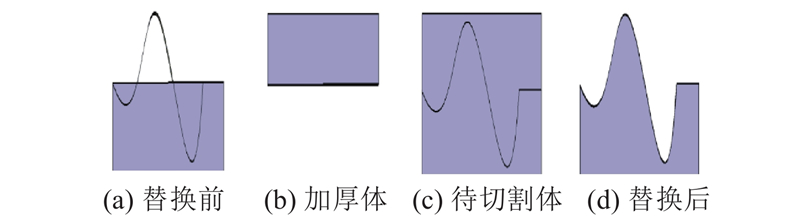
2)基于BREP/CSG的曲面替换. 虽然CATIA、UG和Pro/E等CAD软件均具有基于BREP的曲面替换功能,但是复杂的BREP结构使得曲面替换的局限性较大、计算稳定性和效率较差[23]. 为了实现直观、稳定、高效的曲面替换,设计基于BREP/CSG的曲面替换方法,如图5所示. 交互选取设计模型的原曲面,并遍历模型的BREP拓扑结构,检索出对应的拓扑面;将该拓扑面沿原曲面的法向加厚一个实测偏差极值单位,得到如图5(b)所示的原曲面加厚体;将拓扑面加厚体和模型布尔加,得到如图5(c)所示的待切割体. 确保重构曲面完全“陷入”设计模型;最后用重构的NURBS曲面切割待切割体,实现对原曲面的替换,如图5(d)所示.
图 5
1.4. 数字化预装配仿真验证
图 6
1)定制预装配XML文档.(a)装配信息提取. 借助CAA函数库解析装配体模型,提取出如表1所示的装配信息,并以链表的形式记录在XML文档中,如图7所示.(b)基于关键装配工艺的XML文档轻量化处理. 装配工艺包括装配容差要求、零件装配顺序、零件定位方案等内容. 装配容差要求是装配精度控制的目标,零件装配顺序和定位方案决定了装配偏差传递和累积的方向[25]. 关键的装配工艺由工厂根据装配经验和装配需求进行定制. 本研究借助Protégé本体编译器和Jess(Java Expert Shell System)推理引擎,将XML文档中与关键装配工艺无关的零件或信息标记为非关键信息,并给予删除. 例如,为了保证滑动轴承的间隙配合,与该配合精度无关联的零件均可以标记为非关键信息. 该方法在一定程度上减轻装配体的“重量”,达到节约存储空间和加快处理速度的目的,为提高装配体重构效率奠定基础.
表 1 装配信息提取
Tab.1
| 装配信息 | 提取的元素 |
| 零件 | 零件的装配顺序 |
| 零件间约束关系 | 约束类型、约束值、被约束的几何要素 |
| 三维标注 | 尺寸、公差、基准、关联的几何要素 |
| 零件的加工特征 | 特征类型、设计参数、构成的几何要素 |
图 7
表 2 形状特征组合与匹配参数
Tab.2
| 形状特征组合 | 匹配参数 |
| 旋转面+平面 | 旋转轴+平面中心 |
| 旋转面+球面 | 旋转轴+球心 |
| 2个旋转面+拉伸面 | 2旋转轴+拉伸方向+拉伸起点 |
| 3个球面 | 3球心 |
| 2个球面+平面 | 2球心+平面中心 |
| 球面+2个平面 | 球心+2个平面中心 |
| 球面+平面+拉伸面 | 球心+平面中心+拉伸方向 |
2. 实验验证
表 3 组件开发环境与工具
Tab.3
| 组件 | 型号 | 组件 | 型号 | |
| 系统硬件 | Intel(R)Core(TM) i5-6500 CPU @3.2 GHz(16 G) | 设计工具 | CATIA V5R18 | |
| 操作系统 | Windows 7,64 bit | 开发环境 | RADEV5R18 | |
| 开发语言 | C/C++ | 函数库 | CAA V5R18 | |
| 开发工具 | VS 2005 | − | − |
图 8
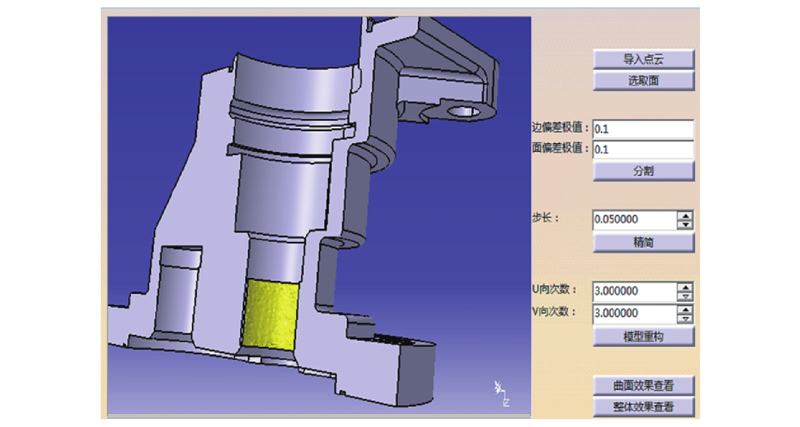
图 8 基于CAA开发的设计模型重构界面
Fig.8 Interface of design model reconstruction based on CAA development
2.1. 关键技术验证
2.1.1. 数据准备
图 9
表 4 PTS-HS717激光手持三维扫描仪技术参数
Tab.4
| 参数 | 取值 | 参数 | 取值 | |
| 尺寸 | 147×80×310 mm | 光源 | 14束激光线 | |
| 扫描速率 | 480000点/秒 | 分辨率 | 0.02 mm | |
| 工作距离 | 300 mm | 工作温度 | −10°~40° | |
| 测量范围 | 0.1~8.0 m | 测量精度 | 0.02 mm |
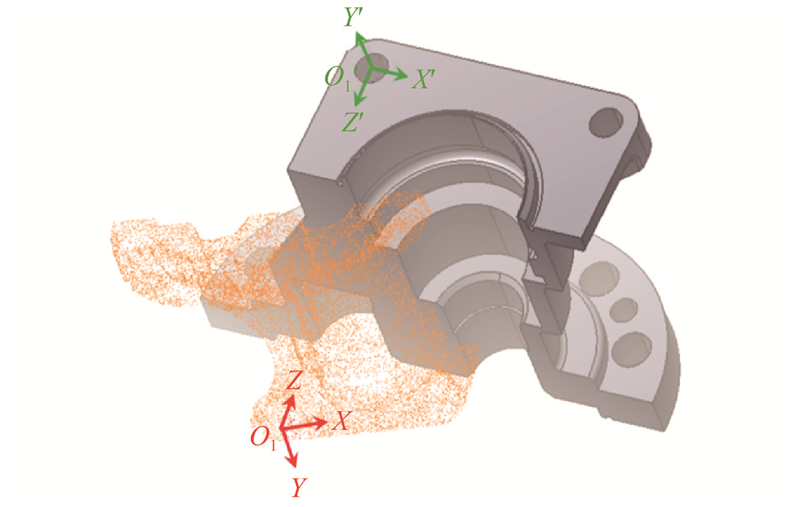
2.1.2. 点云配准验证分析
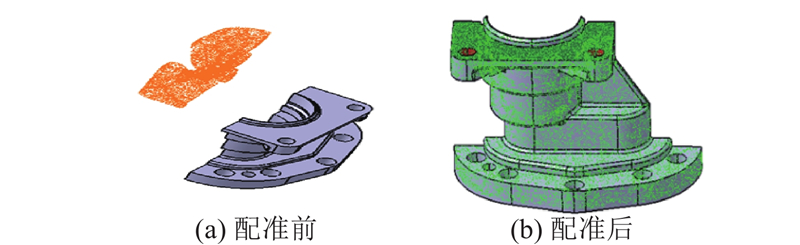
图 10
图 10 一面两孔配准示意图
Fig.10 Schematic diagram of ane-plane and two-hole registration
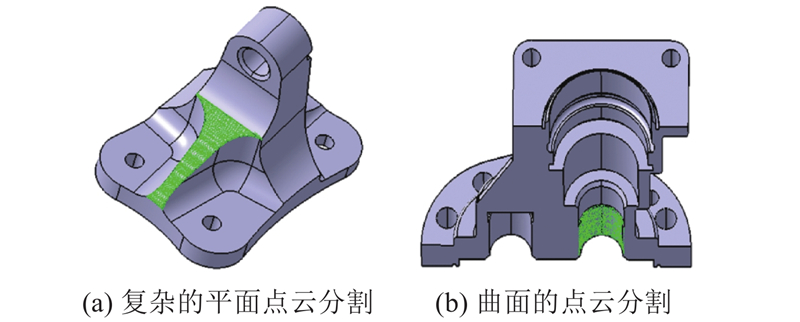
2.1.3. 点云分割验证分析
图 11
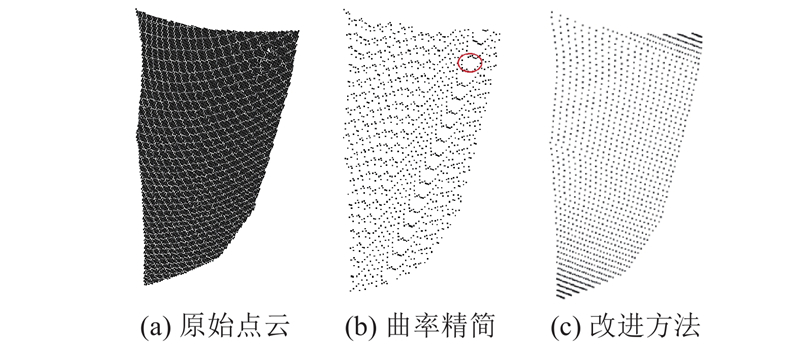
2.1.4. 点云精简验证分析
图 12
2.1.5. 曲面重构验证分析
如图13所示为对25万个数据点采用不同精简步长s的曲面重构效果. 可以看出,随着s的增大,重构曲面分辨率变低,但是重构用时t明显减少. 因此,调节精简步长,可以满足对不同重构精度和重构速度的需求,为后续实物表面特征精确和快速的构建提供可能.
图 13
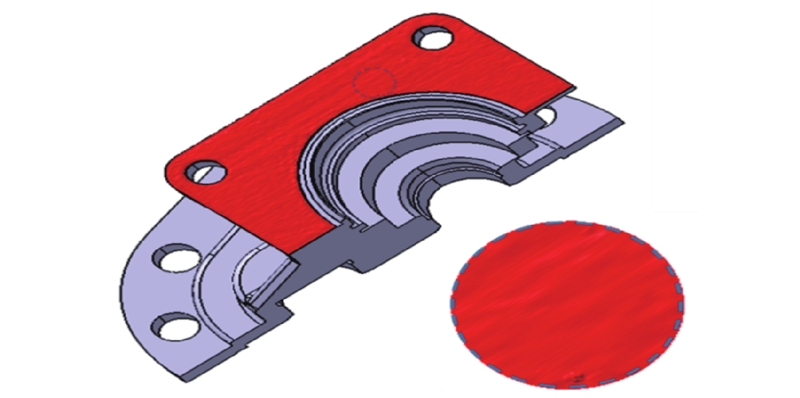
2.1.6. 曲面替换验证分析
如图14所示为NURBS曲面替换. 图中,红色面为对25万个点进行NURBS曲面拟合的效果,右下角处为局部放大视图,可以清晰看到上面的小凸起、凹坑以及刀痕. 用该NURBS曲面切割模型,实现曲面替换,达到NURBS曲面在模型上的精确定位. 该算法具有以下优势:1)实现零件表面质量的可视化呈现;2)面可以按需替换交互式选中的表面,避免重构整体模型,提高重构的速度;3)保留模型的设计边界,保证零件模型信息的完整性.
图 14
2.2. 模型重构速度和精度验证
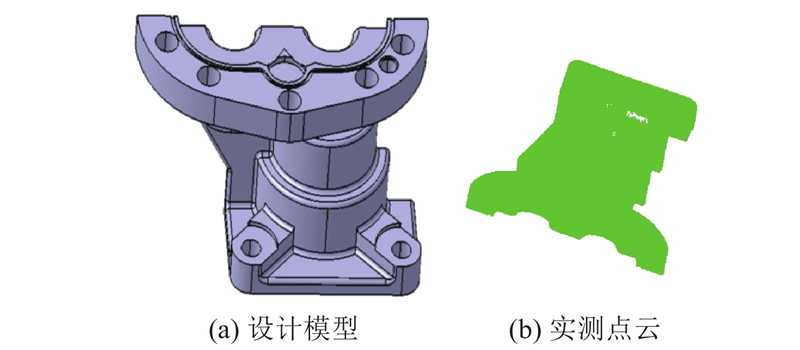
为了验证分析本研究方法的重构速度和精度,设计某航空企业典型零件上端面重构的对比实验.
图 15
图 16
2.2.1. 模型重构速度对比分析
统计传统重构方法和提出的重构方法各个步骤用时,如表5所示. 可以看出,1)在点云配准方面,本研究重构算法用时约为传统重构方法的15.50%,这是由于本研究重构方法无须人为在点云中绘制特征点、直线、面等的匹配约束;2)在点云提取方面,本研究重构算法用时约为传统重构方法的14.90%,这是由于本研究利用设计模型边界作为提取约束,无须重新拟合提取点云的边界;3)在曲面重构方面,本研究重构算法用时增加的时间仅占传统方法整体重构时间的1.34%,影响较小,但是大幅度提升了重构精度;4)在曲面替换方面,本研究算法用时约为传统方法的2.40%,这是由于本研究基于BREP/CSG的切割操作模型实现了零件模型的表面替换,避免了曲面和模型的边界匹配问题.
表 5 不同重构方法的用时对比表
Tab.5
| 方法 | 传统重构方法用时/s | 本研究重构算法用时/s |
| 点云配准 | 192.3 | 28.6 |
| 点云提取 | 37.4 | 5.8 |
| 曲面重构 | 5.7 | 12.0 |
| 曲面替换 | 235.8 | 5.6 |
| 合计 | 471.2 | 52.0 |
综上分析,以该模型为例,本研究提出的重构方法在点云配准、点云提取及曲面替换方面显著缩短了时间,总体速度得到了大幅度的提高.
2.2.2. 重构精度验证分析
为了定量检测和分析本研究重构算法的精度,以点云作为标准值,分别对已定位在模型上的三角网格面和NURBS曲面进行沿曲面法向的偏差分析.
图 17
2.3. 数字化预装配仿真验证
表 6 舱门装配的关键零件精度要求
Tab.6
| 关键零件精度 | 指标 |
| 蒙皮外形轮廓度 | |
| 边框垂直度 | |
| 主轴孔的同轴度 | |
图 18
图 19
图 20
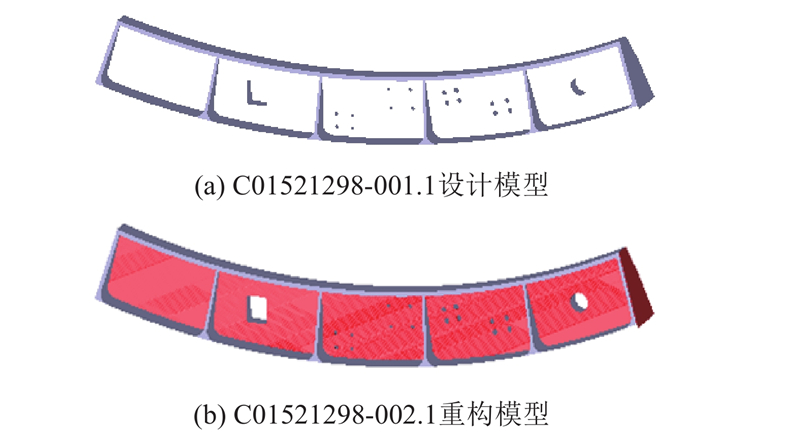
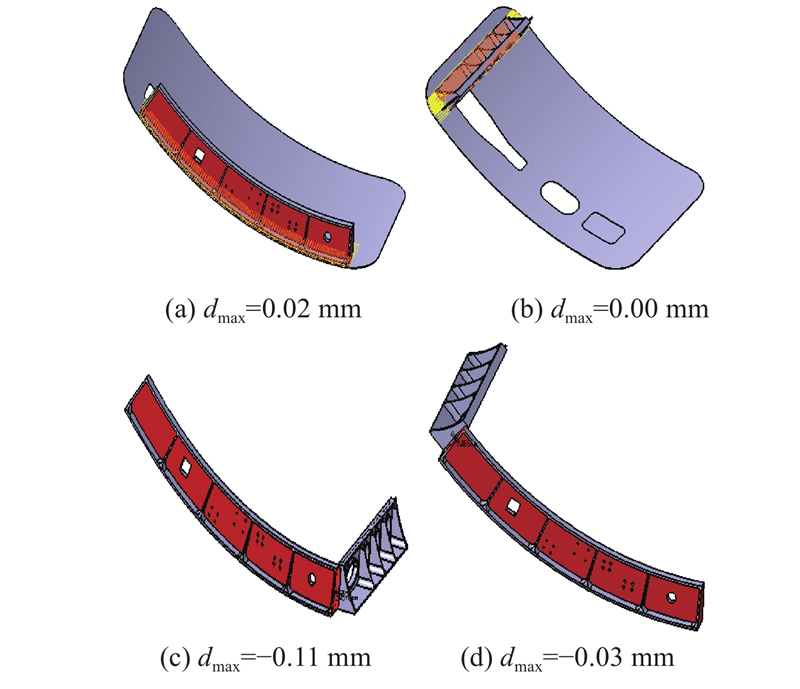
图 20 重构前、后的模型对比
Fig.20 Model comparison diagram before and after reconstruction
图 21
图 22
图 23
如表7所示为舱门预装配各项数据统计. 可以看出,轻量化方法减少了装配零件,并提高了装配体模型重构的效率,舱门的预装配仿真用时提高了79.3%. 而基于点云和设计模型的仿真模型重构与替换方法,实现了装配精度的自动检测,与工厂提供的实测装配精度间的误差小于0.03 mm,并显著缩短了工厂精度检测用时. 因此,本研究提出的仿真模型重构方法可以满足数字化预装配仿真的高精度和高效率的需求,具有一定的工程应用价值.
表 7 舱门预装配各项数据统计
Tab.7
| 统计项 | 零件数量/个 | 占用内存/kB | 装配体模型重构用时/s | 精度检测用时/s | 装配精度/mm | ||
| 蒙皮轮廓度 | 边框垂直度 | 主轴同轴度 | |||||
| 轻量化前 | 97 | 47022 | 243.2 | 6.5 | 0 | 0 | 0 |
| 轻量化和模型替换后 | 16 | 8237 | 50.3 | 6.7 | 0.27 | 0.31 | 0.38 |
| 工厂检测 | 97 | − | − | 7200.0 | 0.29 | 0.34 | 0.37 |
3. 结 论
本研究借助CAA技术,实现了基于设计模型的点云配准、基于设计模型边界的点云分割和精简、基于仿真需求的NURBS曲面拟合及基于BREP/CSG的曲面局部替换,达到了对仿真模型的高精度和快速重构的目的. 相比模型的传统重构方法,本研究所述的方法有如下改进:
(1)点云配准方面. 以设计模型作为参照,通过“一面两孔配准”方法将点云配准到设计模型上,有效减少手动绘制点云的特征点、线、面等约束特征造成的人为误差和时间浪费.
(2)点云提取方面. 以设计模型的面边界作为参照,保留点云的有效边界,避免传统点云分割时的特征识别和曲率计算等耗时运算;通过改进的均匀网格精简算法,满足曲面不同分辨率的重构需求.
(3)曲面替换方面. 结合BREP和CSG,构建待切割体,实现表面刀痕、轮廓度、粗糙度等质量信息的可视化表达. 相比基于BREP的曲面替换,本研究方法更直观和高效.
(4)仿真模型重构方法的应用价值方面. 通过XML文档的轻量化和基于特征完全匹配的零件替换,验证了仿真模型重构方法对装配质量评估的高效性和准确性.
不过,复杂曲面的点云分割相对较慢,对计算机性能要求较高,后续可以开展复杂曲面的点云分割算法的优化,从而进一步提高曲面重构的速度.
参考文献
一种基于关键点选择的快速点云配准算法
[J].
A fast point cloud registration algorithm based on key point selection
[J].
建模与仿真技术发展趋势分析
[J].DOI:10.3969/j.issn.1004-731X.2004.09.014 [本文引用: 1]
The analysis of modeling and simulation development direction
[J].DOI:10.3969/j.issn.1004-731X.2004.09.014 [本文引用: 1]
Q-Morph: an indirect approach to advancing front quad meshing
[J].DOI:10.1002/(SICI)1097-0207(19990330)44:9<1317::AID-NME532>3.0.CO;2-N [本文引用: 1]
NURBS curve and surface fitting for reverse engineering
[J].DOI:10.1007/BF01179082 [本文引用: 1]
A feature-based method for tire pattern reverse modeling
[J].DOI:10.1016/j.advengsoft.2018.08.008 [本文引用: 1]
批量复杂结构毛坯的快速逆向建模技术研究
[J].DOI:10.3969/j.issn.1004-132X.2014.14.018 [本文引用: 1]
Rapid reverse modeling of batched complex blanks
[J].DOI:10.3969/j.issn.1004-132X.2014.14.018 [本文引用: 1]
基于假设检验匹配约束的点云配准算法研究
[J].
Research of point cloud registration algorithm based on hypothesis test matching constraints
[J].
A method for registration of 3D shapes
[J].
一种基于点对应的激光扫描仪外方位参数检校方法
[J].
A calibration method for laser scanner's external orientation by corresponding points
[J].
工件定位特征识别与定位方案自动推理算法
[J].DOI:10.3321/j.issn:0367-6234.2005.02.027 [本文引用: 1]
Focating feature recognition and locating design automation
[J].DOI:10.3321/j.issn:0367-6234.2005.02.027 [本文引用: 1]
复杂曲面零件散乱点云特征点提取
[J].
Extracting feature points in scattered point cloud of complex surface parts
[J].
一种判断点与多边形关系的快速算法
[J].DOI:10.3321/j.issn:0253-987X.2007.01.014 [本文引用: 1]
Fast method to determine spatial relationship between point and polygon
[J].DOI:10.3321/j.issn:0253-987X.2007.01.014 [本文引用: 1]
基于NURBS的轨道板点云外形尺寸检测研究
[J].
Research on track slab point cloud dimensional deviation inspection based on NURBS
[J].
CAD surface data exchang using STEP
[J].DOI:10.1016/0010-4485(91)90067-7 [本文引用: 1]
Modifying the shape of rational B-splines, part 2: surface
[J].DOI:10.1016/0010-4485(89)90014-6 [本文引用: 1]
Processing of topological BIM queries using boundary representation based methods
[J].
基于测量数据的飞机数字化预装配技术
[J].DOI:10.3969/j.issn.1671-833X.2013.20.019 [本文引用: 2]
Aircraft digital preassembly technology based on measured data
[J].DOI:10.3969/j.issn.1671-833X.2013.20.019 [本文引用: 2]
基于预装配精度分析的飞机关键装配工序质量控制技术
[J].
Quality control technology for key assembly procedure of aircraft based on preassembly precision analysis
[J].