在齿轮箱工作过程中，齿轮齿面之间的相对滑动摩擦、齿轮与润滑油之间的摩擦均会产生大量热量，其润滑性能的好坏直接关系到传动系统的性能. 飞溅润滑是齿轮箱最常用的润滑方式，在飞溅润滑时，齿轮系统在工作过程中会产生啮合摩擦功率损失、风阻功率损失和搅油功率损失，其中，搅油功率损失约占上述总功率损失的30%^[1]. 降低搅油功率损失可以显著减小齿轮箱的功率损失和发热量，提高齿轮箱的传动效率和使用寿命. 因此，对齿轮箱搅油功率损失的准确预算非常重要. 由于飞溅润滑具有非稳态、油气两相流和流场分布复杂等特点，较难通过理论或实验进行研究.

近年来，随着计算机技术和数值分析方法的高速发展，计算流体动力学(computational fluid dynamics，CFD)已经逐渐成为齿轮箱飞溅润滑研究的重要手段. 目前，针对齿轮箱飞溅润滑研究的主要方法为基于欧拉坐标系的有限体积法(finite volume method，FVM)和基于拉格朗日坐标系的无网格法. 前者为传统的研究方法，大量学者采用该方法进行研究；后者为新兴的研究手段，目前，较少有学者将该方法应用于齿轮箱飞溅润滑的研究. 在FVM法方面，Gorla等^[2-3]通过实验验证基于FVM的CFD法用于预测齿轮箱搅油功率损失是有效可行的. Liu等^[4-5]运用高速摄像机采集FZG空载试验台飞溅润滑流场照片，与FVM数值仿真结果进行对比，发现数值仿真结果与实验结果具有高度一致性，同时发现FVM法获取的搅油功率损失与实验值较吻合. 沈林等^[6]对一对啮合齿轮空载时的搅油损失进行研究，分析齿轮转速、传动比和齿轮类型对搅油损失的影响. Hu等^[7-9]使用动网格技术，运用多相流模型和湍流模型对直升机中减速器模型进行仿真分析，实现了减速器内部流场的可视化，分析了齿轮浸油深度和转速对关键部位体积流量的影响，同时验证分析了中减速器内液位高度、齿轮转速、油温、直升机倾斜角等对搅油功率损失的影响. Hu等^[10]发现动态运动的变速箱会对齿轮箱搅油损失和齿轮啮合区域供油量产生重大影响，甚至造成润滑不良风险. 在无网格法方面，主要通过光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)法和移动粒子半隐式法(moving particle semi-implicit method，MPS)对齿轮箱飞溅润滑进行研究. Groenenboom等^[11]运用SPH法与有限元(finite element method，FEM)耦合的方法对涌浪、变速箱飞溅润滑和心血管进行研究，结果表明，SPH-FEM法在湍流和流固耦合模型上具有良好应用. 赵迁等^[12]运用SPH法对4种工况下纯电动车减速器进行仿真分析，从整体上得到了齿轮箱飞溅润滑的可视化效果. Ji等^[13]用SPH法研究3个液位高度和3个雷诺数一共9种工况下单对啮合齿轮搅油的油液流场分布情况，并定性分析齿轮箱内空化气泡的数量和大小. Liu等^[14]运用SPH法研究单级齿轮箱飞溅润滑的油液分布和搅油损失情况，发现油液分布、搅油损失与实验结果存在较大误差. 皮彪等^[15]应用MPS法分析某重型汽车主减速器润滑系统，首次将MPS法成功应用到减速器润滑分析中，为润滑系统分析提供了新方法. 李晏等^[16]将MPS法应用到单齿搅油损失研究中，通过公式拟合不同因素对搅油功率损失的影响，为齿轮搅油损失研究提供了新方法.

综上可知，对于FVM法，众多学者主要集中在对FZG空载实验台模型进行数值仿真，研究试验台齿轮箱飞溅润滑流场分布和搅油损失情况. 少量学者对小型工程应用的简单几何结构的齿轮箱进行分析. 可以看到，FVM法在齿轮箱飞溅润滑方面具有广泛应用，且具有较高的准确性. 然而FVM法在处理齿轮箱飞溅润滑这种强非线性变化的问题时仍存在较大困难，比如齿轮啮合处间隙小须进行齿面移动处理、啮合处网格划分困难、对计算机硬件要求高、计算速度缓慢等，对于几何结构复杂的大型工程问题，其往往难以处理. 对于无网格法，SPH法对齿轮箱流场分布具有较好仿真效果，但对于搅油功率损失的预测效果有待提高. 有学者^[15]初次将MPS方法应用到齿轮箱飞溅润滑流场模拟和搅油损失中，但模拟效果较差，搅油功率损失的准确性有待验证.

本研究以FZG空载实验台模型为研究对象，运用MPS法对不同转速、不同润滑油型号和温度工况下齿轮箱飞溅润滑流场分布进行数值仿真，从细节上还原齿轮的搅油形态；通过与试验结果对比验证MPS法在齿轮箱流场分布形态上的准确性；分析对比高转速时不同油温工况下搅油力矩损失仿真值与实验值，验证其在搅油损失预测方面相对于SPH法的优越性. 为MPS法应用于齿轮箱的研究和开发提供了有效支撑.

MPS法是Koshizuka^[17]提出的与早期SPH方法基本思想类似的数值计算法，用于计算不可压缩流体的运动. 该方法利用具有位置和速度特性的有限数量的粒子代表流体，通过粒子法对流体进行整体模拟，是基于拉格朗日形式的无网格计算方法. 在MPS法中，每个计算步分为显式和隐式2步，对计算结果进行2次修正. 第1次对粒子的速度和坐标进行显式修正，在通过求解压力泊松方程得到压力场后，对粒子进行第2次隐式修正，可以严格保证流体的不可压缩性. MPS法通过核函数表达粒子之间的相互作用关系，使用梯度模型、拉普拉斯模型、粒子密度模型、粒子光滑模型等对控制方程进行离散. 由于该方法是无网格法，省去了繁杂的前处理和计算过程中网格的重构更新过程，且具有易于追踪捕捉大变形和强非线性化的自由液面优点，在大变形水力研究中获得广泛应用.

对于连续不可压缩的牛顿流体，MPS方法的基础控制方程为连续性方程和Navier-Stokes方程，形式如下：

(1) ${{{\rm{d}}\rho }}/{{{\rm{d}}t}} = 0,$

(2) ${{{\rm{d}}{{u}}}}/{{{\rm{d}}t}} = - \frac{1}{\rho }\nabla {{p}} + \upsilon {\nabla ^2}{{u}} + {{g}}.$

式中： ${{u}}$为速度， ${{p}}$为压力， $\upsilon $为运动黏性系数， ${{g}}$为重力加速度， $\;\rho $为流体密度， $t$为时间.

在MPS法中，通过梯度模型、拉普拉斯模型、粒子密度模型等各模型来离散控制方程，而这些模型则需要核函数来充当权重函数，用以表征粒子之间相互作用的强弱关系. 粒子之间相隔越近，核函数 $w({{r}})$越大，相互作用越强；相隔越远，核函数 $w({{r}})$越小，作用越弱. 选用核函数如下：

(3) $w({{{r}}_{\rm{p}}}) = \left\{ \begin{array}{*{20}{c}} {{{{{r}}_{\rm{e}}}}}/{{{{{r}}_{\rm{p}}}}} - 1,\;&{\rm{0}} < {{{r}}_{\rm{p}}} < {{{r}}_{\rm{e}}}; \\ 0,\; &{{{r}}_{\rm{p}}} \geqslant{{{r}}_{\rm{e}}} . \end{array} \right.$

式中： ${{{r}}_{\rm{p}}}$为粒子之间的间距， ${{{r}}_{\rm{e}}}$为粒子的作用半径.

在基于网格的Euler法中，须对对流项连续插值从而容易导致数值扩散，而MPS法用粒子相互作用的梯度模型和Laplace来离散控制方程，无须离散N-S方程的对流项，有效避免了数值扩散问题. 梯度模型用来离散一阶导数项，拉普拉斯模型用来离散二阶导数项^[18]. 梯度模型是粒子 $i$和其作用域内所有邻域粒子 $j$的梯度向量的加权平均值^[19]，示意图如图1所示，表达式如下：

(4) ${\left\langle {\nabla f} \right\rangle _i} = \frac{d}{{{n^0}}}\sum\limits_{j \ne i} {\left[ {\frac{{{f_j} - {f_i}}}{{{{\left| {{{{r}}_j} - {{{r}}_i}} \right|}^2}}}\left({{{{r}}_j} - {{{r}}_i}} \right)w\left({\left| {{{{r}}_j} - {{{r}}_i}} \right|} \right)} \right]}. $

式中： ${{{r}}_i}$、 ${{{r}}_j}$为粒子的坐标矢量， $d$为求解问题的空间维数， ${n^0}$为粒子数密度常数， $f$为粒子物理参数.

基于非正常扩散，利用拉普拉斯模型将粒子 $i$的物理量根据邻域粒子的距离进行分配. 表达式如下：

(5) ${\left\langle {{\nabla ^2}f} \right\rangle _i} = \frac{{2d}}{{\lambda {n^0}}}\sum\limits_{j \ne i} {\left({{f_j} - {f_i}} \right)} w\left({\left| {{{{r}}_j} - {{{r}}_i}} \right|} \right).$

式中： $\lambda $为修正因子.

(6) $\lambda = \frac{{\displaystyle \sum\limits_{j \ne i} {w\left({\left| {{{{r}}_j} - {{{r}}_i}} \right|} \right){{\left| {{{{r}}_j} - {{{r}}_i}} \right|}^2}} }}{{\displaystyle \sum\limits_{j \ne i} {w\left(\left|{{{{r}}_j} - {{{r}}_i}}\right| \right)} }}.$

在MPS法中，通过保证粒子的密度数恒定来确保流体的不可压缩性，粒子数密度 ${n_i}$指粒子 $i$在核函数作用范围内，该粒子和其相邻粒子的函数值的叠加^[18]，表达式如下：

(7) ${n_i} = \sum\limits_{j \ne i} {w{\left(\left| {{{{r}}_j} - {{{r}}_i}} \right|\right)} } .$

MPS采用时间步积分法，数值计算就是迭代的预测和校正过程^[18]. 在校正过程中须使用到压力Poisson方程：

(8) ${\langle {\nabla ^{\rm{2}}}{p^{k + 1}}\rangle _i} = - \frac{\rho }{{{{(\Delta t)}^2}}}\frac{{{{({n^*})}_i} - {n^0}}}{{{n^0}}}.$

式中： $\Delta t$为计算时间步长， $k$为计算步数，n^*为介于2个时间步的中间粒子密度.

在MPS法中，将自由面粒子的压力设为零作为压力的边界条件. 因此，自由表面的确定对计算的准确性很重要. 根据流体的物理形态，自由表面外的粒子密度应小于流体内的粒子密度，则当 $n_i^ * < \beta {n^0}$时，粒子被认定为自由表面粒子， $\;\beta \in [0.8,\;1.0]$，本研究取0.97.

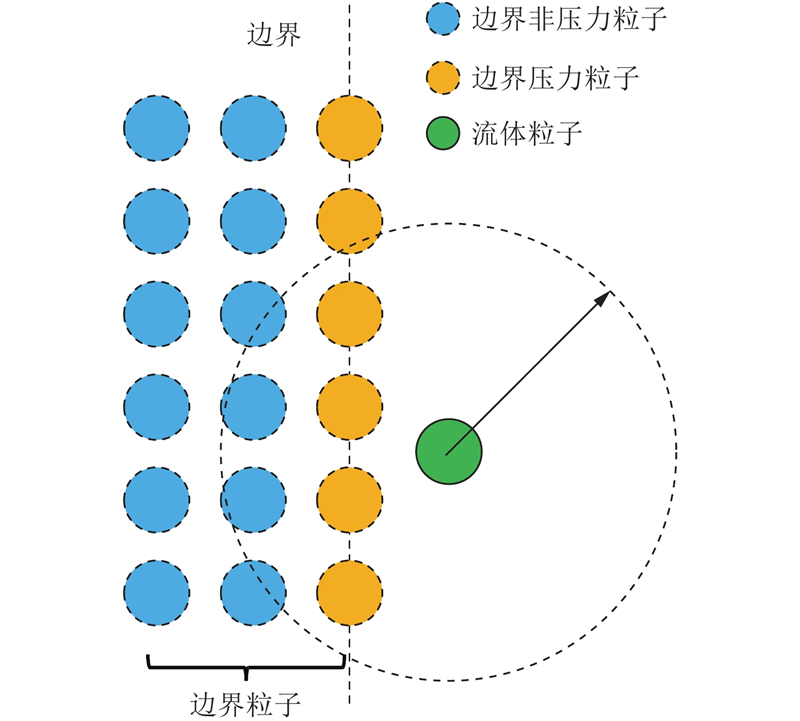
在模拟仿真时，须设置边界粒子以防止靠近边界的粒子穿越边界，由于该层边界粒子与流体粒子紧密接触，在实际计算中也会参与压力泊松方程的求解，具有压力值，所以称之为边界压力粒子. 为了避免自由表面的误判，一般情况下，在边界压力粒子之外，还须布置2层虚拟的边界非压力粒子. 因此，在仿真模型中边界均采用3层粒子的布置方法. 如图2所示.

在仿真过程中，为了保证计算的稳定性，时间步长的确定须满足如下条件：

(9) $\Delta t = \min \;\left\{{\Delta {t_i},\;\frac{{C{l_0}}}{{{u_{\max }}}},\;\frac{{{d_i}{l_0}^2}}{{2(\upsilon + {\upsilon _{\max }})}}} \right\}.$

式中： $\Delta {t_i}$为初始时间步长， $C$为克朗数， ${l_0}$为粒子直径， ${u_{\max }}$为粒子最大速度， ${d_i}$为扩散系数， ${\upsilon _{\max }}$为流体的动力黏度最大值. ${{C{l_0}}}/{{{u_{\max }}}}$保证 $\Delta t$满足Courant-Friedrichs-Lewy (CFL)条件^[20]， $\dfrac{{{d_i}{l_0}^2}}{{2(\upsilon + {\upsilon _{\max }})}}$保证黏度计算的稳定性.

MPS的每个计算步分为显示和隐式，是半隐式计算方法. 计算过程如下. 1）输入初始条件并对粒子进行初始化，得到粒子的速度初始值 ${u_i}^0$、位移初始值 ${r_i}^0$和初始粒子数密度 ${n^0}$；2）通过显示求解方法进行计算，得到在重力和黏滞力作用下粒子的速度估算值 ${u_i}^{\rm{*}}$和位移估算值 ${r_i}^{\rm{*}}$；3）通过隐式求解方法计算压力Piosson方程和压力梯度项，以此修正粒子的速度和位置，得到下一时间步的速度 ${u_i}^{{{n}} + {\rm{1}}}$和位置 ${r_i}^{{{n}} + {\rm{1}}}$. 依照上面得到的速度和位置值继续向下循环计算，直至求解结束.

由于实验条件限制，引用文献[4]采集的6张润滑油飞溅照片，建立与其相同的几何模型，设置相同的边界条件，运用MPS进行数值仿真，将两者结果进行比较，验证MPS法在飞溅润滑流场分布上的准确性. 引用文献[14]采集的6种工况的齿轮搅油损失力矩，建立与其相同的几何模型，设置相同的边界条件，运用MPS进行数值仿真，将两者结果进行比较，研究MPS法在搅油力矩损失预测上的准确性.

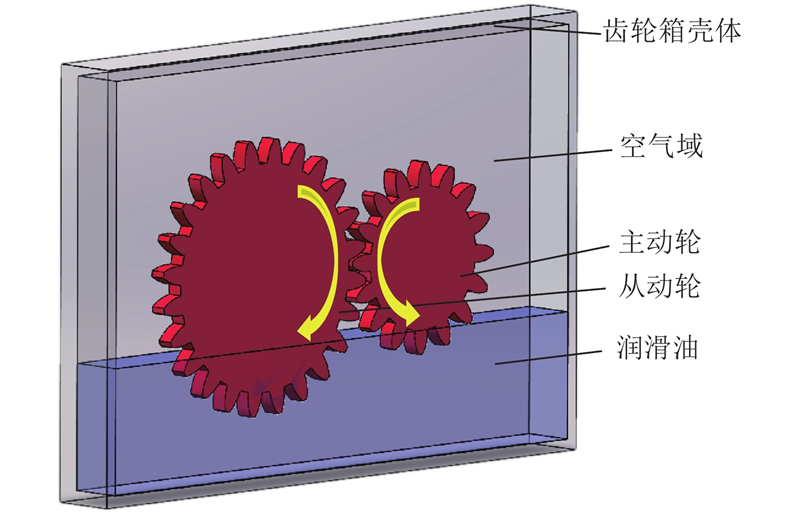
参考文献[4]，采用FZG齿轮实验机. 采用闭环能量施加原理给精密实验齿轮提供所需载荷，主要由电机、伺服齿轮箱、扭矩测量离合器、透明测试齿轮箱、实验主从动齿轮等构成. 通过该试验机可以获得啮合齿轮的搅油功率损失. 为了获得高速润滑油飞溅照片，在齿轮箱前配备Photron品牌下的 FASTCAM Mini AX200 型号高速摄像头，拍摄频率为5000帧/s. 实验齿轮采用FZG C-PT型齿轮，其几何参数如表1所示. 表中， ${m_{\rm{n}}}$为法向模数， $a$为中心距， $b$为齿宽， ${\alpha _{\rm{n}}}$为压力角， ${\;\beta _0}$为螺旋角， $z$为齿数， ${d_{\rm{a}}}$为齿顶圆直径， $x$为齿顶修正系数. FZG齿轮实验机示意图如图3所示.

主要研究验证MPS方法在齿轮箱飞溅润滑流场分布应用上的准确性，以及其在齿轮搅油力矩损失预算方面的正确性. 在飞溅润滑时，当齿轮在转速较低时，润滑油分布形态简单，易于捕捉和分析对比；在转速较高时，润滑油分布形态复杂，不易捕捉分析，但齿轮副的搅油功率损失较大，方便对其进行分析研究. 因此设置3种低转速、2种型号润滑油和2种油温共9种工况条件，用来分析不同转速和润滑油黏度下齿轮箱飞溅润滑流场的分布情况. 低转速工况具体参数如表2所示. 表中，−32.2 mm表示齿轮中轴线下32.2 mm， ${n_{\rm{o}}}$为主动轮转速， $\theta $为润滑油油温， $h$为液位高度. 设置2种高转速和3种油温一共6种工况用来分析齿轮的搅油功率损失，高转速工况具体参数如表3所示. 表中， ${n_{\rm{w}}}$为从动轮转速. 与文献[14]不同的是，本研究未考虑油温差异带来的初始液位高度的细微差异. 3种低转速分别为240、360、540 r/min，对应的齿轮周向速度分别为0.9、1.4、2.1 m/s. 2种高转速分别为1444、3474 r/min，对应的齿轮周向速度分别为8.3、20.0 m/s. 润滑油属性如表4所示. 表中， $\gamma $为运动黏度.

利用Particleworks软件对模型进行油液单相数值仿真. 综合考虑计算机性能和仿真结果精度，经过粒子直径参数测试，将低转速工况粒子直径设置为0.8 mm，高转速工况粒子直径设置为1.5 mm，采用双精度条件求解. 在仿真过程中，考虑粒子受到的重力，重力加速度设置为9.8 m²/s. 为了保证仿真过程的稳定性，压力和黏度项均采用隐式算法. 液体的表面张力采用Potential模型. 由于在飞溅润滑过程中，润滑油运动形态剧烈复杂，采用大涡模拟法(LES)湍流模型. 仿真的初始时间步长设置为5×10⁻⁵ s，Courant数设置为0.2，满足CFL条件. 粒子自由表面判断系数取0.97.

MPS法在处理齿轮副齿面接触时容易造成发散，用齿面移动法对齿轮的齿面切除1%厚度可以有效保证仿真的顺利进行. 即在保留所有轮齿和不改变齿轮安装位置的基础上，通过改变轮齿厚度来增大啮合区域间隙，以保证计算的正常进行^[21]. 目前，针对齿轮啮合处间隙狭小，给流体域网格划分和求解带来困难的问题，常用的齿轮建模处理方法包括无齿法、单向切齿法、双向切齿法和分离法. 根据彭钱磊等^[21]的研究，相对以上的齿轮处理方法，齿面移动法无须改变齿轮副的安装位置，且获得的润滑油飞溅效果符合实际情况，搅油功率与试验结果基本一致，最大误差小于8%.

本研究MPS法数值仿真的所有工况均在普通PC端完成，配置如下：graphics card: NVIDIA GTX1050Ti, CPU: Intel Core i5-9400 6-cores, RAM capacity: 8 GB.

每种工况求解至从动轮旋转10圈为止. 求解耗时如表5所示. 表中， ${t_{\rm{s}}}$为耗时.

数值仿真几何模型参数与上述FZG实验箱参数保持一致，几何模型主要包括齿轮箱壳体、主动轮、从动轮、空气域和液体域. 在数值仿真前，对液体域进行粒子化，不同液位高度下MPS粒子个数如表6所示. 仿真几何模型半剖图如图4所示. 参考文献[14]中使用SPH粒子法对FZG试验台进行数值仿真，其仿真的基本参数如表7所示. 表中， ${d_{\rm{p}}}$为粒子直径， ${t_{\rm{p}}}$为仿真物理时长.

为了验证MPS法在齿轮箱飞溅润滑油液分布上的细节表现和预测能力，选取低转速工况下，油温为40 ℃时的6种工况结果进行分析.

对粒子化的油液进行表面化后处理，使得仿真结果在液体的形态特征上表现得更加贴切. 将获得的6种工况的数值仿真结果（润滑油分布图片）与文献[4]采集的高速摄像FZG试验机搅油图片进行对比分析，以验证MPS法在流场分布形态预测上的准确性. 仿真图片与实验图片中的齿轮旋转状态选取为同一时刻. 如图5所示为主动轮旋转0.450圈时的油液分布形态. 仿真与试验对比如图6、7所示. 图6中从左至右3种工况展示的分别为主动轮旋转至0.360、0.376、0.450圈时的油液分布形态；图7中从左至右3种工况展示的分别为主动轮旋转至0.360、0.412、0.386圈时的油液分布形态.

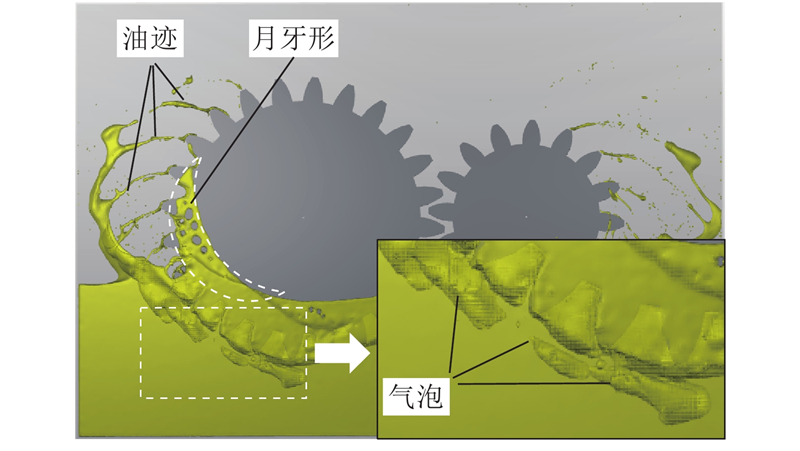
由图5可以看到，由于齿轮副的旋转，浸没在润滑油中的轮齿产生低压区，箱体上部的空气被吸入油中，在轮齿附近产生大小不一的气泡，甚至在齿顶圆周处形成明显的弧形气液交界线. 随着齿轮旋转角度的增大，可以看到，一部分油液由于黏性附着在轮齿根部，在轮齿上形成一个月牙形区域，而从动齿轮更多的浸没在油液中，相对于主动齿轮，其月牙形区域覆盖面积更大，表现得更明显；另一部分油液由于齿轮旋转时离心力的作用和液体表面张力的作用，在主从动轮两侧的齿顶处分别形成清晰可见的油迹.

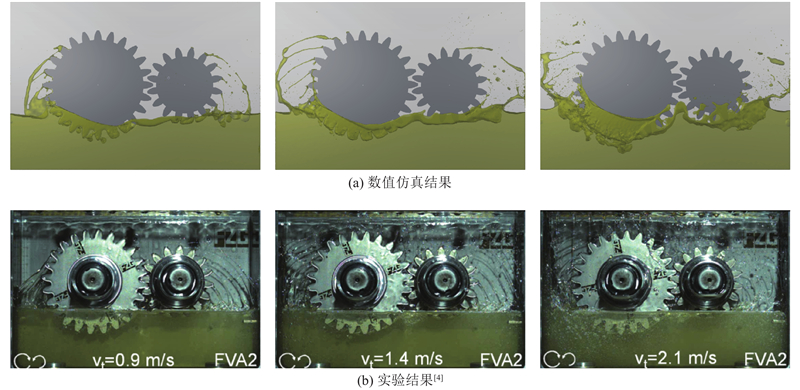
在图6、7中，从动轮侧面的每一个齿顶上均有一条清晰均匀的油迹，而主动齿轮侧面的油迹相对散乱，这是由于齿轮运转时，主动轮受到的离心力较大，约为从动轮的1.5倍，导致黏着在轮齿上的油液受到更大的作用力而更容易向外飞溅. 分别对比圆周转速v_t=0.9、1.4、2.1 m/s的工况，可以发现速度越大，齿轮侧面的油迹被甩开的张角越大，油液被甩的越远；同时，油迹的形状由圆滑连续变得零散间断，甚至油迹消失，在空中形成散乱分布的油粒. 这是由于 ${v_{\rm{t}}}$=1.4 m/s时齿轮所受离心力为 ${v_{\rm{t}}}$=0.9 m/s时的2.25倍， ${v_{\rm{t}}}$=2.1 m/s时所受离心力为 ${v_{\rm{t}}}$=1.4 m/s时的2.25倍. 速度增大，齿轮所受离心力逐渐增大，油液更容易脱离齿轮而向外飞溅.

为了分析黏度对油液飞溅分布的影响，设置FVA3和FVA2这2种型号润滑油的对比工况，在40 ℃时，两者的密度相近，而FVA2动力黏度约为FVA3的1/3. 对比图6、7，可以看出，由于低黏度润滑油的抗剪切应力能力较差，在油液分布形态上存在3点区别. 1）当润滑油黏度较高时，齿顶形成的油迹厚而连续，当黏度较低时，形成的油迹薄而间断，甚至呈油粒状. 2）当润滑油黏度较高时，轮齿附近产生的气泡数量少、体积大且形状规整；当黏度较低时，轮齿附近产生的气泡数量变多，体积变小且形状不规则. 3）当润滑油黏度较高时，黏着在轮齿根部的月牙形油液区域面积大，说明其从轮齿上滑落的速度慢；当黏度较低时，月牙形区域面积明显变小，且形状接近于弓形，说明油液滑落的速度快.

对比试验所得的图片，可以看到数值仿真方法可以较准确地捕捉到浸没在油液中的齿间气泡以及在齿轮对两侧散开的弧形油迹之类的油液分布细节特征，同时可以清晰表现出不同转速和润滑油黏度工况下齿轮箱内油液分布形态的差异，说明MPS法在齿轮箱飞溅润滑油液分布形态的预测上具有较好效果.

相对传统的试验方法，CFD方法可以容易地获得油液的相关数据信息，比如液体的速度场云图、压力场云图和迹线分布状况等. 为了更好地了解流场特性，提取低转速工况下润滑油速度场分布云图，结果如图8所示.可以看出，在各工况中，具有速度的粒子主要为齿轮搅动区域附近的粒子和被甩到空中的粒子，而齿轮箱中大部分粒子的速度均约为零. 在油位以下齿轮附近的粒子速度较低，随着其被旋转的齿轮逐渐搅起，更多的能量传递到油液粒子中，粒子动量逐渐增大，速度逐渐增大，最终与附着处齿轮的局部速度大小一致. 部分齿顶处粒子在速度等于齿顶圆圆周速度后，在离心力和重力作用下脱离齿顶，并在惯性作用下继续飞溅. 这表明该计算具有较好的物理一致性，因为根据Stocks黏性条件，运动壁上的牛顿流体粒子的速度与壁速相同.

此外，与预想的一样，在润滑油黏度一定时，随着齿轮转速的提高，润滑油粒子的速度逐渐增加. 在40 ℃时，FVA3型号润滑油黏度约为FVA2的3倍；在100 ℃时，FVA3型号润滑油黏度约为40 ℃时FVA2润滑油的1/3. 对比分析图8可以看到，随着润滑油黏度的逐渐降低，油液粒子的分布逐渐变得分散，因为黏度减低，油液之间的作用力变小，油液会很快分散，变成小的油滴颗粒. 尤其FVA3型润滑油油温在100 ℃时，相比于40 ℃时，齿轮对两侧的清晰油迹已经基本消失，粒子以散乱的形式分布在空气中.

综上，试验与MPS法数值仿真具有较好的一致性. 同时，仿真的流场分布与试验结果也存在些许差异，差异的产生主要与如下4个方面相关：1)MPS法使用基于纯拉格朗日法的粒子法，具有较高的求解效率，在求解强非线性自由液面问题和复杂模型时具有较大优势，但在求解精度上有待进一步提高；2)考虑到计算资源，只进行了油液单相求解，造成求解精度有所降低；3)从数值仿真来看，湍流效应是该方法常见的误差来源^[22]；4)误差还可能与曝气效应和试验温度存在一定联系. 总的来说，MPS法较好地捕捉到了流场流动的主要特征，并且准确展现了粒子的速度分布云图，在齿轮箱飞溅润滑流场分布上具有较好的预测作用.

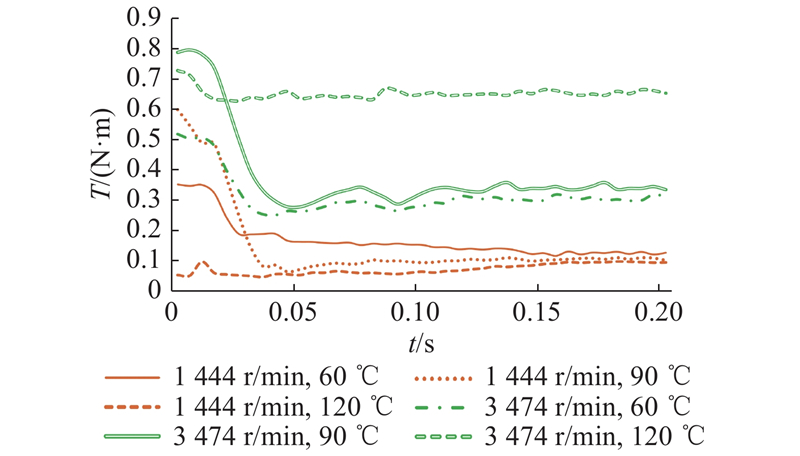
MPS方法通过插值方法将流体力作用到齿轮表面，齿轮表面受到的反作用力与力臂乘积即为搅油力矩损失. 不同工况下力矩损失的时域变化曲线如图9所示. 图中， $T$为搅油损失力矩， $t$为时间. 可以看出，力矩损失是随时间波动的曲线，在前期，齿轮搅油还未达到稳态，曲线波动幅度较大，随着时间推移，齿轮搅油逐渐达到稳态，力矩损失趋于稳定.

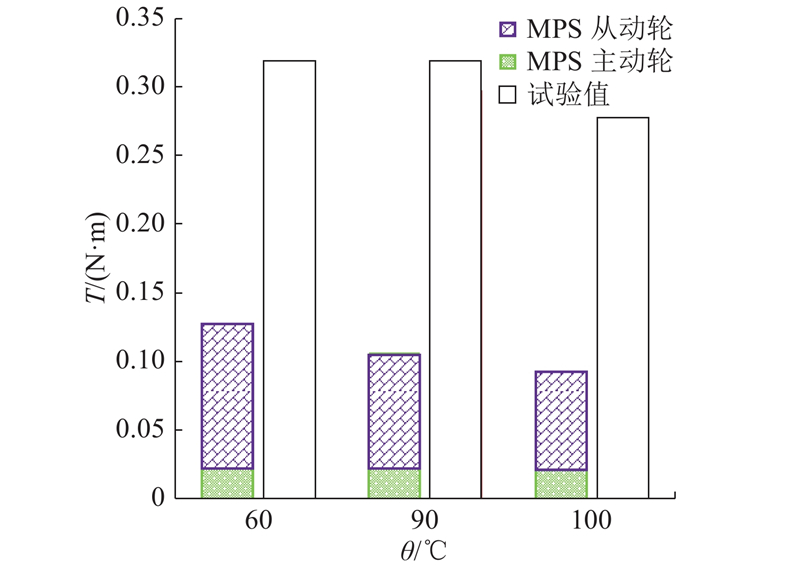
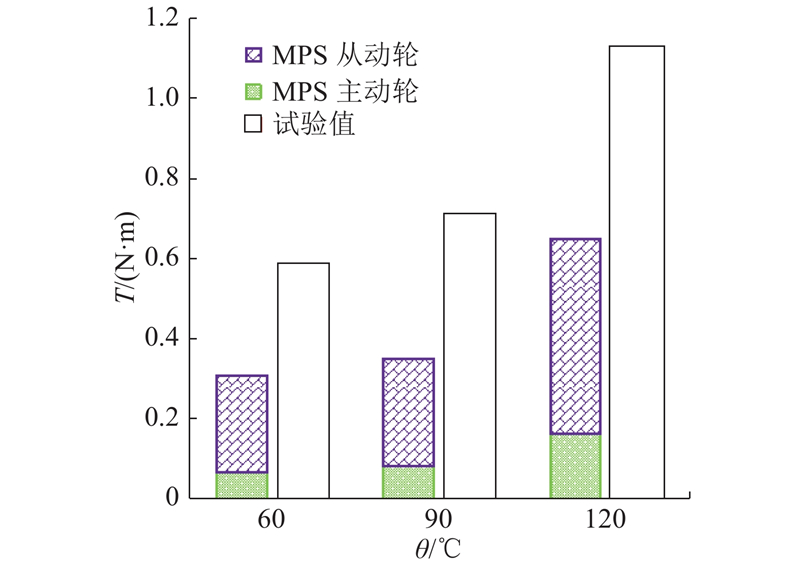
力矩损失在齿轮搅油后期会达到稳定状态，取各个工况从动轮旋转至第7~10圈(即1444 r/min时的第0.291~0.416 s，3474 r/min时的第0.121~0.173 s)的数据作均值处理，得到各工况的搅油力矩损失. 参考文献[14]的力矩损失结果，高转速工况时试验与MPS数值仿真力矩损失对比如图10、11所示. 可以看出，数值仿真结果与试验结果的变化趋势一致. 在转速为1444 r/min（圆周速度约为8.3 m/s）时，搅油损失力矩随油温的增高而降低. 这主要是由于随着油温从60 ℃增加到120 ℃，润滑油黏度降低至1/9，其阻力矩降低. 这与Seetharaman^[23]提出的在低转速时阻力矩随润滑油黏度降低而降低相符. 在转速为3474 r/min（圆周速度约为20 m/s）时，搅油损失力矩试验值随油温增高而增高，这与Liu^[14]提出的圆周转速约为5 m/s时，阻力矩随润滑油黏度增高而增高，圆周转速约为20 m/s时，阻力矩随润滑油黏度降低而增高的规律相一致. 因为油液黏度越大，流体越容易沿齿轮方向运动^[24]. 在齿轮转速高时，油液雷诺数高，其受惯性力影响大于黏滞力，油液黏度越大，会有更多油液被带入齿轮上部或甩到空中，齿轮浸入油液的部分变小，从而使得搅油损失力矩降低. 在转速低时，油液雷诺数小，其受黏滞力影响大于惯性力，油液黏度变大，油液被带入齿轮上部或甩至空中的油量变化不大，此时，搅油力矩损失主要受油液阻力矩影响，因此，油温增高，搅油力矩损失降低. Chernoray等^[25]也观察到了相同的规律.

另外，无论从试验还是仿真结果，均可以看到齿轮箱在高转速时的搅油损失力矩更大. 这与Otto^[26]的试验结果一致：速度对搅油功率损失的影响最大，随着齿轮转速提升，齿轮箱内油液的湍流区域增加，齿轮箱空余空间也逐渐充满油液，同时齿面与油液的相互作用力也更大，导致了更高的搅油损失. 同时，从图10、11中的MPS仿真值可看到，主动轮搅油损失力矩仅占总损失的约16~24%，主要可能与如下两方面有关：1）与从动轮相比，主动轮体积和表面积较小，浸油深度浅，导致齿轮搅油时与油液的接触表面积相对更少；2）主动轮离心力更大，将更多油液甩向空中，导致液位下与齿轮接触的油液更少.

为了分析MPS数值方法和SPH方法在搅油力矩损失预测上的准确性，参考文献[14]中SPH数值仿真结果. 如表8所示为不同工况下试验与仿真结果误差. 表中， ${T_{\rm{m}}}$为MPS法力矩损失， ${T_{\rm{s}}}$为SPH法力矩损失， ${T_{\rm{e}}}$为试验力矩损失， ${\delta _{\rm{m}}}$为MPS误差， ${\delta _{\rm{s}}}$为SPH法误差. 由表8、图10、图11可以看出，当转速较低，为1444 r/min时，MPS法误差为60%~66%，SPH法误差为61%~69%，2种数值方法结果与试验结果变化趋势一致；当转速较高，为3474 r/min时，MPS法误差为43%~ 51%，SPH法误差为55%~ 82%，且MPS法仿真结果与试验结果变化趋势一致，而SPH法结果与试验结果变化趋势相反. 对比分析可知，MPS数值方法在搅油力矩损失的预测上比SPH数值方法准确，但与试验结果相比，仿真误差较大.

试验与仿真误差大概与如下4个方面有关. 1）试验误差，试验过程中难免存在测量误差以及数据采集数量有限导致的处理精度误差. 2）文献[4]中的力矩损失是通过空载损失减去密封和轴承损失得到的，其中轴承和密封损失必然存在一定误差，这给力矩损失试验值带来了误差. 3）限于计算机硬件条件，本研究只对油液单相进行数值仿真，忽略了气相对齿轮的作用，导致搅油功率损失的仿真值偏低. 4）MPS数值仿真方法存在的缺点带来的误差.

针对MPS数值仿真方法带来的误差，根据低转速工况的流场特性分析，推测主要存在如下3点原因：1) 湍流模型. 齿轮副的搅油力矩损失主要来源于齿轮齿面、端面与润滑油相互作用之间的剪切力，且相互作用力的大小与湍流密切相关. 在仿真时，MPS法使用的是大涡模拟（LES）湍流模型. 目前，湍流的数值模拟还不成熟，大涡模拟是新的解决湍流的研究方法，解决湍流问题的效果相对较好. 大涡模拟在完全模拟的基础上忽略了小涡模拟，对内存的要求降低，计算速度提高. 然而在齿轮箱飞溅润滑流场中存在一定数量的小涡，大涡模拟湍流模型仿真时未捕捉到这些湍流特征，给搅油力矩损失带来了误差. 2)压力震荡现象. 压力震荡是MPS法的常见现象，主要是由粒子运动的随机性导致的. 若存在该现象说明仿真精度不高，从而带来力矩损失误差. 可以通过修改压力泊松方程缓解该现象. 3)核函数. 核函数是MPS方法中的最基本模型，粒子间的相互作用就是通过核函数实现的. 因此，更优的核函数对仿真精度的提高至关重要.

运用MPS法分析低转速时，不同润滑油型号、转速和油温工况下齿轮箱飞溅润滑流场和速度场分布情况，对比研究高转速工况时，3种润滑油温度下MPS和SPH这2种数值仿真结果与试验结果的齿轮搅油力矩损失.

(1)通过对比分析齿轮箱润滑油流场分布和速度场可知，MPS法可以较好地捕捉到流场流动的主要特征，同时可以较准确地展现粒子的速度分布云图，在齿轮箱飞溅润滑流场分布上具有较好的预测作用.

(2)在低转速工况时，MPS法与SPH法的搅油力矩损失误差区别较小，在高转速工况时，MPS法比SPH法误差低约17%. 相对于SPH法，MPS法能准确预测搅油力矩损失趋势，且精度相对较高. 但与实验值相比，MPS法在搅油力矩损失预测上的误差较大，须对误差进行仔细分析.

(3)本研究仿真及实验组数有限，未对仿真误差开展统计学分析和评估. 接下来可以对误差开展系统分析，或针对具体工程应用多级齿轮箱开展研究.