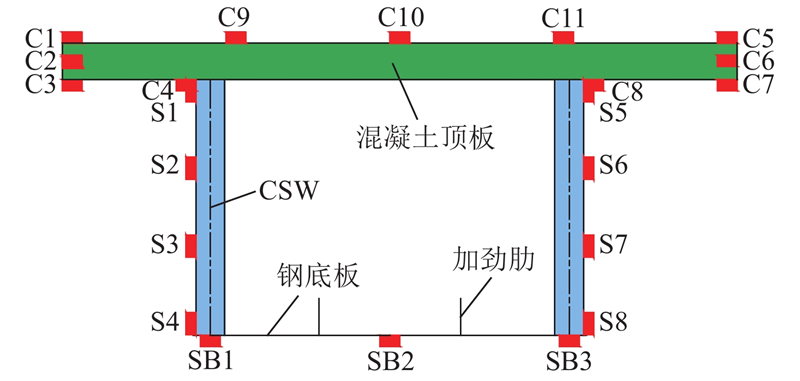
波形钢腹板(corrugated steel web,CSW)组合箱梁因其自重轻、力学性能好和造型美观等特点,近年来在我国公路桥梁建设中被广泛应用,但该组合结构下翼缘混凝土置于梁底,构造复杂,施工难度较大. 为了克服混凝土底板浇筑困难,减轻结构自重的问题,Nie等[1]提出用带肋钢底板代替传统CSW组合箱梁混凝土底板的新型CSW组合箱梁结构.
目前,国内外针对桥梁温度效应的的研究对象主要针对混凝土结构,对组合结构桥梁的相关研究相对较少. 各国规范[4-7]对组合梁桥竖向温度梯度模式的规定并非针对组合梁桥专门制定,而是对混凝土箱梁修正或变异得到的,因此对组合梁结构的适用性不强. 陈彦江等[8-11]基于现场实测数据拟合了组合梁的竖向温度梯度函数,利用有限元法计算组合梁温度效应,与规范梯度下的温度效应进行对比,分析实测温度梯度与规范梯度的差异性. 对于传统CSW组合箱梁结构,徐向锋等[12-14]基于CSW组合梁桥的现场温度实测数据,建立该类梁桥的温度场二维模型. 赵品等[15]对某CSW连续箱梁桥进行长期温度效应观测,提出CSW箱梁温差计算模式,结果表明,温度效应产生的横向应力与车辆荷载结果相当. 迄今,针对CSW组合箱梁桥温度效应居多采用现场实测拟合温度梯度与有限元模拟计算温度响应相结合的方式,通过理论推导对CSW组合箱梁结构进行温度效应计算的研究成果较少. Shan等[16]结合CSW预应力混凝土组合箱梁的力学特性,忽略波形腹板剪切变形,推导CSW简支梁桥温度应力的计算公式,分别讨论了连接件为刚性和柔性时的最大温度应力计算方法. CSW组合箱梁腹板的褶皱效应使得该类组合箱梁剪切变形较一般混凝土箱梁更显著[17],因此忽略剪切变形影响可能给温度效应的计算结果带来一定偏差,不利于结构设计.
我国西北干寒地区干燥少雨、太阳辐射强、日温差大,组合结构桥梁温度效应问题突出,新型CSW组合箱梁桥温度效应计算尚无专门规范可依. 本文通过现场实测、拟合,得到新型CSW组合箱梁温度梯度模式. 考虑腹板剪切变形效应和子梁间滑移效应,建立新型CSW组合箱梁温度效应的计算方法,为设计计算和推广应用提供必要的理论依据.
1. 计算理论
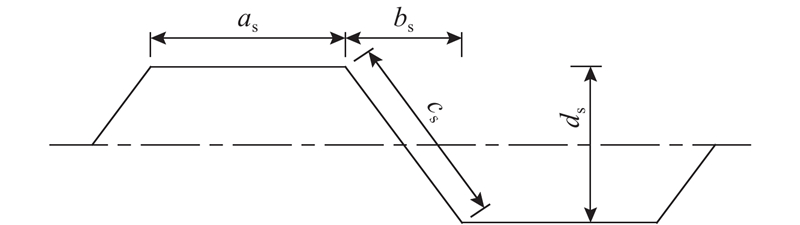
1.1. CSW的特性
式中:
图 1
1.2. CSW组合箱梁温度效应计算理论
在理论推导过程中,将子梁(混凝土顶板和波形腹板钢箱梁)所受轴力、剪力、弯矩、拉压刚度、抗弯刚度、接触面剪力和滑移分别表示为
CSW组合箱梁温度效应计算理论的基本假设如下.
1)组合箱梁各子梁材料均为线弹性.
2)钢-混凝土接触面上剪力连接件均匀布置,剪力钉所受剪力与层间相对滑移成正比.
3)子梁之间不会发生竖向掀起,子梁曲率和挠度相等.
4)温度沿梁纵向不发生变化,各子梁温度沿高度方向呈线性变化.
由组合箱梁截面上内力平衡条件,可得
式中:
根据组合梁微元体内力平衡条件,可知
CSW和混凝土顶板在接触面上的变形条件为
式中:
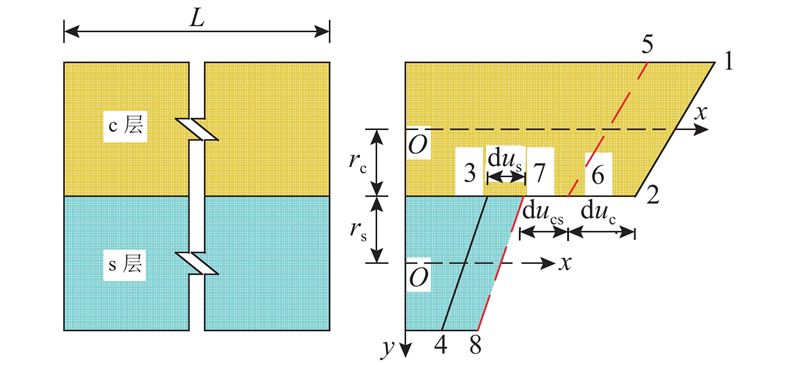
图 2
图 2 新型波形钢腹板组合箱梁的轴向变形
Fig.2 Axial deformation of new corrugated steel web composite box girder
根据假定2,可知
式中:
将式(7)~(9)代入式(6),整理得到
式中:
联立式(2)、(10),可得
式中:
假设混凝土顶板和波形腹板钢箱梁的曲率在温度梯度作用下保持相等,即
式中:
根据等曲率假设,推得
式中:
式中:
对4阶微分方程(16)进行求解,可得通解为
式中:
根据双曲函数的性质,将式(17)转换为
式中:
在组合箱梁跨中位置建立笛卡尔坐标系,设梁计算跨径为L,故在梁跨中的界面剪力
将上述内力边界条件代入式(14),可得
代入边界条件求出待定常数
将钢-混凝土接触面上离散的剪力键简化为连续均匀分布,且组合梁为弹性工作状态. 接触面相对滑移
若不计CSW剪切变形的影响,则在式(15)中将
由组合箱梁温度作用下的内力响应,可得混凝土板和波形腹板钢箱梁的上、下缘温度应力:
式中:下标t、b分别表示子梁的上缘和下缘.
2. 有限元模拟
2.1. 模型概况
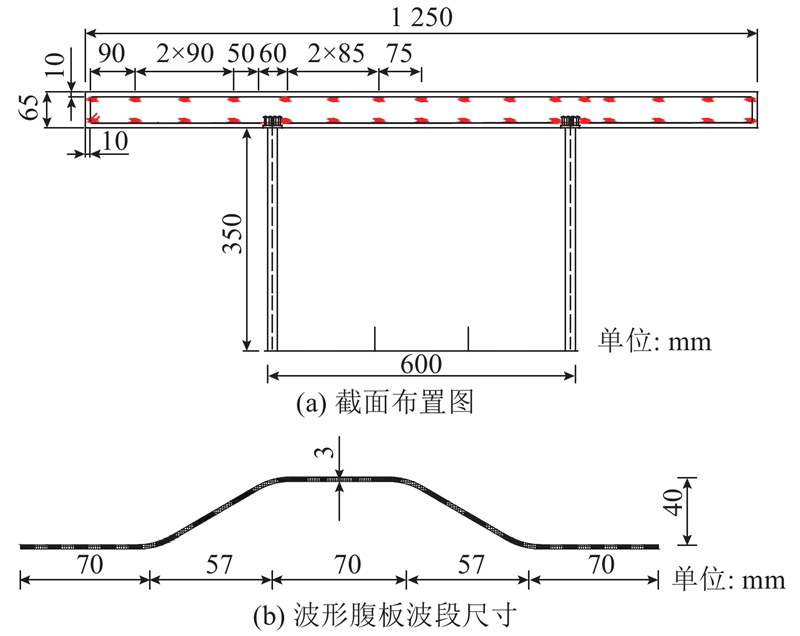
试验梁为单箱单室新型波形钢腹板组合箱梁(L=8.0 m). 梁高415 mm,顶板宽1 250 mm,底板宽600 mm. 顶板采用C50混凝土浇筑,试验室测得混凝土翼板28 d抗压强度平均值为51.3 MPa. 波形钢腹板厚3 mm,底板及底板加劲肋厚5 mm,均采用Q235钢材制作. 试验梁的基本尺寸如图3所示.
图 3
图 3 新型波形钢腹板组合箱梁的几何参数
Fig.3 Geometric parameters of new-type corrugated steel web composite box girder
2.2. 有限元建模
表 1 20 °C时的材料特性
Tab.1
| 材料 | 混凝土 | Q235钢材 |
| 弹性模量E/MPa | 3.45×104 | 2.1×105 |
| 质量密度ρ/(kg·m−3) | 2550 | 7850 |
| 线膨胀系数 | 1.0 | 1.2 |
| 导热系数/(W·m−1·°C−1) | 2.3 | 58.2 |
| 泊松比 | 0.2 | 0.33 |
图 4
3. 新型CSW组合箱梁温度梯度拟合
国内在钢-混凝土组合箱梁温度设计中主要参照《钢-混凝土组合桥梁设计规范》(GB 50917—2013),现行各类规范中均未给出专门针对CSW组合箱梁温度梯度分布模式. 鉴于该类新型桥梁的特点和桥梁地域差异性,在实际应用中不宜简单套用规范梯度. 对试验梁进行1 a(2018−12—2019−11)的温度测试,通过实测数据建立新型波形钢腹板组合箱梁的竖向温度分布函数.
图 5
图 6
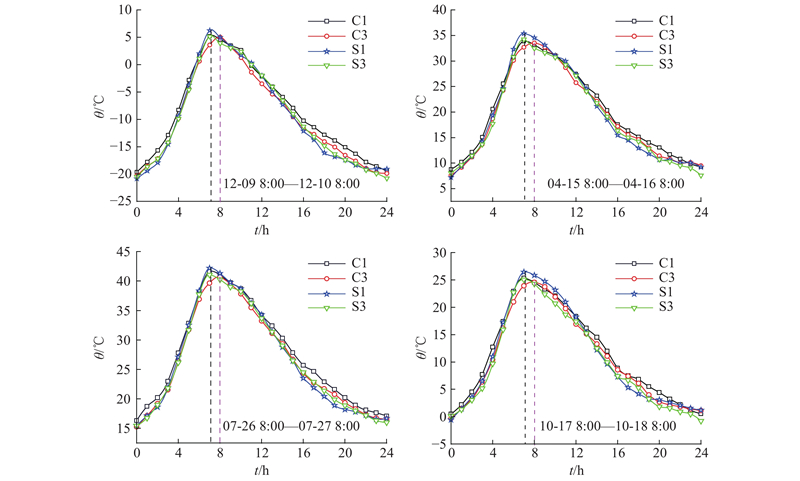
图 7
由图7可知,试验梁各测点的温度随着环境温度的变化呈正弦曲线变化. 由于钢与混凝土导热性能的显著差异,在同一时刻,钢-混凝土结合处存在一定的温差. 混凝土顶板和钢腹板最高温时间为15:00,混凝土底板最高温时间为16:00. 采用测试顶面温度达到最大值时刻(15:00)的结构温度分布形式作为最不利温度梯度,以混凝土顶板上表面平均温度
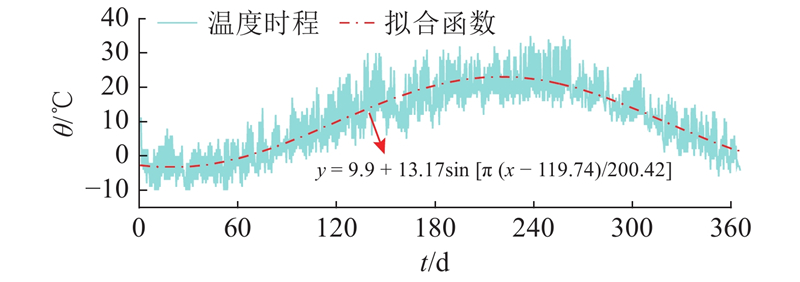
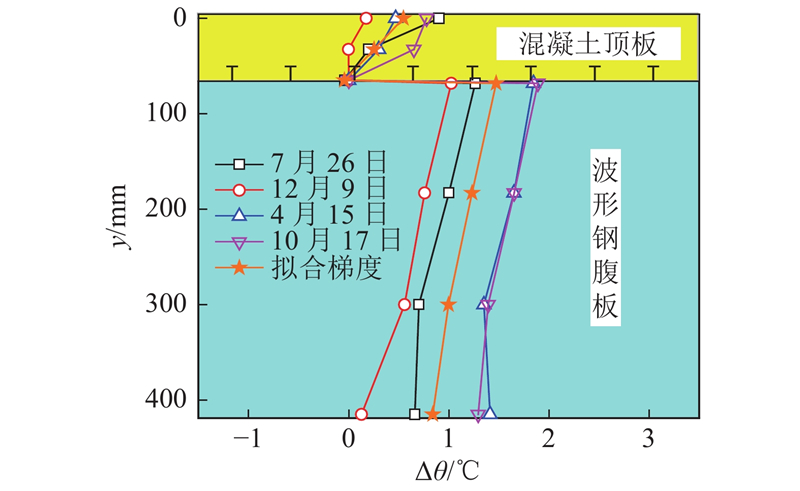
式中:y为温度测点到箱梁顶面的距离. 拟合结果如图8所示. 图中,
图 8
4. 温度效应结果分析
4.1. 温度效应分析
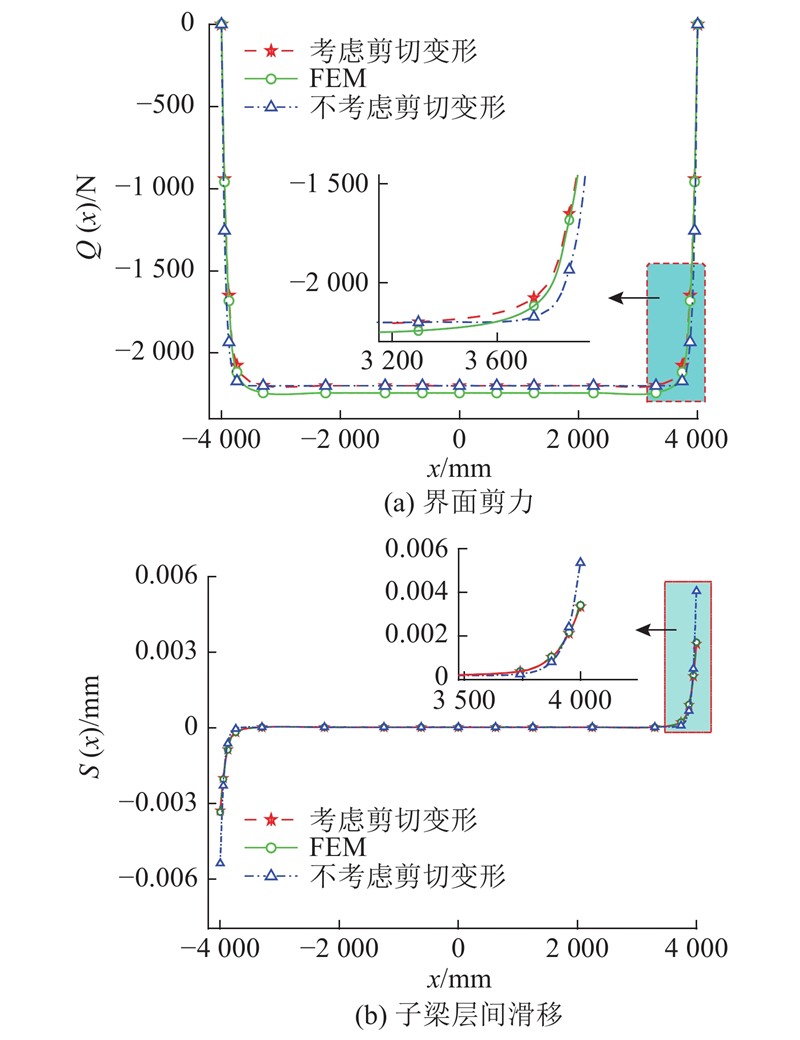
运用本文的理论计算方法,对新型波形钢腹板组合箱梁展开温度效应研究. 运用有限元模型数值模拟(FEM),验证本文方法的可靠性. 组合箱梁沿梁纵向的界面剪力和层间相对滑移分布如图9所示.
图 9
从图9可以看出,采用考虑腹板剪切变形效应、不考虑腹板剪切变形效应和FEM方法,计算得到界面剪力均沿梁纵向服从双曲余弦函数分布,子梁层间滑移均沿梁纵向服从双曲正弦函数分布. 总体来看,3种方法在L/10~9L/10梁段范围内计算结果的最大偏差仅为2.01%,在剩余梁段内,考虑腹板剪切变形效应的计算值略小于有限元值,最大偏差仅为2.4%,与不考虑腹板剪切变形效应计算值的最大偏差可达56.7%. 由此可见,本文计算方法的可靠性较高.
表 2 组合箱梁温度效应主要计算结果
Tab.2
| 位置/m | 是否考虑剪切变形 | Q(x)/kN | S(x)/(10−3 mm) | Mc /(105 N·mm) | Ms /(N·mm) | σc,t /MPa | σc,b /MPa | σs,t /MPa | σs,b /MPa |
| 跨中 | 是 | −2.701 | 0 | 5.55 | −5785.98 | −0.66 | 0.60 | 9.94 | −8.40 |
| 跨中 | 否 | −2.701 | 0 | 5.55 | −5785.98 | −0.66 | 0.60 | 9.94 | −8.40 |
| x=3.2 | 是 | −2.700 | 0.002 | 5.54 | −5784.14 | −0.66 | 0.60 | 9.94 | −8.40 |
| x=3.2 | 否 | −2.701 | 0 | 5.55 | −5785.89 | −0.66 | 0.60 | 9.94 | −8.40 |
| x=3.75 | 是 | −2.549 | 0.245 | 5.23 | −5547.94 | −0.63 | 0.56 | 9.52 | −8.06 |
| x=3.75 | 否 | −2.668 | 0.082 | 5.48 | −5630.46 | −0.66 | 0.59 | 9.69 | −8.16 |
| x=3.875 | 是 | −2.024 | 1.089 | 4.15 | −4727.64 | −0.50 | 0.45 | 8.07 | −6.91 |
| x=3.875 | 否 | −2.375 | 0.803 | 4.89 | −4260.98 | −0.58 | 0.53 | 7.43 | −6.07 |
| x=3.95 | 是 | −1.150 | 2.495 | 2.35 | −3358.67 | −0.28 | 0.25 | 5.65 | −4.99 |
| x=3.95 | 否 | −1.542 | 2.854 | 3.20 | −364.87 | −0.38 | 0.34 | 1.02 | −0.14 |
| x=4.0 | 是 | 0 | 4.240 | 0 | 0 | 0 | 0 | 0 | 0 |
| x=4.0 | 否 | 0 | 6.647 | 0 | 0 | 0 | 0 | 0 | 0 |
4.2. 参数分析
图 10
图 10 混凝土线膨胀系数对组合箱梁滑移和界面剪力的影响
Fig.10 Effect of linear expansion coefficient of concrete on slip and interfacial shear of composite box girder
图 11
图 11 层间滑移刚度对组合箱梁滑移和界面剪力的影响
Fig.11 Effect of sliding stiffness between layers on slip and interfacial shear of composite box girder
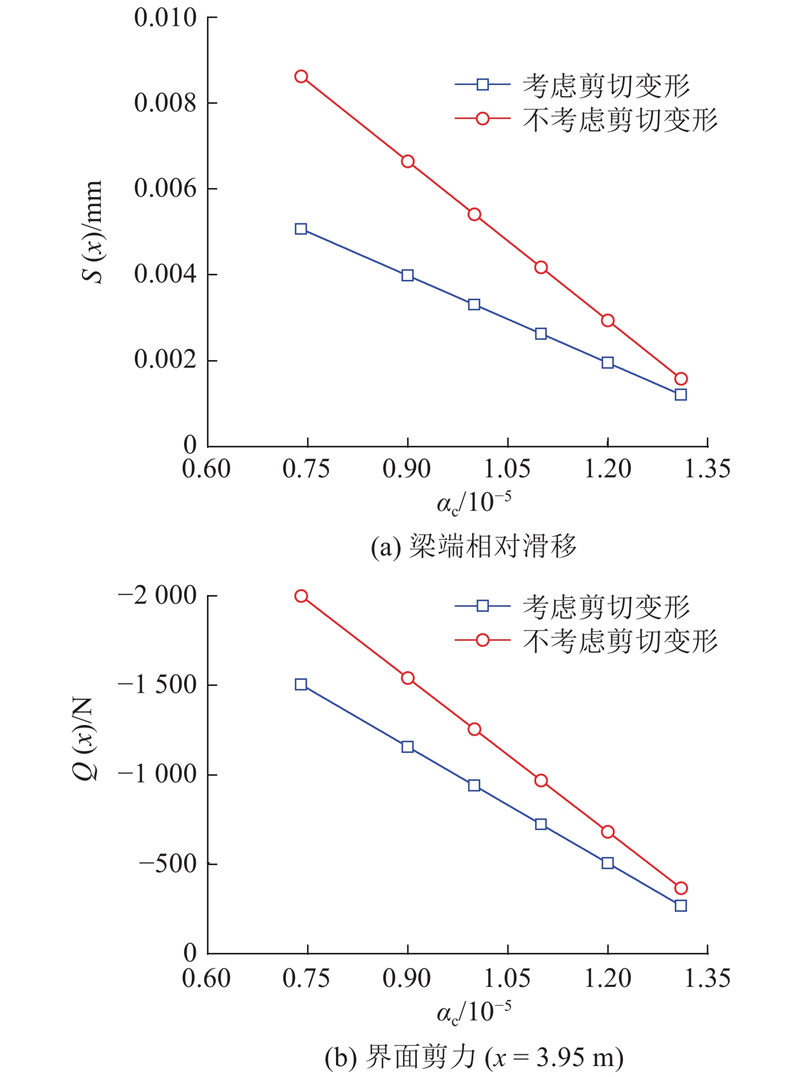
4.2.1. 混凝土线膨胀系数
图 12
图 12 界面温差对组合箱梁滑移和界面剪力的影响
Fig.12 Effect of interface temperature difference on slip and interfacial shear of composite box girder
由图10可得如下结论. 1)梁端相对滑移和界面剪力与
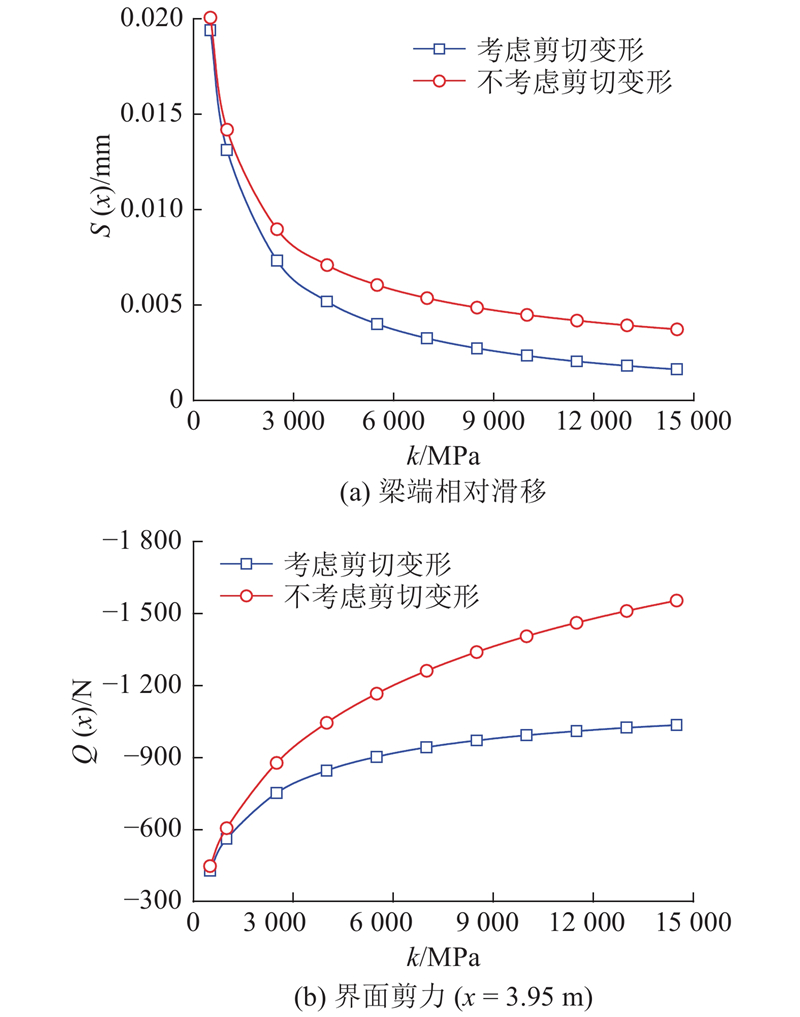
4.2.2. 层间滑移刚度k
层间滑移刚度是确保组合箱梁各子梁协同受力和整体结构性能最大化的关键因素. 如图11所示为层间滑移刚度改变时,组合箱梁梁端滑移和剪力的变化情况.
从图11可得如下结论. 1)接触面滑移刚度与梁端相对滑移呈负相关,与界面剪力呈正相关. 2)考虑腹板剪切变形效应后,梁端相对滑移和界面剪力响应均小于不考虑剪切变形工况,因此不考虑剪切变形会过大估计波形钢腹板组合箱梁的温度效应. 3)当k<1 000 MPa时,是否考虑腹板剪切变形效应求得梁端滑移和界面剪力相对误差小于10%,尚可满足工程精度要求. 当k进一步增大时,不考虑剪切变形的相对滑移和界面剪力响应分别可达考虑剪切变形效应时的2.3倍和1.5倍.
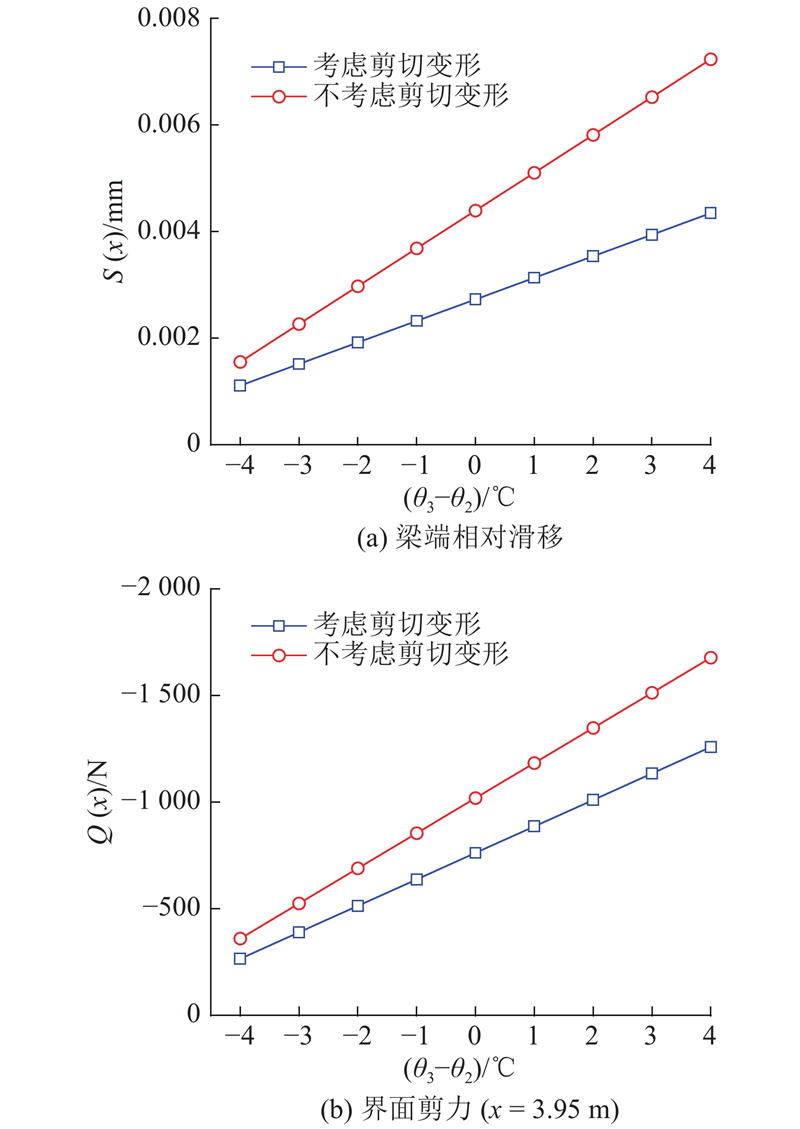
4.2.3. 界面温差
由图12可得如下结论. 1)界面温差与梁端相对滑移、界面剪力均呈正相关. 在考虑腹板剪切变形效应后,梁端相对滑移和界面剪力响应均小于不考虑剪切变形工况. 2)界面温差从−4~4 °C逐渐增大时,2种计算方法的相对误差从39.8%逐渐增至66.4%,剪力相对误差保持为34%.
综上分析表明,混凝土线膨胀系数、层间滑移刚度和界面温差对钢-混接触面剪力和相对滑移的影响较大. 混凝土线膨胀系数和层间滑移刚度减小或界面温差增大,均会引起梁端滑移增大. 在工程结构分析计算中,应考虑混凝土线膨胀系数的变异性,否则可能导致较大误差. 不考虑腹板剪切变形效应的温度效应计算结果普遍偏大. 在该类组合结构温度效应的计算分析中,应考虑上述因素的影响.
5. 结 论
(1)考虑组合箱梁子梁微段平衡条件、子梁间变形协调条件和波形钢腹板剪切变形效应,建立竖向温度梯度下新型波形钢腹板组合箱梁温度效应计算方法,利用有限元模拟验证了本文方法的可靠性.
(2)在实测温度梯度下,界面剪力沿梁纵向呈双曲余弦函数分布,层间相对滑移沿梁纵向呈双曲正弦函数分布. 是否考虑腹板剪切变形效应对组合梁梁端向跨中0.8 m(L/10)范围的温度效应影响较大,对组合梁中部的影响可以忽略不计.
(3)混凝土线膨胀系数、组合箱梁层间滑移刚度和界面温差对新型波形钢腹板组合箱梁温度效应的影响较大. 在设计中,应合理排布层间剪力连接件,考虑混凝土线膨胀系数的变异性,对该类结构进行温度效应计算.
参考文献
Optimized prestressed continuous composite girder bridges with corrugated steel webs
[J].
波形钢腹板PC组合箱梁几个特殊问题研究进展
[J].
Review on special issues in prestressed concrete box girders with corrugated steel webs
[J].
钢-混凝土组合梁温度效应的解析解
[J].DOI:10.3969/j.issn.1671-1637.2017.04.002 [本文引用: 1]
Analytical solution of temperature effects of steel-concrete composite girder
[J].DOI:10.3969/j.issn.1671-1637.2017.04.002 [本文引用: 1]
钢-混凝土组合梁桥温度场及温度效应研究
[J].DOI:10.3969/j.issn.1002-0268.2014.11.014 [本文引用: 1]
Research of temperature field and its effect of steel-concrete composite girder bridge
[J].DOI:10.3969/j.issn.1002-0268.2014.11.014 [本文引用: 1]
高原高寒地区钢-混凝土组合梁斜拉桥温度效应分析
[J].DOI:10.3969/j.issn.1673-2049.2016.01.016
Temperature effect analysis of steel-concrete composite girder cable-stayed bridge in arctic-alpine region
[J].DOI:10.3969/j.issn.1673-2049.2016.01.016
组合高墩大跨连续刚构桥箱梁日照温度场观测与效应分析
[J].DOI:10.3969/j.issn.1672-7029.2014.01.002
Observation and study of temperature distribution in combination of high pier large span continuous and rigid frame bridge
[J].DOI:10.3969/j.issn.1672-7029.2014.01.002
Experimental and finite element investigation of temperature distributions in concrete-encased steel girders
[J].
波形钢腹板箱梁温度分布
[J].DOI:10.3969/j.issn.1674-0696.2018.12.01 [本文引用: 1]
Temperature distribution of box girder with corrugated steel webs
[J].DOI:10.3969/j.issn.1674-0696.2018.12.01 [本文引用: 1]
波形钢腹板组合桥梁温度效应研究
[J].
Study of temperature effect on the composed bridge with corrugated steel webs
[J].
大跨波形钢腹板箱梁桥日照温度场及温差效应研究
[J].
Research on sunlight temperature field and thermal difference effect of long span box girder bridge with corrugated steel webs
[J].
波形钢腹板箱梁桥面板横向温度效应分析
[J].
Analysis of transverse temperature effects on the deck of box girder with corrugated steel webs
[J].
Temperature stress analysis of prestressed concrete box girder with corrugated steel webs
[J].DOI:10.1007/s12209-012-1626-8 [本文引用: 1]
基于剪切附加挠度的波形钢腹板组合箱梁挠度计算
[J].DOI:10.3969/j.issn.1671-6264.2019.02.016 [本文引用: 1]
Deflection calculation of composite box girder with corrugated steel webs based on shear additional deflection
[J].DOI:10.3969/j.issn.1671-6264.2019.02.016 [本文引用: 1]
Bending strength of steel beams with corrugated webs
[J].DOI:10.1061/(ASCE)0733-9445(1997)123:6(772) [本文引用: 1]
Finite element static and dynamic analyses of folded plates
[J].
耐火钢-混凝土组合梁耐火极限和承载力
[J].
Fire resistance and bending bearing capacity of fire resistant steel-concrete composite beams
[J].