式中: $k$ $\lambda $ $k = {{2 {\text{π}} } / \lambda }$ $I\left( {x,y} \right)$ $A(x,y)$ $I\left( {x,y} \right) = {A^2}\left( {x,y} \right)$ $\nabla $ $I(x,y)$ $\phi (x,y)$ ${{\partial I(x,y)} / {\partial z}}$
[1]
SIMPSON J, LOPEZ L, ACAR P, et al Three-dimensional echocardiography in congenital heart disease: an expert consensus document from the European Association of Cardiovascular Imaging and the American Society of Echocardiography
[J]. Journal of the American Society of Echocardiography , 2017 , 30 (1 ): 1 - 27
DOI:10.1016/j.echo.2016.08.022
[本文引用: 1]
[2]
MUSARRA G, LYONS A, CONCA E, et al Non-line-of-sight three-dimensional imaging with a single-pixel camera
[J]. Physical Review Applied , 2019 , 12 (1 ): 011002
DOI:10.1103/PhysRevApplied.12.011002
[本文引用: 1]
[3]
陈妮, 左超, BYOUNGHO L 基于深度测量的三维成像技术
[J]. 红外与激光工程 , 2019 , 48 (6 ): 199 - 223
URL
[本文引用: 1]
CHEN Ni, ZUO Chao, BYOUNGHO L 3D imaging technology based on depth measurement
[J]. Infrared and Laser Engineering , 2019 , 48 (6 ): 199 - 223
URL
[本文引用: 1]
[4]
BORN M, WOLF E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light [M]. Heading Hill Hall, Oxford OX3 0BW, England: Pergamon Press, 2013.
[本文引用: 1]
[5]
GERSHUN A The light field
[J]. Journal of Mathematical Physics , 1939 , 18 : 51151
URL
[本文引用: 1]
[6]
LAM E Y Computational photography with plenoptic camera and light field capture: tutorial
[J]. Journal of the Optical Society of America , 2015 , 32 : 2021 - 2032
DOI:10.1364/JOSAA.32.002021
[本文引用: 1]
[7]
黄坦. 基于强度传输方程的凸优化相位恢复算法研究[D]. 武汉: 华中科技大学, 2019.
[本文引用: 1]
HUANG Tan. Study of convex optimization phase retriev- al algorithm based on transport of intensity equation[D]. Wuhan: Huazhong University of Science and Technology, 2019.
[本文引用: 1]
[8]
纵榜铭. 基于PIE相位恢复的成像光学元件检测技术研究[D]. 无锡: 江南大学, 2019.
[本文引用: 1]
ZONG Bang-ming. Aberration measurement on optical imaging element with ptychographic iterative engine[D]. Wuxi: Jiangnan University, 2019.
[本文引用: 1]
[9]
沈成. 基于多图像迭代相位恢复技术的计算成像特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[本文引用: 1]
SHEN Cheng. Computational imaging based on iterative multi-image phase retrieval techniques[D]. Harbin: Harbin Institute of Technology, 2018.
[本文引用: 1]
[10]
TEAGUE M R Deterministic phase retrieval: a Green’s function solution
[J]. Journal of the Optical Society of America , 1983 , 73 (11 ): 1434 - 1441
DOI:10.1364/JOSA.73.001434
[本文引用: 1]
[11]
程鸿, 熊帮玲, 王金成, 等 基于配准递进补偿的相位恢复
[J]. 光子学报 , 2019 , 48 (4 ): 0410002
URL
[本文引用: 1]
CHENG Hong, XIONG Bang-ling, WANG Jin-cheng, et al Phase retrieval based on registration progressive compensation algorithm
[J]. Acta Optica Sinica , 2019 , 48 (4 ): 0410002
URL
[本文引用: 1]
[12]
左超, 陈钱, 孙佳嵩, 等 基于光强传输方程的非干涉相位恢复与定量相位显微成像: 文献综述与最新进展
[J]. 中国激光 , 2016 , 43 (6 ): 227 - 257
URL
[本文引用: 1]
ZUO Chao, CHEN Qian, SUN Jia-song, et al Non-interferometric phase retrieval and quantitative phase microscopy based on transport of intensity equation: a review
[J]. Chinese Journal of Lasers , 2016 , 43 (6 ): 227 - 257
URL
[本文引用: 1]
[13]
高要利. 双波长下基于强度传输方程的相位恢复和相位解缠研究[D]. 合肥: 安徽大学, 2019.
[本文引用: 1]
GAO Yao-li. Research on phase retrieval and phase unwrapping based on transport of intensity equation at two wave lengths[D]. Hefei: Anhui University, 2019.
[本文引用: 1]
[14]
CHENG H, WANG R, YE Y Q, et al Transport of intensity equation method based on edge detection and duty ratio fusion
[J]. Journal of Optics , 2020 , 22 (4 ): 045302
DOI:10.1088/2040-8986/ab7ae9
[本文引用: 1]
[15]
SUI L, ZHAO X, HUANG C, et al An optical multiple-image authentication based on transport of intensity equation
[J]. Optics and Lasers in Engineering , 2019 , 116 : 116 - 124
DOI:10.1016/j.optlaseng.2019.01.006
[16]
HU J, WEI Q, KONG Y, et al Higher order transport of intensity equation methods: comparisons and their hybrid application for noise adaptive phase imaging
[J]. IEEE Photonics Journal , 2019 , 11 (3 ): 1 - 14
URL
[本文引用: 1]
[17]
FAYED M, ELHADARY M, ABDERRAHMANE H A, et al The ability of forecasting flapping frequency of flexible filament by artificial neural network
[J]. Alexandria Engineering Journal , 2019 , 58 (4 ): 1367 - 1374
DOI:10.1016/j.aej.2019.11.007
[本文引用: 1]
[18]
CHENG II H, LIU Y, ZHANG II Q. Phase retrieval algorithm based on the neural network and the GS[C]// Holography, Diffractive Optics, and Applications IX . Hangzhou: ISOP, 2019: 1118809.
[本文引用: 1]
[19]
NEHMETALLAH G T, AYLO R, WILLIAMS L. Analog and digital holography with MATLAB [M]. Bellingham: SPIE, 2015.
[本文引用: 1]
[20]
左超. 基于光强传输方程的非干涉相位恢复与定量相位显微成像方法研究[D]. 南京: 南京理工大学, 2014.
[本文引用: 1]
ZUO Chao. Research on non-interferometric phase retrieval and quantitative phase microscopy based on transport of intensity equation[D]. Nanjing: Nanjing University of Science and Technology, 2014.
[本文引用: 1]
[21]
GLOROT X, BENGIO Y. Understanding the difficulty of training deep feedforward neural networks[C]// Proceedings of the 13th International Conference on Artificial Intelligence and Statistics . Sardinia, Italy: PMLR, 2010: 249-256.
[本文引用: 1]
[22]
RUDER S. An overview of gradient descent optimization algorithms [DB/OL]. (2017-06-15)[2021-02-19]. https://arxiv.org/abs/1609.04747.
[本文引用: 1]
[23]
HECHT-NIELSEN R. Theory of the backpropagation neural network [M]// Neural networks for perception . Oval Road: Academic Press, 1992: 65-93.
[本文引用: 1]
Three-dimensional echocardiography in congenital heart disease: an expert consensus document from the European Association of Cardiovascular Imaging and the American Society of Echocardiography
1
2017
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
Non-line-of-sight three-dimensional imaging with a single-pixel camera
1
2019
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
基于深度测量的三维成像技术
1
2019
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
基于深度测量的三维成像技术
1
2019
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
1
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
The light field
1
1939
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
Computational photography with plenoptic camera and light field capture: tutorial
1
2015
... 现今,由于三维(3D)成像技术能够更直观地表达出现实世界中的大量信息,该技术的应用越来越广泛,尤其是在生物医学领域[1 ] 和信息科学领域[2 ] . 为了进行三维成像,需要获取物体的三维信息. 所谓三维信息,通常是指物体的深度或者形状信息,三维信息是包含在物体光波场之中. 三维成像在某些情况下可以看成是物体光波前的振幅和相位成像,也称为波前成像或光波场成像. 除此之外,三维成像可以看作是光线场成像[3 ] . 光线和光波是不同光层面的表示,两者分别属于几何光学和波动光学范畴,Eikonal方程给出两者之间的联系[4 ] . 从几何光学来看,可以将光视为光线,从而通过几何关系来描述光的传播和反射情况. 通过记录物体发出的光线及方向,可以重构出物体的三维表面形态[5 -6 ] . ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
1
... 无论是光波场成像中的“相位”还是光线场成像中的“光线”,都无法被直接获取. 在光学领域内,完整的光场信息由强度和相位构成,通常用二维复振幅来描述,即振幅的平方称为强度,幅角称为相位[7 ] . 根据相关研究表明,相位信息包含了物体的深度、形状等表面信息,重要程度远超于强度信息. 目前市场上主要的光传感设备只能获取物体强度信息,丢失了相位信息,因此相位恢复技术[8 -9 ] 具有重要的研究意义. ...
Deterministic phase retrieval: a Green’s function solution
1
1983
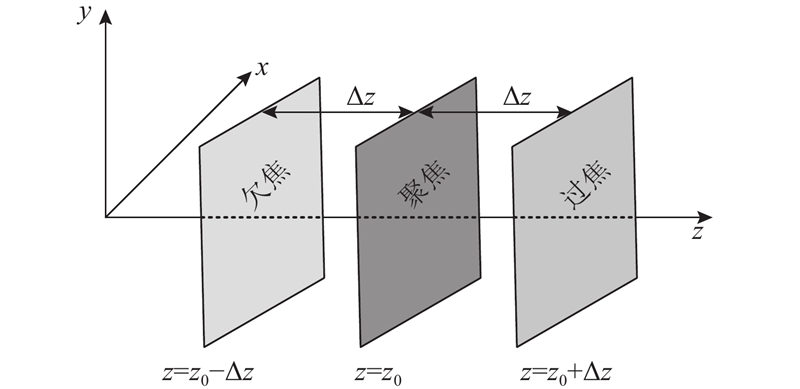
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
基于配准递进补偿的相位恢复
1
2019
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
基于配准递进补偿的相位恢复
1
2019
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
基于光强传输方程的非干涉相位恢复与定量相位显微成像: 文献综述与最新进展
1
2016
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
基于光强传输方程的非干涉相位恢复与定量相位显微成像: 文献综述与最新进展
1
2016
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
1
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
1
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
Transport of intensity equation method based on edge detection and duty ratio fusion
1
2020
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
An optical multiple-image authentication based on transport of intensity equation
0
2019
Higher order transport of intensity equation methods: comparisons and their hybrid application for noise adaptive phase imaging
1
2019
... 基于强度传输方程(transport of intensity equation,TIE)的相位恢复[10 ] 是典型的非干涉相位恢复方法. 该方法克服了传统成像技术中系统装置复杂、实验条件要求高等缺点[11 -12 ] ,且基于该方法所得到的相位恢复结果不存在相位缠绕问题[13 ] ,吸引了大量学者的研究及应用[14 -16 ] . TIE求解过程中存在一些近似处理,例如需要利用至少2个垂直于光轴的平面上的强度信息进行差分近似. 除此以外,在采集这些信息时会引入采样误差,因此基于TIE的相位恢复算法存在结果不够精确的缺点. ...
The ability of forecasting flapping frequency of flexible filament by artificial neural network
1
2019
... 人工神经网络(artificial neural networks,ANN)是基于生物神经网络对信息进行自动优化的方法,该方法具有很高的容错性、鲁棒性及自组织性[17 ] . 目前,该方法已经广泛应用于自然语言处理、人工智能等领域. Cheng等[18 ] 提出基于人工神经网络和Gerchberg-Saxton迭代的相位恢复算法,该方法可以明显地改善原有迭代方法的精度,但是未应用于基于TIE的相位恢复中,也未验证人工神经网络恢复相位用于三维重构的可行性. ...
1
... 人工神经网络(artificial neural networks,ANN)是基于生物神经网络对信息进行自动优化的方法,该方法具有很高的容错性、鲁棒性及自组织性[17 ] . 目前,该方法已经广泛应用于自然语言处理、人工智能等领域. Cheng等[18 ] 提出基于人工神经网络和Gerchberg-Saxton迭代的相位恢复算法,该方法可以明显地改善原有迭代方法的精度,但是未应用于基于TIE的相位恢复中,也未验证人工神经网络恢复相位用于三维重构的可行性. ...
1
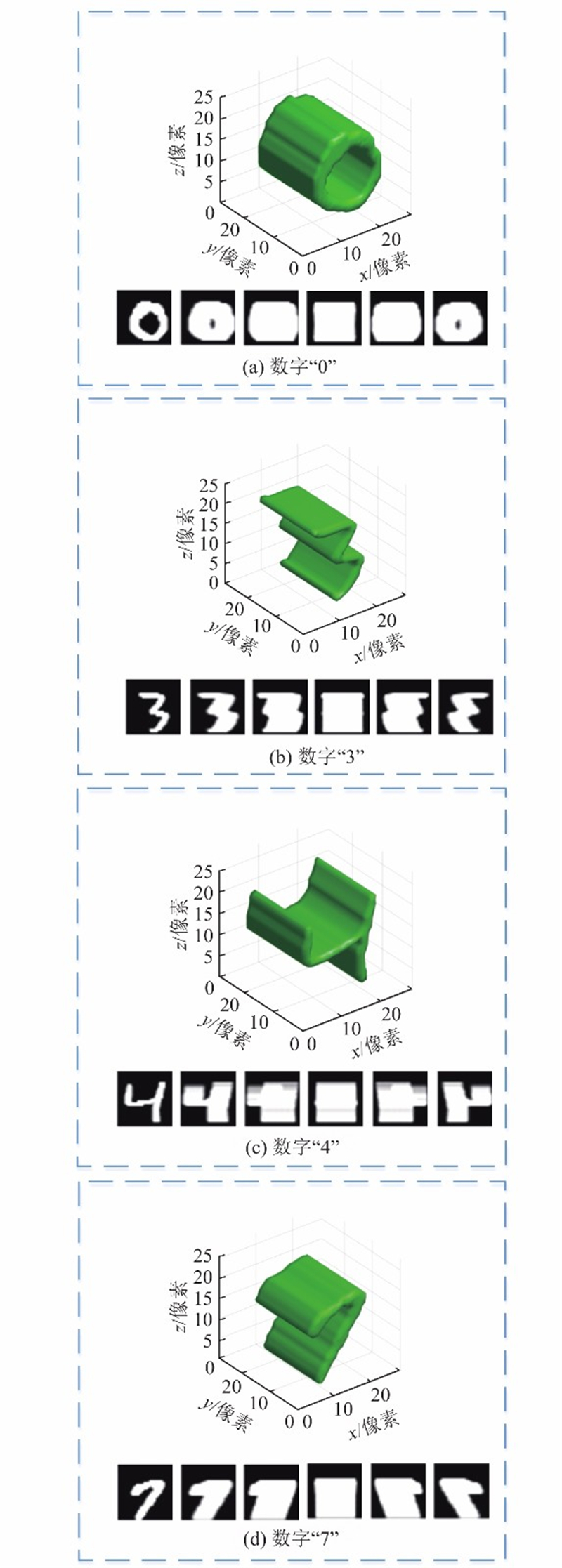
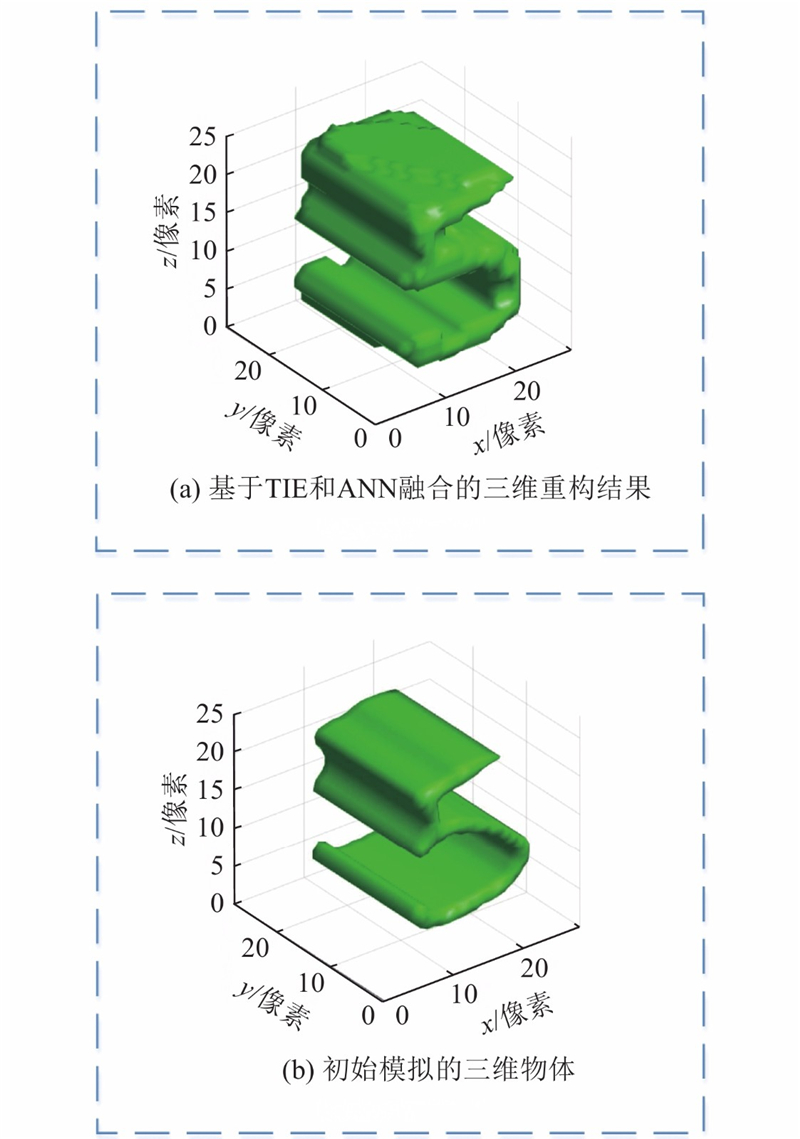
... 层析重建是常用的三维重建方法,在医疗、文娱、工业等领域具有广泛的应用场景. 乘法技术(multiplicative technique,MT)[19 ] 作为层析重建的一种,最大的特点是方便快速且非侵入. 本文结合MT技术,提出基于强度传输方程和人工神经网络融合的三维成像技术. ...
1
... 通过获取平面波在不同成像平面上的强度信息,利用傅里叶解法[20 ] 求解方程,可得相位信息. ...
1
... 通过获取平面波在不同成像平面上的强度信息,利用傅里叶解法[20 ] 求解方程,可得相位信息. ...
1
... 当训练神经网络时,通常将 ${{{W}}_{\rm{1}}}$ ${{{W}}_{\rm{2}}}$ ${{{b}}_{\rm{1}}}$ ${{{b}}_{\rm{2}}}$ [21 ] . 采用sigmoid函数作为激活函数. 为了衡量网络的误差,采用均方误差函数作为损失函数(loss function),如下: ...
1
... 式中: ${{\varphi }}_{i,j}^{{\rm{ex}}}$ i 行第j 列的值, ${{\varphi }}_{i,j}^{{\rm{out}}}$ i 行第j 列的值. 通过不断地迭代修改 ${{W}}$ ${{b}}$ ${{L}}$ [22 ] 的方式来优化神经网络,使得网络的损失函数尽快收敛至较小值. 参数 ${{W}}$ ${{b}}$ ${{W}}$
1
... 式中: ${{W}}_n^i$ $i$ $n$ ${{W}}$ $\eta $ ${{\partial {{L}}}}/{{\partial {{{W}}_n}}}$ [23 ] 计算: ...