地表水水质监测站点能够实时获取所处水域的水质状况. 基于获取的地表水水质数据并结合其他环境大数据可以实现高精度地表水水质预测,具有重大的实际应用意义. 例如监察人员能够提前感知流域的污染风险,向上下游站点发送预警信号,并回溯可能的污染来源. 对于预测值和实际值相差较大的点位,可以联动相关人员发起人工排查,提高线下执法效率.
实现高精度水质预测面临许多挑战. 水质数据在时间和空间2个维度上有复杂的依赖关系. 比如在时间维度上,站点某时刻的污染情况可能会与前一天的同一时刻相似;在空间上,站点的污染情况会受到周围水域的影响,传统的数据分析方法难以建模这种复杂的关联性.
许多研究者已经提出过一些方法解决地表水水质预测问题. 现有的预测方法可以粗略分为基于物理模型的方法和基于机器学习的方法2类.
1. 模型简介
1.1. 问题定义
定义
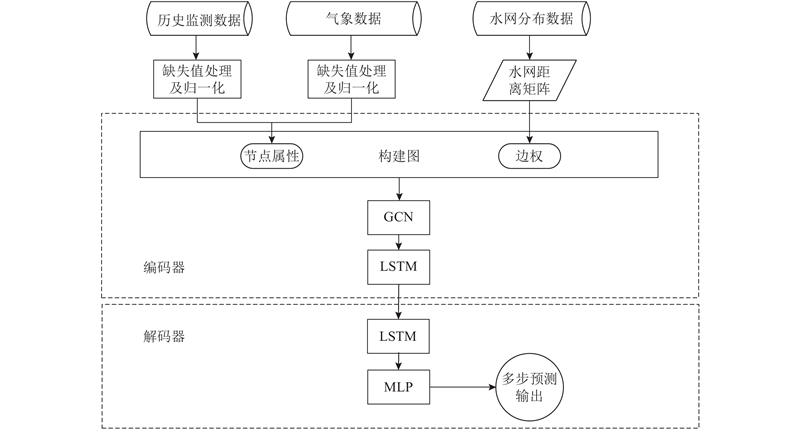
1.2. 框架分析
图 1
1.3. 数据预处理
水质预测模型使用的数据输入包括地表水水质监测站点历史监测数据和气象数据.
表 1 站点监测数据指标及有效值范围
Tab.1
| 水质指标 | 有效值 |
| PH值 | 0~14 |
| 氨氮质量浓度 | 0~3 mg/L |
| 总磷质量浓度 | 0~0.6 mg/L |
| 高锰酸盐指数 | 0~22.5 mg/L |
| 溶解氧质量浓度 | 0~12 mg/L |
2)气象数据. 气象因素对水污染物的产生与扩散有很大影响. 将气象因素引入模型计算中,能够基于深度学习技术,学习从气象因素到地表水水质的复杂影响关系.
气象数据的数据格式如表2所示,其中包含4个与水质相关性较大的气象指标,分别为气温、气压、湿度和降雨量. 本文为气象指标设定了对应的有效值范围(根据气象指标的实际含义). 与站点监测数据类似,所有不在上述有效值范围内的站点监测数据将被认为是异常值,在后续处理流程中视同缺失值.
表 2 气象数据数据指标及有效值范围
Tab.2
| 气象指标 | 有效值 |
| 气温 | −20~50 °C |
| 气压 | 900~1100 hPa |
| 湿度 | 0~100% |
| 降雨量 | 0~60 mm |
3)缺失值处理与归一化. 实际数据采集中出现的许多问题都会带来数据的缺失和异常,其中异常数据经过有效范围的判断后,可以视同缺失值,在实现时采用线性插值法实现缺失值填充. 线性插值法假设包含缺失值的一段连续序列满足线性变化关系,以线性函数去拟合数据变化,线性插值法的计算公式如下:
式中:
模型输入数据的分布存在较大差异,在数据预处理中加入归一化操作,可以有效加速模型收敛,缓解潜在的梯度问题,归一化计算公式为
式中:
1.4. 模型设计
1)站点图构建. 在输入时间窗口内的每个时刻,通过构建站点图
图 2
式中:
2)图卷积计算. 在完成图的构建过程后,通过GCN实现节点间的信息交互,以建模站点间的空间依赖关系. 具体的计算公式为
式中:
3)序列编解码. 在输入时间窗口内的所有图上完成图卷积操作后,每一个站点更新后的信号可以按时间顺序组成序列
式中:
编码LSTM得到的
该任务的损失函数定义为均方误差(MSE),具体的计算方式如下:
式中:
2. 实验分析
2.1. 数据集
采集杭嘉湖地区24个站点从2018年1月至2020年5月的历史水质指标监测数据和相应地区的气象数据. 地表水水质监测站点在地理上的分布如图3所示,地表水水质监测站点在地图上以圆点标注.
图 3
图 3 杭嘉湖地区水质监测站点分布图
Fig.3 Distribution diagram of water quality monitoring stations in Hangzhou-Jiaxing-Huzhou area
2.2. 实验设置
模型的超参数设置如下:batch size设定为64,GCN的输出维度为16,LSTM的隐状态长度为32,GCN层数为1. 采用Adam优化器[17]优化模型参数,学习率设定为0.002,训练epoch设定为150. 为了减少随机性,模型将独立训练5次,在实验部分取5次实验结果的平均值作为最终结果.
按照任务目标,预测任务定义为利用所有站点24个值(
该实验以训练集的样本优化模型参数,以在评估集上的运行结果优化超参数,在测试集上验证该模型的性能.
性能评价指标包括平均绝对误差(MAE)和平均相对误差(MRE),计算方法如下:
MAE直接计算真实值与预测值之间的绝对值. MRE在MAE的基础上除以真实值得到相对的误差率,结果更加直观,但不适用于数值范围在0附近的数据指标(相对误差会非常大).
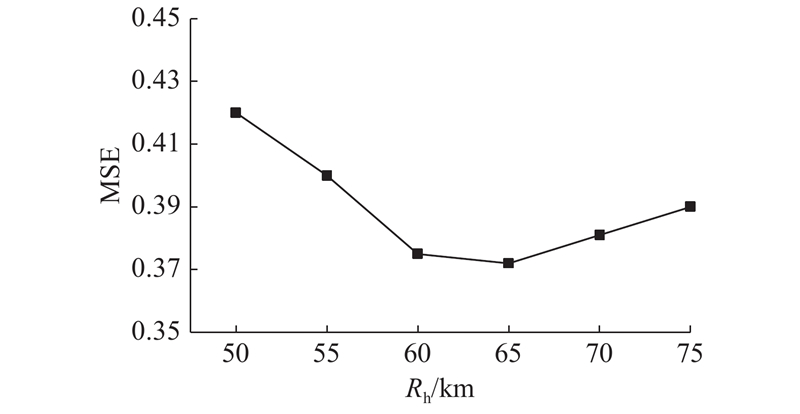
2.3. 距离阈值 ${R}_{{\rm{h}}}$
图 4
从实验结果可以看出,当
2.4. 气象数据及水网距离的影响
除了历史水质指标监测数据外,模型还用到了气象数据和水网分布数据. 为了验证这2种数据的有效性,引入2个变体模型w/o wea和w/o water. 其中w/o wea去除了站点图节点信号的气象数据输入,w/o water以站点间的欧式空间距离代替水网距离来构建距离矩阵.
表 3 变体实验结果
Tab.3
| 方法 | PH监测值 | 高锰酸盐指数 | 溶解氧质量浓度 | |||||
| MAE | MRE | MAE | MRE | MAE | MRE | |||
| 本文模型 | 0.099 | 1.4% | 0.468 | 10.7% | 0.478 | 7.5% | ||
| w/o wea | 0.109 | 1.6% | 0.478 | 10.9% | 0.484 | 7.6% | ||
| w/o water | 0.123 | 1.7% | 0.608 | 13.3% | 0.662 | 10.7% | ||
从实验结果可以看出,该模型较2个变体模型具有性能上的优势,这说明模型中引入的气象数据和水网分布数据有助于实现水质指标预测. 水网分布数据比气象数据的影响更大,原因是基于空间欧式距离定义的相关性不仅不能充分表达站点间的依赖关系,还会引入错误的先验知识,造成模型无法正确地拟合真实的映射关系,而基于站点在水网上分布所构建的水网距离矩阵能够更加真实地反映站点间的相关性.
2.5. 基线对比
将提出的地表水水质预测模型与现有的基于机器学习方法的模型进行对比. 用于对比的基线模型如下.
1)支持向量回归机(SVR)[5]. 该方法是传统支持向量机(SVM)的回归版本,目标是在特征空间内寻找最优的超平面,使得特征空间中的所有数据样本到该平面的距离最近. 原始版本的SVR只支持单变量输出,作为实验对比基线,本文为每个指标和预测步长建立SVR模型.
2)差分整合移动平均自回归模型(ARIMA)[3]. 该方法将时间序列转化为平稳时间序列,将因变量对它的滞后值以及随机误差项进行回归拟合,是时间序列线性分析中最常见的模型之一.
3)长短期记忆网络(LSTM)[10]. LSTM在序列建模过程中保持记忆性,较RNN与GRU有更加复杂的门控结构,设定遗忘门和输入门用以控制长期记忆的保留与更新,设定输出门用以得到每个时刻的输出结果. LSTM缓解了RNN模型中的梯度消失问题,是深度学习中建模时间序列最常用的神经网络.
表 4 PH监测值的预测结果
Tab.4
| 方法 | | | | | | |||||||||
| MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | |||||
| 本文模型 | 0.081 | 1.2% | 0.090 | 1.3% | 0.096 | 1.4% | 0.097 | 1.4% | 0.110 | 1.6% | ||||
| SVR | 0.101 | 1.5% | 0.125 | 1.8% | 0.135 | 1.9% | 0.144 | 2.0% | 0.167 | 2.2% | ||||
| ARIMA | 0.079 | 1.1% | 0.143 | 2.0% | 0.138 | 1.9% | 0.135 | 1.8% | 0.167 | 2.2% | ||||
| LSTM | 0.089 | 1.3% | 0.125 | 1.8% | 0.110 | 1.6% | 0.105 | 1.6% | 0.126 | 1.8% | ||||
表 5 高锰酸盐指数的预测结果
Tab.5
| 方法 | | | | | | |||||||||
| MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | |||||
| 本文模型 | 0.410 | 8.2% | 0.455 | 10.5% | 0.474 | 10.8% | 0.497 | 11.1% | 0.520 | 11.4% | ||||
| SVR | 0.624 | 13.7% | 0.673 | 14.6% | 0.680 | 14.8% | 0.671 | 14.6% | 0.681 | 14.8% | ||||
| ARIMA | 0.571 | 12.9% | 0.712 | 15.5% | 0.695 | 15.1% | 0.743 | 16.0% | 0.850 | 17.7% | ||||
| LSTM | 0.521 | 11.4% | 0.532 | 11.7% | 0.589 | 13.2% | 0.641 | 14.0% | 0.674 | 14.7% | ||||
表 6 溶解氧质量浓度的预测结果
Tab.6
| 方法 | | | | | | |||||||||
| MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | MAE | MRE | |||||
| 本文模型 | 0.354 | 5.7% | 0.451 | 7.1% | 0.466 | 7.3% | 0.517 | 8.3% | 0.582 | 9.2% | ||||
| SVR | 0.525 | 8.4% | 0.731 | 11.5% | 0.803 | 12.0% | 0.897 | 13.9% | 0.876 | 13.7% | ||||
| ARIMA | 0.501 | 8.0% | 0.818 | 12.3% | 0.802 | 12.0% | 0.865 | 13.6% | 0.891 | 13.8% | ||||
| LSTM | 0.467 | 7.3% | 0.672 | 10.9% | 0.675 | 10.8% | 0.742 | 11.7% | 0.839 | 12.7% | ||||
实验结果表明,与时间序列分析模型ARIMA和通用回归模型SVR相比,基于深度学习技术的LSTM和该模型在预测准确率上具有明显的优势. 这是因为在该场景中,输入数据的维度高达216维(24×9),开展特征工程的难度较大,而基于深度学习的模型支持多源异构数据输入,通过堆叠多层神经网络实现了自动化的特征学习. 该模型的预测性能比LSTM模型更好,这是因为该模型能够通过GCN建模站点在空间上的复杂依赖关系,例如水污染物在水网上的传播过程,相比深度单序列建模模型更完整地考虑了水质监测数据在时空两方面的复杂依赖关系.
3. 结 语
本文提出新的地表水水质预测模型,使用图神经网络建模地表水水质监测站点在空间上的复杂依赖关系. 使用长短时记忆网络建模历史指标序列在时间上的复杂依赖关系,实现所有地表水水质站点水质指标的多步预测输出. 实验结果表明,与传统回归方法相比,利用该模型能够显著提高预测性能,与时间序列分析方法、通用回归方法和一般深度学习方法相比,该模型能够实现23.3%、26.6%和14.8%的性能提升.
本文提出的预测模型有进一步的拓展空间. 对于今后的工作,将重点探索以下3个方向. 1)引入更多影响地表水水质的因素,如站点周边污染源的实时排放信息、地表水文信息. 2)现有方法通过人为定义规则的方式实现图的构建,未来可以在图上实现节点间关系的自动推理,减少因预定义图带来的信息损失. 3)进一步扩大现有的建模范围,将区域从杭嘉湖局部区域扩展到整个浙江省水域或者是跨省域水网,以建模更加复杂的地表水水质监测站点间的空间依赖关系.
参考文献
MIKE 11 model-based water quality model as a tool for the evaluation of water quality management plans
[J].DOI:10.2166/aqua.2015.048 [本文引用: 1]
Water quality modeling for a typical urban lake based on the EFDC model
[J].DOI:10.1007/s10666-016-9519-1 [本文引用: 1]
A hybrid neural network and ARIMA model for water quality time series prediction
[J].DOI:10.1016/j.engappai.2009.09.015 [本文引用: 2]
Water quality management using statistical analysis and time-series prediction model
[J].DOI:10.1007/s13201-014-0159-9 [本文引用: 1]
A hybrid approach of support vector regression with genetic algorithm optimization for aquaculture water quality prediction
[J].
Support vector machines in water quality management
[J].
Water quality monitoring method based on TLD 3D Fish tracking and XGBoost
[J].
Improving prediction of water quality indices using novel hybrid machine-learning algorithms
[J].
Water quality prediction based on recurrent neural network and improved evidence theory: a case study of Qiantang River, China
[J].
Analysis and prediction of water quality using LSTM deep neural networks in IoT environment
[J].
Long short-term memory
[J].DOI:10.1162/neco.1997.9.8.1735 [本文引用: 1]