统计分析法基于大量历史统计数据,直接建立输入量与输出量的非线性映射关系,再根据实测数据或NWP进行预测,可分为时间序列法和人工智能法等. 其中,时间序列法是将风速或功率作为单一输入序列,人工智能法考虑输出与多变量之间的关系. 总体趋势表明,人工智能法更准确[7]. 人工神经网络(artificial neural network,ANN)在仿真、图像识别、预测等任务中取得了很好的效果,也是风电预测中最常用的人工智能方法[8],在历史样本充足的条件下,通常具有较高的预测精度和较强的泛化能力. BP神经网络(back-propagation artificial neural network,BP-ANN)按误差逆向传播算法进行训练,理论上可逼近任何非线性函数[9]. 范高锋等[9]根据风电场输出功率的影响因素,建立了基于BP-ANN的风电功率预测模型. 师洪涛等[10]在不同尺度上利用小波分解了风速与功率序列,再分别利用多个BP-ANN对各频率的分量进行预测,最后经过重构得到完整预测结果. 循环神经网络(recurrent neural network,RNN)具有循环反馈的框架,能够利用历史信息中的时序相关性,改进RNN得到的长短期记忆法(long short-term memory,LSTM)网络具有记忆、遗忘模式,解决了RNN梯度消失的问题,可应用于时间序列数据的预测[11],朱乔木等[12]基于LSTM网络建立了风电场功率预测模型,对多变时间序列进行动态时序建模.
不论是物理分析法还是统计分析法,都把功率预测作为预测变量连续的回归问题处理,通常以最小化均方差(mean square error,MSE)损失函数为训练目标. 但是MSE更适用于高斯分布,不能反映一般概率分布情况下的峰度与偏度信息[13]. 此外,风场变化巨大,纯回归的方法没有充分利用风场大幅变化导致的输出功率层级的差异性. 为了克服MSE损失函数的局限性,并充分利用数据的原始信息,本研究提出将回归与基于功率分段的分类相组合的风电功率预测模型. 在MSE损失函数监督的传统BP-ANN模型的基础上,考虑回归问题与分类问题之间的关联,引入交叉熵(cross entropy,CE)损失函数和排序(rank,RK)损失函数,建立以最小化组合损失函数为训练目标的预测模型. 使用CE损失函数监督模型的分类效果,使用RK损失函数加强分类效果,从而进一步改进预测模型. 与BP-ANN模型和LSTM模型进行对比实验,验证所提出模型的预测精度.
1. 基于BP-ANN和组合损失函数的风电预测方法
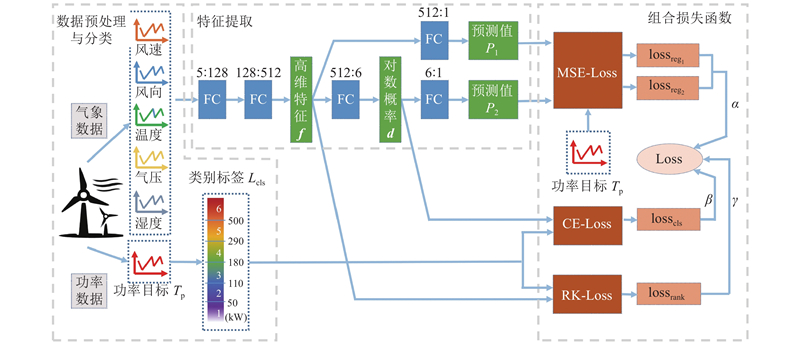
本研究方法包括数据预处理与分类部分、特征提取部分、组合损失函数评估部分,所提出的神经网络模型结构如图1所示. 组合损失函数值来自3个通道. 1)第一通道类似监督学习中的神经元网络结构,网络输入为气象数据
图 1
图 1 基于BP-ANN和组合损失函数的风电预测模型示意图
Fig.1 Schematic diagram of wind power prediction model based on BP-ANN and combined loss function
表 1 风电功率、类别及样本数的列表
Tab.1
| 风电功率/kW | 类别 | 样本数 |
| <50 | 1 | 2094 |
| 50~110 | 2 | 2120 |
| 110~180 | 3 | 2008 |
| 180~290 | 4 | 2356 |
| 290~500 | 5 | 2169 |
| >500 | 6 | 2165 |
1.1. 数据预处理与分类
输入历史数据包括由数据采集与监控系统获取的实测输出功率和NWP系统提供的风速、风向(风向角正弦值)、温度、湿度和气压等
为消除不同变量的量纲,让模型更好更快收敛,对各项数据通过最大值归一化到[0,1.0]. 根据风电机组的容量和样本数量,将风电功率值按照样本数量均匀且足量的原则进行区间划分,以实现回归问题向分类问题的转化,获得如表1所示的
气象数据
1.2. 特征提取
将样本表示为向量
式中:
如图1所示,维度为5的气象数据
图 2
1.3. 组合损失函数评估
以组合损失函数计算得到的组合损失
2. 人工神经网络中的组合损失函数
2.1. MSE损失函数
在监督学习中,损失函数用于衡量预测值和实际值之间的差距,并以损失函数最小为训练目标,对预测模型参数进行迭代求解[15]. MSE损失函数是标准BP-ANN的损失函数,将其定义为
式中:
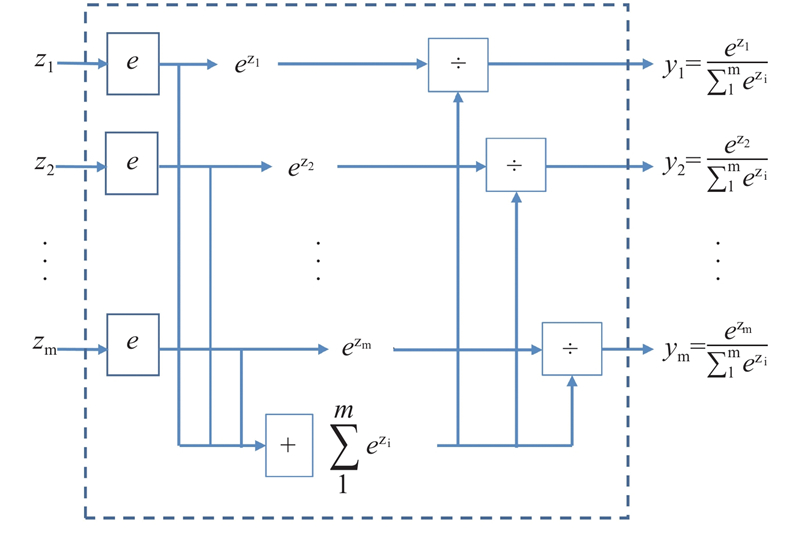
2.2. CE损失函数
考虑训练模型与真实模型的概率性误差,通过引入CE损失函数衡量误差大小[16]:
式中:
CE损失函数经常用于分类问题,表征2个概率模型之间的相似程度,CE损失函数越小,表征训练出的概率模型越接近真实的概率模型[14].
2.3. RK损失函数
中心损失函数
式中:第
式中:
式中:当
其中,条件函数
排序损失函数示意如图3所示.
图 3
当类内特征分散而远离中心时,
2.4. 组合损失函数
用风电功率预测值
式中:
3. 算例分析
3.1. 实验方法
实验样本来自江苏某地风电机组在2011年上半年的实测数据,额定容量为1200 kW,共有近13000条数据.
根据实际的气象数据维度和类别数量,及经典网络结构中神经元个数设置的经验[20],设置网络结构. 初始化方式为高斯随机,激活函数采用Sigmoid函数,训练周期(epoch)的数目设置为10,学习率(learning rate)初始化为0.001,训练过程和测试过程的批次(batch)分别设置为40、1;联合损失函数的权重系数分别取1、1、0.001,RK损失函数中的边距值
本研究使用可变的学习率,初期学习速度较快以大幅更新连接权值,在训练进行到第3个周期时,学习率乘以0.1,进行到第6个周期时,再乘以0.1,使学习速度逐渐减小以缓慢稳定地更新网络.
3.2. 评价指标
采用平均绝对误差
式中:
3.3. 预测性能分析
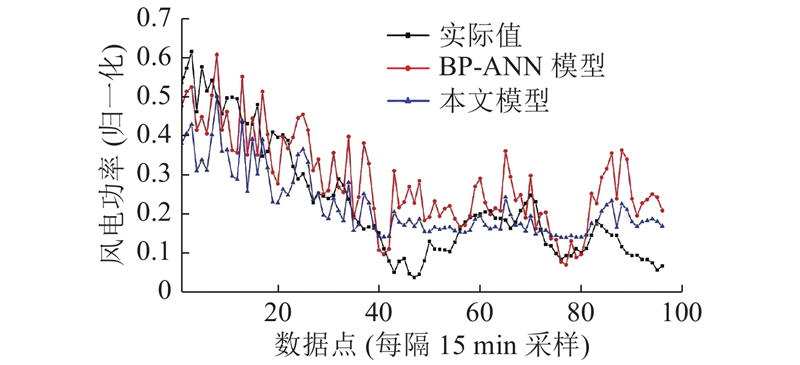
取2011年1月6日0:00至15日24:00的样本数据作为训练集,取1月16日0:00~24:00的样本数据作为测试集,实际功率曲线与采用BP-ANN模型、组合损失函数模型(本文模型)得到的预测功率曲线如图4所示. 由图可知,本文模型能有效预测风电出力.
图 4
图 4 实际功率曲线与采用BP-ANN模型、本文模型得到的预测功率曲线
Fig.4 Actual power curve and the predicted power curve obtained by using the BP-ANN model and proposed model
为了进一步验证组合损失函数的作用,在不同的数据量规模下比较本文模型、BP-ANN模型和LSTM模型的风电功率预测效果. BP-ANN模型和LSTM模型均采用3层隐层网络结构. 为减小随机性初始化对结果的影响,采用6次独立实验的误差结果平均值,
表 2 模型的预测性能对比
Tab.2
| 训练集样本数 | 模型 | | | 训练时间/s |
| 900 | BP-ANN | 131.9 | 150.5 | 1.8 |
| LSTM | 154.0 | 179.1 | 5 | |
| 本文 | 110.0 | 133.9 | 3.1 | |
| 1800 | BP-ANN | 126.2 | 144.4 | 3.0 |
| LSTM | 222.9 | 259.7 | 16.5 | |
| 本文 | 131.7 | 141.6 | 4.5 | |
| 4500 | BP-ANN | 152.6 | 186.8 | 5.4 |
| LSTM | 120.9 | 147.5 | 26.6 | |
| 本文 | 118.1 | 144.1 | 8.8 | |
| 7200 | BP-ANN | 133.3 | 185.2 | 8.3 |
| LSTM | 131.6 | 161.5 | 42.9 | |
| 本文 | 94.5 | 105.2 | 13.8 | |
| 9000 | BP-ANN | 125.9 | 187.7 | 10.2 |
| LSTM | 109.2 | 130.9 | 78.8 | |
| 本文 | 103.2 | 128.9 | 16.6 |
本文模型的计算量大于BP-ANN模型,在3.60 GHz Intel(R)Core(TM)i7-4790/8G RAM的测试平台上,学习速度略低于BP-ANN模型,但优于LSTM模型. 原因是LSTM模型每一时刻的计算都依赖于前一时刻的计算和输出结果.
3.4. 功能验证
为了进一步测试组合损失函数的效果,利用以下3种损失函数训练模型:1)单独MSE损失函数;2)MSE+CE损失函数;3)组合损失函数,其余的设置相同. 基于五类训练数据规模最终得到的
在某一训练集规模下,改变组合损失函数的权重系数
表 3 训练后的模型的预测功率误差对比
Tab.3
| 训练集样本数 | | ||
| MSE | MSE+CE | MSE+CE+RK | |
| 900 | 121.7/145.0 | 119.5/138.3 | 110.0/133.9 |
| 1800 | 153.9/162.6 | 146.1/155.1 | 131.7/141.6 |
| 4500 | 134.3/161.0 | 128.5/150.9 | 118.1/144.1 |
| 7200 | 104.2/113.3 | 98.5/108.7 | 94.5/105.2 |
| 9000 | 146.6/171.9 | 134.0/159.3 | 103.2/128.9 |
表 4 不同损失函数权重系数的预测误差对比
Tab.4
| | | | | | | ||
| 1/0.5/0.001 | 138.9 | 1/1/0.0005 | 144.1 | 1/1/0.005 | 142.3 | ||
| 1/1/0.002 | 144.2 | 1/1/0.01 | 126.4 | 1/5/0.001 | 148.8 | ||
| 1/10/0.001 | 133.9 | 2/1/0.001 | 130.5 | 10/1/0.001 | 166.7 |
4. 结 论
(1)与BP-ANN模型、LSTM模型的对比实验,证明了本文模型具有更强的学习与泛化能力,能够获得更高的预测精度,且训练速度快于LSTM模型.
(2)引入CE损失函数,将分类的思维引入回归问题,弥补了MSE作为损失函数的局限性. 与仅用MSE来训练的方法相比,MSE+CE联合训练的预测精度有所提高.
(3)引入RK损失函数,通过提高同类别样本高维特征的集中度与不同类别样本高维特征的区分度,进一步加强分类的效果. 并通过与MSE+CE联合训练方法的对比,充分验证了本文模型的效果.
参考文献
风电集群短期及超短期功率预测精度改进方法综述
[J].
A summary of the state of the art for short-term and ultra-short-term wind power prediction of regions
[J].
风电功率预测方法综述
[J].
Review of wind power forecasting method
[J].
Long-term wind speed and power forecasting using local recurrent neural network models
[J].
基于OS-ELM和Bootstrap方法的超短期风电功率预测
[J].DOI:10.7500/AEPS20130830010 [本文引用: 1]
Ultra-short-term wind power prediction based on OS-ELM and bootstrap method
[J].DOI:10.7500/AEPS20130830010 [本文引用: 1]
基于PCA-LSTM模型的风电机网相互作用预测
[J].
Prediction of interaction between grid and wind farms based on PCA-LSTM model
[J].
风电场功率预测物理方法研究
[J].
Study on the physical approach to wind power prediction
[J].
A review on the selected applications of forecasting models in renewable power systems
[J].
关于短期及超短期风电功率预测的评述
[J].DOI:10.7500/AEPS20141218003 [本文引用: 1]
A review on short-term and ultra-short-term wind power prediction
[J].DOI:10.7500/AEPS20141218003 [本文引用: 1]
基于人工神经网络的风电功率预测
[J].DOI:10.3321/j.issn:0258-8013.2008.34.019 [本文引用: 2]
Wind power prediction based on artificial neural network
[J].DOI:10.3321/j.issn:0258-8013.2008.34.019 [本文引用: 2]
基于小波—BP神经网络的短期风电功率预测方法
[J].
A short-term wind power prediction method based on wavelet decomposition and BP neural network
[J].
基于GRU-NN模型的短期负荷预测方法
[J].
Short-term load forecasting method based on GRU-NN model
[J].
基于长短期记忆网络的风电场发电功率超短期预测
[J].
Short-term wind power forecasting based on LSTM
[J].
Entropy and correntropy against minimum square error in offline and online three-day ahead wind power forecasting
[J].
Optimization of computer simulation models with rare events
[J].
基于交叉熵理论的风电功率组合预测方法
[J].
A combination method for wind power predication based on cross entropy theory
[J].