浙江大学学报(工学版)

浙江大学学报(工学版), 2021, 55(3): 500-510 doi: 10.3785/j.issn.1008-973X.2021.03.010

土木与交通工程

粉质黏土层直埋铸铁管道爆破地震效应

朱斌,, 蒋楠,, 周传波, 贾永胜, 罗学东, 吴廷尧

1. 中国地质大学 工程学院，湖北 武汉 430074

2. 江汉大学 工程爆破湖北省重点实验室，湖北 武汉 430024

3. 武汉爆破有限公司，湖北 武汉 430024

Blasting seismic effect of buried cast iron pipeline in silty clay layer

ZHU Bin,, JIANG Nan,, ZHOU Chuan-bo, JIA Yong-sheng, LUO Xue-dong, WU Ting-yao

1. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China

2. Hubei Key Laboratory of Blasting Engineering, Jianghan University, Wuhan 430024, China

3. Wuhan Explosion and Blasting Co. Ltd, Wuhan 430024, China

通讯作者: 蒋楠，男，副教授. orcid.org/0000-0003-2709-840X. E-mail： jiangnan@cug.edu.cn

收稿日期: 2020-02-15  

基金资助: 国家自然科学基金资助项目（41807265，41972286）；爆破工程湖北省重点实验室开放基金资助项目（HKLBEF202001）；湖北省自然科学基金资助项目（2019CFB224）

Received: 2020-02-15  

Fund supported: 国家自然科学基金资助项目（41807265，41972286）；爆破工程湖北省重点实验室开放基金资助项目（HKLBEF202001）；湖北省自然科学基金资助项目（2019CFB224）

作者简介 About authors

朱斌（1996—），男，博士生，从事地下工程、爆破工程研究.orcid.org/0000-0003-0629-6757.E-mail：b.zhu@cug.edu.cn , E-mail：b.zhu@cug.edu.cn

摘要

针对武汉市区内常见直埋球墨铸铁管道，设计实施邻近预埋管道的全尺寸爆破实验. 结合有限元数值计算方法，考虑管道不同埋深，研究爆破地震作用下粉质黏土地层内直埋管道动力响应. 研究结果表明，管道和地表峰值振速（PPVs）随爆源与管道距离的减小而增大，在管道正下方爆破为最危险工况. 管道中心截面为危险截面，危险截面PPVs以管腰和管底较大，动态应变以轴向拉伸应变为主，环向应变次之，峰值有效应力以底部单元最大，管道肩部最小. 管道不同埋置深度和PPVs具有比例关系，通过实测地表振速与管道有效应力关系可以预测管道截面爆破峰值有效应力，计算关系式可以为岩土爆破施工中邻近管道的安全性评价提供计算方法.

关键词： 直埋管道 ; 爆破地震 ; 质点速度 ; 峰值有效应力 ; 安全评价

Abstract

A full-scale blasting experiment of adjacent pre-buried pipes was designed and implemented, aiming at the common direct-buried ductile iron pipes in the urban area of Wuhan. Combined with the finite element numerical calculation method and considering the different buried depth of the pipeline, the dynamic response of the directly buried pipeline in the silty clay layer under the action of the blasting vibration was studied. Results show that the pipeline and the surface peak particle velocities (PPVs) increase with the decrease of the blast distance, and the most dangerous working condition is blasting directly below the pipeline. The central section of the pipeline is dangerous. The PPVs at the waist and bottom of the tube are larger for the dangerous section. The dynamic strain is mainly the axial tensile strain and the hoop strain is smaller. The peak effective stress in the bottom element is the largest and that of the pipe shoulder is the smallest. There is a functional relationship between PPVS and different embedded depth of pipeline. By measuring the relationship between the surface PPVs and the peak effective stress, the peak effective stress of the pipeline section can be predicted, which provides a calculation method for the safety determination of related pipelines in engineering construction.

Keywords： directly buried pipeline ; blasting seismic effect ; particle velocities ; peak effective stress ; safety evaluation

PDF (1861KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

朱斌, 蒋楠, 周传波, 贾永胜, 罗学东, 吴廷尧. 粉质黏土层直埋铸铁管道爆破地震效应. 浙江大学学报(工学版)[J], 2021, 55(3): 500-510 doi:10.3785/j.issn.1008-973X.2021.03.010

ZHU Bin, JIANG Nan, ZHOU Chuan-bo, JIA Yong-sheng, LUO Xue-dong, WU Ting-yao. Blasting seismic effect of buried cast iron pipeline in silty clay layer. Journal of Zhejiang University(Engineering Science)[J], 2021, 55(3): 500-510 doi:10.3785/j.issn.1008-973X.2021.03.010

爆破作为坚硬岩土体开挖的重要方式在城市岩土工程建设中受到广泛应用. 随着我国城市地下空间不断开发，直埋管道邻近爆破工程的安全性问题日益凸显. 爆破施工中产生的中、远区爆破地震波经过岩土介质传播到管道和地表，当爆破地震效应引起的管道动力响应超过本身的安全承受能力时，管道就会发生破坏. 我国现有的爆破安全规程中[1]缺少针对直埋管道的爆破振动安全控制标准以及有效的安全评价方法. 在实际爆破施工中，管道的振动安全控制值和评价方法往往根据经验进行，可靠性和经济性得不到保证. 因此，研究城区爆破工程邻近直埋管道的地震效应对于保证城市管道的安全运行，指导城市地下空间工程的高效建设具有重要意义.

目前，相关学者针对岩土工程爆破开挖邻近埋地管道的地震效应进行了大量研究[2-4]. 张黎明等[5]利用现场爆破实验，根据管道破坏的应变准则建立爆破振动质点峰值速度与管道破坏的对应关系. Xia等[6]基于现场工程测试利用动力有限元数值计算软件，研究不同装水状态的输水管道爆破动力响应；Jiang等[7]根据现场监测数据，建立三维数值模型，分析并探讨管道和管道周围土体的振动效应. Scott等[8]通过2次全尺寸控制爆破实验，评价侧向扩展作用管道的性能. 在相关研究中，针对目前服役时间较长，更易受破坏的球墨铸铁管道研究较少，关于实际工程现场管道不同埋置深度对其动力响应影响的研究不足. 因此，有针对性地开展不同埋置深度下直埋球墨铸铁管道的爆破地震效应研究尤为重要.

本研究依托武汉市区直埋管道邻近爆破工程，开展全尺寸预埋管道邻近爆破实验，分析直埋球墨铸铁管道邻近爆破工程中的爆破地震波传播特性以及管道动力响应规律，并结合LS-DYNA有限元数值软件，建立不同埋深管道的数值计算模型对现场实验进行补充研究，研究结论可以为城市爆破工程安全评价提供指导.

1. 邻近管道全尺寸爆破实验

1.1. 场地条件

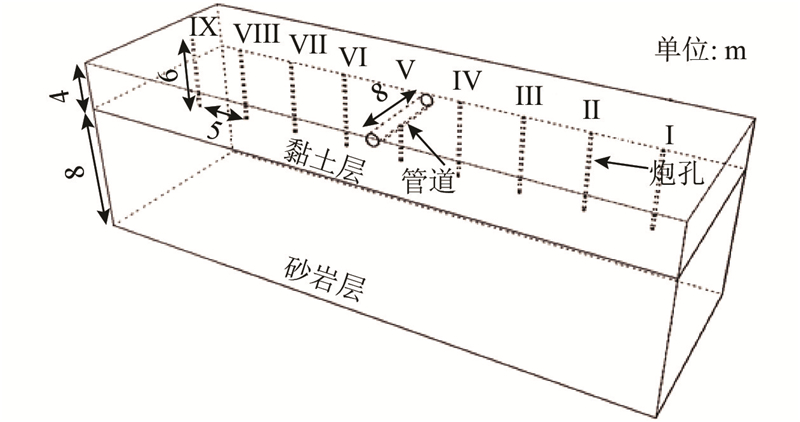
根据现场实验要求，对武汉市在建或已建成的直埋管道邻近爆破工程的开挖场地条件、管道类型以及爆破数据进行大量调查研究[9-11]. 研究表明，武汉市范围内现役输气、输水管多为球墨铸铁管道，管径为40~2600 mm，该类管道多直接埋于粉质黏土层中，埋深为1.5~2.5 m. 管道邻近的爆破开挖工程多为轨道交通下穿爆破工程，开挖爆源具有沿水平方向动态推进的特点，炸药类型为岩石乳化炸药.

基于上述数据，选取武汉市经济技术开发区硃山路与硃山一路交汇处的场地平整项目作为爆破实验场地. 该场地上部覆土层为杂填土、粉质黏土层，下部为砂岩层，主要地层和参数如表1所示. 表中，ρ为天然重度，φ为摩擦角，c为内聚力，fk为承载力. 对比分析可知，该场地中的粉质黏土层与武汉市主城区粉质黏土层参数相近，下部爆破岩层与实际爆破工程开挖岩体接近，因此该实验场地可以充分满足现场爆破实验场地要求.

表 1   爆破场地岩土参数

Tab.1  Rock and soil parameters of blasting site

地层 ρ /（kN·m−3） φ /（°） c /kPa fk /kPa
填土 19.2 18.0 8 120~160
粉质黏土 19.3 12.0 25 160~180
石英砂岩 26.8 5.5 43 2000~4000

新窗口打开| 下载CSV


1.2. 设计方案

对爆破实验进行适当的简化设计以减小实验难度. 实验设计示意如图1所示. 根据场地条件，实验土层选用粉质黏土层，厚度为4 m，下部开挖岩层为强、中风化砂岩层. 实验研究管段选用武汉城区常见的直埋球墨铸铁管，管道相关物理力学参数如表2所示. 表中，E为弹性模量，h为埋深，d为管径，δ为壁厚，μ为泊松比.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   现场实验设计示意图

Fig.1   Schematic diagram of field experiment design


表 2   实验用直埋球墨铸铁管道相关参数

Tab.2  Ductile iron pipe parameters for experiment

管材 E /GPa h /m d /mm δ /mm μ
球墨铸铁 195 2 1 000 10 0.3

新窗口打开| 下载CSV


根据实验设计，管道埋置于场地的粉质黏土层中，埋深为2.0 m，在直埋时开挖沟槽，在填埋时保证管道回填土的密实度，使土壤与管周土紧密接触. 管道沿轴向长度取8.0 m，远大于管道直径，管道两端留出小沟槽保证管道轴线两端自由，实验条件可以满足管道周围以及两端的实际约束条件，不对管道进行加压处理. 爆破使用的炸药为爆破工程中常用的2#岩石乳化炸药，药卷直径为70 mm，长度为350 mm，采用孔底集中装药，非电导爆管单孔单段起爆，以充分保证实际爆破开挖工程中爆破地震波的产生条件，实验共设计I~IX组炮孔，依次分别对应实验工况编号1~9，炮孔布置顺序为从右到左依次下穿直埋球墨铸铁管道，药量为8 kg，孔深为6 m.

1.3. 监测与操作

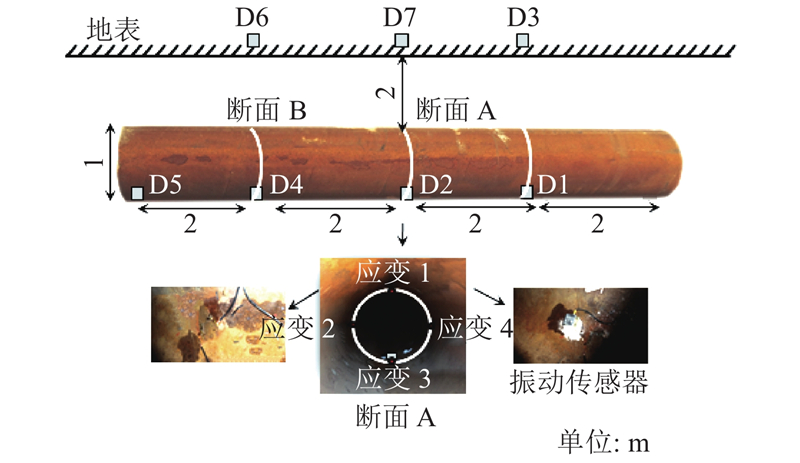
振动特征以及应力应变数据是实验中主要监测和研究的物理量. 根据研究需求，管道以及地表振动数据采用常用的TC-4850爆破测振仪进行测试，振动监测点布置如图2所示. 图中，D1~D7为振动监测点，应变1~4为应变测点. 管道动态应变通过在管道内壁黏贴环向和轴向的应变片来测量，管道内壁共设置2个应变监测断面，应变测点处分别黏贴环向和轴向应变片.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   实验监测点布置图

Fig.2   Arrangement diagram of experimental monitoring point


如图3所示，根据爆破实验设计以及监测方案，在选定的实验场地用小型挖土机在预定位置开挖长宽约为1.2 m，深约为3.0 m的沟槽（均须大于管道直径，保证管道顺利埋设）. 按照预先的炮孔设计，利用直径为90 mm的开山液压钻机进行炮孔钻凿. 按照预先设计测点布设方案，依次在管道内部黏贴上述动态应变片，并安装管道内部振动速度传感器，预留连接线接头.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   现场实验实施图

Fig.3   Field experiment implementation diagram


将已经布置好监测点的研究管段安放在开挖沟槽内，并分层夯实回填上方土体至地表标高，回填时用简易密实度测试仪测定覆土密实度，保证沟槽填土密实度不小于90%~95%，使管道覆土与管道紧密接触且密实稳定,管道两端留出小沟槽，保证管道轴向两端自由. 回填后在预先设计好的地表位置安装地面振动速度传感器. 按照装药设计依次进行装药堵塞，连接雷管与起爆器. 将数据测试接收仪器与传感器连接，并放置于安全范围内. 依次起爆上述炮孔，进行现场实验并进行应变、振速、频率等数据的采集，单个炮孔起爆时间间隔为30 min，在每次起爆前检查前一次爆破效果并调试仪器初始状态.

2. 数值计算模型及参数设置

2.1. 数值模型

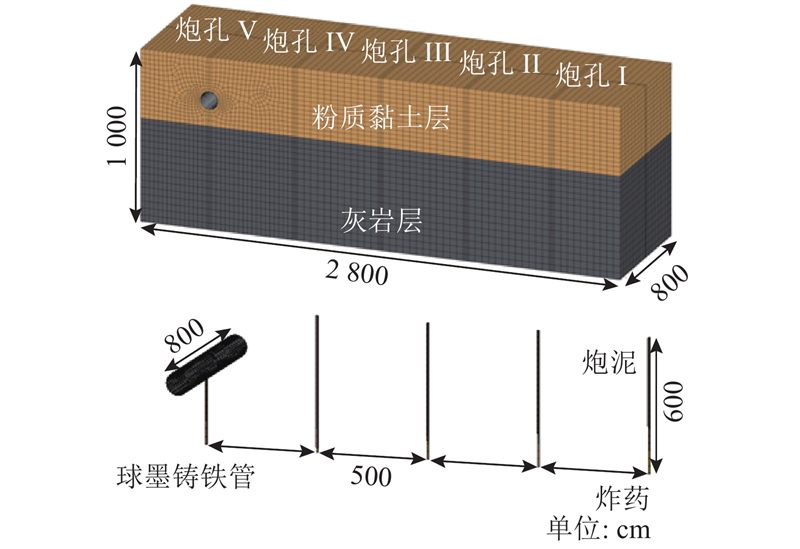
根据现场实验场地条件和布置情况，爆破过程中管道动力响应沿轴线具有对称性. 因此为了简化计算模型，拟建立管道正下方以及右侧I~V炮孔，分别模拟爆破工况1~5的数值模型. 管道、柱状炮孔作为埋置于土层中的孔洞结构，为了保证所选取的模型不受边界尺寸效应的影响，根据圣维南原理，模型中管道及炮孔周围尺寸取值均大于3~5倍洞径[12]. 数值计算整体模型如图4所示，模型整体尺寸为28 m×8 m×10 m，模型单元采用8节点SOLID164实体单元，cm-g-μs单位制[13]. 数值计算模型包括炸药、管道、土层、岩层. 粉质黏土层厚度为5 m，强风化粉质砂岩层厚为5 m. 球墨铸铁管道内直径为1 m，厚度为1 cm，轴向长度为8 m，管道埋置深度为2 m. 炮孔深为6 m，直径为90 mm，单孔装药量为8 kg.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   现场爆破实验数值模型示意图

Fig.4   Numerical model of field blasting experiment


为了保证数值计算模型的准确性，模型中的炸药、炮泥、岩层和土层采用任意拉格朗日-欧拉网格Arbitrary Lagrangian-Eulerian（ALE）划分，管道采用拉格朗日Lagrangian网格划分，ALE网格自适应方法使得网格脱离材料独立流动，网格在整个分析过程中保持较好的状态，更适用于爆炸冲击材料的计算模拟[14]. 根据网格敏感性分析结果，模型网格尺寸定为15~40 cm不等，并对管道、管周土体和炸药部分的网格进行细化. 管道与土体接触部分设置为自动面面接触，根据实验管土特性设置接触面参数保证管道环向的约束条件. 模型中土层与管道采用流-固耦合算法，其他部分采用多物质ALE算法求解. 根据工程现场特点，将计算模型顶面设置为自由边界，其他各面设置为无反射边界. 在管道两端不设置约束，仅设置为无反射边界，以充分满足实际管道轴向约束条件.

2.2. 材料及参数

根据室内力学参数测试结果以及相关实验材料参数，对研究范围的材料性质进行均质单一性简化，如表3所示. 表中，σt为抗拉强度.

表 3   爆破实验数值模型材料参数

Tab.3  Numerical simulation parameter of blasting experiment

材料 ρ /（g·m−3） E /GPa μ c /MPa φ /（°） σt /MPa
管道 7.85 195.000 0.30 − − 235.000
粉质黏土 1.98 0.039 0.35 0.035 15 0.028
砂岩 2.68 52.000 0.25 5.500 43 2.580

新窗口打开| 下载CSV


模型中的土壤作为松散多孔的非均质材料，其物理力学性能受多种因素影响. LS-DYNA材料模型库中提供的*MAT_DRUCKER_PRAGER模型[15]，能较好地模拟有关于土壤介质的相关模型. 这种材料模型使用改进的德鲁克-普拉格（Drucker-Prager）屈服准则，使屈服表面的形状可以扭曲成更真实的土壤模型.

岩体介质是非连续、不均匀的，数值模拟通常将围岩假设为连续的、各向同性的弹塑性材料. LS-DYNA中的*MAT_PLASTIC_KINEMATIC材料模型[16]，用来模拟岩石材料的应力应变行为较为准确. 此外本实验中所采用的球墨铸铁管道，其材料的物理力学模型仍可以采用上述岩石介质的*MAT_PLASTIC_KINEMATIC材料模型，此模型的屈服条件为

$\left. \begin{array}{l} {\sigma _{\rm{y}}} = \left[ {1 + {{\left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon C}} \right. \kern-\nulldelimiterspace} C}} \right)}^{{1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-\nulldelimiterspace} p}}}} \right]\left( {{\sigma _0} + \beta {E_{\rm{p}}}\varepsilon _{{\rm{eff}}}^{\rm{p}}} \right),\\ {E_{\rm{p}}} = {{{E_{\rm{t}}}E} \mathord{\left/ {\vphantom {{{E_{\rm{t}}}E} {\left( {E - {E_{\rm{t}}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {E - {E_{\rm{t}}}} \right)}}. \end{array} \right\}$
(1)

式中：σy为屈服强度，σ0为初始屈服强度，ԑ为应变率， $\varepsilon _{{\rm{eff}}}^{\rm{p}} $为有效塑性应变，p、C为应变率参数，β为硬化参数，Ep为塑性硬化模量，Et为切线模量.

模型中的炸药材料与实验现场采用的2号岩石炸药保持一致，采用LS-DYNA软件自带的高能炸药材料*MAT_HIGH_EXPLOSIVE_BURN来模拟炸药模型[16]，通过定义炸药状态方程（*EOS_JWL）准确描述炸药在爆炸过程中的压力、体积和能量特性，以模拟真实炸药爆炸过程. JWL[14]方程可以对炸药的爆轰压力与相对体积和内能的关系进行描述，表达式为

$p_{\rm{e}} = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){{\rm{e}}^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){{\rm{e}}^{ - {R_2}V}} + \frac{{\omega {E_0}}}{V}.$
(2)

式中：pe为爆炸产物压力，V为爆炸产物相对体积，R1、R2、ω、A、B为炸药材料参数，E0是初始比内能，炸药爆轰产物相关参数如表4所示.

表 4   爆轰产物参数

Tab.4  Detonation product parameter

ρ /（g·cm−3） A /GPa B /GPa R1 R2 ω E0 /GPa V /cm3
1.25 214 18.2 4.2 0.9 0.15 4.19 1.0

新窗口打开| 下载CSV


3. 数值模拟计算结果可靠性分析

3.1. 振动特征分析

参考现场实验测点布置，合理选择数值计算模型中相对应的质点进行对比验证分析，并对现场实验进行相关的补充研究. 数值计算模型管道和地表监测质点选取如图5所示. 图中，管道正下方炮孔V爆破时（工况5）管道底部质点H27（实验测点D2）各方向振动波形和振动频率如图6、7所示. 图中，vpx、vpy、vpz、vpr分别为管道测点x、y、z、合振动方向的振速，vE、vN分别为实验和数值模拟中测点峰值振速，MSA为质点功率，f cE为实验得到的主振动频率，f cN为数值模拟得到的主振动频率.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   爆破实验数值模拟质点示意图

Fig.5   Diagram of numerical measurement points for blasting experiments


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   实验与数值模拟管道底部质点振动波形对比图

Fig.6   Experimental and numerical simulation of vibration waveform of mass at bottom of pipe


图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   实验与数值模拟管道底部质点振动频率对比图

Fig.7   Experimental and numerical simulation of vibration frequency of mass at bottom of pipe


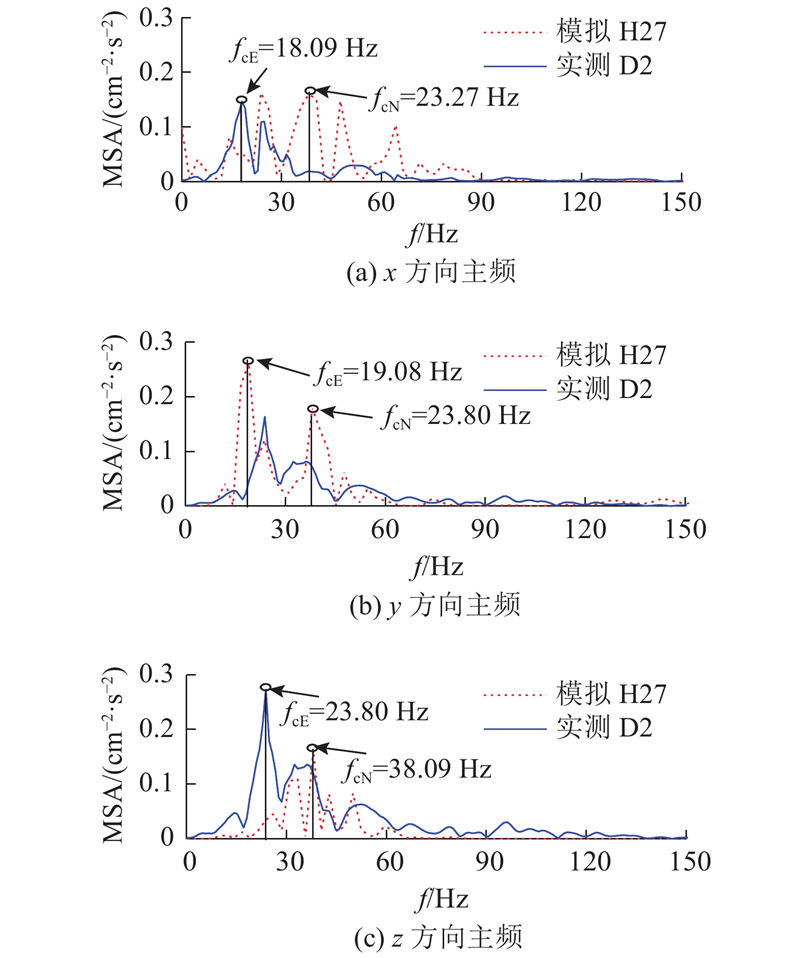
可以看出，在数值计算中，监测点振动速度起始响应时间约为15 ms，即在爆破振动起爆后，由爆源传播至监测点位置所需时间约为15 ms；质点振动时间持续100 ms，现场监测质点振动速度峰值略小于数值计算结果，合振速误差率最高为15.77%. 根据实验数据分析，现场实验管道以及地表地震波传播振动主频率fcE=15~100 Hz，数值计算振动主振频率fcN=20.63~128.25 Hz，现场监测振动频率略小于数值计算结果，误差约为10%. 分析存在以上现象的原因：在数值模拟过程未考虑岩土体内可能存在节理弱面对爆破振动速度峰值及频率衰减的影响. 综上分析，数值计算模型及参数选取合理，数值计算模型的振动速度峰值以及频率特征与现场实测爆破地震波振动规律一致，通过上述模型研究直埋管道的爆破地震效应是可行的.

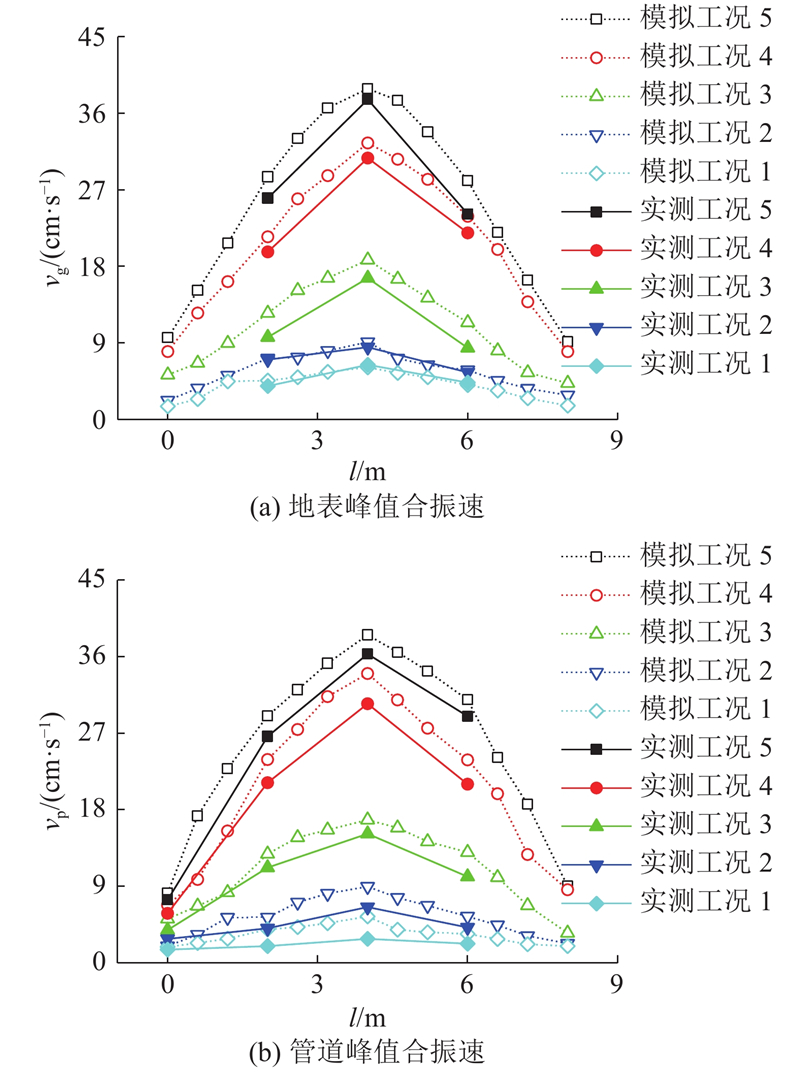
根据现场实验监测点的布置，沿管道轴线方向的振动测点布置不足，为了全面分析管道的振动特征，根据数值计算模型，沿管道轴线选取底部以及正上方地表土体质点，统计其合速度峰值振动速度，如图8所示. 图中，vg为地表振速，vp为管道振速，l为从管道端部起沿轴线方向的距离. 可以看出，在不同爆破工况下，管道、地表3个方向的峰值振动速度呈现出随爆源距离减小而不断增大的趋势，其中以炮孔V（工况5）爆破时的振动速度最大. 这与实际工程中下穿爆破施工位于管道正下方的工程实际情况一致. 因此可以确定正下方爆破为最危险工况. 此外沿管道轴线方向，管道、地表峰值振动速度均呈现出以管道中心截面为对称面沿两端不断减小的趋势，管道中心截面为振动危险截面. 对比数值模拟与现场实验数据可知，数值模型计算结果与实测数据基本一致，数值模拟计算结果稍大于实测结果，但在误差允许范围内，进一步验证了数值模型的准确性.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

图 8   管道轴线方向振速分布图

Fig.8   Vibration velocity in axial direction of pipeline


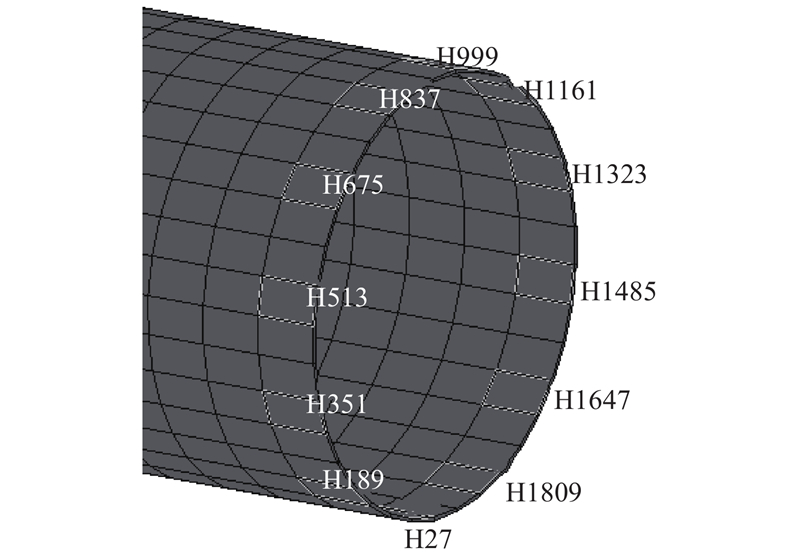
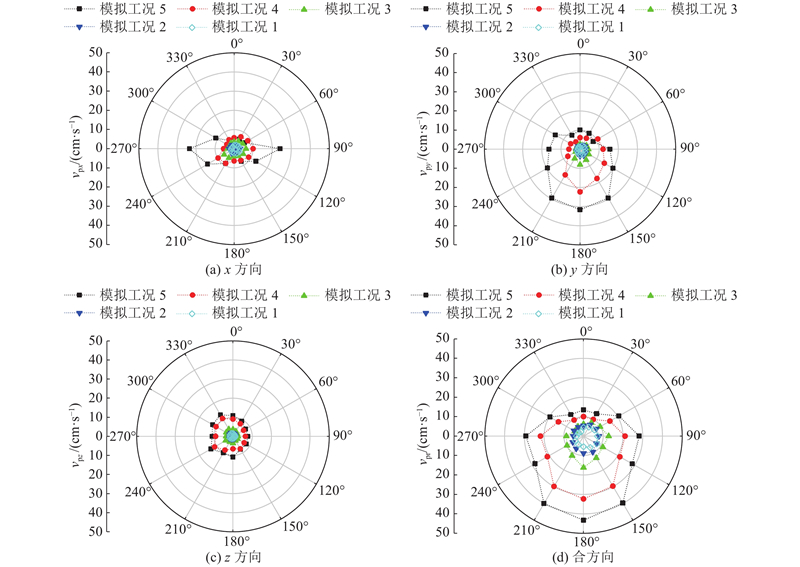
为了研究管道在爆破地震波影响下全截面的振动分布特征，根据不同爆破工况所建立的数值模型，选取管道中心截面为研究截面，沿着管道截面顺时针方向每30°选取管道截面单元H，如图9所示. 统计管道全截面单元x、y、z方向的峰值振动速度如图10所示. 可以看出，管道截面峰值振动速度随着爆破距离的减小而不断增大，且不同方向的振动规律有所不同. 以竖直y方向的振动为主，x方向次之，z方向最小. 随着爆源从右往左的靠近，管道截面的x方向的峰值振动速度的最大值均出现在管道腰部两侧，y方向的峰值振速最大值出现在管道底部，z方向的峰值振速最大值出现在背爆一侧的管道腰部. 为了便于研究，将3个方向的振动速度做矢量合，如图6、10（d）所示. 可以看出，合振动速度传播振动时间与达到峰值速度的时间与三向速度是同步的，合振动速度略大于三向振速. 实际工程中较大的振动速度对于实际工程应用具有一定的安全储备，对于管道安全评价更加合理. 因此在考虑振动速度的分析中，均采用三向矢量合速度峰值来表征质点的振动特征.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   管道截面单元示意图

Fig.9   Schematic diagram of pipe section unit


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   管道截面振速分布数值模拟结果

Fig.10   Simulation results of pipe section velocity distribution


3.2. 应力应变分析

根据弹塑性力学相关理论，管道这种具有一定壁厚的圆筒状结构，其力学性能不仅与管道结构材料相关，还与管道结构本身的直径和壁厚相关，按照管道外径与内径之比 ${\varDelta } $可以将其分为薄壁与厚壁结构[17]， ${\varDelta } $计算式为

$\varDelta {\rm{ = }}{{{D_0}}}/{{{D_{\rm{i}}}}}.$
(3)

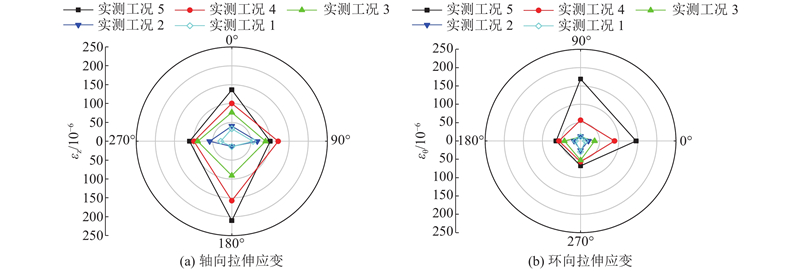
式中：D0为管道外径，Di为管道内径. 当 ${\varDelta } $≤1.2时，管道结构为薄壁结构. 本实验中管道直径为1 m，管道壁厚为1 cm，根据上式计算的 ${\varDelta } $=1.02，可以判断本实验管道为薄壁结构.

根据现场实验应变监测数据，实验所测动态应变数据包括管道截面A、B相应测点的环向εθ以及轴向应变εz，其中炮孔V（工况5）爆破下应变监测断面A的轴向和环向拉伸应变分布情况如图11所示. 可以看出，管道截面A上的4个监测点的动态应变以轴向拉伸应变为主，环向应变为辅，且在不同工况下，管道应变随爆源距离的减小逐渐增大，在正下方爆破时管道轴向拉伸应变达到最大，且在4个监测点中以管道底部以及顶部测定的应变值较大.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   实测管道截面应变分布图

Fig.11   Measured pipe section strain distribution


根据数值计算模型，在最危险工况5下，管道有效应力分布如图12所示. 图中，σe为有效应力. 可以看出，爆破地震波在约0.04 s时开始在管道中传播并引起管道单元有效应力的改变，管道振动增强，管道有效应力也逐渐增大. 在约0.10 s时到达管道上的爆破地震波的能量达到峰值，管道有效应力也达到峰值. 随后应力波在管道结构内不断震荡，引起管道有效应力的变化. 在0.20 s后管道介质中的爆破地震波能量逐渐消失，管道有效应力逐渐减小并趋于稳定. 爆破地震波在管道中传播时，管道中心截面上的有效应力最大，且有效应力以管道中心截面为对称面沿管道轴线不断减小，管道中心截面为危险截面，可以看出有效应力与管道的振动速度分布规律相对应.

图 12

新窗口打开| 下载原图ZIP| 生成PPT

图 12   管道有效应力分布图

Fig.12   Effective stress distribution of pipeline


根据材料力学相关理论，管道截面单元环向应力以及轴向应力表达式为

${\sigma _{\text{θ}} } = E {\varepsilon _{\text{θ}} },$
(4)

${\sigma _{\rm{z}}} = E{\varepsilon _{\rm{z}}}.$
(5)

式中：E=195 GPa，ε为测试应变. 根据弹塑性力学理论，薄壁圆筒结构径向应力可以近似忽略不计，由此可知管道截面单元处于平面受应力状态. 因此可以认为管道单元主应力σ1=σθ，σ2=0，σ3=σz. 管道有效应力σe可以采用Mises屈服准则[17]，表达式为

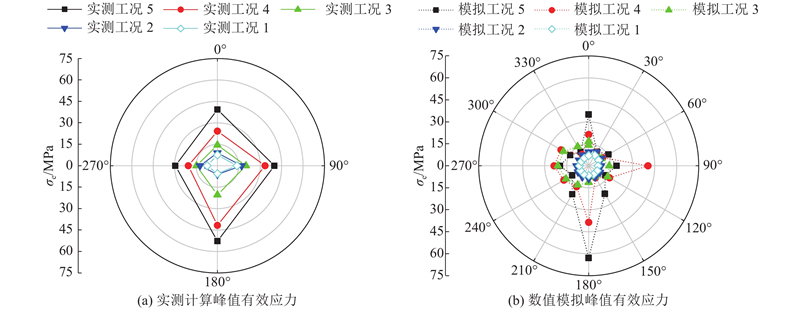
${\sigma _{\rm{e}}} ={\left( {\sigma _{\text{θ}} ^2 - {\sigma _{\text{θ}}}{\sigma _{\rm{z}}} + \sigma _{\rm{z}}^2} \right)}^{1/2} . $
(6)

将上述应变监测截面A各监测点的轴向、环向应变数据分别代入式（4）~（6）计算可得现场实验管道截面A应变监测测点的Mises有效应力如图13所示. 可以看出，现场监测管道截面有效应力分布以管道底部和顶部较大. 根据现场实验，按照图9选取数值计算模型中研究管道的中心截面单元，其不同工况下管道截面单元v-mises有效应力统计如图13（b）所示. 根据图13（a）、（b）对比分析可知，数值模拟计算值与现场实测值相比基本一致，误差在允许范围内. 根据数值模型，在不同爆破工况下管道危险截面Mises有效应力随爆破距离的增大而不断减小，且随着爆源的逐渐接近，管道截面的有效应力由管道腰部逐渐转移到管道顶部和管道底部，当管道位于最危险工况5时，管道截面Mises有效应力达到最大，且以底部单元最大，管道顶部、腰部次之，管道肩部数值最小.

图 13

新窗口打开| 下载原图ZIP| 生成PPT

图 13   截面有效应力分布示意图

Fig.13   Effective stress distribution of section


4. 爆破地震效应影响管道安全控制

4.1. 管道与地表振速关系

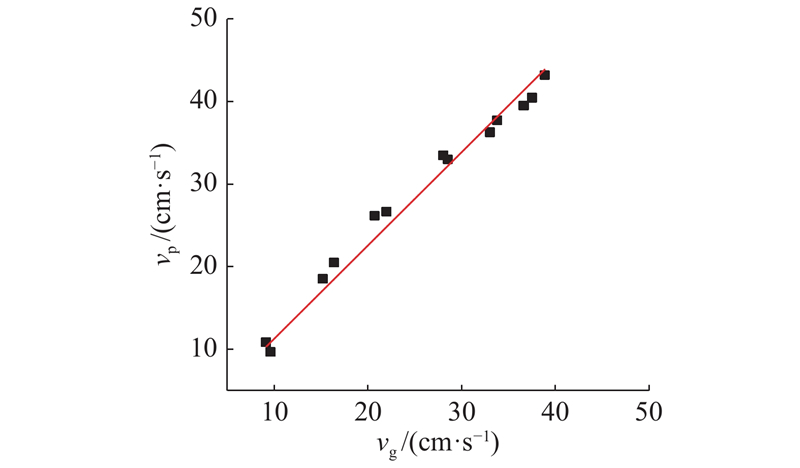
在实际工程中，针对管道结构本身的爆破振动监测几乎难以实现，往往以管道邻近地表振动速度作为表征来反映管道的振动速度. 但这一做法仅为经验操作，缺少实验和相关研究理论的支撑. 为了验证这一假设的合理性，根据上述实测以及数值模型，对管道、地表的峰值合振动速度进行统计分析，发现在同一爆破工况下，两者均呈现出以爆源与管道的垂直平面为对称面不断衰减的规律，两者最大振动速度均出现在爆源位于正下方的最危险工况条件. 根据最不利工况原则，选取工况5爆破时管道单元以及地表峰值合振动速度进行统计，如图14所示. 可以看出，管道与地表振动速度之间的关系可以表示为

${v_{\rm{p}}} = 1.128{v_{\rm{g}}}.$
(7)

根据式（7）可以定义管道与地表振速之比：

$K = {{{v_{\rm{p}}}}}/{{{v_{\rm{g}}}}}.$
(8)

由式（8）计算可以得到现场实验管土振速比为1.10，数值模型管土振速比约为1.16，两者较接近，进一步验证数值计算模型的可靠性. 根据上述分析可知，地表振动速度在一定程度上可以反映其正下方管道截面质点的振动速度特征，在实际工程管道的爆破振动安全监测中可以将地表振速作为下部埋地管道振动速度的监测量.

图 14

新窗口打开| 下载原图ZIP| 生成PPT

图 14   管道与地表振动速度关系示意图

Fig.14   Relationship between pipe and surface vibration velocity


4.2. 峰值应力与振速关系

大量工程实际表明，埋地管道中、远区爆破振动破坏，主要为爆破地震波在管道介质中传播引起的管道应力变化而产生的管道材料本身的失效破坏. 根据波动学理论[18-19]，波在无限介质中传播时产生的应力为

$\sigma = \rho c_{\rm{p}}v.$
(9)

式中：σ为正应力；ρ为传播介质密度；cp为纵波在介质中的传播速度，按照波的类型可以分为纵波和横波，与传播介质的弹性模量和泊松比有关；v为波传播过程中引起的介质质点的振动速度. 在本实验中，爆破地震波在管道中传播引起管道单元应力的变化，管道传播介质一定，因此ρ、cp可以近似看作比例定值. 根据式（9）定义管道单元有效应力表达式为

${\sigma _{\rm{e}}} = C_0{v_{\rm{p}}}.$
(10)

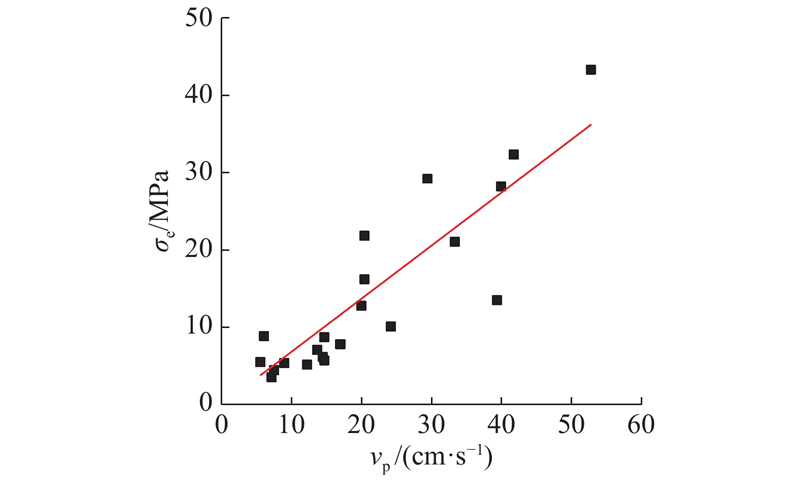
式中：C0为管道应力与振速的比例系数. 根据上述数值计算模型，管道截面单元有效应力与合振动峰值速度关系如图15所示.

图 15

新窗口打开| 下载原图ZIP| 生成PPT

图 15   有效应力与振速关系示意图

Fig.15   Relationship between effective stress and vibration speed


由图15可以得到本实验中埋地球墨铸铁管道有效应力为

${\sigma _{\rm{e}}} = 0.685{v_{\rm{p}}}.$
(11)

式（11）表明，本实验中埋地管道应力振速比C0=0.685. 将式（9）与式（11）联立，可以得到管道应力与地表振动速度的关系式为

${\sigma _{\rm{e}}} = C_0 K{v_{\rm{g}}}.$
(12)

将本实验中所确定的相关比例系数C0、K代入式（12），可以得到本实验中管道有效应力的预测公式为

${\sigma _{\rm{e}}} = 0.766{v_{\rm{g}}}.$
(13)

4.3. 不同埋深管道安全评价

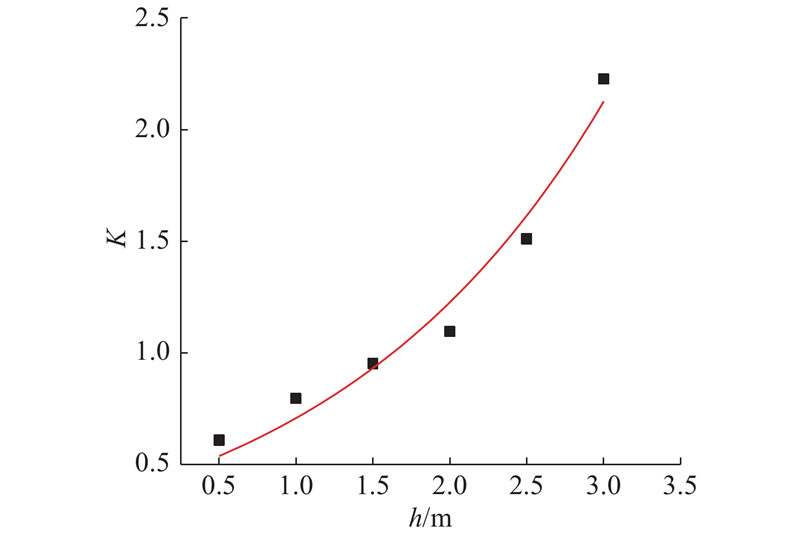
式（13）表明，管道单元有效应力与比例系数C0、K有关，根据上述分析，当管道材料一定时C0是一定的，K为不同介质的振速之比，其大小与波的传播与衰减路径有关，因此管道埋深h（上部覆土层厚度）是影响K的重要因素. 根据工程调查，武汉市球墨铸铁管道主要埋置深度为0.5~2.5 m，根据上述现场实验结果，按照最不利工况原则，在上述埋深2.0 m的数值计算模型的基础上改变管道埋置深度分别建立管道埋深为0.5、1.0、1.5、2.0、2.5 m时的数值计算模型进行研究，得到不同埋深条件下K的变化，如表5所示.

表 5   不同管道埋深下的振速统计

Tab.5  Vibration velocity with different pipeline buried depth

h /m vp /（cm·s−1） vg /（cm·s−1） K
0.5 27.56 45.320 0.60
1.0 33.35 43.340 0.76
1.5 38.15 40.120 0.95
2.0 43.99 37.123 1.18
2.5 50.35 33.330 1.51
3.0 59.45 28.140 2.11

新窗口打开| 下载CSV


由表5可知，管道峰值振速与地表峰值振动速度之比随管道埋深增加而增加，根据统计学原理，其关系示意如图16所示：

图 16

新窗口打开| 下载原图ZIP| 生成PPT

图 16   管表比与埋深关系示意图

Fig.16   Relationship between pipeline and ground surface vibration velocity ratio and buried depth


$K = 0.408{{\rm{e}}^{0.55h}}.$
(14)

结合式（13）、（14）可以得到本实验中管道有效应力与埋深、地表振动速度的关系式：

${\sigma _{\rm{e}}} = 0.905{v_{\rm{g}}} {{\rm{e}}^{0.55h}}.$
(15)

由式（15）可知，在考虑管道埋深影响下，可以根据管道上方地表峰值振速预测管道峰值有效应力. 根据现场实验测试数据可知，当管道埋深内为2.0 m时，将地表监测振速为vg=38.48 cm/s代入式（15）计算可得管道有效应力σe=104.61 MPa. 根据文献[20]，球墨铸铁管道安全运行有效应力应该满足

${\sigma _{\rm{e}}} \leqslant 0.90{\sigma _{\rm{s}}}.$
(16)

式中：σs为管材标准规定的最小屈服强度. 根据文献[21]，本实验中球墨铸铁管道σs=300 MPa. 由此计算得到[σ]=270 MPa，由于σe<[σ]，故管道材料未破坏，管道处于安全状态，根据现场实验后检查可知，管身均无明显变形破坏，故上述公式具有合理性.

综上所述，在实际工程现场中，在爆破作业时由于不便于开挖揭露管道，往往采用管道上方地表土体振动速度作为监测数据. 式（15）为考虑埋深影响下管道的有效应力与地表监测速度之间的预测关系式，为工程现场提供了可以预测评价爆破振动邻近埋地管道安全性的计算方法，对指导岩土爆破工程安全作业具有重要意义.

5. 结　论

（1）在不同爆破工况下，管道、地表峰值振动速度随爆源距离减小而不断增大，管道正下方爆破为最危险工况；沿管道轴线方向，管道、地表峰值振动速度以管道中心截面为对称面沿两端不断减小，管道中心截面为危险截面；管道截面单元三向振动规律有差异，以合振动速度作为表征是合理的.

（2）管道截面应变以轴向拉伸应变为主，环向应变为辅；在不同工况下，管道应变随爆源距离的增大逐渐减小；管道截面有效应力随爆破距离的增大而不断减小，在危险工况下，管道截面有效应力以底部单元最大，管道顶部、腰部次之，管道肩部最小.

（3）管道与地表振速具有对应关系，在工程实际中以地表振速预测下方埋地管道振速是合理的，管表振速比随着管道埋置深度的增大而增大；管道单元应力与振速具有对应关系，通过地表振动速度与管道应力关系预测管道在爆破地震波作用下的峰值有效应力是可靠的，可以为爆破邻近管道的安全评价提供计算方法.

（4）研究成果适用于计算黏性土中不同深度埋地铸铁管道的爆破振动速度及有效应力，由于实验条件限制，本研究并未考虑管道运行状态及不同土层参数因素，因此研究具有一定的不足. 在后续的研究中须针对不同土层性质（黏性土、砂土、填土）下、不同运行状态下的埋地管道的动力响应及安全控制方法进行进一步研究.

参考文献

中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 爆破安全规程: GB6722—2014[S]. 北京: 中国标准出版社, 2015: 7.

[本文引用: 1]

管晓明, 张良, 王利民, 等

隧道近距下穿管线的爆破振动特征及安全标准

[J]. 中南大学学报: 自然科学版, 2019, 50 (11): 2870- 2885

[本文引用: 1]

GUAN Xiao-ming, ZHANG Liang, WANG Li-min, et al

Blasting vibration characteristics and safety standards of tunnels passing through pipelines at short distances

[J]. Journal of Central South University: Science and Technology, 2019, 50 (11): 2870- 2885

[本文引用: 1]

夏宇磬, 蒋楠, 周传波, 等

下穿地铁隧道爆破振动作用下给水管道动力响应特性研究

[J]. 爆破, 2019, 36 (1): 6- 13

XIA Yu-qing, JIANG Nan, ZHOU Chuan-bo, et al

Study on the dynamic response characteristics of water supply pipelines under the blasting vibration of subway tunnels

[J]. Blasting, 2019, 36 (1): 6- 13

王栋, 何历超, 王凯

钻爆法施工对邻近埋地管道影响的现场实测与数值模拟分析

[J]. 土木工程学报, 2017, 50 (Suppl.2): 134- 140

[本文引用: 1]

WANG Dong, HE Li-chao, WANG Kai

Field measurement and numerical simulation analysis of the impact of drilling and blasting construction on adjacent buried pipelines

[J]. Journal of Civil Engineering, 2017, 50 (Suppl.2): 134- 140

[本文引用: 1]

张黎明, 赵明生, 池恩安, 等

爆破振动对地下管道影响实验及风险预测

[J]. 振动与冲击, 2017, 36 (16): 241- 247

[本文引用: 1]

ZHANG Li-ming, ZHAO Ming-sheng, CHI En-an, et al

Experiment and risk prediction of impact of blasting vibration on underground pipelines

[J]. Vibration and Shock, 2017, 36 (16): 241- 247

[本文引用: 1]

XIA Y, JIANG N, ZHOU C, et al

Safety assessment of upper water pipeline under the blasting vibration induced by subway tunnel excavation

[J]. Engineering Failure Analysis, 2019, 104 (6): 626- 642

[本文引用: 1]

JIANG N, GAO T, ZHOU C B, et al

Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel

[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research, 2018, 81 (11): 590- 601

[本文引用: 1]

SCOTT A A, TEERAWUT J

Response of single piles and pipelines in liquefaction–induced lateral spreads using controlled blasting

[J]. Earthquake Engineering and Engineering Vibration, 2002, 1 (2): 181- 193

DOI:10.1007/s11803-002-0064-3      [本文引用: 1]

高坛, 周传波, 蒋楠, 等

基坑开挖爆破下邻近管道振动速度安全阈值研究

[J]. 安全与环境学报, 2017, 17 (6): 2191- 2195

[本文引用: 1]

GAO Tan, ZHOU Chuan-bo, JIANG Nan, et al

Study on the safety threshold of adjacent pipeline vibration speed under foundation pit excavation blasting

[J]. Journal of Safety and Environment, 2017, 17 (6): 2191- 2195

[本文引用: 1]

张震, 周传波, 路世伟, 等

超浅埋地铁站通道爆破暗挖地表振动传播特征

[J]. 中南大学学报: 自然科学版, 2017, 48 (8): 2119- 2125

ZHANG Zhen, ZHOU Chuan-bo, LU Shi-wei, et al

Propagation characteristics of ground vibration induced by subsurface blasting excavation in an ultra–shallow buried underpass

[J]. Journal of Central South University: Science and Technology, 2017, 48 (8): 2119- 2125

屈若枫, 徐光黎, 王金峰, 等

武汉地区典型软土物理力学指标间的相关性研究

[J]. 岩土工程学报, 2014, 36 (Suppl.2): 113- 119

[本文引用: 1]

QU Ruo-feng, XU Guang-li, WANG Jin-feng, et al

Correlation between physical and mechanical indices of typical soft soils in Wuhan area

[J]. Chinese Journal of Geotechnical Engineering, 2014, 36 (Suppl.2): 113- 119

[本文引用: 1]

袁松, 王峥峥, 周佳媚

隧道地震动力计算边界取值范围研究

[J]. 土木工程学报, 2012, 45 (11): 166- 172

[本文引用: 1]

YUAN Song, WANG Zheng-zheng, ZHOU Jia-mei

Research on boundary value range of tunnel seismic dynamic calculation

[J]. Journal of Civil Engineering, 2012, 45 (11): 166- 172

[本文引用: 1]

尚晓江, 苏建宇. ANSYS/LS–DYNA动力分析方法与工程实例[M]. 北京: 中国水利水电出版社, 2006.

[本文引用: 1]

刘小鸣, 陈士海

隧道掘进中掏槽孔爆破引起的地表振动波形预测

[J]. 岩土工程学报, 2019, 41 (9): 1731- 1737

[本文引用: 2]

LIU Xiao-ming, CHEN Shi-hai

Prediction of surface vibration waveform caused by blasting in tunnel excavation

[J]. Chinese Journal of Geotechnical Engineering, 2019, 41 (9): 1731- 1737

[本文引用: 2]

鲁稳, 潘卫东

Drucker–Prager系列屈服准则在稳定分析中的应用研究

[J]. 汕头大学学报: 自然科学版, 2014, 29 (1): 73- 80

[本文引用: 1]

LU Wen, PAN Wei-dong

Application of Drucker-Prager series yield criterion in stability analysis

[J]. Journal of Shantou University: Natural Science Edition, 2014, 29 (1): 73- 80

[本文引用: 1]

许名标, 彭德红

某水电站边坡开挖爆破震动动力响应有限元分析

[J]. 岩土工程学报, 2006, (6): 770- 775

[本文引用: 2]

XU Ming-biao, PENG De-hong

Finite element analysis of blasting dynamic response of slope excavation of a hydropower station

[J]. Chinese Journal of Geotechnical Engineering, 2006, (6): 770- 775

[本文引用: 2]

周琪, 陈永强

轴对称薄壁结构自由振动的边界元分析

[J]. 力学学报, 2019, 51 (1): 146- 158

[本文引用: 2]

ZHOU Qi, CHEN Yong-qiang

Boundary element analysis of free vibration of axisymmetric thin-wall structures

[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51 (1): 146- 158

[本文引用: 2]

李兴华, 龙源, 纪冲, 等

爆破地震波作用下隧道围岩动应力集中系数分析

[J]. 岩土工程学报, 2013, 35 (3): 578- 582

[本文引用: 1]

LI Xing-hua, LONG Yuan, JI Chong, et al

Analysis of dynamic stress concentration factor of tunnel surrounding rock under blasting seismic wave

[J]. Chinese Journal of Geotechnical Engineering, 2013, 35 (3): 578- 582

[本文引用: 1]

黄强兵, 彭建兵

基于地震波入射角的地下管道地震应力计算

[J]. 地下空间与工程学报, 2008, (5): 979- 984

[本文引用: 1]

HUANG Qiang-bing, PENG Jian-bing

Study on seismic stress calculation of underground pipeline based on incident angle of seismic wave

[J]. Chinese Journal of Underground Space and Engineering, 2008, (5): 979- 984

[本文引用: 1]

中华人民共和国住房和城乡建设部. 输气管道工程设计规范: GB 50251—2015 [S]. 北京: 中国标准出版社, 2015: 7.

[本文引用: 1]

国家市场监督管理总局, 国家标准化管理委员会. 水及燃气用球墨铸铁管、管件和附件: GB/T 13295—2019 [S]. 北京: 中国标准出版社, 2019: 1.

[本文引用: 1]

/

〈 〉