岩体广泛分布于自然界各处，几乎所有工程建设都要准确获取岩体的强度参数. 岩体由岩块和结构面组成，结构面强度对岩体强度有决定性的影响. 岩体结构面粗糙度的定量评价是获取岩体结构面峰值抗剪强度的基础，在生产实践和工程建设中具有重要的意义.

岩体结构面粗糙度系数（joint roughness coefficient, JRC）由Barton^[1]通过测试岩体结构面抗剪强度得到. 在针对136组结构面强度测试的基础上，Barton等^[2]总结了10条标准剖面线，JRC为0~20. 至此，工程师可以通过视觉类比的方法获取结构面大致的JRC. 该方法被国际岩石力学学会采纳作为估算JRC的标准方法^[3]. 视觉类比往往会产生较大的误差，通过直剪试验测定JRC较烦琐. 为此，大量学者开展了结构面统计参数与JRC关系的研究. Patton等^[4]基于规则锯齿状结构面，研究起伏角度与结构面剪切强度的关系. Myers等^[5-9]提出结构面的坡度均方根参数与结构面JRC之间的定量关系. Yu等^[7]提出岩体结构面起伏角标准差与JRC之间的定量关系. Barton等^[10-11]研究结构面表面相对起伏高度与JRC的关系. 葛云峰等^[12]提出基于光亮面积百分比的岩体结构面JRC表征方法. 陈世江等^[13-15]提出用岩体结构面分形维数表征JRC的新方法. 蔡毅等^[16]研究岩体结构面在垂直方向投影面积与水平投影面积之比，将其定义为粗糙度指标，提出描述结构面三维粗糙程度的新参数. 上述研究均是基于单一或少量结构面剖面线形态参数，建立综合多种形态参数的JRC评价模型尚待开展.

岩体结构面粗糙度研究经历了从力学试验到统计参数研究的过渡，不但使JRC的评价更加便捷，而且节约了大量成本. 在大数据信息化的时代，如若能够建立基于智能算法的多参量JRC评价预测模型，则能够将JRC的研究再次向前推进一步. 在结构面JRC评价预测方面，Wang等^[17-19]作了初步尝试. 其中，Wang等^[17-18]通过支持向量机模型（support vector machine, SVM）建立各统计参数与结构面JRC的隐式关系. 宋康明等^[19]提出基于随机森林(random forest，RF)算法研究JRC的新方法. 由于机器学习所构建的隐式模型的局限性，Wang等^[17-19]建立的模型均不具有普遍性与可推广性. 本研究尝试采用Boosting-决策树（decision tree, DT）C5.0模型，建立岩体结构面统计参数与JRC的决策树模型，并致力于推广其在岩土工程中的应用. 决策树是流行的分类算法和决策支持方法. 在分类和预测方面遵循一系列树状图规则，其中树状图的结点为样本属性，分支为属性取值. 决策树的算法很多，DT C5.0是比较常用的一种. 目前，DT C5.0模型在岩土工程领域中的应用多集中在滑坡与岩石力学的研究方面. 王朋伟^[20]建立滑坡主要诱发因素与稳定性状态的决策树模型，结合规律与滑坡地质环境特征解释滑坡演化趋势. 乔建平等^[21]提出基于不确定决策树算法在滑坡危险性预测的方法. 王正海等^[22]建立基于决策树的SVM多类分类器，利用矿区采集的野外实测岩性波谱数据进行分类实验. 陈顺满等^[23]建立岩石3种评价指标与岩爆烈度之间的决策树模型.

本文搜集112条岩体结构面JRC值，统计包括结构面平均相对起伏高度、结构面平均起伏角、结构面剖面线粗糙系数等在内的8种形态参数. 采用主成分分析（principal component analysis，PCA）的方法，对形态参数进行降维处理. 以前102组剖面线数据作为训练样本，基于Boosting-DT C5.0算法构建决策树模型，采用Barton10条标准剖面线进行验证. 选取多种机器学习模型作为对比，验证各模型的预测精度.

决策树模型在估计过程和解释参数方面具有优势，与其他统计方法不同，决策树模型无须作统计假设，可以处理代表不同尺度的数据，且计算速度较快，这是较SVM等模型比较明显的优点. DT C5.0是基于ID 3算法发展而来的. 其计算方法是由熵的概念引出，即在信息源被发出之前的平均不确定性. 假设N为整个样本集合，C是一组目标变量，t为C的分类数. 熵被定义为

(1) ${\rm{Ent}}(N) = - \mathop \sum \limits_{i=1}^t p\left( {{C_i}\mid N} \right){\log _2}\;p\left( {{C_i}\mid N} \right).$

式中： $p({C_i}\left| N \right.)$为 ${C_i}(i = 1,2, \cdots ,t)$的相对概率. 假如某具有属性的变量T被分成K类，则该变量被引入后的条件熵定义为

(2) $ {\rm{Ent}}(N\mid T) = \mathop \sum \limits_{j=1}^k \frac{{\left| {{T_j}} \right|}}{{|N|}} \times {\rm{Ent}}(N).$

新分裂的节点与原节点熵的差值为信息增益，表示为

(3) $ {\rm{Gains}}(N,T) = {\rm{Ent}}(N) - {\rm{Ent}}(N\left| T \right.).$

一般情况下， ${\rm{Ent}}(N) > {\rm{Ent}}(N|T)$. 信息消除的随机不确定性程度由信息增益来表现，因此，决策树的生长是通过选择具有最大信息增益率的最佳分组变量，它的定义如下：

(4) $ {{{\rm{GainRatio}}}} = \frac{{{\rm{Gains}}(N,T)}}{{{\rm{Ent}}(T)}}.$

DT C5.0算法对训练集使用统计的置信区间估计的方法来评估误差. 若节点n包含E_n个预测错误的样本，则该节点的错误率为

(5) $ {f_n} = {{{E_n}}}/{N}.$

定义节点n的估计误差为

(6) $ {e_n} = {f_n} + z\sqrt {\frac{{{f_n}\left( {1 - {f_n}} \right)}}{N}} . $

式中：z为阈值，一般等于1.15. 当待剪子树中叶节点的加权误差大于父节点的估计误差时，可以将该叶节点剪去，表示为

(7) $ \mathop \sum \limits_{n = 1}^r {p_n}{e_n} > e.$

式中：r为还未修剪子树叶节点的数量，p_n为叶节点中样本量占子树样本量的比值，e为父节点的估计误差.

Boosting技术可以提高DT C5.0算法的稳健性，主要包括建模阶段和模型投票阶段.

在建模阶段，该技术通过对现有加权样本进行重复采样来增加模拟样本集. 设整个过程需要k次迭代，训练样本T的样本量为N，则建模过程可以表示如下.

1）初始化样本权重，

(8) ${w_j}(i) = \frac{1}{N};\;i = 1,2, \cdots ,k,\;j = 1,2, \cdots ,N.$

式中： ${w_j}(i)$表示在j个样本在第i次迭代中的权重.

2）根据 ${w_j}(i)$，从T中有放回地抽取n个样本形成训练样本集T_i.

3）根据T_i得到模型C_i，计算该模型的误差e(i).

4）当 $e(i) > 0.5$或者 $e(i) = 0$时结束建模过程，否则根据误差来更新每个样本的权重. 正确分类样本权重为

(9) $ {w_j}(i + 1) = {w_j}(i)\beta (i). $

式中：

(10) $ \beta (i) = \frac{{{e_i}}}{{1 - {e_i}}}. $

错误分类的样本权重保持不变：

(11) $ {w_j}(i + 1) = {w_j}(i). $

进行归一化处理：

(12) $ {w_j}(i + 1) = \frac{{{w_j}(i + 1)}}{{\displaystyle\mathop \sum \limits_{j = 1}^N {w_j}(i + 1)}}. $

5）重复迭代步骤1）~4），得到k个模型和k个误差.

在投票阶段，对新的样本集X的投票过程可以概括如下.

a）对每个模型 ${C_i}(i = 1,2, \cdots ,k)$都给出预测值 ${C_i}(X)$和权重：

(13) $ {w_j}(X) = - \lg \;\left( {\frac{{{e_i}}}{{1 - {e_i}}}} \right). $

k个模型将给出k个 ${C_i}(X)$和 ${w_i}(X)$.

b）根据类别分别计算权重的总和，总和最高的类别即为该集合X的最终分类结果.

结合交叉验证方法与Boosting技术，可以提高DT C5.0模型的泛化能力，防止模型过度拟合.

主成分分析（PCA）是统计学中常见的降维算法. 核心思想是通过正交变换，将可能存在相关性的变量转换为线性不相关的变量，转换后的这组变量叫主成分. PCA基本流程如下：1）求取n维向量各平均值；2）求n维向量特征协方差矩阵，并求解协方差的特征值和特征向量；3）将特征值按从大到小依次排序，选择其中最大的k个特征向量分别作为列向量组成特征向量矩阵；4）将样本点投影到选取的特征向量上. 经过上述处理，可将原始的n维向量降维至k维.

Barton通过试验推导了结构面峰值剪切强度与JRC的经验公式，用于反映结构面粗糙度对峰值强度的影响^[1-2]：

(14) $ \tau = {\sigma _{\rm{n}}}\tan\; \left[ {{\rm{JRC}}\lg \;\left( {\frac{{{\rm{JCS}}}}{{{\sigma _{\rm{n}}}}}} \right) + {\varphi _{\rm{r}}}} \right]. $

式中：τ为结构面峰值剪切强度，σ_n为结构面法向应力，JCS为结构面的壁岩强度，φ_r为结构面的残余摩擦角.

为了便于上式在工程实践中的应用，Barton和Choubey在对136个结构面进行直剪试验的基础上，给出JRC为0~20时的10条标准剖面线，用于视觉对比确定目标结构面的JRC.

上述方法是基于直剪试验测试出来的，后续研究表明，结构面统计参数也可用来获取结构面粗糙度系数^[4-11]. 选取8种常用的结构面粗糙度评价参数.

1）结构面平均相对起伏高度：

(15) $ {R_{{\rm{ave}}}} = \frac{{{h_{{\rm{ave}}}}}}{L} = \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^{ N} \left| {{y_i}} \right|} \Big/ {N}}{L}. $

式中：L为结构面剖面线的取样长度，h_ave为结构面的平均起伏高度，y_i为第i个离散点的y坐标（y轴方向为剖面线起伏方向），N为结构面剖面线上的取样个数.

2）结构面起伏高度标准差：

(16) $ {\rm{S}}{{\rm{D}}_{\rm{h}}} = {\left[ {\frac{1}{{N - 1}}\mathop \sum \nolimits_{i = 1}^{ N - 1} {{\left( {{y_i} - {h_{{\rm{ave}}}}} \right)}^2}} \right]^{1/2}}. $

3）结构面平均起伏角：

(17) $ {i_{{\rm{ave}}}} = \arctan\; \left[ {\frac{1}{{N - 1}}\mathop \sum \nolimits_{i = 1}^{ N - 1} \left| {\frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}}} \right|} \right]. $

式中：x_i为第i个离散点的x坐标（x轴方向为剖面线延伸方向).

4）结构面起伏角标准差：

(18) $ {\rm{S}}{{\rm{D}}_{\rm{i}}} = \arctan {\left[ {\frac{1}{{N - 1}}\mathop \sum \nolimits_{i = 1}^{ N - 1} {{\left( {\frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}} - \tan {i_{{\rm{ave}}}}} \right)}^2}} \right]^{1/2}}. $

5）结构面最大相对起伏高度：

(19) $ {R_{{\rm{max}}}} = \frac{{{h_{\rm{p}}} - {h_{\rm{v}}}}}{L}. $

式中：h_p为结构面剖面线各取样测量点距中心线的最大正高差；h_v为结构面剖面线各取样测量点距中心线的最大负高差，取负值.

6）结构面剖面线粗糙系数R_p. Maerz等^[24]研究表明，JRC与R_p存在一定的线性关系，剖面线粗糙系数如下：

(20) $ {R_{\rm{p}}} = \frac{{{L_{\rm{t}}}}}{L} = \frac{{\displaystyle\mathop \sum \nolimits_{i = 1}^{ N - 1} {{\left[ {{{\left( {{x_{i + 1}} - {x_i}} \right)}^2} + {{\left( {{y_{i + 1}} - {y_i}} \right)}^2}} \right]}^{1/2}}}}{{\displaystyle\mathop \sum \nolimits_{i = 1}^{ N - 1} \left( {{x_{i + 1}} - {x_i}} \right)}}. $

(21) $ {\rm{JRC}} = 411\left( {{R_{\rm{p}}} - 1} \right). $

式中：L_t为结构面剖面线的真实迹线长度.

7）结构面结构函数（structure function）SF. Tse等^[6,8]分别得到JRC与SF之间的线性关系，如下：

(22) $ {\rm{SF}} = \frac{1}{{N - 1}}\mathop \sum \nolimits_{i = 1}^{ N - 1} \left( {y_{i + 1}^2 - y_i^2} \right), $

(23) $ {\rm{JRC}} = 37.28 + 16.58\lg\; {\rm{SF}}, $

(24) $ {\rm{JRC}} = 37.63 + 16.5\lg\; {\rm{SF}}. $

8）结构面坡度均方根参数Z₂. Patton^[4]在研究规则锯齿状结构面的剪切强度时，最先考虑了突起体的起伏角度对结构面剪切强度以及破坏模式的影响. 为了定量描述结构面的起伏角度特征，Myers^[5]提出结构面的坡度均方根参数：

(25) $ {Z_2} = {\left[ {\frac{1}{{N - 1}}\mathop \sum \nolimits_{i = 1}^{ N - 1} {{\left( {\frac{{{y_{i + 1}} - {y_i}}}{{{x_{i + 1}} - {x_i}}}} \right)}^2}} \right]^{1/2}}. $

Yang等^[8]采用傅里叶变换的方法重构标准剖面线，给出相关性更高的JRC与Z₂的回归关系式：

(26) $ {\rm{JRC}} = 32.69 + 32.98\lg \;{Z_2}. $

上述结构面形态参数均是在确定结构面中心线的基础上得到的. 结构面中心线如图1所示，求得上、下部分面积A_u、A_d相等，即可得到结构面中心线.

选用的岩体结构面粗糙度数据来源于文献[25]，共112条剖面线，长度为72.0~119.6 mm，采样间距为0.4 mm. 其中，1~102条剖面线数据为实际统计值；103~112为10条Barton标准剖面线. 8组统计参数与结构面JRC统计如图2所示. 采用1~102条剖面线参数作为训练学习样本，10条Barton标准剖面线（103~112）作为预测样本.

训练样本共有102组，每组由8个输入因子和1 个输出因子组成. 由于输入因子个数相对较多，且可能存在两两相关性，使得决策树模型构建缓慢且支数过多，须对模型的8个输入因子作预处理. 采用PCA方法对输入因子进行降维处理，共得到5个主成分，各主成分均为8个输入因子的线性函数，如下所示.

(27) $ \left. {\!\!\!\!\!\!\!\! {\begin{array}{*{20}{l}} \begin{array}{l} {\rm{P}}{{\rm{C}}_1} = 21.39{R_{{\rm{ave}}}} + 0.31{\rm{S}}{{\rm{D}}_{\rm{h}}} + 0.03{i_{{\rm{ave}}}} + 0.02{\rm{S}}{{\rm{D}}_{\rm{i}}} + \\ 4.68{R_{{\rm{max}}}} +4.38{R_{\rm{p}}} + 10.97{\rm{SF}} + 1.32{Z_2} - 6.11, \end{array}\\ \begin{array}{l} {\rm{P}}{{\rm{C}}_2} = 107.30{R_{{\rm{ave}}}} + 1.50{\rm{S}}{{\rm{D}}_{\rm{h}}} - 0.07{i_{{\rm{ave}}}} - 0.05{\rm{S}}{{\rm{D}}_{\rm{i}}} + \\ 21.49{R_{\max }} - 13.16{{{R}}_{\rm{p}}} - 35.28{\rm{SF}} - 3.39{Z_2} + 14.27, \end{array}\\ \begin{array}{l} {\rm{P}}{{\rm{C}}_3} = 128.20{R_{{\rm{ave}}}} + 2.55{\rm{S}}{{\rm{D}}_{\rm{h}}} - 0.393{i_{{\rm{ave}}}} - 0.28{\rm{S}}{{\rm{D}}_{\rm{i}}} + \\ 5.90{R_{\max }} + 45.13{R_{\rm{p}}} + 171.80{\rm{SF}} - 4.03{Z_2} - 39.2, \end{array}\\ \begin{array}{l} {\rm{P}}{{\rm{C}}_4} = 731.60{R_{{\rm{ave}}}} - 7.92{\rm{S}}{{\rm{D}}_{\rm{h}}} - 0.18{i_{{\rm{ave}}}} - 0.19{\rm{S}}{{\rm{D}}_{\rm{i}}} - \\ 33.52{R_{{\rm{max}}}} + 27.74{R_{\rm{p}}} + 94.14{\rm{SF}} - 1.07{Z_2} - 24.68, \end{array}\\ \begin{array}{l} {\rm{P}}{{\rm{C}}_5} = 420.50{R_{{\rm{ave}}}} + 12.00{\rm{S}}{{\rm{D}}_{\rm{h}}} - 0.27{i_{{\rm{ave}}}} + 0.34{\rm{S}}{{\rm{D}}_{\rm{i}}} - \\ 279.10{R_{\max }} - 1.45{R_{\rm{p}}} - 16.73{\rm{SF }}- 3.53{Z_2} + 0.79. \end{array} \end{array}}} \right\} $

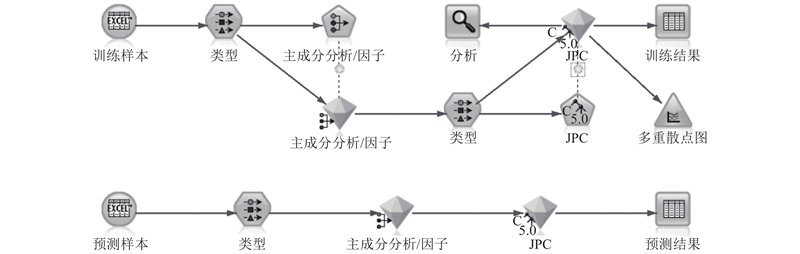
在PCA基础上，将5个主成分作为输入因子、JRC作为目标函数，对102组数据进行训练学习，建立 Boosting-DT C5.0模型. 决策树模型构建完毕后，将10条Barton标准剖面线作为测试样本，检验构建的决策树模型的准确性. 决策树模型训练预测流程如图3所示.

为了提高模型的泛化能力，防止模型过度拟合，在构建决策树模型时，采用将交叉验证与Boosting技术相结合的方法. Boosting的试验次数设置为20，交叉验证折叠次数设置为10，预期噪声设置为10%. 经过对102组数据的学习训练，Boosting-DT C5.0模型构建完毕，共生成了8层、68个节点，各节点判别条件及训练结果如图4所示.

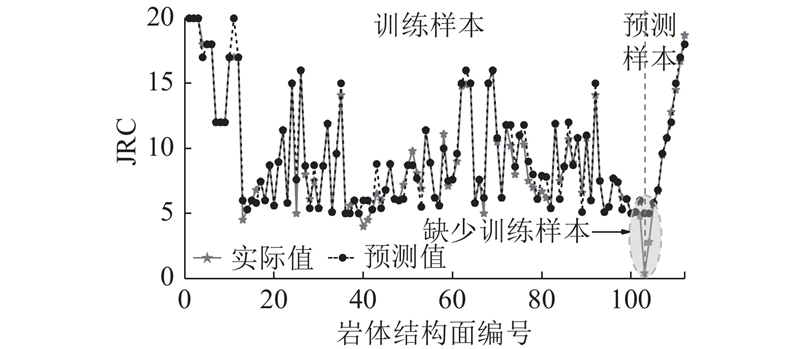
Boosting-DT C5.0模型训练预测结果如图5所示. 由结果可知，训练样本拟合优度为0.896，误差小于1.0的训练样本为83.33%，平均训练误差为0.24，均根误差MSE为1.077，均方根误差为1.038. 在预测样本中，前2组偏差较大. 由模型训练结果可知，最小JRC为5，而在预测样本中，前2组JRC分别为0.4和2.8. 学习样本中的训练组JRC较大，因此，样本预测时将这2组的JRC判别为5，造成了较大的误差. 在预测样本后8组数据中，取得了较理想的效果，误差小于1.0的样本达到100%. 由此可见，构建的Boosting-DT C5.0模型在预测JRC>5的样本时具有良好的效果.

为了验证构建的Boosting-DT C5.0模型的精度，选取DT C5.0模型、CHAID DT模型、SVM模型、人工神经网络（artificial neural network，ANN）模型作为对比，将后8组数据作为预测样本，选取拟合优度R²、误差小于1的样本率E₁、平均误差E_a、均方误差MSE、均方根误差RMSE作为评价指标，各模型的预测精度如图6及表1所示.

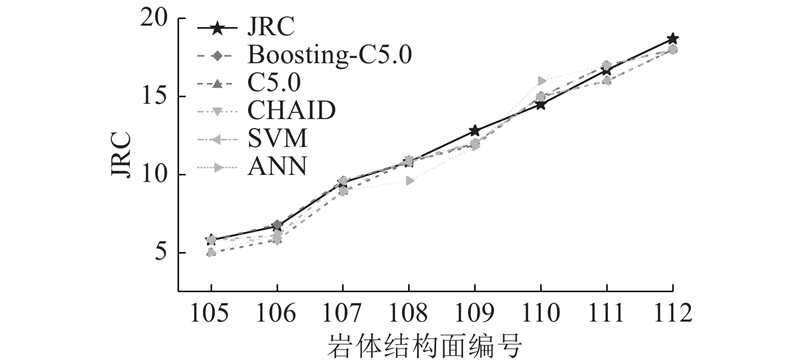
从预测结果的拟合优度上来看，各模型预测结果精度排序为 Boosting- DTC5.0 > SVM > CHAID DT > DT C5.0 > ANN. 从误差小于1的样本率上来看：除了ANN模型，其余4种均为100%. 预测结果误差显示，Boosting-DT C5.0 > SVM > CHAID DT > DT C5.0 > ANN. 综合5种模型预测结果可知，本文构建的Boosting-DT C5.0模型拟合优度最佳，且预测结果平均误差、均方根误差均最小. Boosting-DT C5.0模型可以用于岩体结构面粗糙度指标的预测.

将本文建立的JRC预测模型与文献[17，18]的预测结果相比，在对后8组数据的预测精度上，本文提出的Boosting-DT C5.0模型平均误差达到0.06，远高于文献[17，18]中的0.36，可见Boosting-DT C5.0模型的预测精度较高，具有良好的推广应用价值，可以在生产实践中用于岩体结构面粗糙度指标的预测，对于生产实践中工程岩体的稳定性分析评价具有重要的理论意义和应用价值.

（1）岩体结构面JRC与结构面形态参数具有紧密的联系，选取结构面8种形态参数，采用PCA方法将输入因子降维至5个主成分，大大提高了预测模型构建速度.

（2）相较于DT C5.0模型、CHAID DT模型、SVM模型、ANN模型，基于Boosting-DT C5.0模型的岩体结构面JRC预测精度最高. 因此，Boosting-DT C5.0模型可以用于岩体结构面粗糙度指标的预测.

（3）采用智能算法构建JRC预测模型可更加便捷地获取结构面粗糙度参数，从而有效评价岩体结构面的峰值剪切强度，对于生产实践中工程岩体的稳定性分析评价具有重要的理论意义和应用价值.

（4）由于数据量有限，构建的Boosting-DT C5.0模型仅考虑了结构面剖面线的8种形态参数，未能考虑分形特征参数，需在下一步研究中予以补充.