基于模型定义^[1-3]（model-based definition，MBD）的数字化设计与制造技术已经被很多制造企业采用. 在MBD技术的基础上，数字线（digital thread）和数字孪生（digital twin，DT）成为制造信息化发展的趋势. 数字孪生^[4-5]作为赛博物理系统的关键技术，能够对物理世界进行数字化描述并有效管控产品全生命周期的数据. 数字孪生的产生和应用是对MBD技术的进一步发展，为全三维研制模式下产品研发、生产提供了新的思路. 在“基于模型驱动”的产品研制环节，根据MBD技术构建零件工艺信息模型，并利用工艺信息模型和工序参数快速构建工序模型，满足工艺规划过程对信息处理速度的要求^[6-8]；在产品检验环节，利用工艺/工序模型开发三维数字化检测工艺系统，构建检测工艺模型，解决传统二维检测方法速度慢、效率低、准确率低的问题^[9-10].

上述模型都是利用底层采集所得的数据构建的，如何深度利用这些模型承载的工艺和检测数据逐渐成为当前数字孪生应用研究的焦点. 近年来，已有学者利用制造过程中采集的工艺信息和检测信息进行数据挖掘分析，并将分析结果用于零件质量的预估和工艺参数的优化.

Tirkel^[11]利用机器学习算法建立晶圆加工周期预测模型，提高了产品制造和供应效率. 朱雪初等^[12]研究晶圆智能制造系统的工业大数据挖掘，并根据挖掘所得的有效信息提出了基于工业大数据的晶圆加工周期预测方法框架. 汪俊亮等^[13]基于海量晶圆制造数据设计回归模型，通过对1669个晶圆加工过程参数与订单交货期指标之间关联关系的分析，实现了晶圆制造订单交货期的精准预测. Abajo等^[14]利用对新型马口铁质量诊断数据的分析，提出基于过程数据的马口铁质量诊断模型.

基于数字孪生思想和已有研究的启发，本研究提出机加零件的质量预测与工艺参数优化方法. 以集成工艺信息和检测信息的MBD模型为唯一数据源，采用CATIA组件应用架构（component application architecture，CAA）二次开发技术，完成工艺信息和检测信息的自动提取并存入数据库；利用逻辑回归（logistic regression，LR）、支持向量机（support vector machine，SVM）、极端梯度提升（extreme gradient boosting，XGBoost）等多种分类器构建预测模型并完成数据训练，实现基于工艺参数的零件质量预测；利用梯度提升树（gradient boost decision tree，GBDT）算法构建特征，提升分类模型预测的准确率；基于零件的工艺参数和质量分类标签，结合信息增益算法对影响零件质量的工艺参数进行优先级的排序；最后，通过GBDT回归模型的训练优化零件的工艺参数.

根据工业工程相关理论，影响机加零件质量的主要因素可归纳为加工方法、设备、材料、环境和工艺参数等5个方面. 本研究将在前4个方面因素确定的情况下，从工艺参数对零件质量的影响入手，使用机器学习算法构建零件质量预测模型，通过机加过程中选用的工艺参数预测零件质量.

在实际工业场景中，工艺参数取值对零件质量的影响存在各种不确定性和随机性. 因此，本研究给出通用的工艺信息与检测信息的结构化数据格式、工艺参数优先级排序接口、零件质量模型准确率验证接口以及零件质量预测接口. 基于结构化数据格式对所有工艺参数进行优先级排序，辅助工艺人员进行有效工艺参数选取；针对所选工艺参数，提供多种零件质量预测模型的准确率验证接口，展示模型对工艺参数的拟合情况；选取拟合情况较好的模型作为零件质量预测模型，辅助工艺人员预测零件质量.

设训练数据集为D， $\left| D \right|$为其样本容量，即样本个数. 零件质量有合格和不合格2种状态，即样本有2个类 ${C_1}$和 ${C_2}$， $\left| {{C_k}} \right|$为属于类 ${C_k}$的样本个数， $\sum\limits_{k = 1}^2 {\left| {{C_k}} \right|} = \left| D \right|$. 假设工艺参数 ${x_1}$有 $l$个不同的取值 ${x_{11}},{x_{12}},\cdots,{x_{1l}}$，根据工艺参数 ${x_1}$的取值将 $D$划分为l个子集 $\{ {D_1},{D_2},\cdots,{D_l}\} $， $\left| {{D_i}} \right|$为 ${D_i}$的样本个数， $\sum\limits_{i = 1}^l {\left| {{D_i}} \right|} = \left| D \right|$. 记子集 ${D_i}$中属于类 ${C_k}$的样本的集合为 ${D_{ik}}$，即 ${D_{ik}} = {D_i}\bigcap {{C_k}} $， $\left| {{D_{ik}}} \right|$为 ${D_{ik}}$的样本个数.

用于零件质量预测的结构化数据格式如表1所示. 表中， $x_1^{(i)},x_2^{(i)},\cdots,x_j^{(i)}，\cdots,x_n^{(i)}$表示同一样本机加过程中的不同工艺参数，取值可以为连续型变量也可以为离散型变量，上标 $i = 0,1,\cdots,m$表示机加零件的样本编号，下标 $j = 0,1,\cdots,n$表示不同的工艺参数编号， ${L^{(i)}}(i = 0,1,\cdots,m)$表示零件质量预测标签，取值为离散型变量，有合格/不合格2种状态.

给定训练数据集 $D$和特征 $A$，信息熵^[15]$H(D)$表示对数据集 $D$进行分类时的不确定性；条件熵 $H(D\left| A \right.)$表示在给定特征 $A$的条件下，对数据集 $D$进行分类时的不确定性. 信息熵和条件熵的差值为信息增益，表示因为特征 $A$的给定，对数据集 $D$进行分类时不确定性的减少程度. 该算法的输入为训练数据集 $D$和工艺参数 ${x_j}$，计算步骤为

1）计算数据集 $D$的信息熵：

(1) $H(D) = - \sum\limits_{k = 1}^2 {\frac{{|{C_k}|}}{{|D|}}} {\log _2}\;\frac{{|{C_k}|}}{{|D|}}.$

2）计算给定 ${x_j}$的条件熵：

(2) $H(D\left| {{x_j}} \right.) = - \sum\limits_{i = 1}^n {\frac{{|{D_i}|}}{{|D|}}} \left[\sum\limits_{k = 1}^2 \left({\frac{{|{D_{ik}}|}}{{|{D_i}|}}} {\log _2}\frac{{|{D_{ik}}|}}{{|{D_i}|}}\right)\right].$

3）计算信息增益：

(3) $g(D\left| {{x_j}} \right.) = H(D) - H(D\left| {{x_j}} \right.).$

通过计算机加零件所有工艺参数的信息增益，可以判断不同工艺参数对零件质量的影响程度，信息增益最大的工艺参数对零件质量的影响程度最大.

零件质量预测模型的原理，是利用加工工艺参数实现对零件质量的二分类，因此属于分类问题，可以选用LR、SVM^[16]、XGBoost^[17]和GBDT+LR^[18-19]等常见分类器实现模型构建. 其中，LR、SVM和XGBoost属于通用性较强的分类器，可以作为基础分类器.

GBDT属于Boosting算法，前面的树结构能够构建对多数样本具有区分度的特征，后面的树结构拟合少数样本，因此采用GBDT可以构建具有区分度的特征. 在工艺参数较少的特殊情况下，为了提高零件质量预测模型的准确率，须构建有效特征以弥补人工经验的不足，可以利用GBDT结合LR作为此类情况下的零件质量预测模型.

使用逻辑回归算法构建的零件质量预测模型的输入为零件的工艺参数，输出为零件质量是否合格. 对于样本编号为i的样本，模型的输入为当前编号零件的工艺参数 $x_1^{(i)}, $ $ x_2^{(i)},\cdots,x_j^{(i)},\cdots,x_n^{(i)}$，记为 ${X^{(i)}}$；逻辑回归模型的内部参数，即工艺参数权值 ${\omega _1},{\omega _2},\cdots,{\omega _n}$，记为 $\omega $. 因此用于零件质量预测的分类器为

(4) $P(Y = 1\left| {{X^{(i)}}} \right.) = \frac{{\exp\;\; (\omega {X^{(i)}})}}{{1 + \exp\;\; (\omega {X^{(i)}})}}.$

(5) $P(Y = 0\left| {{X^{(i)}}} \right.) = \frac{1}{{1 + \exp\;\; (\omega {X^{(i)}})}}.$

可以看出， $\omega {X^{(i)}}$的计算值越接近正无穷大，分类结果越趋近于1，即零件质量分类为合格； $\omega {X^{(i)}}$的计算值越接近负无穷大，分类结果越趋近于0，即零件质量分类为不合格. 对于给定的输入实例 ${X^{(i)}}$，求得 $P(Y = 1\left| {{X^{(i)}}} \right.)$和 $P(Y = 0\left| {{X^{(i)}}} \right.)$2个条件概率，将实例 ${X^{(i)}}$分到概率较大的类.

在应用GBDT拟合原始数据集并构建新特征时，须将新特征和原始数据集特征进行拼接后，再对零件质量进行预测. 对于样本编号i，将 $n$维工艺参数作为特征 ${\rm{\{ }}x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)}{\rm{\} }}$，记为 ${X^{(i)}}$，对零件质量标签 ${L^{(i)}}$进行拟合. $T({X^{(i)}};{\theta _m})$表示决策树， ${\theta _m}$表示决策树的初始化参数， $M$表示决策树个数，利用特征 ${X^{(i)}}$求得 $M$棵回归树的总和为

(6) ${f_M}({X^{(i)}}) = \sum\limits_{m = 1}^M {T(x^{(i)};{\theta _m})} .$

首先设定初始 ${f_0}(x^{(i)}) = 0$， $ f_{m-1}(X^{(i)})$是当前的分类器，则第 $m$步分类器为

(7) ${f_m}({X^{(i)}}) = {f_{m - 1}}({X^{(i)}}) + T({X^{(i)}};{\theta _m}).$

通过经验风险极小化对每一棵决策树的初始化参数 ${\theta _m}$进行优化。得到优化后的 ${\mathop \theta \limits^ \wedge {_m}} $为

(8) ${\mathop \theta \limits^ \wedge {_m}} = \arg \mathop {\min }\limits_{{\theta _m}} \;\sum\limits_{i = 1}^N {\rm{Loss}}({L^{(i)}} ,{f_{m - 1}}({X^{(i)}}) + T({X^{(i)}};{\theta _m}))$

式中： ${\rm{Loss}}({L^{(i)}} ,{f_{m - 1}}({X^{(i)}}) + T({X^{(i)}};{\theta _m}))$为第m步分类器与真实零件质量标签的损失值。

应用GBDT对训练数据进行拟合，保存训练后的分类器. 通过分类器重新读入全部数据并构建新特征，对于编号为 $i$的样本，构建特征 $\left\{ {x_{n + 1}^{(i)},} \right.$ $\left.x_{n + 2}^{(i)}, \cdots ,{x_{n + k}^{(i)}} \right\}$. 最后将构建的新特征和原始特征拼接，组成最终的预测特征 ${\rm{\{ }}x_1^{(i)},x_2^{(i)},\cdots,x_{n + k}^{(i)}{\rm{\} }}$，记为 ${X^{(i)}}$，逻辑回归模型的工艺参数权值 ${\rm{\{ }}{\omega _1},{\omega _2},\cdots,$ ${\omega _{n + k}} {\rm{\} }}$则记为 $\omega $. 因此，用于零件质量预测的分类器为

(9) $P(Y = 1|{X^{(i)}}) = \frac{{\exp\; (\omega {X^{(i)}})}}{{1 + \exp \;(\omega {X^{(i)}})}}.$

在机器学习研究中，为了验证模型的准确率，一般情况下会把原始数据分为训练集和测试集. 在样本量不充足的情况下，为了更加充分地利用现有数据测试算法效果，采用随机生成索引的方式将数据集分为10份，一共进行10次试验，每次取其中1份数据作为测试数据，用剩余9份数据作为训练数据进行试验，这种方法称为十折交叉验证（10 fold cross-validation）^[20].

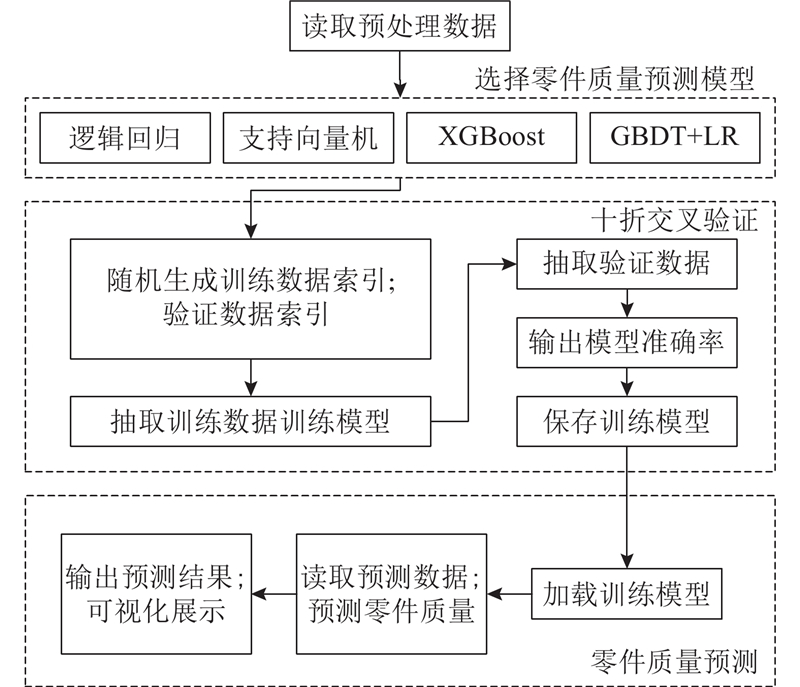
如图1所示为零件质量预测模型的构建流程，共分4个步骤. 1）读取预处理后的数据，分离工艺参数与零件质量标签为2个变量；2）用户选择模型，生成模型训练相应句柄；3）十折交叉验证训练模型，输出对应准确率并保存训练模型；4）加载预训练零件质量预测模型，读取预测数据，输出模型预测结果.

工艺参数优化模型的原理，是利用机器学习算法结合工艺参数和零件质量标签，实现对某一维工艺参数的优化. 具体而言，该模型是在零件试制阶段，计算所有工艺参数的信息增益并排序，在其余参数不变的情况下，使用工艺参数优化模型对信息增益最高者（即对零件质量影响最大的工艺参数）进行预测，实现单点优化.

结合1.1节给出的结构化数据格式，工艺参数优化模型的构建须选定待优化工艺参数，利用机器学习算法构建回归模型；再通过其余工艺参数和零件质量标签对待优化工艺参数进行拟合；最后选取一组待优化工艺参数，并更改零件质量标签为设计设计最优值，将两者输入到模型中，得到优化结果.

用于机器学习的工艺参数优化数据格式如表2所示. 新增列 $x_o^{(i)}$表示待优化工艺参数.

工艺参数优化模型针对的是某一条生产线的某个问题，具有一定的针对性，因此不要求模型的泛化能力，可以直接选用GBDT模型进行构建：对于样本编号 $i$，将 $n$维工艺参数和零件质量标签作为新特征 $\{ x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},{L^{(i)}}\} $，记为 ${X^{(i)}}$，输入1.3.2节给出的GBDT模型进行训练，并保存训练后的模型；取某一条加工数据 $k$，确定待优化的工艺参数 $x_o^{(k)}$，并保持其余工艺参数不变，更改零件质量标签为最优取值 ${L^{(k*)}}$，重新构建特征 $\{ x_1^{(k)},x_2^{(k)},\cdots,x_{o - 1}^{(k)},x_{o + 1}^{(k)},\cdots,x_n^{(k)},{L^{(k*)}}\} $，记为 ${X^{(k)}}$，并输入至训练好的模型中，得到优化后的工艺参数 $x_o^{(k)}$.

为了确认前述零件质量预测模型和工艺参数优化模型的有效性，采用某航空企业提供的铣削实验数据进行验证.该实验采用控制变量法，分别在不同的轴向切深、径向切深参数下，采用变转速的方式对铝合金材料表面进行铣削，通过测量并记录表面粗糙度，研究机床主轴转速、轴向切深和径向切深3个变量对铣削加工表面粗糙度的影响. 该实验的材料为7050-T7415航空铝合金，选用V1-2000-2T五坐标数控龙门铣床和 $\phi $10硬质合金立铣刀进行加工，通过北京吉泰公司的TR200测量仪进行表面粗糙度测量.

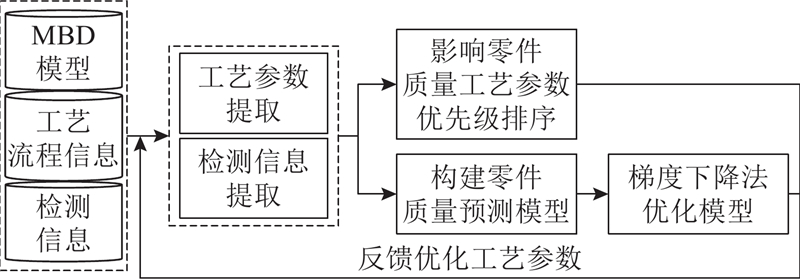
系统整体框架如图2所示，系统的开发以CAA为工具，Microsoft Visual Studio 2005为开发环境，对CATIA V5 R18平台进行二次开发，实现集成工艺信息和检测信息的MBD模型参数自动提取；以Python为工具，Jupyter Notebook为开发环境，实现影响零件质量工艺参数优先级排序、构建零件质量预测模型和优化工艺参数的功能.

实验选择径向切深（0.5~5 mm）、轴向切深（0.5~18 mm）、主轴转速（4000~13000 rpm）3个参数进行实际加工，得到实验数据共380条，结果设定表面粗糙度阈值为3.2 μm，高于阈值视为不合格并记为0，反之合格并记为1.

针对制造过程中采集的工艺和检测数据，MBD模型统一采用结构树的形式进行组织与存储. 其中，检测信息采用以特征为单位节点的形式进行表达和存储，节点下包含检验特征名称、理论值、公差值、实际值以及检验结果等内容，其结构化数据格式如图3所示：

工艺信息的表达和存储与检测信息相同，节点下包含该特征类型、几何尺寸、工艺要求和加工方案等信息. 其中，几何尺寸和工艺要求是指该特征的设计要求；加工方案包含设计特征在实际加工过程中的所有工序信息和工序采用的工艺参数，其结构化数据格式如图4所示.

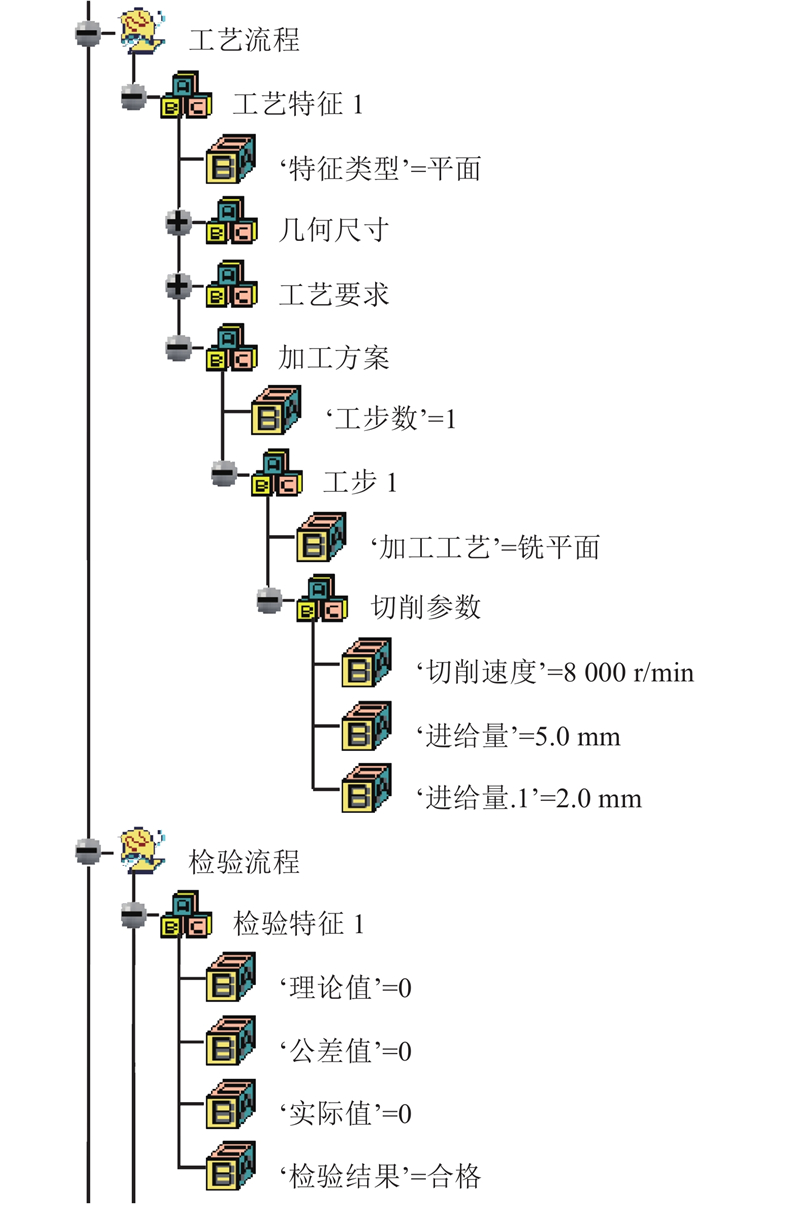
工艺信息中同一特征的工艺参数，按照工步分别添加在对应工步的子节点下. 在添加检验特征时，根据理论值和公差值自动生成零件是否合格的节点. 工艺信息和检测信息在MBD模型中的集成结果如图5所示.

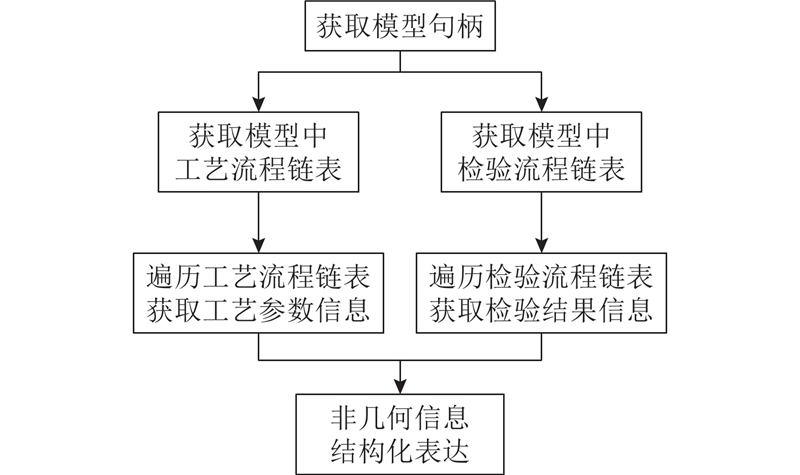
工艺信息和检测信息的提取流程如图6所示，共分为3个步骤. 1）获取MBD模型并遍历工艺流程和检测流程链表；2）分别提取MBD模型指定特征的切削参数和检测结果；3）将所得MBD模型的工艺信息和检测信息结构化表达，为后续机器学习提供数据依据。

为了验证所提出的方法，利用Python开发零件质量预测与工艺参数优化工具集用户界面，如图7所示. 利用信息增益算法对所有工艺参数进行信息增益计算，由结果可知主轴转速的信息增益最大，即主轴转速对零件质量的影响程度最大，具体结果如表3所示. 采用选取的500条实验数据，通过十折交叉验证分别训练LR、SVM、XGBoost 3种分类器，从而实现对零件质量的二分类，并记录各个分类器的平均准确率. 接着，为了进一步提升模型预测的准确率，使用GBDT对原始数据进行拟合后构造新特征，并与原始工艺参数拼接后输入LR分类器. 最终所有模型的平均准确率如表4所示. 由表中数据分析可知，相对简单的LR分类器在特征数量较少的情况下预测准确率较低，而SVM和XGBoost 2种复杂分类器的准确率提升较大；GBDT结合LR分类器的准确率为86.31%，比XGBoost还提升了3.43%，表现出最佳的预测准确率.

在验证完毕分类器准确率的基础上，为了进一步验证模型的可靠性，随机抽取加工数据中的5条原始数据输入到准确率最高的GBDT+LR中进行预测，结果如表5所示. 由表中数据分析可知，对于径向切深和轴向切深确定的情况下转速依次提升的数据，GBDT+LR模型具有较好的拟合效果，验证了预测模型的可靠性.

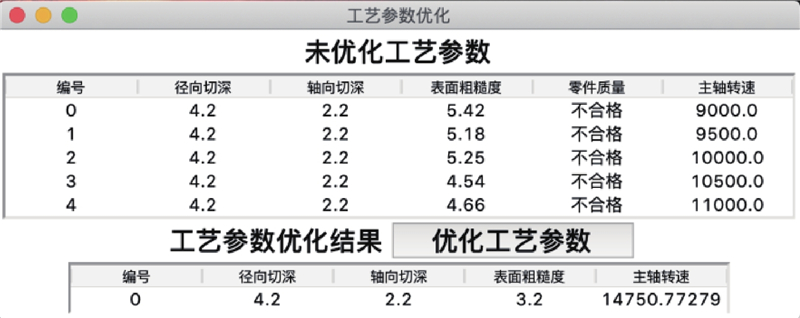
为了验证工艺参数优化方法的有效性，从500条实验数据中随机抽样450条数据，把径向切深、轴向切深和原始采集粗糙度作为特征，主轴转速作为标签，使用GBDT对其进行拟合并保存拟合后的模型；从剩余50条数据中随机抽样5条数据，在预测前把表面粗糙度取值改为理想取值，输出优化后的主轴转速，如图8所示. 优化所得的主轴转速为14750，通过对比原始加工数据可知，GBDT模型对于工艺参数和表面粗糙度数据的拟合效果较好.

本研究结合“基于模型驱动”的产品研制模式和数据挖掘相关理论，探讨将机器学习算法应用于机加零件质量预测与工艺参数优化的方法. 应用信息增益算法进行工艺参数优先级排序，为零件加工工艺优化提供重要依据；筛选出了对零件质量影响最大的工艺参数；基于工艺参数优先级排序的零件定量预测，实现不确定工艺参数对零件质量的质量评估；利用实测加工数据和信息增益算法进行工艺参数优化，有效降低了其对工艺人员经验的依赖性，提升了工艺优化工作的智能化水平.

实例表明，本研究所提出的方法和开发的对应工具集，在实际应用中能够有效并可靠地实现机加零件的质量预测和工艺参数优化，为MBD技术和数字孪生思想的深入应用和推广落地提供了坚实的技术基础。本研究构建的零件质量预测和工艺参数优化模型，只适用于解决单点工艺参数的问题。下一步研究工作的重点，将针对同一道工序中多个参数耦合影响零件质量的问题，前一道工序的工艺参数和零件质量影响后一道工序的问题，以及其他实际加工过程中的复杂场景，开展零件质量预测和工艺参数优化。