分布式系统是由一组通过网络进行信息通信、为了完成共同的任务而协调工作的计算机节点组成的^[1]. 分布式多计算节点训练已经成为大规模深度神经网络（deep neural network，DNN）模型的主要训练方法之一^[2]. 然而，由于在分布式训练中各节点间须频繁地交换和更新DNN模型梯度信息G，通信带宽已经成为限制分布式并行规模的主要瓶颈之一^[3]. 因此，将梯度集合G压缩为稀疏梯度通信集合S以降低对通信带宽压力的研究受到广泛关注. 残差梯度压缩^[4-9]（residual gradient compression，RGC）是最近提出的压缩算法之一. 经过Lin等^[7]对算法的优化，可以在几乎不影响模型训练精度的情况下，实现梯度信息压缩比0.1%，即分布式节点间每次迭代只须交换梯度数据的0.1%，剩余的99.9%梯度数据在本地保存为残差.

与传统非梯度压缩训练相比，RGC稀疏方法选择DNN模型每层（记为层l）原始梯度G^l与残差累加得到累计梯度R^l，从R^l中选取元素组成集合作为该层的通信集S^l，并将剩余梯度保存为新残差累积到新一轮迭代得到的新G^l上，降低通信负荷. 现有梯度稀疏化方法主要包含random-k^[10]、top-k^{[4，6，7，11]}和fixed-v^[12-13]等. random-k通过从R^l随机选择k个梯度元素组成集合S ^l. fixed-v选择R^l中梯度绝对值大于预设固定阈值的梯度元素组成S^l. 不过，一个合适的预设阈值很难确定，因为它取决于模型本身^[3]. top-k根据预设压缩比选择R^l中绝对值最大的第k个梯度元素作为阈值，进而将R^l中绝对值大于该阈值的梯度元素组成S^l，是目前广泛采用的梯度稀疏压缩方法.

由于效率问题，目前将RGC稀疏压缩方法应用到实际的分布式并行系统仍面临着挑战^[4]. 基于多核GPU架构的算法radixSelect^[14]在对top-k梯度选取时开销较大，尤其是在单层参数量达到百万甚至千万级别的DNN模型的梯度稀疏压缩过程中，甚至可能导致稀疏压缩的时间成本高于降低通信带宽的性能收益^[4]. 因此，如何高效地从累计梯度R^l中选择稀疏梯度集S^l，对于基于RGC方法的分布式训练系统的整体性能显得尤为重要. Aji等^[6]提出先随机从R^l中抽样0.1%作为样本，排序得到第k个元素作为样本阈值，再利用该阈值作为整体阈值选择top-k梯度. 然而，随机抽样操作可能导致整体压缩比得不到保证. Lin等^[7]提出的深度梯度压缩（deep gradient compression，DGC）框架采用层级选择top-k梯度的方法，先随机抽样0.1%~1.0%的梯度排序选出阈值，若选出梯度个数远大于top-k，则再在已选出的S^l中进行二次排序选出更准确的阈值，从而保证压缩比. 不过，该方法未考虑因随机操作导致的小于top-k情况，而且这种情况将导致梯度信息丢失. Fang等^[4]提出剪枝top-k方法，利用统计特性去除R^l中大多数绝对值较小的梯度元素，并在删减后的梯度数据子集上使用radixSelect排序选出top-k的稀疏阈值. 不过，对于参数量巨大的网络层，对删减后的数据子集的排序也较耗时.

为了高效地从累计梯度R^l选择稀疏梯度集S^l，避免数据排序操作，尽可能减少额外的稀疏压缩计算时间，提出结合基于Laplacian分布估计阈值（Laplacian distribution-based threshold estimation，LDTE）和二分搜索^[4]（binary search，BS）的梯度稀疏算法LDTE-BS. 结合梯度统计分布特征对分布曲线的特征值进行最大似然估计，进而采用曲线面积积分求取top-k阈值，并采用二分搜索进行修正，实现快速准确的稀疏阈值选取. 同时，该方法支持并行的计算和通信，进一步优化了分布式训练方案.

本研究训练框架采用的RGC方法实现流程^[4]如算法1所示. 假设分布式系统有N个训练节点，每个节点都保存一份DNN模型f（w）全局参数w的副本. 在分布式训练过程中，在迭代周期t，不同节点j从训练数据集χ中随机抽样小批量尺寸为B的不同数据子集x_t^j，进行并行训练，计算梯度集合G并与其他节点交换，最后基于同步随机梯度下降（stochastic gradient descent，SGD）算法更新本地模型参数w.

节点j利用本地模型执行反向传播过程计算所有梯度G_t^j. 每个节点都保留上次迭代未被选为S^j的残差梯度R^j，其初始值为0. ${{R}}_{t - 1}^j $与最新梯度G_t^j进行累加得到累计梯度R_t^j，用于新一轮迭代中top-k梯度的选择. 通过选取每层l累计梯度R_t^j的稀疏阈值，得到该层对应的掩码，然后利用掩码选出S^l，最后将其压缩为稀疏数据格式 $T_t^{j,l} $进行通信传输. 掩码为0/1张量，0对应位置表示未选中的梯度，1表示选中的须通信的梯度，未选中的梯度用作新一轮迭代的新残差梯度 ${{R}}_{t - 1}^j $. 在算法中select操作为top-k阈值选取过程. 全规约（all-reduce）操作实现各节点的同步. 最终，每个节点j对收集到的{T_t¹， T_t^j−1， T_t^j+1， ···， T_t^N}解压缩，并实现参数同步更新，至此便完成一次训练迭代过程.

算法1   RGC方法实现流程

输入：数据集χ，训练节点数N，小批量尺寸B，压缩　　　　 比η，终止条件参数δ；

输出：更新参数 ${{{w}}_{t + 1}}$

1： 初始化参数 ${{w}} = \{ {{w}}[0], {{w}}[1], \cdots , {{w}}[L - 1]\} $

2：初始化 ${{{R}}^j} \leftarrow {\bf{0}}$

3： for $t = 1, 2, \cdots T$ do

4： 　从 $\chi $中随机抽样 $B$个训练数据 ${{x}}_t^j$

5： 　执行反向传播计算梯度： ${{G}}_t^j \leftarrow \nabla f\left( {{{x}}_t^j, {{{w}}_t}} \right)$

6： 　残差梯度求和： ${{R}}_t^j \leftarrow {{R}}_{t - 1}^j + {{G}}_t^j$

7：　for $l = L, L - 1, \cdots , 1$ do

8： 　　top-k阈值选取： ${ p_{\rm th}} \leftarrow {\rm select} \left( {{{R}}_t^{j, l}, \eta , \delta } \right)$

9： 　　 ${\rm Mask} \leftarrow \left| {{{R}}_t^{j, l}} \right| > { p_{\rm th}}$

10： 　　 ${{S}}_t^{j, l} \leftarrow {{R}}_t^{j, l} \odot {\rm Mask} $

11： 　　 ${{T}}_t^{j, l} \leftarrow {\rm all} - {{\rm reduce}}\left( {{\rm compress} \left( {{{ S}}_t^{j, l}} \right)} \right)$

12： 　　 ${{R}}_t^{j, l} \leftarrow {{R}}_t^{j, l} \odot \neg {\rm Mask} $

13：　end for

14： 　 ${{{w}}_{t + 1}} \leftarrow {\rm SGD} \left( {{{{w}}_t}, {{\rm decompress}}\left( {{{T}}_t^j} \right)} \right)$

15：end for

　　该算法中的top-k阈值选取是梯度稀疏压缩过程时间开销的主要部分，本研究提出低复杂度、快速选取top-k阈值的方法，即LDTE-BS算法，避免传统方法基于排序选择top-k的复杂操作.

所提出的LDTE-BS梯度稀疏算法，通过将累计梯度R^l的分布近似为Laplacian分布，先利用其曲线特征求出预定压缩比对应的阈值，并采用二分搜索对阈值进行修正得到对应的S^l.

为了将阈值选择问题转化为统计分析问题，从而避免数据排序，首先研究累计梯度R^l的统计分布特征. 现有研究显示，DNN模型的R^l统计直方图近似符合高斯Gaussian分布^[15-16]或拉普拉斯Laplacian分布^[17]. 为了确定该分布的统计特征，采用Wasserstein距离^[18]对R^l统计分布与Gaussian分布、Laplacian分布的近似度进行评估. Wasserstein距离为2个概率分布P和Q之间距离，值越小，表明2个分布越接近. 定义如下：

(1) ${\rm EMD}\; (P, Q) = \mathop {\inf }\limits_{\gamma \sim {\textit{Π}} (P, Q)} {\kern 1pt} {\kern 1pt} {E_{(x, y) \sim \gamma }}\left[ {\left\| {x - y} \right\|} \right].$

式中：Π（P，Q）为分布P和Q组合的所有可能的联合分布γ的集合；对于每个可能的联合分布γ，可以采样（x，y）~γ得到样本x、y，则这对样本的距离为||x−y||. 在该联合分布γ下，样本对距离的期望值为E_{（x，y）~γ}[||x−y||]， 在所有可能的联合分布中能够对该期望值取到的下界即为Wasserstein距离.

基于CIFAR-10数据集和多个DNN模型，分别计算每个模型所有层的累计梯度分布与Gaussian、Laplacian分布的Wasserstein距离的几何平均值. 如表1所示，相比于Gaussian分布，累计梯度分布与Laplacian分布的Wasserstein距离更小. 也就是说，累计梯度R^l的统计分布特征更接近Laplacian分布.

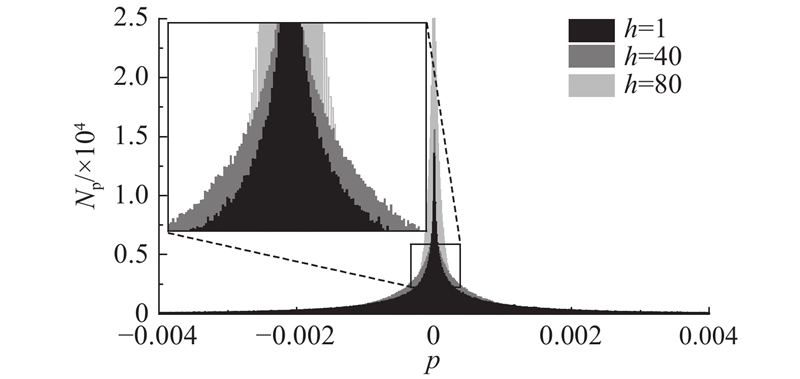
实验发现R^l分布有时也存在不能较好地近似为Laplacian分布的情况. 如图1所示为基于CIFAR-10数据集，ResNet50模型第22层卷积层（参数量为589824）的R^l在不同训练阶段的分布情况. 图中，p为累计梯度的数值，N_p为相应p的数量，h为训练迭代周期. 可以看出，当h=80，逐渐接近收敛时，绝大部分梯度聚集在零点附近，Laplacian分布特征逐渐消失. 此外，数据量较小的偏置层的R^l近似符合均匀分布. 对于该类特殊情况，本研究提出采用二分搜索对阈值进行修正，下一节将详细介绍.

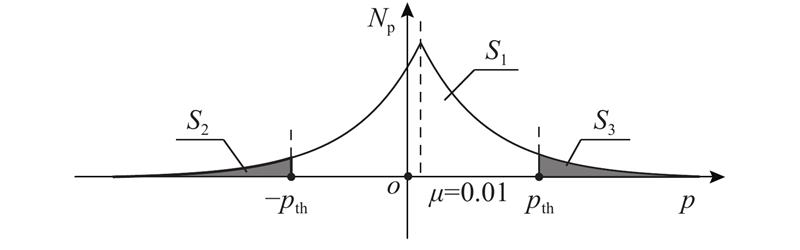
拟选取的top-k梯度对应R^l中绝对值较大的数值，则易知其位于Laplacian分布曲线的两端. 因此，提出基于Laplacian分布估计top-k阈值的LDTE方法，利用分布曲线特征（见图2）确定稀疏阈值，进而选出top-k梯度对应的S^l.

在概率论与统计学中，Laplacian分布又称为双指数分布，若随机变量的概率密度函数分布满足下式，则为Laplacian分布：

(2) $f(x|\mu ,b) = \frac{1}{{2b}}\exp\; \left( { - \frac{{|x - \mu |}}{b}} \right).$

式中：μ 为位置参数；b为尺度参数，b>0；x为随机变量. 对于不同的数据集、不同的训练迭代及不同的网络模型层，由于梯度参数在变化，参数μ 和b也在变化. 因此，每次迭代中不同的网络模型层对应的参数μ 和b须动态地进行计算，后续将详细介绍该过程. 通过对大量梯度参数分布的统计分析可知，Laplacian分布函数的位置参数μ 接近零点，根据其面积特征，可以将top-k问题转换为近似求解问题.

如图2所示，假设top-k梯度稀疏阈值为p_th，当压缩比η=0.1%时，Laplacian函数曲线左端top-k梯度对应的S^l部分与横轴围成的灰色区域的面积分别为S₂（该部分占总面积的0.05%）和S₃（0.05%），两者并集对应范围p∈ （−∞，−p_th）∪（p_th，+∞），对应k个最大的top-k目标梯度，而白色区域面积S₁（99.9%）对应p∈[−p_th，p_th]，为较小的未选中梯度，−p_th和p_th即为所求稀疏阈值.

由上可知，目标梯度、未选中梯度的分布面积和总面积S关系满足η=S_{2, 3}/S，S和S_{2, 3}=S₂+S₃区域面积积分分别如下所示：

(3) $S = \int_{ - \infty }^\mu {f(p|\mu , b)} {\kern 1pt} {\kern 1pt} {\rm{d}}p + \int_\mu ^{ + \infty } {f(p|\mu , b)} {\kern 1pt} {\kern 1pt} {\rm d} p, $

(4) ${S_2}_{,3} = \int_{ - \infty }^{ - {{p_{{\rm{th}}}}}} {f(p|\mu , b)} {\kern 1pt} {\kern 1pt} {\rm d} p + \int_{{{p_{{\rm{th}}}}}}^{ + \infty } {f(p|\mu , b)} {\kern 1pt} {\kern 1pt} {\rm d} p.$

求解稀疏阈值的问题转换为计算曲线面积问题.

根据积分极限定理和牛顿-莱布尼茨公式，由式（2）~（4）可以得出

(5) ${{p_{{\rm{th}}}}}=b\ln \;\left( {\frac{{\cosh \;{u \mathord{\left/ {\vphantom {u b}} \right. } b}}}{\eta }} \right).$

同时，假设梯度样本期望和方差分别为E（X）和D（X），存在D（X）=E（X ²）−E（X）²成立，由最大似然估计可以得到Laplacian分布曲线的特征参数满足

(6) $\mu = E(X),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b = \sqrt {\frac{{D(X)}}{2}} =\sqrt {\frac{{E({X^2}) - E{{(X)}^2}}}{2}} .$

将所得μ 和b分别代入式（5），可知只需梯度样本X、X ²和压缩比常数η，即可以求出稀疏阈值p_th.

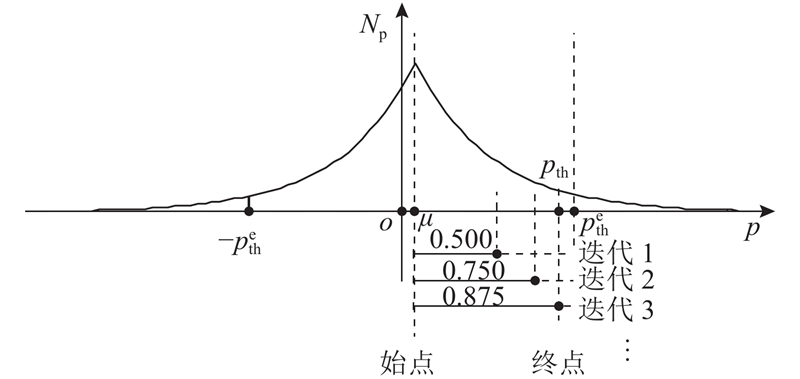
对于2.1节提到的特殊情况，提出基于二分搜索算法对LDTE算法进行修正得到LDTE-BS算法，其算法原理如图3所示. LDTE-BS算法通过从R^l中选择top-k梯度组成S^l. 假设LDTE最初估计的阈值 $p_{{\rm{th}}}^{\rm{e}} $对应的S^l元素个数小于k，处于真实阈值p_th右侧，则将均值μ 和 $p_{{\rm{th}}}^{\rm{e}} $分别作为搜索区间端点，去搜索R^l中第k个最大的数值作为阈值，然后将大于该阈值的梯度组成S^l. 如图3所示，迭代1得到μ 和 $p_{{\rm{th}}}^{\rm{e}} $的中间值，迭代2得到第2个中间值，以此类推逐渐逼近阈值p_th；同样，当 $p_{{\rm{th}}}^{\rm{e}} $ 处在p_th左侧时，则将 $p_{{\rm{th}}}^{\rm{e}} $和R^l中最大数值mx分别作为搜索区间端点，进行类似的搜索过程.

LDTE-BS具体实现如算法2所示，根据预设压缩比η和一维梯度张量R^l的长度计算出对应S^l的元素个数k，并利用式（5）、（6）计算出特征参数μ 和b，进而得到估计阈值. count_nonzero操作利用当前阈值计算通信集S^l元素个数nnz，若nnz $ \notin $k~1.5k，则执行二分搜索进行修正. 设定左指针pl和右指针pr初值分别为0.0和1.0，并计算R^l中元素的最大值mx. 当nnz > 1.5 k，即估计阈值落在真实值左侧时，令始点head和终点tail分别为p_th和mx，否则令head和tail分别为μ 和p_th. 进而利用二分搜索算法搜索一个阈值，使对应的S^l元素个数为k~1.5k. 为了避免过搜索，当左指针和右指针相差小于或等于非常小的值δ时，停止阈值搜索.

算法2   LDTE-BS阈值select算法

输入：一维梯度张量R^l，压缩比η，终止条件参数δ；

输出：top-k稀疏阈值p_th

1：$k \leftarrow {\rm len}\; \left( {{{{R}}^l}} \right) \times \eta$

2：$\;\mu \leftarrow {\rm mean}\; \left( {{{{R}}^l}} \right)$

3：$b \leftarrow {\rm sqrt}\; \left[ {\left( {{\rm mean}\; \left( {{{{R}}^l}^{\rm{T}}{{{R}}^l}} \right) - {\;\mu ^2}} \right)/2} \right]$

4：${ p_{{\rm{th}}}} \leftarrow b \ln\; ({{\cosh \;({\mu \mathord{\left/ {\vphantom {\mu b}} \right. } b})} \mathord{\left/ {\vphantom {{\cosh ({\mu \mathord{\left/ {\vphantom {\mu b}} \right. } b})} \eta }} \right. } \eta })$

5：${\rm nnz} \leftarrow {\rm count} \_{\rm{nonzero}}\;\left( {{\rm abs} \;\left( {{{{R}}^l}} \right) > {{p}}_{{\rm{th}}}} \right)$

6：if nnz < k or nnz > 1.5 k then

7：　${\rm pl} \leftarrow 0.0;{\kern 1pt} {\kern 1pt} {\rm pr} \leftarrow 1.0;{\rm mx} \leftarrow \max\; \left( {{{{R}}^l}} \right)$

8：　if nnz > 1.5k then

9：　　$< {\rm head} , {\rm tail} > {\kern 1pt} \leftarrow {{p}}_{{\rm{th}}} , {\rm mx}$

10：　else

11：　　$< {\rm head} , {\rm tail} > {\kern 1pt} \leftarrow \mu , {{p}}_{{\rm{th}}}$

12：　end if

13：　while ${\rm pr} - {\rm pl} > \delta $ do

14：　　${\rm ratio} \leftarrow {\rm pl} + {{({\rm pr} - {\rm pl} )} \mathord{\left/ {\vphantom {{({\rm pr} - {\rm pl} )} 2}} \right. } 2}$

15：　　${{p}}_{{\rm{th}}} \leftarrow {\rm head} + {\rm ratio} \times ({\rm tail} - {\rm head} )$

16：　　${\rm nnz} \leftarrow {\rm count} \_{\rm{nonzero}}\left( {{\rm abs} \;\left( {{{{R}}^l}} \right) > {{p}}_{{\rm{th}}} } \right)$

17：　　if nnz > k and nnz < 1.5 k then

18：　　　break

19：　　else if nnz < k then

20：　　　pr $ \leftarrow $ ratio

21：　　else

22：　　　pl $ \leftarrow $ ratio

23：　　end if

24：　end while

25：end if

在硬件系统实现时，因随机抽样^[6-7]、排序^[4，6-7]的操作须对所有梯度数据处理，导致须等待DNN每层反向传播计算完之后才可以开始计算，难以实现计算和通信的并行处理，同时因排序涉及的数据量巨大，导致对内存设备读取频繁. 所提出的LDTE-BS算法只涉及遍历一遍R^l数据，计算复杂度为O（n），分别求出X和X ²的均值E（X）和E（X ²）即可. 因此，可以通过流水线方式将DNN每层反向传播、梯度稀疏和梯度通信重叠起来，从而实现并行处理，提高系统整体效率.

如图4所示，在计算阶段，正向传播（forward propagation，FP）计算当前训练数据样本的损失项. 反向传播利用该损失项，依据链式法则逐层计算网络参数梯度G^l（l=L，L−1，···，1）. 梯度稀疏过程将每层的G^l与残差梯度累加得到的R^l进行稀疏化处理并得到T^l. 在通信阶段，梯度通信过程将T^l逐层传输，并在其他节点进行同步及参数更新操作. 针对DNN训练提出并行计算和通信时间的方案. 在DNN训练中正向传播和反向传播具有前后依赖性，反向传播层与层之间也有依赖性. 在对当前层累计梯度R^l稀疏压缩完成后，对该层执行稀疏通信，此层的稀疏压缩计算可以与上一层的稀疏通信重叠，进一步降低时间开销.

本研究还实现了为动量SGD更新策略而设计的动量纠正（momentum correction）和动量因子掩蔽（momentum factor masking）技术，以及在前5个周期分别以压缩比为25.00%、6.25%、1.5625%、0.40%、0.10%逐步递减到目标压缩比0.10%的预热训练（warm-up training），避免模型训练无法收敛^[7].

基于配备一个Intel（R） Xeon（R） E5-2630 v4 CPU和2个NVIDIA Tesla K40C GPU的硬件系统，采用PyTorch（v1.1.0版本）深度学习框架搭建分布式训练平台. GPU通过PCI-E 3.0与CPU通信.

基于CIFAR-10和CIFAR-100数据集，分别训练测试ResNet50、ResNet101、DenseNet121和DenseNet169这4种DNN模型的图片分类性能. 所有DNN模型采用动量SGD更新策略，并设定超参数动量因子为0.9，压缩比η=0.1%（记为top-0.1%），学习率为0.1，小批量尺寸为128以及训练总周期为150. 预热训练技术应用在所有模型训练的前5个训练周期.

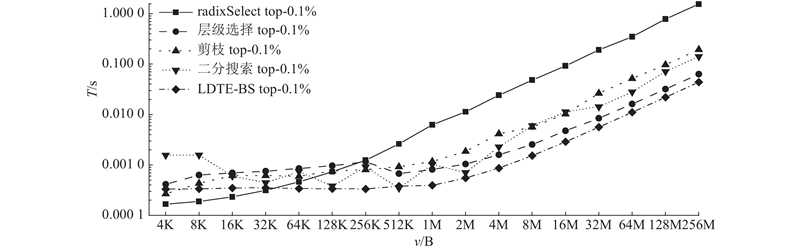
测试数据采用均值和标准差分别为5×10⁻⁴和5×10⁻³的符合Laplacian分布的带噪声的随机生成数据. 如图5所示，对比radixSelect top-0.1%、剪枝top-0.1%、二分搜索top-0.1%、层级选择top-0.1%和LDTE-BS top-0.1%这5种top-k选择方法的运行时间. 图中，T为100次独立操作的平均运行时间（对数坐标），v为数据量大小.

结果表明，当数据量＜64 KB时，radixSelect方法耗时最短. 当数据量＞64 KB时，LDTE-BS算法耗时最短，且随着数据量逐渐变大，时间增长最慢. 当数据量为16 MB时，与radixSelect相比，LDTE-BS达到32倍加速. radixSelect方法采用类似基数排序的算法，每次基于最高位优先法执行直方图统计操作及前缀和操作，计算复杂度为O（d（n+r）），d为数据元素中十六进制的位数，r为基数. 本研究所提方法的计算复杂度为O（n）. 其中，radixSelect方法执行扫描运算和分散操作，所提方法执行相对复杂的阈值求解操作. 因此，当数据量n较小时，由于操作时间较短，radixSelect方法执行速度相对较快；当数据量n逐渐变大时，计算复杂度起决定作用，因而与radixSelect方法相比，本研究方法的运行时间增长速度较慢.

评估DGC层级选择、RGC剪枝top-k、radixSelect和LDTE-BS这4种梯度稀疏方法对不同网络模型的精度及收敛性的影响. 评估以非稀疏传统SGD训练方法结果作为基准. 如图6（a）、 （b）所示分别为5种方法在CIFAR-10数据集上ResNet101和DenseNet169的top-1准确率，如图6（c）、 （d）所示分别为CIFAR-100数据集上ResNet50和DenseNet121的top-1准确率. 图中，P为top-1准确率，N_e为训练周期. 结果表明，4种梯度稀疏方法对应的模型收敛性能基本相当，且模型top-1准确率无显著差异. 不同方法下具体的模型精度如表2所示. 表中，V为模型大小，与其他方法相比，本研究方法在加速梯度稀疏压缩过程后，几乎不影响模型训练精度.

评估radixSelect top-0.1%、层级选择top-0.1%、剪枝top-0.1%和LDTE-BS top-0.1%这4种技术在模型稀疏训练中达到相同精度下的实际训练时间. 其中ResNet101、DenseNet169、ResNet50、DenseNet121的精度分别为92%、92%、72%、70%，如表3所示. 表中，α为计算加速比。可以看出，与radixSelect、层级选择相比，本研究方法最高分别实现了1.62、1.30倍的加速. 由于模型参数量较小，本研究方法与剪枝方法性能相当.

评估ResNet101分别使用传统SGD训练、朴素RGC radixSelect、DGC层级选择和本研究的RGC LDTE-BS这4种训练方法在不同节点规模上的扩展性（即系统吞吐量）. 采用Wen等^[15]提出的性能模型对扩展性进行评估，其中计算时间为单节点每个训练周期的实测平均时间，而多节点的通信时间由性能评估模型计算求得. 该性能模型适用于基于分布式计算平台如GPUs的深度学习系统，不仅支持对称的系统架构，还可以扩展支持异构的系统架构^[15]. Wen等^[15]分别采用NCCL基准和OSU全规约基准对该性能模型进行验证.

该性能模型结合单个节点的轻量级配置和通信分析模型，基于j个工作节点（每个节点i个GPU）和小批量尺寸B对系统吞吐量进行估计. 假设梯度通信量为g，节点内的GPU-GPU间和CPU-GPU间的通信带宽分别为C_gwd、C_cwd，节点间的网络延迟和网络带宽分别为C_ncost、C_nwd，则在全规约通信机制下，总的通信时间如下：

(7) ${T_{{\rm{comm}}}}=\frac{g}{{{C_{{\rm gwd} }}}}{\log _2}\;i + \frac{g}{{{C_{{\rm{cwd}}}}}} + \left( {{C_{{\rm ncost} }} + \frac{g}{{{C_{{\rm{nwd}}}}}}} \right){\log _2}\;j.$

利用单个节点中1个CPU和1个GPU训练大小为B的训练样本消耗的时间T_B来估计计算时间. 每个工作节点总是训练B个训练样本，则系统整体小批量尺寸变为ijB，总的计算时间如下：

(8) ${T_{{\rm{comp}}}}={T_{ B} } - {g \mathord{\left/ {\vphantom {g {{C_{{\rm{cwd}}}}}}} \right. } {{C_{{\rm{cwd}}}}}}.$

系统的扩展性（即吞吐量）如下：

(9) ${T_{{\rm{scal}}}}=\frac{{ijB}}{{{T_{{\rm comm} }} + {T_{{\rm comp} }}}}.$

假设每个节点有4个K40C GPU，分别在以太网带宽为1、10 Gbps的网络环境下测试. 传统SGD为非梯度稀疏通信，radixSelect、层级选择和LDTE-BS为top-0.1%梯度稀疏通信. 3种稀疏通信方法均采用游程编码^[7]对S^l进一步压缩，其中0采用16位编码，而梯度值为32位.

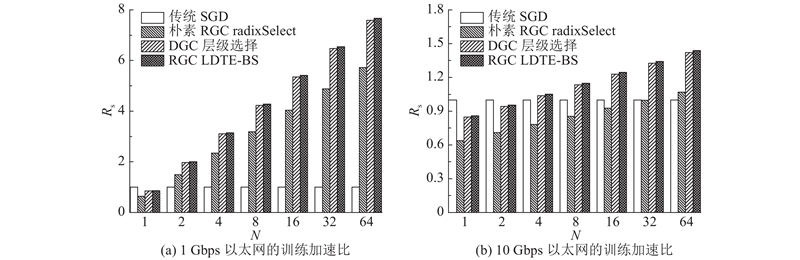
如图7所示为各种稀疏方法与经典训练方法在K40C GPU的扩展性对比. 图中，N为计算节点数目，R_s为4种训练方法对应的系统扩展性，即训练加速比. 其中，比较的基准为传统SGD方法. 如图7（a）所示，在网络环境较差（例如1 Gbps）的情况下，通信带宽成为瓶颈. 与非梯度稀疏通信的传统SGD方法相比，在通信-计算比偏高的条件下，由于各种梯度稀疏通信方法大大降低了梯度通信量，其扩展性随着计算节点数目的增加而增强. 由于不同的梯度稀疏压缩技术的压缩计算效率不同，对应的整体扩展性存在差异. 如图7（b）所示，当网络环境变好（例如10 Gbps甚至更好）时，网络带宽不再受限，与较差网络环境相比，相对于其他梯度稀疏通信方法而言，传统SGD的扩展性提升，各种梯度稀疏通信方法带来的效益降低. 与朴素RGC和DGC相比，LDTE-BS方法计算效率更高，扩展性更好. 例如，当节点为16时，与传统SGD、朴素RGC和DGC相比，在1 Gbps环境下，本研究分别实现5.41、1.34、1.01倍的加速；在10 Gbps环境下，分别实现1.25、1.35、1.01的加速.

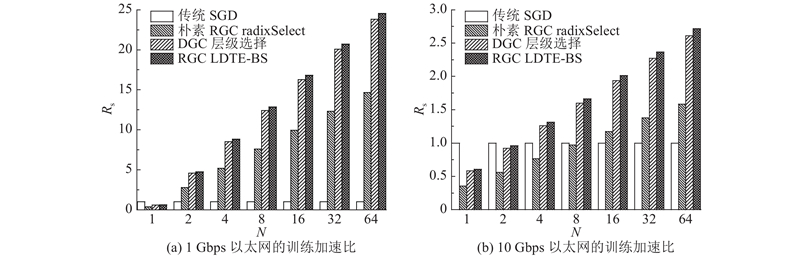
为了进一步在计算和通信能力更高的GPU计算卡上讨论本研究方法的扩展性能，采用目前主流使用的NVIDIA Tesla V100型号GPU进行实验. 每个节点配备一个Intel Xeon（R） Gold 6240 CPU和2个V100 GPU，在节点内GPU通过PCI-E 4.0×16连接到CPU. 根据上述性能模型，节点间采用全规约通信机制，假设每个节点有4个V100 GPU，节点间分别在以太网带宽为1、10 Gbps的网络环境下测试. V100的单精度浮点运算性能是K40C性能的3.5倍，因而V100平台的通信-计算比更高. 对比图7、8可知，与K40C平台相比，各种梯度稀疏通信方法带来的效益提高. 结果显示，与朴素RGC和DGC相比，LDTE-BS方法计算效率更高，扩展性更好. 例如，在节点为32时，与传统SGD、朴素RGC和DGC相比，在1 Gbps环境下，LDTE-BS方法分别实现20.73、1.68、1.03倍的加速；在10 Gbps环境下，LDTE-BS方法分别实现2.37、1.71、1.04倍的加速.

所提出的LDTE-BS梯度稀疏压缩算法将传统基于排序选取top-k的问题转换为统计分布的特征值最大似然估计和二分搜索操作，降低了算法复杂度，在实现降低分布式训练梯度通信量的同时，减少额外的稀疏压缩时间开销. 同时，采用Wasserstein距离为梯度分布近似评估提供了理论支持.

（1）与radixSelect、层级选择相比，达到相同精度，本研究所提LDTE-BS方法最高分别实现了1.62、1.30倍的加速，同时，改善了模型收敛性以及最终模型精度. 当网络层梯度数据量较少时，剪枝top-k以及LDTE-BS选择效率相当. 当数据量较大时，LDTE-BS方法性能更优，与其他方法形成有效互补.

（2）LDTE-BS方法也为其他满足参数对称分布的模型解决top-k问题提供了参考，如高斯分布和稳态分布；该方法还可以从两方面改进：最终选取的S^l满足对称特性，可以通过量化操作（例如，用均值编码）实现进一步压缩降低通信带宽；二分搜索可以用斐波那契查找替代，后者只涉及加法和减法运算，可以加快搜索速度.

（3）本研究结果对分布式训练梯度稀疏压缩方式的选择起到一定的参考作用. LDTE-BS方法更适用于具有大规模参数量的网络模型，因此未来将采用较大的数据集（例如ImageNet数据集）以及其他DNN模型进行验证. 同时，对于并行环境实验，将采用不同计算和通信能力的GPU进行扩展性讨论.