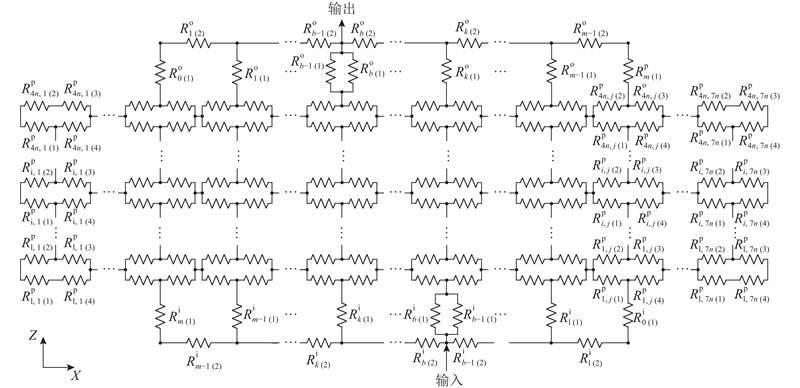
(10) $q_{k(2)}^{\rm{i}}{\rm{ = }}\left\{ \begin{array}{l} q_{k - {\rm{1}}(1)}^{\rm{i}}, \;k = 1 ;\\ q_{k - {\rm{1}}(1)}^{\rm{i}}{\rm{ + }}q_{k - 1(2)}^{\rm{i}},\; k \in \left[ {2,\; b - 1} \right] ;\\ q_{k{\rm{ + }}1({\rm{1}})}^{\rm{i}} - q_{k{\rm{ + 1}}({\rm{2}})}^{\rm{i}},\; k \in \left[ {b,\; m - 2} \right] ;\\ - q_{k + {\rm{1}}(1)}^{\rm{i}},\; k = m - 1 . \\ \end{array} \right.$
(13) $q_{k(2)}^{\rm{o}}{\rm{ = }}\left\{ \begin{array}{l} q_{k - 1(1)}^{\rm{o}},\; k = 1 ; \\ q_{k - 1(1)}^{\rm{o}}{\rm{ + }}q_{k - 1(2)}^{\rm{o}},\; k \in \left[ {2,\; b - 1} \right] ; \\ q_{k{\rm{ + }}1(1)}^{\rm{o}} - q_{k + 1(2)}^{\rm{o}},\; k \in \left[ {b,\; m - 2} \right] ; \\ - q_{k + 1(1)}^{\rm{o}}, \;k = m - 1 . \\ \end{array} \right.$
(19) $\left. { \begin{array}{l} {{U}}_{k\left( 1 \right)}^{\rm{i}} + {{U}}_{1, j + 1(1)}^{\rm{p}}{{ = U}}_{k + 1}^{\rm{i}} + {{U}}_{1, j((4)}^{\rm{p}};\; k \leqslant b - 2 ,\\ {{U}}_{k\left( 1 \right)}^{\rm{i}} = {{U}}_{k + 1\left( 1 \right)}^{\rm{i}};\; k = b - 1 , \\ {{U}}_k^{\rm{i}} + {{U}}_{1, j + 1((4)}^{\rm{p}}{{ = U}}_{k + 1\left( 1 \right)}^{\rm{i}} + {{U}}_{1, j((4)}^{\rm{p}};\; k \geqslant b ,\\ \end{array} } \right\} $
(20) $\left. { \begin{array}{l} {{U}}_{k\left( 1 \right)}^{\rm{o}} + {{U}}_{4n, j(3)}^{\rm{p}}{{ = U}}_{k + 1}^{\rm{o}} + {{U}}_{4n, j + 1(2)}^{\rm{p}};\; k \leqslant b - 2 , \\ {{U}}_{k\left( 1 \right)}^{\rm{o}} = {{U}}_{k + 1\left( 1 \right)}^{\rm{o}};\; k = b - 1 ,\\ {{U}}_k^{\rm{o}} + {{U}}_{4n, j(3)}^{\rm{p}}{{ = U}}_{k + 1\left( 1 \right)}^{\rm{o}} + {{U}}_{4n, j + 1(2)}^{\rm{p}}; \;k \geqslant b , \\ \end{array}} \right\} $
(21) $\left. { \begin{array}{l} {{U}}_{i, j(1)}^{\rm{p}}{{ + U}}_{i, j((4)}^{\rm{p}}{{ = U}}_{i, j(2)}^{\rm{p}}{{ + U}}_{i, j(3)}^{\rm{p}} , \\ {{U}}_{i, j(3)}^{\rm{p}}{{ + U}}_{i, j + 1(2)}^{\rm{p}}{{ = U}}_{i + 1, j((4)}^{\rm{p}}{{ + U}}_{i + 1, j + 1(1)}^{\rm{p}} . \\ \end{array} } \right\}$
[1]
FATHY A, ELAZIZ M A, ALHARBI A G A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell
[J]. Renewable Energy , 2020 , 146 : 1833 - 1845
DOI:10.1016/j.renene.2019.08.046
[本文引用: 1]
[2]
汪翼东. 面向PEMFC的甲醇现场重整制氢系统设计与应用研究[D]. 杭州: 浙江大学, 2019.
WANG Yi-dong. Design and application study of methanol fuel processing system for PEMFC [D]. Hangzhou: Zhejiang University, 2019.
[3]
易邹东一. 面向PEMFC的自热型甲醇重整制氢反应器的研发[D]. 杭州: 浙江大学, 2019.
[本文引用: 1]
YI Zou-dong-yi. Development of a self-heated methanol steaming reforming reactor for PEMFC [D]. Hangzhou: Zhejiang University, 2019.
[本文引用: 1]
[4]
YAN Y, ZHANG Z, ZHANG L, et al Investigation of autothermal reforming of methane for hydrogen production in a spiral multi-cylinder micro-reactor used for mobile fuel cell
[J]. International Journal of Hydrogen Energy , 2015 , 40 (4 ): 1886 - 1893
DOI:10.1016/j.ijhydene.2014.11.140
[本文引用: 1]
[5]
PALO D R, DAGLE R A, HOLLADAY J D Methanol steam reforming for hydrogen production
[J]. Chemical Reviews , 2007 , 107 (10 ): 3992 - 4021
DOI:10.1021/cr050198b
[6]
WANG F, WANG G Performance and cold spot effect of methanol steam reforming for hydrogen production in micro-reactor
[J]. International Journal of Hydrogen Energy , 2016 , 41 (38 ): 16835 - 16841
DOI:10.1016/j.ijhydene.2016.07.083
[7]
贺行. 面向甲醇重整供氢系统的自热式CO去除微反应器[D]. 杭州: 浙江大学, 2017.
[本文引用: 1]
HE Xing. Self-heated microreactor for CO removal from hydrogen supply system via methanol reforming [D]. Hangzhou: Zhejiang University, 2017.
[本文引用: 1]
[8]
HUANG Y X, JANG J Y, CHENG C H Fractal channel design in a micro methanol steam reformer
[J]. International Journal of Hydrogen Energy , 2014 , 39 (5 ): 1998 - 2007
DOI:10.1016/j.ijhydene.2013.11.088
[本文引用: 1]
[9]
钱淼, 梅德庆, 刘宾虹, 等 微凸台阵列型重整微反应器的传热传质特性
[J]. 浙江大学学报: 工学版 , 2011 , 45 (8 ): 1387 - 1392
[本文引用: 1]
QIAN Miao, Mei De-qing, LIU Bin-hong, et al Heat and mass transfer characteristics in reforming micro-reactor with micro-pin-fin arrays
[J]. Journal of Zhejiang University: Engineering Science , 2011 , 45 (8 ): 1387 - 1392
[本文引用: 1]
[10]
梁灵威. 甲醇重整制氢A型微通道反应器流场优化与传热传质特性研究[D]. 杭州: 浙江大学, 2015.
LIANG Ling-wei. Research on flow field optimization and heat and mass transfer capacity of the A-type microchannel reactor for hydrogen production via methanol reforming [D]. Hangzhou: Zhejiang University, 2019.
[11]
MEI D, FENG Y, QIAN M, et al An innovative micro-channel catalyst support with a micro-porous surface for hydrogen production via methanol steam reforming
[J]. International Journal of Hydrogen Energy , 2016 , 41 (4 ): 2268 - 2277
DOI:10.1016/j.ijhydene.2015.12.044
[12]
ZHOU W, KE Y, WANG Q, et al Development of cylindrical laminated methanol steam reforming microreactor with cascading metal foams as catalyst support
[J]. Fuel , 2017 , 191 (3 ): 46 - 53
DOI:10.1016/j.fuel.2016.11.058
[13]
LIU Y, ZHOU W, CHEN L, et al Optimal design and fabrication of surface microchannels on copper foam catalyst support in a methanol steam reforming microreactor
[J]. Fuel , 2019 , 253 : 1545 - 1555
DOI:10.1016/j.fuel.2019.05.099
[14]
KE Y, ZHOU W, CHU X, et al Porous copper fiber sintered felts with surface microchannels for methanol steam reforming microreactor for hydrogen production
[J]. International Journal of Hydrogen Energy , 2019 , 44 (12 ): 5755 - 5765
DOI:10.1016/j.ijhydene.2019.01.141
[本文引用: 1]
[15]
TANG Y, ZHOU W, PAN M, et al Porous copper fiber sintered felts: an innovative catalyst support of methanol steam reformer for hydrogen production
[J]. International Journal of Hydrogen Energy , 2008 , 33 (12 ): 2950 - 2956
DOI:10.1016/j.ijhydene.2008.04.006
[本文引用: 3]
[16]
ZHOU W, WANG Q, LI J, et al Hydrogen production from methanol steam reforming using porous copper fiber sintered felt with gradient porosity
[J]. International Journal of Hydrogen Energy , 2015 , 40 (1 ): 244 - 255
DOI:10.1016/j.ijhydene.2014.10.139
[本文引用: 2]
[18]
AMIRI E O, HORMOZI F, KHOSHANDAM B Methanol steam reforming integrated with oxidation in a conical annulus micro-reactor
[J]. International Journal of Hydrogen Energy , 2014 , 39 (2 ): 761 - 769
DOI:10.1016/j.ijhydene.2013.10.130
[本文引用: 1]
[19]
TONOMURA O, TANAKA S, NODA M, et al CFD-based optimal design of manifold in plate-fin microdevices
[J]. Chemical Engineering Journal , 2004 , 101 (1 ): 397 - 402
[本文引用: 1]
[20]
AMADOR C, GAVRIILIDIS A, ANGELI P Flow distribution in different microreactor scale-out geometries and the effect of manufacturing tolerances and channel blockage
[J]. Chemical Engineering Journal , 2004 , 101 (1 ): 379 - 390
[21]
MEI D, QIAN M, LIU B, et al A micro-reactor with micro-pin-fin arrays for hydrogen production via methanol steam reforming
[J]. Journal of Power Sources , 2012 , 205 (2 ): 367 - 376
[本文引用: 1]
[22]
LIU H, LI P Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels
[J]. International Journal of Heat and Fluid Flow , 2013 , 40 (4 ): 165 - 179
[本文引用: 1]
[23]
郑帅, 谭大鹏, 李霖, 等 微反应器计算流体力学与离散元建模及调控
[J]. 浙江大学学报: 工学版 , 2019 , 53 (7 ): 1237 - 1251
[本文引用: 1]
ZHENG Shuai, TAN Da-peng, LI Lin, et al Ultrasonic coupled microreactor CFD-DEM dynamic modeling and regulating method
[J]. Journal of Zhejiang University: Engineering Science , 2019 , 53 (7 ): 1237 - 1251
[本文引用: 1]
[24]
冯艳冰. 表面多孔微通道制氢反应器的设计与制造基础研究[D]. 杭州: 浙江大学, 2019.
FENG Yan-bing. Fundamental study on the design and fabrication of micro channel reactor with porous surface for hydrogen production [D]. Hangzhou: Zhejiang University, 2019.
[25]
QIAN M, MEI D, YI Z, et al Fluid flow and heat transfer performance in a micro-reactor with non-uniform micro-pin-fin arrays for hydrogen production at low Reynolds number
[J]. International Journal of Hydrogen Energy , 2017 , 42 (1 ): 553 - 561
DOI:10.1016/j.ijhydene.2016.10.150
[26]
WANG Y, HUANG L, MEI D, et al Numerical modeling of microchannel reactor with porous surface microstructure based on fractal geometry
[J]. International Journal of Hydrogen Energy , 2018 , 43 (49 ): 22447 - 22457
DOI:10.1016/j.ijhydene.2018.10.135
[本文引用: 1]
[27]
PAN M, TANG Y, YU H, et al Modeling of velocity distribution among microchannels with triangle manifolds
[J]. Aiche Journal , 2010 , 55 (9 ): 1969 - 1982
[本文引用: 6]
[28]
TONDEUR D, FAN Y, COMMENGE J M, et al Uniform flows in rectangular lattice networks
[J]. Chemical Engineering Science , 2011 , 66 (21 ): 5301 - 5312
DOI:10.1016/j.ces.2011.07.027
[29]
MEI D, LIANG L, QIAN M, et al Modeling and analysis of flow distribution in an A-type microchannel reactor
[J]. International Journal of Hydrogen Energy , 2013 , 38 (35 ): 15488 - 15499
DOI:10.1016/j.ijhydene.2013.09.105
[本文引用: 1]
[30]
CHENG X, SASTRY A M, LAYTON B E Transport in stochastic fibrous networks
[J]. Journal of Engineering Materials and Technology , 2001 , 123 (1 ): 12 - 19
[本文引用: 2]
[31]
LUU H T, PERROT C, MONCHIET V, et al Three-dimensional reconstruction of a random fibrous medium: geometry, transport, and sound absorbing properties
[J]. Journal of the Acoustical Society of America , 2017 , 141 (6 ): 4768 - 4780
DOI:10.1121/1.4989373
[本文引用: 1]
[33]
DIDARI S, HARRIS T A L, HUANG W, et al Feasibility of periodic surface models to develop gas diffusion layers: a gas permeability study
[J]. International Journal of Hydrogen Energy , 2012 , 37 (19 ): 14427 - 14438
DOI:10.1016/j.ijhydene.2012.06.100
[本文引用: 2]
[34]
XU Z J, YANG S, HU G H, et al Numerical study of flow distribution uniformity for the optimization of gradient porosity configuration of porous copper fiber sintered felt for hydrogen production through methanol steam reforming micro-reactor
[J]. International Journal of Hydrogen Energy , 2018 , 43 (9 ): 4355 - 4370
DOI:10.1016/j.ijhydene.2018.01.083
[本文引用: 2]
[35]
DJILALI N Computational modelling of polymer electrolyte membrane (PEM) fuel cells: challenges and opportunities
[J]. Energy , 2007 , 32 (4 ): 269 - 280
DOI:10.1016/j.energy.2006.08.007
[本文引用: 1]
[36]
COMMENGE J M, FALK L, CORRIOU J P, et al Optimal design for flow uniformity in microchannel reactors
[J]. Aiche Journal , 2002 , 48 (2 ): 345 - 358
DOI:10.1002/aic.690480218
[本文引用: 1]
A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell
1
2020
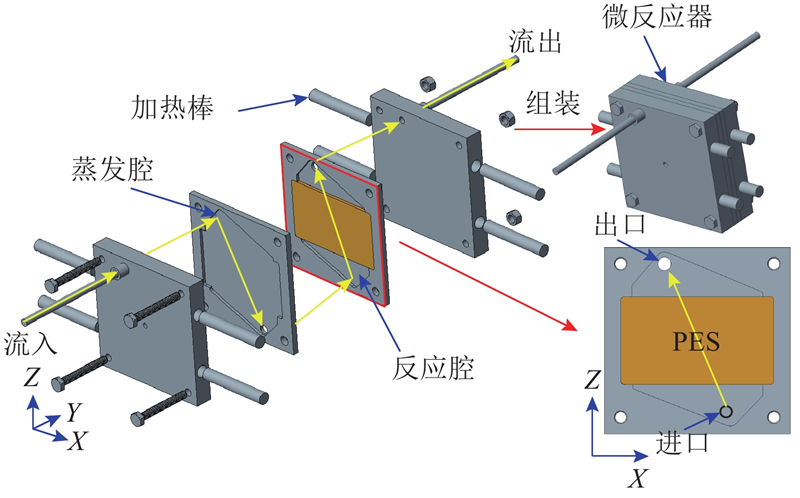
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
1
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
1
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
Investigation of autothermal reforming of methane for hydrogen production in a spiral multi-cylinder micro-reactor used for mobile fuel cell
1
2015
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
Methanol steam reforming for hydrogen production
0
2007
Performance and cold spot effect of methanol steam reforming for hydrogen production in micro-reactor
0
2016
1
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
1
... 质子交换膜燃料电池(proton exchange membrane fuel cell, PEMFC)是理想的能量转换装置,可以直接将氢气中的化学能转化为电能,在以新能源汽车为代表的移动领域应用前景广阔[1 -3 ] . 甲醇蒸汽重整制氢微反应器凭借紧凑、轻量化的结构与高能量密度,可以为PEMFC提供更为安全、高效、低成本的氢源,是有效的移动制氢解决方案[4 -7 ] . ...
Fractal channel design in a micro methanol steam reformer
1
2014
... 催化剂载体是微反应器中实现甲醇蒸汽重整制氢的关键构件,其结构设计是提升制氢性能的重要课题. 因此,新型微通道、泡沫金属、多孔金属纤维等新型催化剂载体层出不穷[8 -14 ] . 其中,华南理工大学Tang等[15 ] 结合切削和固相烧结法开发的多孔金属纤维结构工艺简单、比表面积高,表现出良好的催化反应性能(以下将其简称为纤维载体). 更进一步,Zhou等[16 ] 开发了梯度纤维载体,在提升制氢性能的同时,通过引入梯度界面和孔隙率分布2个变量,提高其结构设计的自由度. 但该设计方式依赖于实验,缺乏明确的设计依据. ...
微凸台阵列型重整微反应器的传热传质特性
1
2011
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
微凸台阵列型重整微反应器的传热传质特性
1
2011
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
An innovative micro-channel catalyst support with a micro-porous surface for hydrogen production via methanol steam reforming
0
2016
Development of cylindrical laminated methanol steam reforming microreactor with cascading metal foams as catalyst support
0
2017
Optimal design and fabrication of surface microchannels on copper foam catalyst support in a methanol steam reforming microreactor
0
2019
Porous copper fiber sintered felts with surface microchannels for methanol steam reforming microreactor for hydrogen production
1
2019
... 催化剂载体是微反应器中实现甲醇蒸汽重整制氢的关键构件,其结构设计是提升制氢性能的重要课题. 因此,新型微通道、泡沫金属、多孔金属纤维等新型催化剂载体层出不穷[8 -14 ] . 其中,华南理工大学Tang等[15 ] 结合切削和固相烧结法开发的多孔金属纤维结构工艺简单、比表面积高,表现出良好的催化反应性能(以下将其简称为纤维载体). 更进一步,Zhou等[16 ] 开发了梯度纤维载体,在提升制氢性能的同时,通过引入梯度界面和孔隙率分布2个变量,提高其结构设计的自由度. 但该设计方式依赖于实验,缺乏明确的设计依据. ...
Porous copper fiber sintered felts: an innovative catalyst support of methanol steam reformer for hydrogen production
3
2008
... 催化剂载体是微反应器中实现甲醇蒸汽重整制氢的关键构件,其结构设计是提升制氢性能的重要课题. 因此,新型微通道、泡沫金属、多孔金属纤维等新型催化剂载体层出不穷[8 -14 ] . 其中,华南理工大学Tang等[15 ] 结合切削和固相烧结法开发的多孔金属纤维结构工艺简单、比表面积高,表现出良好的催化反应性能(以下将其简称为纤维载体). 更进一步,Zhou等[16 ] 开发了梯度纤维载体,在提升制氢性能的同时,通过引入梯度界面和孔隙率分布2个变量,提高其结构设计的自由度. 但该设计方式依赖于实验,缺乏明确的设计依据. ...
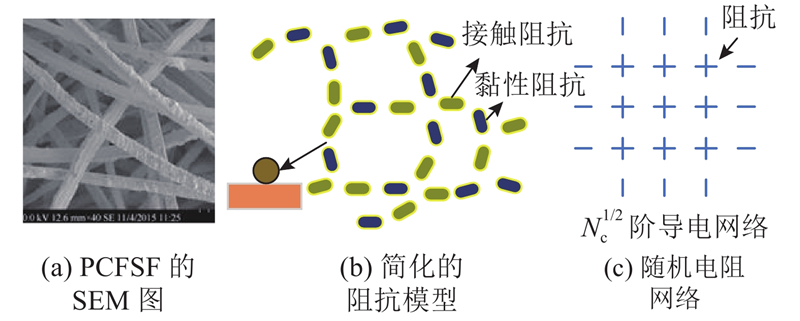
... 纤维载体由长度为10~20 mm、当量直径约为100 μm、随机分布的铜纤维段经模压和固相烧结工艺制得(见图1 (a) 、(b) )[15 ] . 对于其内部复杂的孔隙通道(见图1(c) 、(d) )缺乏统一的描述方法;切削加工工艺使得铜纤维表面形貌丰富(见图1 (d) ),但也使得纤维表面对流动阻力的影响难以量化. ...
... 式中:E 为纤维载体的孔隙率,可以按文献[15 ]计算. ...
Hydrogen production from methanol steam reforming using porous copper fiber sintered felt with gradient porosity
2
2015
... 催化剂载体是微反应器中实现甲醇蒸汽重整制氢的关键构件,其结构设计是提升制氢性能的重要课题. 因此,新型微通道、泡沫金属、多孔金属纤维等新型催化剂载体层出不穷[8 -14 ] . 其中,华南理工大学Tang等[15 ] 结合切削和固相烧结法开发的多孔金属纤维结构工艺简单、比表面积高,表现出良好的催化反应性能(以下将其简称为纤维载体). 更进一步,Zhou等[16 ] 开发了梯度纤维载体,在提升制氢性能的同时,通过引入梯度界面和孔隙率分布2个变量,提高其结构设计的自由度. 但该设计方式依赖于实验,缺乏明确的设计依据. ...
... 须注意的是,由于纤维载体的厚度(2 mm)远小于其长度和宽度,同时,其中的流动一般呈低速层流状态[16 ] ,以单层纤维结构的流道划分结果作为纤维载体的整体流道结构. 该层纤维结构处在纤维载体厚度方向中心面上. 对于该层纤维结构,本研究不加推导地给出式(1)中的纤维根数为 ...
Micro-channel reactor for steam reforming of methanol
1
2007
... 催化剂载体要求具有较好的传热传质能力[17 -18 ] ,而这与载体中流体的流动分布密切相关. 流动不均会导致反应物停留时间不均,严重影响反应效率;均匀的体积流量分布有利于反应速率和目标产物选择性的提高. 因此均匀的流动分布是催化剂载体结构优化的重要目标[19 -22 ] . ...
Methanol steam reforming integrated with oxidation in a conical annulus micro-reactor
1
2014
... 催化剂载体要求具有较好的传热传质能力[17 -18 ] ,而这与载体中流体的流动分布密切相关. 流动不均会导致反应物停留时间不均,严重影响反应效率;均匀的体积流量分布有利于反应速率和目标产物选择性的提高. 因此均匀的流动分布是催化剂载体结构优化的重要目标[19 -22 ] . ...
CFD-based optimal design of manifold in plate-fin microdevices
1
2004
... 催化剂载体要求具有较好的传热传质能力[17 -18 ] ,而这与载体中流体的流动分布密切相关. 流动不均会导致反应物停留时间不均,严重影响反应效率;均匀的体积流量分布有利于反应速率和目标产物选择性的提高. 因此均匀的流动分布是催化剂载体结构优化的重要目标[19 -22 ] . ...
Flow distribution in different microreactor scale-out geometries and the effect of manufacturing tolerances and channel blockage
0
2004
A micro-reactor with micro-pin-fin arrays for hydrogen production via methanol steam reforming
1
2012
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
Even distribution/dividing of single-phase fluids by symmetric bifurcation of flow channels
1
2013
... 催化剂载体要求具有较好的传热传质能力[17 -18 ] ,而这与载体中流体的流动分布密切相关. 流动不均会导致反应物停留时间不均,严重影响反应效率;均匀的体积流量分布有利于反应速率和目标产物选择性的提高. 因此均匀的流动分布是催化剂载体结构优化的重要目标[19 -22 ] . ...
微反应器计算流体力学与离散元建模及调控
1
2019
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
微反应器计算流体力学与离散元建模及调控
1
2019
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
Fluid flow and heat transfer performance in a micro-reactor with non-uniform micro-pin-fin arrays for hydrogen production at low Reynolds number
0
2017
Numerical modeling of microchannel reactor with porous surface microstructure based on fractal geometry
1
2018
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
Modeling of velocity distribution among microchannels with triangle manifolds
6
2010
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
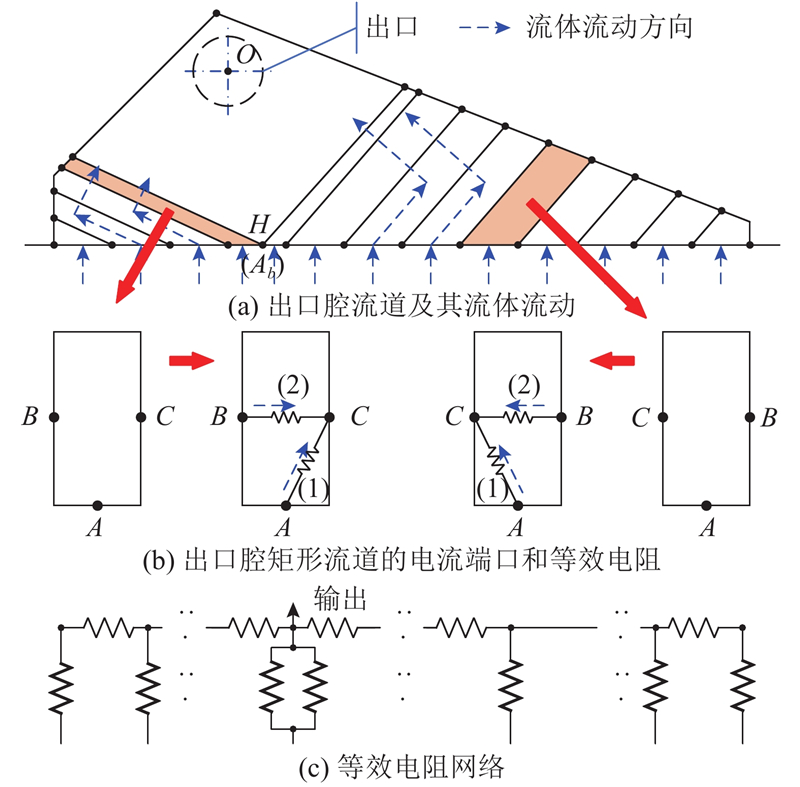
... 研究表明,反应物在纤维载体中的扩散速度、停留时间以及与催化剂的接触面积都会影响甲醇重整制氢反应效率[27 ] . 因此,该区域的流动分布状态对微反应器性能具有重要影响. 鉴于纤维载体直接与进出口腔相连,本研究中纤维载体的整体流道结构包括其本身的流体微通道和进出口腔流道. ...
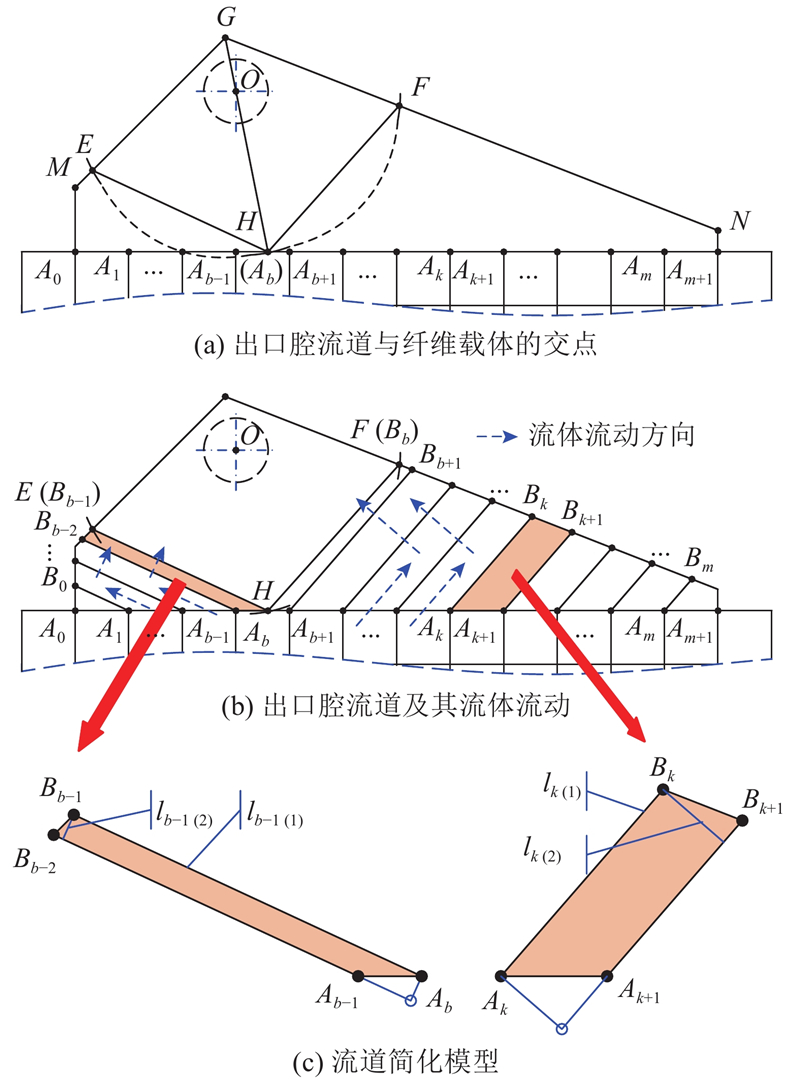
... 进出口腔流道的划分方法已经较为成熟[27 ] ,本研究亦采用相同的方法. 由于进出口腔具有中心对称性,以下仅以出口腔为例对该方法进行简要说明. ...
... 式中: $L$ ${{k}}$ 27 ];下标A 、B 如图5 所示. ...
... 对于进出口腔的矩形单元(见图5 ),由腔体内壁面的剪切应力引起的摩擦损失导致的压力降占主导作用,可以采用哈根-泊肃叶方程进行计算[27 ] : ...
... 如表2 所示,进一步对比2种方法获得的纤维载体流速场信息. 表中,v avg、 v max、 v min 分别为平均流速、流速峰值、流速谷值,t 为计算时间. 可以看出,2种流速场的平均流速基本一致,因此它们在整体流速上基本没有偏移;2种流速场对应的峰值与谷值 $v_{\text{min}}$ [27 ] . 在将纤维载体孔隙简化为网格单元时,并未考虑单元之间因不同流速流体之间摩擦力造成的压降损失. 这使得等效电阻网络模型的流速分布数据在靠近纤维载体与进出口腔边界交点处的起伏稍大. 尽管如此,对比2种流速场的均方差可知其整体数值及变化趋势仍然具有较高的拟合度. ...
Uniform flows in rectangular lattice networks
0
2011
Modeling and analysis of flow distribution in an A-type microchannel reactor
1
2013
... 计算流体力学(CFD)仿真是研究微流道中流动分布的重要手段[9 , 23 -26 ] ,但其计算量大、求解速度慢. 为此,基于等效电阻网络的方法在微流道、微翅片结构的流动分析中得到了发展[21 , 27 -29 ] . 该方法借鉴基尔霍夫定律,在建立微流道模型的基础上,将其中的体积流量和流动阻力分别等效为电流和电阻,并根据电压和电流守恒建立微流道的近似压降模型,进而对流速场快速求解. 尽管效果较好,但要将等效电阻网络方法应用于纤维载体仍然存在极大挑战. 原因在于,纤维载体的微流道结构是三维连通的,流道形状不规则、数目众多,长度和方向都具有随机性. 这使得纤维载体的流道形状难以描述、流道阻力难以确定,无法直接应用已有的等效电阻网络模型. ...
Transport in stochastic fibrous networks
2
2001
... 在随机分布纤维结构研究中,研究者们发展了一种统计分析方法,其核心是将纤维结构简化为规则的统计网络[30 -32 ] . 但该方法面向的是纤维实体结构,而非其中的孔隙结构. 为了发展面向纤维载体流速场快速分析的等效电阻网络模型, 本研究借鉴这一统计网络方法对纤维载体的流道结构进行简化;基于基尔霍夫定律,建立有效的等效电阻网络模型,进行高效求解;通过实例验证方法的有效性. ...
... 纤维随机分布的纤维结构内部纤维搭接点数N c 符合以下统计关系[30 -31 ] : ...
Three-dimensional reconstruction of a random fibrous medium: geometry, transport, and sound absorbing properties
1
2017
... 纤维随机分布的纤维结构内部纤维搭接点数N c 符合以下统计关系[30 -31 ] : ...
基于随机电阻网络碳毡复合层力阻建模
2
2013
... 在随机分布纤维结构研究中,研究者们发展了一种统计分析方法,其核心是将纤维结构简化为规则的统计网络[30 -32 ] . 但该方法面向的是纤维实体结构,而非其中的孔隙结构. 为了发展面向纤维载体流速场快速分析的等效电阻网络模型, 本研究借鉴这一统计网络方法对纤维载体的流道结构进行简化;基于基尔霍夫定律,建立有效的等效电阻网络模型,进行高效求解;通过实例验证方法的有效性. ...
... 基于式(1),可以将纤维随机分布的纤维结构简化为阶数为 $N_{\rm{c}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}$ [32 ] ,如图3 (c) 所示. 其中,网格节点之间是纤维段. ...
基于随机电阻网络碳毡复合层力阻建模
2
2013
... 在随机分布纤维结构研究中,研究者们发展了一种统计分析方法,其核心是将纤维结构简化为规则的统计网络[30 -32 ] . 但该方法面向的是纤维实体结构,而非其中的孔隙结构. 为了发展面向纤维载体流速场快速分析的等效电阻网络模型, 本研究借鉴这一统计网络方法对纤维载体的流道结构进行简化;基于基尔霍夫定律,建立有效的等效电阻网络模型,进行高效求解;通过实例验证方法的有效性. ...
... 基于式(1),可以将纤维随机分布的纤维结构简化为阶数为 $N_{\rm{c}}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}$ [32 ] ,如图3 (c) 所示. 其中,网格节点之间是纤维段. ...
Feasibility of periodic surface models to develop gas diffusion layers: a gas permeability study
2
2012
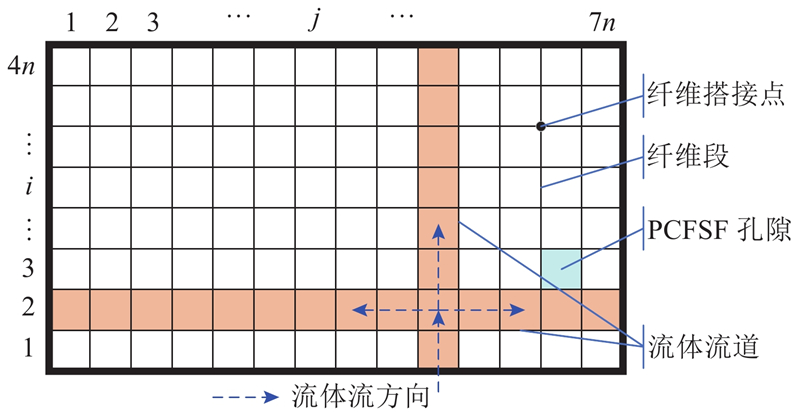
... 显然,在如图4 所示的流道结构中,每个网格单元都代表由纤维段包围形成的孔隙. 由于网格单元满足均匀性标准[33 ] ,将反应物在其中的流动阻力等价为孔隙中纤维段产生的平均阻力. ...
... 纤维载体中的流动阻力与压力降有关. 由于流体在其中的流动为层流[34 ] ,可以利用达西定律来描述纤维载体的整体压力降[33 , 35 ] : ...
Numerical study of flow distribution uniformity for the optimization of gradient porosity configuration of porous copper fiber sintered felt for hydrogen production through methanol steam reforming micro-reactor
2
2018
... 纤维载体中的流动阻力与压力降有关. 由于流体在其中的流动为层流[34 ] ,可以利用达西定律来描述纤维载体的整体压力降[33 , 35 ] : ...
... 为了验证纤维载体等效电阻网络模型的有效性和求解效率,与前期CFD方法[34 ] 进行对比. 以孔隙率E =70%、80%、90%的纤维载体为例进行介绍. 其网格划分阶数n 按式(1)~(3)计算分别为13、9、5,渗透因子K =1.19×10−10 、2.17×10−10 、5.92×10−10 m−2 . ...
Computational modelling of polymer electrolyte membrane (PEM) fuel cells: challenges and opportunities
1
2007
... 纤维载体中的流动阻力与压力降有关. 由于流体在其中的流动为层流[34 ] ,可以利用达西定律来描述纤维载体的整体压力降[33 , 35 ] : ...
Optimal design for flow uniformity in microchannel reactors
1
2002
... 式中:ξ 、D 分别为非圆系数和横截面当量直径,可以通过矩形单元在垂直流动方向的截面深度和宽度表示,具体方法参见文献[36 ]; $A_{\rm{t}}^{{\rm{io}}} $ $q_{\rm{t}}^{{\rm{io}}} $ $R_{\rm{t}}^{{\rm{io}}} $