异质材料模型是指在内部由不同的材料组分或拓扑结构组成的实体模型,典型例子包括多材料模型、梯度渐变材料模型和多孔结构等[1]. 其中,多材料模型具有离散的材料分布类型,通常用有限的整数值来标识各均质材料组分;梯度渐变材料模型具有在空间上逐渐变化的材料分布特性,需要定义相关的材料分布函数来拟合材料组分在欧氏空间的分布信息.
计算机辅助设计的传统建模方法侧重于表示模型的几何形状和拓扑结构,忽略了密度变化、材料分布和复杂拓扑结构等模型内部信息,限制了异质材料模型在制造和工程中的应用,因此适用于设计、分析和制造异质材料模型的系统性建模方案对于充分发挥异质材料模型的卓越性能至关重要. 与传统的均质材料模型相比,表征异质材料模型的重要属性包括几何结构、材料分布、微观结构等.
增材制造技术通过将三维模型离散为一簇二维分层切片,利用不同的制造原理、制造设备及材料性能逐层实施加工制造. 对于任意复杂的几何结构和内部材料分布,选取适当的制造设备和制备工艺并完成相应的基本工艺规划步骤:选择制造方向、离散分层切片、逐层路径规划,可得满足目标需求的制造结果. 现有的切片方法研究主要集中于从不同的表面模型中分层得到精确的切片轮廓,不包含材料分布、密度变化等内部信息.
若提升相关制造工艺来实现多种材料组分在模型内部不同位置的连续变化,则增材制造技术能够通过定制材料性能制造出异质材料物件. 适用于制造异质材料的增材制造技术有很多种,这些技术的不同之处在于所使用的材料性能、机器结构及制造原理[2]. 立体光刻技术通过紫外线光逐层固化均匀分布的光聚合物液体树脂,沿着制造方向改变工艺参数,能够固化得到材料组分呈现梯度变化的异质材料物件. 熔融沉积成型技术的制造原理是将热塑性塑料细丝通过加热喷嘴熔融并挤出,当加热喷嘴允许不同热塑性材料的任意混合时,装配多个喷嘴的FDM机器可以制造出具有梯度材料特性的物体. 基于激光的增材制造技术可以根据使用的机器类型和材料性能来调整工艺参数,制造得到具有相当结构强度和制造精度的异质金属物件. 与传统的制造技术相比,这些适用于制造异质材料物件的增材制造技术均提供了灵活的工艺原理,设计并制造复杂的异质材料分布类型.
本文着重于几何结构和材料分布这2种基本属性,提出基于三维T样条的异质材料实体重建框架. 基于三维T型控制网格的自适应结构,重建过程通过最小化相应的能量泛函来逐步拟合四面体网格的几何结构及材料属性分布,达到降低拟合误差的目的.
1. 异质材料建模技术研究现状
材料属性在实体模型的传统表达中添加了额外的维度,使得高效地表达实体内部的材料分布信息具有一定的难度和复杂性. 传统的CAD建模方法侧重于表示模型的几何形状和拓扑结构,没有直接定义材料信息.
随着等几何分析技术[6]的提出和发展,具有指定材料属性的三变量样条模型实现了对材料分布的高阶连续性表达,可以通过等几何分析技术直接应用于分析过程. Hua等[7-8]定义三变量单纯形样条模型来表示具有任意拓扑结构的复杂异质材料模型,但是计算这种三变量单纯形样条的混合函数及其导数不简单高效. 三维B样条模型和三维NURBS模型被广泛地应用于构建具有高阶连续性的异质材料模型. Zhang等[9]提出基于三维NURBS模型的建模方法,用于构建患者的特定血管模型. Sasaki等[10]介绍基于三维B样条的异质材料实体建模方法,在后续应用中对其直接切片,用于增材制造. B样条模型和NURBS模型都定义在一个规则的张量积域上,这使得它们在拓扑结构方面受到极大的限制. 当细化一个特定的区域时,需要在其邻近区域引入许多额外的自由度来维持张量积拓扑结构. 为了克服这一限制,T样条[11-12]被提出并定义为NURBS模型的一种特殊结构,通过在参数域中引入T型网格结构实现了局部细化. 三维T样条作为T样条的衍生模型,它可以对具有复杂几何结构的实体实施基于局部细化的直接建模. 到目前为止,基于三维T样条的几何实体建模研究包含:基于体参数化方法来构造复杂三维T样条的方法[13];基于广义多立方体结构来参数化构造三维T样条的方法[14-15];针对亏格为零的几何实体提出有理三维T样条实体构造方法[16],将其推广为适用于任意亏格的通用表示方法[17]. 尽管这些研究对异质材料建模过程的讨论较少,但为利用三维T样条更高效地表示实体内部材料属性分布提供了必要的理论基础.
2. 基于三维T样条的异质材料实体重建
2.1. 异质材料实体的三维T样条模型表示
在异质材料模型的建模过程中,当材料分布的定义与几何结构无关时,被归类为与几何无关的材料定义,可以依据材料分布函数直接计算材料组分信息. 对于这类异质材料模型,几何结构和材料分布之间的独立无关性可以允许定义高度复杂的几何结构或材料分布,几何结构的表示不会指导或限制材料分布的表示,反之亦然. Martin等[18]通过使用不同的三变量样条,独立地表示实体模型的几何结构和材料分布. 在该框架下,几何模型和材料模型对应的2个控制网格共享相同的参数域,但是它们的控制点属性、基函数阶次和节点矢量等信息都是独立的. 利用该框架,通过使用共享相同控制网格的2类三维T样条,即几何三维T样条
式中:
2.2. 异质材料实体的体参数化映射
在体参数化的过程中,在四面体网格的边界三角网格通过求解伞算子来定义表面参数化映射:
式中:函数值
其中
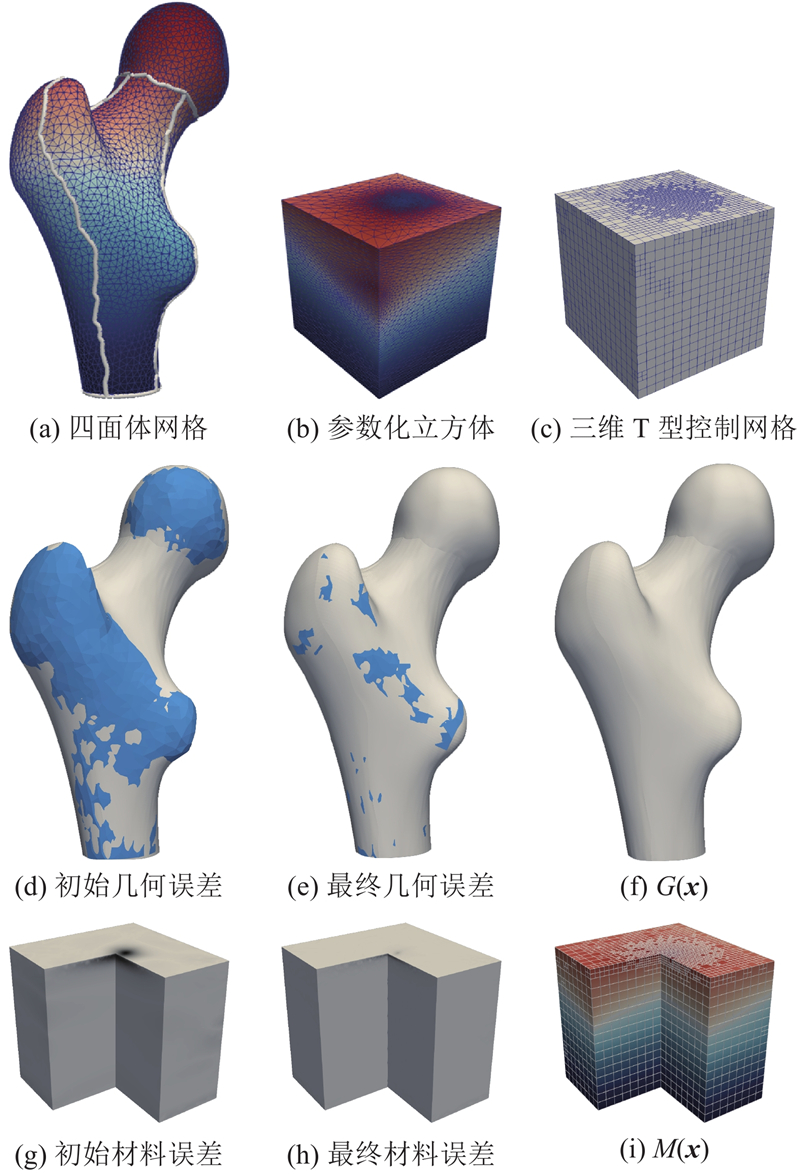
图 1
图 1 异质材料实体的重建框架
Fig.1 Modeling framework for solids with heterogeneous materials
在四面体网格中,
2.3. 异质材料实体重建过程
2.3.1. 三维T型控制网格的自适应初始化过程
基于四面体网格的异质材料实体模型表示为一簇四面体网格单元的集合,每个四面体网格单元分别表示为一簇顶点的集合,每个顶点内可以同时存储相应的几何坐标和材料组分信息. 为了精确表示异质材料实体,四面体网格模型需要在几何特征和材料特征处生成大量的细分网格结构. 基于几何特征和材料特征得到的网格单元自适应分布可以指导三维T型控制网格的自适应初始化过程.
在三维T型控制网格的自适应初始化过程中,以参数域包围的单位立方体网格为初始控制网格实施均匀细分. 如图2所示,在均匀细分的控制网格内部实施基于八叉树结构的自适应细分过程,直至细分得到的每个子网格单元内部至多包含一定数目的四面体网格单元,得到可以精确表示几何特征和材料特征分布情况的三维T型控制网格.
图 2
图 2 三维T型控制网格的自适应初始化过程
Fig.2 Adaptive initialization process for trivariate T-mesh
在三维T型控制网格中计算初始几何三维T样条
2.3.2. 基于三维T样条的能量泛函定义
最小化能量泛函的方法被广泛应用在图像配准领域. 与异质材料的实体重建过程不同,图像配准通过空间变换来构建2幅图像之间的最佳对应映射. 其中,二维图像配准[20-21]和三维图像配准[22-23]等非刚性图像配准方法均定义了相应的配准能量泛函来用于捕获大变形或拓扑结构变化. 本文将能量泛函的定义扩展到异质材料实体的重建过程,利用能量泛函来度量输入的四面体网格和几何三维T样条
在几何建模过程中使用的能量泛函
式中:
式中:
式中:
速度约束项
式中:
在以上2个能量泛函
2.3.3. 基于最小化能量泛函的重建过程
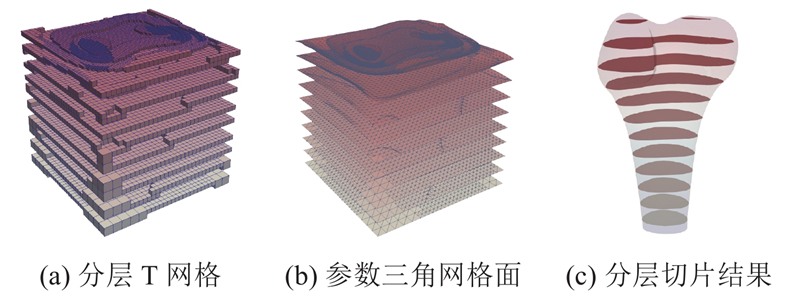
图 3
图 3 股骨下端模型的渐进式重建过程
Fig.3 Progressive modeling framework implemented on lower extremity of femur
在最小化能量泛函的过程中,计算能量泛函对控制点的微分结果,可得
引入时间步长
式中:
式中:
式中:
通过计算
可以动态更新控制点,生成拟合精度更高的三维T样条. 在进一步实施迭代拟合步骤之前,计算当前的拟合相似度,与上一步的拟合相似度进行比较. 若相似度的变化低于给定容差,则迭代循环终止;反之,则进一步实施迭代拟合,直至满足给定容差.
3. 异质材料实体的直接切片过程
按照三维模型的表达方式,对分层切片方法的研究主要分为2类:网格模型切片和直接切片方法. 基于网格的模型易于建模和操作,在选择制造方向、添加支持结构等过程具有更好的灵活性. 网格模型缺乏高阶连续性,在网格化过程中需要添加大量的网格单元来表示复杂的几何特征;随着引入复杂的异质材料属性,数据量过大的情况会更加严重. 相反,直接切片方法直接应用于精确的模型表示,在不涉及网格化过程的情况下,不仅可以减少预处理时间,而且能够保持模型从原始输入到分层切片结果乃至最终制造产品的一致性.
随着各种制造设备和工艺的发展,适用于异质材料模型的制造方法得到了广泛的关注和研究. 为了实现异质材料实体模型在增材制造领域的应用,制造方向选择、离散分层切片及逐层路径规划等相关工艺步骤亟需研究. 本文采用适用于异质材料实体模型的直接切片算法[24],可以沿着给定的制造方向实施直接分层切片,得到基于三角网格表示的二维切片结果.
3.1. 自适应细分生成分层T网格
以股骨下端模型为例,选择Z轴为制造方向,具体说明分层切片的实施过程. 对于任意给定的Z轴坐标值
基于八叉树结构自适应细分生成分层T网格包含以下步骤.
1)综合考虑目标模型的几何结构及实际制造过程中的工艺参数、目标制造精度等,给定细分精度
2)在参数域包围的立方体网格中进行初始化均匀细分,得到初始分层T网格. 初始化均匀细分的阶数是一个经验参数值,需要综合考虑目标模型的几何结构及实际制造过程中的工艺参数等进行实验性设置. 细分阶数越高,算法实施过程中的数据存储量越大,但后续步骤的计算过程会越快;反之,细分阶数越低,算法实施过程的数据存储量越小,但后续步骤的计算过程会越慢. 在本例的具体实施过程中,初始化均匀细分的阶数设置为1.
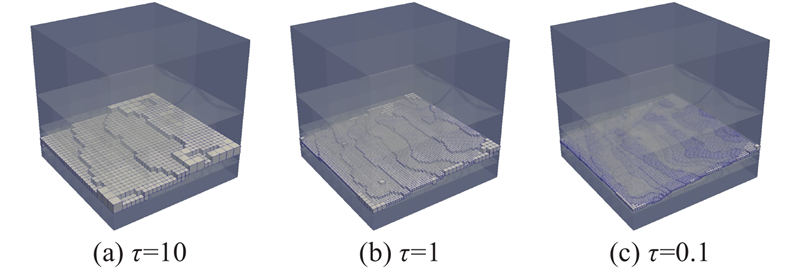
图 4
图 4 基于3种不同的细分精度的分层T网格
Fig.4 Slicing T-meshes based on three different tolerances
4)以标记后的分层T网格为基础,利用
3.2. 基于分层T网格实施直接切片
图 5
图 5
基于
Fig.5
Direct slicing results based on slicing T-meshes in
4. 实验与讨论
以具有异质材料信息的四面体网格为输入模型,在C++中实现了模型重建与切片流程,以股骨下端和上端模型及橡皮鸭模型为例进行数值实验.
图 6
图 6 股骨上端模型的渐进式重建过程
Fig.6 Progressive modeling framework implemented on upper extremity of femur
图 7
图 7 橡皮鸭模型的渐进式重建过程
Fig.7 Progressive modeling framework implemented on Rubber Duck
4.1. 异质材料实体的重建实验
在基于最小化能量泛函的重建过程中,在每一次迭代拟合步骤结束之后,需要对当前的拟合精度采用相似度(similarity ratio, RS)进行度量。较高的RS对应较好的拟合结果,RS=100%对应完美的拟合结果. 几何三维T样条
式中:
在三维T型控制网格的自适应初始化过程中,初始化控制网格直至自适应细分得到的每个子网格单元内部至多包含5个四面体网格单元. 在渐进式重建过程中,
三维NURBS模型定义在基于均匀细分的三维控制控制网格上. 如表2所示,在异质材料实体建模过程中需要大量的冗余控制点来满足张量积拓扑约束,控制点的数量明显高于三维T样条. 尤其是当几何结构或者材料分布中存在复杂特征时,三维NURBS模型需要在拟合精度和数据量之间进行权衡;三维T样条模型能够利用局部控制性质,在某些复杂特征分布的区域中自适应地插入节点,以改善模型的自由度,从而可以在达到相似甚至更优的拟合精度的前提下减少冗余控制点的数量,使得表达方式更加紧凑.
表 1 基于三维T样条的异质材料实体建模结果
Tab.1
| 实验模型 | 三维T样条 | nc | | ni | RS/% |
| 股骨下端 | | 17 409 | 0.6 | 20 | 86.76 |
| 股骨下端 | | 17 409 | 0.6 | 25 | 90.13 |
| 股骨上端 | | 21 659 | 0.6 | 23 | 85.33 |
| 股骨上端 | | 21 659 | 0.6 | 27 | 88.03 |
| 橡皮鸭 | | 27 455 | 0.4 | 23 | 80.47 |
| 橡皮鸭 | | 27 455 | 0.4 | 16 | 88.66 |
表 2 基于三维NURBS的异质材料实体建模结果
Tab.2
| 实验模型 | 三维NURBS | nc | | ni | RS/% |
| 股骨下端 | | 68 921 | 0.6 | 25 | 84.57 |
| 股骨下端 | | 68 921 | 0.6 | 27 | 82.66 |
| 股骨上端 | | 64 000 | 0.6 | 28 | 84.62 |
| 股骨上端 | | 64 000 | 0.6 | 27 | 85.92 |
| 橡皮鸭 | | 54 872 | 0.4 | 31 | 83.84 |
| 橡皮鸭 | | 54 872 | 0.4 | 19 | 90.27 |
4.2. 异质材料实体的直接切片实验
图 8
图 9
图 10
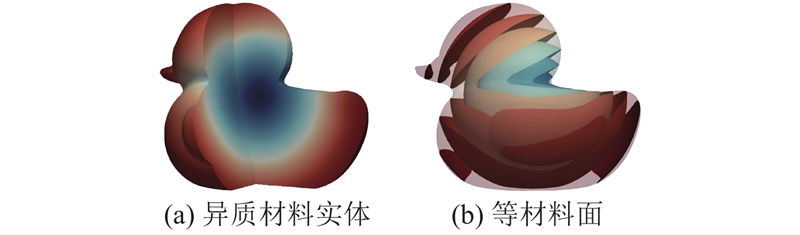
4.3. 异质材料实体的等材料面提取实验
基于4.2节的直接切片方法,如图11~13所示,沿着材料三维T样条
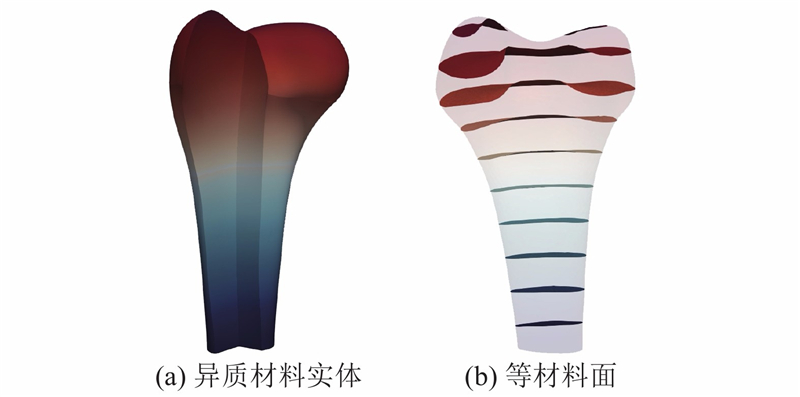
图 11
图 11 股骨下端模型的等材料面提取结果
Fig.11 Results of extracting iso-material surfaces from lower extremity of femur
图 12
图 12 股骨上端模型的等材料面提取结果
Fig.12 Results of extracting iso-material surfaces from upper extremity of femur
图 13
图 13 橡皮鸭模型的等材料面提取结果
Fig.13 Results of extracting iso-material surfaces from Rubber Duck
5. 结 语
本文提出用于异质材料实体的建模和切片工艺,将几何结构和材料分布由基于相同三维T型控制网格的2类三维T样条定义. 通过最小化能量泛函来逐步迭代拟合控制点,降低构造的三维T样条与输入的四面体网格之间的拟合误差. 针对异质材料实体在增材制造中的切片工艺,采用基于八叉树结构的自适应细分过程,在参数域生成分层T网格,应用移动立方体方法生成三角网格切片结果. 数值结果表明,三维T型控制网格能够局部自适应控制几何结构和材料分布,使得异质材料实体的重建过程和切片工艺可以得到较高的拟合和切片精度.
本文所采用的体参数化方式很难捕获尖锐突起之类的复杂几何特征,使得材料建模过程无法进一步提高拟合精度. 采用基于Polycube的复杂参数域结构,实施适用于亏格非零的复杂实体模型的体参数化过程. 在直接切片过程中,制造方向是预先给定的. 虽然这种方式对整个直接切片过程没有影响,但是为了实现设计-分析的无缝集成,如何自动获得最佳制造方向是亟待解决的问题.
参考文献
Heterogeneous object modeling: a review
[J].DOI:10.1016/j.cad.2006.12.007 [本文引用: 1]
Additive manufacturing of functionally graded material objects: a review
[J].
A framework for object modeling
[J].DOI:10.1016/S0010-4485(99)00051-2 [本文引用: 1]
An automatic 3D mesh generation method for domains with multiple materials
[J].
Adaptive tetrahedral mesh generation of 3D heterogeneous objects
[J].DOI:10.1080/16864360.2015.1014736 [本文引用: 1]
Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement
[J].DOI:10.1016/j.cma.2004.10.008 [本文引用: 1]
Trivariate simplex splines for inhomogeneous solid modeling in engineering design
[J].DOI:10.1115/1.1881352 [本文引用: 1]
Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow
[J].
Adaptive direct slicing of volumetric attribute data represented by trivariate B-spline functions
[J].DOI:10.1007/s00170-016-9800-0 [本文引用: 1]
T-splines and T-NURCCs
[J].DOI:10.1145/882262.882295 [本文引用: 1]
T-spline simplification and local refinement
[J].DOI:10.1145/1015706.1015715 [本文引用: 1]
A new approach to solid modeling with trivariate T-splines based on mesh optimization
[J].
Restricted trivariate polycube splines for volumetric data modeling
[J].DOI:10.1109/TVCG.2011.102 [本文引用: 1]
Solid T-spline construction from boundary representations for genus-zero geometry
[J].DOI:10.1016/j.cma.2012.01.014 [本文引用: 1]
Trivariate solid T-spline construction from boundary triangulations with arbitrary genus topology
[J].DOI:10.1016/j.cad.2012.10.018 [本文引用: 1]
Constructing B-spline solids from tetrahedral meshes for isogeometric analysis
[J].DOI:10.1016/j.cagd.2015.03.013 [本文引用: 1]
Medical image interpolation based on multi-resolution registration
[J].DOI:10.1016/j.camwa.2013.04.026 [本文引用: 1]
A novel dynamic multilevel technique for image registration
[J].DOI:10.1016/j.camwa.2015.02.010 [本文引用: 1]
DTHB3D_Reg: dynamic truncated hierarchical B-spline based 3D nonrigid image registration
[J].
Joint image segmentation and registration based on a dynamic level set approach using truncated hierarchical B-splines
[J].DOI:10.1016/j.camwa.2019.04.026 [本文引用: 1]
Slicing heterogeneous solid using octree-based subdivision and trivariate T-splines for additive manufacturing
[J].DOI:10.1108/RPJ-11-2018-0287 [本文引用: 1]
Marching cubes: a high resolution 3D surface construction algorithm
[J].DOI:10.1145/37402.37422 [本文引用: 1]