自然灾害、事故等事件因其突发性、不确定性给应急救援工作开展造成困难，导致严重的生命财产损失. 统计表明，有效的应急救援系统可以将事故损失降低约40%^[1]，其中应急设施选址和资源配置是该系统建设的重要组成部分.

应急设施选址影响救援覆盖区域，该问题一般分为确定性选址、动态选址、随机选址和鲁棒性选址^[2]等. 确定性选址问题通过输入事先已知且不随时间变化的参数，以优化系统成本、救援效率等为目标，决策应急设施选址^[3-9]. 动态选址问题是长期决策过程，须在不同周期对易变化的参数更新^[10]. 随机选址问题的核心思想是假设不确定性参数遵循一定的概率分布，可以将不确定的需求转化为多场景下的确定性需求^[11]，或将不确定的参数通过数学方法转化为期望与方差^[12-14]. 鲁棒性选址问题偏向提高解对不同场景的适应力^[15].

应急资源配置问题影响系统救援能力，与设施选址密切关联. Rawls等^[16-18]建立基于反馈机制的选址-配置双层规划模型，其中Caunhye等^[17]考虑了物资在设施之间的转运，使方案更加灵活. Baharmand等^[19-20]将选址和配置问题集成在同一层优化模型中进行求解. 现有研究较多关注于资源配置数量的优化，但在实际中资源种类的选取匹配对救援能力和成本产生影响，值得讨论.

救援覆盖可靠度作为反映应急系统在不确定因素影响下完成救援任务概率的重要指标，在近年来的应急选址与资源配置研究中逐渐得到关注^[21-25]. 其中Ai等^[21-22]运用并联系统原理计算覆盖可靠度，秦进等^[23]将可靠度转化为应急系统为需求点提供资源的概率. 多数考虑了可靠性的研究中，可靠度计算过程往往不考虑救援设备失效时可采用系统内其他设备替代的可能，无法较好地反映系统可靠性，模型的实用价值存在提升空间.

应急系统内的救援设备，例如车辆，往往不止配置一种类型. 本文基于使用可用车辆替代失效车辆完成救援任务的思想，通过构建虚拟车辆资源池，考虑不同场景下设施内和设施间的车辆替代可能，提出救援覆盖可靠度的计算方法. 使用该方法为建立的应急配置与需求分配双层优化模型提供重要参数，与基于传统可靠度计算方法的优化结果进行对比. 探讨车辆类型匹配对系统总成本的影响，为最优的车辆类型匹配提供依据.

假设某片区域中存在多个潜在的灾害救援需求点（以下简称需求点），已知每个需求点发生突发事件时的预计物资需求量和应急设施（以下简称设施）候选点位置. 通过对设施的新建和升级改造以及不同型号救援车辆的合理配置，在保障每个需求点的救援覆盖可靠度前提下，最小化救援系统的总成本. 对该问题作出如下合理假设：1）救援所用车辆分为大车和小车，对应不同单位购置成本、速度、容量和可靠度；2）突发事件不损坏设施.

部分参数、变量定义如下：I为需求点集合； $J$为设施候选点集合， $J'$为现有设施点集合， $J' \subseteq J$； $t$为覆盖条件下的最大可接受应急响应时间（以下简称响应时间）； ${O_i}$为在响应时间内能够覆盖需求点 $i$的设施候选点集合； ${D_j}$为在响应时间内能够被设施候选点 $j$覆盖的需求点集合；A为设施级别集合， $a$指示设施等级， $a_j^{\rm{e}}$为 $j$处现有设施的级别； $B$为车辆种类集合， $b$表示车辆种类， $b = 1$为大车， $b = 2$为小车； ${l_{ij}}$为需求点 $i$与设施 $j$之间的距离； ${\mu _b}$、 $v_b^{\max }$分别为 $b$类车的可靠度和最大行驶速度， $v_2^{\max } < v_1^{\max }$. 为了考虑道路交通量 ${u_{ij}}$对行驶速度的影响，采用王炜^[26]建立的双车道公路车速-流量模型. 通过下式对2种车辆在需求点和设施之间的行驶速度 $v_b^{ij}$进行修正，可以得到集合 ${O_i}$和 ${D_j}$：

(1) $v_b^{ij} = v_b^{\max }\exp\; ( - 0.000\;225{u_{ij}}).$

当车辆因故障、维修等原因无法完成救援任务时，承担的任务可以由该设施或其他设施的车辆替代完成. 小车可由其他相同或不同类型的车辆替代；大车受限于容量和速度属性，仅可由其他大车替代. 定义救援覆盖可靠度（以下简称可靠度） ${\tau _i}$：救援系统在响应时间内能够为需求点 $i$提供数量不低于需求总量 ${d_i}$的救援物资的概率. 对可靠度计算作出如下合理假设：1）同一时刻仅1处需求点需要救援，不考虑多点同时救援的情况；2）小车可在响应时间内将物资运至需求点时，优先使用小车.

为了充分考虑设施内及设施间的车辆替代可能，在不考虑车辆失效的情况下为每个需求点 $i$构造虚拟车辆资源池 ${P_i}$，池内车辆来自各个与需求点 $i$有救援需求分配关系的设施. 由于本文所提的可靠度计算方法基于车辆运输能力角度，应先以设施内实际物资储存量（即物资配置角度）为约束对各设施的入池车辆数进行讨论，确保入池车辆可由所属设施配备充足物资以完成救援任务.

1）当设施 $j$内物资储存总量 ${w_j}$≥需求 ${d_i}$时，在极端情况下仅用 $j$中的车辆和物资仍可完成救援任务，此时物资储存约束为宽松约束. 若该设施可以通过小车在响应时间内覆盖需求点 $i$，设施内所有车辆均进入资源池 ${P_i}$；若由于距离较远或设施内未配置小车，该设施仅可通过大车覆盖需求点，此时设施内所有大车进入资源池 ${P_i}$.

2）当 ${w_j}<{d_i}$时. 若该设施入池车辆对应的运输能力大于 ${w_j}$，可能出现车辆数满足运输能力需求但实际可运物资数不足的情况，特别是当使用该设施内的车辆替代其他设施的失效车辆时，更无法保证完成救援. 利用下式计算该设施的入池车辆数，以避免上述情况的发生：

(2) $\max \sum\limits_{ b \in B} {{k_b}{z_{ijb}}} \cdot $

(3) $ \sum\limits_{ b \;\in\; B} {{k_b}{z_{ijb}}} \leqslant {w_j}; $

(4) $ {z_{ijb}} \leqslant {e_{ijb}}{x_{jb}},\; b \in B ; $

(5) ${z_{ijb}} \in {\bf{N}} \cdot $

式中： ${k_b}$为 $b$类车的容量； ${e_{ijb}}$为车辆覆盖能力变量，设施 $j$可在响应时间内通过 $b$类车为需求点 $i$运输物资时等于1，否则等于0； ${z_{ijb}}$为设施 $j$中进入资源池 ${P_i}$的 $b$类车数量.

式（2）表示最大化入池车辆对应的运输能力；式（3）表示入池车辆对应的总运输能力不超过该设施的物资储备量；式（4）表示入池的各型号车数不超过设施内的配置数，且某类车辆受限于速度无法在响应时间内到达需求点 $i$时，该类车不会进入 $i$的资源池；式（5）为决策变量取值约束.

至此各潜在需求点的虚拟车辆资源池构建完毕，池内车辆在符合前文所述规则的前提下均可替代失效车辆进行救援. 根据入池车辆情况和对应需求点的物资需求量划分场景，计算考虑替代救援的救援覆盖可靠度.

计算所用参数包括： ${\tau _i}$为需求点 $i$的预期救援覆盖可靠度； ${\mu _b}$为 $b$类车的可靠度； $n$为大车与小车间的容量倍数， ${k_1}{\rm{ = }}n{k_2}$. 相关概念的定义如下.

1）资源池车辆数：资源池 ${P_i}$包含b类车辆的总数， ${z_{{P_i}b}^{\rm{}}}{\rm{ = }}\displaystyle\sum\nolimits_{j \in {O_i}} {{z_{ijb}}}$.

2）车辆失效数：车辆因故障或其他原因无法完成救援任务时即为失效，失效概率为 $1{\rm{ - }}{\mu _b}$. ${s_{{P_i}b}}$为在保证完成 $i$点救援任务前提下，资源池 ${P_i}$中 $b$类车的可能失效数.

3）车辆空闲数：不考虑失效时，池内车辆数减去完成任务所需的最小车辆数即为车辆空闲数， ${P_i}$中 $b$类车的空闲数用 ${q_{{P_i}b}^{\rm{}}}$表示.

根据不同任务对车辆的需求，可能出现仅需小车运输、同时需要大车和小车运输、仅需大车运输3类场景，下面对各场景的可靠度计算进行分类讨论.

不考虑失效时，仅使用资源池内的小车即可完成 $i$点的救援任务. 此时大车空闲数 ${q_{{P_i}1}^{\rm{}}} = {z_{{P_i}1}^{\rm{}}}$，小车空闲数 ${q_{{P_i}2}^{\rm{}}} = {z_{{P_i}2}^{\rm{}}} - \left\lceil {{d_i}/{k_2}} \right\rceil$.

当小车失效数不超过池内空闲小车总数时，可以由空闲小车进行替代，可靠度为

(6) $ {\tau _i} = \sum\limits_{{s_{{P_i}2}^{\rm{}}} = 0}^{{q_{{P_i}2}^{\rm{}}}} {{\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}{\mu _2}^{{z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}}}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}} . $

当小车失效数超过池内空闲小车总数时，需空闲大车参与替代救援，应考虑大车面临失效的可能，可靠度为

(7) $ \begin{split} {\tau _i} = & \sum\limits_{{s_{{P_i}2}^{\rm{}}} = {q_{{P_i}2}^{\rm{}}} + 1}^{\min \;\left\{ {n {q_{{P_i}1}^{\rm{}}} + {q_{{P_i}2}^{\rm{}}},\;{z_{{P_i}2}^{\rm{}}}} \right\}} {\Bigg\{ {{\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}}} \times } } \\ & \left. {\left[ {\sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}} \!-\! \left\lceil {[\left\lceil {{d_i}/{k_2}} \right\rceil \!-\! ({z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}})]/n} \right\rceil } {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}\left( {1 \!-\! {\mu _1}} \right)\!{^{{s_{{P_i}1}^{\rm{}}}}}{\mu _1}^{\! {{z_{{P_i}1}^{\rm{}}}\! -\! {s_{{P_i}1}^{\rm{}}}} \!}} } \right]} \right\}\!. \end{split} $

“仅需小车”时的可靠度由式（6）、（7）加和计算.

当不考虑失效时，需资源池内2种车辆共同运输才能完成 $i$点的救援任务. 在优先使用小车的原则下，此时资源池内已无空闲小车，可能存在若干空闲大车和1辆未装满的大车，剩余容量 ${k_{1{\rm{w}}}}{\rm{ = }}{k_1} - \{ {d_i} - {k_2}{z_{{P_i}2}^{\rm{}}} - {k_1}[\lceil ({d_i} -$ ${k_2}{z_{{P_i}2}^{\rm{}}})/ {k_1} \rceil - 1]\}$，可能用于替代失效小车. 该场景可以进一步细分为池内“无空闲大车”和“仅剩余空闲大车”.

1）无空闲大车时，仅存在未装满的大车替代失效小车的可能.

a）未装满的大车剩余容量不足以替代1辆小车时，池内所有车辆都不失效才能完成救援任务，可靠度为

(8) $ {\tau _i} = \mu _1^{{z_{{P_i}1}^{\rm{}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}}} \cdot $

b）未装满的大车剩余容量可替代小车时，仅可接受较少数量的小车失效，可靠度为

(9) $ \begin{split} {\tau _i} = & \sum\limits_{{s_{{P_i}2}^{\rm{}}} = 1}^{\min \;\left\{ {\left\lfloor {{k_{1{\rm{w}}}}/{k_2}} \right\rfloor ,\;{z_{{P_i}2}^{\rm{}}}} \right\}} {\left[{\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}\mu _2^{({z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}})}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}}}\right]} {\rm{ + }} \\ & \mu _1^{{z_{{P_i}1}^{\rm{}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}}}.\\[-13pt] \end{split} $

2）剩余空闲大车时，空闲的大车数量为 ${q_{{P_i}1}^{\rm{}}} = {z_{{P_i}1}^{\rm{}}} - \left\lceil {({d_i} - {k_2}z{}_{{P_i}2}^{\rm{}})/{k_1}} \right\rceil$.

a）未装满的大车剩余容量不足以替代1辆小车时，仅空闲大车可替代失效车辆. 可能出现无车辆失效、仅大车失效、仅小车失效和大小车同时失效4种情况. 前2种情况的可靠度为

(10) $ {\tau _i} = \sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}}} {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}{{(1 - {\mu _1})}^{{s_{{P_i}1}^{\rm{}}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}} - {s_{{P_i}1}^{\rm{}}}}} \mu _2^{{z_{{P_i}2}^{\rm{}}}} \cdot $

后2种情况的可靠度为

(11) $ \begin{split} {\tau _i} = & \sum\limits_{{s_{{P_i}2}^{\rm{}}} = 1}^{\min\; \left\{ {n {q_{{P_i}1}^{\rm{}}},\;{z_{{P_i}2}^{\rm{}}}} \right\}} \Bigg\{ {\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}}} \times \\ & \left.\left[\sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}} - \left\lceil {{s_{{P_i}2}^{\rm{}}}/n} \right\rceil } {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}{{(1 - {\mu _1})}^{{s_{{P_i}1}^{\rm{}}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}} - {s_{{P_i}1}^{\rm{}}}}} \right] \right\}. \end{split} $

当池内仅剩空闲大车且未装满的大车剩余容量不足以替代小车时，可靠度由式（10）、（11）加和计算.

b）当未装满的大车剩余容量可以替代小车时，可能出现上述4种情况. 前2种情况的可靠度通过式（10）计算.

当小车失效数较小时，只需未装满的大车进行替代. 此时后2种情况的可靠度为

(12) $ \begin{split} {\tau _i} = & \sum\limits_{{s_{{P_i}2}^{\rm{}}}{\rm{ = }}1}^{\min\; \left\{ {\left\lfloor {{k_{1{\rm{w}}}}/{k_2}} \right\rfloor ,\;{z_{{P_i}2}^{\rm{}}}} \right\}} \Bigg\{ {\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}}} \times \\ & \left.\left[\sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}}} {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}{{(1 - {\mu _1})}^{{s_{{P_i}1}^{\rm{}}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}} - {s_{{P_i}1}^{\rm{}}}}} \right] \right\} . \end{split} $

当小车失效数超过未装满大车的剩余容量时，需要额外空闲大车进行替代. 此时后2种情况的可靠度为

(13) $ \begin{split} {\tau _i} = & \sum\limits_{{s_{{P_i}2}^{\rm{}}} = \left\lfloor {{k_{1{\rm{w}}}}/{k_2}} \right\rfloor + 1}^{\min\; \left\{ {n {q_{{P_i}1}^{\rm{}}} + \left\lfloor {{k_{1{\rm{w}}}}/{k_2}} \right\rfloor ,\;{z_{{P_i}2}^{\rm{}}}} \right\}} \Bigg\{ {\rm{C}}_{{z_{{P_i}2}^{\rm{}}}}^{{s_{{P_i}2}^{\rm{}}}}{{(1 - {\mu _2})}^{{s_{{P_i}2}^{\rm{}}}}}\mu _2^{{z_{{P_i}2}^{\rm{}}} - {s_{{P_i}2}^{\rm{}}}} \times \\ & \left.\left[\sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}} - \left\lceil {({s_{{P_i}2}^{\rm{}}} - \left\lfloor {{k_{1{\rm{w}}}}/{k_2}} \right\rfloor )/n} \right\rceil } {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}{{(1 - {\mu _1})}^{{s_{{P_i}1}^{\rm{}}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}} - {s_{{P_i}1}^{\rm{}}}}} \right] \right\} . \end{split} $

当池内仅剩空闲大车且未装满的大车剩余容量可以替代小车时，可靠度利用式（10）、（12）、（13）加和计算.

由于池内车辆所属设施距离较远或车辆种类配置限制，仅大车能完成 $i$点的救援任务. 此时大车空闲数 ${q_{{P_i}1}^{\rm{}}} = {z_{{P_i}1}^{\rm{}}} - \left\lceil {{d_i}/{k_1}} \right\rceil$，该场景下的可靠度为

(14) $ {\tau _i} = \sum\limits_{{s_{{P_i}1}^{\rm{}}} = 0}^{{q_{{P_i}1}^{\rm{}}}} {{\rm{C}}_{{z_{{P_i}1}^{\rm{}}}}^{{s_{{P_i}1}^{\rm{}}}}\mu _1^{{z_{{P_i}1}^{\rm{}}} - {s_{{P_i}1}^{\rm{}}}}{{(1 - {\mu _1})}^{{s_{{P_i}1}^{\rm{}}}}}} \cdot $

以最小化应急救援系统的总成本为目标，建立双层规划模型. 上层模型优化应急设施选址与车辆配置方案，下层模型在上层模型的基础上优化需求点和设施之间的物资需求分配.

上层模型所需参数、变量定义如下： ${f_{ja}}$为在 $j$处新建或升级至 $a$级设施的建设成本； ${k_{ja}}$为 $j$处 $a$级设施最多可配置车辆总数； ${c_b}$为 $b$类车的单位购置成本； ${\eta _i}$为需求点 $i$的重要度； ${\eta _{\rm{l}}}$为需求点的重要度阈值. 决策变量包括： ${x_{jb}}$为设施 $j$中配置 $b$类车的数量； ${y_{ja}}$为选址决策变量，在 $j$处新建或升级至 $a$级设施时等于1，否则等于0. 本文的上层规划模型如下.

(15) ${\min\;{{Z}} _1}{\rm{ = }}\sum\limits_{ j \in J} {\sum\limits_{ a \in A} {{f_{ja}}{y_{ja}}} } {\rm{ + }}\sum\limits_{ j \in J} {\sum\limits_{ b \in B} {{c_b}{x_{jb}}} + } {Z_2} \cdot $

(16) $\sum\limits_{j \in {O_i}} {{y_{ja}}} \geqslant 1{\rm{ }},\; i \in I ; $

(17) $\sum\limits_{j \in {O_i}} {{y_{ja}}} \geqslant 2,\;{\rm{ }}i \in I,{\eta _i} \geqslant {\eta _{\rm{l}}} ; $

(18) $\sum\limits_{b \in B} {{x_{jb}}} \leqslant \sum\limits_{a \in A} {{k_{ja}}{y_{ja}}} ,\; j \in J ; $

(19) $\sum\limits_{a \in A} {a{y_{ja}}} \geqslant a_j^{\rm{e}},\; j \in J' ; $

(20) $ {x}_{ja}\in {\bf{N}},\;{y}_{ja}\in \left\{0,1\right\}, \;j\in J, \;a\in A. $

目标函数（15）表示最小化系统总成本Z₁，前两部分分别为系统设施建设和车辆购置成本，第3部分为物资储存成本和系统预期需求不满足惩罚成本之和，取下层模型目标函数值Z₂. 式（16）、（17）为需求点覆盖约束，式（16）保证每个需求点在响应时间内至少被1个设施覆盖，式（17）保证每个重要度较高的需求点至少被2个设施覆盖. 式（18）为设施车辆配置约束，配置总数不可超过该级别设施的车辆可配置数上限。式（19）保证系统内现有设施不能拆除。式（20）为决策变量取值约束.

下层模型所需参数、变量定义如下： ${h_i}$为需求点 $i$的预期需求短缺量； ${g_j}$为设施 $j$的应急物资单位储存成本； $p$为物资需求短缺的单位惩罚成本； ${\tau ^*}$为需求点预期覆盖可靠度阈值； $M$为1个较大的正数； ${d_{ij}}$为下层模型的决策变量，表示需求点 $i$和设施点 $j$之间的物资需求分配量. 运用上文所述考虑替代救援的可靠度计算方法计算救援覆盖可靠度 ${\tau _i}$，作为下层模型约束条件之一，将救援覆盖可靠度转化为预期需求不满足惩罚成本加入到目标函数中. 本文的下层规划模型目标函数如下.

(21) ${\min\;{{Z}}_2}{\rm{ = }}\sum\limits_{ j \in J} {{g_j}{w_j}} {\rm{ + }}\sum\limits_{ i \in\; I} {{h_i}p} \cdot $

(22) ${w_j}{\rm{ = }}\sum\limits_{i \in {D_j}} {{d_{ij}},\; j \in J }; $

(23) ${h_i}{\rm{ = }}{d_i}(1 - {\tau _i}),\; i \in I ; $

(24) ${\tau _i} \geqslant {\tau ^*},\; i \in I ; $

(25) $\sum\limits_{i \in {D_j}} {{d_{ij}}} \leqslant \sum\limits_{b \in B} {{k_b}{x_{jb}}},\; j \in J ; $

(26) $ {\displaystyle \sum _{i\in {D}_{j}}{d}_{ij}\left( {{e}_{ij1}-{e}_{ij2}} \right)}\leqslant {k}_{1}{x}_{j1},\; j\in J; $

(27) ${d_{ij}} \leqslant M \sum\limits_{b \in B} {{e_{ijb}}},\; j \in J,\; i \in I ; $

(28) $\sum\limits_{j \in {O_i}} {{d_{ij}}} \geqslant {d_i},\; i \in I; $

(29) ${d_{ij}} \geqslant 0,\; j \in J,\; i \in I . $

目标函数（21）最小化系统内物资储存总成本和预期需求不满足惩罚成本. 式（22）计算设施物资储存总量。式（23）计算需求点的预期需求不满足数。式（24）保证需求点覆盖可靠度应高于可接受下限。式（25）保证分配给设施的需求总量不超过该设施内车辆的总运输能力。式（26）保证分配给设施仅能用大车运输的需求总量不可超过该设施内大车的总运输能力。式（27）表示若设施无法在响应时间内覆盖需求点，两者间无需求分配关系。式（28）表示需求点与各设施之间的需求分配之和不小于总需求量。式（29）为决策变量取值约束.

所建应急配置优化与需求分配双层规划模型是NP-Hard问题. 随着设施候选点数量、需求点数量、设施类型、设施内可配置车数量范围的增加，问题解空间规模呈指数增长，一般的数学方法很难在有效时间内进行求解. 设计双层启发式算法，上层模型采用基于矩阵编码的遗传算法，下层采用粒子群算法进行求解.

矩阵编码方法是将矩阵整体作为遗传个体，不需要将矩阵展开成遗传元素. 每个设施候选点对应3个决策变量，因此遗传个体为 $3 \times |J|$的矩阵，上层模型染色体结构如图1所示. 下层模型粒子编码如图2所示.

算法流程如图3所示，具体步骤如下.

1）上层初始解生成. 保证现有设施处的设施级别不为零，根据取值要求随机生成其他候选点的设施级别及每个设施候选点的车辆配置数.

2）下层需求分配方案寻优. 将上层染色体信息输入至下层模型，利用粒子群算法求解该染色体对应的需求分配方案，输出最优值作为反馈.

3）选择. 采用带有精英保留策略的轮盘赌方法，选择进入下一代的个体.

4）交叉. 随机选择2个个体，交换基因矩阵中某个设施所在列的全部信息.

5）变异. a）设施等级变异，改变染色体中某处设施等级，根据该等级要求随机生成设施内车辆配置数。b）车辆配置数变异，不改变设施等级，在该等级要求范围内随机改变车辆配置数.

6）重复步骤2）~5），直到满足最大迭代次数，输出最优个体对应的编码矩阵和目标函数值.

使用文献[21]中某区域内需求点与设施候选点的距离数据，构建包含23个需求点、16个设施候选点的网络. 将设施分为2个级别：一级设施最多可配置4辆救援车，二级设施最多可配置8辆，其中1号和16号候选点已有一级设施. 小车容量为40单位，购置成本为30万元/辆，通过调查救援运输车辆的相关数据可知，当大车与小车间的容量关系为 ${k_1} = n{k_2}$时，单位购置成本关系取 ${c_1} = $ $ 0.85n{c_2}$，2种车辆的可靠度分别为0.8和0.7；物资需求不满足的单位惩罚为3.5万元；预期覆盖可靠度阈值 ${\tau ^*} = 0.8$；应急设施的相关成本如表1所示.

以大车容量为小车容量的2倍为例，模型求解得到系统成本最优值为2 896.73万元，其中设施建设成本为1 072.50万元，车辆购置成本为873.00万元，物资储存成本为919.79万元，需求不满足惩罚成本为31.44万元，系统内各需求点的平均救援覆盖可靠度为98.85%. 对应的上层模型最优解如表2所示，新建一级设施5处，升级设施1处，保留原有级别设施1处，共配置13辆大车、7辆小车.

当大车容量倍数较大时，对小车的替代作用更加显著，有利于提高系统的整体可靠度. 大型车辆对应更高的购置成本，因此车辆的类型匹配选择是在系统成本和可靠度之间的博弈过程，较优的车辆类型匹配方案须在保证系统可靠度的前提下减少系统总成本. 通过调查救援运输车辆的相关数据可知， $n$的取值为1.2~3.0，步长为0.1，单位购置成本关系取 ${c_1} = 0.85n{c_2}$. 在每个容量倍数下连续对模型进行15次求解，分析算法稳定性；提取最优解，对成本与车辆容量倍数进行敏感性分析.

如图4所示，随着容量倍数的增加，每个车辆类型匹配场景下的求解结果与最优解的最大差异百分比G_max和平均差异百分比G_ave有扩大趋势，主要原因是容量倍数较小时对应的可行解空间规模较小，因此算法的稳定性相对较强. 整体而言，不同容量倍数下解平均差异百分比的均值为1.63%，最大差异百分比的均值为3.17%，使用该算法求解所建立的模型具有较强的稳定性.

如图5所示，随着容量倍数在合理范围内增加，系统总成本呈现下降趋势，由 $n = 1.2$时的3315万元降至 $n = 2.9$时的最低值2 702万元，“大车容量为小车容量的2.9倍”为本案例最优的车辆种类搭配，因此提出的模型可以为实际车辆配置种类选取提供指导性意见. 当 $n = 1.2\sim 2.0$和 $n = 2.7$时，系统总成本下降较快；当容量倍数超过2.7后，稳定在2 710万元左右. 在考虑车辆替代救援可靠性的背景下，救援车辆类型的选择对系统总成本具有显著影响，合理的救援车辆类型匹配十分重要.

如图6所示，随着大车容量倍数的增加，大车配置数N_b和车辆配置总数N_t的减少趋势较明显，小车配置数N_s处于波动状态. 主要原因是大车单位购置成本随着容量倍数同步增长，为了在满足可靠度约束的同时进一步优化系统成本，模型偏向于减少大车数量. 图7中，N₁、N₂分别为1、2级设施数. 如图7所示，2种设施的数量关系由高级设施多于低级设施，逐渐变为低级设施多于高级设施，两者数量差异随着车辆容量倍数的增加而扩大并在后期趋于稳定. 在多数情况下系统内设施总数为7处，在 $n = 2.6$后稳定为6处.

图8中，C_v、C_f、C_s、C_p分别为车辆购置成本、设施建设成本、物资储存成本、需求不满足时的惩罚成本. 如图8所示，随着容量倍数的增加，设施建设成本显著减少，需求不满足时的惩罚成本增加。结合表3，对于各分项成本的走势具体分析如下.

1）车辆购置成本. 虽然2种车辆配置数均有减少趋势，但大车的单位购置成本增长，两者共同作用导致车辆购置成本仅在小范围内波动，总体保持稳定.

2）物资储存成本. 当 $n = 1.2\sim 2.4$时，物资储存成本整体呈现缓慢下降的趋势，主要原因是单位储存成本较高的第13号设施等级降低，且设施内2种车辆的配置数减少，物资储存能力下降. 当 $n = 2.4$时，单位储存成本较低的第7号设施中车辆配置总数增加，以较低的成本储存更多物资. 当 $n = 2.6\sim 3.0$时，系统设施总数较之前减少，原本单位储存成本较低的第12号设施取消，同时单位储存成本较高的第10号设施中车辆配置数增加，更多需求被分配至第10号设施，导致物资储存成本增长.

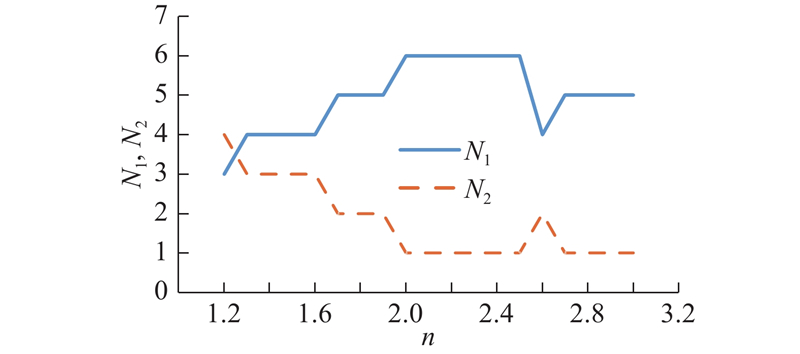
3）设施建设成本：作为系统总成本的重要组成部分，设施建设成本下降趋势明显，是导致系统总成本降低的主要原因. 当n=1.3、1.7和2.0时，设施建设成本显著降低，主要原因是在设施总量不变的情况下，低级设施逐渐增多同时高级设施逐渐减少. 当 $n = 2.1\sim 2.5$时，虽然部分设施位置选择有差异，但变化的设施位置对应的建设成本差异较小，故该阶段设施建设成本稳定. 当 $n = 2.6$时，系统内总设施数由7处减为6处，设施建设成本大幅降低.

4）预期需求不满足惩罚成本. 整体而言，系统预期需求不满足惩罚成本在波动中呈现上升趋势，主要原因是系统可靠度始终处于较高水平，远超过模型中的预期可靠度阈值，因此预期需求不满足惩罚成本的优化空间较小，进一步提高可靠度所需增加其他类成本的代价高于惩罚减小的收益.

将5.2节的求解结果与基于传统救援覆盖可靠度计算方法的结果进行对比，以验证考虑车辆替代作用的必要性. 为了保证合理性，对照组采用文献[23]的救援覆盖可靠度计算方法，其余参数均同前文；不同车辆容量倍数下的应急选址结果如表4所示. 利用2种可靠度计算方法得到的系统总成本对比如图9所示.

在不同的容量倍数下，采用所提可靠度计算方法时的系统总成本均优于对照组. 其中最高优化程度为11.83%，整体平均优化程度为9.01%，说明使用该方法对系统成本的优化具有普遍性. 从各分项成本来看，可以帮助模型有效减少设施建设、预期需求不满足惩罚和车辆购置3项成本，平均优化程度分别为8.10%、50.98%和10.32%.

对于设施建设成本，如表4所示，当 $n = 1.2\sim 1.8$时，使用对照组方法的模型偏向于在第13号或第14号设施处建立高等级设施，且在 $n = 1.20\sim 1.30$时系统设施总数为8，多于使用所提可靠度计算方法得到的结果；虽然在n>2.4后对照组结果中总设施数已下降为6处，但多数情况下高等级设施数仍为2，而基于所提可靠度计算方法的结果中，多数情况仅含1处高等级设施.

随着容量倍数的增加，需求不满足时惩罚成本的优化程度逐渐降低，由 $n = 1.3$时的64.76%降至 $n = 2.8$时的20.13%，即在大车容量倍数较小且配置成本较低时，考虑其替代能力的性价比更高，该阶段使用所提方法的优势更加明显；当大车容量倍数较大时，受单位购置成本的影响，削弱了大车替代作用对系统成本的影响，导致预期需求不满足惩罚成本优化程度降低. 对于车辆配置成本，在不同的容量倍数下，考虑车辆替代时的系统车辆配置总数均少于对照组. 综合来看，提出的可靠度计算方法对车辆的运用更加灵活，利用车辆容量关系，可以在有效减少设施等级、车辆配置数的同时，增加系统救援覆盖的可靠度.

（1）在考虑车辆替代救援可靠度的背景下，应急设施选址与配置是在系统成本与可靠度之间的博弈过程. 随着大车容量倍数在合理范围内增长，系统总成本呈现先下降后平稳的趋势，其中车辆购置和物资储存成本基本保持稳定，设施建设成本显著降低，预期需求不满足惩罚成本受限于车辆单位购置价格变化在可接受范围内增加.

（2）通过对车辆容量倍数的敏感性分析，建立的模型可以为实际救援车辆种类的匹配选择提供依据，在满足可靠度约束的前提下选取系统总成本较低的方案.

（3）与以往类似研究中使用的传统可靠度计算方法对比发现，考虑车辆替代作用在对系统总成本具有普遍优化作用的同时，较大幅度地提高了系统内的救援覆盖可靠度水平.

研究未来工作将在救援覆盖可靠度计算中考虑多个需求点同时发生突发事件的可能，进一步提升所建模型的实用性.