反射镜与支撑结构的粘接有3种工艺[3]. 第1种是“面”粘接方式,即反射镜背面与支撑板(背板)粘接,背板再连接到桁架;西班牙GemaSolar电站、美国CrescentDunes电站、北京延庆DAHAN电站采用了这种方式[4]. 第2种是“点”粘接方式,即桁架上的多个独立连接片与同一块反射镜粘接;美国Ivanpah电站、中控德令哈电站采用了这种方式[5]. 第1种粘接方式的反射镜与背板接触点多,通过控制背板的面形,可获取理想的反射镜面形. 采用这种方式粘接的定日镜质量较好且成形精度较高,但是背板的造价提高了整机的制造成本. 第2种粘接方式,由于粘接点个数有限,反射镜载荷集中在连接片粘接处,形成较大的局部应力,此外该方式的成形效果较差,适合于小型定日镜. 第3种是“线”粘接方式. 该方式将型材与反射镜背面粘接,利用型材(视为梁)的弯曲变形特性形成整机在高度方向的微弧形,各组型材在相对扭矩管上的高低错落分布,形成整机在宽度方向的微弧形. 采用这种粘接方式的定日镜其反射镜面形在现场装配时自然形成,避免了一系列机加工序,降低了生产成本. 此外,相比于第2种粘接方式,这种方式增加了粘接的接触面积,降低了反射镜的局部应力及其破损率.
为了提高“线”粘接型定日镜的光斑质量,本文研究了反射镜面形支撑结构优化的技术路线. 为了验证此方法,试制定日镜,进行了光斑实验,并与标准球面镜面形进行对比分析.
1. 面形规格和宽高比最优化
1.1. 光学因素
镜场一般呈环形布局,故定日镜投射到吸热器表面的光斑尺寸随当地时间、定日镜的分布位置而变化. 为了降低太阳辐射的溢出损失,要求光斑尺寸及方差最小.
式中:
图 1
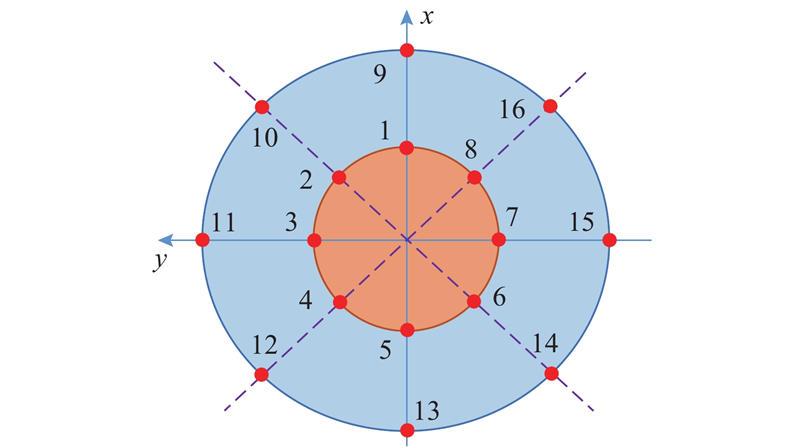
表 1 定日镜坐标表
Tab.1
| 编号 | x | y | z |
| 1 | 200 | 0 | 3 |
| 2 | 141 | 141 | 3 |
| 3 | 0 | 200 | 3 |
| 4 | −141 | 141 | 3 |
| 5 | −200 | 0 | 3 |
| 6 | −141 | −141 | 3 |
| 7 | 0 | −200 | 3 |
| 8 | 141 | −141 | 3 |
| 9 | 1 200 | 0 | 0 |
| 10 | 849 | 849 | 3 |
| 11 | 0 | 1 200 | 3 |
| 12 | −849 | 849 | 3 |
| 13 | −1 200 | 0 | 3 |
| 14 | −849 | −849 | 3 |
| 15 | 0 | −1 200 | 3 |
| 16 | 849 | −849 | 3 |
若镜场的太阳辐照度为1 000 W/m2,太阳像散误差为2.51 mrad,定日镜的镜面反射率为0.92,镜面误差为2.50 mrad,则可确定Ssun(x,y)和Es(x,y) [8].
根据式(1),可得每台定日镜投射到吸热器靶面上的光斑能流密度分布函数.
图 2
图 3
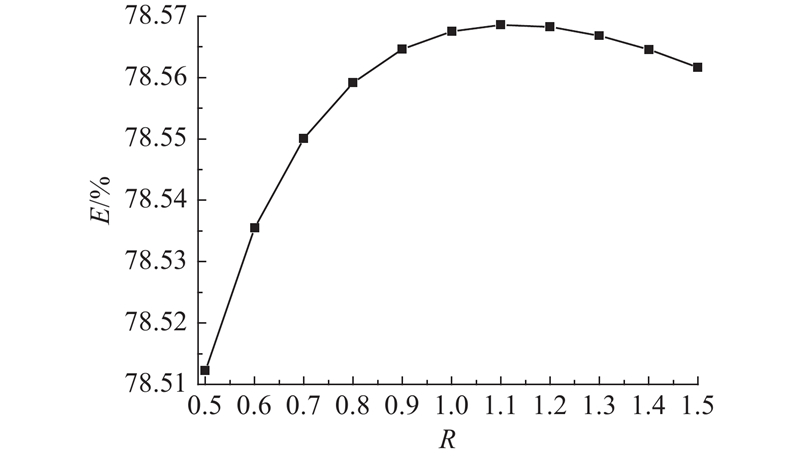
图 3 定日镜宽高比与平均光学效率曲线图
Fig.3 Curve of heliostat ratio and average optical efficiency
1.2. 风荷载因素
式中:
图 4
由式(2)可知,当A为定值时,Fx是zo的单调函数. 根据定日镜的结构特点可知,zo随宽高比的增大而减小, 即Fx随宽高比的增大而减小.
1.3. 结果分析
1)根据图2可知,镜场内圈的定日镜,当宽高比为0.8~1.3时,光斑尺寸平均值及方差最小,光斑质量最好.
2)根据图3可知,镜场外圈的定日镜,当宽高比为0.9~1.4时,光学效率最高.
3)根据式(2)可知,定日镜宽高比越大,表面的风荷载推力越小.
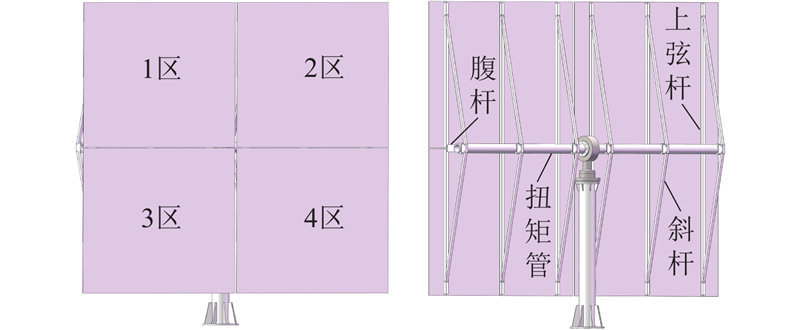
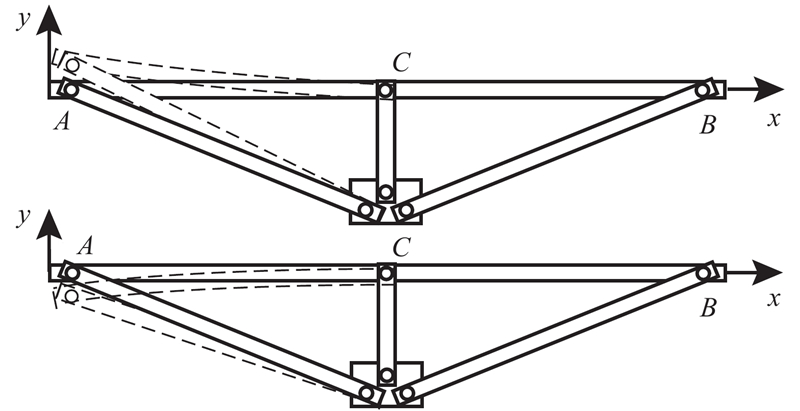
根据以上分析可知,当定日镜宽高比取0.9~1.3时,光斑质量和光学效率较优。若宽高比取1.2,即20 m2反射镜宽4.9 m、高4.1 m,并取镜厚4 mm. 如图4所示,定日镜子镜采用2×2布局,背面粘接6组平面桁架组件,各节点采用铰接方式,材料为Q235.
2. 上弦杆截面矩定义
图 5
表 2 定日镜支撑结构材料参数表
Tab.2
| 材料 | E/Pa | μ | ρm /(kg·m−3) |
| 钢 | 200×109 | 0.30 | 7 800 |
| 反射镜 | 7×1010 | 0.20 | 2 500 |
| 双面胶带 | 60 000 | 0.49 | 710 |
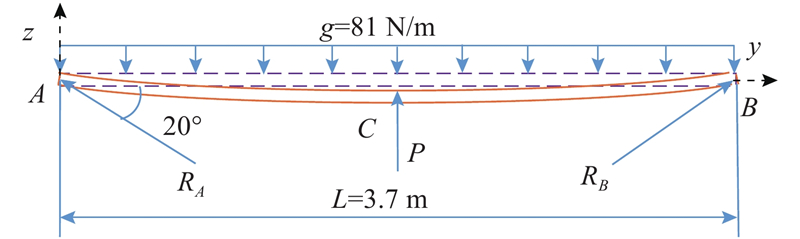
式中:E为弹性模量,z为上弦杆的挠度,T为纵向分力,I为截面矩.
由于上弦杆在A点的挠度z(0)=0、弯矩M(0)=0、剪力
式中:
由式(4)可知,C点的弯曲要素表达式为
式中:f0(u)、f1(2u)、
假设集中力P取100~200 N,I取2×104~1.5×105 mm4,则T<270 N,u<0.48,因而f0(u)>0.91,f1(2u)>0.92,
式(6)与杆简单弯曲的表达式一致[13],故可认为上弦杆变形近似于简单弯曲,以求取上弦杆截面矩最优解,再以此解校核纵向力对此杆弯曲要素的影响大小.
在简单弯曲模式下,上弦杆的挠曲线方程:
式(7)中,P和I为未知量,最优解是使得z(y)与半径500 m的圆弧最佳拟合,可以采用最小二乘法解算. 以0.01 m间距生成理想圆弧切向的数据集Ai={A1,A2,···,An},zdi是式(7)挠曲线上对应点的切向数据集. 设向量t=[P,I],则两者的残差函数和目标函数分别为
式中:fi(t)=zdi(t)−Ai,i=1,2,···,n.
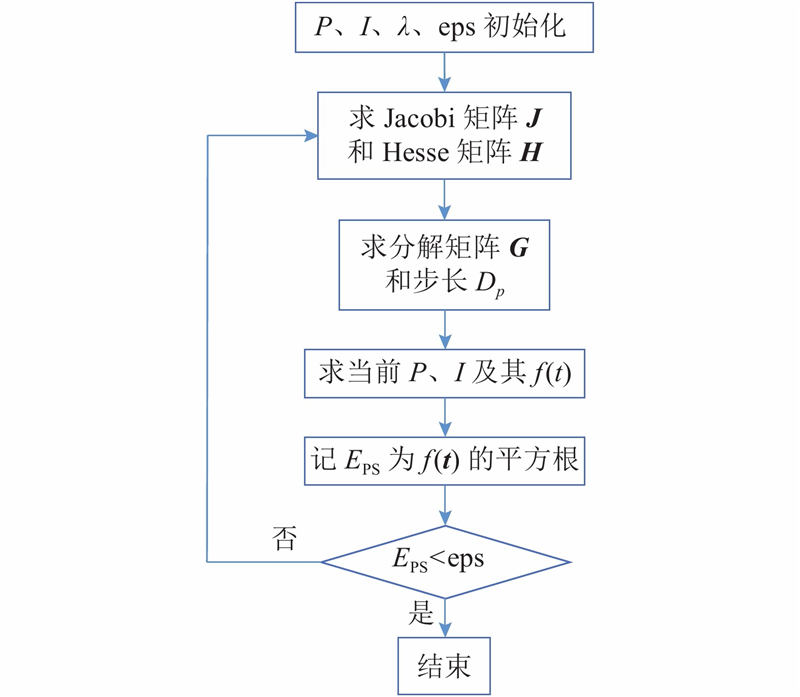
利用式(9)求t=[P,I ]的最小二乘最优解属于非线性问题. 该类解法中LM算法采用阻尼系数改变Hesse矩阵的性态,同时具有梯度法和牛顿法的优点,因而收敛速度快.
设式(8)中残差函数f(t)的Jacobi矩阵为J、Hesse矩阵为H. 定义LM算法的分解矩阵为
由于目标数据Ai具有单调性的特点,故阻尼系数λ取较大值1 000,可以达到较快的收敛速度,该算法的流程图如图6所示. 令初值P0=10 N,I0=1 000 mm4,允许误差eps=2×10−6,经过10次迭代计算,得最优值P=125 N,I=96 930 mm4,则f(t)的标准误差为0.12 mrad.
图 6
图 6 上弦杆截面参数优化算法流程图
Fig.6 Flow chart of section parameter optimization algorithm
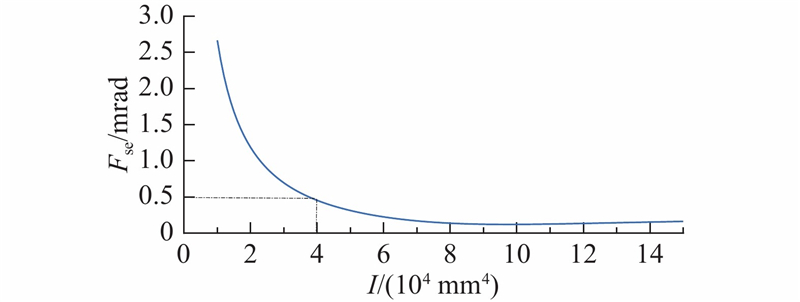
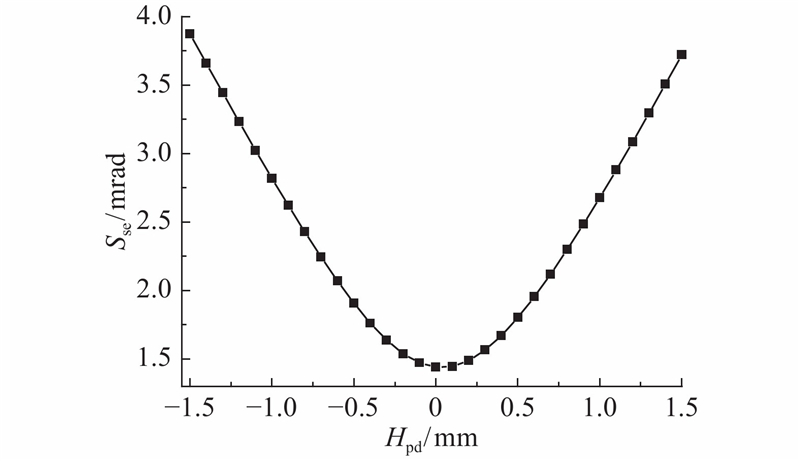
当上弦杆截面形状相似时,I越大则其截面积越大,将占用更多材料. 若I取(104,1.5×105),则得到f(t)的标准误差Fse曲线,如图7所示. 当标准误差取允许最大值0.5 mrad,则对应I为40 000 mm4,此时集中力为170 N.
图 7
根据图5可知,上弦杆的纵向分力T=370 N,由复杂弯曲辅助系数
当反射镜呈竖直姿态时,上弦杆与反射镜的粘接处集中承受反射镜的自重和风荷载推力. 由我国规范[14],工况取乡村地区,则式(2)中地面粗糙度指数α=0.15;由行业推荐检测标准[10],则式(2)中参考点高度zref=10 m、工作风速vref=14 m/s;由实验结论[11],则式(2)中风阻系数
图 8
3. 平面桁架布局定义
由于定日镜左、右侧对称,故平面桁架组若沿横向对称、沿纵向平行布局,将有利于发挥桁架结构的抗弯特性,这就产生了平面桁架组的最优间距问题,即布局定义. 由于反射镜属于薄板,抗弯刚度小,在重力的作用下,反射镜非粘接区域有下凹的趋势. 此外,由于定日镜的俯仰运动,将使得反射镜同时发生面形的微观变化. 所以平面桁架的布局影响面形误差大小,要求在整个俯仰行程范围内,面形标准误差最小.
有限元方法是结构分析的有力工具. 定日镜支撑结构材料参数如表2所示,添加铰接约束和重力负荷后,在Ansys中进行有限元计算,从计算结果可提取反射镜变形数据. 数据以离散点格式保存后,导入Matlab中拟合成曲面. 以50 mm间隔提取该拟合曲面的法向量集,这个法向量集与理想球面相应法向量的夹角集是当前模型的面形误差集,整机面形误差以它的标准误差表征.
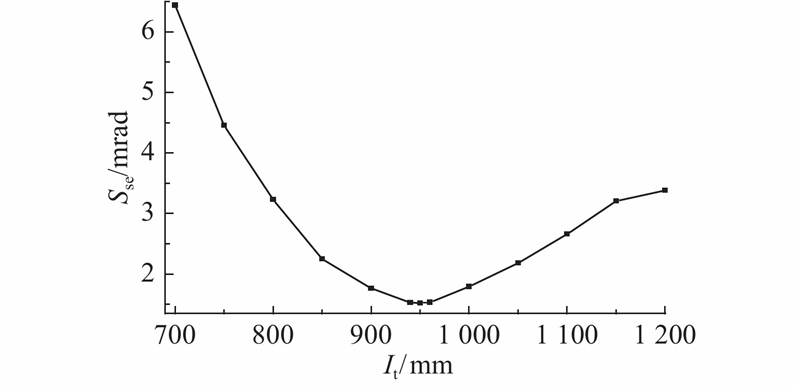
如图9所示为反射镜水平姿态时,平面桁架不同间距It布局时的面形标准误差Sse. 由图可知,当上弦杆间距为950 mm时,整机面形标准误差为最小值1.5 mrad.
图 9
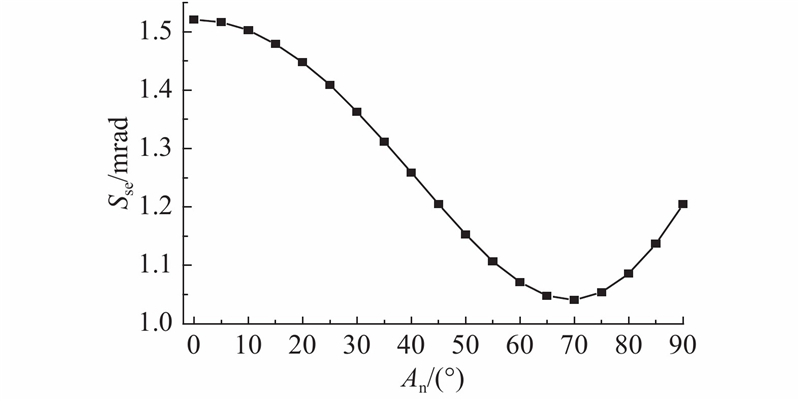
如图10所示为当平面桁架间距为950 mm,俯仰角An为0~90 °时,整机面形误差的变化曲线. 可知,随着俯仰角的增大,整机的面形标准误差先减小再增大,这是由于不同位姿时,反射镜的水平和竖直自重分力大小变化不同. 当俯仰角为0°时适宜进行平面桁架的布局,可校核最大整机面形标准误差,该模型的平面桁架布局取950 mm.
图 10
4. 反射镜强度校核
图 11
根据Kirchhoff假设可知,反射镜薄板的弯曲微分方程可以表示为:
式中:
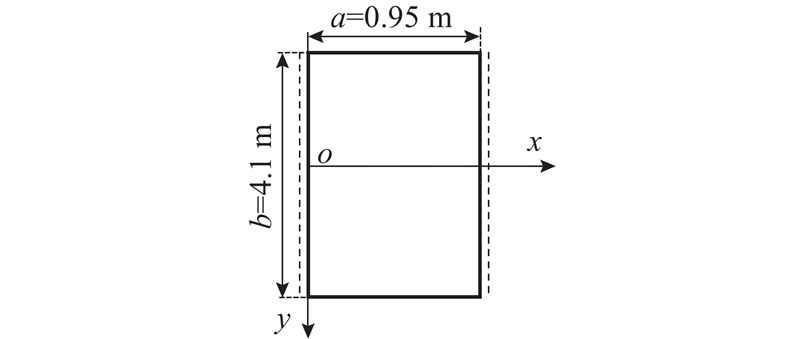
根据图11的反射镜的边界条件,式(11)可以采用莱维法表达.
反射镜薄板的另一对边是自由边,因而ω是偶函数,由薄板弯曲理论可知,式(12)可以进一步表达为
由式(13),解得
根据八面体应力理论[15]可知,单块反射镜薄板中心的应力最大,即中心点是反射面强度的校核点,即
图 12
图 12 2种方式下反射镜中心应力计算对比图
Fig.12 Comparison chart of central stress of mirror between two kinds of ways
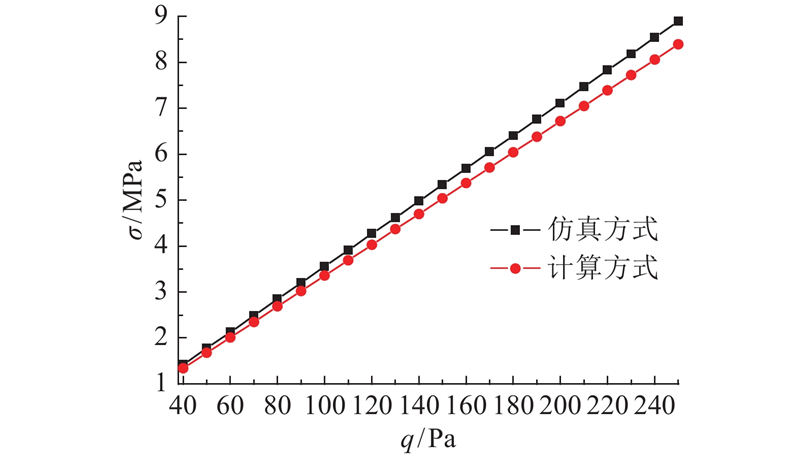
由图12可知,在一定区间范围内,镜面中心应力与横向载荷近似呈线性关系;理论计算方式与仿真结果的差值小于5.6%,所以式(15)得到的镜面中心应力与仿真方式下基本一致,用于强度校核时是可信的.
由于反射镜的超白玻璃材料的抗拉强度为41 MPa,重力、最大工作风速载荷作用下,反射镜整体模型的强度充分.
5. 机加工中工艺控制要点分析
平面桁架精度是整机面形精度的基础. 平面桁架的各部件通过铰接方式连接,但由于机加工不可避免的误差,将造成各部件上孔的尺寸和位置存在偏差. 上弦杆和斜杆的长度较大,机加工时易产生较大定位误差,因而是孔偏差的主要来源. 如图13所示,铰接点A或B的空间位置偏差导致平面桁架弯曲线形误差.
图 13
图 13 铰接孔误差导致的上弦杆弯曲线形误差
Fig.13 Bending alignment error of upper chord with hinge hole
图 14
图 14 孔位置偏差与面形标准误差曲线
Fig.14 Curve of hole position deviation and surface profile standard error
6. 定日镜面形实验
由上述形成平面桁架构建的定日镜面形支撑结构的设计技术路线,如图15所示.
图 15
6.1. 定日镜主要参数定义
在反射镜背面贴标记点,并利用三维扫描仪HSCAN331得到标记点的点云数据,以获取实验定日镜的实际面形. 点云数据在Geomagic环境中进行干扰区域删除、整体降噪和平滑等处理,以及坐标系的对齐等操作,使z轴垂直于镜面中心切平面,并以stl格式封装数据. 将此stl数据导入Matlab环境,以5 mm的数据间距,求取这个数据集的法向量集. 以半径74 m的球面相应点的法向量为真值,处理得到镜面整体的标准误差为2.7 mrad. 如图16所示.
表 3 实验定日镜主要参数
Tab.3
| 宽/mm | 高/mm | 面形 半径/m | 弦杆 材料 | 上弦杆截 面矩/mm4 | 上弦杆 间距/mm | 双面 胶宽/mm |
| 800 | 1 400 | 74 | 铝型材 | 3 000 | 380 | 20 |
图 16
如表4所示为光斑实验条件。在目标位置放置朗伯靶,并调整定日镜的位姿,使得光斑投射在朗伯靶内.
表 4 光斑实验条件
Tab.4
| 地理位置 | 时间 | 距离 | 朗伯靶方位 | 朗伯靶尺寸 |
| 北纬31.25东经121.47 | 2019-03-15 | 37 m | 正南高4 m | 1.5 m×1.5 m |
6.2. 定日镜光斑的仿真模型
单个定日镜的能流特性分析中,为了得到准确的结果,一般采用蒙特卡罗(Monte Carlo)法. 蒙特卡罗法是以概率统计理论为基础的数值计算方法,当样本容量足够大时能够得到高精度的计算结果.
定日镜光斑特性主要由入射光的能流密度分布、反射镜的面形及其误差分布这2个因素决定.
6.2.1. 太阳辐射分布模型
图 17
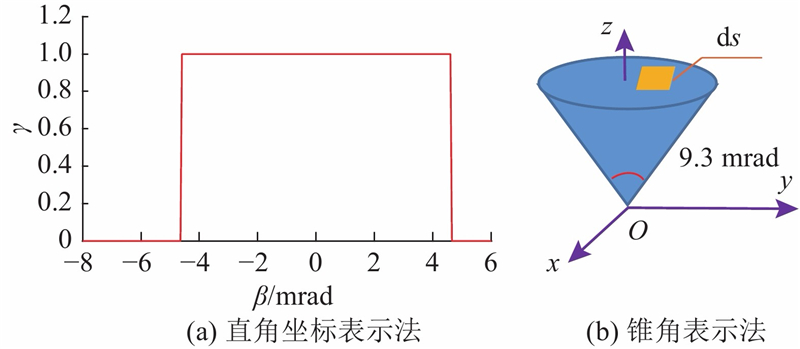
式中:γ(β)为圆锥角β的太阳辐射密度概率.
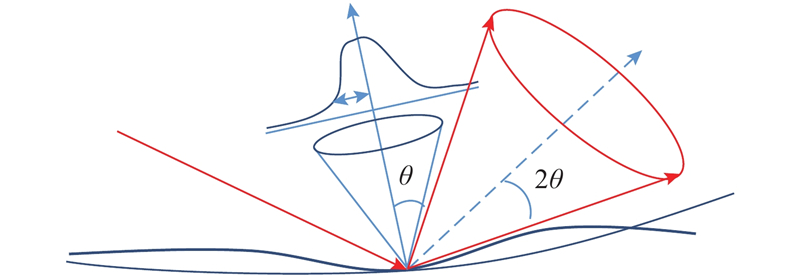
设图17右侧的坐标系oxyz中的ds是单位光锥球面上的一个微元,圆锥角为9.3 mrad,z轴是光锥的对称中心轴. 设oxyz相应的球坐标系中,该微元的方位角为
对于任意位置点的微元ds相等,则
式中:r1、r2为均匀随机变量,这时式(17)成立.
当某一时刻太阳方位角为
6.2.2. 斜率误差模型
图 18
斜率误差分布符合圆形高斯概率特性[17],即误差分布函数
式中:σ为斜率误差的标准偏差,本文取2.7 mrad.
式(20)不是以镜面法向误差作为自变量,故不能直接生成满足圆形高斯分布的镜面法向随机向量. 如果用球坐标方式表达斜率误差,则斜率误差的径向分量和轴向分量可独立表达. 径向误差在[0,2π)内均匀分布,即
式中:u1为[0,1.0]的均匀分布随机变量,
误差的轴向密度函数不能直接表达,须先对式(20)进行径向积分,以求取轴向分布函数为
故式(20)沿轴向分布的密度函数为
根据概率积分变换定理[19],式(22)运用反变换法可得
可表达为
式中:u2为[0,1.0]的均匀分布随机变量,θe为镜面法向误差数值.
式(21)、(23)是标准偏差为σ的反射面斜率误差在球面坐标系下的误差表达式. 与式(19)相似,反射面任一点的法向量进行相应旋转后,即符合误差圆形高斯分布特性.
6.2.3. 光斑能流密度计算公式
由光的反射定律可知,已知入射光方向矢量和镜面上反射点坐标,则根据几何运算可得吸热器上交点的坐标值. 如果认为每根入射光所带能量相同,则吸热器上任一区域的能流密度为
式中:Ni为该区域的入射光交点数,I为每根太阳光所带的能量,Si为该区域的表面积.
式(18)、(19)、(21)、(23)、(24),即为定日镜的光斑能流密度分布公式,记为SolHelioSpot模型.
6.3. 实验结果对比分析
图 19
图 20
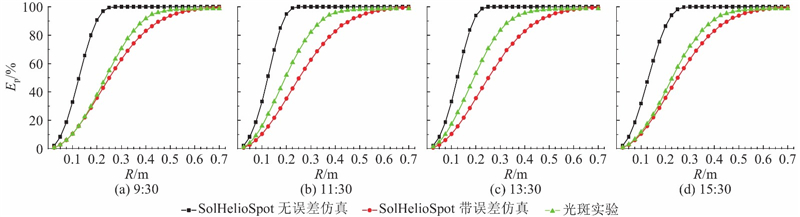
图 20 仿真和实验光斑沿径向的能量占比
Fig.20 Energy ratio of simulated and experimental spots along radial direction
图 21
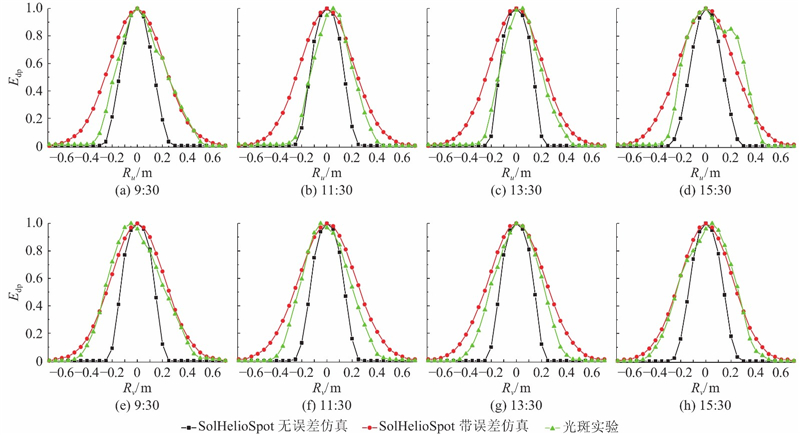
图 21 仿真和实验光斑沿u、v方向的能流密度概率
Fig.21 Flux density of simulated and experimental spots along u,v direction
1)由图16可知,面形标准误差分布总体较均匀,两侧的误差较大. 这是由于粘接位置处,成形过程中存在一定的内应力导致镜面发生非理想的微小变形.
3)由图20可知,相对于无面形成型误差的SolHelioSpot仿真光斑,实验方式和带面形成型误差仿真光斑的能量沿径向分布曲线较相似. 这是由于两者的面形标准误差相同. 相对于带面形成型误差的SolHelioSpot仿真光斑,随着时间的变化,实验方式光斑的能量径向分布率曲线存在一定变化. 这是由于实验定日镜的面形不是理想球面,误差分布不规则所致.
7. 结 论
(1)反射镜宽高比为1.2,能够得到最优的光学和效率属性,且节点通过铰接方式连接.
(2)上弦杆和斜杆呈小角度夹角,上弦杆的弯曲适用于简单弯曲理论求解,截面矩约为40 000 mm4,能够得到较优的弯曲线形.
(3)反射镜水平状态是面形误差最佳评价姿态,平面桁架组间距为950 mm,能够使得面形标准误差最小,且反射镜最大应力达标.
(4)机加工的控制要点是上弦杆和斜杆的开孔偏差,建议公差小于0.9 mm.
(5)按照上述技术路线,试制小定日镜,分析光斑形状、尺寸和能流分布特性,证实平面桁架构建的定日镜面形支撑方式,从原理和实践上都是可行的.
定日镜承受的载荷是一个随机过程,故面形支撑结构的激励响应是动态的,这是面形质量的影响因素,需要后续型号迭代中加以考虑,通过仿真和实验方式确定.
参考文献
塔式太阳能定日镜聚光成像建模与仿真
[J].
Modeling and simulation of sun image formed by CSP heliostat
[J].
塔式太阳能热发电站定日镜单元子镜面形研究
[J].
Finite element analysis and test on reflecting mirror surface shape of the heliostat facet
[J].
An analytic function for the flux density due to sunlight reflected from a heliostat
[J].DOI:10.1016/0038-092X(86)90078-2 [本文引用: 3]
One-point fitting of the flux density produced by a heliostat
[J].DOI:10.1016/j.solener.2010.01.019 [本文引用: 1]
定日镜反射板力学模型及设计方法
[J].
Mechanical model and design method for reflector plate of heliostat
[J].
On the analysis of an elliptical Gaussian flux image and its equivalent circular Gaussian flux images
[J].DOI:10.1016/j.solener.2011.03.010 [本文引用: 1]
Optical performance of a heliostat in the DAHAN solar power plant
[J].DOI:10.1016/j.egypro.2014.03.026 [本文引用: 1]