理解人脑的工作机制是21世纪最具挑战性的前沿课题. 脑功能连接刻画不同脑区之间神经元活动的动态关联性，为研究人脑的工作机制提供了崭新的视角^[1]. 功能磁共振脑成像(functional magnetic resonance imaging，fMRI)具有无创伤、可重复以及高空间分辨率等优点，是当前脑功能连接研究中重要的神经影像技术^[2]. 基于机器学习的fMRI脑功能连接分类由于可以提取fMRI数据中带有判别信息的脑功能连接特征，对脑疾病的早期诊断和病理研究具有重要意义，已成为脑疾病分类的研究热点^[3-4]. fMRI脑功能连接的高维小样本特性所引发的维灾难问题给脑疾病分类模型的构建提出了巨大挑战^[5].如何对fMRI脑功能连接进行特征归约已经成为脑疾病分类研究的重要课题.

目前，研究人员已经提出多种fMRI脑功能连接特征归约方法，这些方法大致可以分为fMRI脑功能连接特征提取和fMRI脑功能连接特征选择2类. 其中，特征提取方法通常利用变换或映射方式，将原始数据从高维特征空间投影到一个低维空间，从而降低特征维数. Mohanty等^[6]采用主成分分析方法(principal component analysis，PCA)将高维脑功能连接特征通过正交变换的方式变为低维脑功能连接特征. Shen等^[7]利用局部线性嵌入方法(locally linear embedding，LLE)将原始的脑功能连接特征映射到低维空间. 这类方法能够快速完成特征归约任务，但是得到的特征归约结果不易理解，不利于给出神经学的解释. 特征选择方法依据某种度量指标从特征集中挑选出拥有最优评价指标的特征子集，不改变特征的原始表达，因此能够保持原始特征的含义，有利于人们的理解和判断. Hamdi等^[8]使用最大相关最小冗余(minimal redundancy maximal relevance，mRMR)的特征选择方法从脑功能连接数据中获得重要的脑功能连接特征，为脑疾病的病理研究提供生物标志物. Cheng等^[9]利用双样本T检验方法从感兴趣的功能连接区域中选取差异显著的特征. Kong等^[10]使用非模型评价打分方法(F-score)衡量每个特征的分类判别能力，选择评分高的特征输入到深度神经网络进行脑疾病的分类. 利用这些已有的特征选择方法可以快速获得可解释的特征子集，但是它们只根据单个判别标准选择相对重要的脑功能连接特征，没有考虑特征之间的联系，容易影响得到的特征子集的分类判别能力.

粗糙集是Pawlak^[11]提出的用于处理不完整、不精确数据的数学工具. 该理论不需要任何先验知识，仅使用数据本身蕴含的信息就能分析特征之间的关系，现已被广泛应用到特征选择、数据挖掘、决策与分析等领域.付志耀等^[12]利用粗糙集得到计算机漏洞的强关联特征集. Liu等^[13]提出基于群体粗糙集的数据分析方法SRS，该方法通过观察粒子在搜索空间中正域的变化，有效地发现特征组合. Sarkheyli等^[14]利用粗糙集自动选择相关特征，实现实时态势识别. 近年来，随着数据环境的变化，已经涌现出不少粗糙集扩展模型，例如模糊粗糙集^[15]、决策粗糙集^[16]、邻域粗糙集^[17]等. 其中，邻域粗糙集(neighborhood rough set，NRS)结合邻域模型和粗糙集理论，根据实数空间中点的邻域来粒化邻域空间，能够处理连续型数据，有效避免离散化数据带来的损失. 作为有效的粗糙集扩展模型，邻域粗糙集目前在图像分割、基因选择、模式识别等众多领域得到了成功应用^[18-20].

鉴于脑功能连接是衡量不同脑区间神经元活动在时间上关联性的连续型数据，而邻域粗糙集可以直接处理连续型数据且具有强大的归约能力，可能在脑功能连接特征归约上发挥作用. 潜在的问题是现有的邻域粗糙集方法大多利用贪心算法搜索候选特征子集，这种方式比较容易陷入局部最优，影响得到的特征子集的分类判别能力. 近年来，基于群智能的搜索方法由于具有结构简单、鲁棒性强、易于与领域知识结合等优点，得到研究者的广泛关注. 鱼群算法作为新型群智能算法，采用自上而下的寻优模式，通过鱼群中各个体的局部寻优，使得全局最优解在群体中突现出来，是解决全局优化问题的有效工具^[21-23]. 若在利用邻域粗糙集进行脑功能连接特征归约时，使用鱼群算法对候选特征子集进行搜索，有望克服利用贪心算法搜索候选特征子集时易陷入局部最优的不足.

为了提高脑功能连接特征的分类判别能力，探索高效的邻域粗糙集方法，本研究提出基于鱼群算法的脑功能连接邻域粗糙集特征归约方法(feature reduction of neighborhood rough set based on fish swarm algorithm in brain functional connectivity). 该方法使用邻域粗糙集挖掘脑功能连接特征与标签特征之间的依赖度，并依据该信息初始化种群，然后采用综合特征子集依赖度和长度的适应度函数来评价个体的优劣，最后执行觅食、聚集、追尾、交叉和迁徙机制来优化种群的脑功能连接特征.

在邻域粗糙集中，邻域信息表由五元组 ${\rm{NIS}} = (U,A,V,f,\varepsilon )$表示. 其中， $U = \{ {u_1},{u_2}, \cdots ,{u_n}\} $为非空有限的样本对象集； $A$为非空有限的属性集； $V = \cup {V_a}$为所有属性值域的并集， ${V_a}$为属性 $a$的值域； $f:U \times A \to V$为信息函数，表示样本与其属性取值的映射关系； $\varepsilon $为邻域半径. 当属性集 $A$由条件属性集 $C$和决策属性集 $D$构成时，邻域信息表又称为邻域决策表 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$，简记为 ${\rm{NDS}} = (U,C,D,\varepsilon )$.邻域粗糙集的相关定义^[18-20]如下所示.

定义1 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中，样本集空间 $U \times U$关于条件属性集 $B = \{ {b_1},{b_2}, \cdots ,{b_m}\} \subseteq C$的邻域关系定义为

(1) ${{\rm{NR}} ^\varepsilon } = \left\{ {\left( {{u_i},{u_j}} \right) \in U \times U\left| {{d_B}\left( {{u_i},{u_j}} \right)} \right. \leqslant \varepsilon } \right\} .$

式中： ${d_B}({u_i},{u_j})$表示对象 ${u_i} \in U,{u_j} \in U$在条件属性集 $B$上的距离. ${d_B}({u_i},{u_j})$常用如下的欧氏距离来表示：

(2) ${d_B}\left( {{u_i},{u_j}} \right){\rm{ = }}{\left( {{{\sum\nolimits_{k{\rm{ = 1}}}^m {\left| {f\left( {{u_i},{b_k}} \right) - f\left( {{u_j},{b_k}} \right)} \right|} }^2}} \right)^{1/2}} .$

式中： $f\left( {{u_i},{b_k}} \right)$为对象 ${u_i}$在属性 ${b_k}$上的取值.

定义2 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中， ${u_i} \in U$在条件属性集 $B \subseteq C$上的邻域定义为

(3) $N_B^\varepsilon \left( {{u_i}} \right){\rm{ = }}\left\{ {{u_j}\left| {{u_j} \in U,} \right.{d_B}\left( {{u_i},{u_j}} \right) \leqslant \varepsilon } \right\} .$

定义3 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中， $\forall Z \subseteq U$关于条件属性集 $B \subseteq C$的邻域上近似集和邻域下近似集的定义分别为

(4) $\overline {{\rm{NB}} } _B^\varepsilon \left( Z \right) = \left\{ {\left. {{u_i}} \right|N_B^\varepsilon \left( {{u_i}} \right) \cap Z \ne \varnothing ,{u_i} \in U} \right\} ,$

(5) $\underline {{\rm{NB}} } _B^\varepsilon \left( Z \right) = \left\{ {\left. {{u_i}} \right|N_B^\varepsilon \left( {{u_i}} \right) \subseteq Z,{u_i} \in U} \right\} .$

定义4 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中，决策属性集D将对象集U划分为g个等价类： ${D_1},{D_2}, \cdots ,{D_g}$，则决策属性集D关于条件属性集 $B \subseteq C$的邻域上近似集和邻域下近似集定义分别为

(6) $\overline {{\rm{NB}} } _B^\varepsilon \left( D \right) = \cup _{i = 1}^g\overline {{\rm{NB}} } _B^\varepsilon \left( {{D_i}} \right) ,$

(7) $\underline {{\rm{NB}} } _B^\varepsilon \left( D \right) = \cup _{i = 1}^g\underline {{\rm{NB}} } _B^\varepsilon \left( {{D_i}} \right) .$

邻域下近似集也称为决策正域，记为 ${{\rm{POS}} _B}(D)$. 决策正域的大小反映分类问题在给定属性空间中的可分离程度.

定义5 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中，决策属性集D对条件属性集 $B \subseteq C$的依赖度的定义为

(8) $\gamma _B^\varepsilon \left( D \right) = {{\left| {{{{\rm{POS}} }_B}\left( D \right)} \right|}}/{{\left| U \right|}} .$

式中： $|U|$为集合内元素的个数.

定义6 　在 ${\rm{NDS}} = (U,C \cup D,V,f,\varepsilon )$中，若条件属性 $a \in C$且 $a \notin B$，那么属性a相对 $B \subseteq C$关于D的重要度定义为

(9) ${\rm{SIG}} \left( {a,B,D} \right) = \gamma _{B \cup a}^\varepsilon \left( D \right) - \gamma _B^\varepsilon \left( D \right) .$

受鱼类觅食行为的启发，李晓磊等^[21]提出在空间中寻求全局最优解的鱼群算法(fish swarm algorithm，FSA). 面对具体的优化问题，鱼群算法将每个人工鱼位置表示为求解问题的一个可行解，并定义适应度函数来衡量个体位置的优劣，然后执行觅食、聚集和追尾机制来搜索最优位置. 算法的主要机制如下.

1) 觅食机制. 鱼类在水中自由游动，可以快速地游向食物所在位置. 令X_i、Y_i为人工鱼 $i$的位置和适应度，X_j、Y_j为人工鱼 $j$的位置和适应度， ${R_{\rm{s}} }$为随机步长， ${{X}}_i^{{\rm{new}} }$为人工鱼 $i$的新位置，则人工鱼 $i$执行觅食机制的表达式如下：

(10) ${{X}}_i^{{\rm{new}} } = \left\{ \begin{array}{l} {{{X}}_i} + {R_{\rm{s}} } \dfrac{{{{{X}}_j} - {{{X}}_i}}}{{||{{{X}}_j} - {{{X}}_i}||}}, \; {Y_j} > {Y_i}; \\ {{{X}}_i} + {R_{\rm{s}} }{{I}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{其他}. \end{array} \right. $

式中：I为与X_i同维的单位向量.

2) 聚集机制. 鱼类在寻找食物的过程中，会自发地聚集在一起，以避免伤害，保证生存. 对于任意人工鱼 $i$，定义 $P'$为人工鱼 $i$视野范围内的人工鱼数目， ${{{X}}_{{\rm{cen}}}}$为人工鱼视野范围的中心位置，Y_cen为中心位置处人工鱼的适应度， $ \delta $为拥挤度. 若 ${{{Y_{\rm{cen} }}} / { P'}} > \delta {Y_i}$，即中心位置的适应度较高且该位置不太拥挤时，人工鱼 $i$向中心位置前进一步，否则执行觅食机制. 其中，人工鱼 $i$向中心位置 ${{{X}}_{{\rm{cen}}}}$前进的表达式如下：

(11) ${{X}}_i^{{\rm{new}} } = {{{X}}_i} + {R_{\rm{s}} } \frac{{{{{X}}_{{\rm{cen}}}} - {{{X}}_i}}}{{{\rm{||}}{{{X}}_{{\rm{cen}}}} - {{{X}}_i}{\rm{||}}}}; \; \frac{{{Y_{\rm{{\rm{cen}}} }}}}{{ P'}} > \delta {Y_i} .$

3) 追尾机制.当一条鱼发现某区域的食物丰富且该区域不太拥挤时，附近鱼类会尾随其后，快速到达该区域. 对于任意人工鱼 $i$，定义 ${{{X}}_{\max }}$为人工鱼 $i$视野内适应度最高的人工鱼i_max的位置. 若 ${{{Y_{\max }}} / { P'}} > \delta {Y_i}$，即当人工鱼 $i_{\rm{max}}$的适应度较高且该位置不太拥挤时，人工鱼 $i$向 ${{{X}}_{\max }}$位置前进一步，否则执行觅食机制. 其中，人工鱼 $i$向 ${{{X}}_{\max }}$位置前进的表达式如下：

(12) ${{X}}_i^{{\rm{new}} } = {{{X}}_i} + {R_{\rm{s}} } \frac{{{{{X}}_{\max }} - {{{X}}_i}}}{{{\rm{||}}{{{X}}_{\max }} - {{{X}}_i}{\rm{||}}}};\; \frac{{{Y_{\max }}}}{{ P'}} > \delta {Y_i} .$

NRSFSA利用邻域粗糙集与鱼群算法实现脑功能连接特征归约. 该算法的主要思路如下：建立脑功能连接数据的邻域决策表；依据功能连接特征与标签特征之间的依赖度初始化种群，并采用综合特征子集依赖度和长度的适应度函数来评价个体的优劣；执行觅食、聚集、追尾、交叉和迁徙5种机制来不断优化个体，直到获得最优或近似最优的脑功能连接特征子集为止. 其中，觅食、聚集和追尾机制是鱼群算法的核心优化机制，交叉和迁徙机制是为了改善鱼群算法搜索后期个体趋同、早熟现象而引入的新机制. 下面对NRSFSA算法涉及的主要步骤和机制进行详细介绍.

NRSFSA算法中每条人工鱼的位置代表一个候选的脑功能连接特征子集，用长度为m(m为脑功能连接特征总数)的二进制向量来表示，当第k个脑功能连接特征被选择时，该向量第k个分量的值为“1”，否则为“0”.

个体初始化的步骤如下：1）建立脑功能连接数据的邻域决策表 ${\rm{NDS}} = (U,C,D,\varepsilon )$；2）根据式(7)计算标签特征集 $D$关于每个脑功能连接特征 $a \in C$的邻域下近似集，进而计算标签特征集 $D$关于每个特征的依赖度；3）将所有的脑功能连接特征按照依赖度大小降序排列，选出前几个脑功能连接特征构成初始特征集合；4）依据初始特征集合来初始化种群. 具体来说，对于任意人工鱼个体，定义一个 $m$维的零向量，从初始集合中随机选择一个特征，若该特征位于 $m$维零向量的第 $k$个分量位置，则将该分量的值由“0”变为“1”，其余分量的值保持不变，完成个体的初始化.

对于脑功能连接特征归约问题，总希望得到分类能力较强且长度较短的特征子集，因此定义如下综合脑功能连接特征子集依赖度和特征子集长度的适应度函数：

(13) ${Y_i} = \left\{ \begin{array}{l} \!\!\!\left| C \right| \gamma _B^\varepsilon \left( D \right) + \left( {\left| C \right| - \left| B \right|} \right),\;\;\;\;\;\;\;\;\;\; \gamma _B^\varepsilon \left( D \right) \ne \gamma _C^\varepsilon \left( D \right) ; \\ \!\!\! \left| C \right| \gamma _B^\varepsilon \left( D \right) + \left( {\left| C \right| - \left| B \right|} \right) + \left| C \right|, \; \gamma _B^\varepsilon \left( D \right) = \gamma _C^\varepsilon \left( D \right) . \\ \end{array} \right.\!\!\!\!\!\!\!$

式中： $|C|$为原始脑功能连接特征总数； $|B|$为人工鱼i的位置的已选特征的数目， $ \gamma _B^\varepsilon (D)$为标签特征集 $D$对人工鱼i的位置的对应的特征子集B的依赖度.可以看出，当 $ \gamma _B^\varepsilon (D)$越大并且 $|B|$越小时，个体的适应度越高.

觅食机制使种群中每条人工鱼在自身周围随机游动. 该机制的实现过程如下：对于任意人工鱼 $i$，从 ${{{X}}_i}$中值为“0”的分量中随机选择一位，将其值由“0”变为“1”，并将变化后的新位置作为人工鱼i游动的候选位置. 如果该位置的适应度优于原来人工鱼i的适应度 ${Y_i}$，则将人工鱼i移动至该位置，得到人工鱼i的新位置，否则重复以上过程，若在 $\mu $次尝试后仍无法满足前进的条件，则从 ${{{X}}_i}$中值为“1”的分量中随机选择一位，将其值由“1”变为“0”，即随机删除一个特征得到人工鱼i的新位置 ${{X}}_i^{{\rm{new}} }$.

在聚集机制中，鱼群中心对鱼个体具有一定的吸引力，当鱼群中心位置的适应度较高且不太拥挤时，个体使用差异移动规则向鱼群中心聚集. 在这一过程中，视野范围的确定、个体之间距离的度量、中心位置的定义以及差异移动规则的确定是实现该机制的关键.这4个关键部分的实现方法如下所示.

1)视野范围.为了平衡算法的全局搜索能力与局部搜索能力，使用自适应的线性函数自动调整视野范围，表达式如下：

(14) ${G_q} = G - Wq/Q .$

式中： ${G_q}$为当前视野范围， $G$为最大视野范围， $Q$为最大迭代次数， $W$为视野权重， $q$为当前迭代次数. 在鱼群优化的早期阶段，视野范围相对较大，可以增加算法的全局搜索能力；随着迭代的进行，视野范围逐渐减小，有利于提高算法的局部搜索能力.

2)鱼个体之间的距离.鉴于脑功能连接的稀疏性，使用Jaccard距离来衡量鱼个体之间的距离，具体表达式如下：

(15) ${\rm{dis}}\;\left( {{{{X}}_i},{{{X}}_j}} \right) = \frac{{\left| {E \cup H} \right| - \left| {E \cap H} \right|}}{{\left| {E \cup H} \right|}} .$

式中：E、H分别为个体 ${{{X}}_i} = \left[ {{x_{i,1}},{x_{i,2}}, \cdots ,{x_{i,k}}, \cdots ,{x_{i,m}}} \right]$和个体 ${{{X}}_j} = [{x_{j,1}},{x_{j,2}}, \cdots ,{x_{j,k}}, \cdots ,{x_{j,m}}]$对应的特征子集， $E = \{ \left. k \right|{x_{i,k}} = 1,1 \leqslant k \leqslant m\} ,H = \{ \left. k \right|{x_{j,k}} = 1,1 \leqslant k \leqslant m\} $.

3)中心位置.令 $X = \left\{ {{{{X}}_1},{{{X}}_2}, \cdots ,{{{X}}_i}, \cdots ,{{{X}}_{^{P'}}}} \right\}$为 $P'$条人工鱼位置组成的群体. 定义鱼群的中心位置 ${{{X}}_{\rm{cen} }} = \left[ {{x_{{\rm{cen} } ,1}},{x_{{\rm{cen} } ,2}}, \cdots ,{x_{{\rm{cen} } ,k}}, \cdots ,{x_{{\rm{cen} } ,m}}} \right]$表达式如下：

(16) ${x_{{\rm{cen}},k}} = \frac{{\displaystyle\sum\nolimits_{i = 1}^{P'} {{x_{i,k}}} }}{{P'}},\; {x_{{\rm{cen}},k}} = \left\{ \begin{array}{l} 1, \; {x_{{\rm{cen}},k}} \geqslant 0.5; \\ 0, \; {x_{{\rm{cen}},k}} < 0.5 . \\ \end{array} \right. $

式中： ${x_{{\rm{cen} } ,k}}$为中心位置 ${{{X}}_{{\rm{cen}}}}$第 $k$个分量的值， ${x_{i,k}}$为人工鱼位置 ${{{X}}_i}$中第 $k$个分量的值.

4）差异移动规则. 当人工鱼i向中心位置 ${{{X}}_{{\rm{cen}}}}$移动时，定义一个m维零向量作为人工鱼i移动后的新位置 ${{X}}_i^{{\rm{new}} }$，比较 ${{{X}}_i}$和中心位置 ${{{X}}_{{\rm{cen}}}}$每个分量的值，对于值相等的分量，新位置相应分量的值直接取自 ${{{X}}_i}$；根据式(9)计算每个差异分量对应的特征相对于新位置的重要度，从中选择重要度最大的特征，若该特征的重要度为正值，将新位置相应分量的值由“0”变为“1”，确定一个差异分量的值. 之后重新计算其他差异分量的特征相对于新位置的重要度，以相同的方式确定下一个差异分量的值，重复以上过程，直到新位置中所有差异分量的值都被确定为止.

聚集机制的实现过程描述如下：对于任意人工鱼i，根据式(14)确定 ${{{X}}_i}$的视野范围；根据式(15)衡量当前位置 ${{{X}}_i}$与其他个体之间的距离，得到 ${{{X}}_i}$视野范围内的人工鱼个体，进而根据式(16)确定中心位置 ${{{X}}_{{\rm{cen}}}}$. 如果中心位置 ${{{X}}_{{\rm{cen}}}}$适应度较高且不太拥挤，比较 ${{{X}}_i}$与中心位置 ${{{X}}_{{\rm{cen}}}}$之间各分量的值，依据差异移动规则使人工鱼i向中心位置移动，得到人工鱼i的新位置 ${{X}}_i^{{\rm{new}} }$，否则执行觅食机制.

追尾机制是为了使种群中每条人工鱼朝着适应度较高个体所在的方向移动. 该机制的实现过程描述如下：对于任意人工鱼 $i$，根据式(14)确定 ${{{X}}_i}$的视野范围，并计算所有个体的适应度，找到当前种群的最优个体；根据式(15)衡量 ${{{X}}_{\max }}$与种群其他个体之间的距离，求得 ${{{X}}_{\max }}$视野范围内人工鱼个体的数目. 如果 ${{{X}}_{\max }}$的适应度较高且不太拥挤，比较 ${{{X}}_i}$与 ${{{X}}_{\max }}$中各分量的值，依据差异移动规则使人工鱼i向 ${{{X}}_{\max }}$移动，得到人工鱼i的新位置 ${{X}}_i^{{\rm{new}} }$，否则执行觅食机制.

在算法优化后期，种群多样性严重丧失，使得个体容易陷入局部最优. 在算法中执行交叉机制，可以生成新的个体，增加种群的多样性. 该机制的实现过程如下：对于任意人工鱼位置 ${{{X}}_i}$，在种群中随机选择另一人工鱼位置 ${{{X}}_j}$，根据式(17)、(18)对2个个体的每个分量进行交叉操作，最终得到新位置 ${{{{X}}}_i'}{\text{、}}{{{{X}}}_j'}$. 如果新位置的适应度高于原来位置的适应度，用新位置替换原来位置，否则保留原来位置不变.

(17) ${x'_{i,k}} = \left\{ \begin{array}{l} {x_{j,k}}, \; r < \lambda ||l = k; \\ {x_{i,k}}, \; \text{其他}. \\ \end{array} \right. $

(18) ${x'_{j,k}}{\rm{ = }}\left\{ \begin{array}{l} {x_{i,k}}, \; r < \lambda ||l = k; \\ {x_{j,k}}, \; \text{其他}. \\ \end{array} \right. $

式中： ${x'_{i,k}}{\text{、}}{x'_{j,k}}$分别为新位置 ${{{{X}}}_i'}$和新位置 ${{{{X}}}_j'}$第 $k$个分量的值； ${x_{i,k}}{\text{、}}{x_{j,k}}$分别为位置 ${{{X}}_i}$和位置 ${{{X}}_j}$第 $k$个分量的值； $ \lambda $为交叉概率； $ r$为 $[0,1.0]$的随机数； $l$为 $[1,m]$的随机整数，它确保新位置 ${{{{X}}}_i'}$、 ${{{{X}}}_j'}$分别从 ${{{X}}_j}$、 ${{{X}}_i}$中获得至少一个分量值.

在鱼类的觅食活动中，那些找不到足够食物的个体可能会迁徙到其他地方去寻找更多的食物.因此，执行迁徙机制剔除搜索性能较低的个体，提高算法的全局搜索能力.该机制的实现过程如下：将种群个体按照其适应度连续不变的次数降序排列，移除连续 $M$次迭代后适应度仍未提高的个体；假设移除的个体数量为 ${P_M}$，则重新随机初始化 ${P_M}$个新个体，保证种群规模不变；比较种群个体和公告牌最优个体的适应度，如果两者相等，将该个体随机移动一步，帮助其跳出局部最优.

NRSFSA算法利用邻域粗糙集与鱼群算法实现脑功能连接特征归约.核心思想是首先建立脑功能连接数据的邻域决策表，计算每个特征与标签特征之间的依赖度信息，初始化种群，并综合特征子集的依赖度和特征子集的长度来评价个体，接着执行觅食、聚集、追尾、交叉和迁徙机制不断优化种群. 具体流程如算法1所示.

算法1.NRSFSA算法

输入：脑功能连接

输出：脑功能连接特征子集

1. 参数设置. 设置种群规模 $P$、拥挤度 $\delta $、尝试次数 $\mu $、最大视野范围 $G$、视野权重W、迁移阈值M、交叉概率λ、最大迭代次数 $Q$、最优解保持不变的最大迭代次数 $T$；

2. 初始化种群. 根据式(8)计算每个特征的依赖度，选出排列在前的特征初始化种群；

3. 优化种群. 根据式(13)计算每条人工鱼个体的适应度；将种群最优个体及其适应度 ${Y_{{\rm{best}} }}$记入公告牌；开始的迭代次数 $q = 1$；最优人工鱼个体适应度不变的次数 $t = 1;$

While $q \leqslant Q \; \& \; t \leqslant T$ do

For $i = 1$ to $P$ do

对个体尝试：执行觅食、聚集、追尾机制；执行3种机制中最好的机制，更新个体位置；执行交叉机制；

End for

执行迁徙机制，生成新鱼群；计算鱼群中最优个体及其适应度 ${Y_{\rm{g}} }$；

If ${Y_{\rm{g}} } > {Y_{{\rm{best}} }}$

更新公告牌的最优个体及其适应度； $t = 0;$

Else

$t = t + 1;$

End If

$q = q + 1;$

End While

4. 输出公告牌最优解表示的脑功能连接特征子集.

基于算法1的描述，对NRSFSA进行时间复杂度分析：在初始化过程中，计算所有特征依赖度的时间复杂度为 $O({m^2} {n^2})$，个体编码的时间复杂度为 $O(P m)$，则初始化种群的时间复杂度为 $O({m^2} {n^2} + P m)$，其中 $n$为被试样本数；在种群优化过程中，主要须重新计算脑功能连接特征的重要度，这最多须花费 $O({m^2} {n^2})$的计算时间，因此种群优化的时间复杂度为 $O(P {m^2} {n^2})$. 综上所述，算法的时间复杂度为 $O({m^2} + {n^2} + P m + Q P {m^2} {n^2}) \approx $ $O(Q P {m^2} {n^2})$.

实验在处理器为Intel (R) Core (TM) i3 CPU 3 120M 2.50 GHz、RAM为4.00 G、操作系统为Windows 10的环境下，利用Matlab2017a运行工具编写的Matlab代码完成.

使用如下3种脑疾病的静息态fMRI数据：阿尔茨海默症神经影像学联盟在平台上发布的ADNI数据集(http://www.adni-info.org)、注意力缺陷多动症联盟提供的ADHD数据集(http://fcon_1000.projects.nitrc.org/indi/adhd200)和孤独症脑成像数据交换联盟发布的ABIDE数据集(http://fcon_1000.projects.nitrc.org/indi/abide/). 3种脑疾病静息态fMRI数据的具体信息如表1所示. 其中，ADNI数据集含有阿尔茨海默症(AD)、认知功能障碍症(MCI)和正常被试(NC)3组被试，ABIDE和ADHD数据集均含有2组被试，分别为孤独症(ASD)组和正常(NC)组、注意力缺陷多动症(ADHD)组和正常 (NC)组. 由于将ADNI数据集的3组被试两两对照，本研究对比实验中共有ABIDE、ADHD、NC-AD、NC-MCI和AD-MCI这5组数据.

在实验中，首先对3种脑疾病静息态fMRI数据进行预处理，得到fMRI脑功能连接数据. 具体来说，对于每个fMRI数据集下的每组被试，利用AAL(anatomical automatic labeling)模板将大脑划分为90个脑区，然后分别计算2个脑区之间平均时间序列的皮尔森相关系数，得到 90×90的功能连接矩阵，其中每个元素表示相应2个脑区之间的功能连接强度. 因为功能连接矩阵是对称矩阵，所以原始的不同脑功能连接特征数为4 005.

特征归约的评价标准主要有两方面：归约所得脑功能连接特征的数目；特征子集的分类判别能力.利用SVM分类学习算法来检验脑功能连接特征子集的分类判别能力，SVM参数值由libsvm工具箱提供的网格搜索策略自适应确定，并使用如下4种常用的分类评价指标：准确率(accuracy, Acc)、精确率(precision, Pr)、召回率(recall, Re)以及F度量(F-measure, Fm). 定义如下：

(19) ${\rm{Acc}} = {{\left({\rm{TP}} + {\rm{TN}}\right)}}/{{\left({\rm{TP}} + {\rm{FP}} + {\rm{TN}} + {\rm{FN}}\right)}},$

(20) $\Pr = {{{\rm{TP}}}}/{{\left({\rm{TP}} + {\rm{FP}}\right)}},$

(21) ${\rm{Re}} = {{{\rm{TP}}}}/{{\left({\rm{TP}} + {\rm{FN}}\right)}},$

(22) ${\rm{Fm}} = {{2 {\rm{\Pr}} \times {\rm{Re}} }}/{{\left(\Pr + {\rm{Re}} \right)}} .$

式中：TP为将患者预测为病人的数目；TN为将正常人预测为正常人的数目；FP为将正常人预测为病人的数目；FN为将患者预测为正常人的数目. 准确率、精确率、召回率以及F度量4项指标越高，特征子集的分类判别能力越强.

NRSFSA算法在5组数据上的参数设置如下： $ P = 150$、 $ \delta {\rm{ = 0}}{\rm{.9}}$、 $ T = 30$、 $ \mu {\rm{ = 16}}$、 $ Q = 200$、 $ G = 0.8$、W = 0.4、 $ M = 4$、 $ \lambda = 0.75$. 此外， $\varepsilon $决定数据操作的粒度，对脑功能连接数据的分布较敏感，因此 $\varepsilon $在ABIDE、ADHD、AD-NC、NC-MCI和AD-MCI数据上的设置各不相同，分别为0.450、0.425、0.350、0.400、0.625. 对算法参数设置的分析如下.

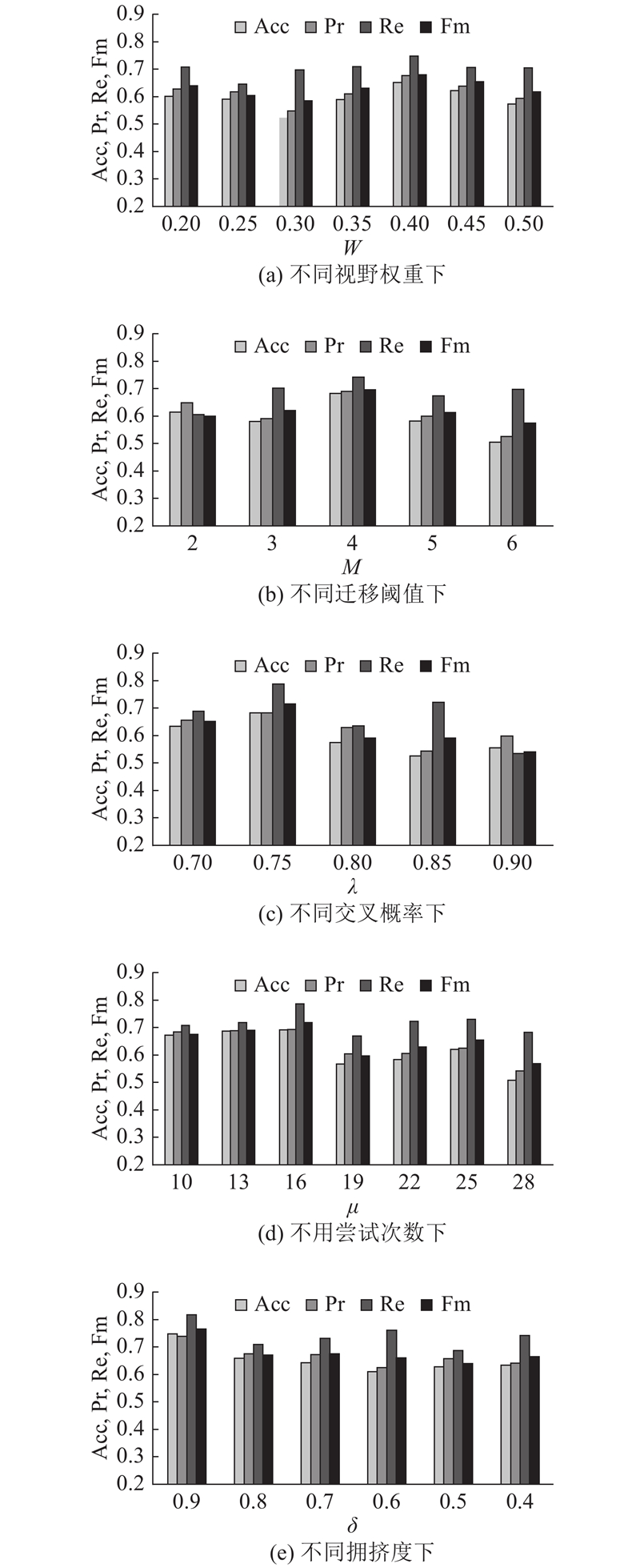
在数据上测试视野权重、迁徙阈值、交叉概率、尝试次数及拥挤度对算法的影响. 在测试过程中保持其余参数不变，仅变动待测试参数，结果如图1所示.具体来看，参数W影响算法全局搜索与局部搜索之间的平衡，随着W的增加，Acc、Pr、Re、Fm总体呈现先增后减的趋势，在 $ W = 0.4$时取得较好的结果，因此算法最终选定 $ W = 0.4$. 参数 $ M$影响算法的迁徙机制，当参数设置较小时，个体随机初始化的概率会提升，在一定程度上限制其搜索能力；当参数设置较大时，种群个体后期容易趋同. 当 $ M= {\rm{ 4}}$时，表征特征子集分类能力的4项指标最高. 参数 $ \lambda $影响算法的交叉机制，当 $ \lambda = 0.75$时，算法在4项指标上取得较好的值，因此本研究设置 $ \lambda = 0.75$. 参数 $ \mu $影响算法执行觅食机制的尝试次数，当 $ \mu = {\rm{ 16}}$时，算法得到的特征子集的分类判别能力最强，因此设置 $ \mu {\rm{ = 16}}$. 同理，依据图1(e)的结果，设置 $ \delta {\rm{ = 0}}{\rm{.9}}$.其他参数的取值也采用此方法选取，不再具体列出.

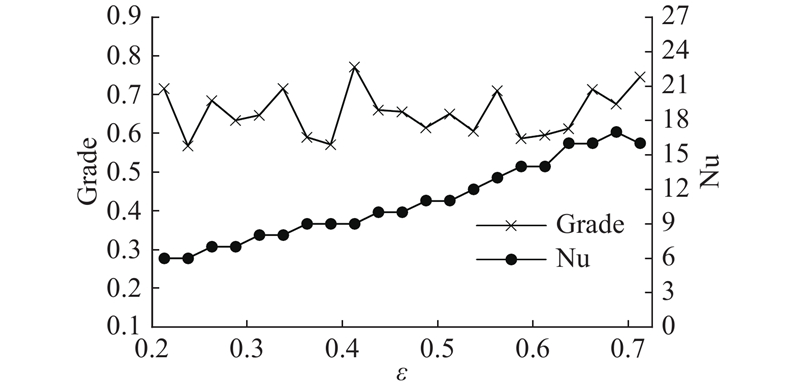
经过初步实验得到每个数据集上 $ \varepsilon $的取值区间，然后以步长为0.025在每个邻域半径下进行特征归约. NRSFSA算法在不同邻域半径下的实验结果如图2所示. 图中，Grade为准确率、精确率、召回率、F度量的平均值，Nu为特征数量.可以看出，随着 $ \varepsilon $的增加，特征数量总体呈上升趋势，在 $ \varepsilon {\rm{ = 0}}{\rm{.4}}$时，算法得到Grade较高并且数量较少的脑功能连接特征. 本研究综合特征的分类判别能力和特征的数量，在NC-MCI数据集上设置 $ \varepsilon {\rm{ = 0}}{\rm{.4}}$. 同理，以相同方式确定NRSFSA算法在其他数据集上的邻域半径参数.

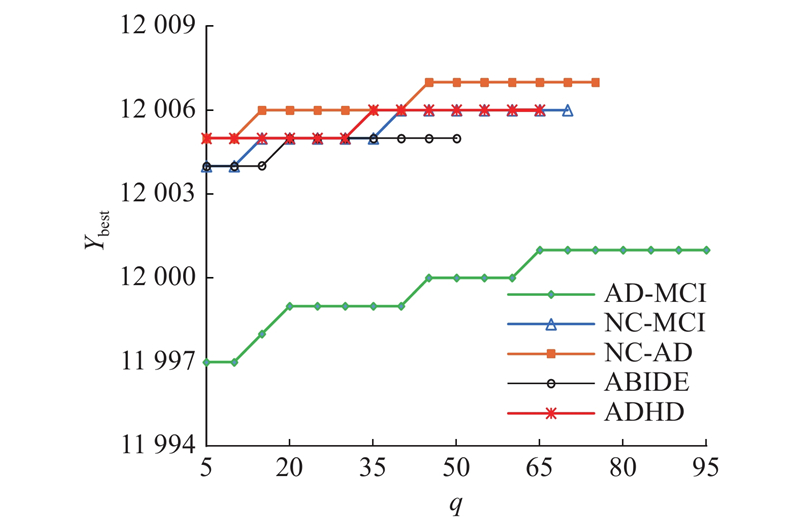
NRSFSA算法通过鱼群逐步迭代获得最优或最近最优的脑功能连接特征子集. 为了展示算法的收敛特性，提供NRSFSA算法在5组fMRI脑功能连接数据上的迭代过程，如图3所示.可以看出，随着迭代次数的增加，纵坐标的适应度也逐步提高，最后算法收敛于最优值或近似最优值.

为了验证NRSFSA算法的有效性，将NRSFSA与PCA、LLE、mRMR、NRS、F-score、SRS以及使用邻域粗糙集替代SRS中粗糙集的SNRS共7种方法进行对比.

如表2所示为8种方法在5组实验数据集上的特征归约结果. 须注意的是，SRS、SNRS、NRS、PCA、LLE方法在进行特征归约时，能够自动得到一个具体的Nu指标；mRMR、F-score特征归约方法使用互信息和F-score值衡量脑功能连接特征的重要度，并依据重要度将脑功能连接降序排列，得到一个脑功能连接特征的排序列表. 本研究参照相关文献的实验设置，选取与NRSFSA算法所得数目相同的前Nu个脑功能连接特征作为归约结果^[24-25].

由表2可知，在ADHD数据集上，与其他7种算法相比，NRSFSA算法获得的脑功能连接特征数最少，并且在Acc、Pr、Re和Fm指标上的取值最优. 在ABIDE数据集上，NRSFSA算法获得10个脑功能连接特征，在Acc和Pr上均取得第2的成绩，在Re和Fm上均取得第3的成绩；由于在阿尔兹海默症的数据集上出现了多个适应度相同的候选脑功能连接特征子集，NRSFSA算法的输出具有一定的随机性，性能有所下降，不过实验结果相比于其他算法也大多排名前3. 具体来说，在NC-AD数据集上，NRSFSA算法在Pr指标上排名第2，在Acc、Re和Fm指标上均排名第3；在NC-MCI数据集上，NRSFSA算法在Acc、Pr、Fm指标上均排名第3，在Re指标上以较小差距排名第4；在AD-MCI数据集上，NRSFSA算法在Re和Fm上分别取得第2、3的成绩，在Acc和Pr指标上的结果有所下降，分别取得第5、6的成绩. NRSFSA算法在NC-AD、NC-MCI、AD-MCI数据集上获得的特征数均是最少的. 此外，为了更好地展示NRSFSA算法在fMRI脑功能连接特征归约方面的整体性能，在表格最后一部分展示了每个算法在5组数据集上的平均指标值. 从整体平均值来说，与其他7种特征归约算法相比，NRSFSA算法不仅获得的脑功能连接特征数最少，而且在准确率、精确率、召回率和F度量4项指标上均取值最优.

如表3所示为8种算法在每个数据集上运行所消耗的时间. 由于在不同数据集上算法消耗的时间不同，根据平均结果对算法的时间性能进行整体分析.可以看出，相较于PCA、LLE、F-score等特征归约方法，NRSFSA、SRS、SNRS这些迭代类特征归约方法的运行时间较长.在NRSFSA、SRS、SNRS算法中，本研究所提出的算法在时间性能上排名第3. 这是由于算法在迭代时须重新计算鱼个体差异位置的特征重要度，时间复杂度较高. 虽然本研究算法在时间性能上表现一般，但是相比于其他算法，NRSFSA算法的特征归约能力较强，得到的脑功能连接特征子集的分类能力较好. 总体而言，NRSFSA算法在高维的fMRI脑功能连接数据中具有一定的应用价值.

为了探讨NRSFSA算法得到的脑功能连接特征代表的生物意义，首先将其放回原始的功能连接矩阵中，得到已选特征的脑功能连接矩阵；通过对照ALL模板，发现NRSFSA算法获得的脑功能连接特征所涉及的脑区包括后扣带回、背外侧前额叶、角回和海马等. 在大脑的神经活动中，后扣带回是记忆系统的重要组成部分，参与情景记忆的信息加工过程. 位于顶下小叶的角回属于视野语言中枢，具有理解看到的符号和文字的作用. 海马位于大脑丘脑和内侧颞叶之间，属于边缘系统的一部分，主要负责长时记忆和空间定位等功能. 这些脑区均属于大脑默认网络(default mode network, DMN)，目前已有研究发现在阿尔兹海默症、注意力缺陷多动症、自闭症等患者的大脑中均存在DMN的异常活动^[26-27]. 由上可知，NRSFSA算法可以有效降低脑功能连接数据的维度，获得带有判别信息的脑功能连接特征.

利用邻域粗糙集的特征归约能力与鱼群算法的全局寻优能力，提出新的脑功能连接特征归约方法NRSFSA. 该方法基于邻域粗糙集的依赖度评价脑功能连接特征子集和标签的相关性，并使用鱼群的觅食、聚集、追尾、交叉和迁徙机制来不断搜索较好的特征子集.在3种脑疾病fMRI数据上的实验表明，所提方法不仅能降低脑功能连接的特征维度，而且能获得分类判别能力较强的脑功能连接特征.该方法的研究，不仅拓展了鱼群算法和邻域粗糙集理论的应用领域，而且对其他高维数据的分析与研究也有一定的借鉴意义.

本研究是邻域粗糙集在脑功能连接特征归约上的新探索.由于脑功能连接数据特征维度较高，又采用种群迭代的方式搜索候选特征子集，新算法的效率不高.如何基于邻域粗糙集定义更好的适应度函数，并融合更多的生物信息来提高鱼群算法搜索特征子集的效率，进而提高脑功能连接特征的分类判别能力是未来工作的主要方向.