可破坏拆卸须保证目标再制造毛坯的完整性和高效拆解,国内外的学者对此从不同角度进行了深入研究.
在破坏方法方面,Feldmann等[13]通过破坏连接件或者零部件来提高目标拆卸体的拆卸效率;Lee等[14]提出基于切割平面法的拆卸序列规划方法,该方法定义了零部件间的交互面,并根据交互面生成含有可行拆卸方向集合的高斯球来获取拆卸方向;Geun等[15]采用弹性波方式摧毁螺栓和螺栓头,弹性波是指将能量冲击传递给安装有弹性介质的突出螺栓头,这种方式可以在短时间内破坏螺栓及螺栓头部,特别适用于退役产品;Umeda等[16]对Geun等[15]的方法进行了优化,使用分割线将产品破坏成所需形状后再拆卸目标组件;Reap等[17]使用机器强制破坏连接件对产品再制造回收,提出面向破坏拆卸的设计方法,并讨论可破坏拆卸的价值.
在可破坏性拆卸序列规划方面,潘兴兴[18]针对电子产品提出通过去除一定约束的局部破坏方法以获得最短物理拆卸路径的方法;周伟东[19]提出识别拆卸序列中不可拆卸(unable to disassembly,UTD)组件的方法,并应用破坏操作去除这些组件;宋小文等[20]从拆卸经济性和环保方面研究部分破坏模式下的串行拆卸序列规划问题,基于无向图和面向对象的目标回溯法获得最优序列;在此研究基础上,陈旭玲等[21]应用有向图表示产品拆卸信息,获得部分破坏模式下的拆卸序列最优解;Wang等[22]通过分析不可拆卸组件以及约束类型建立多层约束矩阵和紧固件矩阵来获取可行串行拆卸序列解;Zhou等[23]通过分析破坏性拆卸方法定义规则来重构产品拆卸混合图,提出扩展的FLOYD算法搜索可破坏模式下的最优串行拆卸序列解;Liang等[24]认为自动化程度和破坏性拆卸是解决报废产品拆卸序列的有效方法之一,并提出拆卸信息模型自动生成方法. 已有研究在可破坏拆卸序列规划方面取得了一定的成果,为了进一步提高求解效率,魏伟杰等[25]通过分析零件寿命对零件进行分类,采用粒子群算法求解破坏模式下的串行拆卸序列规划问题.
已有文献主要针对可破坏模式下的串行序列规划问题进行研究,且忽略实际拆卸过程中许多零部件存在故障问题对拆卸序列的影响,例如,部分产品由于磨损、变形、腐蚀、老化等多种故障造成连接失效导致产品不可拆卸或拆卸困难问题. 此外,在实践中,大型复杂产品的拆卸往往需要多人并行协作完成,并通过局部破坏低价值、不可拆卸零件(例如铆接、焊接)以提高拆卸效率. 可破坏模式下的再制造并行拆卸序列规划(remanufacturing parallel disassembly sequence planning,RPDSP)问题及求解方法的相关研究尚未见报道.
与可破坏模式下的串行拆卸序列规划问题相比,RPDSP问题的难点在于可破坏零件不确定、拆卸任务并行性. 本研究以拆卸连接失效为对象,通过产品故障来确定各零部件的拆卸方式和可破坏拆卸点,结合改进的遗传算法实现可破坏模式下的再制造并行拆卸序列寻优,降低拆卸的盲目性,为大型复杂产品的自动化拆卸提供技术支撑.
1. 层次式多重故障传递链模型
1.1. 绕弯现象和不可拆卸性
图 1
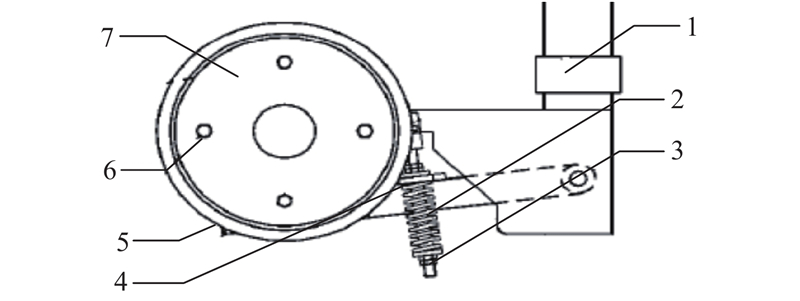
图 1 某摩擦驱动装置示意图
1-安装台;2-弹簧;3-螺栓1;4-调节轴;5-主动臂;6-螺栓2;7-主动轮 Schematic diagram of friction drive device
图 2
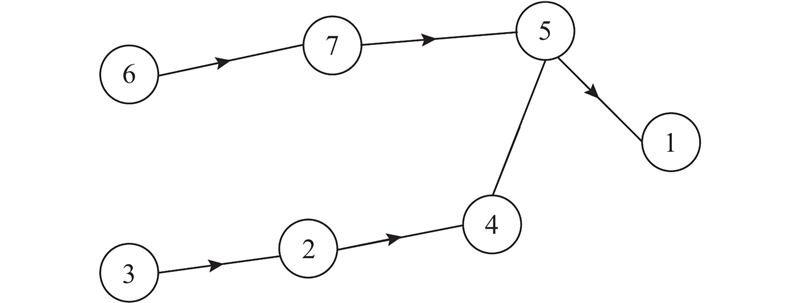
图 2 某摩擦驱动装置拆卸混合图
Fig.2 Disassembly hybrid graph model of friction drive device
如图1所示装置含有7个零件,其中,调节轴4和主动臂5通过铆接固定在一起. 假设以零件5为目标组件,在采用常规拆卸时,零件5与零件4固定在一起导致无法拆卸. 当以零件1为目标组件时,最短物理拆卸路径为6−7−5−1. 但是零件4使用常规拆卸无法进行拆除从而将会被绕过,拆卸路径将变为(3,6)−(2,7)−(4,5)−1,所有零件将会被拆除. 这种由于不可拆卸性导致的拆卸序列冗长的现象被称为绕弯现象[32]. 由上述案例可知,已有的拆卸信息模型会造成后续序列规划中的绕弯现象,无法表示不可拆卸问题. 同时,已有研究在选取破坏拆卸点和拆卸方式时主要以人为选择为主,主观性强,效率低. 为此,本研究构建层次式多重故障传递链模型来描述产品零件故障信息与回收决策、拆卸模式间的映射关系,通过回收决策来规划拆卸方式.
1.2. 产品故障信息与回收决策
表 1 零件故障信息及回收决策信息
Tab.1
| 故障特征 | 故障程度 | 报废原因 | 回收决策 |
| 老化( | 轻微故障( | 尺寸不合格( | 废弃( |
| 磨损( | 一般故障( | 残余价值低( | 材料回收( |
| 腐蚀( | 中等故障( | 性能不足( | 再制造( |
| 变形( | 严重故障( | 无法修复( | 重用( |
| 无失效( | − | 材料缺失( | − |
| 断裂( | − | 配对零件丢失( | − |
| 孔洞( | − | 无( | − |
| 烧伤( | − | − | − |
| 其他( | − | − | − |
1.3. 层次式多重故障传递链的构建
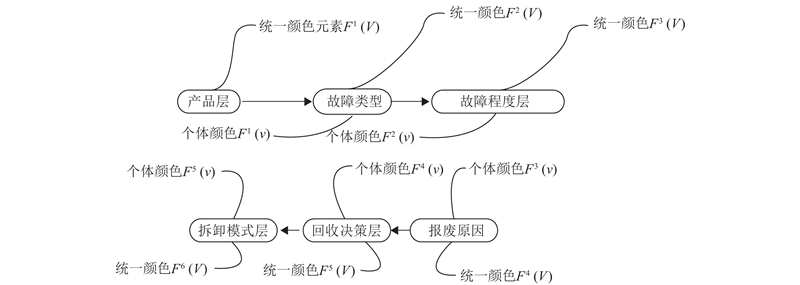
大型复杂退役产品的故障往往具有层次性和耦合性的特点,为了分析退役产品的故障机理,须将产品的各个层次和不同的故障类型都以相互关联的方式组织和表示,以反映各个故障类型和失效机理之间的层次对应关系,以及各个层次故障之间的因果逻辑关系. 为此,提出基于故障失效机理的层次式多重故障传递链模型,该模型描述产品零件故障信息与回收决策、拆卸模式间的映射关系. 该传递链由故障类型、故障程度、报废原因、回收决策、拆卸模式组成,如图3所示. 零部件具有多种故障,根据故障程度不同,主要分为轻微故障、一般故障、中度故障、严重故障4种,理论上,根据故障程度即可判断产品回收决策,但是由于实际中零部件报废原因的不确定性,故障程度与回收决策并非一一对应关系,须结合如表1所示的报废原因来综合判断. 如对于一般故障,可以进行再制造,但是,如果同时存在配对零件丢失的报废模式,则在实践中一般进行材料回收. 回收决策信息主要分为废弃、材料回收、再制造、重用4种方式. 回收决策的不同意味着选择拆卸零部件的方式不同,针对于某些可再制造和重用的组件,尽量选择非破坏拆卸方式以获取完整的组件;对于部分废弃和材料回收的组件,可以有选择性、针对性的采用破坏拆卸来快速获取再制造或重用组件.
图 3
2. 故障传递链模型的多色映射与推理
传统集合只描述集合中各元素的名称,无法表示元素本身的性质. 维·维·巴伏洛夫等[35]提出多色集合的概念,通过对集合整体及其组成元素涂上不同“颜色”来描述集合本身及其组成元素的不同性质.
2.1. 层次式多重故障传递链的多色集合映射
由于层次式多重故障传递链中各元素关系复杂且不利于计算机编程,为此,应用多色集合形式化描述多重故障传递链.
根据多色理论,将产品零件描述为产品围道:
图 4
图 4 层次式多重故障传递链映射机制
Fig.4 Hierarchical multiple failover chain mapping mechanism
2.2. 多色推理
层次式多重故障传递链的多色模型用于分析产品零部件故障程度与回收决策、拆卸方式间的关系,以零件的失效模式为前提,通过逐层推理获取零件的回收决策和拆卸方式. 推理矩阵运算如下:
式中:
式中:第i行第j列元素为零件i的故障类型
零部件的故障程度一般难以精确量化,对于老化、断裂、变形等故障类型,无论故障程度轻重该零部件都不能重用,须按照完全失效处理. 根据领域知识建立故障类型与故障程度的围道矩阵:
式中:第i行第j列元素为故障
将式(2)、(3)代入式(1),推理获得故障程度关联矩阵:
为了消除式(4)中部分零部件故障程度的不确定性,按照
根据专业知识,构建故障程度与报废原因的围道矩阵:
式中:第i行第j列元素为故障程度
将式(5)、(6)代入式(1),推理获得报废模式关联矩阵:
构建报废模式围道矩阵:
将式(7)、(8)代入式(1),推理获得回收决策关联矩阵:
式中:
表 2 摩擦装置回收决策与拆卸模式
Tab.2
| 序号 | 名称 | 回收决策 | 拆卸模式 |
| 1 | 安装台 | 重用 | 非破坏操作 |
| 2 | 弹簧 | 再制造 | 非破坏操作 |
| 3 | 螺栓1 | 报废 | 破坏操作 |
| 4 | 调节轴 | 再制造 | 非破坏操作 |
| 5 | 主动臂 | 再制造 | 非破坏操作 |
| 6 | 螺栓2 | 报废 | 破坏操作 |
| 7 | 主动轮 | 再制造 | 非破坏操作 |
3. 考虑故障的可破坏性拆卸信息模型
在实际拆卸过程中,待拆卸退役产品存在多种故障,导致其回收价值过低、拆卸难度增加. 为了考虑产品零部件故障对拆卸序列的影响,须将故障信息融入拆卸信息模型中,构建可破坏性拆卸信息模型.
3.1. 可破坏性拆卸信息模型的构建
可破坏性拆卸是指在实际拆卸过程中采取可破坏拆卸的方式拆除零部件的过程. 根据产品多层故障传递链模型,可以将产品的拓扑结构表示为可破坏性拆卸信息模型,
3.1.1. 接触矩阵
为了描述拆卸节点
以图1为例,接触矩阵
3.1.2. 约束优先级矩阵
为了描述拆卸节点
以图1为例,约束优先级矩阵为
3.1.3. 回收决策矩阵
回收决策信息可以直接通过层次式多重故障传递链的多色模型推理可知. 为了描述拆卸节点
如图1所示摩擦装置的回收决策矩阵为
3.1.4. 考虑回收决策的综合优先关系矩阵
在实际拆卸过程中,待拆卸产品的质量状态通常较差,存在多个故障,导致回收决策信息不同. 在拆卸序列规划中,既要考虑拆卸优先关系,又要考虑其自身的质量以及回收价值. 根据产品故障类型对拆卸序列造成的影响,建立考虑回收决策的综合优先关系矩阵
以图1为例,拆卸任务综合优先关系矩阵为
M4中含有采取破坏拆卸的零件以及拆卸优先级信息. 当满足式(5)时,表示该零件为采取破坏拆卸模式,删除该零件所在行和列,获得矩阵
3.1.5. 可拆卸性条件
假设产品由n个零件构成,则拆卸节点Vi可拆卸必须满足:
3.2. 拆卸并行度
将某个时刻可以同时拆卸的最小拆卸单元定义为拆卸并行度,记为para. 由拆卸并行度定义可知,RPDSP的并行度与可拆卸节点数量以及操作人员有关,设操作人员集合
以图1为例,由式(5)可知,第1步可拆卸的节点为2、7,第2步可拆卸节点为5,第3步可拆卸节点为1,则拆卸并行度可以选择为2.
4. 故障驱动的RPDSP求解
4.1. 问题描述
已知产品的层次式多重故障传递链,通过多色集合理论以及多色推理获取零部件的故障信息以及回收决策,从而决定拆卸模式. 拆卸模式是指通过分析零件的故障程度决定零部件的回收决策信息从而选择采用破坏操作还是非破坏操作,可破坏模式下的并行拆卸介于破坏操作和非破坏操作之间. 基于产品故障特征的RPDSP问题就是求解某约束下的以再制造毛坯为目标组件的最佳节点并行拆卸序列,该问题须满足以下条件:1) 最小化目标函数(总拆卸时间);2) 最大化拆卸并行度,每步可拆卸的零部件节点数不能超过给定的并行度;3) 拆卸过程允许破坏某些不可拆卸零件和低价值零件.
为了减少多重故障驱动的并行拆卸序列规划问题的复杂性,进行如下假设:1) 同时执行的拆卸操作不能互相干涉;2) 每步拆卸任务同时执行.
4.2. 基于遗传算法的RPDSP问题求解
4.2.1. 多层染色体编码
再制造并行拆卸的染色体编码一般包含2个信息,即拆卸序列和拆卸步长[38]. 基于产品失效特征的多重故障驱动的并行拆卸序列不仅含有节点拆卸优先级信息,而且含有破坏性零件信息. 所以,传统的染色体编码无法使用. 本研究提出多层染色体编码方法.
定义
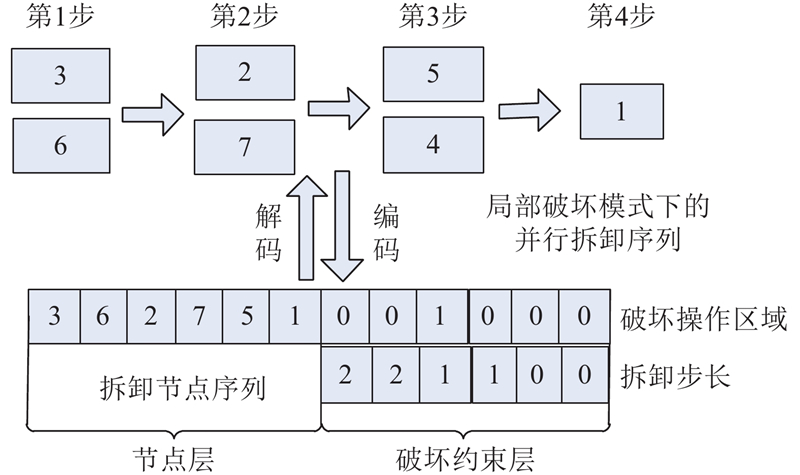
式中:n为节点层,记录拆卸序列,采用基于优先权的自然数编码方法;p为破坏约束层,由破坏操作区域和拆卸步长两部分组成,分别采用0-1编码和自然数编码,保证染色体的可读性;在破坏操作区域中,
图 5
图 5 可破坏拆卸步骤与染色体编码的映射过程
Fig.5 Mapping process of process of partial destructive disassembly steps and chromosome code
4.2.2. 融入零部件回收决策的初始种群获取
1) 根据废旧产品的装配信息,构建接触矩阵M1和拆卸优先关系矩阵M2;由多色推理确定回收决策矩阵M3,推出拆卸任务综合优先关系矩阵M4. 定义初始种群矩阵为Q,定义拆卸节点层次矩阵G为
流程图如图6所示.
图 6
图 6 融入零部件回收决策的初始种群获取
Fig.6 Initial population acquisition incorporating component recycling decision
以图1为例,图中层次G为
由式(13)、(14)可知,在将其零件3、4、6破坏之后,第1步拆卸零件7和2,第2步拆卸零件5,第3步获取目标组件1.
4.2.3. 适应度的定义
再制造并行拆卸旨在以最小的成本和最短时间获得复杂产品中指定的多目标零部件,因此拆卸成本和拆卸时间直观反映和体现拆卸效率. 以基本拆卸时间和破坏操作时间设定适应度函数[39]:
式中:r为序列,l为拆卸步长,L为可破坏并行拆卸序列长度,
4.2.4. 交叉算子和变异算子
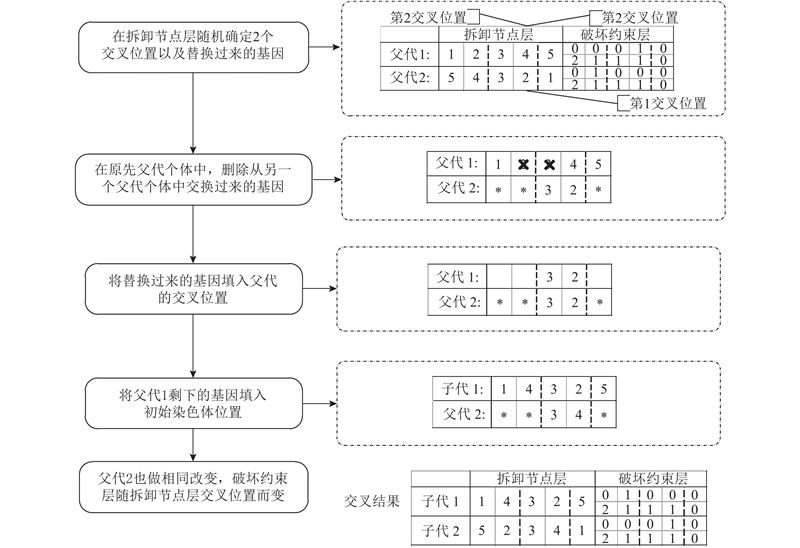
交叉进化是产生新个体的主要方法,采用单点交叉算子针对多层染色体中的拆卸节点序列部分进行交叉操作. 针对多层染色体的交叉,交叉过程示意图以及具体步骤如图7所示. 变异操作是指分别在染色体中的拆卸节点层和破坏约束层中确定2个变异位置,将基因信息交换,得到新染色体.
图 7
5. 案例研究
5.1. 波轮洗衣机回收决策
表 3 零件原始拆卸信息表
Tab.3
| 编码 | 名称 | tb /s | td /s | 拆卸方向 | Cu /元 | Cd /元 |
| 1 | 前盖板 | 112 | 46 | −X | 0.160 | 0.310 |
| 2 | 配重 | 30 | 12 | −X | 0.080 | 5.110 |
| 3 | 进水管 | 200 | 40 | +Z | 0.320 | 0.760 |
| 4 | 进水控制阀 | 132 | 34 | +Z | 0.310 | 0.370 |
| 5 | 外筒盖 | 314 | 88 | − | 0.510 | 3.760 |
| 6 | 上盖板 | 80 | 32 | +Z | 0.220 | 0.286 |
| 7 | 内筒 | 304 | 64 | +Y | 0.290 | 0.840 |
| 8 | 叉形架 | 2 | 2 | +Y | 0.006 | 0.006 |
| 9 | 平衡块 | 10 | 4 | +Y | 0.028 | 0.170 |
| 10 | 大带轮 | 10 | 4 | +Y | 0.028 | 0.170 |
| 11 | 后盖板 | 128 | 52 | +Y | 0.360 | 0.360 |
| 12 | 小带轮 | 100 | 20 | +Y | 0.280 | 0.280 |
| 13 | 电机 | 114 | 28 | +Y | 0.250 | 0.450 |
| 14 | 外筒主体 | 440 | 102 | − | 0.570 | 0.170 |
| 15 | 洗衣机排水管 | 402 | 84 | +Y | 0.340 | 1.120 |
| 16 | 箱体 | 150 | 60 | − | 0.320 | 0.420 |
| 17 | 排水泵 | 40 | 16 | −Y | 0.110 | 0.110 |
| 18 | 阻尼器 | 40 | 16 | −Y | 0.110 | 0.170 |
| 19 | 外筒排水管 | 110 | 24 | −Y | 0.230 | 0.310 |
| 20 | 温控器 | 40 | 16 | −Y | 0.110 | 3.210 |
| 21 | 加热器 | 100 | 20 | −Y | 0.280 | 3.190 |
图 8
为了便于进行拆卸序列规划,通过分析波轮式洗衣机存在的故障以及故障程度获得波轮洗衣机回收决策数据,如表4所示. 可以看出,零件7、8、15为再制造零件对其进行回收,以零件7、8、15为目标组件进行多目标拆卸;对于零件3、5、11、14,根据零件价值或故障严重程度采用破坏操作.
表 4 波轮洗衣机回收决策数据
Tab.4
| 序号 | 名称 | 回收决策 | 拆卸模式 |
| 3 | 进水管 | 报废 | 破坏操作 |
| 5 | 外筒盖 | 报废 | 破坏操作 |
| 7 | 内筒 | 再制造 | 非破坏操作 |
| 8 | 叉形架 | 再制造 | 非破坏操作 |
| 11 | 后盖板 | 报废 | 破坏操作 |
| 14 | 外筒主体 | 材料回收 | 破坏操作 |
| 15 | 排水管 | 再制造 | 非破坏操作 |
5.2. 基于产品故障特征的拆卸序列规划
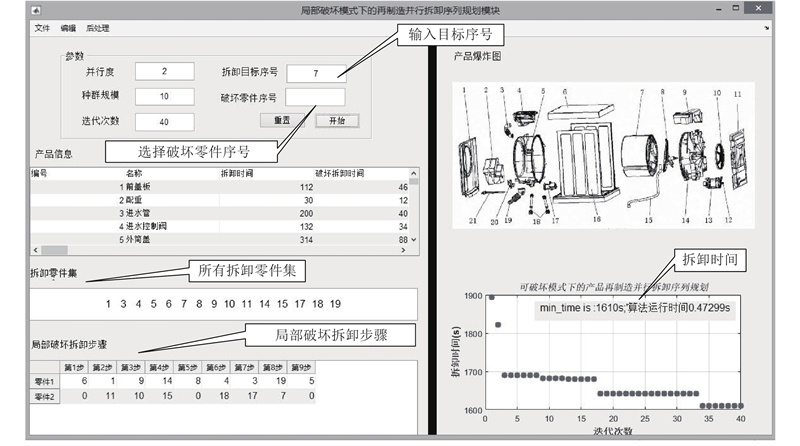
在Win10 Intel(R)Core(TM)i5-4210U @ 1.70 GHz环境下,以上述理论方法为基础使用Matlab R2016a在课题组研究的基础上进行系统开发. 通过计算得到非破坏拆卸下的产品再制造并行拆卸序列以及拆卸时间,如图9所示. 由表4可知,零件3、5、11、14回收价值过低,可以采取破坏操作进行拆卸. 在确定破坏性零件后使用上文所述方法进行拆卸序列规划,获取可破坏模式下的迭代次数iter和拆卸时间t,如图10所示. 以破坏零件11为例,种群规模M=40,迭代次数最大为100,系统连续运行10次得到的运行结果如图11所示. 波轮式洗衣机不同类型拆卸序列规划结果如表5所示.
表 5 波轮式洗衣机不同类型拆卸序列规划结果
Tab.5
| 类型 | 目标组件 | t /s | 最优序列 |
| 无故障 影响 | 零部件7 | 1632 | (6)−(1, 11)−(9, 10)−(14, 15)−(8)− (4, 18)−(3, 17)−(9, 8)−(7) |
| 考虑故 障影响 | 破坏零件11 | 1388 | (10, 6)−(3, 1)−(9)−(14, 15)−(8, 18)− (17)−(19, 7)−(5) |
| 考虑故 障影响 | 破坏零件5 | 884 | (11)−(10, 9)−(14)−(8)−(7) |
图 9
图 9 可破坏模式下的产品再制造并行拆卸序列规划
Fig.9 RPDSP for product under partial destructive mode
图 10
图 10 可破坏拆卸序列规划时间
Fig.10 Partial destruction disassembly sequence planning time
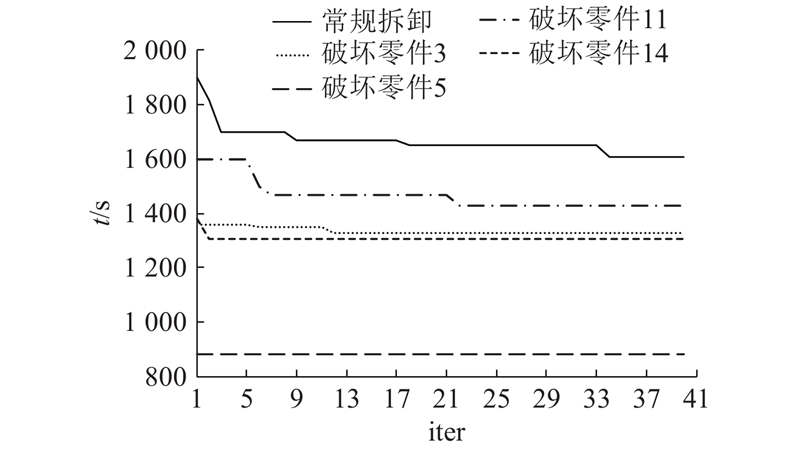
图 11
图 11 可破坏拆卸下总拆卸时间随迭代次数的变化规律
Fig.11 Change rule of total disassembly time with iteration number under RPDSP
5.3. 结果讨论
5.3.1. 不同拆卸模式对解的影响
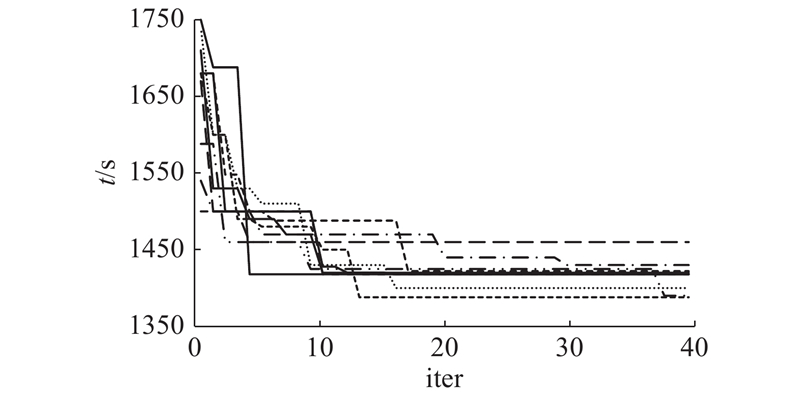
在遗传算法中,很难保证一次实验寻找到最优解,每次实验的最优解须经系统连续运行多次后得到. 以破坏零件11为例,设置种群规模为40,最大迭代次数为100,系统连续运行10次得到的运行结果如图11所示. 可以看出,在运行10次后,算法均趋于1388 s,基本在40代时收敛.
5.3.2. 并行度对拆卸时间的影响
随着破坏拆卸深度的增大,拆卸并行度越大,总拆卸时间越短. 因此,在操作者和操作空间允许的范围内,尤其是对于拆卸深度较深的目标组件,尽可能提高拆卸并行度有助于提高拆卸效率.
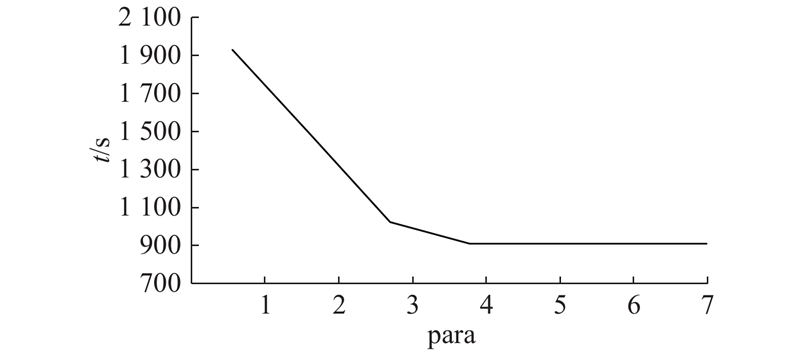
为了分析可破坏拆卸并行度与总拆卸时间的关系,在算法种群规模为100,迭代次数为100,目标组件为第7号零件并且零件11选择破坏的情况下,可以得到如图12所示的实验结果. 可以看出,当
图 12
图 12 可破坏拆卸并行度与拆卸时间的关系
Fig.12 Relationship between partial destruction disassembly parallelism and disassembly time
5.3.3. 结果
图 13
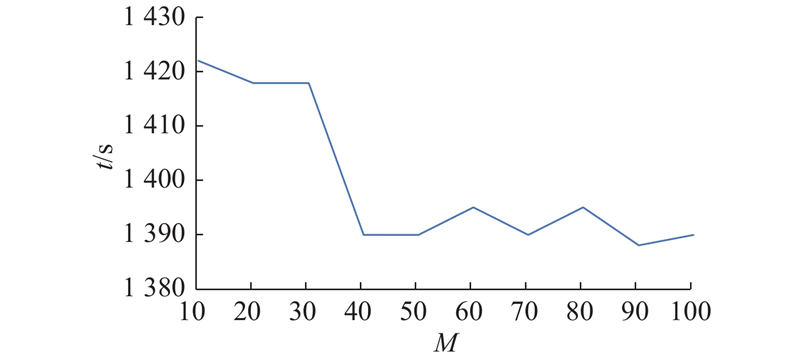
图 13 种群规模与拆卸序列规划结果的关系
Fig.13 Relationship between population size and results of disassembly sequence planning
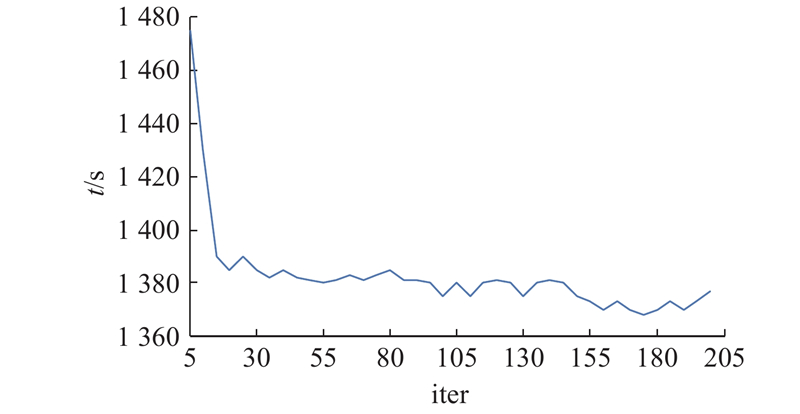
图 14
图 14 迭代次数与拆卸序列规划结果的关系
Fig.14 Relationship between number of iterations and results of disassembly sequence planning
6. 结 论
(1) 建立层次式多重故障传递链模型,为了便于计算机处理进行多色集合形式化描述,通过多色推理确定零部件的回收决策和拆卸模式,克服人工指定可破坏组件的主观性、效率低、盲目性等不足,为问题的自动化求解提供技术支持.
(2) 提出双层染色体编码方法,节点层采用基于优先权的自然数编码,破坏约束层采用二进制编码方法,实现局部破坏模式下的并行拆卸序列规划问题的遗传映射,为该问题的智能算法求解提供思路.
(3) 提出融入零部件回收决策的初始种群获取方法,剔除不合理解,提高初始种群质量,为拆卸序列解的快速求解提供基础.
该方法需要故障程度、报废原因、回收决策等因素及其相关知识的支持,如何精确提取和量化零部件故障信息对于退役产品再制造并行拆卸序列规划问题有着重要的工程意义,下一步工作将围绕此方面展开.
参考文献
废旧产品再制造质量控制研究
[J].
Quality control in remanufacturing waste product
[J].
Disassembly sequence planning for products with defective parts in product recovery
[J].
基于遗传蝙蝠算法的选择性拆卸序列规划
[J].
Selective-disassembly sequence planning based on genetic-bat algorithm
[J].
Disassembly sequence planning based on the simulated annealing and genetic algorithm
[J].
Selective cooperative disassembly planning based on multi-objective discrete artificial bee colony algorithm
[J].DOI:10.1016/j.engappai.2017.06.025
Disassembly information model incorporating dynamic capabilities for disassembly sequence generation
[J].
Selective disassembly sequence generation based on lowest level disassembly graph method
[J].
Integrated multi-layer representation and ant colony search for product selective disassembly planning
[J].DOI:10.1016/j.compind.2015.10.011
考虑作业空间约束的并行拆卸序列规划算法
[J].DOI:10.3724/SP.J.1089.2018.16858
Parallel disassembly sequence planning method considering operation space constraints
[J].DOI:10.3724/SP.J.1089.2018.16858
基于粒子群算法的产品拆卸序列规划方法
[J].
Product disassembly sequence planning based on particle swarm optimization algorithm
[J].
Disassembly sequence planning for electromechanical product under a partial destructive mode
[J].
Innovative disassembly strategies based on flexible partial destructive tools
[J].DOI:10.1016/S1367-5788(99)00017-6 [本文引用: 1]
Destructive disassembly to support virtual prototyping
[J].
Destructive disassembly of bolts and screws by impact fracture
[J].DOI:10.1016/S0278-6125(02)80170-4 [本文引用: 2]
Proposal of a design method for semi-destructive disassembly with split lines
[J].
部分破坏模式下的机电产品拆卸序列规划
[J].
Electromechanical product disassembly sequence planning based on partial destruction made
[J].
部分破坏拆卸模式下拆卸规划
[J].DOI:10.3969/j.issn.1005-2615.2014.06.019 [本文引用: 1]
Product disassembly sequence planning based on partial destruction made
[J].DOI:10.3969/j.issn.1005-2615.2014.06.019 [本文引用: 1]
Research of partial destructive based selective disassembly sequence planning
[J].DOI:10.2174/1874155X01509010605 [本文引用: 1]
Value recovery from end-of-use products facilitated by automated dismantling planning
[J].DOI:10.1007/s10098-017-1370-9 [本文引用: 1]
零件分类条件下废旧产品拆卸序列多目标优化
[J].
Multi-objective optimization method for disassembly sequence of used product under the condition of parts classification
[J].
A hierarchical approach to disassembly sequence planning for mechanical product
[J].
Determining optimum disassembly sequences in electronic equipment
[J].DOI:10.1016/S0360-8352(02)00125-0 [本文引用: 1]
Fuzzy-Petri-net based disassembly planning considering human factors
[J].DOI:10.1109/TSMCA.2005.853508 [本文引用: 1]
考虑产品故障特征的目标选择性拆卸序列规划
[J].DOI:10.11918/j.issn.0367-6234.201807074 [本文引用: 1]
Objective selective disassembly sequence planning considered product fault features
[J].DOI:10.11918/j.issn.0367-6234.201807074 [本文引用: 1]
基于自适应粒子群的产品再制造拆卸规划
[J].
Product remanufacture disassembly planning based on adaptive particle swarm optimization algorithm
[J].
Rule-based recursive selective disassembly sequence planning for green design
[J].DOI:10.1016/j.aei.2010.03.002 [本文引用: 1]
支持再制造设计的产品失效模式信息传递模型
[J].DOI:10.3901/JME.2017.03.201 [本文引用: 1]
Product failure mode information transfer polychromatic model for remanufacture
[J].DOI:10.3901/JME.2017.03.201 [本文引用: 1]
基于失效特征的机械零部件可再制造度评价方法
[J].
Remanufacturability evaluation method of mechanical parts based on failure features
[J].
多色集合在加工系统建模与分析时的应用
[J].DOI:10.3321/j.issn:0253-987X.2001.09.011 [本文引用: 1]
Application of the polychromatic sets for modeling and analysis of manufacturing system
[J].DOI:10.3321/j.issn:0253-987X.2001.09.011 [本文引用: 1]
An asynchronous parallel disassembly planning based on genetic algorithm
[J].DOI:10.1016/j.ejor.2018.01.055 [本文引用: 1]
随机型拆卸线平衡问题的局部邻域遗传算法
[J].
Local neighborhood genetic algorithm for stochastic disassembly line balancing problem
[J].
Optimal design of flux diverter using genetic algorithm for axial short circuit force reduction in HTS transformers
[J].
支持再制造的选择性并行拆卸序列规划方法
[J].DOI:10.3724/SP.J.1089.2018.16317 [本文引用: 1]
Selective parallel disassembly sequence planning method for remanufacturing
[J].DOI:10.3724/SP.J.1089.2018.16317 [本文引用: 1]