高密度聚乙烯(high-density polyethylene,HDPE)管道由于其较好的抗震、无毒、耐腐蚀等性能,以及相对其他材质管道较低廉的成本,被广泛应用于燃气运输、城市给排水工程中. 随着国内城市地铁及其他地下空间工程开发的快速发展,常有临近管道工程施工的现象. 由于城区地质条件的复杂性,若岩土体在开挖过程遇到坚硬岩层,常采用爆破碎岩的方式进行施工,在爆破施工过程中如何控制爆破振动对临近管道的影响是重点关注内容. 研究爆破荷载对埋地HDPE给排水管道的影响,探讨埋地HDPE管道振动破坏的控制标准,具有理论研究价值及工程实际意义.
当前,对于振动荷载对邻近管道的影响,许多学者已开展相关研究工作[1-2]. 其中,在通过室内试验的方法研究管道力学性能方面,Ha等[3]利用离心机试验研究HDPE管道变形规律,并结合应力应变数据得到管道横向力和变形关系. Abdoun等[4]利用离心机试验研究HDPE管道不同埋深和管径的受力性能. 王海涛等[5]开展室内相似模型试验,研究地铁隧道钻爆法施工时岩体和邻近埋地管道的振动特性. 在爆破振动作用下管道的响应特征现场试验研究方面,朱斌等[6]通过现场试验的方式提出球墨铸铁燃气管道在爆破振动作用下的动力响应;夏宇磬等[7]通过现场试验研究承插式混凝土管道动力响应特征,并提出该管道的振动速度安全判据;钟冬望等[8]利用现场模型试验得到爆炸荷载下聚乙烯(polyethylene,PE)管道的动力响应. 此外,还有大量学者利用数值模拟的方法来研究埋地管道的动力响应[9-10]. Francini等[11]利用爆破数值计算研究邻近埋地管道以及其上方地表的振动规律,提出相应的安全判据. Jiang等[12]利用现场监测和ANSYS/LS-DYNA研究燃气管道下穿隧道爆破的动力响应. Xia等[13]通过现场监测以及LS-DYNA数值模拟得出,在爆破振动荷载下混凝土管道满水状态的振动速度及等效应力要小于空管状态下的. Wu等[14]利用ABAQUS软件模拟开挖荷载静力作用下HDPE管道的应力应变特性. 张震等[15]通过数值计算,利用监测数据研究爆破邻近埋地混凝土管道动力响应特征.
目前,关于管道动力响应研究多针对混凝土、铸铁等质地较硬的管道,关于HDPE波纹管这种材质软、韧性强的管道研究较少;同时,较少有研究针对临近爆破振动荷载对不同运营充水状态管道的影响.
以武汉市城区典型土层埋置的给排水管道系统为工程依托,通过全尺度预埋HDPE管道现场爆破试验及数值模拟方法,分析爆破振动荷载作用下埋地HDPE波纹管道在不同运营充水状态下的动力响应特征;结合管道运营状态环向容许应力控制准则,提出HDPE波纹管爆破振动速度安全控制标准.
1. 现场爆破试验
以在建的武汉地铁8号线洪小区间竖井基坑爆破工程为背景,邻近基坑的为中科院武汉岩土所新建高层建筑,该建筑排水管道利用HDPE波纹管,直径为500 mm,埋置深度为1.5 m,埋置土层为粉质黏土,管道与基坑直线距离为15 m,基坑爆破工程最大单段药量约为9.6 kg. 根据上述工程特点,选取武汉爆破公司位于武汉市经济技术开发区硃山路与硃山一路交汇处的爆炸荷载与振动作用下埋地管道动态响应与防护技术试验场作为试验场地,爆破区域长、宽分别约为100、60 m.
1.1. 试验尺寸参数
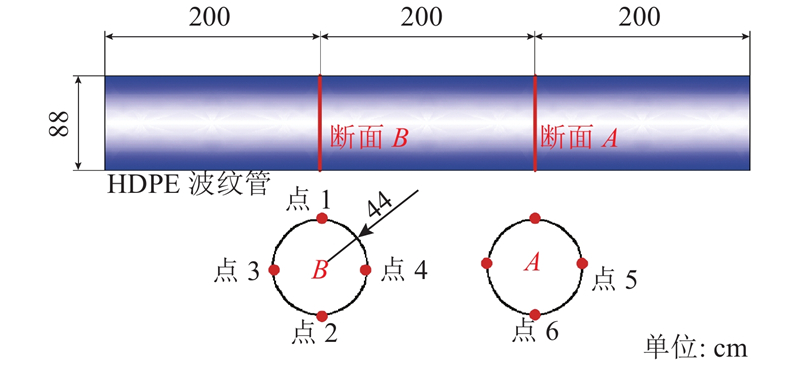
根据武汉市地区地层地质勘察资料与工程实际[16-17],武汉市的埋地HDPE波纹管道广泛埋置于深度约为1~3 m的粉质黏土地层,直径为100~2 600 mm. 该土层具有水的质量分数较高、孔隙比较大、强度较低等特点,动剪切模量与阻尼比受水的质量分数的影响较大,地震波在其中传播的动力特性与岩石介质具有较大的不同. 因此研究粉质黏土地层中埋地管道的爆破动力响应特征对武汉市爆破工程邻近埋地管道的安全性具有重要指导意义. 选取试验场地为粉质黏土层,管道埋深(管顶至地面距离)为2.0 m. HDPE波纹管尺寸如图1所示,外径D=88 cm,内径d=80 cm,壁厚为1 cm,波高为3 cm,波峰宽为5 cm,波峰间距为3 cm. HDPE波纹管参数如下:泊松比μ=0.46,密度ρ=936 kg/m3,弹性模量E=834.9 MPa,环刚度SN=8 kPa,强度极限σu=31.6 MPa,延伸率
图 1
图 1 爆破试验所用HDPE管道尺寸示意图
Fig.1 Schematic diagram of HDPE pipe size used in blasting test
表 1 爆破试验的工况参数
Tab.1
| 工况 | 炸药埋深/m | 炸药量/kg | 水平距离/m |
| 1 | 6.5 | 8.0 | 25 |
| 2 | 6.5 | 8.0 | 20 |
| 3 | 6.5 | 8.0 | 15 |
| 4 | 6.5 | 8.0 | 10 |
| 5 | 4.0 | 8.0 | 25 |
| 6 | 4.0 | 8.0 | 20 |
| 7 | 4.0 | 8.0 | 15 |
| 8 | 4.0 | 8.0 | 10 |
| 9 | 4.0 | 9.6 | 5 |
图 2
1.2. 试验测试系统
根据试验设计方案,为了研究HDPE波纹管爆破振动效应的动态规律,利用动态测试仪器对管段中以及管段周围岩土层的相关数据进行实时动态量测. 试验中的主要测试项目有管道动态应变ε、管道质点振动速度vP、管道上方地表振动速度vG等.
为了研究埋地管道与管道上方地表的振动速度,选用TC-4850爆破测振仪作为振动速度测试系统. 根据实际需要在管道内部以及管道对应的正上方地表设置多个监测截面以布置多个振动速度测点,振动速度测试点布置示意图如图3所示. 图中,断面A、B分别为管道三等分点截面,即管口截面与断面A、B之间距离为2 m,D1~D7为振动测点.
图 3
为了研究管道在爆破振动振动过程中的动态应变,通过在管道内表面黏贴不同方向的应变片来进行测量. 使用敏感栅长为80 mm,电阻为120 Ω的单轴应变片,接1/4桥,通过连接线与DH5956动态信号采集仪相连. 在爆破试验过程中进行实时动态数据的采集,采样频率设置为20 kHz. 参考振动测点,管道动态应变截面测点布置如图4所示.
图 4
1.3. 测试结果分析
表 2 振动速度的现场试验与数值模拟结果对比
Tab.2
| 监测点 | 现场试验 | 数值模拟 | EVR /% | |||||||
| vX /(cm·s−1) | vY /(cm·s−1) | vZ /(cm·s−1) | vR /(cm·s−1) | vX /(cm·s−1) | vY /(cm·s−1) | vZ /(cm·s−1) | vR /(cm·s−1) | |||
| D1 | 18.99 | 4.12 | 2.47 | 19.58 | 15.44 | 7.25 | 3.51 | 17.41 | −11.08 | |
| D2 | 7.25 | 2.67 | 7.63 | 10.86 | 9.34 | 5.65 | 3.23 | 11.38 | 4.85 | |
| D3 | 10.39 | 5.33 | 3.24 | 12.12 | 11.60 | 5.88 | 3.11 | 13.37 | 10.32 | |
| D4 | 17.81 | 8.66 | 3.91 | 20.19 | 16.43 | 6.42 | 3.55 | 17.99 | −10.87 | |
| D5 | 8.51 | 5.12 | 3.41 | 10.50 | 11.55 | 2.03 | 2.89 | 12.08 | 14.98 | |
| D6 | 13.34 | 4.51 | 5.73 | 15.20 | 10.50 | 8.44 | 4.23 | 14.12 | −7.11 | |
| D7 | 15.19 | 4.95 | 4.30 | 16.54 | 13.20 | 6.11 | 6.33 | 15.86 | −4.11 | |
图 5
图 5 爆破试验工况9测点2轴向与环向动应变
Fig.5 Axial and circumferential dynamic strain in blasting test condition 9 measuring point 2
2. 管道数值模拟及验证
为了研究充水HDPE管道在爆破振动荷载作用下的动力响应,利用LS-DYNA软件结合工况8建立数值模型,采用LS-DYNA软件自带的炸药模型以及Jones-Wilkins-Lee(JWL)状态方程,模拟爆破振动荷载下管道空管状态下的动力响应特性. 模型整体尺寸为15.0 m×6.0 m×6.0 m,管道尺寸与现场比例为1∶1,炮孔直径为90 mm,耦合装药. 在模型中,埋置管道土体为均质粉质黏土层,基岩为强风化粉质砂岩;由于模型尺寸有限,除模型上表面为自由面外,其他面均为无反射边界. 管道与粉质黏土的接触形式设为面面接触,管道与液体之间界面采用流固耦合界面. 建立的计算模型及网格如图6所示.
2.1. 粉质黏土的材料模型
粉质黏土的材料模型选用MAT_DRUCKER_PRAGER[16]. Mohr-Coulomb准则在偏平面的屈服面为六棱锥面,而MAT_DRUCKER_PRAGER能构造光滑没有棱角的屈服曲面内切于M-C准则的六棱锥面,有利于数值计算. 该材料模型的力学表达式为
式中:f为塑性势函数;I1(σij)为应力张量第1不变量,σij为应力张量;I2(Sij)为应力偏张量第2不变量;Sij为柯西应力张量;α、k为材料常数,是材料黏聚力c、内摩擦角φ的函数. 在计算时具体输入参数如表3所示. 表中,ρ为密度,E为弹性模量,G为剪切模量,μ为泊松比,σt为抗拉强度.
图 6
图 6 管道爆破试验整体数值模型及网格划分
Fig.6 Numerical model and meshing of pipeline blasting test
表 3 管道、粉质黏土与砂岩材料模型参数表
Tab.3
| 材料 | ρ /(g·m−3) | E /GPa | G /GPa | μ | c /MPa | φ /(°) | σt /MPa |
| 管道 | 0.936 | 0.834 9 | − | 0.46 | − | − | 31.600 |
| 粉质黏土 | 1.980 | 0.039 0 | 4.3 | 0.35 | 0.035 | 15 | 0.028 |
| 砂岩 | 2.680 | 52.000 0 | 11.2 | 0.25 | 5.500 | 43 | 2.580 |
2.2. 强风化粉质砂岩的材料模型
强风化粉质砂岩以及堵泥均采用*MAT_PLASTIC_KINEMATIC材料模型[17]. 该材料模型的屈服条件表达式为
式中:σY为屈服应力,σ0为初始屈服应力,
2.3. HDPE管的材料模型
HDPE材料是黏弹性材料,力学性能受到应力、形变、温度和时间4个因素的影响,本研究中不考虑温度对HDPE材料的影响,即认为其力学性能与应变率相关. 因此,材料模型可以采用*MAT_PLASTICITY_POLYMER,该模型可以模拟高聚物在高应变率下的动力响应问题. 在计算时管道的具体输入参数如表3所示.
2.4. 水的材料模型
在模型中水采用关键字*MAT_NULL定义,状态方程采用关键字*EOS_GRUNEISEN,表达式为
式中:p为流体所受的压力;c0为水中声速;u=ρ1/ρ0−1,ρ1为扰动后水密度,ρ0为水初始密度;E1为比内能;γ0为GRUNEISEN系数;b为体积修正系数;S1、S2、S3分别为该状态方程激波速度与粒子速度曲线的斜率系数. 计算时具体输入参数如表4所示.
表 4 水材料模型参数
Tab.4
| ρw/ (g·cm−3) | c0 / (m·s−1) | S1 | S2 | S3 | γ0 |
| 1.0 | 1 500 | 2.560 0 | 1.986 0 | 1.226 8 | 0.5 |
2.5. 炸药的材料模型
模型中的炸药材料与试验现场采用的2#岩石炸药保持一致,采用LS-DYNA软件自带的高能炸药材料*MAT_HIGH_EXPLOSIVE_BURN来模拟炸药模型. JWL方程可以描述炸药的爆轰压力与相对体积和内能的关系:
式中:pe为爆炸产物压力,V为爆炸产物相对体积,R1、R2、ω、A、B为炸药材料参数,E0为初始比内能. 炸药爆轰产物相关参数如表5所示. 表中,ρe为炸药密度.
表 5 爆轰产物参数表
Tab.5
| 参数 | ρe /(g·cm−3) | A /GPa | B /GPa | R1 | R2 | ω | E0 /GPa | V /cm3 |
| 数值 | 1.25 | 214.0 | 18.2 | 4.2 | 0.9 | 0.15 | 4.19 | 1 |
2.6. 数值模拟结果验证
为了验证数值模拟参数及结果的可靠性,依据现场试验,在数值模型同样的位置处选取监测点,数值模拟结果与现场实测数据在X、Y、Z方向上的峰值振动速度与峰值合振速的对比结果如表2所示. 可以看出,数值模拟结果与现场试验结果差距不大,最大误差为14.98%,证明数值模拟结果与参数准确可靠. 另外,可以发现3个方向的振动速度为X方向最大,Y方向次之,Z方向最小.
3. 不同水位状态数值模拟
为了充分反映实际爆破工程中,HDPE给排水管道充水运营时的动力响应特性,分别建立0.25d=20 cm、0.5d=40 cm、0.75d=60 cm、d=80 cm,4种水位高度的数值模型,与前文所建立无水空管的模型组成5种不同水位高度的工况,计算不同水位状态下管道的动力响应规律,其中半水和满水工况下管道及其内部水的网格划分如图7所示. 图中,R、r分别为管道外、内半径.
图 7
3.1. 振动速度
管道轴对称中心截面为危险截面,为了探究不同水位高度对管道振动速度及主频率的影响,统计5种数值模拟工况下危险截面X、Y、Z方向的峰值振速与峰值合振速及各个方向上的主频,如表6所示. 表中,fX为X方向主频,fY为Y方向主频,fZ为Z方向主频,H为水位高度. 可以看出:1)空管的X方向振动速度与主频率最大,随管内水位高度的增加,X方向的振动速度与主频率均降低;2)Y、Z方向上的主频率及振动速度均随水位高度的增加而升高,且Y方向振动速度与频率的增长速度大于Z方向;3)5种工况下的振动主频均高于管道自振频率(按照文献[18]对PE管道进行的快速傅氏变换,得到当激振频率为4~9 Hz时,管道的峰值应变最明显,故可以认为管道自振频率小于10 Hz),所以管道不会发生共振现象而受到破坏;4)地表振动速度大于管道振动速度,符合现场试验测得的数据,满水管道峰值合振速为16.5 cm/s,空管峰值合振速为19.4 cm/s,即充水管道更安全. 将合振速与管道水位高度所占管道内径高度比例系数进行拟合,结果如图8所示. 图中,i为管内水位高度与管道内径d的比值. 发现两者之间具有较好的线性相关关系,拟合直线公式为
表 6 5种数值模拟工况下危险截面振动速度与主频
Tab.6
| H/cm | vX /(cm·s−1) | fX/Hz | vY /(cm·s−1) | fY /Hz | vZ /(cm·s−1) | fZ /Hz | vR /(cm·s−1) |
| 0 | 18.35 | 72 | 6.03 | 31 | 2.21 | 37 | 19.44 |
| 20 | 17.33 | 61 | 6.91 | 45 | 3.02 | 58 | 18.90 |
| 40 | 15.83 | 52 | 8.52 | 68 | 3.41 | 69 | 18.30 |
| 60 | 14.37 | 38 | 9.41 | 87 | 3.99 | 82 | 17.63 |
| 80 | 12.21 | 26 | 10.21 | 103 | 4.33 | 99 | 16.49 |
图 8
图 8 振动速度与管道水位高度拟合图
Fig.8 Fitting curve of vibration velocity and pipeline water level height
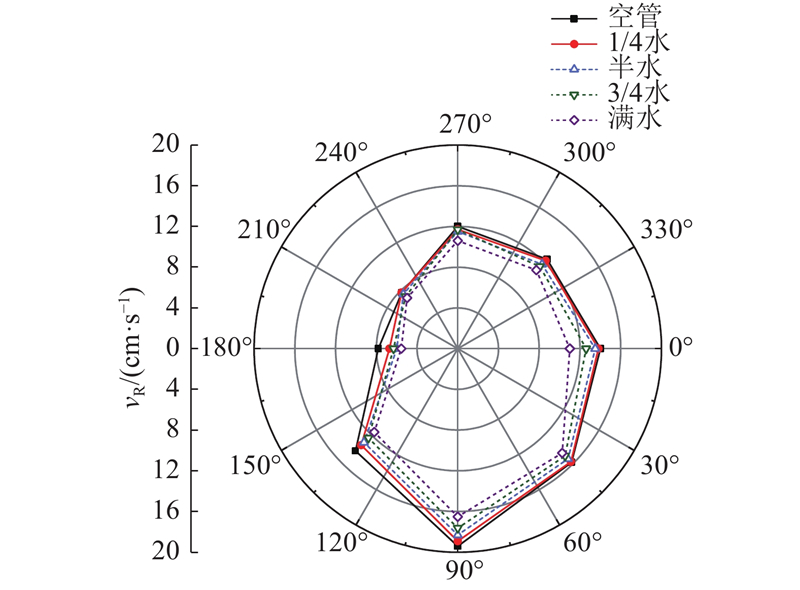
为了直观显示同一截面不同位置处的动力响应特点,将危险截面位置等分为8部分,以观察不同工况条件下,管道同一截面不同位置上的质点峰值振动速度,结果如图9所示. 迎爆侧即危险截面0°~90°振动速度更大,振速最大的位置位于管道正下方90°处,并且离迎爆侧距离越远,质点振动速度越小.
图 9
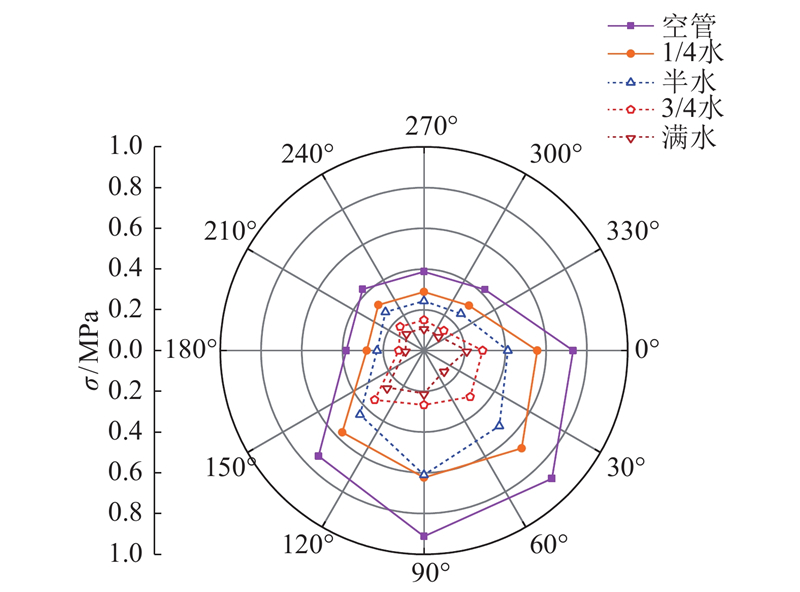
3.2. 等效应力
图 10
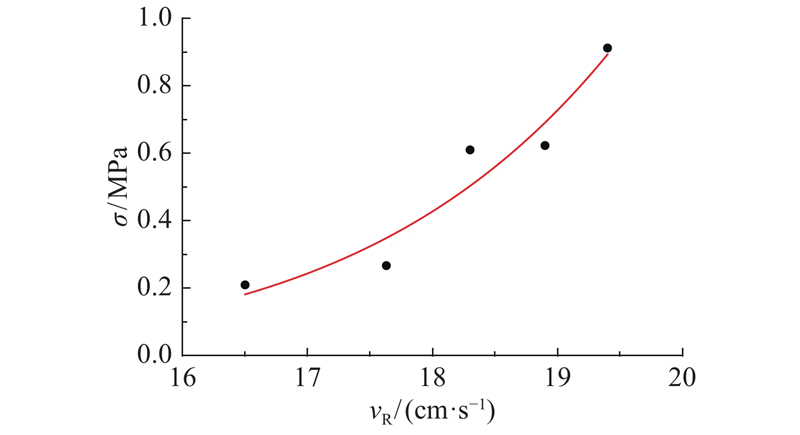
图 11
图 11 等效应力与峰值合振速拟合图
Fig.11 Fitting curve of equivalent stress and resultant peak velocity
拟合曲线的R2=0.93,拟合度较好.
4. HDPE给排水管道运营时安全评估
为了计算HDPE给排水管道运营时控制振速,须进行如下假设:1)假设土壤为线弹性均质,且在爆破地震波作用时管土无相对滑动,管材为非线性黏弹性且满足各向同性;2)不考虑埋置土层的深度、水的质量分数的影响;3)计算对象为直埋管道管身处,不考虑管道接口与弯管,因为按照规范要求,须通过法兰、套筒、热熔等方式处理接口、弯道、三通等薄弱环节,使其强度大于管身部分,以管身作为研究主体计算其控制振速是合理的.
为了得到爆破振动作用下HDPE波纹管道充水运营时的最大控制速度,利用规范给出的HDPE管道最大允许工作压力计算公式[19]:
式中:MOP为最大允许工作压力;PN为公称压力,取0.8 MPa;ft为50年寿命要求时,温度引起的压力折减系数,其中,当温度取20、30、40 °C时,折减系数分别为1.00、0.87、0.74(本研究中取温度为30 °C时的折减系数0.87). 在管道系统正常工作状态下,选用的管材最大设计内水压力pwd,且pwd=1.5MOP,结合前文MOP计算公式得到最大允许工作压力为1.044 MPa.
在设计内水压力作用下的管壁环向应力设计值为
式中:γQ为设计内水压力的作用分项系数,取1.2;D0为管截面计算直径;en为管壁计算厚度. 计算得到管壁环向应力设计值为26.31 MPa.
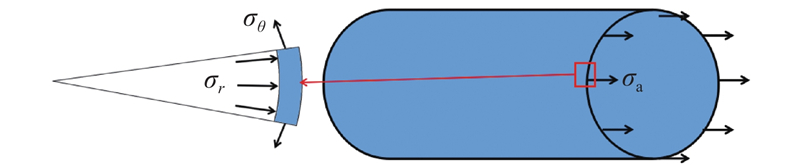
根据田峰等[20]提出的热力、动力管道在内压及外载作用下的应力计算公式,利用薄壁圆筒原理进行受力分析得到环向应力、轴向应力、径向应力的表达式:
式中:
图 12
设环向应力为已知量,可以利用环向应力来表示其他2个方向的应力:
考虑到PE管道的破坏形式以屈服时效为主,故利用米塞斯屈服准则进行评估[21]:
式中: σ1为第1主应力,σ2为第2主应力,σ3为第3主应力. 当
由前文拟合得到的管道危险截面处等效应力与峰值合振速之间的关系(式(7)),结合管道环向应力设计值[σθ]=26.31 MPa,可以得到运营状态管道安全控制速度为27.62 cm/s.
考虑到振动速度随水位的降低而增大,故假设当管道处于空管状况时的安全控制速度为27.62 cm/s,为了保证管道安全,通过振动速度与管道水位高度所占管道内径高度比例系数i之间的关系式(式(6)),计算得到满水时的安全控制速度为25.79 cm/s,以此作为管道运营时的安全控制速度是合理的.
5. 结 论
(1)通过现场试验发现,HDPE管在受爆破振动影响时,管道振速随爆心距增大、药量的减少而降低,环向压应变最大,管道更易在环向发生受压破坏.
(2)管道合振速与等效应力随着管内水位高度的增加而降低,且管道同一截面处迎爆侧的合振速和等效应力大于背爆侧,空管状态时合振速最大为18.56 cm/s,等效应力最大为0.912 MPa.
(3)在管道危险截面最低点处,X方向振动速度最大,Y方向次之,Z反向最小,且X方向振动速度与主频率随着水位高度升高而降低,Y、Z方向的振动速度与主频率随着水位高度的升高而增加;无论是满水还空管状态,主频均高于管道自振频率,管道不会发生共振破坏.
(4)通过管道环向应力、径向应力、轴向应力计算公式,结合等效应力与合振速拟合,利用米塞斯屈服强度准则得到管道运营状态安全控制速度为25.79 cm/s.
致谢 感谢武汉爆破有限公司谢先启院士及其团队姚颖康、刘昌邦、黄小武、钱坤、王威、岳端阳等对本研究给予的大力支持.
参考文献
Blast response of composite pipeline structure using finite element techniques
[J].DOI:10.1177/0021998315618768 [本文引用: 1]
Blast-induced dynamic response on the interface of a multilayered pipeline
[J].DOI:10.1080/15732479.2012.699532 [本文引用: 1]
Centrifuge modeling of earthquake effects on buried high-density polyethylene (HDPE) pipelines crossing fault zones
[J].DOI:10.1061/(ASCE)1090-0241(2008)134:10(1501) [本文引用: 1]
Factors influencing the behavior of buried pipelines subjected to earthquake faulting
[J].DOI:10.1016/j.soildyn.2008.04.006 [本文引用: 1]
地铁隧道钻爆法施工对邻近埋地管道影响的模型试验研究
[J].
Model test study on the influence of subway tunnel drilling and blasting construction on adjacent buried pipelines
[J].
下穿燃气管道爆破振动效应现场试验研究
[J].
Field experiment on blasting vibration effect of underpass gas pipeline
[J].
爆破荷载下埋地PE管道动力响应的试验研究
[J].DOI:10.3963/j.issn.1001-487X.2018.04.001 [本文引用: 1]
Experimental study on buried PE pipeline under blasting loads
[J].DOI:10.3963/j.issn.1001-487X.2018.04.001 [本文引用: 1]
Buckling failure of a buried pipeline subjected to ground explosions
[J].DOI:10.1016/j.psep.2017.11.017 [本文引用: 1]
Numerical simulation of dynamic response of water in buried pipeline under explosion
[J].
Blasting and construction vibrations near existing pipelines: what are the appropriate levels?
[J].
Effect of excavation blasting vibration on adjacent buried gas pipeline in a metro tunnel
[J].DOI:10.1016/j.tust.2018.08.022 [本文引用: 1]
Safety assessment of upper water pipeline under the blasting vibration induced by Subway tunnel excavation
[J].DOI:10.1016/j.engfailanal.2019.06.047 [本文引用: 1]
Stress and strain analysis of buried PE pipelines subjected to mechanical excavation
[J].DOI:10.1016/j.engfailanal.2019.104171 [本文引用: 1]
爆破振动作用下邻近埋地混凝土管道动力响应特性
[J].DOI:10.11918/j.issn.0367-6234.201611089 [本文引用: 1]
Dynamic response characteristics of adjacent buried concrete pipelines under blasting vibration
[J].DOI:10.11918/j.issn.0367-6234.201611089 [本文引用: 1]
超浅埋地铁站通道爆破暗挖地表振动传播特征
[J].
Characteristics of surface vibration propagation in tunnels of ultra-shallow buried subway stations
[J].
基坑爆破预留层对围护桩的保护作用数值分析
[J].DOI:10.3969/j.issn.1006-7051.2017.05.001 [本文引用: 2]
Numerical analysis of the protective effect of the reserved layer of foundation pit blasting on retaining piles
[J].DOI:10.3969/j.issn.1006-7051.2017.05.001 [本文引用: 2]
Monitoring the dynamic response of a buried polyethylene pipe to a blast wave: an experimental study
[J].DOI:10.3390/app9081663 [本文引用: 1]
动力管道的应力分析及管壁厚计算
[J].
Stress analysis and pipe wall thickness calculation of power pipeline
[J].