随着战场环境的复杂化和多样化,相控阵雷达的探测任务逐渐加重,这会使得不同的雷达工作方式对系统资源有竞争的需求. 对于搜索和跟踪2种主要工作方式,若搜索资源缺乏,则低可观测目标可能不能及时被发现. 若不利用足够的资源跟踪已发现目标,则可能导致目标航迹缺失甚至失跟. 为了充分发挥雷达系统的性能,制定合理的资源分配策略是必不可少的.
近些年来,很多方法被应用到相控阵雷达SATRA策略中. 对于搜索问题,重点是利用尽量少的资源来扩大监视区域或提高目标检测能力,Hoffmann等[1-4]通过控制搜索参数,实现了搜索RA策略. 对于跟踪问题,重点是提高跟踪质量或跟踪目标数量,学者们利用协方差控制[5-7]和克拉美罗界(Cramer-Rao low bound, CRLB)控制[8-13]的方式,实现了对波束指向[8-11]、驻留时间[11]和发射功率[9,12-13]等参数的优化. 现有工作对SATRA问题的解决方案大多是基于优化规则的[14-16],问题被描述为一个最优控制过程,目标函数通常设置为搜索能力和跟踪质量的加权和,这些方法的缺点是权重的选定和非对称指标的无意义聚合,不能相对客观准确地反映问题的本质.
从上述分析可知,在有限的时间资源约束下最大化搜索能力和跟踪质量是2个相互冲突但必须同时考虑的问题. Charlish等[17]将雷达资源分配问题建模为连续双重拍卖问题,通过相应机制确定Karush-Kuhn-Tucker条件的竞争市场均衡,产生的最优解明显改善雷达的整体工作性能. Yan等[18]将SATRA问题制定在双目标约束优化的框架下,使用Pareto理论确定其多个最优解,以便在不同的场景下选择最优的分配策略. Shi等[19]在非合作博弈理论的框架下,在目标检测信噪比和最大干扰容限的约束下,实现了分布式雷达的功率分配. 目前,基于博弈论的资源分配策略在通信领域取得了很好的成果,有一定的借鉴意义. 王妍等[20-22]在合作博弈的理论指导下,完成了对链路信道及服务器容量的分配. Jiang等[23-24]将链路网络能量分配问题建模为非合作博弈模型,提高了网络的能量利用效率.
从上述研究可以看出,对相控阵雷达SATRA问题的研究还很缺乏. 事实上,相控阵雷达在不同情况下对SAT有不同的偏好,博弈论框架给RA策略提供了多角度的解决方案来满足决策者的需求,故博弈视角下SATRA策略具有更大的意义与优势. 本文在有限的时间资源约束下,将SATRA建模为非合作博弈问题,将其子资源的分配建模为合作博弈问题. 为了快速找到满足决策者偏好的解,将其转化为单目标优化问题,利用并行的混合遗传算法(genetic algorithm,GA)和粒子群算法(particle swarm optimization,PSO)求解上述问题的最优解,通过仿真验证了本文策略的有效性和先进性及寻优算法的优越性.
1. 相控阵雷达搜索和跟踪模型
相控阵雷达的任务是发现责任区内的未检测目标并更新已知目标的跟踪状态,责任区是根据外部环境和作战任务划定的雷达监视空域范围. 为了最大化雷达同时管理2类任务的能力,资源管理器必须动态地改变这2类任务之间有限资源的分配情况.
雷达部署在
1.1. 搜索模型
假设在第
式中:
考虑到检测概率
1.2. 跟踪模型
第
式中:
当目标被照射后,可以从目标
式中:
其中
式中:
2. 博弈视角下SATRA问题建模
从上述模型可以看出,当搜索资源增加时,搜索信噪比提高;当跟踪资源增加时,跟踪误差降低,在有限的时间资源下,搜索和跟踪任务必然存在竞争关系,非合作博弈理论为其提供了很好的解决方案. 多空域搜索间和多目标跟踪过程中存在子资源分配问题,考虑其间是一种协同合作的关系,将上述问题分解为合作博弈的子空域(sub-airspace,SA)和多目标(multiple object,MO)间RA问题和非合作博弈的SATRA问题.
2.1. 非合作博弈的SATRA问题分析
非合作博弈模型
式中:
则局中人
对于本文问题,搜索和跟踪作为局中人. 对于搜索,信噪比越大,检测概率越大,越容易发现远距低可探测目标,故搜索效用函数
对于跟踪,状态估计误差越小,目标的跟踪精度越高. 为了更好地体现目标跟踪误差,根据文献[26]可知,目标状态估计的CRLB为
式中:
式中:
其中
2.2. 合作博弈的SARA和MORA问题分析
合作博弈中不存在统一的解,其中Shapley值是具有不同良好性质的解中最重要的一种,它将成本按照边际成本进行分摊,体现了分配的公平性和平等性. 利用Shapley值对SARA和MORA问题进行分析建模. 合作博弈
为局中人
对于搜索区域,搜索空域越大,应分配到更多的资源,故定义搜索的特征函数为搜索空域的面积;对于跟踪目标,跟踪误差越大,下一周期应分配更多的资源,故定义跟踪的特征函数为跟踪目标的CRLB,即
式中:
2.3. 联合优化模型建立
在非合作博弈中,每个局中人都是选择对自己最有利的策略,形成大家都不愿意去改变的稳定局势,即纳什均衡局势,数学描述如下:设
则称
综合上述分析可知,本文资源分配问题的纳什均衡解可以通过求解双目标优化问题得到,即最大化
式中:
上述双目标优化的非劣解集即为所求的纳什均衡点集,实际资源分配结果是解集中最能体现决策者偏好的某个解. 为了提高决策效率并兼顾决策偏好,利用理想点法将上述双目标优化问题转化为单目标优化问题,即使各目标值尽可能逼近理想值;由于
式中:
其中,
为了实时反映决策者的偏好,须对系数
式中:
3. 混合遗传粒子群算法
3.1. PSO算法
PSO将每个优化问题的潜在解作为搜索空间中的“粒子”,所有粒子都有一个被优化的函数决定的适应度,每个粒子还有一个速度决定它们飞翔的方向和距离;通过迭代寻优,每个粒子通过跟踪2个极值来更新自己在解空间中的位置和速度. 结合上述优化问题,对粒子群算法介绍如下.
假设在一个由
式中:
3.2. GA算法
GA通过对当前群体施加选择、交叉和变异等一系列遗传操作,从而产生新一代的群体,并逐步使群体进化到包含或接近最优解的状态. GA把可行解空间转换到其所能处理的搜索空间中的操作,称作编码. 常用的编码方式有二进制编码和实数编码,本文采用实数编码,该方式适合于精度较高的问题,同时降低了计算复杂度. 群体由
3.2.1. 适应度函数设计
适应度函数是度量个体适应度的函数,其值定义为非负,故通过目标函数
式中:
相控阵雷达搜索和跟踪过程的目标函数随资源变化是非线性的,为了提高算法的性能,须对适应度函数进行改进,借鉴文献[30],即
式中:
3.2.2. 选择算子、交叉算子和变异算子
选择又称为复制,是在群体中选择生命力强的个体产生新的群体的过程. 利用比例选择方法,则个体i被选择的概率Pi为
通过上述方式会破坏适应度较高的优良个体,使得问题收敛速度慢甚至陷入局部最优,故引入最优保存策略保护优秀个体. 基本思想概括如下:当前种群中适应度最高的个体不参与进化,而是用它替换掉本代种群中经过杂交、变异等遗传后所产生的适应度最低的个体.
交叉算子是个体间交配重组的过程,对于实数编码方式,常采用算术交叉方式开展. 假设在两个体
式中:
变异算子是个体间染色体等位基因替换的过程,为了增加种群的多样性,采用均匀变异的方式. 上述操作过程描述如下:依次指定个体中每个基因座为变异点,对每个变异点,以变异概率
3.3. PHGAPSO算法
为了整合PSO和GA在寻优时各自的优势,提出PHGAPSO. 该方法将个体(粒子)用混合概率
图 1
4. 仿真实验
为了说明博弈策略求解SATRA问题的有效性和先进性,揭示问题内在机制,在设定的场景下将博弈论(game theory,GT)方法与文献[18]的帕累托双目标优化(Pareto bi-objective optimization,PBO)方法进行对比分析.
4.1. 对比方法[18]介绍
该方法将相控阵雷达SATRA分配问题建模为双目标优化问题,从模型的帕累托解中寻求资源分配方案. 为了减少可行方案的数目,选取以最小检测信噪比和最大CRLB水平下的帕累托前沿面,求得搜索和跟踪所需的最少资源,在有限的资源约束下利用比例法寻求最优分配方案.
4.2. 仿真场景
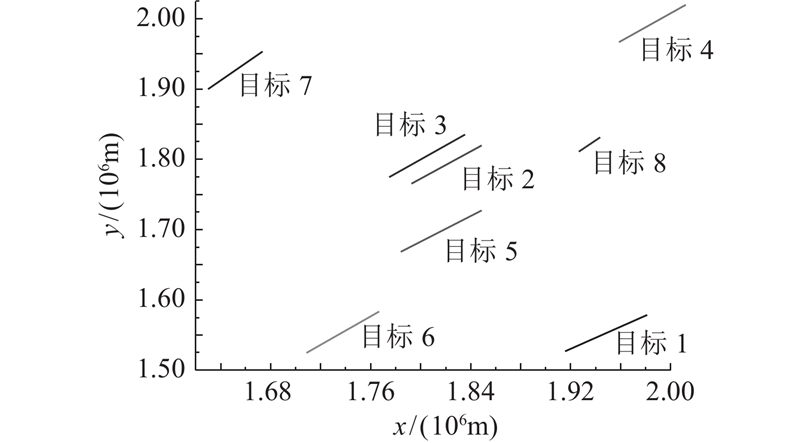
假设雷达固定在坐标(0,0)位置,信号带宽Bk=1 MHz,3 dB波束宽度βk=1º,当目标σ=1 m2时,系统常数ρ=2.28×1026,决策周期设置为T0=1 s,时间利用率取η=0.9,仿真总时间为20T0;最小可检测概率Pdmin=0.9,虚警概率Pf=10-6,跟踪误差门限Pthr=500 m. 在实际情况下,雷达搜索空域和跟踪目标数目是变化的,具体场景如下:初始跟踪目标为5个,1~10周期内,搜索空域布置如表1所示,同时,在第6周期时,跟踪目标增加2个;在11~15周期,搜索空域布置情况的变化如表2所示,在第16周期时,跟踪目标增加1个. 目标飞行速度为10~12马赫,目标空间的分布情况如图2所示.
表 1 1~10周期搜索空域1布置参数
Tab.1
| 空域序号 | Rm,k / (103 km) | φm,k / (°) |
| 1 | 2.5 | 10 |
| 2 | 2.5 | 12 |
| 3 | 2.7 | 10 |
| 4 | 2.8 | 8 |
| 5 | 3.0 | 10 |
| 6 | 2.9 | 6 |
表 2 11~20周期搜索空域2布置参数
Tab.2
| 空域序号 | Rm,k / (103 km) | φm,k / (°) |
| 1 | 2.4 | 6 |
| 2 | 2.4 | 8 |
| 3 | 2.6 | 8 |
| 4 | 2.8 | 8 |
| 5 | 3.0 | 16 |
| 6 | 3.0 | 10 |
| 7 | 2.7 | 6 |
| 8 | 2.5 | 8 |
图 2
图 2 雷达责任区内的目标运动轨迹示意图
Fig.2 Schematic diagram of target motion trajectory in radar area of responsibility
对PHGAPSO算法的关键参数值进行设置,如表3所示. 表中,Pres为时间资源分配比例.
表 3 PHGAPSO算法参数设计
Tab.3
| 参数 | 数值 | 参数 | 数值 | |
| L | 100 | c1 | 2 | |
| Pc | 0.4 | c2 | 2 | |
| Pm | 0.05 | Pres | 0~1.0 | |
| T | 50 | v | 0.002~0.010 | |
| ω | 0.7 | PH(t) | 0.5 |
4.3. 仿真结果分析
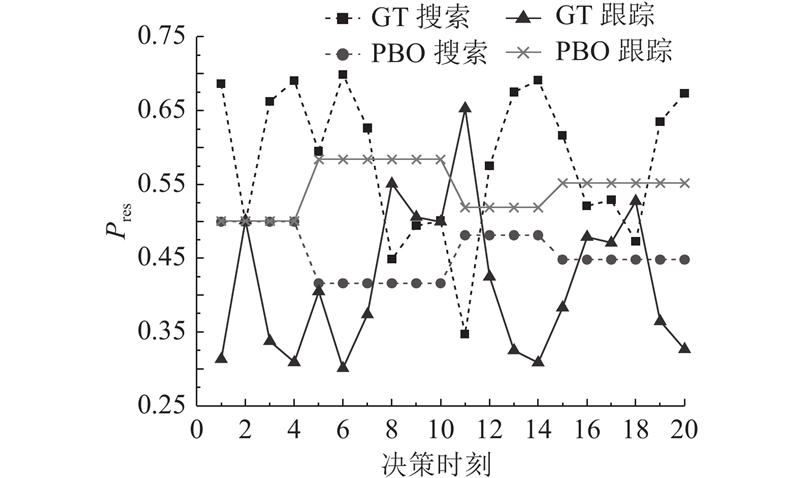
在上述场景下,博弈分配方法和帕累托双目标优化方法下的搜索和跟踪资源分配结果如图3所示. 可以看出,GT方法不仅可以在搜索空域和跟踪目标数变化时及时采取合适的资源分配方案,而且能够在系统状态发生变化时对资源分配方案进行调整,更具有灵活性. PBO方法仅仅是在搜索空域和跟踪目标数量发生变化时进行资源分配调整,在其他决策时刻时的资源分配方案基本保持不变.
图 3
图 3 GT和PBO方法的资源分配结果对比
Fig.3 Comparison of resource allocation results between GT and PBO methods
在图3分配方案下得出的2种方法的搜索和跟踪效用函数值,如图4、5所示. 图中,SCRLB为克拉美罗下界. 在初始时刻,雷达资源较充足,目标的初始跟踪误差较小,GT方法相比PBO方法分配搜索工作方式更多资源;当第6周期跟踪目标增加时,GT方法相比PBO方法分配给跟踪工作方式更多资源;当第11周期搜索区域扩大时,GT方法相比PBO方法分配给搜索工作方式更多资源,如此往复. 经过计算可知,GT方法的平均搜索信噪比和跟踪CRLB分别为26.49 dB和172.56 m,PBO方法的平均搜索信噪比和跟踪CRLB分别为26.22 dB和175.21 m,平均搜索信噪比提高了1.02%,平均跟踪目标误差降低了1.55%.
图 4
图 4 GT和PBO方法的搜索效用对比
Fig.4 Comparison of search utility between GT and PBO methods
图 5
图 5 GT和PBO方法的跟踪效用对比
Fig.5 Comparison of track utility values between GT and PBO methods
从上述分析可以看出,GT方法能够根据搜索和跟踪系统的变化情况实时地调整资源分配情况,达到搜索和跟踪性能的最佳平衡. 这是因为GT方法将大部分资源流动分配给搜索和跟踪工作方式,提高了各个决策时刻资源的可利用率,PBO方法时刻保证2种工作方式具有一定的资源,这是限制PBO方法调度性能的根本原因.
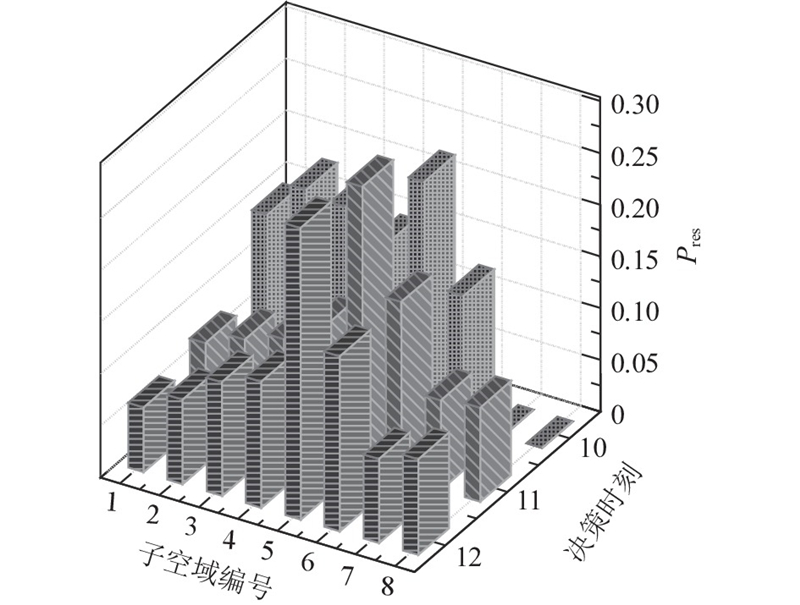
图 6
图 6 典型帧周期实际子空域资源分配图
Fig.6 Actual subspace resource allocation map at typical frame period
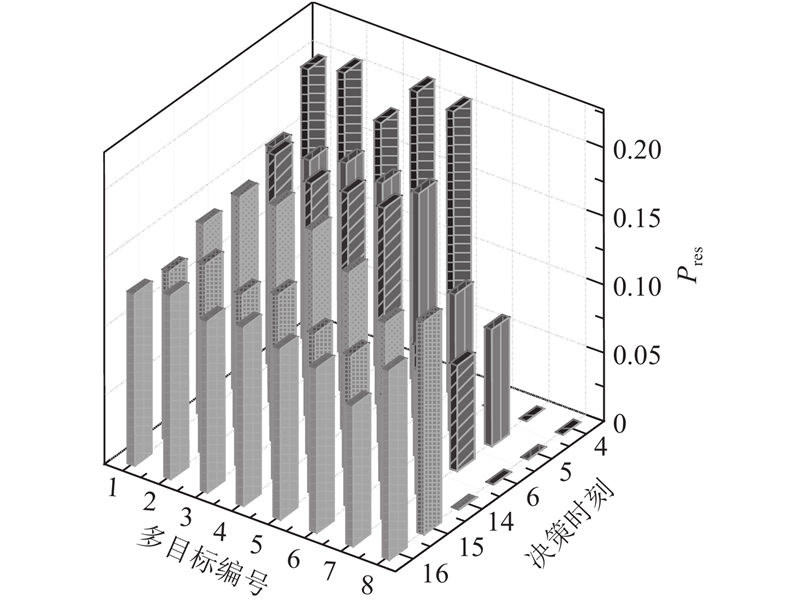
图 7
图 7 典型帧周期实际多目标资源分配图
Fig.7 Actual multi-target resource allocation map at typical frame period
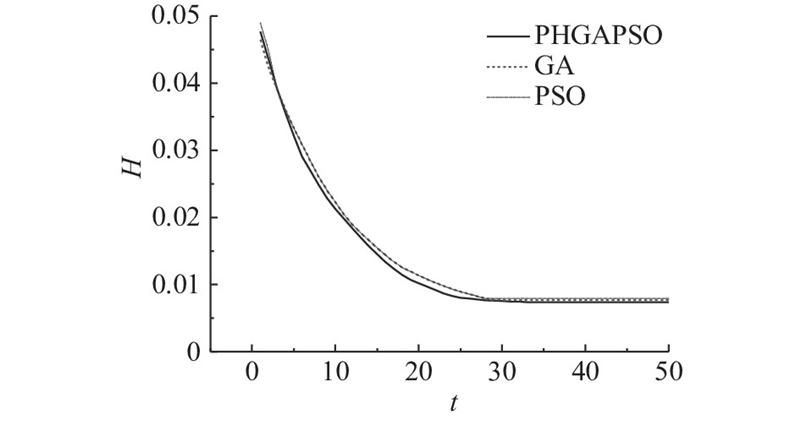
给出PHGAPSO算法与GA和PSO寻优性能的对比曲线,如图8所示. 可以看出,在迭代次数相同的条件下,PHGAPSO的寻优精度更高;在适应度相同的条件下,所需的迭代次数更低. 为了反映算法寻优的实时性,各算法的寻优时间和性能指标如表4所示. 表中,Hmax为适应度最优值,tcom为算法运行时间. 实验平台为Windows1 064位操作系统,计算机配置为Intel Core i5-8250U CPU,主频为1.6 GHz,显示适配器为NVIDIA GeForce MX150;在相同的条件下,PHGAPSO的寻优精度较GA提高了4.26%,较PSO提高了7.30%,各算法的运行时间均满足资源分配的实时性.
表 4 各算法寻优性能指标统计表
Tab.4
| 算法 | Hmax | tcom/s |
| PHGAPSO | 0.007 368 | 3.505 643 |
| GA | 0.007 682 | 1.842 562 |
| PSO | 0.007 906 | 1.822 971 |
图 8
图 8 各寻优算法性能曲线的对比图
Fig.8 Comparison curve of performance curves of various optimization algorithms
5. 结 论
(1)利用博弈视角下资源分配问题解的非唯一性,为相控阵雷达资源分配问题提供了有效的多解决方案.
(2)利用动态加权的理想点法将双目标优化模型转化为单目标优化模型,为快速获得满足决策者偏好解提供了解决思路.
(3)提出混合并行遗传粒子群算法,提高了模型求解的效率和精度.
(4)提出的解决问题的理论框架具有良好的拓展性,可以解决多功能相控阵雷达多工作方式下的资源分配问题.
参考文献
相控阵雷达资源受限时最优搜索性能研究
[J].
Research on optimal search performance of phased array radar under resource constraints
[J].
Search optimization for minimum load under detection performance constraints in multi-function phased array radars
[J].
Joint beam and waveform selection for the MIMO radar target tracking
[J].
多目标跟踪中自适应时间资源调度
[J].
Adaptive time resource scheduling in multi objective tracking
[J].
Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept
[J].
Simultaneous multibeam resource allocation scheme for multiple target tracking
[J].DOI:10.1109/TSP.2015.2417504 [本文引用: 1]
Scaled accuracy based power allocation for multi-target tracking with colocated MIMO radars
[J].DOI:10.1016/j.sigpro.2019.01.014
基于多目标跟踪的相控阵雷达波束和驻留时间联合分配方法
[J].
Phased array radar beam and dwell time joint allocation method based on multi-target tracking
[J].
Joint node selection and power allocation strategy for multi-target tracking in decentralized radar networks
[J].DOI:10.1109/TSP.2017.2777394 [本文引用: 1]
Receive-beam resource allocation for multiple target tracking with distributed MIMO radars
[J].DOI:10.1109/TAES.2018.2818579 [本文引用: 2]
Cognitive radar network: cooperative adaptive beamsteering for integrated search-and-track application
[J].DOI:10.1109/TAES.2013.6494389 [本文引用: 1]
Distributed multi-target search and track assignment with consensus-based coordination
[J].DOI:10.1109/JSEN.2014.2355200 [本文引用: 1]
Phased array radar resource management using continuous double auction
[J].DOI:10.1109/TAES.2015.130558 [本文引用: 1]
Resource allocation for search and track application in phased array radar based on pareto bi-objective optimization
[J].DOI:10.1109/TVT.2019.2894960 [本文引用: 3]
Non-cooperative game theoretic power allocation strategy for distributed multiple-radar architecture in a spectrum sharing environment
[J].DOI:10.1109/ACCESS.2018.2817625 [本文引用: 1]
Shapley值的LTE系统下行QoS感知资源调度
[J].
Downlink QoS aware resource scheduling for LTE systems with Shapley values
[J].
Cooperative game based resource allocation in hybrid D2D cellular network
[J].DOI:10.14257/ijfgcn.2017.10.3.08
Cost sharing of cooperating queues in a Jackson network
[J].DOI:10.1007/s11134-012-9336-4 [本文引用: 2]
Resource allocation in energy constrained cooperative cognitive radio network
[J].
Energy-efficient uplink resource allocation based on game theory in cognitive small cell networks
[J].DOI:10.1007/s11277-016-3927-z [本文引用: 1]
Posterior Cramér-Rao bounds for discrete-time nonlinear filtering
[J].DOI:10.1109/78.668800 [本文引用: 1]
基于混合遗传-粒子群算法的相控阵雷达调度方法
[J].
Phased array radar scheduling method based on hybrid genetic-particle swarm optimization
[J].
Optimal allocation of cooperative jamming resource based on hybrid quantum-behaved particle swarm optimisation and genetic algorithm
[J].
Optimization of antenna array deployment for partial discharge localization in substations by hybrid particle swarm optimization and genetic algorithm method
[J].