实时城市配送具有点对点、小批量、多频次的特点,故对物流配送的及时响应和灵活性皆均有较高的技术要求. 实时城市配送决策高度依赖于动态环境,须及时处理配送系统中由各种动态事件带来的实时变化,因此出现了带时间窗的动态取送货问题(dynamic pick-up and delivery problem with time windows,DPDP-TW). 近年来,对于DPDP-TW的研究备受关注,实时城市配送的发展也极为迅速. 针对该问题,在传统的DPDP-TW基础上,考虑4种实时信息,即新请求出现、旧请求的改变或取消、交通拥堵和车辆抛锚,称为考虑真实场景多项动态事件的动态取送货问题(dynamic pick-up and delivery problem considering multiple dynamic events in a real-world environment,DPDP-MDE),尝试揭示动态事件对真实场景取送货问题的影响规律,提高实时动态决策能力和快速响应能力.
针对DPDP-TW以及DPDP-MDE建模问题,大多数研究者为了简化问题,考虑单项动态事件的影响. 较少有文献如Francesco等[1]同时响应和有效处理新请求到达、交通拥堵和车辆扰动3种动态事件,提出实时控制方法以实现制定路径规划与执行运输服务(需求)同步控制,并采用禁忌搜索算法进行规划调整. 针对新请求出现的单项动态事件,Fabri等[2]采用新请求插入方法,在新请求出现后算法会更新目前路径计划,将新请求分配给每一辆车,转化为单车路径规划问题. Mitrovic´-Minic´等[3]采用最小值插入算法等待策略插入新增请求,比较研究多种请求增加时的等待策略. Branke等[4-7]采用缓冲策略,在请求出现后将该请求搁置一段时间或者令车辆移动到未来请求较容易到达的节点. Pureza等[8]证明在无容量限制的动态取送货问题中采用等待策略和缓冲策略整合新请求的优势. 针对交通拥堵单项动态事件,Kok等[9]采用选择替代路线、更改客户访问顺序和更改车辆分配等措施,提出反映交通拥堵高峰时段车辆速度模型,消除路径规划中87%的交通拥堵. Sun等[10]从运输服务商通过选择运输请求来取得最大化利润和利用交通状况的周期性两方面优化DPDP-TW的运输服务,在交通流较少时段对车辆进行路径规划. 针对车辆抛锚单项动态事件,Mamasis等[11]针对城市单一产品配送过程中车辆抛锚问题,在团队定向问题模型的基础上考虑最大时间约束、最大距离约束和车辆容量约束,重构路径规划模型,采用快速标记算法几乎可以实时得到有效解.
关于时变条件下的DPDP-TW问题,Bruce等[12]围绕行驶时间建模、应用和求解,系统进行时变条件下路径规划问题文献解析. Sun等[10]研究一系列时变条件下的DPDP-TW问题,采用分支定界的算法求解,通过数值算例对改进算法框架的有效性和加速技巧的影响进行评估. Kritzinger等[13]评价时变条件下车辆路径规划问题的算法,采用可变邻域搜索算法显著改善解的质量. Gerardo等[14]总结时变条件下DPDP-TW的2种优化方法,即时法和滚动时域法. Michel等[15]在解决DPDP-TW时采用即时法,即每出现一个新信息(新的请求或请求取消),就进行全局重新优化,这样会造成计算时间过长不适合实时情景. 滚动时域法相继由Mitrovic´-Minic´等[3, 16]提出,该方法将调度时域分解为更小的时间间隔,在调度时域开始时按照静态问题的算法求出初始解,之后当信息到来时采用插入法或删除法这类启发式算法更新初始解. Pisinger等[17]采用滚动时域的框架和分割调度时域,解决动态车辆路径规化问题. 可见,滚动时域法与静态问题的算法深度结合在求解真实场景DPDP-MDE问题时具有独特优势,在其动态算法框架中,静态问题求解算法及其优化对于实时场景问题快速求解具有重要作用. 本研究在完善动态算法框架的同时,通过禁忌搜索算法(TS)和自适应大规模邻域搜索算法(ALNS)改善初始可行解质量,并运用动态插入法解决未固定请求和新请求同步处理问题.
本研究综合考虑新请求出现、旧请求改变或取消、交通堵塞和配送车辆抛锚4种真实场景动态事件的影响重构规划模型;将滚动时域法与禁忌搜索算法和自适应大规模邻域搜索算法相结合,完善动态算法框架.
1. 模型建立
1.1. 问题描述
本研究提出的DPDP-MDE数学规划模型如下:假定所有相应的服务请求由车场调度车辆去完成,每一辆车在调度期开始时从车场出发,在调度期结束之前必须返回车场. 每辆车必须先访问请求的取货点然后运送至相应的送货点完成一个完整的请求. 每一个请求对取货点和送货点都有时间窗要求,而且在整个模型中动态出现. 假定每个间隔为
在规划路径时,考虑传统模型以外的4种因素,即请求改变、新请求出现、交通拥堵和车辆抛锚. 在调度时域
1.2. 符号表示
1.2.1. 常量
DPDP-MDE数学规划模型中常量定义如下:
1.2.2. 变量
DPDP-MDE数学规划模型中变量定义如下:
1.2.3. 决策变量
DPDP-MDE数学规划模型中决策变量定义为
式中:
1.3. 模型建立
所提出的考虑4种实时信息的动态取送货问题单目标规划模型建立如下:
限制条件如下:
式(1)为目标函数,表示
式(2)~(17)为约束条件,详细说明如下:
1)车辆路径问题基本式. 式(2)确保每一个节点只被访问一次,动态问题中的节点是指在新增请求、修改请求和车辆抛锚这些动态事件发生后未固定请求的取送货节点;式(3)、(4)确保每一辆车从车场或时刻车辆位置出发,最后返回车场. 在动态问题建模中,车辆的位置除了车场位置和上一个间隔结束位置,还有无法进行生产活动的抛锚车辆在路径规划中被剔除的位置;式(5)为流平衡式,即确保一辆车访问了一个节点后就必须从这个节点离开.
2)取送货式. 式(6)为取送货问题特有的配对式,即确保一个请求的取货点和送货点只能由同一辆车访问;式(12)为取送货问题特有的优先式,即确保一个请求的取货点在送货点之前被访问.
3)时间窗式. 时间窗式由式(10)、(11)表示,式(10)表示车辆
4)容量式. 式(7)~(9)共同为容量式,在考虑车辆的运载能力下满足顾客货运需求,从而设计路径方案;容量式表明在任何时刻车辆的负载不超过车辆的最大容量,须特别注意的是,在动态问题中,已经执行任务的车辆在重新规划时车辆是有负载的,这与静态问题不同.
5)调度时域式. 式(13)确保服务时间不超过动态问题的调度时域的最大长度.
6)距离式. 式(14)、(15)确保在任何时间车辆的总行驶距离不超过车辆的最大行驶距离;式(16)、(17)确保车辆在最大行驶距离内返回车场;须特别注意的是,在动态问题中,已经执行任务的车辆在重新规划时车辆已经行驶了一定距离,这与静态问题不同.
2. 动态算法框架设计
动态算法或在线算法本质上是动态环境中的算法框架. 本研究的动态算法的流程图如图1所示,即将问题分割成许多静态子问题,以方便利用构造型算法和改善型算法求得静态子问题的解.
图 1
在动态算法中,采用启发式算法求解调度时域子间隔. 其中求解分为2个阶段:第1阶段,采用构造型算法求出调度时域子间隔问题的初始解,详见2.1节;第2阶段,采用改善型算法,即禁忌搜索算法和自适应大规模邻域搜索算法这2种智能算法,改善第1阶段的初始解的质量,详见2.2节. 在构造和改善初始解之后,在2.3节中使用动态插入法重新规划路径.
2.1. 构造初始解
作为经典车辆路径问题的衍变,基于实时信息的动态取送货问题要求:与1个请求相关的2个节点须满足同车服务,取货节点在送货节点前访问,这些复杂约束条件须采用构造型算法构造初始可行解.
从一条空路径开始,随机选择一个未安排的请求插入. 对于每一个请求而言,检查现存路径中所有可行的取货点和送货点插入位置. 这里的可行位置是指满足取货点在送货点之前的约束、取货点与相应送货点在同一条路径上的约束、容量约束和时间窗约束. 并且,初始化一条新的路径插入该请求. 比较所有可行位置,选择适应度函数(式(1))最小的插入位置,将所有未被安排的请求插入到路径中.
2.2. 改善初始解
初始解通常具有较大的改善空间. 考虑到该问题是NP-hard问题,在第2阶段采用对求解效率和质量有着较好协调能力的智能算法改进初始解.
2.2.1. 禁忌搜索算法
禁忌搜索算法是对人类思维过程的模拟,通过对一些局部最优解的禁忌(也可以说是记忆)达到接纳一部分较差解,以保证多样化的有效探索,从而实现全局搜索.
1)邻域移动. 采用邻域移动获得候选解. 如图2所示,从初始解的一条路径中随机移除一对取货点和送货点,再重新插入到初始解中的一条路径中,判断邻域解的可行性,并选择所有可插入位置中使得适应度函数最小的位置,得到的解就是候选解.
图 2
2)禁忌对象. 禁忌对象为边,如图2所示,转换后的红色虚线为禁忌对象. 边AB为间接取货边,边DE为间接送货边,边GH为直接取货边,边HE为直接送货边. 所有引起这些边发生变化的邻域移动都是禁忌的.
3)禁忌表长度和停止准则. 禁忌表长度和停止准则与静态子问题中须重新规划的请求数量成正比. 静态子问题中须规划的请求数量在求解过程中是动态的,须在每一次运行禁忌搜索算法前实时确定.
4)选择策略. 以候选解集为整个邻域,从中选择适应度函数为最小的解,作为下一次迭代的初始解.
5)渴望水平. 当邻域中存在一个解的适应度函数的值最小,且比此次迭代的初始解的适应度函数值小,则无论这个移动是否是禁忌的,都接受这个解.
2.2.2. 自适应大规模邻域搜索算法
自适应大规模邻域搜索算法的主要依据是根据破坏算子和修复算子扩大搜索范围. 通过给每个破坏算子和修复算子分配一个权重,再根据算子的表现调节权重,从而控制每个算子在搜索期间的使用频率,这样的自适应调节能够更快找到更优邻域.
1)动态选择算子. ALNS根据算子以前的表现选择破坏操作和修复操作的组合以产生邻域. 为了扩大邻域的搜索范围,表现较差的算子将以较低的概率继续生成邻域,本研究采用轮盘赌的方式生成选择各算子的概率. 假定有
在迭代开始时每一个算子
为了更新权重,
式中:
2)破坏算子.(a)最差请求去除(worst removal). 先计算每一个请求去除后的成本减少量,再随机选择r%的请求去除. 这里被选择的概率随成本减少量的增加而增加.(b)随机去除(random removal). 随机选择r%的请求从目前的解中去除.(c)相关节点去除(related removal). 去除相关节点,2个请求的相关性与取货点和送货点的距离、服务时间的差和需求量的差有关. 为了适于本研究问题,设相关度为
式中:
3)修复算子. 采用基于最佳插入和遗憾原则的2种插入法.(a)最佳插入法. 在每次迭代时,计算每一个移除请求的最佳插入成本,最低插入成本的请求放在最后的插入位置. 直到所有请求都被插入到路径中.(b)遗憾插入法. 基于后悔的算法,
4)接受和停止准则. 若新解的适应度函数值f(s′)小于当前解f(s),则接受这个解;若新解的适应度函数值f(s′)大于当前解,根据模拟退火准则接受新解. 在每一次迭代时,模拟退火方法以
5)自适应方面. 采用破坏和修复操作生成邻域,邻域
2.3. 动态插入法
动态算法框架将整个调度时域分为多个间隔,在间隔之间,存在已经完成的路径、上一个间隔已经规划还未访问的请求和新请求. 须采用动态插入法重新规划路径,本研究采用未固定请求插入法. 如果在时间
未固定请求插入法是指,在间隔之间,先从原路径中移除所有未固定请求,再采用2.2节中的构造型算法将这些未固定请求和新请求重新插入到路径中. 如图3所示为未固定请求插入法重新插入动态新请求的例子. 图中,蓝色虚线为已经完成的路径,黑色实线为已规划但还未执行的路径,Depot代表车场,以p结尾的节点代表取货点,以d结尾的节点代表送货点,相同的数字代表同一个请求.
图 3
3. 算例分析
3.1. 实验数据
以Li等[7]在研究静态的PDPTW时所生成的数据为基础,数据来源为
本研究所有程序用MATLAB9.5编写,实验环境为Intel(R)Core(TM)i7-4790 CPU 3.60 GHz.
3.1.1. 请求出现时间
相比于普通的静态问题,动态问题中每一个请求都有一个出现时间. 本研究的请求出现时间表达式为
式中:
紧迫度
3.1.2. 实时交通状况下车辆的速度
本研究在解决动态问题时,将调度时域分割成许多间隔,进行多次路径与调度的规划. 在每次开始规划时,系统会根据此刻每一辆车所在的时段和位置,采用智能交通系统获取每一辆车的车速. 间隔时间越短车速越准确,规划方案越准确. 在本研究中,在时段T内,位于区域c的车速表达式为
式中:
例如,当新请求出现时,通过式(21)中的参数
3.2. 数值分析与比较
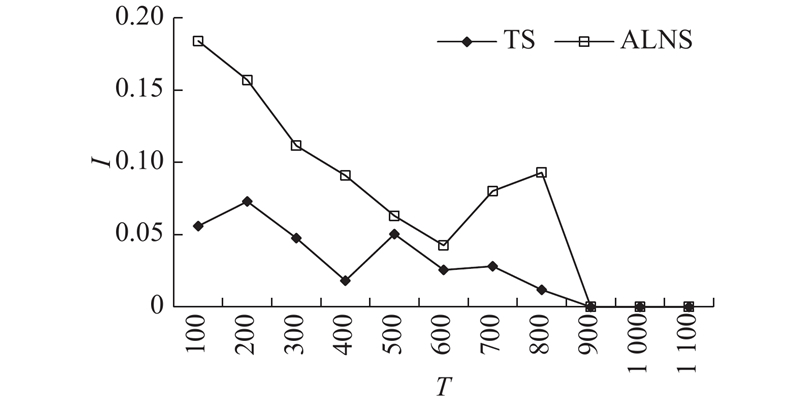
3.2.1. 调度时域 $T$
图 4
图 5
图 5 不同间隔下TS和ALNS的改善程度
Fig.5 Degree of improvement of TS and ALNS at different scheduling time horizon
3.2.2. 不同紧迫度下解改善程度的比较
图 6
图 6 不同紧迫度下2种算法的解的改善程度对比
Fig.6 Comparison of improvement degree of solution of two algorithms under different urgency degrees
图 7
图 7 不同紧迫度下2种算法的计算时间对比
Fig.7 Comparison of computation time of two algorithms under different urgency degrees
相比自适应大规模邻域搜索算法,禁忌搜索算法的解的质量虽然不高,但计算时间较少且相对稳定;在紧迫度较高时,自适应大规模邻域搜索算法的计算时间与禁忌搜索算法相近,同时解的质量更高.
3.2.3. 不同请求规模的比较
在不同请求规模下,2种改善算法的对比如表1所示. 采用第2节的算法求出请求规模分别为50、100、200、300(即节点数分别为100、200、400、600)的算例,其中自适应大规模邻域搜索算法的缺省处为计算时间过长(超过1 h),因此不再列出具体时间. 通过对比禁忌搜索算法和自适应大规模邻域搜索算法这2种智能算法对解的改善程度和计算时间,可以得出以下结论.
表 1 不同请求规模下2种改善算法的对比
Tab.1
| 请求规模 | 数据来源 | 初始解 | 改善解 | 改善程度/% | 计算时间/s | |||||
| TS | ALNS | TS | ALNS | TS | ALNS | |||||
| 50 | lc101 | 13499.29 | 12685.16 | 10765.53 | 6.03 | 20.25 | 0.72 | 8.87 | ||
| 50 | lr101 | 5334.35 | 4463.41 | 4405.10 | 16.33 | 17.42 | 12.72 | 66.74 | ||
| 50 | lrc101 | 5690.40 | 5170.15 | 4953.49 | 9.14 | 12.95 | 23.47 | 93.83 | ||
| 100 | LC1_2_1 | 28761.62 | 27062.05 | 25699.91 | 5.91 | 10.65 | 4.01 | 741.44 | ||
| 100 | LR1_2_1 | 17411.13 | 15640.55 | 14755.93 | 10.17 | 15.25 | 5.74 | 633.92 | ||
| 100 | LRC1_2_1 | 18524.11 | 16154.23 | 15645.90 | 12.79 | 15.54 | 12.26 | 1026.40 | ||
| 200 | LC1_4_1 | 17411.13 | 15640.55 | 15003.17 | 10.17 | 13.83 | 10.16 | 1218.88 | ||
| 200 | LR1_4_1 | 18524.11 | 16154.23 | 15856.64 | 12.79 | 14.40 | 15.46 | 4711.36 | ||
| 200 | LRC1_4_1 | 43170.27 | 40406.39 | 38145.25 | 6.40 | 11.64 | 68.78 | 12203.84 | ||
| 300 | LC1_6_1 | 77561.53 | 73369.65 | − | 5.40 | − | 19.39 | − | ||
| 300 | LR1_6_1 | 90873.69 | 83317.97 | − | 8.31 | − | 46.48 | − | ||
| 300 | LRC1_6_1 | 48895.00 | 43278.83 | − | 11.49 | − | 58.03 | − | ||
1)禁忌搜索算法在4种规模下都能够得到优化结果,其计算时间基本小于60 s;自适应大规模邻域搜索算法在请求规模达到300时,计算时间超过3600 s,对于求解动态问题无实际意义.
2)由表1可知,在改善程度中,自适应大规模邻域搜索算法一列的数据都大于禁忌搜索算法,即在自适应大规模邻域搜索算法可以应用的规模下(即请求规模小于200时),其对于初始解的改善程度比禁忌搜索算法要好.
3)当请求规模为50时,自适应大规模邻域搜索算法的计算时间小于100 s,当请求规模为100时,自适应大规模邻域搜索算法的计算时间为1026.40 s,当请求规模为200时,计算时间最多为12 203.84 s. 也就是说,自适应大规模邻域算法的计算时间随着请求规模的增加而骤然增加,验证了NP-hard问题的计算复杂度随着数据规模的增大而增大的既知事实.
4. 结 语
本研究重新定义考虑真实场景多项动态事件的动态取送货问题,尝试揭示多项动态事件经典模型带时间窗取送货问题的不同影响,提高实时动态决策能力和快速响应能力. 构建考虑新请求出现、请求改变、交通拥堵和车辆抛锚4种动态事件的实时场景取送货动态车辆路径规划模型,即DPDP-MDE,该模型以调度时域
本研究在考虑交通拥堵状况时,限于问题涵盖了真实场景的多项动态事件,较为复杂,因而未能细分车辆速度在不同的时段和区域有所不同的情景。在车辆规划路径时仅根据车辆所处的时段和区域类推车辆的速度,未来为了更符合实际情况,可以考虑车辆速度伴随线路拥堵情况呈某种递减规律的情况。同时,动态问题求解对算法的时效性要求较高,未来尝试采用并行思想设计新算法,以降低算法运行时间,提高决策快速响应能力。
参考文献
Real-time control of express pickup and delivery processes in a dynamic environment
[J].
On dynamic pickup and delivery vehicle routing with several time windows and waiting times
[J].DOI:10.1016/j.trb.2005.04.002 [本文引用: 1]
Waiting strategies for the dynamic pickup and delivery problem with time windows
[J].
Waiting strategies for dynamic vehicle routing
[J].DOI:10.1287/trsc.1040.0095 [本文引用: 1]
Double-horizon based heuristics for the dynamic pickup and delivery problem with time windows
[J].
Exploiting knowledge about future demands for real-time vehicle dispatching
[J].
A metaheuristic for the pickup and delivery problem with time windows
[J].
Waiting and buffering strategies for the dynamic pickup and delivery problem with time windows
[J].
Vehicle routing under time-dependent travel times: the impact of congestion avoidance
[J].DOI:10.1016/j.cor.2011.05.027 [本文引用: 1]
The time-dependent pickup and delivery problem with time windows
[J].
Managing vehicle breakdown incidents during urban distribution of a common product
[J].DOI:10.1057/jors.2012.93 [本文引用: 1]
Using traffic information for time-dependent vehicle routing
[J].DOI:10.1016/j.sbspro.2012.03.103 [本文引用: 1]
Dynamic pickup and delivery problems
[J].DOI:10.1016/j.ejor.2009.04.024 [本文引用: 1]
Neighborhood search heuristics for a dynamic vehicle dispatching problem with pick-ups and deliveries
[J].DOI:10.1016/j.trc.2006.03.002 [本文引用: 1]
Ant colony system for a dynamic vehicle routing problem
[J].DOI:10.1007/s10878-005-4922-6 [本文引用: 1]
A general heuristic for vehicle routing problems
[J].DOI:10.1016/j.cor.2005.09.012 [本文引用: 1]