管桩底部开口，在成桩过程中其底部会被土塞填充，而土塞高度与管桩直径、土体性质和成桩方式密切相关. 在桩基动力研究中，较多学者针对土塞建立计算模型^[1-2]，研究土塞对管桩振动特性的影响. 刘润等^[3]将管桩土塞假定为作用于管桩内壁的弹簧和阻尼器并联的Voigt体；Zheng等^[4-5]利用三维连续介质模型，模拟桩芯土与桩身的动力相互作用；Li等^[6-7]采用考虑土体竖向波动的连续介质模型，研究桩周土与桩芯土径向非均质的桩土动力响应问题，但是上述模型均无法模拟桩芯土对桩身计算波速的影响. Wu等^[8-10]提出附加质量模型，将桩芯土与管桩内壁用弹簧阻尼器连接，考虑桩与桩芯土之间的差异变形，但是对于水泥土这种强度逐渐增长和黏结性较高的土来说，适用性不强.

Zhou等^[11-13]的研究表明，水泥土对桩身的黏结性远强于普通土，并且水泥土强度随龄期逐渐增长，对桩身动力响应的影响更加复杂. 另外，水泥土在振动过程中会产生较大的阻尼，相关文献研究^[14]表明，相比于滞回阻尼，采用土体的黏性阻尼更加实用，但是目前尚无直接测定材料黏性阻尼的方法.

针对上述问题，考虑水泥土与桩身的强黏结性，提出桩侧虚土桩模型，将桩芯土塞分成2个部分：靠近桩身的较小区域土环视为虚土桩，该部分与桩身紧密相连，使用桩段的动力模型进行描述；中心的水泥土采用平面应变模型进行模拟，两者的材料参数均按照水泥土取值. 将桩土系统纵向划分为有限单元层，使用阻抗函数传递法，得到桩顶动力响应频域内的解析解和时域内的半解析解；对该模型进行参数分析，得到桩身动力响应的变化规律；将以上模型计算结果与静钻根植竹节桩的现场试验结果进行拟合，得到虚土桩尺寸系数和水泥土黏性阻尼系数，进一步验证该模型的实用性.

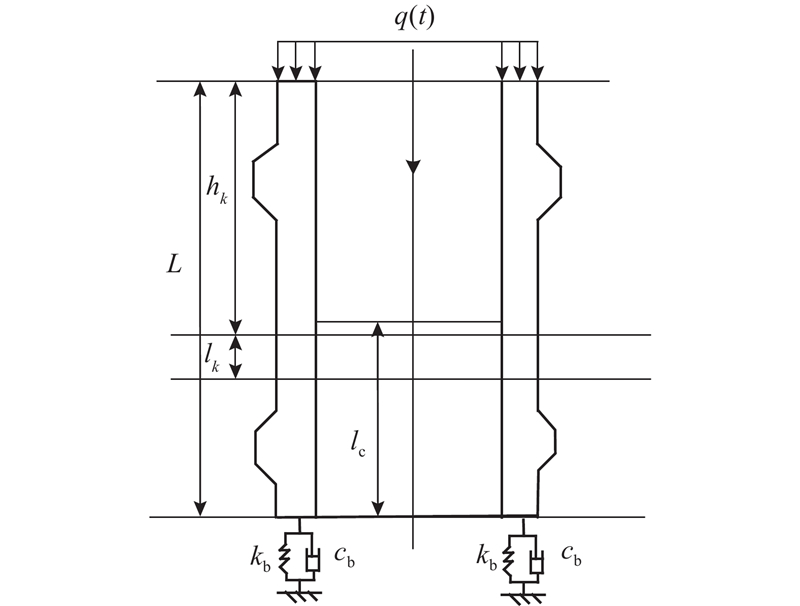
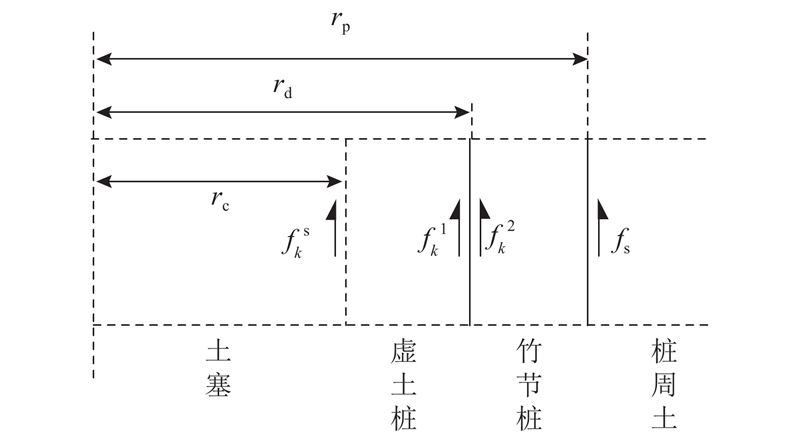
根据所提出的桩侧虚土桩模型，建立竹节桩与土塞的竖向振动计算模型，如图1所示为竹节桩与桩芯土整体模型图（已省略部分竹节），根据土塞高度和竹节桩身特性，将桩土系统由下而上划分为 $n$层. 图中， $L$为桩长， ${l_k}$、 ${h_k}$分别为第 $k$段桩（虚土桩）的长度和第 $k$段桩（虚土桩）顶部到桩顶的距离， ${l_{\rm{c}} }$为桩芯土塞的总高度， ${k_{\rm{b}} }$、 ${c_{\rm{b}} }$分别为桩底土的弹性和阻尼系数， $q\left( t \right)$为桩顶荷载. 如图2所示为第k层桩土计算简图. 图中， ${r_{\rm{p}} }$为无竹节处桩身外半径； ${r_{\rm{d}} }$为桩身内径； ${r_{\rm{c}}}$为桩芯土塞与虚土桩分界面的半径， ${r_{\rm{c}} } = \left( {1 - \theta } \right){r_{\rm{d}} }$， $\theta $为虚土桩尺寸系数； $f_k^{\rm{s}} $、 $f_k^1$、 $f_k^2$、 ${f_{\rm s}}$分别为第 $k$段桩（虚土桩）中土塞对虚土桩、虚土桩对竹节桩、竹节桩对虚土桩、桩周土对竹节桩的摩擦力. 根据吴文兵等^[15-16]研究楔形桩的理论，对于竹节桩的斜面而言，当每个斜面划分层数超过200时，采用台阶式的划分方法可以较为精确地模拟该斜面.

采用的假设条件如下：1）桩与水泥土为均质黏弹性材料；2）桩周土体采用平面应变模型，桩周土层无穷远处位移为零，土体上表面自由，桩与桩底土相互作用简化为Voigt体；3）桩芯土与虚土桩之间的应力通过剪切复刚度传递，材料参数完全一致；4）虚土桩与桩身内侧接触面位移和力连续，且相同桩和虚土桩段竖向位移相等.

重点研究竹节桩桩芯土塞的影响，因此假设桩周土体为均质，采用平面应变模型进行模拟，根据Novak^[17]提出的土体纵向振动时的平面应变模型，对于桩土系统的每一个分层，假设 ${u_{\rm s}}\left( {r,s} \right)$为桩周土体竖向位移的拉普拉斯变换形式，可以得到桩周土动力方程：

(1) ${r^2}{{{{\rm{d}} ^2}{u_{\rm{s}}}}}/{{{\rm{d}} {r^2}}} + r{{{\rm{d}} {u_{\rm{s}}}}}/{{{\rm{d}} r}} - {\left( {{\alpha _{\rm{s}}}} \right)^2}{r^2}{u_{\rm{s}}} = 0.$

式中： $r$为半径； $s$为拉普拉斯变量； ${\alpha _{\rm{s}}} = \dfrac{{{\rm{i}} \omega }}{{{V_{\rm{s}}}\sqrt {1 + {\rm{i}} {D_{\rm{s}}}} }}$， $\omega $为角频率， ${\rm{i}} = \sqrt { - 1} $为虚数单位， ${V_{\rm{s}} }$、 ${D_{\rm{s}}}$分别为桩周土体的剪切波速和阻尼比， ${V_{\rm{s}} } = \sqrt {{{{G_{\rm{s}}}}}/{{{\rho _{\rm{s}}}}}} $， ${G_{\rm{s}}}$、 ${\rho _{\rm{s}}}$分别为桩周土体的切变模量和密度.

求解方程可以得到桩周土任意一点土体的纵向位移：

(2) ${u_{\rm{s}}} = {A_{\rm{s}}}{{{K}} _0}\left( {\alpha r} \right) + {B_{\rm{s}}}{{{I}} _0}\left( {\alpha r} \right).$

式中： ${{{I}} _0}\left( \cdot \right)$、 ${{{K}} _0}\left( \cdot \right)$分别为零阶第1、2类虚宗量贝塞尔函数；α为贝塞尔函数的特征值； ${A_{\rm{s}}}$、 ${B_{\rm{s}} }$为常数，由边界条件决定. 根据平面应变假定，桩周土体无穷远处位移为零，可知 ${B_{\rm{s}}} = 0$.

竹节桩桩侧任意一点的竖向剪切力为

(3) $\tau = G_{\rm{s}} ^*{{{\rm{d}} {u_{\rm{s}} }}}/{{{\rm{d}} r}} = - G_{\rm{s}} ^*{A_{\rm{s}}}\alpha {{{K}} _1}\left( {\alpha r} \right).$

式中： $G_{\rm{s}} ^* = {G_{\rm{s}}}\left( {1 + {\rm{i}} {D_{\rm{s}}}} \right)$.

根据弹性力学知识，竹节桩与桩周土接触面单位长度方向的竖向剪切刚度为

(4) ${K_{\rm{s}}} = {{ - 2\pi r\tau }}/{{{u_{\rm{s}}}}} = 2\pi rG_{\rm{s}} ^*\alpha {{{{{K}} _1}\left( {\alpha r} \right)}}/{{{{{K}} _0}\left( {\alpha r} \right)}}.$

$r$根据竹节桩的截面外半径进行取值.

考虑水泥土的黏性阻尼，可以得到桩芯水泥土塞的纵向振动平衡方程：

(5) $G_k^{\rm{s}}\frac{{{\partial ^2}u_k^{\rm{s}} }}{{\partial {r^2}}} + \frac{{G_k^{\rm{s}}}}{r}\frac{{\partial u_k^{\rm{s}} }}{{\partial r}} + \delta _k^{\rm{s}} \frac{{{\partial ^3}u_k^{\rm{s}} }}{{\partial {r^2}\partial t}} + \frac{{\delta _k^{\rm{s}} }}{r}\frac{{{\partial ^2}u_k^{\rm{s}} }}{{\partial r\partial t}} - \rho _k^{\rm{s}} \frac{{{\partial ^2}u_k^{\rm{s}} }}{{\partial {t^2}}} = 0.$

式中： $G_k^{\rm{s}} $、 $\delta _k^{\rm{s}} $、 $\rho _k^{\rm{s}} $分别为第 $k$层水泥土的切变模量、黏性阻尼系数和密度， $u_k^{\rm s} $为桩芯水泥土任意点的竖向位移.

对上式进行Laplace变换并化简，可以得到

(6) ${r^2}\frac{{{\partial ^2}U_k^{\rm{s}} }}{{\partial {r^2}}} + r\frac{{\partial U_k^{\rm{s}} }}{{\partial r}} - {\left( {\alpha _k^{\rm{s}} } \right)^2}{r^2}U_k^{\rm{s}} = 0.$

式中： ${\left( {\alpha _k^{\rm{s}} } \right)^2} = \dfrac{{ - \rho _k^{\rm{s}} {\omega ^2}}}{{G_k^{\rm{s}} + {\rm{i}} \omega \delta _k^{\rm{s}} }}$， $U_k^{\rm{s}} $为 $u_k^{\rm{s}} $的Laplace变换形式.

求解式（6）可以得到桩芯水泥土任意一点的竖向位移：

(7) $u_k^{\rm{s}} = D_k^{\rm{s}} {{{K}} _0}\left( {\alpha _k^{\rm{s}} r} \right) + B_k^{\rm{s}} {{{I}} _0}\left( {\alpha _k^{\rm{s}} r} \right).$

式中： $D_k^{\rm s} $、 $B_k^{\rm s} $为常数. 当桩芯土中心 $r = 0$时，土体位移为有限值，可以得到 $D_k^{\rm{s}} = 0$.

由弹性力学知识，可以得到土塞内任意径向位置的竖向切应力为

(8) $\tau _k^{\rm{s}} = \left( {G_k^{\rm{s}} + {\rm i}\omega \delta _k^{\rm{s}} } \right)\frac{{{\rm{d}} u_k^{\rm{s}} }}{{{\rm{d}} r}} = \left( {G_k^{\rm{s}} + {\rm{i}} \omega \delta _k^{\rm{s}} } \right)B_k^{\rm{s}} \alpha _k^{\rm{s}} {{{I}} _1}\left( {\alpha _k^{\rm{s}} r} \right).$

水泥土与虚土桩接触面的竖向剪切刚度为

(9) $\begin{split}K_k^{\rm{s}} = & 2\pi {r_{\rm{c}} }\frac{{\tau _k^{\rm{s}} }}{{u_k^{\rm{s}} }} = \\ &2\pi {r_{\rm{c}} }\left( {G_k^{\rm{s}} + {\rm{i}} \omega \delta _k^{\rm{s}} } \right)\alpha _k^{\rm{s}} {{{{{I}} _1}\left( {\alpha _k^{\rm{s}} {r_{\rm{c}} }} \right)} / {{{{I}} _0}\left( {\alpha _k^{\rm{s}} {r_{\rm{c}} }} \right)}}.\end{split}$

式中：I₁为一阶第1类虚宗量贝塞尔函数.

由上述假设可知，在振动过程中，同一深度处的竹节桩与虚土桩竖向位移完全相等. 假设 ${w_k}\left( {z,t} \right)$为第 $k$段桩与虚土桩的纵向位移，可以分别建立桩身及虚土桩的纵向振动控制方程，同时考虑竹节桩和虚土桩的横向惯性效应和黏性阻尼，可以得到

(10) $\begin{split}& E_k^{\rm{p}} A_k^{\rm{p}} \frac{{{\partial ^2}{w_k}}}{{\partial {z^2}}} + \delta _k^{\rm{p}} A_k^{\rm{p}} \frac{{{\partial ^3}{w_k}}}{{\partial t\partial {z^2}}} - \rho _k^{\rm{p}} A_k^{\rm{p}} \frac{{{\partial ^2}{w_k}}}{{\partial {t^2}}} +\\ &\quad \rho _k^{\rm{p}} A_k^{\rm{p}} {\left( {\nu _k^{\rm{p}} {R_k}} \right)^2}\frac{{{\partial ^4}{w_k}}}{{\partial {z^2}\partial {t^2}}} - {f_{\rm{s}} }\left( {z,t} \right) - f_k^1\left( {z,t} \right) = 0 , \end{split} $

(11) $\begin{split} &E_k^{\rm{s}} A_k^{\rm{s}} \frac{{{\partial ^2}{w_k}}}{{\partial {z^2}}} + \delta _k^{\rm{s}} A_k^{\rm{s}} \frac{{{\partial ^3}{w_k}}}{{\partial t\partial {z^2}}} - \rho _k^{\rm{s}} A_k^{\rm{s}} \frac{{{\partial ^2}{w_k}}}{{\partial {t^2}}} + \\ &\quad \rho _k^{\rm{s}} A_k^{\rm{s}} {\left( {\nu _k^{\rm{s}} {r_k}} \right)^2}\frac{{{\partial ^4}{w_k}}}{{\partial {z^2}\partial {t^2}}} - f_k^{\rm{s}} \left( {z,t} \right) -\\&\quad f_k^2\left( {z,t} \right) = 0;\; {k = 1,2, \cdot \cdot \cdot ,n} . \end{split} $

式中： ${f_{\rm{s}} }\left( {z,t} \right)$为桩周土对竹节桩外侧的作用力， ${f_{\rm{s}} }\left( {z,t} \right) = {K_{\rm{s}} }{w_1}$； $f_k^{\rm{s}} \left( {z,t} \right)$为桩芯土塞虚土桩内壁的作用力， $f_k^{\rm{s}} \left( {z,t} \right) = K_k^{\rm{s}} {w_1}$； $f_k^1\left( {z,t} \right)$、 $f_k^2\left( {z,t} \right)$分别为第 $k$段虚土桩对竹节桩的作用力和第 $k$段竹节桩对虚土桩的作用力； ${R_k}$、 $E_k^{\rm{p}} $、 $A_k^{\rm{p}} $、 $\delta _k^{\rm{p}} $、 $\nu _k^{\rm{p}} $、 $\rho _k^{\rm{p}} $分别为第 $k$个桩段的外半径、弹性模量、横截面积、黏性阻尼系数、泊松比和密度；r_k、 $E_k^{\rm{s}}$、 $A_k^{\rm{s}} $、 $v_k^{\rm s} $分别为虚土桩的外半径、弹性模量、横截面积、泊松比. 其中， $\delta _k^{\rm{p}} $为常数， $\delta _k^{\rm{s}} $随水泥土模量变化而变化. 由牛顿第三定律可知

(12) $f_k^1\left( {z,t} \right) = - f_k^2\left( {z,t} \right).$

结合式（10）、（11），可以得到桩与虚土桩共同振动的动力控制方程：

(13) $\begin{split}& \left( {E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} } \right)\frac{{{\partial ^2}{w_k}}}{{\partial {z^2}}} + \left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right)\frac{{{\partial ^3}{w_k}}}{{\partial t\partial {z^2}}}+ \\ &\quad \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right)\frac{{{\partial ^4}{w_k}}}{{\partial {z^2}\partial {t^2}}} - \\ &\quad \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} + \rho _k^{\rm{s}} A_k^{\rm{s}} } \right)\frac{{{\partial ^2}{w_k}}}{{\partial {t^2}}} - \left( {{K_{\rm{s}} } + K_k^{\rm{s}} } \right){w_k} = 0 . \end{split} $

根据假设条件，可知桩身两端边界条件为

(14) $\begin{split} &{\left. {\left( {E_n^{\rm{p}} {A_n^{\rm p}}\frac{{{\partial ^2}{w_n}}}{{\partial z^2}} + \delta _n^{\rm{p}} {A_n^{\rm p}}\frac{{{\partial ^2}{w_n}}}{{\partial t\partial z}} + \rho _n^{\rm{p}} A_n^{\rm{p}} {{\left( {\nu _n^{\rm{p}} {R_n}} \right)}^2}\frac{{{\partial ^3}{w_n}}}{{\partial z\partial {t^2}}}} \right)} \right|_{z = 0}} = \\ &\quad\quad - q\left( t \right) , \\[-10pt] \end{split} $

(15) $ \begin{split} &\Bigg({k_{\rm{b}} }{w_1} + {c_{\rm{b}} }\dfrac{{\partial {w_1}}}{{\partial t}} + E_1^{\rm{p}} {A_1^{\rm p}}\dfrac{{{\partial ^2}{w_1}}}{{\partial z^2}} + \delta _1^{\rm{p}} {A_1^{\rm p}}\dfrac{{{\partial ^2}{w_1}}}{{\partial t\partial z}} + \\ &\quad\quad \rho _1^{\rm{p}} A_1^{\rm{p}} {\left( {\nu _1^{\rm{p}} {R_1}} \right)^2}\dfrac{{{\partial ^3}{w_1}}}{{\partial z\partial {t^2}}} \Bigg)\Bigg|_{z=l}=0. \end{split} $

${k_{\rm{b}} }$、 ${c_{\rm{b}} }$可以根据Lysmer&Richart^[18]弹性半空间理论推导出的公式计算：

(16) ${k_{\rm{b}} } = \frac{{4{G_{\rm{b}} }{R_1}}}{{1 - {v_{\rm{b}} }}},$

(17) ${c_{\rm{b}} } = \frac{{3.4R_1^2\sqrt {{\rho _{\rm{b}} }{G_{\rm{b}} }} }}{{1 - {v_{\rm{b}} }}}.$

式中： ${G_{\rm{b}} }$、 ${\rho _{\rm{b}} }$、 ${v_{\rm{b}} }$分别为桩底土的切变模量、密度和泊松比.

由相邻桩段分界面两侧的桩身位移和截面力连续条件，对于无土塞段：

(18) ${\left. {{w_k}} \right|_{z = {h_k}}} = {\left. {{w_{k + 1}}} \right|_{z = {h_k}}},$

(19) $\begin{split} &{\left. {\left( {E_k^{\rm{p}} {A_k^{\rm p}}\dfrac{{{\partial ^2}{w_k}}}{{\partial z}} + \delta _k^{\rm{p}} {A_k^{\rm p}}\dfrac{{{\partial ^2}{w_k}}}{{\partial t\partial z}} + \rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2}\dfrac{{{\partial ^3}{w_k}}}{{\partial z\partial {t^2}}}} \right)} \right|_{z = {h_k}}} = \\ &\quad \quad\quad \Bigg( E_{k + 1}^{\rm{p}} {A_{k + 1}^{\rm p}}\dfrac{{{\partial ^2}{w_{k + 1}}}}{{\partial z^2}} + \delta _{k + 1}^{\rm{p}} {A_{k + 1}^{\rm p}}\dfrac{{{\partial ^2}{w_{k + 1}}}}{{\partial t\partial z}} + \\ &\quad\quad\quad \rho _{k + 1}^{\rm{p}} A_{k + 1}^{\rm{p}} {\left( {\nu _{k + 1}^{\rm{p}} {R_{k + 1}}} \right)^2}\dfrac{{{\partial ^3}{w_{k + 1}}}}{{\partial z\partial {t^2}}} \Bigg) \Bigg|_{z = {h_k}}. \\[-17pt] \end{split} $

对于有土塞段：

(20) ${\left. {{w_k}} \right|_{z = {h_k}}} = {\left. {{w_{k + 1}}} \right|_{z = {h_k}}},$

(21) $\begin{split} & \Bigg[ \left( {E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} } \right)\dfrac{{{\partial ^2}{w_k}}}{{\partial z^2}} + \left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right)\dfrac{{{\partial ^2}{w_k}}}{{\partial t\partial z}} + \\ &\quad \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right)\dfrac{{{\partial ^3}{w_k}}}{{\partial z\partial {t^2}}}\Bigg] \Bigg|_{z = {h_k}}= \\ &\quad \Bigg[ \left( {E_{k + 1}^{\rm{p}} A_{k + 1}^{\rm{p}} + E_{k + 1}^{\rm{s}} A_{k + 1}^{\rm{s}} } \right)\dfrac{{{\partial ^2}{w_{k + 1}}}}{{\partial z}} + \\ &\quad \left( {\delta _{k + 1}^{\rm{p}} A_{k + 1}^{\rm{p}} + \delta _{k + 1}^{\rm{s}} A_{k + 1}^{\rm{s}} } \right)\dfrac{{{\partial ^2}{w_{k + 1}}}}{{\partial t\partial z}}+ \\ &\quad \left( {\rho _{k + 1}^{\rm{p}} A_{k + 1}^{\rm{p}} {{\left( {\nu _{k + 1}^{\rm{p}} {R_{k + 1}}} \right)}^2} + \rho _{k + 1}^{\rm{s}} A_{k + 1}^{\rm{s}} {{\left( {\nu _{k + 1}^{\rm{s}} {r_{k + 1}}} \right)}^2}} \right)\times\\&\quad\dfrac{{{\partial ^3}{w_{k + 1}}}}{{\partial z\partial {t^2}}} \Bigg] \Bigg|_{z = {h_k}}. \end{split} $

竹节桩与虚土桩段的初始条件为

(22) ${\left. {{w_k}} \right|_{t = 0}} = 0,{\left. {\frac{{\partial {w_k}}}{{\partial t}}} \right|_{t = 0}}=0\;\;\;{\rm{,}}\;\;\;\;k = 1,2, \cdots ,n.$

令 ${W_k}\left( {z,s} \right)$为 ${w_k}\left( {z,t} \right)$关于时间的Laplace变换形式，结合初始条件（式（22）），对式（13）进行Laplace变化，可以得到

(23) $\begin{split} &\left( {E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} } \right)\frac{{{\partial ^2}{W_k}}}{{\partial {z^2}}} + s\left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right)\frac{{{\partial ^2}{W_k}}}{{\partial {z^2}}} +\\ &\quad \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right){s^2}\frac{{{\partial ^2}{W_k}}}{{\partial {z^2}}} - \\ &\quad \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} + \rho _k^{\rm{s}} A_k^{\rm{s}} } \right){s^2}{W_k} - \left( {K_k^{\rm{s}} + {K_{\rm{s}} }} \right){W_k} = 0 . \end{split} $

经化简可得

(24) $\begin{split} & \Bigg[E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} + s\left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right) + \\ &\quad{s^2}\left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right) \Bigg] \frac{{{\partial ^2}{W_k}}}{{\partial {z^2}}} - \\ &\quad \left( {{s^2}\left( {\rho _k^{\rm{p}} A_k^{\rm{p}} + \rho _k^{\rm{s}} A_k^{\rm{s}} } \right) + K_k^{\rm{s}} + {K_{\rm{s}} }} \right){W_k} = 0 . \end{split} $

上式的通解可以表示为

(25) $W_k^{\rm{p}} = {C_k}\cos\; \left( {{\lambda _k}z} \right) + {D_k}\sin\; \left( {{\lambda _k}z} \right);\;\;\;\ {k = 1,2, \cdots ,n} ,$

(26) $\begin{split} {\lambda _k} = \Bigg\{ \Bigg. -& \Bigg[{s^2}\left( {\rho _k^{\rm{p}}A_k^{\rm{p}} + \rho _k^{\rm{s}}A_k^{\rm{s}}} \right) + K_k^{\rm{s}} + {K_{\rm{s}}}\Bigg]\Big/\\ & \Bigg[E_k^{\rm{p}}A_k^{\rm{p}} + E_k^{\rm{s}}A_k^{\rm{s}} + s\left( {\delta _k^{\rm{p}}A_k^{\rm{p}} + \delta _k^{\rm{s}}A_k^{\rm{s}}} \right) + \\ & {s^2}\left( {\rho _k^{\rm{p}}A_k^{\rm{p}}{{\left( {\nu _k^{\rm{p}}{R_k}} \right)}^2} + \rho _k^{\rm{s}}A_k^{\rm{s}}{{\left( {\nu _k^{\rm{s}}{r_k}} \right)}^2}} \right)\Bigg] \Bigg. \Bigg\}^{1/2};\\ & k = 1,2, \cdot \cdot \cdot ,n \end{split}$

式中： ${C_k}$、 ${D_k}$为复常数，可以由桩顶和桩底边界条件得到.

结合阻抗函数的定义（力除以位移），可以得到第 $k$桩段桩顶的阻抗函数：

(27) $\begin{split} {Z_k} =& - {\lambda _k}\Big[ {E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} + s\left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right)} \Big]\tan\; \left( {{\lambda _k}{h_k} - {\varphi _k}} \right) - \\ & \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right){s^2}{\left( {{\lambda _k}} \right)^2}.\\[-15pt] \end{split} $

${\varphi _k}$可以由第 $k - 1$段桩桩顶复阻抗求得：

(28) ${\varphi _k} \!=\! \arctan\; \left( {\frac{{{Z_{k - 1}} + \left( {\rho _k^{\rm{p}} A_k^{\rm{p}} {{\left( {\nu _k^{\rm{p}} {R_k}} \right)}^2} + \rho _k^{\rm{s}} A_k^{\rm{s}} {{\left( {\nu _k^{\rm{s}} {r_k}} \right)}^2}} \right){s^2}{{\left( {{\lambda _k}} \right)}^2}}}{{{\lambda _k}\left( {E_k^{\rm{p}} A_k^{\rm{p}} + E_k^{\rm{s}} A_k^{\rm{s}} + s\left( {\delta _k^{\rm{p}} A_k^{\rm{p}} + \delta _k^{\rm{s}} A_k^{\rm{s}} } \right)} \right)}}} \right).$

根据上述桩顶阻抗函数递推关系，结合桩底边界条件 ${Z_0} = {k_{\rm{b}} } + s {c_{\rm{b}} }$，可以得到桩顶复阻抗函数：

(29) ${Z_n} = K + {\rm{i}} C.$

式中： $K$、 $C$分别为桩顶的动刚度和动阻尼.

令 $s = {\rm{i}} \omega $，可以得到桩顶速度导纳函数：

(30) ${H_{\rm{v}} }\left( \omega \right) = {{{\rm{i}} \omega }}/{{{Z_n}\left( \omega \right)}}.$

当桩顶受到半正弦脉冲激励时， $q\left( t \right) = {q_{\max }}\times \sin\; \left( {{\text{π}} t/T} \right){\rm{ }}\left( {0 \leqslant t \leqslant T} \right)$，经过傅里叶逆变换（inverse Fourier transform，IFT），可以求得桩顶速度时域响应

(31) $V\left( t \right) = {\rm{IFT}} \; \left[ {{H_{\rm v}}\left( \omega \right){q_{\max }}\frac{{T{\text{π}} }}{{{{\text{π}} ^2} - {T^2}{\omega ^2}}}\left( {1 + {{\rm{e}} ^{ - {\rm{i}} \omega T}}} \right)} \right].$

对于桩芯水泥土的黏性阻尼系数，目前尚无直接测量土体黏性阻尼系数的有效手段，EL Naggar等^[19-20]通过理论研究，认为桩周土对桩身的等效黏性阻尼系数表达式可以写为

(32) ${\delta _{\rm{s}} } = 2\pi {r_0}{\rho _{\rm{s}} }{V_{\rm{s}} } \cdot {\rm{Im}} \; \left[ {\frac{{{{H}} _1^{\left( 2 \right)}\left( {{a_0}} \right)}}{{{{H}} _0^{\left( 2 \right)}\left( {{a_0}} \right)}}} \right].$

式中： ${r_0}$为桩身半径； ${a_0}$为频率参数， ${a_0} = {r_0}\omega /{V_{\rm{s}} }$； ${{H}} _1^{\left( 2 \right)}\left( \cdot \right)$、 ${{H}} _0^{\left( 2 \right)}\left( \cdot \right)$均为汉克尔函数.

须注意的是，这个阻尼系数并不是某种材料的固有属性，而是体现土对桩身阻尼效果的等效值，与桩身半径、振动频率相关. 即使是同样一种土，对不同尺寸的桩，其等效阻尼系数也不一致.

胡志广等^[21-22]通过模型试验进行反演，得到竖向应力条件下各类土的黏性阻尼系数，与上述公式进行对比，发现具体数值与公式计算所得存在一定差异，差异大小随土体性质而不同. 本研究考虑桩芯土的阻尼特性，由于与桩周土体相比，桩土相互作用模式不同，土体边界条件也不一致，桩芯水泥土的等效阻尼系数与桩周土等效阻尼系数计算公式所得结果必然有较大差异，因此在本研究中，水泥土阻尼系数的计算是在上述公式的基础上，乘一个系数，系数的具体取值须根据实测曲线拟合得到. 记阻尼系数常数为 $\beta $，得到桩芯土阻尼系数的表达式为

(33) $\delta _k^{\rm{s}} = \beta {\delta _{\rm{s}} }.$

为了对本研究解的合理性进行验证，采用ABAQUS软件建立竹节桩和土塞的三维有限元模型，如图3所示. 当桩芯有土塞时，在竹节桩内壁和土塞外侧设置接触面，接触类型为Tie（紧约束），以模拟桩土的较强黏结性，桩顶激振力与拾振点的相对位置夹角为90°. 当采用理论模型和有限元模型分别模拟桩基动力响应时，由于激振方式不一样，相同材料的计算波速也不一样，为了调和这一矛盾，先对无土时竹节桩的解析曲线进行拟合反演，得到有限元模型中的竹节桩材料参数，再建立有土塞时的数值模型，进行验算.

在本次验证和接下来的参数分析中，如无特别说明，解析模型中竹节桩和水泥土塞的基本参数取值如下：竹节桩尺寸采用标准的（550-400-90-12）桩型，桩身无竹节处半径 ${r_{\rm{p}} } = 0.2\;{\rm{m}} $，内径 ${r_{\rm{d}} } = 0.105\;{\rm{m}} $，竹节厚度 $d = 0.075\;{\rm{ m}}$，竹节间距 ${l_{\rm{d}} } = 1\;{\rm{ m}}$，桩长 $L = 12\;{\rm{ m}}$，桩身弹性波速为4000 m/s，密度为 $2\;500\;{\rm{ kg/}}{{\rm{m}}^3}$，阻尼系数为 $576\;000\;{\rm{ N}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm{s}} $，泊松比为0.2；水泥土剪切波速为 $100\;{\rm{ m/s}}$，密度为 $2\;000\;{\rm{ kg/}}{{\rm{m}}^3}$，阻尼系数常数 $\beta = 30$，土塞高度为6 m，水泥土泊松比为0.3，虚土桩尺寸系数 $\theta = 0.2$；桩周土和桩底土对竹节桩系统的作用取为零.

在无土塞状态下，使用有限元模型对解析解进行拟合，得到有限元模型中桩身弹性模量为 $43.1\;{\rm{ GPa}}$，瑞利阻尼系数分别为 $\alpha_0 = 150$， $\beta_0 = 0$. 对桩芯土塞高度为 $6\;{\rm{ m}}$时建立有限元数值模型，设置tie接触面，得到桩顶动力响应曲线.

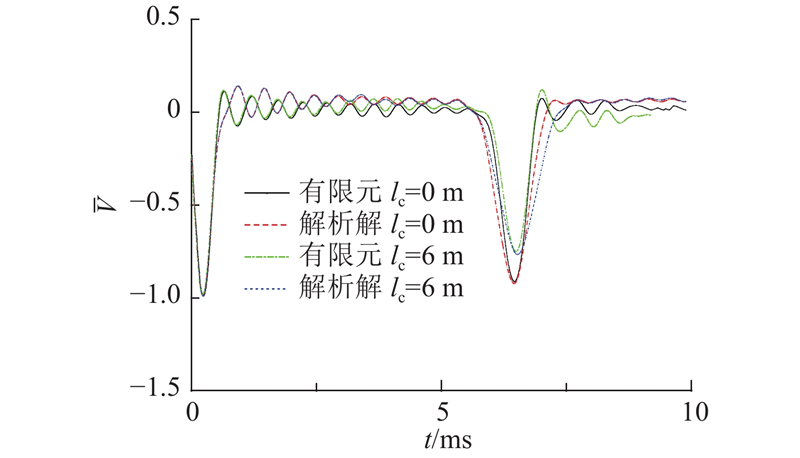
如图4所示为解析解与有限元解的对比，图中， $\overline V $为归一化后的速度时域响应. 可以看出，有限元模型计算得到的曲线与本研究解析解计算得到的曲线基本相符，但是由于桩顶激振方式有差异，得到的曲线桩身段的波动存在一定相位差；对于桩底反射的信号幅值和到达时间这2个关键因素，2条曲线较吻合.

在设置了高度为 $6\;{\rm{ m}}$的桩芯土塞后，可以看到解析解和有限元解曲线在距离桩顶深度 $6\;{\rm{ m}}$处均出现轻微的扩颈反射，但是有限元曲线中反射信号略大于解析解中的；在设置土塞后桩底反射信号幅值有一定减小，桩底反射信号的到达时间也有一定延迟. 上述对比说明本研究解的合理性，也初步表现了土塞对竹节桩动力响应曲线的影响.

对竹节桩-土塞系统的相关参数进行分析，研究其对桩顶速度时域响应的影响规律. 为了与后续的现场试验进行对比分析，在参数分析中假设无桩周土和桩底土作用，桩周土剪切复刚度和桩底土弹性支承复刚度均为零.

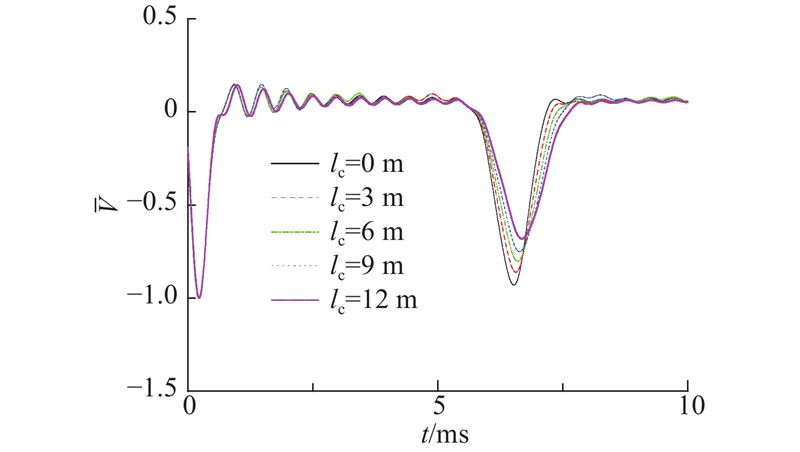
1）土塞高度. 在实际工程中，土塞高度往往受到桩身内径、施工方法和水泥土性质等影响. 改变土塞的高度，得到各土塞高度下的桩顶速度时域响应曲线，并且与无土塞时曲线对比，如图5所示. 可以看出，在竹节桩桩芯填充水泥土后，动力响应曲线中桩底反射信号有一定的延迟，引起桩身的计算综合波速减小，而且随着土塞高度增加，这种延迟效应越来越显著，同时桩底反射信号的幅值也逐步减弱. 在桩芯土塞上表面深度处，出现了类似扩颈的反射信号，反射曲线在该位置处有略微上抬. 当土塞高度靠近桩顶或填充整个桩身时，扩颈反射信号与浅层竹节反射信号叠加，逐渐无法辨别.

2）土塞模量. 维持土塞高度不变，改变水泥土塞的剪切波速 ${V_{{\rm{sc}} }}$，得到桩顶动力响应曲线，如图6所示. 可以看出，随着水泥土切变模量增加，动力响应曲线在桩底的反射信号幅值逐渐减弱，在土塞表面处的反射信号有轻微增强；随着土塞模量增加，桩底反射信号逐渐提前，但是幅度并不大，而土塞上表面处的反射信号峰值位置没有变化. 说明土塞模量的增加会导致含土塞段桩身的综合波速增加，但不会影响不含土塞段的桩身波速.

3）阻尼系数比例常数. 如图7所示为阻尼系数常数对速度时域响应的影响. 可以看出，随着土塞阻尼系数增大，桩底反射信号逐渐减弱，但是桩底和土塞表面处反射信号到达时间没有受到影响，这是因为逐渐增加的水泥土阻尼引起了更多的能量消耗，不过这种能量消耗不会引起桩身综合波速的改变.

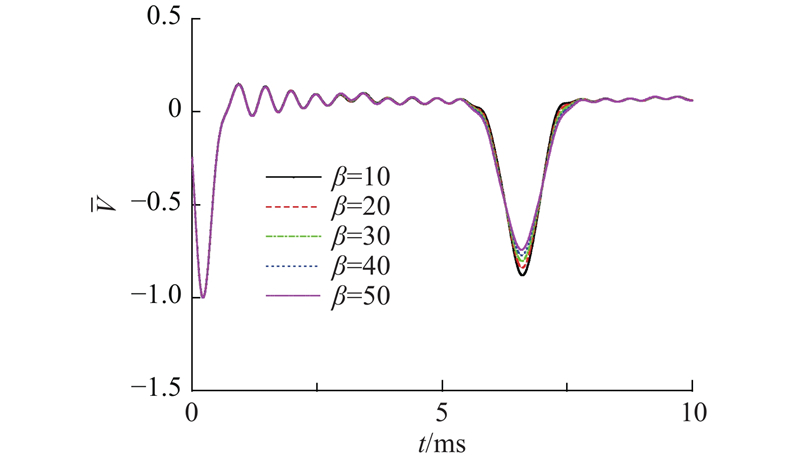
4）虚土桩尺寸系数. 如图8所示为虚土桩尺寸系数对速度时域响应的影响. 可以看出，桩底反射信号幅值随着虚土桩尺寸系数增大而逐渐减小，并且有适当的延迟，表明当考虑为虚土桩的土塞体积越大时，桩身综合波速的降低越明显.

为了测得现场试验中竹节桩周和桩芯土塞水泥土的切变模量随龄期的变化规律，按照现场和规范要求在实验室配置同等配比的水泥土. 参考试验现场情况和周佳锦^[23]的相关研究，所配制的水泥浆中水灰比为1.0，水泥浆与泥浆的体积比为0.5∶1. 选用来自于施工现场的淤泥质软土，烘干测得水的质量分数后进行研磨，形成粉末，水泥采用425硅酸盐普通水泥.

如图9所示为研磨后土样与拌合后的水泥土. 为了测试前期水泥土切变模量，将材料按配合比充分拌合均匀后，浇入与三轴仪配套的圆柱形模具中，成型后在试样两端插入弯曲元传感器，如图10所示. 在试样顶部施加较小的轴压，在不同龄期对该试样进行剪切波速测试.

通过软件读取剪切发射波与接收首波之间的时差 $\bar t $，根据试样长度 $\bar l $，可以得到每次测试时试样的剪切波速 ${v_{{{\rm{cs}}}} } = {{\bar l } / {\bar t }}$. 如图11所示为典型的波速测试曲线. 图中， $\bar H $为归一化信号值. 如图12所示为水泥土试样压缩试验. 以水泥土成型后第1次测试时龄期 $T = 0$，得到各龄期水泥土剪切波速. 根据公式可以得到各龄期水泥土切变模量：

(34) ${G_{\rm{cs}} } = {\rho _{\rm{cs}} }{V_{\rm{cs}} }^2.$

式中： ${G_{\rm{cs}} }$、 ${\rho _{\rm{cs}} }$、 ${V_{\rm{cs}} }$分别为水泥土的切变模量、密度和剪切波速.

由于弯曲元测试仪器的读数精确度对试样模量要求较高，当水泥土强度继续增加时，此测试方法不再适用. 在水泥土形成一定强度后，使用万能压缩试验机对水泥土试块的弹性模量和泊松比进行测试. 切变模量与弹性模量之间的换算公式为

(35) ${E_{\rm{cs}} } = 2\left( {1 + {\gamma _{\rm{cs}} }} \right){G_{\rm{cs}} }.$

式中： ${E_{\rm{cs}} }$、 ${\gamma _{\rm{cs}} }$分别为水泥土的弹性模量和泊松比. 由式（35）可以得到水泥土切变模量随龄期发展的变化规律，如图13所示. 可以看出，水泥土的切变模量在前期有较大的增长，随着龄期增加，模量增大幅度逐渐减缓，在龄期为7 d处由于测试方式改变，模量在该处变化较大，但是后期整体增长的趋势与前期较为一致.

地表竹节桩桩芯土现场试验在宁波中淳高科地基基础公司场地进行.

1）选取常用尺寸（550-400-95-12）竹节桩，桩底用钢板焊接防止漏浆，在地表时对其进行低应变动力测试得到响应曲线. 2）在场地中钻孔，将竹节桩放入孔中，按照试验配比配置水泥土灌入桩芯填满，土塞高度为12 m，在水泥土达到初凝状态不流动后，将竹节桩拔出放置于地表. 3）在水泥土的不同龄期，对放在地表的竹节桩进行低应变动力测试，在每次测试时位置固定不变，激振点与拾振点夹角为90°，得到各龄期桩顶的动力响应曲线. 如图14所示为竹节桩桩芯土现场试验.

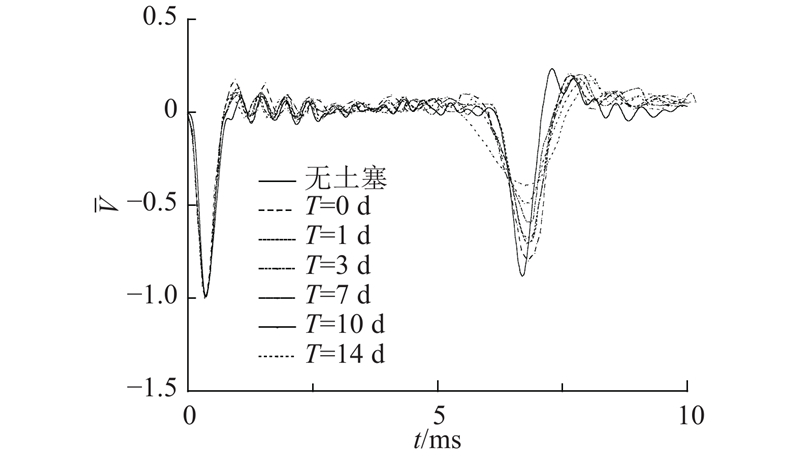
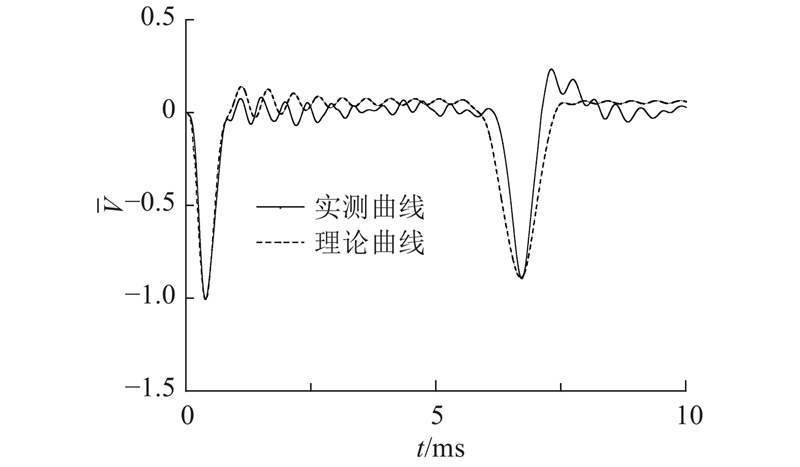
在对地表竹节桩水泥土各龄期的动力响应曲线进行分析后，进行归一化处理，得到典型的响应曲线，如图15所示. 可以看出，在桩芯填充水泥土后，竹节桩桩底反射信号的幅值有一定减小，随着水泥土龄期增长，反射信号幅值逐渐减弱；当桩芯填充土塞后，桩底反射信号到达时间有一定延迟，桩身综合波速减小，随着水泥土龄期增长，桩身波速有轻微增大.

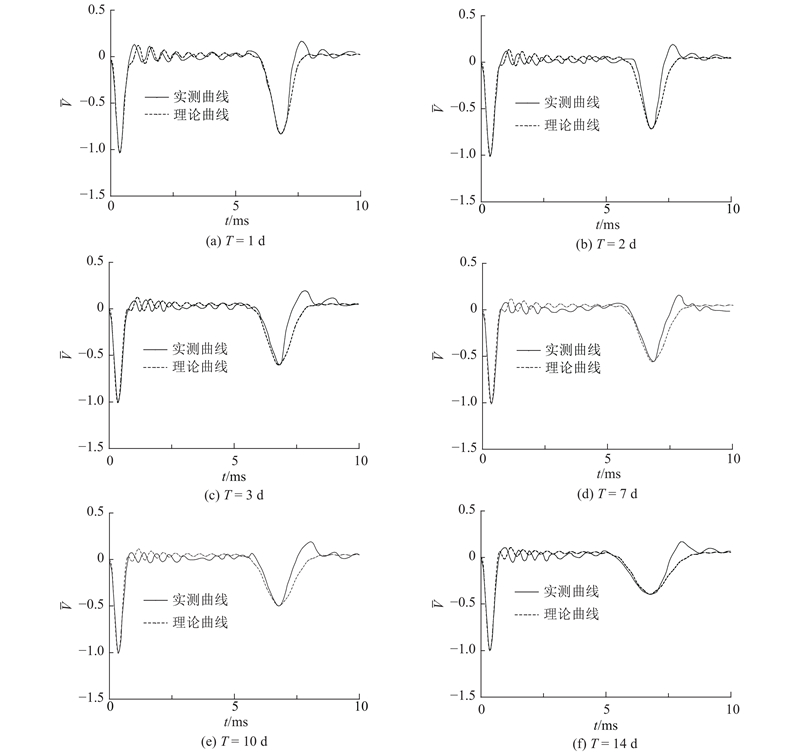
为了对本研究模型进行进一步验证，对比解析解与实测曲线，采用以下步骤对现场试验结果进行处理和拟合：1）对竹节桩位于地表时的曲线进行反演拟合. 在低应变测试时，对于特定的桩，动力响应曲线中入射信号的宽度由激振宽度决定，桩底反射波的到达时间由桩身弹性模量决定，桩底反射波的幅值由材料的黏性阻尼系数决定. 根据动力响应曲线的以上3个主要特性，使用第2节中理论模型，对实测曲线进行多次反演，分别得到激振宽度、桩身材料的弹性模量和黏性阻尼系数分别为 $0.52\;{\rm{ ms}}$、 $39.6\;{\rm{GPa}} $和 $516\;000\;{\rm{ N}} \cdot {{\rm{m}}^{ - 2}} \cdot {\rm{s}} $. 如图16所示为无土塞竹节桩实测与拟合曲线. 2）对照水泥土室内试验得到的对应龄期的水泥土切变模量，对不同龄期的竹节桩动力响应曲线进行拟合. 由上文参数分析结果可知，对于特定龄期的桩土系统，桩底反射信号的到达时间主要由桩侧虚土桩模型的尺寸系数决定，而桩底反射信号的幅值由虚土桩尺寸系数和水泥土的黏性阻尼系数共同决定. 因此先根据综合计算波速反演得到虚土桩尺寸系数，再据此反演得到该龄期水泥土的黏性阻尼系数. 对不同龄期的动力响应曲线重复以上步骤，得到不同龄期虚土桩尺寸系数和水泥土黏性阻尼系数. 几个典型龄期的实测曲线和反演曲线对比如图17所示.

3）统计不同龄期下竹节桩低应变响应曲线的综合波速和桩底响应幅值，以及反演拟合得到的各龄期下理论模型的虚土桩尺寸系数与水泥土黏性阻尼系数，结果如图18所示.

由图18（a）可以看出，根据实测曲线拟合得到的虚土桩尺寸系数总体来说较小，即在桩与土塞竖向振动过程中，只有较小范围内的水泥土可以等效为虚土桩，而且该系数在前期增长较快，后期逐渐趋于平稳，与预期中的逐渐增大存在一定差异，原因可能是实验室水泥土强度随龄期变化规律与现场水泥土强度发展规律之间存在一定差异. 由图18（b）可以看出，阻尼常数系数取值较大，桩芯土塞的等效阻尼系数取值与桩周土体等效阻尼系数计算公式得到的数值相差甚远，一方面是桩周土与桩芯土和桩身相互作用的振动特性和边界条件不同，即使是同样的土体对桩身的阻尼效果也不同，导致等效阻尼系数存在较大差异；另外，即使同是桩周土，不同土质的阻尼系数与公式计算值都有一定差异，水泥土本身材料特性与普通土不一致，导致等效阻尼系数与桩周土阻尼经验公式计算值相差较大.

（1）通过与有限元三维模型的对比，初步证明了所提出模型的可靠性，通过参数分析，得到了桩与土塞参数对桩顶动力时域响应曲线的影响规律.

（2）通过对现场试验数据的分析，发现桩芯填充土塞后，桩身综合波速有一定下降；随着水泥土龄期增长，波速又有轻微增大；上述现象与参数分析结果一致，说明本模型可以较好地模拟实际桩土相互作用.

（3）通过对计算模型中虚土桩尺寸系数和水泥土等效阻尼系数进行拟合，发现虚土桩尺寸并未表现出逐渐增长的趋势，可能与水泥土在现场和实验室条件的差异有关；桩芯水泥土拟合得到的数值与桩周土近似计算公式得到的数值相差较大，一方面与桩土系统振动特性有关，另一方面与水泥土的材料特性有关，具体的计算规律须进一步研究.

（4）本研究的桩侧虚土桩模型适用于与桩身黏结性较强的土体，而且土体黏结性越强，模型中的虚土桩尺寸系数越大；对于相对松散、与桩身黏结性较弱的土体来说，本研究模型不一定适用.