随着科技的发展，人们能够方便地对图像进行编辑处理，因此，一幅图像可能存在拷贝版本，也可能存在被局部篡改的版本. 如何区分拷贝或篡改图像非常重要. 图像哈希技术是用于解决上述问题的重要方法. 图像哈希是将一幅图像单向映射为一串简短的数字序列. 理想的图像哈希算法应满足2个基本性能：鲁棒性，即视觉相同或者相似的2幅图像对应的哈希序列应相同或相似，即哈希算法应对保持内容的图像处理稳健；区别性，即视觉完全不同的2幅图像对应的哈希序列应不同.

近年来，已有许多研究者提出多种图像哈希算法. 这些方法可以大致分为基于图像变换^[1-6]和基于数据降维^[7-12]. 基于图像变换的哈希方法如下. Venkatesan等^[1]利用离散小波变换（discrete wavelet transform，DWT）后的低频信息和高频信息来构建哈希，算法对伽马校正和对比度变换鲁棒性较差. 沈麒等^[2]利用多次小波变换的统计特征值构建哈希算法，算法具有较好的图像分类性能. Tang等^[3]提出利用离散余弦变换（discrete cosine transform，DCT）来获取图像哈希序列，算法对图像进行分块，并提取每一块的主要DCT系数，最后通过矩阵压缩来生成哈希序列. Qin等^[4]利用离散傅里叶变换（discrete Fourier transform，DFT）变换和非均匀采样提取图像特征，在鲁棒性和区别性上达到较好的平衡. 李新伟等^[5]通过Gabor变换获取图像的结构图，并结合极坐标变换提高算法的旋转鲁棒，最后将结构子图量化为哈希序列，算法具有较好的紧凑性和区别性. Tang等^[6]提出结合Gabor变换和DWT变换的方法构建哈希序列，算法对大角度的旋转不具有鲁棒性. 基于数据降维的算法如下. Hermandez等^[7]对子图像应用奇异值分解（singular value decomposition，SVD）得到稳健的图像特征，然后进行压缩量化得到最终的哈希序列，算法对噪音较敏感. Ghouti^[8]提出利用四元数奇异值分解（quaternion singular value decomposition，QSVD）来获取图像哈希，相较于SVD获取的哈希序列具有更好的分类性能. 唐振军等^[9]提出基于主成分分析（principal component analysis，PCA）特征距离的哈希算法，该算法有较好的分类性能，但效率不高. Tang等^[10]利用DCT变换获取图像的稳健特征，然后对特征矩阵应用局部线性嵌入（local linear embedding，LLE）进行压缩，对压缩结果的方差进行量化构建哈希算法，算法能够抵抗常见的数字操作，具有较好的区分能力. Tang等^[11]研究多维尺度变换（multidimensional scaling，MDS）在图像哈希领域的应用，该算法首先通过极坐标变换和DFT变换来获取旋转不变稳健特征，然后利用MDS来获取简洁的哈希序列，算法对任意角度的旋转具有较好的鲁棒性. Tang等^[12]探索张量分解在哈希算法中的应用，该算法提取图像在CIE L^*a^*b^*颜色空间下的L^*分量作为亮度分量，利用亮度分量构建张量，对张量进行Tucker分解生成哈希序列，该方法鲁棒性较好，但分类性能须进一步提高.

除了以上方案，还有一些其他技术被应用于图像哈希领域，例如Ring分割^[13]、图像矩^[14]、图像纹理^[15-16]和颜色特征^[17]等方式. Tang等^[13]利用Ring分割技术对图像进行分环处理，提取每一环的均值、方差、偏态和峰态表示每一环像素的分布情况，联合所有图像环内的统计特征来构建哈希算法，该算法具有较好的旋转鲁棒性，但分类性能有所欠缺. Zhao等^[14]结合图像Zernike矩和局部特征提出应用于图像认证的图像哈希算法. 实验结果表明该算法具有较低的碰撞率，能够检测出图像的局部篡改. Davarzani等^[15]利用中心对称局部二值模式描述符和奇异值分解构建图像哈希，与只使用中心对称局部二值模式描述符作为图像特征构成的图像哈希相比较，鲁棒性得到显著提升. Tang等^[17]提出利用HSI和YCbCr颜色空间的各个通道的统计值构建哈希序列，算法对大部分图像的处理操作较稳健，但对大角度旋转不具有鲁棒性.

在图像哈希算法提取过程中，以上大部分算法都是将图像作为二维平面来考虑特征的提取，本研究从三维视角理解图像的特征信息. 在三维视角下，提取图像在不同观测点下的峰顶峰谷曲线特征来得到图像的外形结构，获取峰顶与峰谷的位置信息来提取其内部结构，外形结构和内部结构共同构成图像的结构特征；提取图像的横向梯度与纵向梯度，通过矩阵相乘得到梯度信息矩阵，将梯度信息矩阵的量化特征与矩阵在三维视角下的结构特征联合起来构成图像的梯度特征；结合图像的结构与梯度特征得到最终的哈希序列.

结合结构特征与梯度特征的图像哈希算法生成框图如图1所示，主要由图像预处理、结构特征提取、梯度特征提取和哈希生成4个部分组成.

通过双线性内插法将输入图像的原始尺寸调整为 $N \times N$，可以使不同大小的图像具有相同的哈希长度，同时提高算法对图像缩放的鲁棒性；对图像进行高斯低通滤波处理，减小噪声、压缩这些细微操作的影响^[13]；本研究算法提取的结构特征与梯度信息是基于灰度图像的，因此将RGB彩色空间转换为YCbCr颜色空间，取亮度分量Y进行后续特征提取. 如图2所示为图像预处理示例，图2（a）为原始彩色图像，大小为205×153，图2（b）为预处理后灰度图像，大小为95×95.

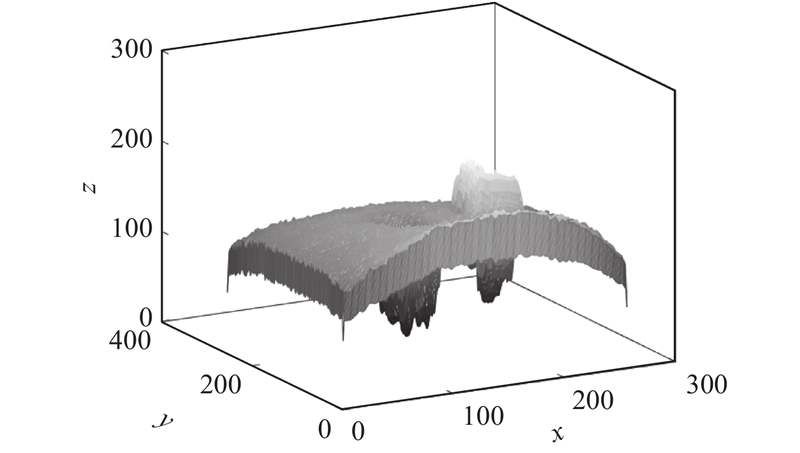
在图像特征提取中，通常将图像作为平面来提取特征. 本研究将图像放在三维视角下提取特征. 如图3所示为图2（b）在三维视角下的图像. 图中，x为图像的横向位置信息，y为纵向位置信息，z为坐标（x，y）对应的像素. 如图4所示为不同视角下的图像. 从如图4（a）所示的2个视角A、B观察图像，会有不同的视觉效果，如图4（b）、（c）所示为在不同视角下图3的峰顶曲线和峰谷曲线. 相似图像具有相似的峰顶与峰谷曲线，不同图像的峰顶与峰谷曲线则明显不同. 在图像经过JPEG压缩、图像缩放和亮度调整等保持内容的图像处理操作后，其峰顶与峰谷曲线之间的间距几乎不变. 将预处理后的图像分割为一系列大小为b×b的非重叠小块，计算每个子块的均值得到特征矩阵F₁，在三维视角A、B下矩阵F₁的峰顶与峰谷曲线的间距也应该不变. 不同视角下的峰顶和峰谷曲线如下：

(1) ${{f}}_{\rm{p}}^1 = \max \;({{{F}}_1},1),$

(2) ${{f}}_{\rm{v}}^1 = \min \;({{{F}}_1},1),$

(3) ${{f}}_{\rm{p}}^2 = \max \;({{{F}}_1},2),$

(4) ${{f}}_{\rm{v}}^2 = \min \;({{{F}}_1},2).$

式中： ${ f}_{\rm{p}}^1 $、 ${ f}_{\rm{v}}^1$分别为视角A下的峰顶与峰谷曲线； ${ f}_{\rm{p}}^2 $、 ${ f}_{\rm{v}}^2$分别为视角B下的峰顶与峰谷曲线；max （·，1）、min （·，1）分别为对矩阵按行取最大值和最小值操作；max （·，2）、min （·，2）分别为对矩阵按列取最大值和最小值操作.

对获得的峰顶与峰谷曲线进行计算，得到A、B视角下的特征矩阵 ${{F}}_{\rm{e}}^1$、 ${{F}}_{\rm{e}}^2$：

(5) ${{F}}_{\rm{e}}^1 = {{f}}_{\rm{p}}^1 - {{f}}_{\rm{v}}^1,$

(6) ${{F}}_{\rm{e}}^2 = {{f}}_{\rm{p}}^2 - {{f}}_{\rm{v}}^2.$

将 ${{F}}_{\rm{e}}^1$、 ${{F}}_{\rm{e}}^2$联合起来构成外在结构特征矩阵 ${{{F}}_{\rm{e}}}$，并进行量化处理得到H_e=[H_e(1)，H_e(2)，H_e(3)，···，H_e(i)]：

(7) ${{{F}}_{\rm{e}}} = [{{F}}_{\rm{e}}^1,{{F}}_{\rm{e}}^2],$

(8) ${H_{\rm{e}}}(i) = \left\{ {\begin{array}{*{20}{c}} 1,&{{{{F}}_{\rm{e}}}(i + 1) > {{{F}}_{\rm{e}}}(i)};\\ 0,&{{\text{其他}}}. \end{array}} \right.$

式中： ${{{F}}_{\rm{e}}}(i)$为结构特征 ${{{F}}_{\rm{e}}}$的第i列元素.

特征矩阵 ${{{F}}_{\rm{e}}}$只描述图像在三维视角下的外在结构而没有反映出三维视角下的内部结构. 因此提取矩阵F₁在视角A下的所有峰顶坐标 ${{{P}}^v} = {[p_1^v,p_2^v,p_3^v]^{\rm{T}}}$（v=1，2，···，N/b）与峰谷坐标 ${{{Q}}^v} = {[q_1^v,q_2^v,q_3^v]^{\rm{T}}}$得到坐标矩阵Z_d=[P¹，P²，···，P^（N/b），Q¹，Q²，···，Q^（N/b）]. 计算坐标矩阵Z_d到Z轴的距离得到特征矩阵F_i¹，如果在视角A下有多个峰顶或峰谷，计算该列的多个最大值或最小值到Z轴的距离，然后取均值代替该列的特征值. 同理在视角B下可以得到特征矩阵F_i². 连接不同视角下的特征构成内部特征矩阵F_i=[F_i¹，F_i²]，并按照式（8）将F_i量化为H_i=[H_i（1），H_i（2），H_i（3），···，H_i（i）]. 结合外在结构特征矩阵H_e与内部结构特征矩阵H_i得到结构特征H_S=[H_e，H_i].

图像的梯度信息可以有效地捕捉图像的局部变化，因此对矩阵F₁进行计算，得到相应的横向梯度信息矩阵F_h和纵向梯度信息矩阵F_v：

(9) ${{{F}}_{\rm{h}}} = {{{F}}_1}(x + 1,y) - {{{F}}_1}(x,y),$

(10) ${{{F}}_{\rm{v}}} = {{{F}}_1}(x,y + 1) - {{{F}}_1}(x,y).$

为了获得简洁的特征序列，计算得到特征矩阵F₂：

(11) ${{{F}}_2} = |{{{F}}_{\rm{h}}} \times {{{F}}_{\rm{v}}}|.$

式中：|·|为取绝对值操作.

对F₂按行展开为特征矩阵G，再量化为二进制序列H_g=[H_g（1），H_g（2），H_g（3），···，H_g（i）]：

(12) ${{{H}}_{\rm{g}}}(i) = \left\{ {\begin{array}{*{20}{c}} 1,&{{{G}}(i) > M};\\ 0,&{{\text{其他}}}. \end{array}} \right.$

式中：M为特征矩阵G的均值，G（i）为矩阵G的第i列元素.

如图5所示为图2（b）的特征矩阵F₂的三维视角. 可以看出，不同于图4的峰顶峰谷曲线，矩阵F₂的峰顶峰谷曲线包含图像的梯度信息. 为了充分获取图像的局部特征，按照1.3节结构特征提取方法获取矩阵F₂的结构特征矩阵H_g2，最后将特征序列H_g、H_g2联合起来作为梯度特征矩阵H_G=[ H_g，H_g2].

将结构特征矩阵H_S和梯度特征矩阵H_G联合起来得到中间哈希序列H_m=[H_S，H_G]，由1.3、1.4节可知，所提算法的哈希长度L=12（N/b）+（N/b）²−4个二进制数. 利用密钥Key对中间哈希序列进行扰乱得到最终的哈希序列H. 本研究选择汉明距离来衡量图像的相似程度：

(13) $D = \frac{1}{L}\sum\limits_{i = 1}^L {({{{h}}_1}(i) \oplus {{{h}}_2}(i))} .$

式中：h₁、h₂为2幅图像的哈希序列； $ \oplus $为异或操作. 当2幅图像的汉明距离大于阈值时判断为不同图像，反之为相似图像.

本研究算法的参数设置如下：规格化尺寸为N=256，标准差为1的3×3高斯低通滤波. 图像子块大小b=32，因此哈希长度L=156 bits.

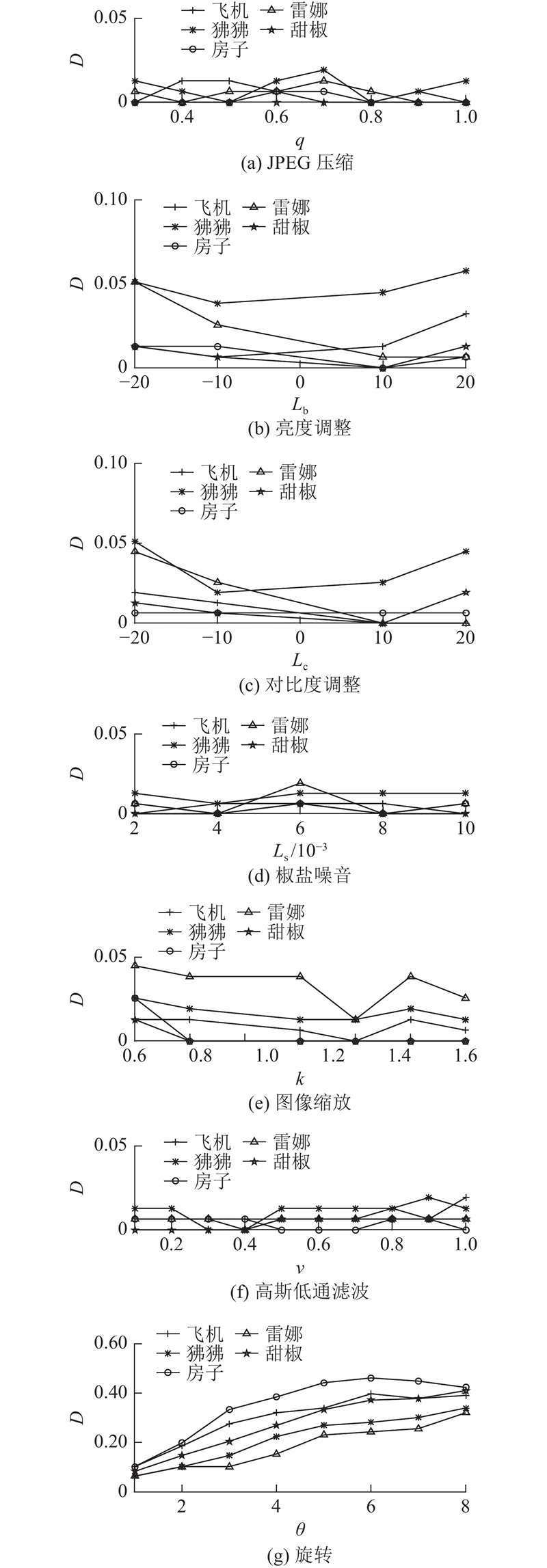
为了验证所提算法的鲁棒性，利用20幅彩色图像作为测试样本，如图6所示为其中一部分图像示例. 对每幅测试图像按照如表1所示的图像处理方式生成相似图像. 用本研究算法提取原始图像与相似图像的哈希序列，并计算两者的汉明距离. 按照不同的处理方式分别绘制汉明距离图，如图7所示为其中5幅图像的鲁棒性实验结果. 图中，q为JPEG压缩质量因子，L_b为亮度调整级别，L_c为对比度调整级别，L_s为椒盐噪音级别，k为图像缩放比例，v为高斯低通滤波方差，θ为旋转角度. 可以看出，JPEG压缩、亮度调整、对比度调整、椒盐噪音、图像缩放和高斯低通滤波的曲线波动范围较小，汉明距离均小于0.10. 在旋转攻击下的鲁棒性实验结果中，1°以内的旋转攻击的汉明距离较小，随着角度的增加，汉明距离有明显上升. 这是因为本研究算法在提取特征时对图像进行分块处理，算法对大角度旋转较敏感. 如表2所示为20幅图像在不同攻击下汉明距离的统计结果，可以看出7种攻击的汉明距离最小值均为0. 当攻击分别为JPEG压缩、亮度调整、对比度调整、椒盐噪音、图像缩放和高斯低通滤波时，汉明距离最大值均不超过0.10，均值和标准差均小于0.05. 旋转攻击的汉明距离的最大值、均值和标准差均超过0.10. 说明本研究算法对除旋转攻击以外的JPEG压缩、亮度调整、对比度调整和椒盐噪音等攻击具有较好的鲁棒性.

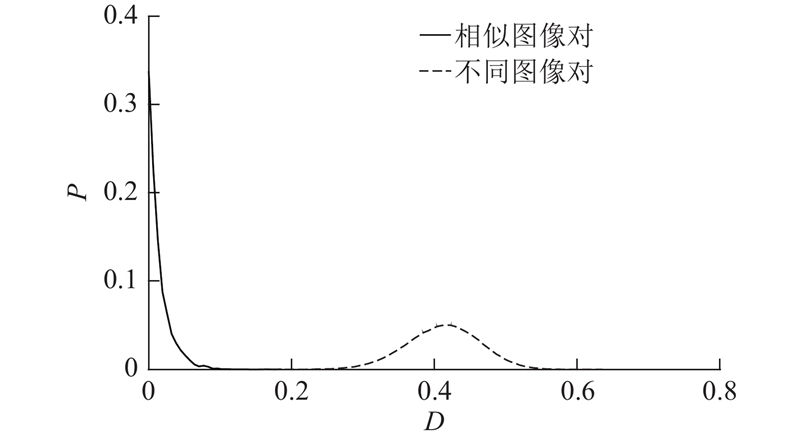
从网络图库中下载1 000幅不同图像构成不同图像库进行算法的区别性实验. 利用本研究算法提取1 000幅图像的哈希序列，并计算两两之间的汉明距离，共有499 500个不同图像对. 按照表3图像处理方式生成相似图像对，每幅图像会得到12幅相似图像，计算相似图像与原始图像的汉明距离，共有12 000个相似图像对. 相似图像对和不同图像对的汉明距离分布图如图8所示. 图中，P为该汉明距离出现的频率. 通过计算发现不同图像之间汉明距离最小值为0.153 8，最大值为0.634 6；相似图像对之间汉明距离最小值为0，最大值为0.185 9. 可以看出，相似图像对与不同图像对的汉明距离在0.150 0~0.190 0重叠，为了获得最优的阈值来区分相似图像对与不同图像对，利用大津法^[18]计算得到最优阈值为0.179 6. 同时引入碰撞率P_C和检错率P_E^[19]分析本研究算法的区别性，表达式分别为

(14) ${P_{\rm{C}}} = {{{N_{\rm{C}}}}}/{{{N_{\rm{D}}}}},$

(15) ${P_{\rm{E}}} = {{{N_{\rm{E}}}}}/{{{N_{\rm{S}}}}}.$

式中：N_C、N_D分别为不同图像对被认为是相似图像对的数目和不同图像对的总数目；N_E、N_S分别为相似图像对被检测为不同图像对数目和相似图像对总数目.

计算结果如表4所示. 可以发现，随着碰撞率的增加，检错率随之减小. 当阈值为0.179 6时，碰撞率、检错率分别为2.20×10⁻⁵、8.33×10⁻⁵，区别性较好. 简单起见，可以取阈值为0.180 0.

为了比较哈希算法的性能，将本研究算法与TD算法^[12]、Ring算法^[13]、CS-LBP算法^[15]和Local Color算法^[17]进行性能比较. 利用哈希算法提取相似图像对和不同图像对的哈希序列，计算它们之间的汉明距离. 通过设定不同的阈值从而得到一系列的错误接受率P_FPR和正确接受率P_TPR构成坐标点（P_FPR，P_TPR），绘制ROC曲线^[20]，实验结果如图9所示. P_FPR、P_TPR表达式分别为

(16) ${P_{{\rm{FPR}}}} = {{{n_1}}}/{{{N_1}}},$

(17) ${P_{{\rm{TPR}}}} = {{{n_2}}}/{{{N_2}}}.$

式中：n₁为不同图像对被误判为相似图像对的数目，n₂为相似图像对被正确判断的数目，N₁、N₂分别为不同图像对和相似图像对的总数目.

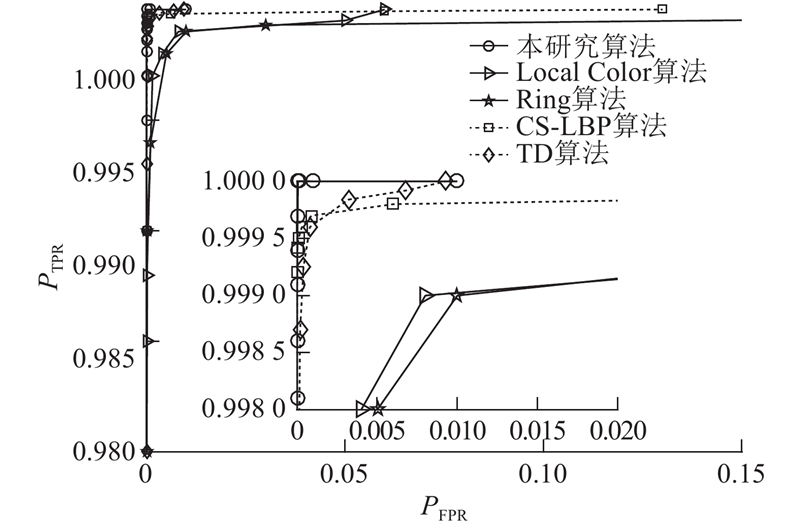
在ROC曲线图中，ROC曲线越接近图像左上角，算法的分类性能越好. 当不同算法取相同的P_FPR时，P_TPR越大的算法的ROC曲线越靠近左上角. 同理，当取相同的P_TPR时，P_FPR越小的算法的ROC曲线越靠近左上角. 当P_FPR=0时，本研究算法的P_TPR=0.998 6，而Local Color算法、Ring算法、CS-LBP算法和TD算法的P_TPR分别为0.960 3、0.974 2、0.998 7、0.982 8. 当P_TPR接近1.0时，本研究算法的P_FPR=1.4×10⁻⁴，Local Color算法、Ring算法、CS-LBP算法和TD算法的P_FPR分别为0.564 1、0.475 0、0.126 4、0.009 3. 当P_FPR=0时，只有CS-LBP算法的P_TPR比所提算法的P_TPR大0.000 1. 由图9可以看出，本研究算法的ROC曲线最靠近左上角，因此相较于对比算法，本研究算法具有更好的图像分类性能. 原因如下：本研究算法充分利用图像的梯度信息来获取图像的稳健特征，并结合图像在三维视角下的结构特征，使得算法在对亮度调整、JPEG压缩和对比度调整等处理操作具有较好的鲁棒性的同时，具有较好的区别性.

哈希生成效率和存储需求也是哈希性能的重要指标，通过Matlab平台，在同一电脑上计算1 000幅图像的哈希序列并记录总时间，总时间除以1 000从而得到计算一副图像哈希序列所需的平均时间，结果如表5所示. 图中，t为平均时间。可以看出，利用本研究算法计算哈希的平均时间为0.02 s，Ring算法所用时间最长为0.69 s. 如表5所示为本研究算法和对比算法的哈希长度，分别为156位、64个十进制数（一个十进制数至少需要4位二进制数表示，因此至少为256位）、440位、64个十进制数（最少256位）和96位. 可以看出，在具有相对较短的哈希长度下，本研究算法的运算时间最短. 综合考虑算法的区分性、运算时间和哈希长度，本研究具有较好的性能.

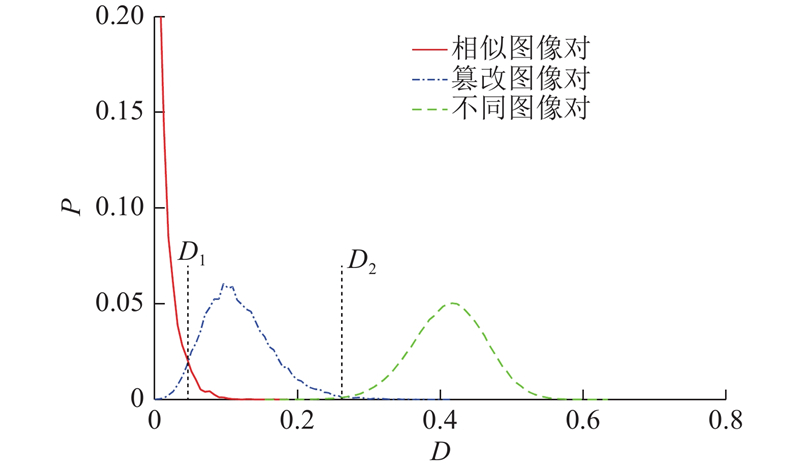
当图像发生局部篡改时，篡改图像与原始图像的汉明距离，应该位于相似图像与不同图像之间. 为了验证本研究算法的篡改检测能力，从VOC2012数据库^[21]中获取15 000幅图像，并对每幅图像添加一个对象，该对象占原图像面积的20%. 如图10所示为一个篡改示例. 绘制相似图像对、篡改图像对和不同图像对的汉明距离分布图，实验结果如图11所示. 相似图像对曲线与篡改图像对曲线的交点横坐标D₁=0.046 8，篡改图像对曲线与不同图像对曲线交点D₂=0.262 3，选择D₁、D₂作为阈值，当待检测图像与原始图像的汉明距离小于D₁时，认为待检测图像为相似图像；当距离为D₁~D₂时，认为是篡改图像；当距离大于D₂时，认为是不同图像. 通过计算发现，本研究算法分别有95.55%、94.69%、99.72%的正确识别率识别相似图像对、篡改图像对和不同图像对. 如表6所示为10个原始图像、篡改图像对以及它们之间的汉明距离. 可以看出，汉明距离均在阈值D₁、D₂之间. 本研究算法可以用于篡改检测.

本研究提出结合结构特征与梯度特征的图像哈希算法. 算法利用三维视角下的峰顶峰谷曲线来描述图像的外在结构，利用峰顶峰谷的位置信息来构建图像的内部结构，结合2种结构作为图像的结构特征来提高算法的区别性；提取图像的梯度信息来得到图像的局部信息；连接结构特征和梯度特征并置乱得到最终的哈希序列. 实验结果表明，本研究算法对亮度调整、JPEG压缩和对比度调整等保持内容的图像处理具有较好的鲁棒性；ROC曲线结果显示，与其他算法相比，本研究算法具有较好的图像分类性能；本研究算法具有较短的哈希长度和较短的运算时间. 在篡改检测实验中，当取2个不同的阈值时，本研究算法分别有95.55%、94.69%、99.72%的识别率识别相似图像对、篡改图像对和不同图像对，具有较好的篡改检测能力. 本研究算法也存在一定不足，例如算法所提取的特征不包含颜色特征，因此无法检测出图像的局部颜色篡改. 下一步研究将结合颜色及结构特征构成稳健的图像哈希.