压入式沉井工法[1]施工时通过由千斤顶组成的反力控制装置提供下压力,在尽量减少井内取土的情况下将沉井平稳地压入土层内,可以克服竖向地层差异性的不利影响并保证下沉的稳定性. 该工法施工时压入式沉井周边及底部土体会挤入井内形成土塞,并随着沉井下沉逐渐增高,使得井壁侧摩阻力和刃脚阻力增大,即产生土塞效应.
目前,国内外对于土塞效应的研究主要是以开口管桩为研究对象. 在理论分析方面,Paikowsky等[2]研究发现,土塞高度在桩内土体闭塞后不随入土深度的增加而增大;Randolph等[3]建立土塞的一维静力平衡方程,引入“有效土塞高度”的概念;杜来斌[4]研究指出,桩内土中楔体的形成是产生土塞的一个关键因素;赵明华等[5]基于太沙基极限承载力理论,推导出管桩沉桩时的土塞高度计算公式. 在数值模拟方面,詹永祥等[6]采用颗粒流程序PFC2D模拟开口管桩的沉桩过程,发现土塞效应随着管桩直径的增大迅速减小;肖勇杰等[7]建立有限元-无限元耦合模型,模拟灌注桩护壁套管高频振动贯入的全过程;董译之等[8]建立耦合欧拉-拉格朗日(CEL)模型,对超长大单桩的高频振动贯入过程进行模拟;王腾等[9]基于CEL模拟发现,钢管桩的土塞效应随着桩-土摩擦系数增大、桩径减小而增强. 在试验研究方面,朱合华等[10]对软土超长PHC桩打桩进行现场试验,发现影响土塞高度的主要因素是土性;周健等[11]通过模型试验,在细观上研究砂土中开口管桩沉桩时土塞的形成机制;张忠苗等[12-13]对淤泥质黏土互层及粉土层静压预应力混凝土管桩进行试验研究,分析土塞效应影响下的径向及桩端土压力变化情况;Tan[14]对比分析了一系列钢管桩静压贯入试验,发现管内土塞完全闭塞后外侧摩阻力约占总摩阻力的2/3. Liu等[15]通过开展粉土地层中开口管桩的沉桩试验,研究沉桩过程中桩内的土塞效应及其影响.
当前关于土塞效应的研究大多局限于开口管桩,对压入式沉井的针对性不足. 本文以压入式沉井为研究对象,采用CEL有限元方法对下沉过程进行数值模拟,分析压入下沉产生的土塞效应,探讨下沉时井内土塞的发展情况及土塞效应对下沉阻力的影响.
1. 压入式沉井概况
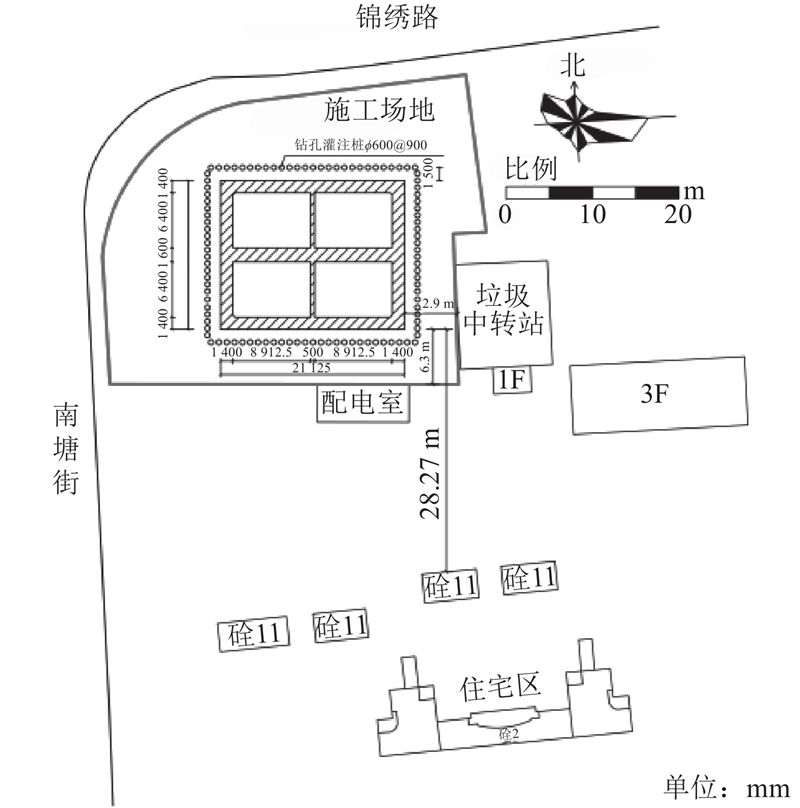
图 1
图 2
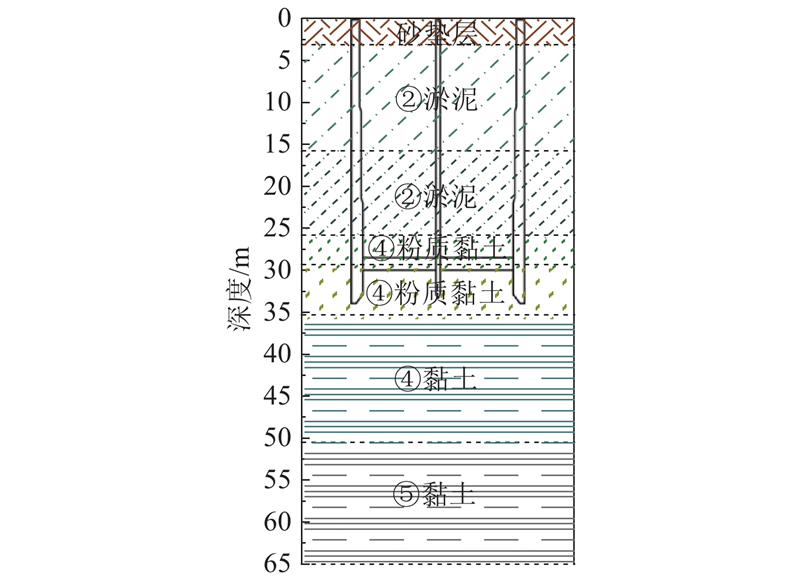
温州是我国沿海的典型深厚软土地区,根据地质勘察结果可知,施工场地自上而下主要由杂填土、淤泥、粉质黏土、黏土等工程地质层组成. 其中,①1杂填土层的均匀性差,压缩性低;②1、②2淤泥层为流塑性,压缩性及灵敏度高,整个淤泥层厚度近25 m,承载能力差,属典型的软弱地基土;④11、④12粉质黏土层为可塑性,中压缩性;④2、⑤2黏土层呈软~可塑状,中~高压缩性. 场地内的平均地下水位约为1.5 m. 施工前,将场地内的①1杂填土层换填为砂垫层. 场地的地质剖面如图3所示,各土层的物理力学参数根据地勘报告取值,如表1所示. 表中,d为层厚,γ为重度,c为黏聚力,φ为内摩擦角,Es1-2为压缩模量,fk为单位摩阻力,fak为地基承载力.
表 1 土层的主要物理力学参数
Tab.1
| 土层名称 | d/m | | 直剪 | | | | |
| | | ||||||
| 砂垫层 | 3.1 | 20.0 | 10.0 | 30.0 | 13.8 | 20 | 120 |
| ②1淤泥 | 12.7 | 15.0 | 8.9 | 8.2 | 1.45 | 10 | 40 |
| ②2淤泥 | 10.0 | 15.7 | 11.3 | 9.2 | 2 | 11 | 50 |
| ④11粉质黏土 | 3.5 | 19.3 | 25.1 | 19.4 | 5.73 | 21 | 140 |
| ④12粉质黏土 | 6.0 | 17.7 | 14.6 | 29.9 | 8.35 | 23 | 150 |
| ④2黏土 | 15.2 | 17.8 | 25.6 | 11.1 | 3.93 | 18 | 120 |
| ⑤2黏土 | 19.5 | 18.1 | 29.4 | 14.2 | 4.96 | 20 | 130 |
图 3
2. 土塞效应的形成机理与力学分析
压入式沉井下沉中周边土体涌入井内不代表井内土体闭塞产生土塞效应,土塞闭塞程度通常用土塞率(plug length ratio,PLR)和土塞增量填充率(incremental filling ratio,IFR)这2个指标[16]来描述:
式中:h为井内土塞高度,H为沉井下沉深度,dh为井内土塞高度增量,dH为沉井下沉深度增量.
PLR、IFR的取值一般为0~1.0,且其值越小,土塞闭塞程度越高:0表示土塞完全闭塞;1.0表示土塞完全不闭塞;0~1.0时表示不完全闭塞. 由于刃脚的切削作用,实际下沉过程中有些沉井的井内有可能出现细长的土柱,使得井内土塞高度大于下沉深度,即PLR、IFR有可能大于1.0. PLR计算容易但仅能反映土柱高度的变化;IFR虽然能够直观地反映土塞闭塞程度的变化,但计算相对复杂.
土塞高度和闭塞程度的变化情况取决于土塞所受的竖直向下的总荷载与底部地基极限承载力之间的相对大小. 当竖直向下总荷载等于底部地基极限承载力时,土塞处于临界平衡状态;当竖直向下总荷载大于底部地基极限承载力时,周边土体无法进入井内,土塞高度不再变化,土塞达到闭塞状态;当竖直向下总荷载小于底部地基极限承载力时,周边土体可以进入井内,土塞高度继续增加,土塞处于非闭塞状态. 随着沉井下沉深度的增加,井壁摩擦力和底部地基极限承载力会不断变化,井内土塞有可能在闭塞与不闭塞状态之间切换,因此土塞的演变过程实质上是土塞平衡状态的不断形成和被打破的过程.
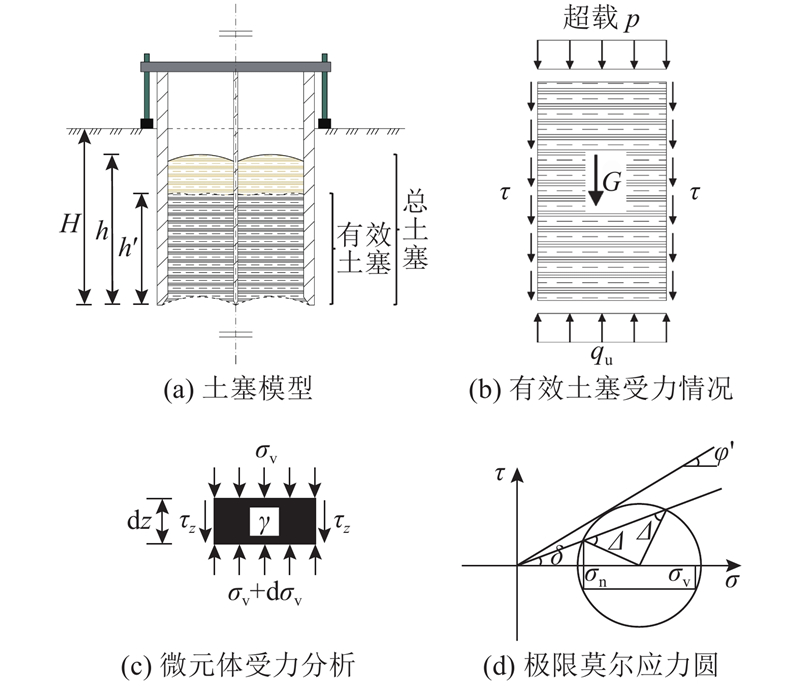
图 4
式中:G为有效土塞自重,
其中
土塞深度z处所受井壁单位摩擦力
式中:
将式(4)~(6)代入式(3),并假设
定义有效土塞高度比如下:
将式(9)代入式(8),可以解得土塞高度为
理论上可以通过式(10)预先求得沉井下沉过程中井内的土塞高度,然而实际情况下式(10)中的参数往往较难取得. 如土塞所受的摩擦力除了与土体的物理力学性质有关外,还与土塞的挤密程度、土塞和井壁间的摩擦角等因素有关. 在工程实践中,可以简单地以地质勘察得到的地基承载力进行深度修正后作为刃脚底地基承载力,并假定
3. 土塞效应数值分析模型建立
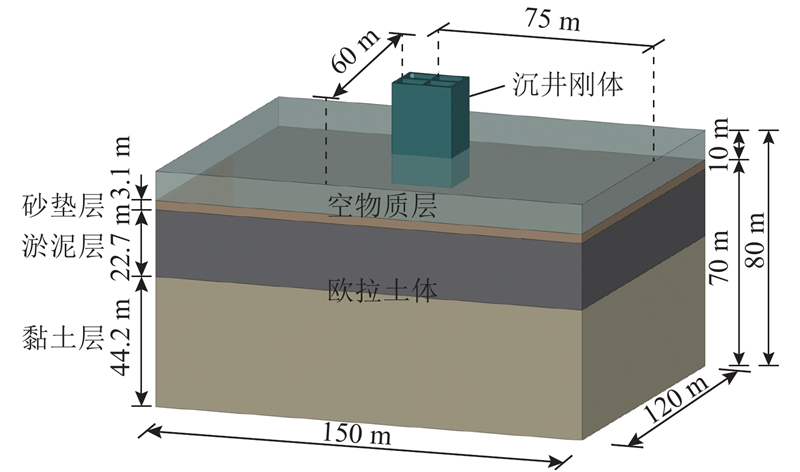
3.1. 模型及边界条件
图 5
针对该工程的特点及地质条件,为了实现对沉井下沉过程的合理模拟,采用如下基本假定.
1)由于沉井刚度远大于周边土体刚度,可将其近似视作刚体,采用拉格朗日网格建模,单元类型为R3D4单元.
2)土体选用DP(Drucker-Prager)弹塑性本构模型并采用欧拉网格建模,单元类型为EC3D8R.
3)采用耦合欧拉-拉格朗日(CEL)方法考虑土体的大变形问题,沉井与土体的接触耦合按罚函数约束来考虑.
4)CEL方法的收敛性对网格密度的依赖较大,参考文献[9],网格尺寸选为沉井壁厚/6.
5)采用位移贯入法,给沉井施加匀速变化的位移曲线进行加载,模拟整个下沉过程,在下沉过程中井内不挖土,且整个过程中沉井结构保持垂直姿态.
由于在CEL方法中欧拉网格不发生变形,实际运动的是网格中的材料,材料的运动趋势体现为通过欧拉网格节点的速度方向和大小. 对于该模型而言,边界条件取为约束模型底面X、Y、Z方向的速度和模型4个侧面X、Y方向的速度.
3.2. 计算参数选取
沉井结构按刚体进行模拟,无需设置材料参数. 地层对应的部分物理力学参数可以由原地层的物理力学参数转换得到. 数值模拟中,DP弹塑性本构模型参数可以由土体抗剪强度参数
式中:
表 2 CEL法的土体计算参数
Tab.2
| 土层 | | | | | | | | | E/kPa | |
| 砂垫层 | 20.0 | 10.0 | 30 | 50.2 | 0.778 | 0 | 34.64 | 13 800 | 41 400 | 0.20 |
| 淤泥层 | 15.3 | 10.0 | 8.6 | 17.5 | 0.905 | 0 | 23.25 | 1 692 | 5 076 | 0.49 |
| 黏土层 | 18.0 | 25.4 | 15.9 | 31.1 | 0.833 | 0 | 67.29 | 5 127 | 15 381 | 0.49 |
3.3. 数值模型验证
图 6
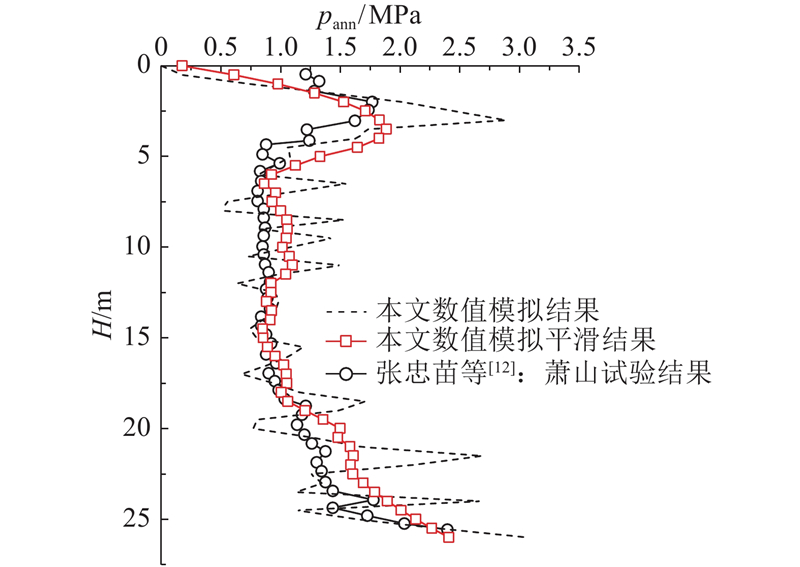
图 6 数值模型与现场试验得到的端阻对比
Fig.6 Comparison of tip resistance between numerical model and field test
从图6可以看出,虽然数值模拟得到的端阻波动较大,但经过平滑处理后的结果与现场试验结果在变化趋势上是较吻合的,表明CEL法的数值模拟结果是比较合理的. 采用CEL法研究压入式沉井下沉过程中的土塞效应是可行的.
4. 土塞效应及其影响的数值分析
4.1. 土塞演化规律
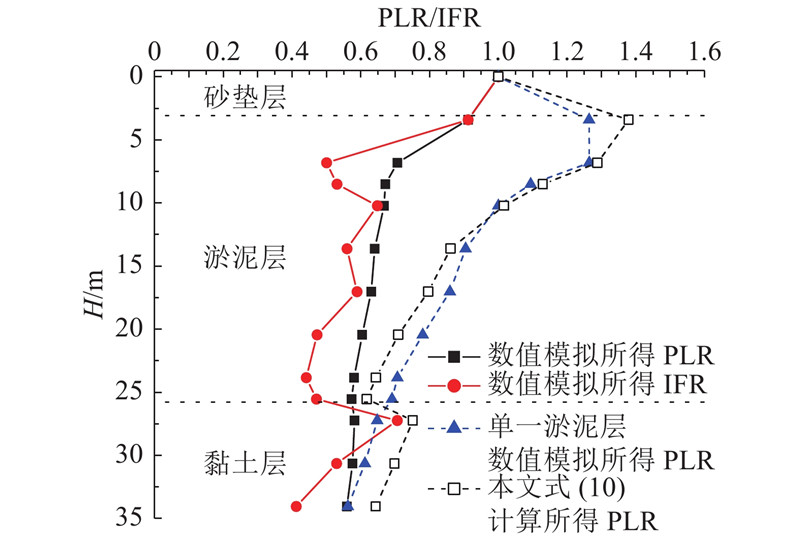
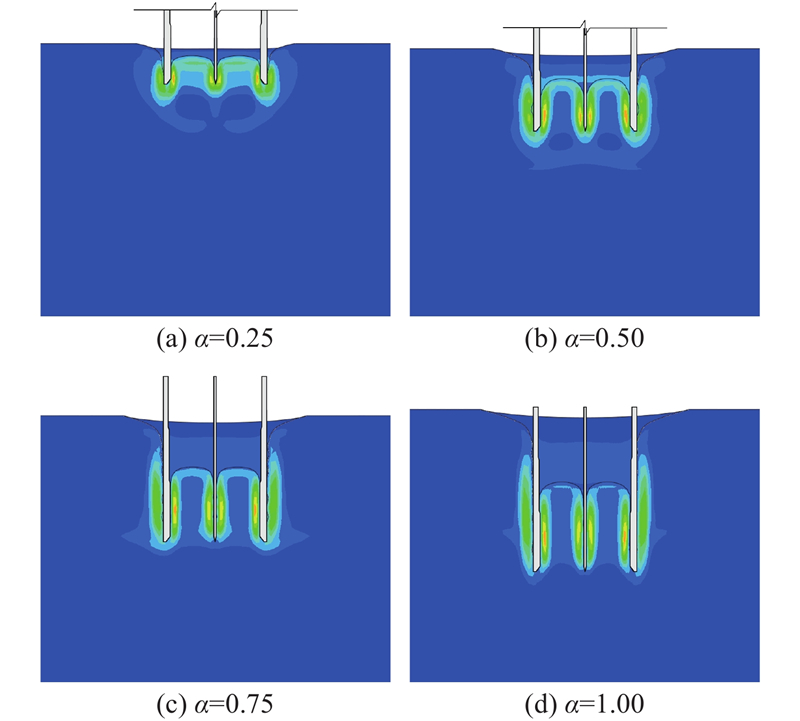
为了分析压入式沉井下沉过程中土塞的演化规律,分别采用式(10)及数值模拟方法,对背景工程计算得到的结果绘制出PLR、IFR随下沉深度的变化情况,如图7所示. 其中,采用式(10)计算土塞高度时,
图 7
淤泥土质软弱、流动性大,加上刃脚的切削作用,使得单一淤泥层时初始贯入阶段井内形成的土柱较高,甚至会超过下沉深度,PLR增加;砂垫层土质较硬、摩擦力大,淤泥上覆砂土垫层井内土塞更容易闭塞,使得初始贯入阶段PLR开始降低. 与仅考虑淤泥层单一土层情况下的PLR变化情况相比,考虑了砂垫层、淤泥层、黏土层多层土层后整个下沉过程的PLR都偏小,这说明软弱淤泥层上覆较硬的砂层会使土塞闭塞程度提高,土塞效应增大. 这一点与王腾等[9]研究发现的上硬下软地层中土塞闭塞情况相符. 在下沉深度达到一定程度后,仅考虑淤泥层单一土层的PLR与考虑砂垫层、淤泥层、黏土层3类土层时的PLR相近. 这表明上覆较硬砂层对土塞效应的影响只是在浅层较显著,在下沉深度较深(约25 m处)时,只考虑淤泥层的土体挤密效果足够使得侧摩阻力大到阻碍周边土体进入井内,井内土塞会达到一定的闭塞程度.
与数值模拟相比,采用本文推导的式(10)计算得到的PLR变化趋势基本一致,尤其在单一土层情况下十分接近,仅数值上偏大. 说明本文推导的土塞高度计算公式具有一定的合理性. 以下沉至设计深度时为例,采用式(10)计算得到的PLR约为0.64,稍大于数值模拟结果. 这是因为通过土塞静力平衡计算土塞高度时,假定土塞所受到的井壁摩擦力仅与竖向应力有关,未考虑挤土效应所引起的土体挤密对井壁摩擦力的影响,导致井壁摩擦力比实际情况偏小.
4.2. 土塞效应对土体运动场的影响
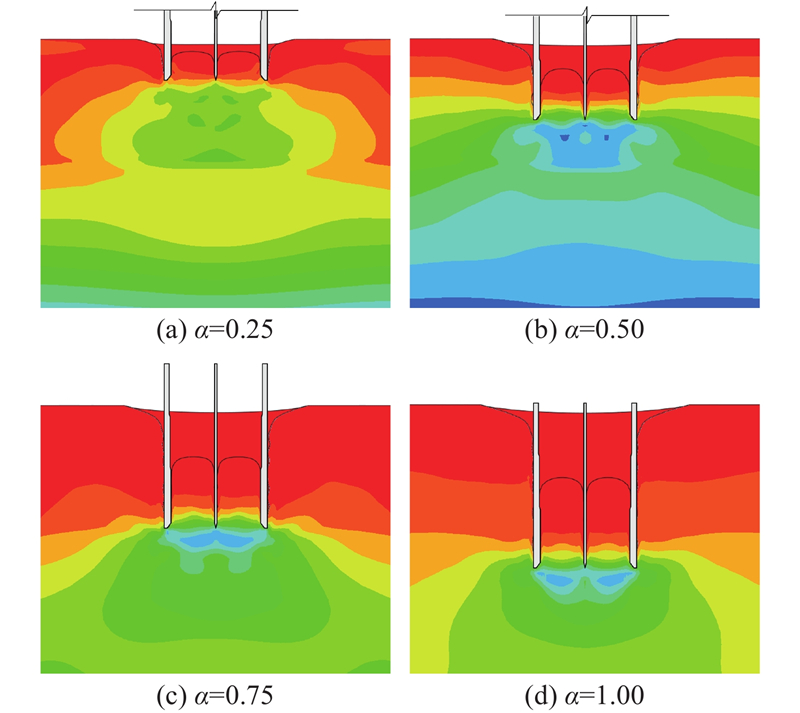
在下沉过程中,土塞效应会对沉井内部及周边土体的运动产生一定的影响. 如图8所示为压入式沉井下沉过程的地层运动速度场分布图,定义下沉深度比
图 8
图 8 下沉过程中的土体速度场分布
Fig.8 Typical distribution of soil velocity field during sinking procedure
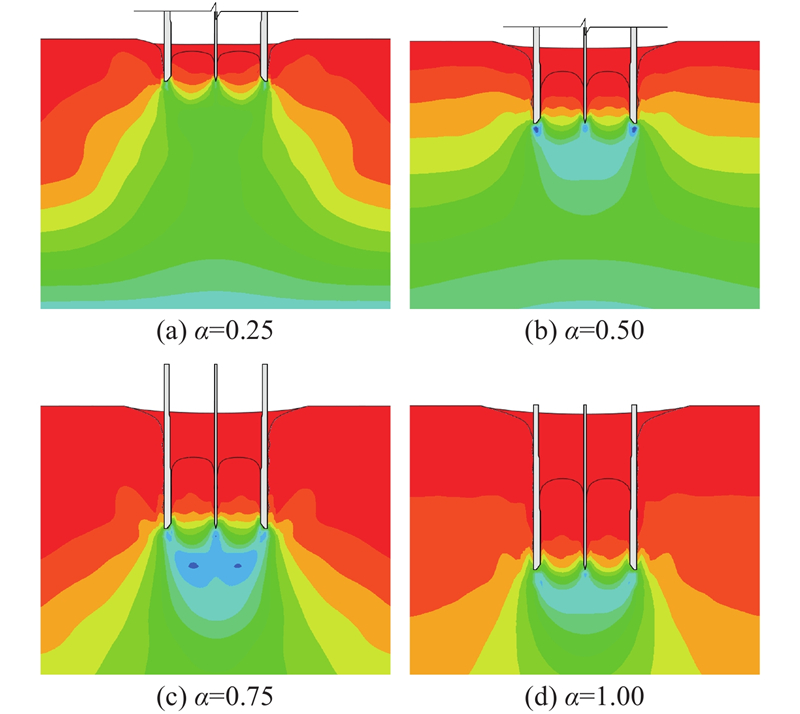
由于CEL方法中网格与材料相互独立,无法直接得到准确的地层变形情况. 采用示踪粒子(tracer particle)技术对地层进行标记,追踪土体颗粒的变形趋势. 如图9所示为压入式沉井下沉各阶段的土体颗粒变形趋势,选取
图 9
图 9 下沉过图程中的土体颗粒变形趋势
Fig.9 Typical deformation trend of soil particles during sinking procedure
4.3. 土塞效应对土体应力应变的影响
图 10
图 11
图 12
从图10可以看出,压入式沉井下沉时对土体的挤压效应会使得周边土体的水平应力增大,水平应力增大越多说明这种挤土效应越明显. 在压入下沉初期,刃脚底面及下方一定范围的土体水平应力增加;随着下沉深度的增加,井内土体的水平应力也有所增加;井内形成土塞后,土塞下部的土体水平应力增加较明显,且土塞闭塞程度越高,水平应力增大的部分越往下.
从图11可以看出,由于挤土效应的存在,压入式沉井下沉对竖向应力的主要影响表现为刃脚底及下方一定范围内土体的竖向应力激增. 井内土塞产生后,刃脚底还会产生向下凸的应力拱,阻碍了周边土体涌入井内. 土塞闭塞程度越高、土塞效应越大,刃脚底的应力拱越大,竖向应力增大越明显. 在沉井下沉至最终深度时,刃脚底应力拱最大的向下应力达到2.8 MPa,远远超过了原先该深度的土体天然自重应力场,土体难以进一步涌入井内,说明此时土塞较闭塞.
由图12可以发现,在压入下沉初期,土体发生的塑性应变主要集中在刃脚底面;当土体挤密到一定程度使得井壁摩擦力增大后,井壁附近土体被带动向下发生变形,产生了一定程度的塑性应变. 从塑性应变的发展趋势来看,井壁附近土体塑性应变不沿着井壁全高度发展,而是主要集中在土塞下部的一定范围. 这说明这部分土塞中的土体比上方的土体所受的井壁摩擦力较大,相应发生的向下运动变形也大,因此该部分的土塞可以视作为有效土塞. 有效土塞占整个土塞的比例越小,表明土塞闭塞程度越高.
4.4. 土塞效应对侧摩阻力的影响
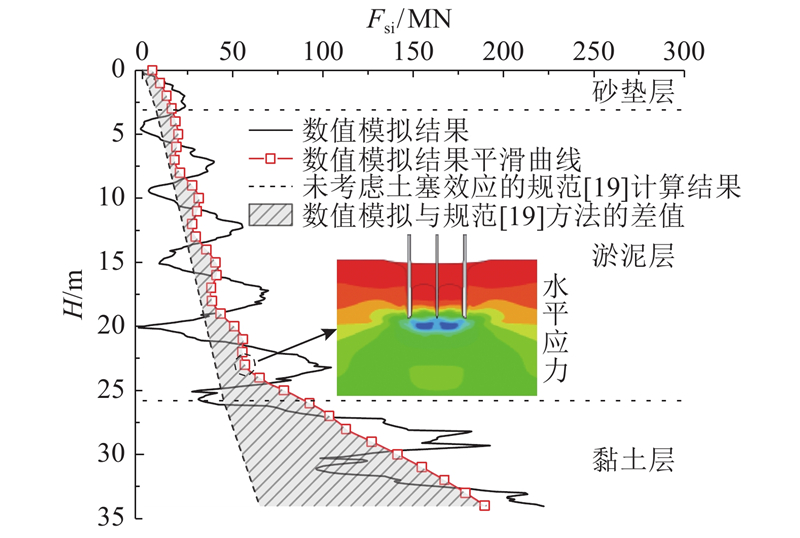
压入式沉井下沉过程中所产生的土塞效应会使得井壁与土体的接触应力增大,从而导致井壁所受的侧摩阻力增大. 为了分析土塞效应对侧摩阻力的影响,分别选取数值模拟所得的内、外井壁侧摩阻力随下沉深度的变化情况,与未考虑土塞效应时的侧摩阻力进行对比,得到沉井内、外壁侧摩阻力随下沉深度的变化关系,分别如图13、14所示. 图中,Fsi、Fso 分别为内壁侧摩阻力和外壁侧摩阻力. 其中数值模拟所得曲线的波动较大,须进行平滑处理. 未考虑土塞效应的侧摩阻力按沉井结构设计规程[19]中的方法计算得到. 简化地层的单位摩阻力可以由表1各层土的单位摩阻力按高度加权平均得到,即:砂垫层为20 kPa,淤泥层为10.44 kPa,黏土层为19.8 kPa.
图 13
图 13 内壁侧摩阻力随下沉深度的变化
Fig.13 Variation of lateral friction force of inner wall along sinking depth
图 14
图 14 外壁侧摩阻力随下沉深度的变化
Fig.14 Variation of lateral friction force of outer wall along sinking depth
由图13可知,内壁侧摩阻力随下沉深度的增加呈不断增大趋势. 考虑土塞效应下数值模拟所得的内壁侧摩阻力比不考虑土塞效应计算得到的内壁侧摩阻力大,这种差距在下沉到底时最明显,增大了约242.1%. 当土塞达到一定闭塞程度时,通过数值模拟所得的内壁侧摩阻力变化曲线出现拐点,约在下沉深度25 m左右,之后内壁侧摩阻力开始急剧增大. 分析此时井壁周边土体的水平应力发现,井壁内侧土体的水平应力相对较大,表明内侧井壁与土体间产生了较大的挤压应力. 土塞效应对内壁侧摩阻力的影响较明显.
由图14可知,外壁侧摩阻力随下沉深度的增加呈不断增大的趋势. 当下沉深度较小时,考虑土塞效应下数值模拟所得的外壁侧摩阻力与不考虑土塞效应计算得到的外壁侧摩阻力相差不大,只有在下沉深度较大时考虑土塞效应的外壁摩阻力才会明显大于不考虑土塞效应的情况,下沉到底时考虑土塞效应后的外壁摩阻力比不考虑土塞效应时增大了约200%. 通过数值模拟所得的外壁侧摩阻力变化曲线的拐点出现在下沉深度25 m左右,之后外壁侧摩阻力开始快速增大. 分析此时井壁周边土体的水平应力发现,井壁外侧土体的水平应力相比内侧较小. 相比内壁侧摩阻力,土塞效应对外壁侧摩阻力的影响较小,仅在土塞闭塞程度较高、土塞效应较大之后才会对外壁侧摩阻力产生显著影响.
4.5. 土塞效应对刃脚阻力的影响
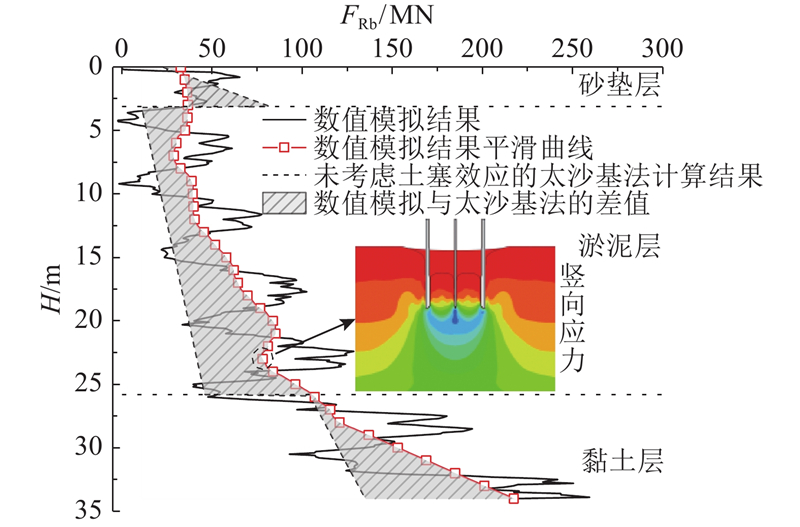
压入式沉井下沉时的土塞效应在竖向上会在刃脚底部产生一个向下的应力拱,阻碍周边土体进入井内. 土塞效应除了会对侧摩阻力产生影响外,还会对刃脚阻力产生影响. 为了分析土塞效应对刃脚阻力的影响,选取数值模拟所得的刃脚阻力FRb随下沉深度的变化情况,与未考虑土塞效应的刃脚极限阻力进行对比,得到FRb随下沉深度的变化关系,如图15所示. 未考虑土塞效应的刃脚极限阻力采用太沙基地基极限承载力乘上刃脚面积进行计算.
图 15
图 15 刃脚阻力随下沉深度的变化
Fig.15 Variation of blade feet resistance force along sinking depth
从图15可以看出,刃脚阻力随下沉深度的增加呈不断增大趋势,且考虑土塞效应下通过数值模拟所得的刃脚阻力比不考虑土塞效应计算得到的刃脚阻力大. 土塞效应引起的刃脚阻力增大在软弱地层如淤泥层中尤为明显,整体上增大了将近1倍. 下沉到底时考虑土塞效应后的刃脚阻力比不考虑土塞效应时增大了约61.9%. 通过数值模拟所得的刃脚阻力变化曲线的拐点出现在下沉深度25 m左右,之后刃脚阻力的增大趋势略有加快,但不如侧摩阻力显著. 分析此时刃脚底部土体的竖向应力发现,刃脚底部的应力拱十分明显. 土塞效应产生后会使得刃脚阻力增大,在软弱地层中尤为明显.
5. 结 论
(1)基于土塞受力机理推导得到土塞高度的理论计算公式,并与数值模拟进行对比,发现在软土地层且各层土之间差异不大时,两者结果基本一致. 该公式能够为现场工程师预估沉井下沉过程中的土塞高度提供一定的计算依据.
(2)在下沉初期,PLR、IFR均较大,土塞闭塞程度低;进入淤泥层瞬间,PLR、IFR急剧减小,土塞闭塞程度显著提高;在淤泥层中下沉时,PLR的减小趋势大大缓和,IFR略有增大;下沉至最终指定深度后,井内土塞的PLR约为0.56,IFR约为0.41. 与单一软弱淤泥层情况相比,上覆较硬砂层会增大土塞效应.
(3)在沉井下沉过程中,作用在井壁上的土体水平应力增加,但主要集中在有效土塞高度范围,刃脚附近的土体竖向应力激增并同时形成一个向下的应力拱. 土体的等效塑性应变主要发生在有效土塞高度范围内,表明这部分的土体所受摩擦力较大,相应产生的滑移变形大.
(4)土塞效应会使得井壁所受的侧摩阻力增大,对内壁侧摩阻力的影响尤为显著,对外壁侧摩阻力的影响仅在土塞效应较大(下沉深度约为25 m)时较明显. 沉井下沉至设计深度后,相比不考虑土塞效应的情况,考虑土塞效应后的内壁侧摩阻力增大约242.1%、外壁侧摩阻力增大约200.1%.
(5)土塞效应会使得刃脚底部产生一个向下的应力拱,阻碍周边土体进一步涌入井内,从而导致刃脚阻力增大. 土塞效应对刃脚阻力的影响在软弱地层(淤泥层)更明显,整体上增大将近1倍. 沉井下沉至设计深度后,相比不考虑土塞效应的情况,考虑土塞效应后的刃脚阻力增大约61.9%.
参考文献
压入式沉井施工对环境影响的现场监测研究
[J].
Field measurement and analysis of influence of jacked open caisson construction on environments
[J].
The effects of plugging on pile performance and design
[J].
One-dimensional analysis of soil plugs in pipe pile
[J].DOI:10.1680/geot.1991.41.4.587 [本文引用: 2]
PHC管桩土塞效应浅析
[J].
Brief analysis of plug effect of PHC pipe piles
[J].
基于太沙基极限承载力理论的管桩土塞高度计算方法
[J].
Study on calculation method of soil plug height of pipe pile based on Terzaghi ultimate bearing capacity
[J].
砂土中开口管桩沉桩过程的颗粒流模拟研究
[J].
Study of process of open-ended pipe pile driven into sand soil by particle flow simulation
[J].
高频振动贯入过程中灌注桩护壁套管土塞效应机理
[J].
Mechanisms of soil plugging effect inside sleeve of cast-in-place piles driven by high frequency vibratory hammers
[J].
超大直径单桩基础高频振动贯入过程中的土塞效应
[J].
Soil plugging effect during driving of large diameter mono-pile by vibratory hammers
[J].
黏土中静压管桩土塞机制研究
[J].
Mechanism of soil plug for jacked pipe pile in clay
[J].
上海软土地基超长打入PHC桩工程性状研究
[J].DOI:10.3321/j.issn:1000-4548.2004.06.004 [本文引用: 1]
Behavior of long PHC piles driven in Shanghai soft clay
[J].DOI:10.3321/j.issn:1000-4548.2004.06.004 [本文引用: 1]
静压开口管桩沉桩过程模型试验及数值模拟
[J].
Model test and numerical simulation of driving process of open-ended jacked pipe piles
[J].
静压预应力混凝土管桩土塞效应试验研究
[J].DOI:10.3969/j.issn.1000-7598.2011.08.005 [本文引用: 4]
Research on plugging effect of jacked prestressed concrete pipe pile
[J].DOI:10.3969/j.issn.1000-7598.2011.08.005 [本文引用: 4]
淤质与粉质互层土中管桩沉桩过程的土压力
[J].
The earth pressure during pile driving in silty soil with mucky soil interbed
[J].
Full-scale testing of open-ended steel pipe piles in thick varied clayey silt deposits along the Delaware river in New Jersey
[J].DOI:10.1061/(ASCE)GT.1943-5606.0000777 [本文引用: 1]
Case history of installing instrumented jacked open-ended piles
[J].DOI:10.1061/(ASCE)GT.1943-5606.0000638 [本文引用: 1]
A new look at the phenomenon of offshore pile plugging
[J].DOI:10.1080/10641198909379869 [本文引用: 1]
分层土中的单桩分析法
[J].
An approach for a single pile in layered soil
[J].