浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(7): 1341-1346 doi: 10.3785/j.issn.1008-973X.2020.07.012

机械与能源工程

变刚度多稳态复合材料结构设计与性能分析

张征,, 张豪, 柴灏, 吴化平, 姜少飞

Design and performance analysis of variable stiffness multi-stable composite laminate structure

ZHANG Zheng,, ZHANG Hao, CHAI Hao, WU Hua-ping, JIANG Shao-fei

收稿日期: 2019-03-9  

Received: 2019-03-9  

作者简介 About authors

张征（1979—），教授，博导，从事智能复合材料结构的研究.orcid.org/0000-0002-1398-7727.E-mail：zzhangme@zjut.edu.cn , E-mail：zzhangme@zjut.edu.cn

摘要

通过研究复合材料层合板结构局部纤维角变化的理论模型与刚度变化的关系，设计2种变刚度多稳态复合材料层合板结构. 对变刚度多稳态复合材料结构进行建模，运用Matlab求出不同的平衡方程解，得到变刚度多稳态复合材料结构的稳态构型. 制备相应的实验试件，测量变刚度多稳态复合材料结构不同稳态转变时的力学性能，通过有限元软件Abaqus模拟变刚度多稳态复合材料结构的降温冷却过程，得到平衡稳定状态的数值解. 结合理论、数值与试验，分析变刚度多稳态复合材料结构的稳态构型、稳态转变最大载荷及载荷-位移曲线的变化规律.

关键词： 变刚度 ; 多稳态复合材料 ; 经典层合板理论 ; 有限元分析

Abstract

Two variable stiffness multi-stable composite laminate structures were designed by analyzing the relationship between the theoretical model of regional fiber angle change and the stiffness change of composite structures. The variable stiffness multi-stable composite structure was modeled, and the stable configuration of the multi-stable composite structures with variable stiffness was obtained by solving different equilibrium equations with Matlab. The experimental specimens were prepared to measure the mechanical properties with different stable transformation. The cooling process were simulated by finite element software Abaqus, and the numerical results of equilibrium stable configuration were obtained. The stable configuration, the stable transformation maximum load and the load-displacement curvatures were analyzed by combining with the theoretical, numerical and experimental results.

Keywords： variable stiffness ; multi-stable composite structure ; classical laminate theory ; finite element analysis

PDF (972KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张征, 张豪, 柴灏, 吴化平, 姜少飞. 变刚度多稳态复合材料结构设计与性能分析. 浙江大学学报(工学版)[J], 2020, 54(7): 1341-1346 doi:10.3785/j.issn.1008-973X.2020.07.012

ZHANG Zheng, ZHANG Hao, CHAI Hao, WU Hua-ping, JIANG Shao-fei. Design and performance analysis of variable stiffness multi-stable composite laminate structure. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(7): 1341-1346 doi:10.3785/j.issn.1008-973X.2020.07.012

变刚度多稳态碳纤维树脂基底复合材料结构是具有多种不同稳定状态的复合材料结构[1-2]. 每种稳定状态都具有一定的承受载荷的能力，在适当的外载荷的作用下稳态之间可以发生转变，不需要持续的外载荷来维持稳定状态. Waldhart[3]对比分析利用平移法和平行法铺设变角度碳纤维层合板的性能表现，发现平移法比平行法既便于制备又能获得更优异的抗屈曲性能. Gurdal等[4-6]通过定义纤维角度沿参考方向线性变化，实现了纤维曲线轨迹的铺设，建立了变刚度复合材料层合板概念. 随着自动铺丝技术的发展，目前已经可以通过曲线铺放丝束的方法，使得复合材料单层的纤维角度不断变化，达到改变结构刚度的目的[7]. 采用该方法制造的层合板称为变刚度多稳态复合材料结构[8-10]. 与传统树脂基碳纤维复合材料结构相比，变刚度多稳态复合材料结构有诸多优点，最显著的是极强的可设计性[11-14]. 到目前为止，国内外学者在变刚度多稳态复合结构的设计和应用上，围绕残余热应力法、预应力法和变刚度设计法3种方法，开展一系列研究[15]，取得了丰硕的成果. 总体上，3种方法各有优缺点，相互之间没有绝对的优势，需要根据具体的应用需求选择相应的方法. 残余热应力法的制备过程简单、易操作，但制得的多稳态板及其结构对湿热环境较敏感；预应力法采用对称铺层，与非对称双稳态层合板相比具有更好的湿热稳定性，但纤维预应力的施加很不方便，且预应力的可控性差，约束预应力法需要提供特殊的模具，装配过程不易操作；变刚度设计法在层合板变刚度设计的基础上往往需要结合前2种方法中的一种，获得多稳态结构. 目前，国内外的学者们围绕其单层材料属性、纤维铺设角度、铺层顺序等进行设计[16-18].

本文运用变刚度法，设计2种多稳态复合材料结构试件. 研究试件的稳态特性，通过施加机械载荷驱动试件在不同稳态间转变，获得试件在稳态转变过程中的载荷-位移曲线. 在经典层合板理论的基础上，结合里兹法推导变刚度结构理论模型，通过Matlab软件得到平衡位置构型. 采用Abaqus建模，对实验过程进行模拟，研究试件的稳态性能，得到变形过程中试件的中面位移云图、稳态转变载荷-位移曲线.

1. 实验研究

1.1. 试验制备

采用实验方法，研究变刚度多稳态复合材料结构在稳态转变时的力学特性. 利用平行法制备变刚度多稳态复合材料结构，试件采用的材料为碳纤维（T700）填充环氧树脂预浸布，结构共5层，单层厚度为0.125 mm，单层板材料参数见表1. 其中2种5层铺设的变刚度多稳态复合材料结构试件的纤维角度定义如图1所示（包含连接层）. 试件分为3块区域，每块区域的纤维角度如图1所示，其中包括45°、−45°、0°和90°的纤维角度.Li (i=1，2，3)和W1分别为每块区域的尺寸长度. 定义纤维铺设方式从左到右为反对称/正交/反对称的结构记为试件1；铺设方式从左到右为正交/反对称/正交的结构为试件2.

表 1   单层板的材料参数[18]

Tab.1  Material properties of carbon fibre laminates

参数 数值
E11/GPa 186
E22/GPa 88
v12 0.3
G12/GPa 7.1
ɑ11/（10−6°C−1） 0.345
ɑ22/（10−6°C−1） 15.3

新窗口打开| 下载CSV


图 1

新窗口打开| 下载原图ZIP| 生成PPT

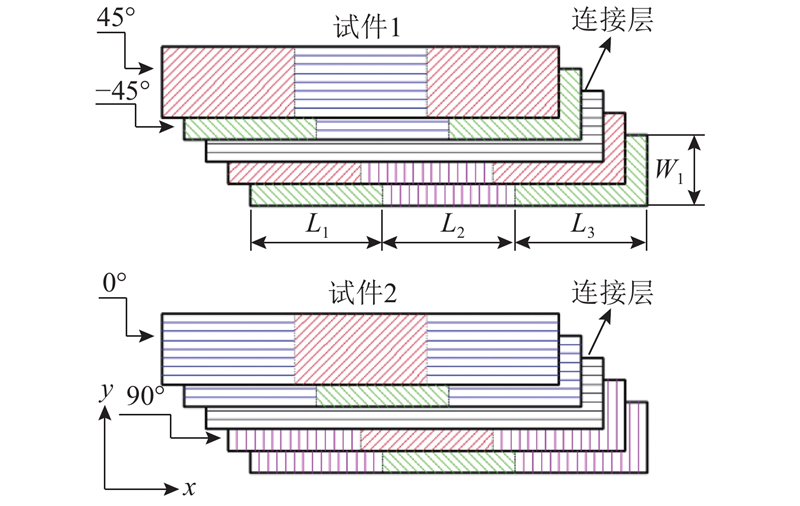
图 1   变刚度多稳态复合材料结构纤维方向示意图

Fig.1   Schematic diagram of fiber direction of variable stiffness multi-stable composite laminate structures


试件1和试件2在平板状态下通过高温保压及冷却固化并脱模的方式制备而得. 制造设备在图2中显示，右边的恒温恒压控制台设定温度与时间，实验中采用的固化温度为200 °C，固化时间为3 h，之后自然冷却至室温20 °C[19]. 2种型号的变刚度多稳态复合材料结构试件尺寸为Li=100 mm(i=1，2，3)，W1=70 mm.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   恒温恒压热压机

Fig.2   Processing equipment with constant temperature and pressure


实验制备的试件如图3、4所示. 图中，2种变刚度多稳态复合材料结构试件表面平顺完整，试件1和试件2呈现2个稳定状态，每个试件在室温状态下均可以保持不同的稳态，且第1稳态到第2稳态转变后不需要外力维持. 在稳态转变过程中会出现1个临界稳定状态，保持该临界稳定状态需要外力维持.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   试件1稳态示意图

Fig.3   Stable diagram of specimen 1


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   试件2稳态示意图

Fig.4   Stable diagram of specimen 2


1.2. 实验方法

借鉴已有的非对称层合板的实验加载方案[20-21]，对变刚度多稳态复合材料结构试件的两端采用光滑的夹具固定，如图5所示. 由于变刚度多稳态复合材料结构试件的中间凸起朝上，故可以通过对试件的中间凸起位置施加载荷，使得试件从1个稳态转变到第2个稳态. 实验中使用的夹具和压头如图6所示，在实验中使用型号为INSRTON-2345电子万能拉伸试验机，配置的机械力传感器量程为0~200 N. 该实验中所测的变刚度多稳态复合材料结构试件在不同稳态转变时的最大载荷小于机械力传感器的最大量程，因此INSRTON-2345型拉伸试验机符合力学测试条件.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   稳态转变实验

Fig.5   Experiment of stable state transformation


图 6

新窗口打开| 下载原图ZIP| 生成PPT

图 6   压头与夹具

Fig.6   Indenter and fixture


1.3. 结果分析

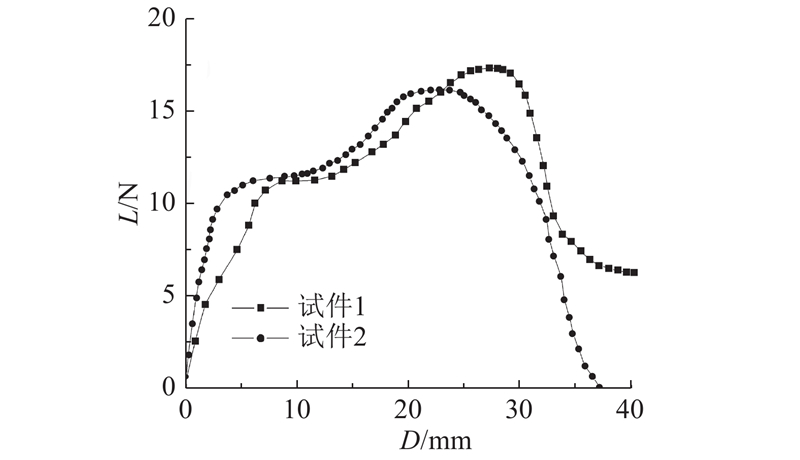
在拉伸实验中，压头以1 mm/min的进给速度对变刚度多稳态复合材料结构试件的中间凸起位置加载，通过INSRTON-2345型拉伸试验机中的力学传感器，可得实验中试件1和试件2所施加载荷随位移的变化情况. 如图7所示为2种变刚度多稳态复合材料结构试件稳态转变时的载荷L-位移D曲线. 在加载初期，试件1的实验载荷随着位移线性增大，然后以类似二次曲线的形式达到最大值，随后突然下降到一个局部最小值，在该过程中从第1稳态转变到第2稳态，完成稳态转变. 试件2在加载初期，实验载荷随着位移线性增大，之后缓慢达到一个局部最大值，然后以类似二次曲线的形式达到最大值，随后快速下降到0，完成第1稳态到第2稳态的转变. 从图7可以看出，试件1和试件2在载荷初期的曲线趋势类似，但在达到第2稳态时的载荷曲线表现不同，表明了2种不同铺设方式的结构差异.

图 7

新窗口打开| 下载原图ZIP| 生成PPT

图 7   2种试件的稳态转变载荷-位移曲线

Fig.7   Load-displacement curvatures of two specimens


2. 理论、模拟与实验对比

2.1. 理论模型与有限元模拟对比

在经典层合板理论的基础上，结合里兹法推导出变刚度结构理论模型，得出纤维铺设方向与铺设组合对层合结构刚度矩阵的关系[5,17]，预测变刚度多稳态复合材料层合结构不同的稳态形状. 碳纤维树脂基材料的热膨胀系数不同，变刚度多稳态复合材料层合结构经过高温固化、自然冷却至室温后会发生翘曲，呈现出多种不同的稳定状态. 基于经典层合板理论公式，可得面内刚度矩阵A、耦合矩阵B和弯曲刚度矩阵D关于位置坐标的详细表达式[22]：

$\begin{split}& \left[ {{{{A}}_{ij}}\left( {x,y} \right),{{{B}}_{ij}}\left( {x,y} \right),{{{D}}_{ij}}\left( {x,y} \right)} \right] = \\ &\quad \int_{ - {{{\rm{th}}}}/{{\rm{2}}}}^{{{{\rm{th}}}}/{{\rm{2}}}} {{{\overline {{Q}} }_{ij}}\left( {x,y} \right) \times \left[ {1,z,{z^2}} \right]{\rm{d}}z} . \end{split} $

式中：th为厚度. 变刚度多稳态复合材料层合结构固化后自然冷却至室温状态，该过程只受热载荷作用，层合结构的响应通过最小势能原理确定[23]. 在没有外部机械作用的情况下层合结构的势能 $\varGamma $由下式给出：

$\varGamma = \int\limits_{\rm{v}} {\left( {\left[\!\! {\begin{array}{*{20}{c}} {{\varepsilon ^0}},&k \end{array}}\!\! \right]\left[N,\;M \right]^{\rm T}} \right)} {\rm{d}}V.$

采用最小势能原理，取 $\varGamma $关于a、b和c的1阶变分之和为0，可得

$\begin{split} {\text{δ}} \varGamma = \left( {\frac{{{\text{δ}} \varGamma }}{{{\text{δ}} a}}} \right){\text{δ}} a + \left( {\frac{{{\text{δ}} \varGamma }}{{{\text{δ}} b}}} \right){\text{δ}} b + \left( {\frac{{{\text{δ}} \varGamma }}{{{\text{δ}} c}}} \right){\text{δ}} c = 0. \\ \end{split} $

式中：a、b分别为x和y方向上的非均匀曲率的负值，c为非均匀扭曲曲率的负值，

$\left.\begin{aligned} a =& {{{\partial ^2}{\omega ^0}}}/{{\partial {x^2}}} = - k_x^0 , \\ b =& {{{\partial ^2}{\omega ^0}}}/{{\partial {y^2}}} = - k_y^0, \\ c =& 2{{{\partial ^2}{\omega ^0}}}/{{\partial x\partial y}} = - k_{xy}^0. \\ \end{aligned}\right\} $

层合结构在固化冷却之后的位移取决于需要确定的未知数 ${d_i}$. 对于从固化温度到室温的差 $\Delta T$，总势能的表达式为

$\varGamma = \varGamma ({d_i});\;\;i = 0,1,2,3,\cdots.$

为了在冷却过程（ $\Delta T < 0$）期间计算变刚度多稳态层合结构的最终稳态形状，使用最小势能原理，引入牛顿-拉夫逊法求解一组高度非线性的平衡方程组[24-25].

${{\partial \varGamma ({d_i})}}/{{\partial {d_i}}} = 0;\;\;i = 0,1,2,3,\cdots.$

通过构造雅可比矩阵评估非线性的平衡方程组解的稳定性，其中

$J = \frac{{{\partial ^2}\varGamma }}{{\partial {d_i}\partial {d_j}}} = 0;\;i,j = 0,1,2,3,\cdots,\;i \ne j.$

当且仅当雅可比矩阵是正定的时，平衡解才稳定. 面内位移 ${u^0}$、 ${v^0}$的表达式为

$\left.\begin{split} {u^0}(x,y) =& \int {\left( {\varepsilon _x^0 - {{({{\partial {w^0}}}/{{\partial x}})}^2}}/2 \right)} {\rm d}x + \\ & {d_{25}}y + {d_{26}}{y^2} + {d_{27}}{y^3} , \\ {v^0}(x,y) = &\int {\left( {\varepsilon _y^0 - {{({{\partial {w^0}}}/{{\partial y}})}^2}}/2 \right)} {\rm d}y+ \\ & {d_{28}}x + {d_{29}}{x^2} + {d_{30}}{x^3}. \end{split} \right\}$

以上的面内位移 ${u^0}$、 ${v^0}$中包含多个未知参数，通过非线性的平衡方程组可以一一确定，得到变刚度多稳态复合材料层合结构的稳态构型数据. 在有限元模拟软件Abaqus中，采用壳单元定义复合材料层合板的厚度以及改变铺设方式. 建立壳模型，模型的大小为300 mm×70 mm，以图1设计的试件1为例，从左到右的3块区域对应的角度为[45°, −45°, 0°, 45°, −45°]、[0°, 0°, 0°, 90°, 90°]和[45°, −45°, 0°, 45°, −45°]，单层厚度为0.15 mm的模型建立完成后，输入对应区域的材料属性，具体的材料属性如 表1所示. 理论结果通过Matlab软件计算得到，对2种方式得到的试件1稳态位置数据进行分析，理论结果与有限元模拟的数值结果对比如图8所示. 图中，离散点表示理论解，曲面表示有限元数值解.

图 8

新窗口打开| 下载原图ZIP| 生成PPT

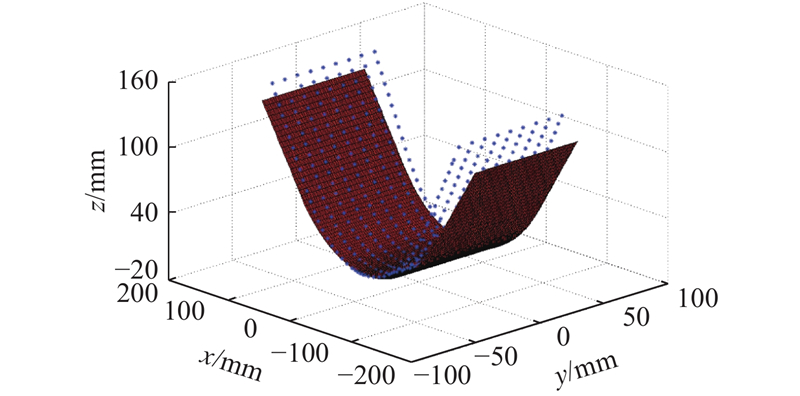
图 8   试件1第2稳态构型理论结果与有限元数值解的对比

Fig.8   Comparison of second stable configuration of theoretical and simulation results for specimen 1


从图8可以看出，结合经典层合板理论和里兹法的理论模型得到的稳态位置数据与有限元模拟所得的结果对比误差较小，2种变刚度多稳态复合材料结构的稳态趋势基本吻合. 数值模拟在边界的最大误差为98.31 mm，理论模型在边界的最大误差为103.46 mm，理论与模拟的最大误差为5.24%.

2.2. 有限元模拟与实验对比

如图9、10所示为2种结构有限元模拟与实验结果对比图. 利用有限元模拟试件从高温高压固化后的降温冷却过程，此时试件的整体环境温度从200 °C逐渐降至20 °C[26]. 从每个稳态位置中可以看出，有限元模拟与实验中的平衡位置稳态构型比较吻合，试件1在左右两侧区域均呈现扭转现象，第2稳态在中间弯曲；试件2的2个稳态中间区域均出现扭转，且扭转方向相反.

图 9

新窗口打开| 下载原图ZIP| 生成PPT

图 9   试件1两个稳态构型有限元与实验试件对比

Fig.9   Two different stable configurations of specimen 1 in simulation and experiment specimen


图 10

新窗口打开| 下载原图ZIP| 生成PPT

图 10   试件2两个稳态构型有限元与实验试件对比

Fig.10   Two different stable configurations of specimen 2 in simulation and experiment specimen


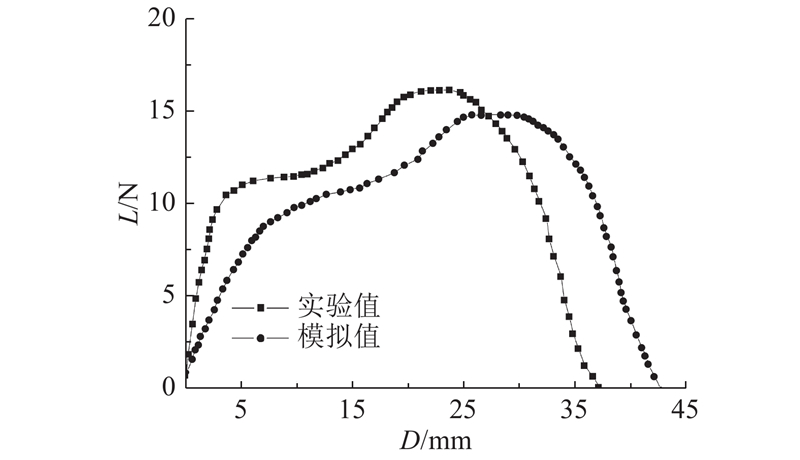
试件1在有限元模拟与实验中的载荷-位移曲线如图11所示，有限元模拟的最大载荷为16.11 N，理论模型的最大载荷为14.79 N，相对误差为8.19%. 通过实验与有限元模拟均能够使试件完成稳态转变，实验与有限元模拟中的载荷-位移曲线趋势吻合，造成有限元模拟和实验误差的原因可能如下：1）在试件制备时3块区域铺设角度精度不够；2）试件本身有扭转现象，在载荷-位移测量中与夹具接触不完整，导致压头初始高度与模拟中有偏差；3）模拟过程中简化的实验模型，实验中的夹具与试件表面的摩擦力、压头上的力传感器精度会造成误差. 试件2的载荷-位移曲线在有限元模拟与实验的起始趋势相同，有限元模拟过程中载荷迅速上升到一个值；之后平缓地到达最大载荷，最大载荷小于实验中的最大载荷，相对误差为8.19%；然后到达第2稳态时下降到最小值，最后的位移大于实验中的最大位移.

图 11

新窗口打开| 下载原图ZIP| 生成PPT

图 11   试件2载荷-位移实验与有限元模拟对比

Fig.11   Comparison of load-displacement with experiment and simulation for specimen 2


3. 结　语

制备2种变刚度多稳态复合材料结构试件，研究变刚度多稳态复合材料层合结构的稳态特性. 施加机械载荷驱动试件在不同稳态间转变，获得试件在稳态转变过程中的载荷-位移曲线，试件1与试件2由于纤维铺设角度的不同造成载荷-位移曲线的差异，导致最大载荷不同. 在经典层合板理论的基础上，结合里兹法推导出变刚度结构理论模型，通过MATLAB软件得到平衡位置构型. 采用ABAQUS建模，对实验过程进行模拟，研究试件的稳态性能，得到变形过程中试件的中面位移图、稳态转变载荷-位移曲线. 稳态数值构型在理论和模拟的对比中误差较小，整体构型相同，表明了理论模型的可行性. 稳态转变时的载荷-位移曲线在模拟与实验中吻合较好，但由于试件与夹具及压头的接触与摩擦等影响导致两者有微弱的误差. 以上研究会进一步提升复合材料的应用范围，为多功能的变刚度多稳态复合材料层合结构提供重要的参考.

参考文献

KUDER I K, ARRIETA A F, RIST M, et al

Aeroelastic response of a selectively compliant morphing aerofoil featuring integrated variable stiffness bi-stable laminates

[J]. Journal of Intelligent Material Systems and Structures, 2016, 27 (14): 1949- 1966

DOI:10.1177/1045389X15620038      [本文引用: 1]

SOUSA C S, CAMANHO P P, SULEMAN A

Analysis of multistable variable stiffness composite plates

[J]. Composite Structures, 2013, 98 (3): 34- 46

[本文引用: 1]

WALDHART C. Analysis of tow-placed, variable-stiffness laminates [D]. Virginia: Virginia Tech, 1996.

[本文引用: 1]

GURDAL Z, OLMEDO R

In-plane response of laminates with spatially varying fiber orientations-variable stiffness concept

[J]. American Institute of Aeronautics and Astronautics Journal, 1993, 31 (4): 751- 758

DOI:10.2514/3.11613      [本文引用: 1]

GURDAL Z, TATTING B F, WU C K

Variable stiffness composite panels: effects of stiffness variation on the in-plane and buckling response

[J]. Composites Part A: Applied Science and Manufacturing, 2008, 39 (5): 911- 922

DOI:10.1016/j.compositesa.2007.11.015      [本文引用: 1]

BLOM A W, STICKLER P B, GURDAL Z

Optimization of a composite cylinder under bending by tailoring stiffness properties in circumferential direction

[J]. Composites Part B: Engineering, 2010, 41 (2): 157- 165

DOI:10.1016/j.compositesb.2009.10.004      [本文引用: 1]

邵忠喜. 纤维铺放装置及其铺放关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2010.

[本文引用: 1]

SHAO Zhong-xi. Research on fiber laying device and its key technologies [D]. Harbin: Harbin University of Technology, 2010.

[本文引用: 1]

LE H M, CAO L, DO T N, et al

Design and modelling of a variable stiffness manipulator for surgical robots

[J]. Mechatronics, 2018, 53: 109- 123

DOI:10.1016/j.mechatronics.2018.05.012      [本文引用: 1]

PEETERS D M J, HESSE S, ABDALLA M M

Stacking sequence optimization of variable stiffness laminates with manufacturing constraints

[J]. Composite Structures, 2015, 125: 596- 604

DOI:10.1016/j.compstruct.2015.02.044     

NIK M A, FAYAZBAKHSH K, PASINI D, et al

Optimization of variable stiffness composites with embedded defects induced by automated fiber placement

[J]. Composite Structures, 2014, 107: 160- 166

DOI:10.1016/j.compstruct.2013.07.059      [本文引用: 1]

KUDER I K, ARRIETA A F, ERMANNI P

Design space of embeddable variable stiffness bi-stable elements for morphing applications

[J]. Composite Structures, 2015, 122: 445- 455

DOI:10.1016/j.compstruct.2014.11.061      [本文引用: 1]

KHANI A, IJSSELMUIDEN S T, ABDALLA M M, et al

Design of variable stiffness panels for maximum strength using lamination parameters

[J]. Composites Part B: Engineering, 2011, 42 (3): 546- 552

DOI:10.1016/j.compositesb.2010.11.005     

孔斌, 顾杰斐, 陈普会, 等

变刚度复合材料结构的设计、制造与分析

[J]. 复合材料学报, 2017, 34 (10): 2121- 2133

KONG Bin, GU Jie-fei, CHEN Pu-hui, et al

Design, manufacture and analysis of variable stiffness composite structures

[J]. Journal of Composite Materials, 2017, 34 (10): 2121- 2133

DURAN A V, FASANELLA N A, SUNDARARAGHAVAN V, et al

Thermal buckling of composite plates with spatial varying fiber orientations

[J]. Composite Structures, 2015, 124: 228- 235

DOI:10.1016/j.compstruct.2014.12.065      [本文引用: 1]

RAHMAN T, IJSSELMUIDEN S T, ABDALLA M M, et al

Postbuckling analysis of variable stiffness composite plates using a finite element-based perturbation method

[J]. International Journal of Structural Stability and Dynamics, 2011, 11 (4): 735- 753

DOI:10.1142/S0219455411004324      [本文引用: 1]

ARRIETA A F, KUDER I K, RIST M, et al

Passive load alleviation aerofoil concept with variable stiffness multi-stable composites

[J]. Composite Structures, 2014, 116: 235- 242

DOI:10.1016/j.compstruct.2014.05.016      [本文引用: 1]

COBURN B H, WU Z, WEAVER P M

Buckling analysis of stiffened variable angle tow panels

[J]. Composite Structures, 2014, 111 (11): 259- 270

[本文引用: 1]

XIONG C, LEI Y, YAO X

Dynamic experimental study of deployable composite structure

[J]. Applied Composite Materials, 2011, 18 (5): 439- 448

DOI:10.1007/s10443-010-9174-7      [本文引用: 2]

ZHANG Z, WU H, YE G, et al

Experimental study on bistable behaviour of anti-symmetric laminated cylindrical shells in thermal environments

[J]. Composite Structures, 2016, 144: 24- 32

DOI:10.1016/j.compstruct.2016.02.062      [本文引用: 1]

ZHANG Z, WU H, YE G, et al

Systematic experimental and numerical study of bistable snap processes for anti-symmetric cylindrical shells

[J]. Composite Structures, 2014, 112: 368- 377

DOI:10.1016/j.compstruct.2014.02.030      [本文引用: 1]

LEI Y M, YAO X F

Experimental study of bistable behaviors of deployable composite structure

[J]. Journal of Reinforced Plastics and Composites, 2010, 29 (6): 865- 873

DOI:10.1177/0731684408100738      [本文引用: 1]

刘东新, 刘伟. 复合材料力学基础[M]. 西安: 西北工业大学出版社, 2010.

[本文引用: 1]

SCHLECHT M, SCHULTE K

Advanced calculation of the room-temperature shapes of unsymmetric laminates

[J]. Journal of Composite Materials, 1999, 33 (16): 1472- 1490

DOI:10.1177/002199839903301601      [本文引用: 1]

ARRIETA A F, KUDER I K, WAEBER T, et al

Variable stiffness characteristics of embeddable multi-stable composites

[J]. Composites Science and Technology, 2014, 97: 12- 18

DOI:10.1016/j.compscitech.2014.03.017      [本文引用: 1]

HALDAR A, REINOSO J, JANSEN E, et al

Thermally induced multistable configurations of variable stiffness composite plates: Semi-analytical and finite element investigation

[J]. Composite Structures, 2018, 183: 161- 175

DOI:10.1016/j.compstruct.2017.02.014      [本文引用: 1]

TAWFIK S, TAN X, OZBAY S, et al

Anticlastic stability modeling for cross-ply composites

[J]. Journal of Composite Materials, 2007, 41 (11): 1325- 1338

DOI:10.1177/0021998306068073      [本文引用: 1]

/

〈 〉