迄今为止,大部分文献研究同步输出反馈多为动态输出反馈和基于观测器的输出反馈. 动态输出反馈控制本质上是增广系统的静态输出反馈控制问题. 基于观测器的输出反馈称为输入、输出反馈,它有2个反馈信号:基于真实的输出和输出经观测器形成的信号,是一种动态补偿形式.
本文研究线性高阶多智能体系统同步和有限时间同步问题. 基于智能体节点输出构造静态协议,得到使该系统达到同步和有限时间同步的充分条件. 该协议的阶数小、结构简单、易于工程实现. 协议仅利用单一的输出信号改善系统品质,是一种不完全的信息反馈形式. 一般来说,基于Lyapunov理论导出的静态输出反馈控制往往要通过求解双线性不等式得到,计算成本高,是NP-hard问题[20],相关结果较少.
本文通过引入自由变量,有效分离出输出反馈增益矩阵. 采用迭代算法给出最小化性能指标,克服了扰动带来的影响. 通过数值仿真验证了结果的可行性. 研究参数对解空间的影响,得到参数的可行域. 本文给出的方法可以综合满足多个性能要求,对单个智能体系统建模具有很好的鲁棒性.
1. 符号描述
智能体节点间的通信拓扑结构用加权图表示,记为
2. 问题描述
考虑含有扰动的多智能体系统,第
式中:
注1 在实际传感器系统中,不同传感器往往具有不同的技术特征/属性,一般不会使用冗余的传感器(仅在需要时使用,例如在容错系统中). 此外,在理论和应用中,状态变量的数量通常都大于(或等于)传感器的数量,因此关于输出矩阵
基于系统输出反馈设计分布式协议:
若令
注2 在实际运用中,大量智能体是非内省的,自身的状态信息无法获知,但邻居智能体的相对输出往往可测(例如自治的水下车辆、车辆间的相对距离信息可以用声呐传感器测出,技术上容易实现,而且成本低廉). 上述基于系统输出设计的分布式协议不需要测量每一个智能体的状态信息,维度低,运算简便,更符合工程实际.
定义被控输出为
式中:
同步误差
其中
系统(6)结合静态输出反馈协议(3)满足下式:
式中:
在给出主要结论之前,介绍下述引理和定义.
引理1[21] 对给定的标量
则系统(7)渐近稳定,并且具有给定的
定义1[22] 若下述条件满足:
且在零初始条件下,存在标量
则多智能体系统(1)同步,且具有扰动抑制水平
(ii)若同步误差
且在零初始条件下,被控输出
则系统(1)关于
引理2[23] 对于给定的矩阵
1)
2)
3)若
证明:首先证明
令
可得
进而
i)、ii)成立. 下面证明iii). 由于
且
因此
3. 主要结果
3.1. 基于静态输出反馈协议的多智能体系统同步
定理1 对于满足
则多智能体系统(1)同步,且具有
式中:
证明: 对不等式(8)进行合同变换,左右同乘
令
令
可得式(13). 根据引理1可知,
多智能体系统(1)同步,且具有
注3 从定理1的证明可以看出,系统(1)同步问题本质上等价于系统(7)渐近稳定,同步问题可以转化成不等式(16)的求解问题. 不等式(16)是一个高维的非线性矩阵不等式,维数随着网络节点数的增多而逐渐增大,难以求解. 定理1将该不等式的求解问题转化成线性不等式(13)的求解问题,可以通过Matlab中的toolbox直接求解. 反馈增益矩阵可以从
注4 定理1说明扰动抑制能力与网络节点数目有关,网络节点数目越多,系统抗干扰能力越强.
3.2. 基于静态输出反馈协议的有限时间同步
给出多智能体系统(1)在有限时间内同步,且具有
定理2 如果存在标量
成立,则多智能体系统(1)关于
证明: 对不等式(18)左右同乘
构造Lyapunov函数:
对式(21)两边左右同乘
一方面,对式(23)从0到
由式(11)、(19)可知,
结合式(20)可得
则多智能体系统(1)在有限时间
对式(23)从0到
因此
此时
注5 定理2保证了多智能体系统(1)在静态输出反馈协议下有限时间同步,且具有
定理3给出增益
定理3 对于满足
则多智能体系统(1)关于
证明:证明方法类似定理1,此处略.
下面考虑将外部干扰对系统的影响降低到最低水平. 设
有解,则多智能体系统(1)有限时间同步,且性能指标
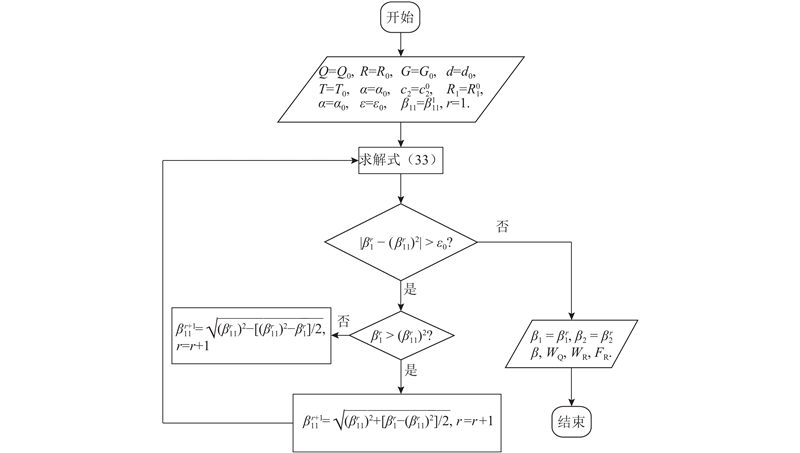
算法:
1)选取
2)给定
3)将上述参数代入式(33),得到一组线性矩阵不等式,相应的变量为
4)若
当
当
图 1
4. 数值算例
通过数值仿真验证提出同步算法的有效性. 仿真在Matlab软件环境下开展. 考虑由4个智能体构成的多智能体系统,如图2所示.
图 2
邻接矩阵
系统矩阵为
外部扰动
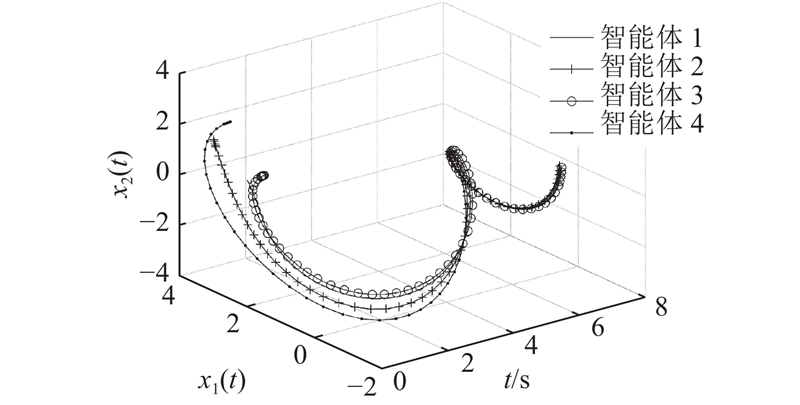
1)多智能体系统同步问题. 当控制输入
图 3
取定
表 1
本文
Tab.1
| 文献 | | |
| 文献[22] | −0.231 5 | 1.205 1 |
| 本文 | −0.474 7 | 0.250 8 |
图 4
2)多智能体系统有限时间同步. 考虑由4个智能体构成的多智能体系统,如图5所示.
图 5
邻接矩阵和拉普拉斯矩阵为
取定
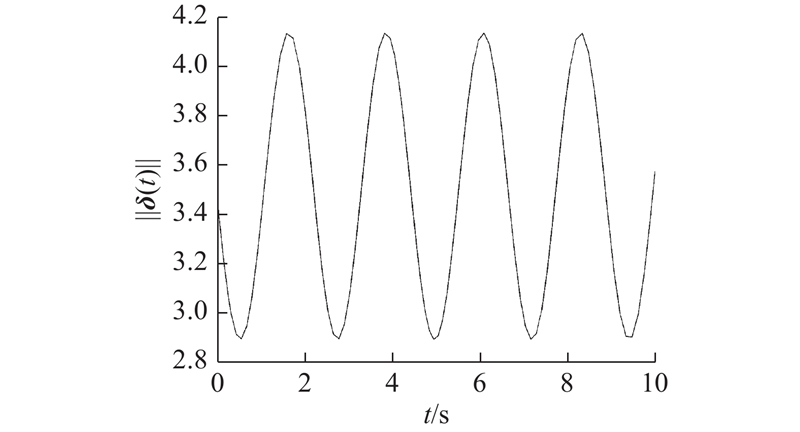
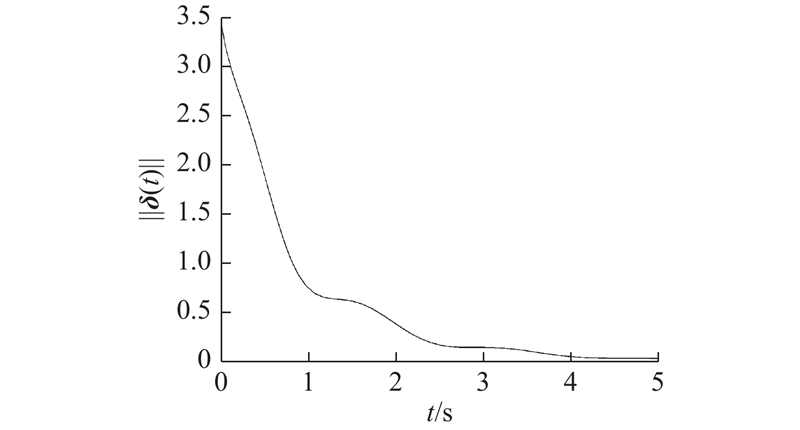
图 6)
图 6) 开环系统(7)同步误差范数轨迹
Fig.6 Synchronization error norm trajectory of open-loop system (7)
图 7
图 8
图 8 闭环系统(7)同步误差范数轨迹
Fig.8 Synchronization error norm trajectory of closed-loop system (7)
改变
图 9
图 9 同步时间不同时同步误差范数轨迹
Fig.9 Synchronization error norm trajectories for different T
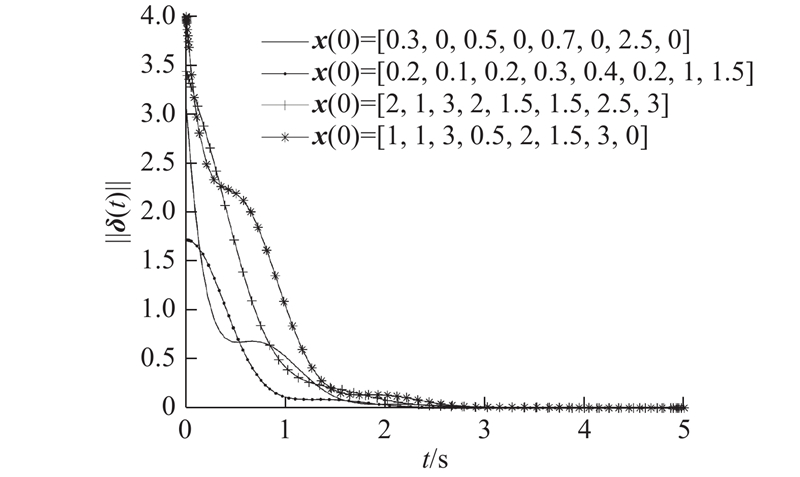
改变各智能体初始状态,分别取
由图10可知,初始状态对收敛速度有影响,但影响不大.
图 10)
图 10) 初始状态不同时同步误差范数轨迹
Fig.10 Synchronization error norm trajectories for different initial state values
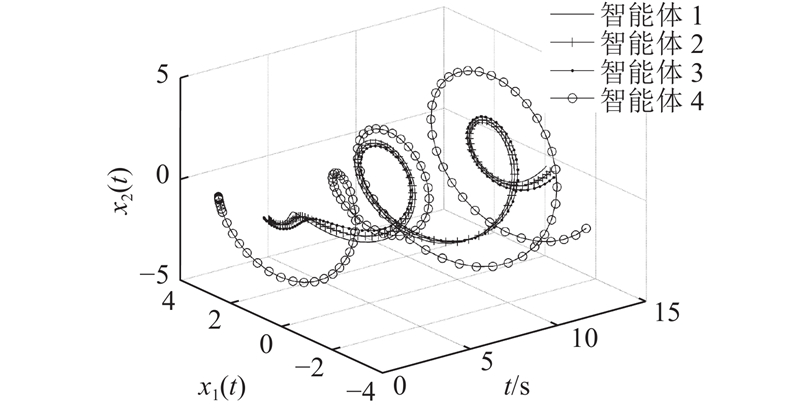
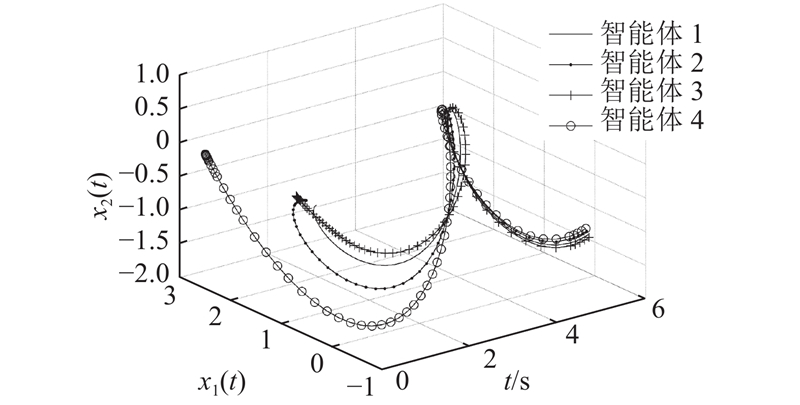
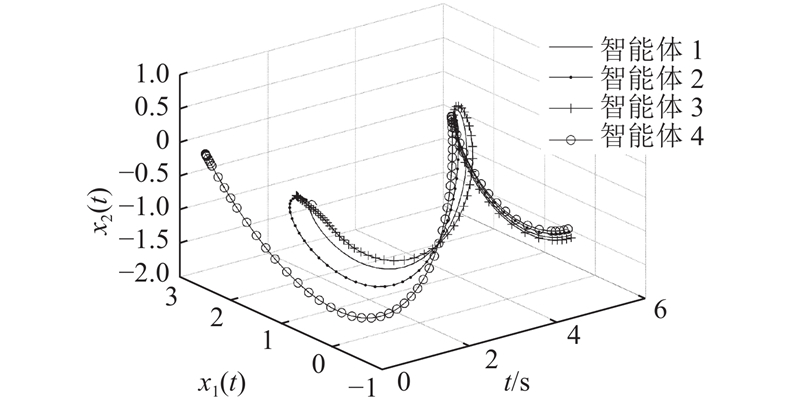
图 11
图 11
Fig.11
State trajectory of closed-loop system (1) for
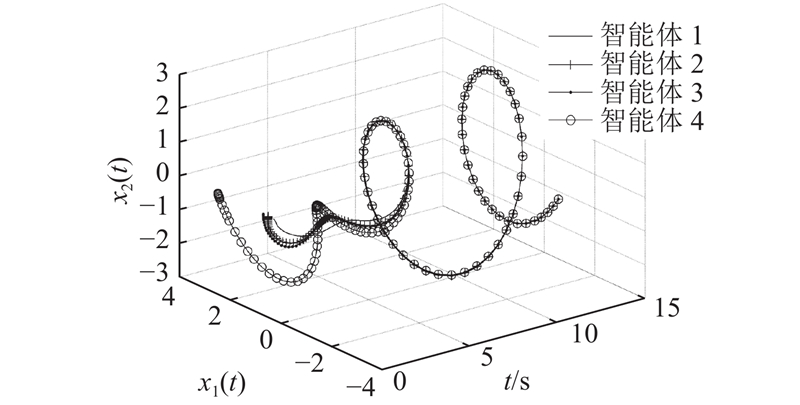
图 12
图 12
Fig.12
State trajectory of closed-loop system (1) for r(t) =
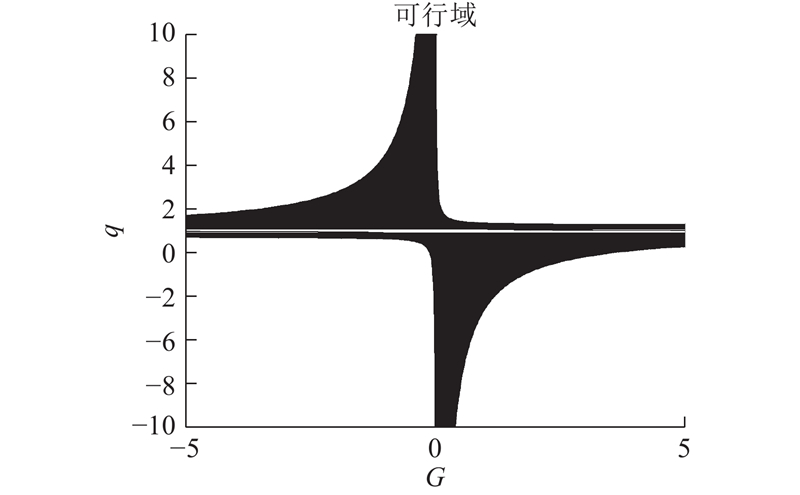
3)参数对解空间的影响. 矩阵
图 13
5. 结 语
本文针对一类多智能体系统,构造静态输出反馈协议,将多智能体系统同步问题转化为一类误差系统的镇定问题. 导出多智能体系统有限时间同步,且具有一定
参考文献
随机复杂网络同步控制研究进展综述
[J].DOI:10.7641/CTA.2017.70221 [本文引用: 2]
Review on synchronization control in stochastic complex networks
[J].DOI:10.7641/CTA.2017.70221 [本文引用: 2]
基于事件触发的三阶离散多智能体系统一致性分析
[J].
Event-triggered consensus of third-order discrete-time multi-agent systems
[J].
二阶多智能体系统快速一致性协议
[J].
Fast consensus protocol of second-order multi-agent systems
[J].
Consensus problems in networks of agents with switching topology and time-delays
[J].DOI:10.1109/TAC.2004.834113 [本文引用: 1]
持续干扰下马尔可夫切换多智能体系统的均方一致性
[J].
Mean square consensus of multi-agent systems under Markovian switching with colored noises
[J].
时间延迟双向耦合的混沌系统的同步与控制
[J].
Control and synchronization of time-delayed bidirectional coupled chaotic systems
[J].
多时滞影响下多智能体网络的分组一致性
[J].
Group consensus of multi-agent networks with multiple time delays
[J].
Stability analysis for a second-order continuous finite-time control system subject to disturbance
[J].DOI:10.1007/s11768-009-8015-4 [本文引用: 1]
On an output feedback finite-time stabilization problem
[J].DOI:10.1109/9.905699 [本文引用: 1]
Bounded synchronization and state estimation for discrete time-varying stochastic complex networks over a finite horizon
[J].DOI:10.1109/TNN.2010.2090669 [本文引用: 1]
Static output feedback control of networked control systems with packet dropout
[J].DOI:10.1080/00207721.2010.517873 [本文引用: 1]
基于参数依赖动态输出反馈鲁棒MPC的混沌系统同步
[J].
Chaos synchronization via parameter-dependent dynamic outputfeedback robust MPC
[J].
Finite-time synchronization of a class of second-order nonlinear multi-agent systems using output feedback control
[J].DOI:10.1109/TCSI.2013.2295012 [本文引用: 1]
Fixed-time leader-follower output feedback consensus for second-order multiagent systems
[J].
Synchronization of multi-agent systems via static output feedback control
[J].DOI:10.1016/j.jfranklin.2016.11.020 [本文引用: 5]
Static output-feedback control under information structure constraints
[J].DOI:10.1016/j.automatica.2012.10.012 [本文引用: 1]
Linear quadratic regulator control of multi-agent systems
[J].DOI:10.1002/oca.2100 [本文引用: 1]