在实际检测中存在维修和不维修2种情况,记系统的实际维修时间序列为 $(t_1^0,t_2^0, \cdots ,t_n^0)$ $t_k^0{\text{、}}t_{k + 1}^0$ m (k )次检测未检测到缺陷,即 $t_{k,m(k)}^0$ k <n )的下一次检测时刻为 $t_{k + 1}^0$ . 在检测时刻 $t_{k,i}^0,i = 1,\cdots,m(k),k = 1,\cdots,n - 1$
(11) $\begin{split} & {P_{\rm{d}}}(t_{k,i}^0|t_k^0) = r\sum\limits_{l = 1}^i {\left\{ {{{(1 - r)}^{i - l}}\int_{t_{k,l - 1}^0 - t_k^0}^{t_{k,l}^0 - t_k^0} {{g_{k + 1}}(u) \times } } \right.} \\ & {[1 - {F_{k + 1}}(t_{k,i}^0 - t_k^0 - u)]{\rm{d}}u} \Bigg\};\;i = 1,\cdots,m(k). \end{split}$
(13) $\begin{split} & {P_{\rm{f}}}(x_{k,i}^0|t_k^0) = \\ & \sum\limits_{l = 1}^i {\left\{ {{{(1 - r)}^{i - l}}\int_{t_{k,l - 1}^0 - t_k^0}^{t_{k,l}^0 - t_k^0} {{g_{k + 1}}(u)[{F_{k + 1}}(t_{k,i + 1}^0 - t_k^0 - u) - } } \right.} \\ & \left. {{F_{k + 1}}(t_{k,i}^0 - t_k^0 - u)]{\rm{d}}u} \right\};\; i = 0,\cdots ,m(k). \end{split}$
[1]
CHEN S, HO T, MAO B, et al A bi-objective maintenance scheduling for power feeding substations in electrified railways
[J]. Transportation Research Part C: Emerging Technologies , 2014 , 44 : 350 - 362
DOI:10.1016/j.trc.2014.04.016
[本文引用: 2]
[2]
ALASWAD S, XIANG Y A review on condition-based maintenance optimization models for stochastically deteriorating system
[J]. Reliability Engineering and System Safety , 2017 , 157 : 54 - 63
DOI:10.1016/j.ress.2016.08.009
[本文引用: 1]
[4]
周炳海, 陶红玉, 綦法群 带随机突变的两阶段退化系统视情维修建模
[J]. 哈尔滨工业大学学报 , 2016 , 48 (1 ): 30 - 35
[本文引用: 1]
ZHOU Bing-hai, TAO Hong-yu, QI Fa-qun Condition-based maintenance modelling for two-stage deteriorating systems with random change
[J]. Journal of Harbin Institute of Technology , 2016 , 48 (1 ): 30 - 35
[本文引用: 1]
[5]
郭驰名, 郭波, 王文彬, 等 非周期不完全检测下的维修优化
[J]. 国防科技大学学报 , 2013 , 35 (4 ): 176 - 181
DOI:10.3969/j.issn.1001-2486.2013.04.031
[本文引用: 1]
GUO Chi-ming, GUO Bo, WANG Wen-bin, et al Maintenance optimization under non-periodic imperfect inspections
[J]. Journal of National University of Defense Technology , 2013 , 35 (4 ): 176 - 181
DOI:10.3969/j.issn.1001-2486.2013.04.031
[本文引用: 1]
[7]
CHRISTER A H, WALLER W M Delay time models of industrial inspection maintenance problems
[J]. Journal of the Operational Research Society , 1984 , 35 (5 ): 401 - 406
DOI:10.1057/jors.1984.80
[本文引用: 1]
[8]
LI Y, MA X, ZHAI Q, et al A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement
[J]. Reliability Engineering and System Safety , 2016 , 150 : 96 - 104
DOI:10.1016/j.ress.2016.01.016
[本文引用: 1]
[9]
ARTS J, BASTEN R Design of multi-component periodic maintenance programs with single-component models
[J]. IISE Transactions , 2018 , 50 (7 ): 606 - 615
DOI:10.1080/24725854.2018.1437301
[本文引用: 2]
[10]
刘学娟, 赵斐. 基于延迟时间理论的n 中取k 系统检测区间模型[J/OL]. 控制与决策, 2020, 35(6): 1469-1475 [2019-03-07]. https://doi.org/10.13195/j.kzyjc.2018.1395.
[本文引用: 1]
LIU Xue-juan, ZHAO Fei. Delay-time-based inspection model for k-out-of-n systems [J/OL]. Control and Decision , 2020, 35(6): 1469-1475 [2019-03-07]. https://doi.org/10.13195/j.kzyjc.2018.1395.
[本文引用: 1]
[11]
STAPELBERG R F. Handbook of reliability, availability, maintainability and safety in engineering design [M]. London: Springer, 2009.
[本文引用: 1]
[12]
WANG W An overview of the recent advances in delay-time-based maintenance modeling
[J]. Reliability Engineering and System Safety , 2012 , 106 : 165 - 178
DOI:10.1016/j.ress.2012.04.004
[本文引用: 1]
[13]
胡海军, 程光旭, 段权, 等 一种包含非理想维修的延迟时间模型
[J]. 西安交通大学学报 , 2009 , 43 (6 ): 103 - 107
DOI:10.3321/j.issn:0253-987X.2009.06.022
[本文引用: 1]
HU Hai-jun, CHENG Guang-xu, DUAN Quan, et al Delay time model based on imperfect maintenance
[J]. Journal of Xi’an Jiaotong University , 2009 , 43 (6 ): 103 - 107
DOI:10.3321/j.issn:0253-987X.2009.06.022
[本文引用: 1]
[14]
WANG L, HU H, WANG Y, et al The availability model and parameters estimation method for the delay time model with imperfect maintenance at inspection
[J]. Applied Mathematical Modelling , 2011 , 35 (6 ): 2855 - 2863
DOI:10.1016/j.apm.2010.11.070
[本文引用: 2]
[15]
CHRISTER A H, WANG W, BAKER R D, et al Modelling maintenance practice of production plant using the delay-time concept
[J]. IMA Journal of Mathematics Applied in Business and Industry , 1995 , 6 (1 ): 67 - 83
[本文引用: 1]
[16]
WANG H, WANG W, PENG R A two-phase inspection model for a single component system with three-stage degradation
[J]. Reliability Engineering and System Safety , 2017 , 158 : 31 - 40
DOI:10.1016/j.ress.2016.10.005
[本文引用: 1]
[17]
DRIESSEN J P C, PENG H, VAN HOUTUM G J Maintenance optimization under non-constant probabilities of imperfect inspections
[J]. Reliability Engineering and System Safety , 2017 , 165 : 115 - 123
DOI:10.1016/j.ress.2017.03.020
[本文引用: 1]
[18]
刘勤明, 李永朋, 叶春明. 基于三阶段时间延迟模型的设备预防维修策略研究[J/OL]. 控制与决策, 2020, 35(7): 1780-1786 [2019-03-08]. https://doi.org/10.13195/j.kzyjc.2018.1692.
[本文引用: 1]
LIU Qin-ming, LI Yong-peng, YE Chun-ming. Research on preventive plan of equipment based on three-stage time delay model [J/OL]. Control and Decision , 2020, 35(7): 1780-1786 [2019-03-08]. https://doi.org/10.13195/j.kzyjc.2018.1692.
[本文引用: 1]
[19]
YANG L, YE Z S, LEE C G, et al A two-phase preventive maintenance policy considering imperfect repair and postponed replacement
[J]. European Journal of Operational Research , 2019 , 274 (3 ): 966 - 977
DOI:10.1016/j.ejor.2018.10.049
[本文引用: 2]
[21]
PARGAR F, KAUPPILA O, KUJALA J Integrated scheduling of preventive maintenance and renewal projects for multi-unit systems with grouping and balancing
[J]. Computers and Industrial Engineering , 2017 , 110 : 43 - 58
DOI:10.1016/j.cie.2017.05.024
[本文引用: 1]
[22]
BOUVARD K, ARTUS S, BERENGUER C, et al Condition-based dynamic maintenance operations planning and grouping: application to commercial heavy vehicles
[J]. Reliability Engineering and System Safety , 2011 , 96 (6 ): 601 - 610
DOI:10.1016/j.ress.2010.11.009
[本文引用: 2]
[23]
杨春节, 童晟, 孙长生, 等 基于可靠度约束的混合预防性维修模型
[J]. 浙江大学学报:工学版 , 2008 , 42 (8 ): 1376 - 1379
[本文引用: 1]
YANG Chun-jie, TONG Sheng, SUN Chang-sheng, et al. Hybrid preventive maintenance model based on reliability constraint
[J]. Journal of Zhejiang University: Engineering Science , 2008 , 42 (8 ): 1376 - 1379
[本文引用: 1]
[24]
LIU G, LONG X, TONG S, et al Optimum consecutive preventive maintenance scheduling model considering reliability
[J]. Journal of Shanghai JiaoTong University: Science , 2019 , 24 (4 ): 490 - 495
DOI:10.1007/s12204-019-2089-z
[本文引用: 1]
A bi-objective maintenance scheduling for power feeding substations in electrified railways
2
2014
... 预防性维修(preventive maintenance)是保证系统状态、提高运行质量的有效方法,合理的预防性维修计划对于减少系统故障和提高可用度有重要意义[1 ] . 状态维修(condition-based maintenance)方法根据检测的状态调整维修计划,以精确地实施预防性维修[2 ] . 检测是状态维修方法的重要内容,已有研究表明预防性维修活动中约80%的任务都是由检测识别并解决的,检测间隔过短或过长会引起维修过度或维修不足等问题,所以合理的检测计划对系统的维护和运行有重要作用[3 ] . ...
... 假设2 系统在一个更新周期内存在最低可靠度约束,表示实际中最大故障概率约束[1 -3 ] . ...
A review on condition-based maintenance optimization models for stochastically deteriorating system
1
2017
... 预防性维修(preventive maintenance)是保证系统状态、提高运行质量的有效方法,合理的预防性维修计划对于减少系统故障和提高可用度有重要意义[1 ] . 状态维修(condition-based maintenance)方法根据检测的状态调整维修计划,以精确地实施预防性维修[2 ] . 检测是状态维修方法的重要内容,已有研究表明预防性维修活动中约80%的任务都是由检测识别并解决的,检测间隔过短或过长会引起维修过度或维修不足等问题,所以合理的检测计划对系统的维护和运行有重要作用[3 ] . ...
基于时间延迟的维修类型优化组合模型及案例分析
2
2013
... 预防性维修(preventive maintenance)是保证系统状态、提高运行质量的有效方法,合理的预防性维修计划对于减少系统故障和提高可用度有重要意义[1 ] . 状态维修(condition-based maintenance)方法根据检测的状态调整维修计划,以精确地实施预防性维修[2 ] . 检测是状态维修方法的重要内容,已有研究表明预防性维修活动中约80%的任务都是由检测识别并解决的,检测间隔过短或过长会引起维修过度或维修不足等问题,所以合理的检测计划对系统的维护和运行有重要作用[3 ] . ...
... 假设2 系统在一个更新周期内存在最低可靠度约束,表示实际中最大故障概率约束[1 -3 ] . ...
基于时间延迟的维修类型优化组合模型及案例分析
2
2013
... 预防性维修(preventive maintenance)是保证系统状态、提高运行质量的有效方法,合理的预防性维修计划对于减少系统故障和提高可用度有重要意义[1 ] . 状态维修(condition-based maintenance)方法根据检测的状态调整维修计划,以精确地实施预防性维修[2 ] . 检测是状态维修方法的重要内容,已有研究表明预防性维修活动中约80%的任务都是由检测识别并解决的,检测间隔过短或过长会引起维修过度或维修不足等问题,所以合理的检测计划对系统的维护和运行有重要作用[3 ] . ...
... 假设2 系统在一个更新周期内存在最低可靠度约束,表示实际中最大故障概率约束[1 -3 ] . ...
带随机突变的两阶段退化系统视情维修建模
1
2016
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
带随机突变的两阶段退化系统视情维修建模
1
2016
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
非周期不完全检测下的维修优化
1
2013
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
非周期不完全检测下的维修优化
1
2013
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
考虑不完美维修的定期检测与备件策略联合优化
3
2017
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... [6 , 13 -14 ]. 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
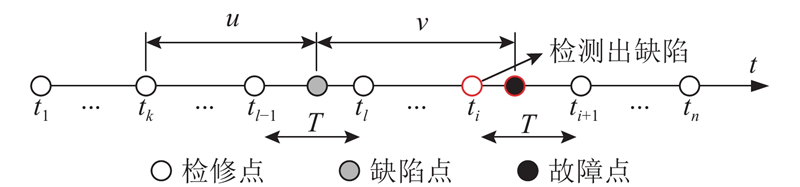
... 根据延迟时间模型[6 ] ,设正常阶段时间为u ,延迟时间阶段时间为v ,此时系统寿命为u +v . 定义随机变量u 和v 的密度函数和累计分布分别为f 1 (u )、F 1 (u )和f 2 (v )、F 2 (v ),并且2个阶段对应的发生率分别为λ (u )和h (u ),称为缺陷率和缺陷发生后的故障率. 系统维修计划取决于检测的状态,当检测需要成本时,有必要首先确定最优的检测策略. 此外,维修不完全性导致系统经多次维修后须对系统进行更换,因此检修计划的另一个重要部分为更换策略. ...
考虑不完美维修的定期检测与备件策略联合优化
3
2017
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... [6 , 13 -14 ]. 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... 根据延迟时间模型[6 ] ,设正常阶段时间为u ,延迟时间阶段时间为v ,此时系统寿命为u +v . 定义随机变量u 和v 的密度函数和累计分布分别为f 1 (u )、F 1 (u )和f 2 (v )、F 2 (v ),并且2个阶段对应的发生率分别为λ (u )和h (u ),称为缺陷率和缺陷发生后的故障率. 系统维修计划取决于检测的状态,当检测需要成本时,有必要首先确定最优的检测策略. 此外,维修不完全性导致系统经多次维修后须对系统进行更换,因此检修计划的另一个重要部分为更换策略. ...
Delay time models of industrial inspection maintenance problems
1
1984
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
A delay time model for a mission-based system subject to periodic and random inspection and postponed replacement
1
2016
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
Design of multi-component periodic maintenance programs with single-component models
2
2018
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... 根据上述分析和更新收益理论[9 ] ,建立以系统平均费用率最小为目标、考虑可靠度和可用度约束的检修计划优化模型(P1),目标函数与约束条件如下. ...
1
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
1
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
1
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
An overview of the recent advances in delay-time-based maintenance modeling
1
2012
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
一种包含非理想维修的延迟时间模型
1
2009
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
一种包含非理想维修的延迟时间模型
1
2009
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
The availability model and parameters estimation method for the delay time model with imperfect maintenance at inspection
2
2011
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... 在不完全检修模型中,除了缺陷分布和故障分布参数,还需确定检出概率和役龄回退因子. 基于文献[14 ],提出维修和检测间隔均不固定的情况下的参数估计方法. ...
Modelling maintenance practice of production plant using the delay-time concept
1
1995
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
A two-phase inspection model for a single component system with three-stage degradation
1
2017
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
Maintenance optimization under non-constant probabilities of imperfect inspections
1
2017
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
1
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
1
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
A two-phase preventive maintenance policy considering imperfect repair and postponed replacement
2
2019
... 在状态维修模型中,随机过程方法可以直接描述退化过程[4 -5 ] . 在实际的维修工作中,常常难以明确具体的退化状态,需要对退化状态进行离散处理[6 ] . 延迟时间模型(delay time model)在多阶段退化方面应用广泛,该模型在1984年首次提出并应用于生产线检修问题[7 ] . 目前,该模型被广泛应用于检修计划优化,如优化检测间隔[8 ] 、检测和更换策略[9 ] ,并开始应用于多部件系统[10 ] . 这一类研究通常假设维修效果是完全的,即检出缺陷或发生故障时进行更换. 在实际情况中维修通常是不完全的(imperfect maintenance)[11 ] ,即维修后系统状态不能恢复至全新. 有效役龄方法是表示不完全维修的常用方法[12 ] ,并已在延迟时间模型中得到应用[6 , 13 -14 ] . 此外,实际维修工作中检测不一定是准确的,不完全检测(imperfect inspection)概念最早由Christer等[15 ] 提出,并逐渐发展为多等级检测[16 ] 、时变检测误差[17 ] 、多阶段延迟时间等模型[18 ] . 目前,综合考虑不完全检测和维修的研究较少,且均假设故障时进行更换,无法有效表达系统的故障概率情况,难以实现长期检修计划的优化[19 ] . ...
... 假设3 检修或故障引起的系统停机时间产生停机损失费用,为了保证系统的可使用时间,系统存在最低可用度约束[19 , 22 ] . ...
Reliable preventive maintenance scheduling
2
1979
... 设系统以固定周期T 进行检测,检测只能以概率r (0<r ≤1)识别已发生的缺陷,但不会将正常情况识别为缺陷. 当检测到缺陷时,系统进行预防性维修,维修后缺陷将被修复. 若检测不到缺陷,则不进行维修. 维修是不完全的,所以维修后系统不能恢复到全新状态,采用有效役龄方法描述维修后的状态[20 ] ,记役龄回退因子为a (0≤a ≤1),表示维修后系统有效役龄的缩减比例. 若系统累计运行时间达到最大可用时间TC或累计检测次数到达次数上限τ ,则进行预防性更换(preventive replacement),更换后系统的状态为全新. 最大可用时间为系统的固有属性,也称为技术寿命,若在之前某时刻进行更换可降低费用,则这一时刻称为经济寿命[21 ] . 系统在运行中发生故障时,通过最小维修(minimal repair)恢复到可运行状态,最小维修不改变系统退化情况,缺陷须在下一次检测时通过预防性维修排除. ...
... 通过役龄回退因子描述不完全维修的效果[20 ] ,设系统在第k 次检修(时间为tk )时累计寿命为Tk ,则不完全维修后系统的累计寿命(即有效役龄)恢复为aTk . 假设役龄回退因子同时作用于正常阶段和延迟时间阶段,则系统在tk 进行维修后的缺陷率λ k +1u )和独立故障率h k +1u )变化分别如下. ...
Integrated scheduling of preventive maintenance and renewal projects for multi-unit systems with grouping and balancing
1
2017
... 设系统以固定周期T 进行检测,检测只能以概率r (0<r ≤1)识别已发生的缺陷,但不会将正常情况识别为缺陷. 当检测到缺陷时,系统进行预防性维修,维修后缺陷将被修复. 若检测不到缺陷,则不进行维修. 维修是不完全的,所以维修后系统不能恢复到全新状态,采用有效役龄方法描述维修后的状态[20 ] ,记役龄回退因子为a (0≤a ≤1),表示维修后系统有效役龄的缩减比例. 若系统累计运行时间达到最大可用时间TC或累计检测次数到达次数上限τ ,则进行预防性更换(preventive replacement),更换后系统的状态为全新. 最大可用时间为系统的固有属性,也称为技术寿命,若在之前某时刻进行更换可降低费用,则这一时刻称为经济寿命[21 ] . 系统在运行中发生故障时,通过最小维修(minimal repair)恢复到可运行状态,最小维修不改变系统退化情况,缺陷须在下一次检测时通过预防性维修排除. ...
Condition-based dynamic maintenance operations planning and grouping: application to commercial heavy vehicles
2
2011
... 假设3 检修或故障引起的系统停机时间产生停机损失费用,为了保证系统的可使用时间,系统存在最低可用度约束[19 , 22 ] . ...
... 维修优化模型通常包括可靠度模型(即退化模型)和维修计划优化模型[22 ] . 首先构建考虑不完全检修的可靠度模型. 检测的不完全性使预防性维修成为随机事件,且在不同时间维修后系统的退化速率不同. 另外,不完全检测使已经发生的缺陷可能延长至下一个检修间隔,系统状态不满足马尔可夫性,因此需要构建基于递推关系的可靠度模型. ...
基于可靠度约束的混合预防性维修模型
1
2008
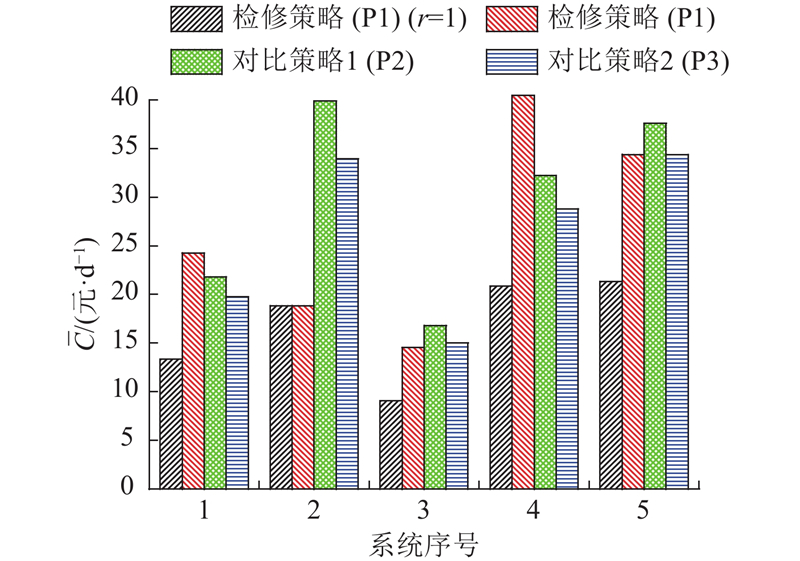
... 模型(P1)同时考虑了检测和维修活动. 为了验证检修模型的效果,基于文献[23 ,24 ]构建2种不考虑检测的预防性维修模型,与模型(P1)的结果进行比较. ...
基于可靠度约束的混合预防性维修模型
1
2008
... 模型(P1)同时考虑了检测和维修活动. 为了验证检修模型的效果,基于文献[23 ,24 ]构建2种不考虑检测的预防性维修模型,与模型(P1)的结果进行比较. ...
Optimum consecutive preventive maintenance scheduling model considering reliability
1
2019
... 模型(P1)同时考虑了检测和维修活动. 为了验证检修模型的效果,基于文献[23 ,24 ]构建2种不考虑检测的预防性维修模型,与模型(P1)的结果进行比较. ...