浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(6): 1210-1217 doi: 10.3785/j.issn.1008-973X.2020.06.019

交通运输

城市区域电动汽车充电设施配置优化

尚夏,, 王美佳, 许刘晓, 章立辉,

Configuration optimization of electric vehicle charging facilities in urban areas

SHANG Xia,, WANG Mei-jia, XU Liu-xiao, ZHANG Li-hui,

通讯作者: 章立辉，男，副教授，博士. orcid.org/0000-0002-7839-1553. E-mail： lihuizhang@zju.edu.cn

收稿日期: 2019-05-21  

Received: 2019-05-21  

作者简介 About authors

尚夏（1996—），男，硕士生，从事交通优化建模研究.orcid.org/0000-0002-7509-0966.E-mail：shangxia@zju.edu.cn , E-mail：shangxia@zju.edu.cn

摘要

综合考虑公共充电设施与私人充电设施特性，根据行程时间、排队时间、等待时间、充电费用等计算车辆充电成本. 采用Logit模型刻画用户的充电设施选择行为，得到各交通小区到各公共充电站、私人充电桩的出行分布量. 以充电总成本最小化为目标，建立城市区域充电设施网络配置优化模型，设计充电设施的布局位置和容量；所得模型为非线性优化模型，可采用现有的求解器（如：Matlab优化工具箱中的相关函数）直接进行求解. 基于杭州市区内的局部路网构建2套算例，来验证提出的充电设施配置优化方法的可行性，并讨论研究区域内外公共充电设施与私人充电设施之间的交互影响. 算例结果显示：所建立的模型可为城市电动汽车充电设施的选址布局和容量设计提供定量决策参考.

关键词： 电动汽车 ; 公共充电站 ; 私人充电桩 ; Logit模型

Abstract

Considering the characteristics of public charging facilities and private charging facilities, the compositions of vehicle charging costs were first elaborated, including vehicle travel time, queuing time, waiting time and charging fee. A Logit model was employed to describe users’ choice behaviors of charging facilities, in order to obtain the charging distribution from each traffic analysis zone to public charging stations and private charging piles. To minimize users ’ total charging cost, an optimization model was built to optimize the configurations of charging facilities in urban areas, which could simultaneously optimize the locations and capacities of public and private charging facilities. The model was in form of a nonlinear program, which could be solved by existing solvers, such as the optimization toolbox provided in Matlab. Two numerical examples based on a portion of Hangzhou network were carried out to demonstrate the proposed approach, and to discuss the interactions of public and private facilities inside and outside of the study area. The numerical test results show that the proposed model has the potential to provide quantitative decision references to optimize the locations and capacities of electric charging facilities in urban areas.

Keywords： electric vehicle ; public charging station ; private charging pile ; Logit model

PDF (847KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

尚夏, 王美佳, 许刘晓, 章立辉. 城市区域电动汽车充电设施配置优化. 浙江大学学报(工学版)[J], 2020, 54(6): 1210-1217 doi:10.3785/j.issn.1008-973X.2020.06.019

SHANG Xia, WANG Mei-jia, XU Liu-xiao, ZHANG Li-hui. Configuration optimization of electric vehicle charging facilities in urban areas. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(6): 1210-1217 doi:10.3785/j.issn.1008-973X.2020.06.019

我国长期将节能减排作为重要的国家发展战略，新能源汽车的出现和发展顺应了这一战略导向. 中国汽车工业协会的报告显示，新能源汽车销量从2012年的1.2万辆增长到了2018年的125.6万辆，其中纯电动汽车销量在2012年仅为1.14万辆，2018年已增长至98.4万辆[1]. 由此可见，发展新能源汽车的关键在于发展电动汽车.

为了促进电动汽车的推广应用和市场规模的进一步扩大，需要建设相应的充电设施服务系统. 现有充电设施难以满足电动汽车长期的发展需要，甚至会阻碍我国电动汽车行业的快速扩张[2]. 充电设施合理定容布局问题亟待解决. 本文对公共充电站和私人充电桩的定容布局进行研究.

1. 问题描述

1.1. 充电设施定容布局问题

我国充电设施的建设速度随着电动汽车行业的快速发展而不断提升. 据中国电动汽车充电基础设施促进联盟数据[3]，截至2018年4月，联盟内成员单位总计上报公共充电桩262 058个，建设安装私人充电桩281 847个，两者的数量还在不断增长之中. 目前公共充电设施与私人充电设施的数量不相上下，私人充电设施由于建设周期短，数量增长相对较快. 两者共同负担了包括公交运营车辆、私家车、出租车等在内的多种电动汽车的充电需求[4]，但充电设施数量规模相对于庞大的电动汽车市场规模而言偏低[5]，这大大降低了电动汽车的使用便利性，从而影响其推广应用[6]. 此外，布桩位置不合理、设施服务水平偏低等现象严重降低了充电设施的利用效率. 充电设施的容量、网络布局需要科学系统的设计思路和优化方案.

1.2. 研究现状

越来越多的国家开始大力进行新能源电动汽车及其充电设施的相关研究. 充电设施布局与规划问题逐渐成为电动汽车领域的研究热点.

基于用户与目的地的出行分布预测可以有效分析充电需求与水平，从而为电动汽车充电站选址布局提供依据. 针对电动汽车出行分布的预测目前有以下一些方法. 首先是传统的交通规划方法. 宋阳[7]利用重力模型建立了出行分布预测，并使用遗传算法模型求解，得到了不同充电设施规模限制下的最优充电站布局方案. Xiang等[8]使用区域变量（如：GDP、人口、补贴、竞争车辆价格和充电时间）来解释车队演变模式并进行敏感性分析. 也有许多学者运用仿真模拟的方法进行规划布局研究. 李颖[9]对电动汽车出行链中的各个出行和充电特征量进行统计性分析，采用蒙特卡洛模拟方法模拟电动汽车在各区域的充电选择，进而得到各区域电动汽车充电站的分配布局情况. Dong等[10]提出了一种基于行为（activity-based）的评价方法来评估不同类型的出行群体采用电动汽车的可行性，运用遗传算法寻找公共充电站的最佳选址，并检验了不同的公共充电站部署水平对减少电动汽车里程焦虑的影响. 邱海[11]采用Agent仿真[12-13]的方法来模拟电动汽车的充电行为，通过建立3个协调互动的Agent子系统，实现充电需求预测、电动汽车路径规划、充电信息发布、充电桩布局优化等功能. 近年来，基于交通大数据分析的方法得到了广泛应用. Cai等[14]利用北京出租车的轨迹数据分析停车需求热点区域，作为充电站选址的重要依据. Tu等[15]从深圳市的海量出租车GPS数据中提取出具有时空属性的公共出租车需求，开发了一种时空需求覆盖方法，来优化时空环境中电动出租车充电站的选址配置. Yun等[16]基于上海市700辆电动汽车的行驶轨迹数据，运用离散选择模型对电动汽车的充电行为进行了研究. 此外，区别于传统的对电动汽车进行充电，Kang等[17]提出了一种在充电站快速更换电池，并对更换下的电池进行集中充电的模式. 该研究设计了一种基于种群的启发式方法来对电动汽车充电站进行布局，使总充电成本最小.

目前已有的充电设施布局模型大多仅对城市中的公共充电站进行布局研究，未考虑到居住宅小区中亦存在许多私人充电桩的情况. 此外，现有文献并没有深入研究充电设施布局发生改变时对其他区域充电设施布局以及周边路网交通的影响. 本文将对以上几个问题展开研究.

2. 模型建立

2.1. 用户充电设施选择模型

本研究同时考虑公共（仅快充）和私人（仅慢充）两类充电设施的定容布局. 一类设施的建设水平必然会影响另外一类设施的发展，因此本文也分析讨论两者之间的相互影响. 使用离散选择模型（Logit模型）[18]来描述用户的充电设施选择行为. 考虑旅行耗时、充电成本、安装成本等，计算每个交通小区 $i$的总充电需求，前往公共充电站 $j$进行快充充电的电动车数量和在本小区 $i$自装慢充充电桩进行充电的电动车数量.

设路网中共有 $m$个交通小区， ${T_i}$为交通小区 $i$内的充电总需求， ${P_{ii}}$为在本小区私人充电桩充电的吸引量， ${P_{ij}}$为交通小区 $i$内用户前往公共充电站 $j$充电的吸引量. 设共有 $n$个可供选择的公共充电站，则有

${T_i} = {P_{ii}} + \sum\nolimits_{j = 1}^n {{P_{ij}}}. $
(1)

根据Logit模型， ${P_{ij}}$、 ${P_{ii}}$可表示为

${P_{ij}} = \frac{{{T_i}\; {\rm{exp\;[}} - (\theta \cdot {u_{ij}} + {\beta _1}){\rm{]}}}}{{{\rm{exp\;[}} - (\theta {u_{ii}} + {\beta _2}){\rm{]}} + \displaystyle\sum\nolimits_{j = 1}^n {{\rm{exp\;[}} - (\theta {u_{ij}} + {\beta _1}){\rm{]}}} }}, $
(2)

$\begin{split} {P_{ii}} =& {T_i} \cdot \frac{{\exp\; [ - (\theta {u_{ii}} + {\beta _2})]}}{{{\rm{exp\;[ - }}(\theta {u_{ii}} + {\beta _2})] + \displaystyle\sum\nolimits_{j = 1}^n {{\rm{exp\;[ - }}(\theta {u_{ij}} + {\beta _1})]} }}=\\ & {T_i} - \sum\nolimits_{j = 1}^n {{P_{ij}}} ,\\[-15pt] \end{split}$
(3)

${u_{ij}} = {c_0} \left(t_{ij}^{\rm{t}} + t_j^{\rm{q}} + t_{ij}^{\rm{w}}\right) + m_j^{\rm{e}}, $
(4)

${u_{ii}} = m_i^{\rm{e}} + m_i^{\rm{f}}.\quad\quad\quad\quad\quad $
(5)

式中： ${u_{ij}}$为小区 $i$电动汽车至公共充电站 $j$充电的单次总成本，由时间成本（行程时间、排除时间、等待时间）和电力成本组成， ${u_{ii}}$为小区 $i$自建慢充充电桩进行充电的单次总成本，主要由电力成本和建设成本组成； $\theta $为效用敏感系数， ${\beta _1}$、 ${\beta _2}$分别为公共充电站和私人充电桩的效用常数； $t_{ij}^{\rm{t}}$、 $t_j^{\rm{q}}$、 $t_{ij}^{\rm{w}}$、 $m_j^{\rm{e}}$分别为 $i$小区电动汽车至公共充电站 $j$单次充电的行程时间、排队时间、等待时间、电力成本； $m_i^{\rm{e}}$、 $m_i^{\rm{f}}$分别为 $i$小区电动汽车进行小区内单次私人充电的电力成本、平均建设成本； ${c_0}$为时间价值换算系数，可通过调查用户平均工资水平确定.

2.2. 充电设施配置优化模型

考虑到公共快充站建设费用昂贵，本研究对快充站所有充电桩总数进行约束，在此约束下分配各快充站中的充电桩数量. 对各交通小区中的私人慢充充电桩数量不作限制.

对于优化目标，文献中通常以电动汽车花费总时间最小行驶总距离最小以及总成本最小等作为目标函数. 考虑到模型中存在电力成本、建设成本，本研究以电动汽车前往所有充电设施进行充电的总成本最小为优化目标. 具体模型如下：

$u=\min \;\left[\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {{P_{ij}}{u_{ij}}} } + \sum\limits_{i = 1}^m {{P_{ii}}} {u_{ii}}\right].\quad\quad\quad\quad\quad$
(6)

$ {\rm{s.t.}}\;\;\;\;\;t_{ij}^{\rm{t}} = \frac{{{d_{ij}}}}{{{v_1}}} \times 2,\;\; \forall i,j.\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;\; $
(7)

$\quad\; t_j^{\,\rm{q}} = g({\lambda _j},\mu ,{N_j}),\;\; \forall j.\quad\quad\quad\quad\quad\quad\quad\quad\;\;\;$
(8)

$\quad\; t_{ij}^{\rm{w}} = \left\{ {\begin{array}{*{20}{l}} {2f\left(\dfrac{{{d_{ij}}}}{{{v_2}}}\right),\quad 2 f\left(\dfrac{{{d_{ij}}}}{{{v_2}}}\right) < t_j^{\rm{\,c}},\quad\forall i,j};\\ {t_j^{\rm{\,c}}, \quad\quad\;\;\;\quad 2 f\left(\dfrac{{{d_{ij}}}}{{{v_2}}}\right) \geqslant t_j^{\rm{\,c}},\quad\forall i,j}. \end{array}} \right. \;\; $
(9)

$\quad\quad\;\;\quad{\lambda _j} = \sum\nolimits_{i = 1}^m {{P_{ij}},\;\; \forall j}. \quad\quad\quad\quad\quad\quad\;\;\quad$
(10)

$0 \leqslant \sum\nolimits_{j = 1}^n {{N_j}} \leqslant {N_{{\rm{all}}}};$
(11)

并加上前文的约束条件（式（2）~（5））. 式中： ${d_{ij}}$为从小区 $i$到公共充电站 $j$的距离， $\mu $为单个公共充电桩的服务率， ${\lambda _j}$为公共充电站 $j$的电动汽车到达率， ${N_j}$为公共充电站 $j$拥有的桩位数量， $t_j^{\rm{c}}$为电动汽车在公共充电站 $j$的充电时间， ${v_{\rm{1}}}$为电动汽车在路网中的行驶速度， ${v_2}$为行人在路网中步行的速度.

式（6）表示模型的目标函数，为各小区电动汽车前往各公共充电站充电的总成本与在小区内使用私人充电桩充电的总成本之和. 优化结果是求出目标函数最小情况下在各公共充电站所布置的公共充电桩以及在各交通小区所布置的私人充电桩的数量. 式（7）表示行程时间，等于用户从小区 $i$驾车往返公共充电站 $j$的行车时间. 式（8）表示在公共充电站 $j$的排队时间 $t\; _j^{\rm{q}}$是电动汽车到达率 ${\lambda _j}$、充电桩服务率 $\mu $、桩位数量 ${N_j}$的函数. 其中，充电桩数量 ${N_j}$为待设计值，到达率 ${\lambda _j}$为中间变量，取决于整个充电系统的配置情况. 式（9）表示当用户从 $j$步行往返 $i$的时间成本小于电动汽车在充电站的充电时间 $t\;_j^{\rm{c}}$时，用户选择回家等待，等待时间由步行时间成本表示；否则，用户选择在充电站等待，等待时间等于充电时间 $t\;_j^{\rm{c}}$. 考虑到步行的体能消耗，单位时间步行产生的负效用和行车时间产生的负效用是不同的. 步行时间产生的负效用可通过函数 $f$转化为等价的行车时间产生的负效用. 式（10）表示公共充电站 $j$的车辆到达率，等于一天内从所有交通小区前往该充电站充电的电动汽车数量之和. 考虑到公共充电站的建设、运营和维护成本费用巨大，基本上是由政府、企业承担，未将其计入用户总成本最小的目标函数中. 式（11）令公共充电桩的总量不超过 ${N_{{\rm{all}}}}$，以限制建设、运营和维护公共充电桩的社会成本.

3. 模型应用示例

3.1. 研究区域介绍和模型参数设定

选取杭州市西湖区纵向余杭塘路至天目山路、横向紫金港路至学院路区域作为基础路网. 将该区域划分为16个交通小区，用Z1~Z16表示，各交通小区中包含了住宅、医院、学校、商场等设施；在该区域内已建公共充电站中选取10个规模较大、地理位置较好的点位作为算例中公共充电站的选址场地，用A1~A10表示，如图1所示. 结合调查数据，假定各小区充电需求如表1所示. 该区域的Logit模型效用敏感系数 $\theta $取0.018，公共充电站的效用常数 ${\beta _1}$取0，私人充电桩的效用常数 ${\beta _2}$取1.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   交通小区划分及公共充电站编号

Fig.1   Traffic analysis zones and public charging stations


表 1   研究区域内各交通小区的充电需求量假设

Tab.1  Assumed charging demand from traffic analysis zones in study area

i Ti /（辆·d−1） i Ti /（辆·d−1）
Z1 580 Z9 380
Z2 270 Z10 290
Z3 380 Z11 250
Z4 290 Z12 300
Z5 310 Z13 820
Z6 370 Z14 540
Z7 320 Z15 270
Z8 190 Z16 310

新窗口打开| 下载CSV


由2019年杭州市薪资水平报告[19]可知，杭州市的平均工资为5 389元/月. 按每天工作8 h、每周工作5 d的工作制进行换算，可得1 h的时间价值约为31 元. 因此，在该路网中， ${c_0}$=31. 假设该区域车辆的平均行车速度 ${v_1}$=36 km/h，行人的平均步行速度 ${v_2}$=6 km/h. 结合该路网的基本情况，假设公共充电桩总量不超过500个.

1）对于公共充电站充电模式，行程时间与路程长度 ${d_{ij}}$及行程速度 ${v_1}$、 ${v_2}$有关. 按照算例中交通小区与公共充电站的位置关系，得到各交通小区到各公共充电站的行程距离 ${d_{ij}}$.

公共充电站充电桩多采用快充模式，经调查，该区域单次充电时间 $\;t_j^{\rm{c}}$平均为2 h，因此充电桩服务率取为0.5辆/h. 目前市场主流的充电桩以电量为单位收费，每度电价格一般集中在1.6~1.8元，行驶200 km的电动汽车电池容量约为31 kWh，需要约31度电，因此单次充电的电力成本为49.6~55.8元，本文取50元. 即对任意的 $j$，有 $m_j^{\rm{e}} = 50$元.

2）对于私人充电桩充电模式，由于私人充电桩的私有属性，无须排队等待，亦无行车成本. 经调查，充电设施用电属于居民用电，每度电价格约为0.58元，同样以行驶200 km为例，单次充电的电力成本约为18元. 考虑到目前普遍存在电动汽车厂家卖车给客户的同时赠送充电桩的情况，暂时认为私人充电桩的安装成本为0. 即对任意的小区 $i$，有 $m_i^{\rm{e}}$=18元， $m_i^{\rm{f}}$=0元.

对于排队时间 ${{t}}_j^{\rm{q}}$，考虑到算例中的车辆充电排队过程与营业场所中的顾客排队过程具有类比性，本算例参考Imgbemena等[20]建立的营业场所客户服务排队时间模型的基本形式，采用如下函数关系：

$t_j^{\rm{q}} = 258.53 \times \left[1 - \exp\; \left( - 0.058\;8 \times \frac{{{\lambda _j}}}{{\mu \cdot {N_j}}}\right)\right]. $
(12)

笔者前期研究[11]对研究范围内部分公共充电站的车辆充电行为进行了小规模调查，包括起始电量、充电时间、结束电量、车型等，发现选择全程在车内等待，至充电完成后才离开的用户极少，因此认为用户的充电活动与其他活动有一定相关性. 本研究假设如下：当充电站比较近时，用户步行回家等待，在家中的时间不计任何成本；当充电站比较远时，用户全程等待直到电量充满. 本文对研究区域内的车主开展随机调查，以获取步行时间 $x$与行车时间 $y$的等价换算关系. 将获得的数据进行拟合，结果如图2所示.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   研究区域内调查所得步行时间与行车时间拟合图

Fig.2   Fitting curve of walking time and driving time from survey in study area


从 ${R^2}$值可以看出，函数拟合效果较好，因此采用如下步行时间与行车时间换算关系：

$y = 0.053\;1{x^2} + 1.939\;5x{\rm{ + 0}}{\rm{.615\;6}}. $
(13)

3.2. 优化结果

采用Matlab中的fmincon优化工具箱[21]对算例中的充电设施配置进行优化. Fmincon是Matlab中用来求解非线性多变量多约束问题最小值的函数，包含多种不同的求解算法. 本算例采用其默认的Interior-point 算法[22]进行求解，求得的充电需求分布情况如表2所示. 各小区设置的私人充电桩数量等于选择在各小区内部进行充电的电动汽车数，即小区内部电动汽车吸引量. 当总成本最小时，各公共充电站的充电桩设置数量、电动汽车到达率、排队时间如表3所示. 此时，优化得出的最小总成本为533 437. 691 7元，其中，516 770. 362 7元为前往公共充电站充电的总成本，16 667. 329 1元为前往私人充电桩充电的总成本.

表 2   从各小区前往各充电站充电的电动汽车数量

Tab.2  Number of charging vehicles from traffic analysis zones to charging stations

辆
i A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 Pii
Z1 97 59 41 40 42 41 41 40 41 39 99
Z2 22 47 29 17 20 21 21 17 17 17 42
Z3 23 37 58 54 23 27 27 29 23 23 56
Z4 19 20 28 50 19 20 20 26 19 20 49
Z5 48 30 18 18 49 26 19 18 21 18 45
Z6 28 57 22 20 36 54 38 21 26 20 48
Z7 19 33 19 37 19 35 35 37 18 22 46
Z8 13 13 13 26 13 13 13 26 13 15 32
Z9 25 27 24 24 65 36 25 25 44 25 60
Z10 17 20 16 16 29 43 44 17 31 17 40
Z11 14 14 14 19 14 28 36 36 15 26 34
Z12 18 19 18 25 19 22 19 47 19 49 45
Z13 59 60 56 57 60 61 61 59 142 59 146
Z14 37 37 36 37 38 39 61 38 88 38 91
Z15 17 17 17 18 17 23 34 32 18 35 42
Z16 20 20 20 21 20 21 22 37 21 57 51

新窗口打开| 下载CSV


表 3   各公共充电站的桩位数量、电动汽车到达率及排队时间情况

Tab.3  Number of charging piles，EV arrival rates and waiting time of each public charging station

j Nj ${\lambda _j}$ /
（辆·min−1） 		$t_j^{\rm{q}}$ /
min 		j Nj ${\lambda _j}$ /
（辆·min−1） 		$t_j^{\rm{q}}$ /
min
A1 47 0.33 12.4 A6 52 0.35 12.17
A2 52 0.35 12.05 A7 53 0.36 12.01
A3 39 0.3 13.71 A8 52 0.35 12.11
A4 48 0.33 12.45 A9 61 0.39 11.22
A5 48 0.34 12.42 A10 48 0.33 12.36

新窗口打开| 下载CSV


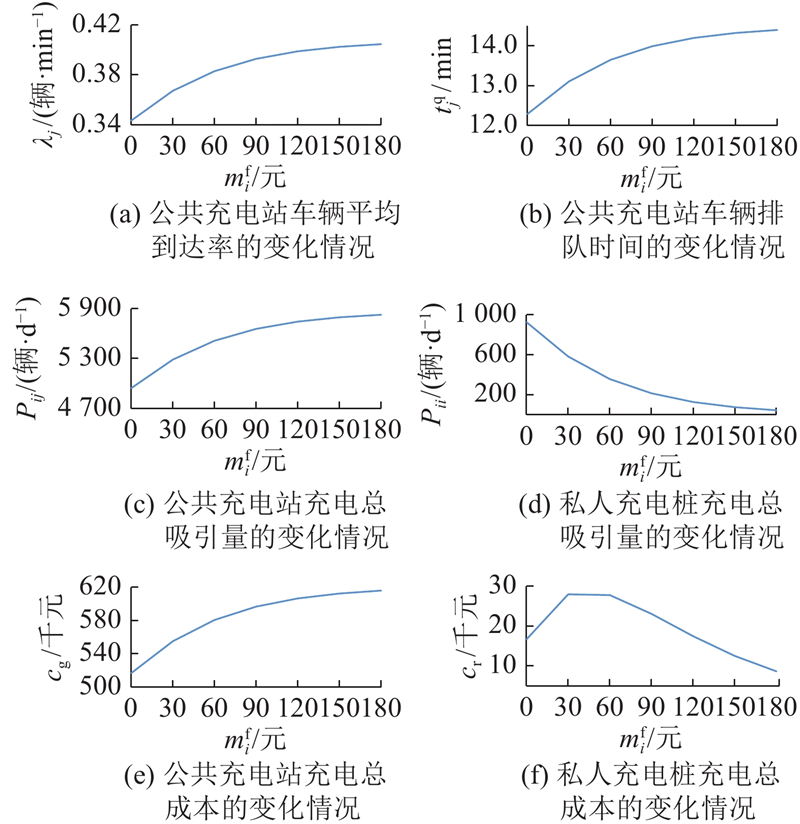
1）对私人充电桩安装成本 $m_i^{\rm{f}}$的敏感性分析.

考虑到未来电动汽车充电市场的发展，厂家在卖车时免费赠送充电桩的情况或将改变，届时充电桩安装成本将由用户承担. 本节对私人充电桩的安装成本 $m_i^{\rm{f}}$开展敏感性分析. $m_i^{\rm{f}}$值在变化0~180，计算结果如图3和表4所示. 其中，cg为公共充电站充电总成本，cr为私人充电站充电总成本.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   对私人充电桩安装成本的敏感性分析结果

Fig.3   Sensitivity analysis results by changing installation cost of private charging pile


表 4   不同私人充电桩安装成本下各公共充电站的最优桩位布置数量

Tab.4  Optimal pile configurations of public charging stations under different installation cost of private charging piles

$m_i^{\rm{f}}$/元 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 $\sum\nolimits_j {{N_j}} $
0 47 52 39 48 48 52 53 52 61 48 500
30 48 52 39 48 48 52 53 51 61 48 500
60 48 52 40 48 48 51 53 51 61 48 500
90 48 52 40 48 48 51 53 51 61 48 500
120 48 52 40 48 48 51 53 51 61 48 500
150 48 52 40 48 48 51 53 51 61 48 500
180 48 52 40 48 48 51 53 51 61 48 500

新窗口打开| 下载CSV


从图3中可以看出，随着私人充电桩安装成本的增加，公共充电站的车辆平均到达率逐渐增加，平均排队时间从12.3 min小幅度增加到14.4 min. 公共充电站的充电总吸引量在不断增加，而私人充电桩的充电总吸引量在不断下降，当安装成本达到180元时，几乎已无用户选择私人充电桩. 随着私人充电桩安装成本的增加，公共充电站充电总成本在增加，私人充电桩充电总成本先增加并在安装费用为30~60元时保持在最大值附近，之后持续下降. 所有总体成本在不断增加，增加幅度不断减少. 公共充电站充电总成本增加是因为公共充电站吸引了更多的电动汽车，引起排队时间成本增加；私人充电桩充电总成本先增加是因为私人充电桩安装成本增加，后下降是因为此时私人充电桩的充电总吸引量在不断下降，此时已无多少车辆选择私人充电桩.

从表4可以看出，随着私人充电桩安装成本的增加，公共充电站的桩位配置变化不大，仅少数站点的桩位数量有所增减. 由于充电站饱和度较高，桩位数总量一直保持不变，等于最大约束值（500个）.

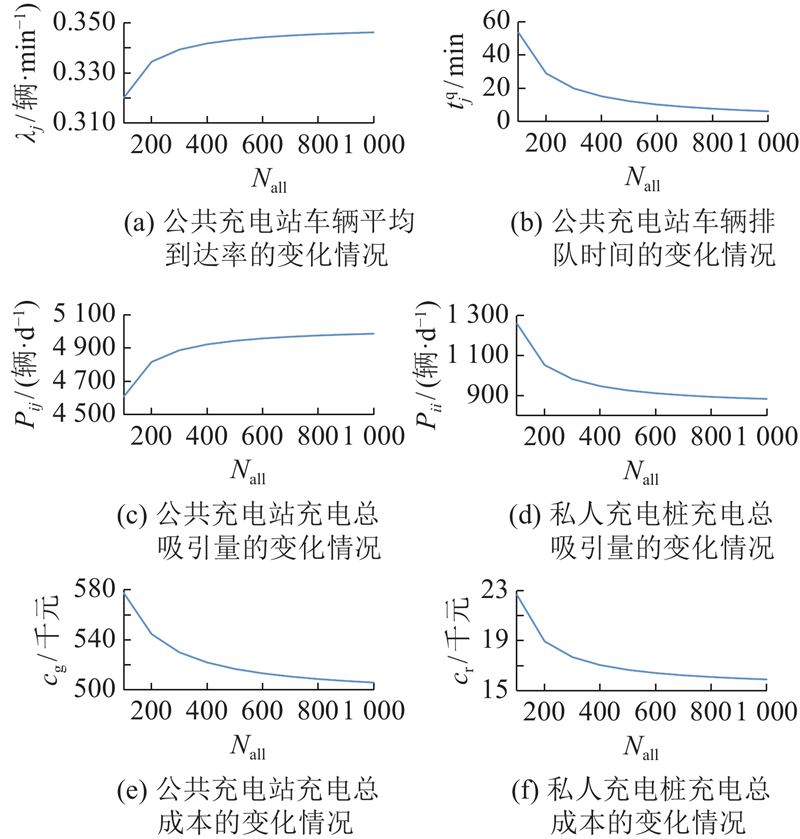
2）对公共充电桩总量 ${N_{{\rm{all}}}}$的敏感性分析.

改变公共充电桩总量限制， ${N_{{\rm{all}}}}$在100~1 000变化. 计算结果如图4和表5所示.

图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   对公共充电桩总量的敏感性分析结果

Fig.4   Sensitivity analysis results by changing total number of public charging piles


表 5   不同总量约束条件下各公共充电站的最优桩位布置数量

Tab.5  Optimal pile configurations of public charging stations with different total amount constraints

${N_{{\rm{all}}}}$ A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 $\sum\nolimits_j {{N_j}} $
100 9 11 5 9 9 11 11 11 14 10 100
200 19 21 15 19 19 21 21 21 25 19 200
300 28 31 23 29 29 31 32 31 37 29 300
400 38 42 31 38 38 42 43 41 49 38 400
500 47 52 39 48 48 52 53 52 61 48 500
600 57 63 46 57 58 62 64 62 73 58 600
700 67 73 54 67 67 73 74 72 86 67 700
800 76 84 62 76 77 83 85 82 98 77 800
900 86 94 70 86 86 93 96 93 110 86 900
1000 95 105 78 95 96 104 106 103 122 96 1000

新窗口打开| 下载CSV


从图4可以看出，随着公共充电桩总量约束的增加，公共充电站的平均到达率逐渐增加，平均排队时间从53.6 min下降到6.3 min，下降幅度明显；公共充电站的充电总吸引量逐渐增加，充电总成本逐渐减小；而私人充电桩的充电总吸引量逐渐下降，充电总成本也逐渐下降. 这是因为，随着公共充电桩位数增加，电动汽车在公共充电站的排队时间减少，使得公共充电桩充电成本减少，从而吸引更多的电动汽车前往公共充电站充电. 这样也降低了私人充电桩的总吸引量，减少了私人充电桩的总体成本. 以上各变化幅度均随着公共充电桩数量的增加而趋于缓和.

从表5可以看出，随着公共充电桩总量约束的增加，各公共充电站配置的桩位数量均在逐渐增加. 由于充电站饱和度较高，所有站点桩位数之和也都达到了最大约束值.

3.3. 算例拓展

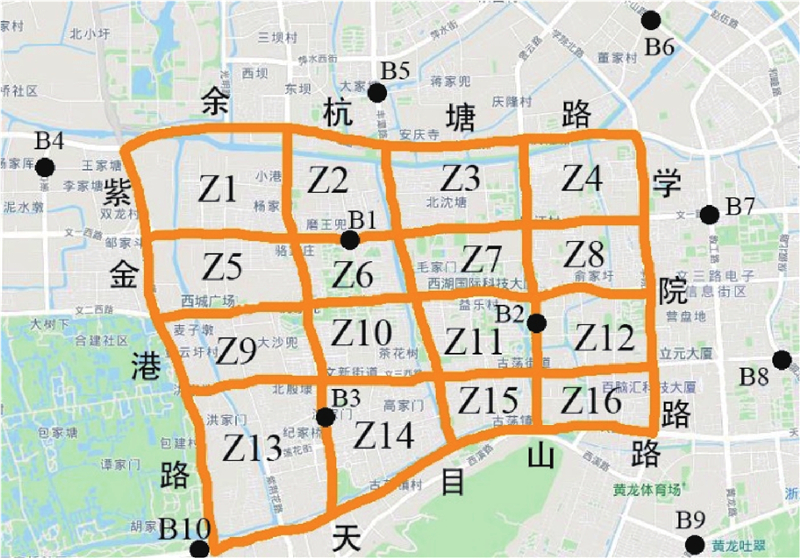
在前述算例的基础上，重新选取公共充电站的可建位置，使其同时分布在研究区域的内部及外部. 分别用B1~B10表示这些公共充电站，其中充电站B1、B2、B3分别与原算例中充电站A2、A8、A9位置相同，B4~B10站的选址如图5所示.

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   拓展算例中公共充电站选址及编号（B1~B10）

Fig.5   Public charging stations（B1 to B10）in extended example


在优化布局时，仍然保持所有公共充电桩总数不超过500个，其他有关参数同第3.1节原始算例参数. 优化得到总成本最小情况下的各公共充电站桩位数量、各交通小区自建私人充电桩数量如表6、7所示. 此时，优化得出的最小总成本为574 174.620 6元，其中，554 890.605 1元为前往公共充电站充电的总成本，19 284.015 6元为前往私人充电桩充电的总成本.

表 6   拓展算例中各公共充电站的桩位数量、电动汽车到达率及排队时间情况

Tab.6  Number of charging piles，EV arrival rate and waiting time of each public charging station in extended example

$j$ ${N_j}$ ${\lambda _j}$ /
（辆·min−1） 		$t_j^{\rm{q}}$ /
min 		$j$ ${N_j}$ ${\lambda _j}$ /
（辆·min−1） 		$t_j^{\rm{q}}$ /
min
B1 76 0.42 10.03 B6 36 0.28 13.93
B2 74 0.42 10.13 B7 34 0.28 14.26
B3 81 0.44 9.78 B8 38 0.29 13.59
B4 38 0.29 13.68 B9 36 0.28 13.89
B5 43 0.31 12.79 B10 44 0.31 12.62

新窗口打开| 下载CSV


表 7   拓展算例各交通小区私人充电桩数量

Tab.7  Number of private charging piles in each traffic analysis zone in extended example

$i$ ${P_{ii}}$ $i$ ${P_{ii}}$
Z1 114 Z9 72
Z2 47 Z10 53
Z3 70 Z11 44
Z4 57 Z12 53
Z5 59 Z13 145
Z6 62 Z14 98
Z7 56 Z15 50
Z8 35 Z16 57

新窗口打开| 下载CSV


优化结果显示，大部分电动汽车被吸引到位于路网内部的3个公共充电站进行充电，因此这3个充电站都配置了数量较多的充电桩. 在研究区域外部，距离较近的B5和B10公共充电站吸引了较多的电动汽车，因而配置的充电站相比其他外部站点要多.

将表7与表2中各交通小区私人充电桩数量进行比较，可以发现，相较于原算例，拓展算例中各交通小区需要布置更多的私人充电桩. 这是由于拓展算例中大部分公共充电站都布置在路网外，路网内的电动汽车若要前往公共充电站进行充电，需要耗费更多的时间成本，导致总成本增加.

4. 结　语

本文建立了一个综合考虑公共充电站（快充）与私人充电桩（慢充）的充电设施定容布局模型. 在用户充电需求稳定的情况下，根据离散选择模型确定了2种类型充电设施的数量及比例，优化目标使得研究区域内电动汽车前往公共和私人充电设施充电的总成本最小.

本文选取杭州市某一实际区域路网，模拟电动汽车充电需求的空间分布，优化充电站的选取和充电桩的分配. 通过对该区域路网的算例分析定量讨论了充电设施与总体效用之间的关系，以及公共、私人、小区间、区域内外充电设施之间的竞争合作关系. 同时，本文通过对私人充电桩安装成本、公共充电桩总量的敏感性分析，进一步挖掘了公共充电站和私人充电桩网络的相互影响. 算例结果表明，本文所建立的模型可为城市电动汽车充电设施的选址布局及容量设计提供定量化的决策参考.

今后多个研究方向值得进一步探索，如：考虑时间、空间等要素的不确定性对模型的影响，建立鲁棒性更强的优化模型；考虑电网负担能力、充电路径有序调度、充电设施建设对交通需求的诱增等多个方面，建立更完备普适的优化模型，进一步提高充电设施的综合服务水平.

参考文献

郑雪芹

2018车市回顾及2019展望

[J]. 汽车纵横, 2019, 94 (1): 24- 28

[本文引用: 1]

ZHEN Xue-qin

Review of car market in 2018 and prospect for 2019

[J]. Auto Review, 2019, 94 (1): 24- 28

[本文引用: 1]

刘志鹏, 文福拴, 薛禹胜, 等

电动汽车充电站的最优选址和定容

[J]. 电力系统自动化, 2012, 36 (3): 174- 175

[本文引用: 1]

LIU Zhi-peng, WEN Fu-shuan, XUE Yu-sheng, et al

Optimal siting and sizing of electric vehicle charging stations

[J]. Automation of Electric Power Systems, 2012, 36 (3): 174- 175

[本文引用: 1]

中国电动汽车充电基础设施促进联盟

充电基础设施月度数据追踪

[J]. 汽车纵横, 2018, (8): 59- 59

[本文引用: 1]

EVCIPA

Monthly data tracking of charging infrastructure

[J]. Auto Review, 2018, (8): 59- 59

[本文引用: 1]

廖振宏. 基于目的地选择的电动出租车充电站规划研究[D]. 北京: 华北电力大学, 2016.

[本文引用: 1]

LIAO Zhen-hong. Study on electric taxi charging station planning based on destination choice [D]. Beijing: North China Electric Power University, 2016.

[本文引用: 1]

宋艳慧

新能源汽车充电服务面临的发展困境及其商业模式研究

[J]. 科技经济市场, 2019, (1): 121- 122

DOI:10.3969/j.issn.1009-3788.2019.01.060      [本文引用: 1]

SONG Yan-hui

Development dilemma and business model of new energy vehicle charging service

[J]. Science and Technology Economy Market, 2019, (1): 121- 122

DOI:10.3969/j.issn.1009-3788.2019.01.060      [本文引用: 1]

任玉珑, 史乐峰, 张谦, 等

电动汽车充电站最优分布和规模研究

[J]. 电力系统自动化, 2011, 35 (14): 53- 57

[本文引用: 1]

REN Yu-long, SHI Le-feng, ZHANG Qian, et al

Optimal distribution and scale of charging stations for electric vehicles

[J]. Automation of Electric Power Systems, 2011, 35 (14): 53- 57

[本文引用: 1]

宋阳. 电动汽车充电站布局优化研究[D]. 成都: 西南交通大学, 2016.

[本文引用: 1]

SONG Yang. Optimization of electric vehicles’ charging station location [D]. Chengdu: Southwest Jiaotong University, 2016.

[本文引用: 1]

XIANG Y, ZHOU H, YANG W, et al

Scale evolution of electric vehicles: a system dynamics approach

[J]. IEEE Access, 2017, 5: 8859- 8868

DOI:10.1109/ACCESS.2017.2699318      [本文引用: 1]

李颖. 基于电动汽车出行随机模拟的充电桩需求研究[D]. 北京: 华北电力大学, 2017.

[本文引用: 1]

LI Ying. Research on demand of charging piles based on stochastic simulation of EV trip chain [D]. Beijing: North China Electric Power University, 2017

[本文引用: 1]

DONG J, LIU C, LIN Z

Charging infrastructure planning for promoting battery electric vehicles: an activity-based approach using multiday travel data

[J]. Transportation Research Part C: Emerging Technologies, 2014, 38: 44- 55

DOI:10.1016/j.trc.2013.11.001      [本文引用: 1]

邱海. 基于Agent仿真的城市电动汽车充电设施布局优化研究[D]. 杭州: 浙江大学, 2019.

[本文引用: 2]

QIU Hai. Research on optimization of charging facilities layout of urban electric vehicles based on agent simulation [D]. Hangzhou: Zhejiang University, 2019.

[本文引用: 2]

NI X, SUN D J, PENG Z

An improved incremental assignment model for parking variable message sign location problem

[J]. Journal of Advanced Transportation, 2015, 49 (7): 817- 828

DOI:10.1002/atr.1305      [本文引用: 1]

NI X, SUN D J

An agent-based simulation model for parking variable message sign location problem

[J]. Transportation Research Record, 2018, 2672 (19): 135- 144

DOI:10.1177/0361198118787387      [本文引用: 1]

CAI H, JIA X, CHIU A S F, et al

Siting public electric vehicle charging stations in Beijing using big-data informed travel patterns of the taxi fleet

[J]. Transportation Research Part D: Transport and Environment, 2014, 33: 39- 46

DOI:10.1016/j.trd.2014.09.003      [本文引用: 1]

TU W, LI Q, FANG Z, et al

Optimizing the locations of electric taxi charging stations: a spatial-temporal demand coverage approach

[J]. Transportation Research Part C: Emerging Technologies, 2016, 65: 172- 189

DOI:10.1016/j.trc.2015.10.004      [本文引用: 1]

YUN B, SUN D J, ZHANG Y, et al

A charging location choice model for plug-in hybrid electric vehicle users

[J]. Sustainability, 2019, 11 (20): 5761

DOI:10.3390/su11205761      [本文引用: 1]

KANG Q, WANG J, ZHOU M, et al

Centralized charging strategy and scheduling algorithm for electric vehicles under a battery swapping scenario

[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17 (3): 659- 669

DOI:10.1109/TITS.2015.2487323      [本文引用: 1]

王炜, 陈学武. 交通规划: 第2版[M]. 北京: 人民交通出版社股份有限公司, 2017.

[本文引用: 1]

新浪云计算. 2019年杭州市薪资水平报告[EB/OL]. (2019-07-01) [2019-07-27]. http://salarycalculator.sinaapp.com/report/杭州.

[本文引用: 1]

IMGBEMENA C E, MGBEMENA C O, CHINWUKO E C

A regression analysis approach to queuing system modelling: a case of banks

[J]. Journal of Applied Sciences Research, 2011, 7: 200- 212

[本文引用: 1]

MathWorks Documentation. Fmincon [EB/OL]. (2019-01-01) [2019-07-27]. https://ww2.mathworks.cn/help/optim/ug/fmincon.html.

[本文引用: 1]

MathWorks Documentation. Fmincon interior point algorithm [EB/OL]. (2019-01-01) [2019-07-27]. https://ww2.mathworks.cn/help/optim/ug/constrained-nonlinear-optimization-algorithms.html#brnpd5f.

[本文引用: 1]

/

〈 〉