在图像去噪问题中,由于高斯噪声比较常见,大多数图像去噪算法都假设噪声服从高斯概率模型. 在天文成像、计算机断层扫描、荧光共焦显微镜成像、CCD固态光电检测等光子计数成像系统中,噪声的概率分布服从泊松概率模型[1],利用高斯噪声模型不能有效描述其概率分布特征,采用面向高斯噪声的去噪方法难以获得理想的去噪效果.
图像泊松噪声去除的经典方法是通过方差变换将泊松噪声转化为近似高斯分布的噪声[2],然后利用成熟的高斯去噪方法,如维纳滤波、全变差模型[3]、非局部均值[4]等进行去噪处理,最后经逆方差变换得到去噪后的图像. 这种方法在一定程度上可以去除泊松噪声,但是去噪效果仍然有待提高. 另一类方法是基于贝叶斯最大后验(maximum a posteriori,MAP)[5]概率的正则化方法,这类方法通常以Richardson-Lucy(RL)算法[6]为基础. 为了解决RL算法多次迭代时产生的噪声放大问题,研究者提出了很多基于变分正则化的改进方法,常用的有吉洪诺夫(Tikhonov)正则项、全变分(total variation,TV)正则项、高阶正则项等[7]. Le等[8]选用TV正则项推导出了经典的泊松全变分去噪模型. 但是,TV模型在去除噪声的同时容易产生阶梯效应,造成部分边缘和细节丢失. 为了解决这一问题,Gilboa等[9]引入了空间变换;张哲等[10]提出了四阶去噪模型;白键等[11]提出了基于积分微分方程的改进方法;胡学刚等[12]提出了一种基于分数阶导数的泊松去噪算法;张峥嵘等[13]提出了一种基于非局部全变差正则化的图像去噪模型.
为了构建能够准确描述自然图像先验概率分布特征的MRF模型,Roth等[16]采用机器学习的方法,建立了一种全新的高阶MRF模型,称之为专家场(fields of experts,FoE)模型,其特点在于构成FoE模型的所有滤波器都是基于自然图像库学习得到的. 因此,FoE模型能够更准确地捕捉复杂自然图像的先验概率分布特点. FoE模型已被应用于一系列视觉图像处理领域,如图像修复、模糊图像复原等,有广阔的研究和应用前景.
本文提出一种基于泊松噪声模型和FoE约束的正则化去噪方法,采用二次惩罚函数对代价函数进行优化求解,并通过仿真实验以及图像评价指标对所提方法的去噪效果进行客观评价.
1. 专家场模型
FoE模型的本质是一种马尔科夫随机场,其邻域系统被定义为包含了K个
式中:
根据Hammersley-Clifford理论[17],整幅图像在FoE模型下的概率分布可以写成下式:
式中:N为图像像素总数,Z为归一化函数.
在FoE模型中,
式中:
在实际问题中,通常采用吉布斯分布形式对式(2)所示FoE模型进行表示:
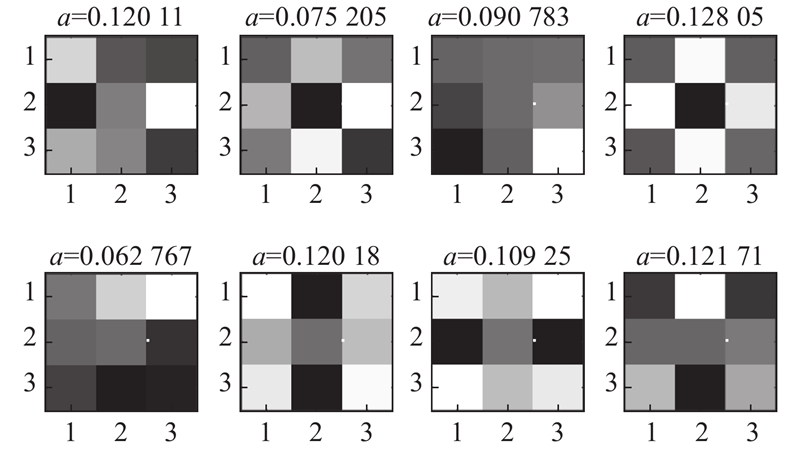
图 1
图 1 构成专家场(FoE)模型的典型邻域系统
Fig.1 Typical domain system for fields of experts(FoE)model
2. 基于专家场模型的去噪问题建模
噪声图像的退化模型可以表示为
式中:
基于噪声的随机特性,根据贝叶斯定律可得
图像去噪问题可以表述为噪声图像已知条件下的最大后验概率估计问题:
对式(7)取负自然对数,上述求最大值问题可转为求最小值问题:
由式(8)可知,求解清晰图像
若
对式(9)进行负对数操作后有
对
将式(10)和(11)代入式(8),可得代价函数:
式中:
3. 去噪模型求解方法
采用二次惩罚函数对如式(12)所示的代价函数进行求解. 引入2组辅助变量:
根据二次惩罚函数原理,当
图 2
1) 初始化:
2) 循环;
6)
7)
8) 输出:
以下依次对求解步骤中涉及的几点问题进行解决,为了便于描述,略去上标
由于步骤3)中的问题不存在解析解,采用Newton-Raphson方法[18]进行求解. 以
根据Newton-Raphson方法可得
对于每一个
针对步骤4)中的问题,设定损失函数
则
当
由于
针对步骤5)中的问题,可在频域中进行求解. 首先,在不考虑非负约束
式中:
由于
式中:
由此,求解过程中的所有问题得到解决,按照求解步骤即可解得清晰图像
4. 实验与分析
为了验证提出的基于FoE模型的泊松噪声去除算法的有效性,针对泊松噪声出现环境,选择大小为
以星云测试图像为例,采用上述不同方法对图像进行去噪的结果分别如图3所示,图中左上角为每幅图像的峰值信噪比(peak signal-noise-ratio,PSNR). 从图3中可以看出,采用GF方法处理后图像整体模糊;采用GTVL2与GGS方法处理后的图像在亮度较高的区域(如:星云中心处)仍含有部分噪声,噪声去除不彻底;PRL方法对噪声的去除效果较差,结果图像中仍含有大量噪声;采用PTVL2、WNNM以及ATFoE方法处理后图像边缘模糊,细节信息丢失;采用PGS方法处理后在高亮度区域(如:星云中心点处)产生不规则花纹,会对接下来的处理产生影响. 采用提出的方法处理后的图像边缘清晰,纹理信息完整,图像中噪声基本得到去除,如图3(k)所示.
图 3
图 3 星云图像在9种去噪方法下的去噪结果局部图
Fig.3 Local nebula images of denoising results by nine denoising methods
图 4
图 4 8幅图像在不同去噪方法下的峰值信噪比对比
Fig.4 Comparison of peak signal-noise-ratio of eight images with different denoising methods
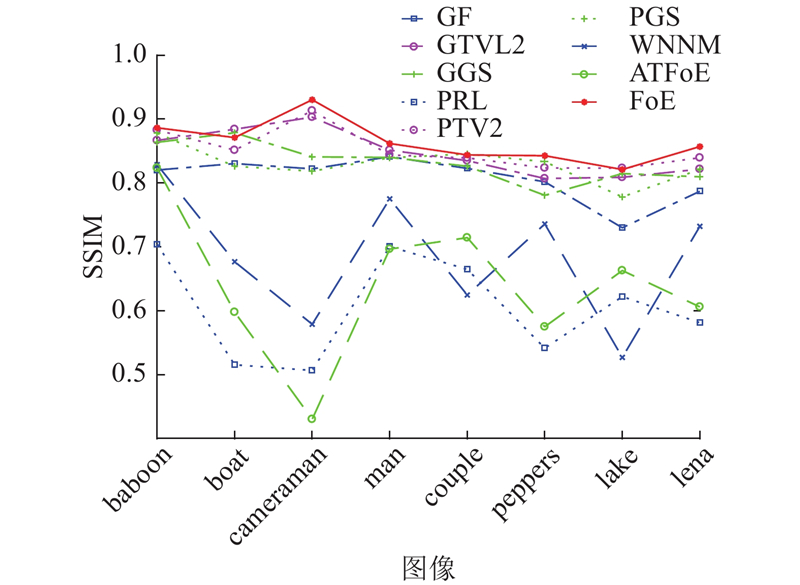
图 5
图 5 8幅图像在不同去噪方法下的结构相似度对比
Fig.5 Comparison of structural similarity of eight images with different denoising methods
由图4和图5可以看出,除少数个别图像以外,使用所提出的方法得到的去噪后图像的PSNR和SSIM值显著优于其他方法. 相较于PGS方法和WNNM方法,所提出的算法在PSNR上平均提升了0.48和0.18 dB. 与文献[22]中同样使用FoE模型的ATFoE算法相比,在PSNR结果上,本文方法优势不明显,但是在SSIM结果上,本文方法具有明显的优越性. 与传统的GF、PRL及TVL2方法相比,本文算法能够更加有效地消除噪声,获得的图像失真度小,边缘纹理结构保留较好,与原始图像相似度高. 以上对比结果充分证明了本文算法的有效性.
5. 结 语
在峰值信噪比方面,本文提出的方法与传统方法相比均有提升,至少提升了0.18 dB. 在结构相似度方面,由于现有的去噪算法大多是直接或间接地利用整数阶积分函数改造的滤波器进行滤波,这样的滤波器会破坏图像中的高频信息致使图像边缘或纹理丢失. 提出的算法所采用的FoE模型主要是利用图像中相邻像素之间的关系,因此边缘纹理得到了保留. 本文在贝叶斯最大后验概率估计的框架下,构建了图像泊松噪声去噪模型. 该模型以泊松概率分布为保真项,以马尔科夫专家场为正则项构造代价函数,利用二次惩罚函数优化求解,能够有效地还原清晰图像,有着不错的泊松噪声去除效果. 但由于求解过程需要多次迭代计算,运算复杂度较高,耗时较长,未来需要考虑精简计算以提高去噪速度.
参考文献
Noise parameter estimation for Poisson corrupted images using variance stabilization transforms
[J].DOI:10.1109/TIP.2014.2300813 [本文引用: 1]
具有全局收敛性的彩色图像去噪模型
[J].
Color image denoising model with global convergence
[J].
A review of image denoising algorithms, with a new one
[J].DOI:10.1137/040616024 [本文引用: 1]
基于卡尔曼滤波的红外图像增强算法
[J].
Enhancement algorithm for infrared images based on Kalman filter
[J].
Richardson-Lucy algorithm with total variation regularization for 3D confocal microscope deconvolution
[J].
欧拉弹性正则化的图像泊松去噪
[J].DOI:10.3969/j.issn.0372-2112.2017.01.025 [本文引用: 1]
Image Poisson denoising based on Euler's elastica regularization
[J].DOI:10.3969/j.issn.0372-2112.2017.01.025 [本文引用: 1]
A variational approach to reconstructing images corrupted by Poisson noise
[J].DOI:10.1007/s10851-007-0652-y [本文引用: 1]
Variational denoising of partly textured images by spatially varying constraints
[J].DOI:10.1109/TIP.2006.875247 [本文引用: 1]
一种基于偏微分方程变分去噪模型
[J].
A denoising model of variation based on PDE
[J].
一种基于积分微分方程的泊松噪声去除算法
[J].
An integro-differential equation approach to reconstructing images corrupted by Poisson noise
[J].
基于分数阶变分的图像泊松去噪模型
[J].DOI:10.3724/SP.J.1087.2013.01100 [本文引用: 1]
Improved image Poisson denoising model based on fractional variation
[J].DOI:10.3724/SP.J.1087.2013.01100 [本文引用: 1]
非局部TV正则化的图像泊松去噪模型与算法
[J].
Image Poisson denoising model and algorithm based on nonlocal TV regularization
[J].
FoE模型的训练方法研究
[J].DOI:10.3969/j.issn.1673-629X.2010.12.022 [本文引用: 1]
A study on training methods of FoE model
[J].DOI:10.3969/j.issn.1673-629X.2010.12.022 [本文引用: 1]
边缘保持专家场模型的自然图像复原
[J].DOI:10.3321/j.issn:1002-008X.2009.09.015 [本文引用: 1]
Natural image restoration of the edge-preserving expert field model
[J].DOI:10.3321/j.issn:1002-008X.2009.09.015 [本文引用: 1]
Fields of experts
[J].DOI:10.1007/s11263-008-0197-6 [本文引用: 3]
Spatial interaction and the statistical analysis of lattice systems
[J].
Non-blind image deconvolution using natural image gradient prior
[J].DOI:10.1016/j.ijleo.2013.05.068 [本文引用: 1]
Weighted nuclear norm minimization and its applications to low level vision
[J].DOI:10.1007/s11263-016-0930-5 [本文引用: 1]
Poisson noise reduction with higher-order natural image prior model
[J].DOI:10.1137/16M1072930 [本文引用: 2]