(1) $ \begin{split} &{{{v}}_{t + 1}},{{{v}}_{t + 2}}, \cdots ,{{{v}}_{t + q}} = \;\mathop {\arg \max }\limits_{{{{v}}_{t + 1}},{{{v}}_{t + 2}}, \cdots ,{{{v}}_{t + q}}} \\ &\quad\left[ {\log\; P\left( {{{{v}}_{t + 1}},{{{v}}_{t + 2}}, \cdots ,{{{v}}_{t + q}}| \;{{{v}}_{t - p + 1}}, \cdots ,{{{v}}_{t - 1}},{{{v}}_t}} \right)} \right]. \end{split} $
[2]
李德仁, 姚远, 邵振峰 智慧城市中的大数据
[J]. 武汉大学学报: 信息科学版 , 2014 , 58 (6 ): 631 - 640
[本文引用: 1]
LI De-ren, YAO Yuan, SHAO Zhen-feng Big data in smart cities
[J]. Journal of Wuhan University: Information Science Edition , 2014 , 58 (6 ): 631 - 640
[本文引用: 1]
[3]
陆化普, 李瑞敏 城市智能交通系统的发展现状与趋势
[J]. 工程研究: 跨学科视野中的工程 , 2014 , 6 (1 ): 6 - 19
[本文引用: 1]
LU Hua-pu, LI Rui-min Development status and trends of urban intelligent transportation systems
[J]. Engineering Research: Engineering in Interdisciplinary Perspectives , 2014 , 6 (1 ): 6 - 19
[本文引用: 1]
[4]
HAJIMOLAHOSEINI H, AMIRFATTAHI R, SOLTANIAN-ZADEH H Robust vehicle tracking algorithm for nighttime videos captured by fixed cameras in highly reflective environments
[J]. IET Computer Vision , 2014 , 8 (6 ): 535 - 544
[本文引用: 1]
[5]
SEN R, MAURYA A, RAMAN B, et al. Kyun queue: a sensor network system to monitor road traffic queues [C] // Proceedings of the 10th ACM Conference on Embedded Network Sensor Systems . Toronto: ACM, 2012: 127-140.
[6]
CHEN C, PETTY K, SKABARDONIS A, et al Freeway performance measurement system: mining loop detector data
[J]. Transportation Research Record , 2001 , 1748 (1 ): 96 - 102
DOI:10.3141/1748-12
[本文引用: 2]
[7]
VLAHOGIANNI E I. Computational intelligence and optimization for transportation big data: challenges and opportunities [M] // Engineering and Applied Sciences Optimization . Cham: Springer, 2015: 107-128.
[本文引用: 1]
[8]
MAKRIDAKIS S, HIBON M ARMA models and the Box–Jenkins methodology
[J]. Journal of Forecasting , 1997 , 16 (3 ): 147 - 163
[本文引用: 2]
[9]
HAMED M M, Al-MASAEID H R, SAID Z M B Short-term prediction of traffic volume in urban arterials
[J]. Journal of Transportation Engineering , 1995 , 121 (3 ): 249 - 254
[本文引用: 1]
[10]
SMOLA A J, SCHOLKOPF B A tutorial on support vector regression
[J]. Statistics and Computing , 2004 , 14 (3 ): 199 - 222
[本文引用: 2]
[11]
HUANG W, SONG G, HONG H, et al Deep architecture for traffic flow prediction: Deep belief networks with multitask learning
[J]. IEEE Transactions on Intelligent Transportation Systems , 2014 , 15 (5 ): 2191 - 2201
DOI:10.1109/TITS.2014.2311123
[本文引用: 1]
[13]
CHO K, VAN MERRIENBOER B, GULVEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation [J]. arXiv Preprint , arXiv: 1406.1078, 2014.
[本文引用: 1]
[14]
CUI Z, KE R, WANG Y. Deep bidirectional and unidirectional LSTM recurrent neural network for network-wide traffic speed prediction [J]. arXiv Preprint , arXiv: 1801.02143, 2018.
[本文引用: 1]
[15]
ZHANG J, ZHENG Y, QI D. Deep spatio-temporal residual networks for citywide crowd flows prediction [C] // Thirty-First AAAI Conference on Artificial Intelligence . San Francisco: AAAI, 2017.
[本文引用: 2]
[16]
LECUN Y, BOSER B, DENKER J S, et al Backpropagation applied to handwritten zip code recognition
[J]. Neural computation , 1989 , 1 (4 ): 541 - 551
[本文引用: 1]
[17]
MA X L, DAI Z, HE Z B, et al Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction
[J]. Sensors , 2017 , 17 (4 ): 818
[本文引用: 1]
[18]
SCARSELLI F, GORI M, TSOI A C, et al The graph neural network model
[J]. IEEE Transactions on Neural Networks , 2009 , 20 (1 ): 61 - 80
[本文引用: 1]
[19]
ZHOU J, CUI G, ZHANG Z, et al. Graph neural networks: A review of methods and applications [J]. arXiv Preprint , arXiv: 1812.08434, 2018.
[本文引用: 1]
[20]
LI Y, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: data-driven traffic forecasting [J]. arXiv Preprint , arXiv: 1707.01926, 2017.
[本文引用: 3]
[21]
YU, YIN H, ZHU Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting [J]. arXiv Preprint . arXiv: 1709.04875, 2017.
[本文引用: 6]
[22]
CUI Z, HENRICKSON K, KE R, et al Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting
[J]. IEEE Transactions on Intelligent Transportation Systems , 2019 ,
[本文引用: 2]
[23]
GUO S, LIN Y, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting [C] // Proceedings of the AAAI Conference on Artificial Intelligence . Hawaii: AAAI, 2019, 33: 922-929.
[24]
ZHANG N, GUAN X, CAO J, et al. A hybrid traffic speed forecasting approach integrating wavelet transform and motif-based graph convolutional recurrent neural network [J]. arXiv Preprint . arXiv: 1904.06656, 2019.
[25]
SUN J, ZHANG J, LI Q, et al. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks [J]. arXiv Preprint . arXiv: 1903.07789, 2019.
[26]
CHEN C, LI K, TEO S G, et al. Gated residual recurrent graph neural networks for traffic prediction [C] // Proceedings of the AAAI Conference on Artificial Intelligence . Hawaii: AAAI, 2019, 33: 485-492.
[27]
ZHENG C, FAN X, WANG C, et al. GMAN: a graph multi-attention network for traffic prediction [J]. arXiv Preprint , arXiv: 1911.08415, 2019.
[本文引用: 1]
[28]
SHUMAN D I, NARANG S K, FROSSARD P, et al The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains
[J]. IEEE Signal Processing Magazine , 2013 , 30 (3 ): 83 - 98
DOI:10.1109/MSP.2012.2235192
[本文引用: 1]
[29]
DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering [C] // Advances in Neural Information Processing Systems . Barcelona: NIPS, 2016: 3844-3852.
[本文引用: 1]
交通流预测方法综述
1
2004
... 为了解决交通拥堵与交通事故、城市敏感区的人群聚集风险以及发生自然灾害后的人群出行等一系列交通问题,世界各国研究者纷纷对智能交通系统(intelligent transportation system,ITS)展开了研究. ITS的核心是交通控制与诱导系统,而实现交通控制与诱导系统的核心工作是实时准确地进行交通流预测,即有效地融合历史交通规律和实时交通数据来预测城市交通系统的运行态势[1 ] . ...
交通流预测方法综述
1
2004
... 为了解决交通拥堵与交通事故、城市敏感区的人群聚集风险以及发生自然灾害后的人群出行等一系列交通问题,世界各国研究者纷纷对智能交通系统(intelligent transportation system,ITS)展开了研究. ITS的核心是交通控制与诱导系统,而实现交通控制与诱导系统的核心工作是实时准确地进行交通流预测,即有效地融合历史交通规律和实时交通数据来预测城市交通系统的运行态势[1 ] . ...
智慧城市中的大数据
1
2014
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
智慧城市中的大数据
1
2014
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
城市智能交通系统的发展现状与趋势
1
2014
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
城市智能交通系统的发展现状与趋势
1
2014
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
Robust vehicle tracking algorithm for nighttime videos captured by fixed cameras in highly reflective environments
1
2014
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
Freeway performance measurement system: mining loop detector data
2
2001
... 精准地感知和预测城市交通态势是ITS领域的一项重要内容[2 -3 ] ,相关研究工作对缓解交通拥堵、减少交通事故及预防人群异常聚集事件等均具有重要应用价值. 现今的交通态势感知和预测研究主要面临以下挑战. 1)交通数据的复杂时空依赖性导致交通态势预测面临实时性困难. 随着时间变化,2个不同地点的空间相关性亦发生变化. 例如,从工作日到周末:在工作日,家庭住所与公司的相关性较强;而在周末,家庭住所与公司的相关性较弱. 此外,对于相同的2个地点,不同时段的时间相关性并不是线性的,即与当前时段最相关的很可能是距离该时段很远的时段. 例如,工作日早高峰时段与其前后平峰时段的相关性较弱,而往往与工作日晚高峰时段的时间相关性更强. 2)交通流量感知设备采集的数据存在缺失、错误等问题. 当前道路状况检测的检测设备(如环形感应线圈、雷达、摄像头等)[4 -6 ] 已经可以获得较高准确度的交通状况数据,但仍存在使用寿命有限及设备故障等问题. 此外,对于检测设备自身的信息(如传感器的邻接信息等)部分,相关数据也难以完全统计. ...
... PeMS项目[6 ] 在加利福尼亚州主要大城市的州际公路上部署了超过39 000个传感器站点,由Caltrans绩效测量系统(PeMS)实时收集数据. 本文所用数据为PeMS项目从2012年5月至同年6月在加利福尼亚州第7区(D7区)以5 min为时间间隔获取的站点流速数据集,共有80 619 552条数据. 同时,该数据集还包括每个站点的地理位置信息,共4 589条数据. 因此,数据可分为两部分:交通流速数据和站点地理位置数据. 本文在D7区随机选择一个包括181个站点的小型数据集和一个包括1 045个站点的大型数据集,分别命名为PeMSD7(S)和PeMSD7(L). ...
1
... 交通流预测方法主要分为2类,分别是动态建模方法和数据挖掘方法. 动态建模方法主要使用数学工具与物理方法,模拟交通系统的动态变化,从而生成预测交通流的公式[7 ] . 数据挖掘方法主要是在交通状况的历史数据中挖掘数据规律,从而对未来的数据走势进行预判. 数据挖掘方法受到更多的关注,逐渐发展成为交通流预测的主流方法. ...
ARMA models and the Box–Jenkins methodology
2
1997
... 统计学方法与机器学习方法是挖掘交通数据的2种主要方法. 在时间序列分析中,传统的统计学方法占有主导地位,自回归积分滑动平均模型(autoregressive integrated moving average model,ARIMA)[8 ] 在短期预测方面表现出明显的优势[9 ] ,然而在中长期预测方面,其准确率大幅度降低. 尽管机器学习算法,如:支持向量机回归(support vector regression,SVR)[10 ] 等,优于传统的统计学方法,但其仅在时间维度挖掘序列数据变化趋势,很难解决复杂的交通流预测问题. 为了挖掘时间序列以外的交通特征,研究人员将注意力逐渐转移到深度学习方法. ...
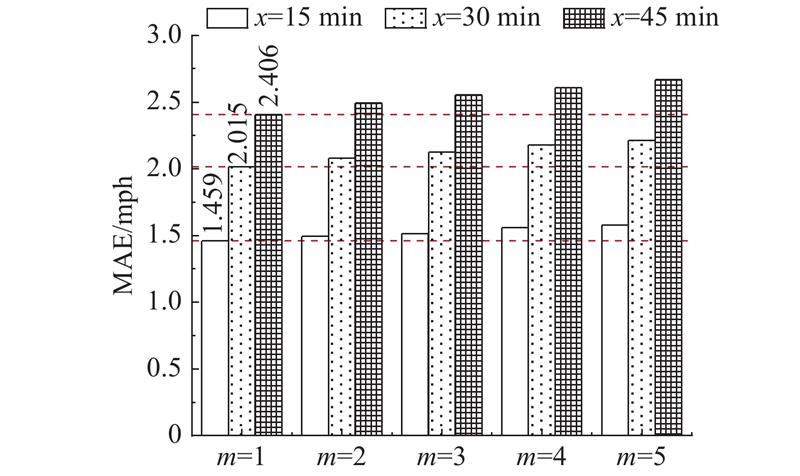
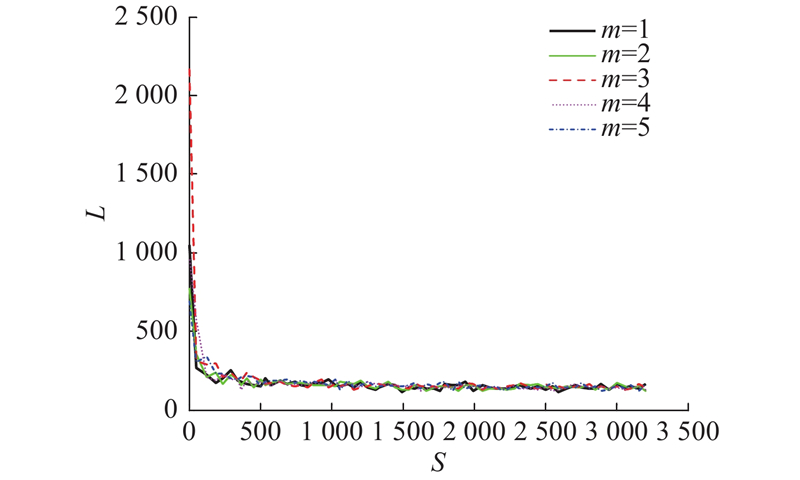
... 基线模型包括以下5种:1)自回归积分滑动平均模型(ARIMA)[8 ] ;2)支持向量机回归(SVR)[10 ] ;3)卷积神经网络(CNN)[15 ] ;4)长短期记忆网络(LSTM)[12 ] ;5)时空图卷积网络(STGCN)[21 ] . ...
Short-term prediction of traffic volume in urban arterials
1
1995
... 统计学方法与机器学习方法是挖掘交通数据的2种主要方法. 在时间序列分析中,传统的统计学方法占有主导地位,自回归积分滑动平均模型(autoregressive integrated moving average model,ARIMA)[8 ] 在短期预测方面表现出明显的优势[9 ] ,然而在中长期预测方面,其准确率大幅度降低. 尽管机器学习算法,如:支持向量机回归(support vector regression,SVR)[10 ] 等,优于传统的统计学方法,但其仅在时间维度挖掘序列数据变化趋势,很难解决复杂的交通流预测问题. 为了挖掘时间序列以外的交通特征,研究人员将注意力逐渐转移到深度学习方法. ...
A tutorial on support vector regression
2
2004
... 统计学方法与机器学习方法是挖掘交通数据的2种主要方法. 在时间序列分析中,传统的统计学方法占有主导地位,自回归积分滑动平均模型(autoregressive integrated moving average model,ARIMA)[8 ] 在短期预测方面表现出明显的优势[9 ] ,然而在中长期预测方面,其准确率大幅度降低. 尽管机器学习算法,如:支持向量机回归(support vector regression,SVR)[10 ] 等,优于传统的统计学方法,但其仅在时间维度挖掘序列数据变化趋势,很难解决复杂的交通流预测问题. 为了挖掘时间序列以外的交通特征,研究人员将注意力逐渐转移到深度学习方法. ...
... 基线模型包括以下5种:1)自回归积分滑动平均模型(ARIMA)[8 ] ;2)支持向量机回归(SVR)[10 ] ;3)卷积神经网络(CNN)[15 ] ;4)长短期记忆网络(LSTM)[12 ] ;5)时空图卷积网络(STGCN)[21 ] . ...
Deep architecture for traffic flow prediction: Deep belief networks with multitask learning
1
2014
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
Long short-term memory
2
1997
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
... 基线模型包括以下5种:1)自回归积分滑动平均模型(ARIMA)[8 ] ;2)支持向量机回归(SVR)[10 ] ;3)卷积神经网络(CNN)[15 ] ;4)长短期记忆网络(LSTM)[12 ] ;5)时空图卷积网络(STGCN)[21 ] . ...
1
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
1
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
2
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
... 基线模型包括以下5种:1)自回归积分滑动平均模型(ARIMA)[8 ] ;2)支持向量机回归(SVR)[10 ] ;3)卷积神经网络(CNN)[15 ] ;4)长短期记忆网络(LSTM)[12 ] ;5)时空图卷积网络(STGCN)[21 ] . ...
Backpropagation applied to handwritten zip code recognition
1
1989
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
Learning traffic as images: a deep convolutional neural network for large-scale transportation network speed prediction
1
2017
... 将深度信念网络(deep belief nets,DBN)应用至交通流预测[11 ] ,能够有效挖掘交通数据的高维特征,从而一定程度地降低预测误差,但其难以从输入数据中提取具体的时空特征. 循环神经网络(recurrent neural network,RNN)、长短期记忆网络(long short-term memory,LSTM)[12 ] 以及门控循环单元(gated recurrent unit,GRU)[13 ] 等基于RNN的模型能够为相邻时刻的交通数据建立联系,并通过门控等方式保存记忆,以学得交通流序列的长期依赖关系,因而在交通流预测问题上表现出强大的优势与潜力[14 ] . 然而这些模型只能从噪声中捕捉复杂的时间特征,并不能够模拟真实世界中的交通路网空间结构. 为了进一步捕捉空间特征,Ma等[15 -16 ] 使用卷积神经网络(CNN)[17 ] 学习交通路网的空间结构. 然而,传统的CNN更适合用于捕捉欧拉数据的空间关系,交通路网属于图结构的非欧拉数据,因此使用CNN学习空间特征并不是学习交通路网结构的最优方法. 可见,早期的交通流预测算法存在局限性,早期算法大多结合基于RNN的模型与基于CNN的模型,将二者分别用于捕捉交通数据的时空特征,然而,基于CNN的方法并不完全适用于捕获图结构的路网空间特征.于捕获图结构的路网空间特征. ...
The graph neural network model
1
2009
... 近年来,由于图在众多领域(如社交网络、知识图谱等)强大的表现力,图神经网络(graph neural network,GNN)[18 ] 受到了越来越多的关注;GNN令人信服的性能和较高的可解释性,使其成为一种应用广泛的图结构分析方法[19 ] . 将图卷积运算扩展到图结构数据中可捕获交通路网信息,Li等[20 -27 ] 利用图卷积神经网络(graph convolutional networks,GCN)对交通流预测问题进行建模. ...
1
... 近年来,由于图在众多领域(如社交网络、知识图谱等)强大的表现力,图神经网络(graph neural network,GNN)[18 ] 受到了越来越多的关注;GNN令人信服的性能和较高的可解释性,使其成为一种应用广泛的图结构分析方法[19 ] . 将图卷积运算扩展到图结构数据中可捕获交通路网信息,Li等[20 -27 ] 利用图卷积神经网络(graph convolutional networks,GCN)对交通流预测问题进行建模. ...
3
... 近年来,由于图在众多领域(如社交网络、知识图谱等)强大的表现力,图神经网络(graph neural network,GNN)[18 ] 受到了越来越多的关注;GNN令人信服的性能和较高的可解释性,使其成为一种应用广泛的图结构分析方法[19 ] . 将图卷积运算扩展到图结构数据中可捕获交通路网信息,Li等[20 -27 ] 利用图卷积神经网络(graph convolutional networks,GCN)对交通流预测问题进行建模. ...
... 利用GCN进行图卷积的方法主要有2类. 第一类方法为图谱卷积,即利用图谱理论,通过设计基于图拉普拉斯矩阵的图谱滤波器完成卷积. Li等[20 ] 融合图谱卷积、Seq2seq体系与预定抽样等技术捕捉交通流的时空依赖性,获得了较高的预测准确率,但时间复杂度较高. Yu等[21 ] 将2个捕捉时间特征的门控卷积层与1个捕捉空间特征的图谱图卷积层结合,组装成时空卷积块进行交通流预测,打造了准确率更高的模型并降低了时间复杂度. 虽然两者均将卷积应用于图结构数据以捕获图的空间特征并取得了良好的效果,但图谱卷积不能完全适应交通网络的物理特性. 第二类图卷积方法是直接在图上定义卷积,从邻居结点中获取信息. Cui等[22 ] 使用自由流动速度计算自由流动可达矩阵,结合关系矩阵、邻接矩阵与自流矩阵,构造图卷积核捕获交通路网的物理特性. 然而,这种方法要求数据集提供传感器的邻接信息,对数据集信息的要求过多,缺乏普适性. ...
... 由于非欧拉的图结构数据不能直接进行常规的网格卷积,研究者对图域内卷积的方法进行了文献探索[20 -21 ] . 目前图域中卷积的主流方法主要有2种:一种是图谱卷积,利用图谱傅里叶变换在谱域中进行操作,在频谱域中应用卷积的频谱框架;另一种是非图谱卷积,扩展卷积的空间定义,即将图的顶点排列为网格形式进行网格卷积. 前者将图数据应用至图谱中模拟图结构,但方法较为固定;后者提取邻居信息的方式更加灵活,更有利于捕捉交通路网独特的物理结构,因此本研究选用非图谱卷积方法模拟路网结构. ...
6
... 利用GCN进行图卷积的方法主要有2类. 第一类方法为图谱卷积,即利用图谱理论,通过设计基于图拉普拉斯矩阵的图谱滤波器完成卷积. Li等[20 ] 融合图谱卷积、Seq2seq体系与预定抽样等技术捕捉交通流的时空依赖性,获得了较高的预测准确率,但时间复杂度较高. Yu等[21 ] 将2个捕捉时间特征的门控卷积层与1个捕捉空间特征的图谱图卷积层结合,组装成时空卷积块进行交通流预测,打造了准确率更高的模型并降低了时间复杂度. 虽然两者均将卷积应用于图结构数据以捕获图的空间特征并取得了良好的效果,但图谱卷积不能完全适应交通网络的物理特性. 第二类图卷积方法是直接在图上定义卷积,从邻居结点中获取信息. Cui等[22 ] 使用自由流动速度计算自由流动可达矩阵,结合关系矩阵、邻接矩阵与自流矩阵,构造图卷积核捕获交通路网的物理特性. 然而,这种方法要求数据集提供传感器的邻接信息,对数据集信息的要求过多,缺乏普适性. ...
... 由于非欧拉的图结构数据不能直接进行常规的网格卷积,研究者对图域内卷积的方法进行了文献探索[20 -21 ] . 目前图域中卷积的主流方法主要有2种:一种是图谱卷积,利用图谱傅里叶变换在谱域中进行操作,在频谱域中应用卷积的频谱框架;另一种是非图谱卷积,扩展卷积的空间定义,即将图的顶点排列为网格形式进行网格卷积. 前者将图数据应用至图谱中模拟图结构,但方法较为固定;后者提取邻居信息的方式更加灵活,更有利于捕捉交通路网独特的物理结构,因此本研究选用非图谱卷积方法模拟路网结构. ...
... 此处,Yu等[21 ] 提出的STGCN算法所使用的图卷积方法为LSGC,所用多项式 ${T_k }({{\varLambda }})$
... 虽然基于RNN的模型(如:LSTM)在时间序列预测方面表现良好,但是均存在模型训练时间开销过大以及对数据的动态变化反应迟缓等问题. CNN在训练模型时具有训练快速、结构简单以及能快速捕捉数据变化等优势,因此本研究参考Yu等[21 ] 提出的方法,使用基于门控线性单元(gated linear unit,GLU)的门控卷积神经网络捕捉交通流的时间动态变化特征,网络结构见图1(c) . 时间门控卷积的定义如下: ...
... 为了融合第3.2节与3.3节分别捕捉的空间特征与时间特征,从而捕获交通数据的时空依赖性,本研究参考Yu等[21 ] 提出的方法,采用瓶颈策略产生1个“时间−空间−时间”结构,如图1(b) 所示,将1个图卷积神经网络嵌入2个门控神经网络中,使两者组成1个时空卷积块,作用于图结构的时间序列数据. 此外,为了防止过拟合问题的出现,本研究还对时空卷积块的输出结果进行归一化处理. ...
... 基线模型包括以下5种:1)自回归积分滑动平均模型(ARIMA)[8 ] ;2)支持向量机回归(SVR)[10 ] ;3)卷积神经网络(CNN)[15 ] ;4)长短期记忆网络(LSTM)[12 ] ;5)时空图卷积网络(STGCN)[21 ] . ...
Traffic graph convolutional recurrent neural network: A deep learning framework for network-scale traffic learning and forecasting
2
2019
... 利用GCN进行图卷积的方法主要有2类. 第一类方法为图谱卷积,即利用图谱理论,通过设计基于图拉普拉斯矩阵的图谱滤波器完成卷积. Li等[20 ] 融合图谱卷积、Seq2seq体系与预定抽样等技术捕捉交通流的时空依赖性,获得了较高的预测准确率,但时间复杂度较高. Yu等[21 ] 将2个捕捉时间特征的门控卷积层与1个捕捉空间特征的图谱图卷积层结合,组装成时空卷积块进行交通流预测,打造了准确率更高的模型并降低了时间复杂度. 虽然两者均将卷积应用于图结构数据以捕获图的空间特征并取得了良好的效果,但图谱卷积不能完全适应交通网络的物理特性. 第二类图卷积方法是直接在图上定义卷积,从邻居结点中获取信息. Cui等[22 ] 使用自由流动速度计算自由流动可达矩阵,结合关系矩阵、邻接矩阵与自流矩阵,构造图卷积核捕获交通路网的物理特性. 然而,这种方法要求数据集提供传感器的邻接信息,对数据集信息的要求过多,缺乏普适性. ...
... 空间特征提取的传统方法主要为CNN,即将交通网络划分为一个个均等的网格,从而对每个网格进行卷积. 然而,这样的交通路网划分方式只考虑到了局部路网连接性,忽略了路网结构的全局连接性. 图谱卷积在提取交通数据空间特征的过程中,将路网作为一个整体,能够成功学得交通路网的全局连接性,然而此种图卷积不能有效挖掘交通路网独特的物理特性. 考虑提取全局连接的交通路网独特的物理特性,本研究参考Cui等[22 ] 提出的交通图卷积方法,使用基于自由流动可达矩阵的非图谱卷积方法对路网进行建模,该方法的详细介绍见第2.2.1节,网络结构见图1(d) . 基于自由流动可达矩阵的非图谱卷积定义如下: ...
1
... 近年来,由于图在众多领域(如社交网络、知识图谱等)强大的表现力,图神经网络(graph neural network,GNN)[18 ] 受到了越来越多的关注;GNN令人信服的性能和较高的可解释性,使其成为一种应用广泛的图结构分析方法[19 ] . 将图卷积运算扩展到图结构数据中可捕获交通路网信息,Li等[20 -27 ] 利用图卷积神经网络(graph convolutional networks,GCN)对交通流预测问题进行建模. ...
The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains
1
2013
... 图谱卷积(spectral graph convolution,SGC)[28 ] 为基于图的拉普拉斯算子的傅里叶域中的卷积运算,定义如下: ...
1
... Defferrard等[29 ] 提出了局部图谱卷积(localized spectral graph convolution,LSGC),其使用多项式滤波器,定义如下: ...