然而,网壳结构的动力特性和响应规律与多高层结构显著不同,传统静力推覆分析方法无法直接被用于网壳结构的地震响应评估. Xiang等[3]的研究表明,传统推覆方法采用基底剪力-顶点位移关系表征能力曲线,不适用于多维耦合显著的大跨度网格结构;并针对网壳结构提出了简化模型与方法[4],采用SRSS方法组合振型位移以确定荷载模式,对结构仅实施一次推覆分析,简化了计算步骤. 但采用该方法构造的固定荷载模式和等效质量物理意义不明确,且未考虑地震动输入特性,这可能导致结构变形模式与实际不符. Ohsaki等[5]针对大跨度结构提出了一种多模态线性组合推覆分析方法;虽然考虑了多维位移耦合,但该方法需要进行多次组合模态推覆分析,计算量较大,实用性不强.
为准确追踪结构的非线性行为,构建合理的能力曲线,Zhu等[6]提出了特征曲线和刚度的概念,用于分析网壳结构的静力稳定,以摆脱对特定节点和特征响应的依赖. 基于此概念,文献[7]提出了改进的模态分析方法,用以评估格构拱结构的地震响应,但该方法仍沿用双线性模型求解目标位移. Chopra等[8-9]提出,可在模态推覆分析(modal pushover analysis, MPA)方法中通过迭代计算确定合理的屈服点;但Gencturk等[10]指出,由于简化模型的屈服后刚度取决于结构达到极限位移时所耗散的能量,而非目标位移处实际耗散的能量,上述双线性模型求解得到的目标性能点精度不高. 由于网壳结构非线性较强,采用不同简化模型或同一简化模型计算得到的不同性能点的实际耗能结果差别较大[11],这降低了静力推覆方法的可靠性.
针对上述问题,本文提出振型刚度概念,通过模态推覆分析确定非线性能力曲线,并基于等效线性化迭代方法求解结构目标位移,从而建立振型刚度法. 将此方法运用于球面网壳和柱面网壳算例的地震反应分析,并将计算结果与时程分析法和传统模态推覆分析法的计算结果进行对比,以验证所提方法的适用性与效率.
1. 振型刚度法基本理论
1.1. 构建结构非线性单自由度体系
对于具有N个节点的网壳结构,在地震作用üg(t)激励下,其非线性动力微分方程为
式中:u(t)为地震作用下的结构动力位移,可写为u(t)=[ux(t),uy(t),uz(t),urotx(t),uroty(t),urotz(t)]T;M为质量矩阵,包括平动质量矩阵m和转动惯量矩阵Io;
将线性体系中的模态分解方法引入非线性分析中[7],假定非线性体系的动力位移可分解为
式中:ϕl和ql (t)为第l阶振型的振型向量和坐标.
将式(2)代入式(1),同时左乘ϕnT/(ϕnT·ϕn),并考虑到质量和经典阻尼的振型正交特性,可得
式中:ωn和ζn分别为第n阶振型频率和阻尼比,mn和Ln分别为振型质量和参量,可表示为
对于第n阶振型,qn(t)可写为qn(t)=ΓnDn(t),Dn(t)为振型位移. 将qn(t)=ΓnDn(t)代入式(3),并考虑到振型参与系数Γn=Ln/mn,第n阶振型动力方程可解耦为以Dn(t)为基本未知量的微分方程,即
令伪加速度为
用于表征恢复力Fs(t)对Dn(t)的贡献. 对于线弹性体系,易证An(t)=ωn2Dn(t),于是,式(5)可写为
式(7)即为与原体系第n阶振型对应的非线性单自由度体系的基本动力方程,该体系的动力特性(质量mn、阻尼比ζn、自振频率ωn、位移响应Dn)与原体系第n阶振型特性相同. 在此基础上,若给定An与Dn的关系,则可借助于能力谱法或时程分析法求得振型位移Dn,进而组合得到结构总响应.
1.2. 结构振型刚度
是否能够合理捕捉结构单自由度体系的非线性力学行为,决定了能否准确求解结构目标性能点. 鉴于此,本文采用模态推覆分析方法跟踪结构非线性力学性态.
根据推覆分析原理,对于线弹性体系,推覆荷载F和位移响应u存在如下关系:
式中:K为结构刚度矩阵.
在推覆加载过程中,第n阶振型所抵抗的荷载以及所产生的位移可分别表示为F和u在该阶振型方向上的投影fn*和un*:
线弹性体系第n阶振型刚度可定义为
对于非线性体系,第i荷载步的推覆荷载增量ΔFi和位移响应增量Δui关系由增量平衡方程给出:
式中:KT,i为结构切线刚度矩阵.
同样地,推覆荷载增量和位移响应增量在第n阶振型方向上的投影增量Δfn,i*和Δun,i*分别为
因此,非线性体系第n阶振型刚度定义为
由式(10)和(13)可知,振型刚度能够反映结构整体刚度矩阵的变化,且与刚度矩阵量纲一致,易于理解,便于计算. 更重要的是,不同于传统模态推覆分析方法(采用基底剪力和顶点位移构建能力曲线),采用振型刚度描述结构非线性特性能够考虑结构整体响应,避免片面地依赖于特定节点或构件的单一响应.
1.3. 单自由度体系能力曲线
根据模态推覆分析原理,对于线弹性体系,第n阶推覆过程中位移响应u和恢复力Fs为
根据文献[3]可知,传统模态推覆分析方法所采用的基底剪力-顶点位移关系无法考虑结构不同方向位移响应的耦联性,这是传统方法无法充分预估网壳结构非线性性能的原因之一. 鉴于此,本文提出在推覆分析时采用如下推覆荷载:
式中:χ为推覆荷载因子.
线弹性体系第n阶振型的刚度为
由式(17)可知,线弹性体系第n阶振型的刚度与本文提出的振型刚度在数值上相等. 相应地,伪加速度An和振型位移Dn为
当结构进入非线性阶段时,由于结构屈服后刚度退化,此时各阶振型已不同于线弹性阶段. 但根据模态推覆分析原理[8],通常仍假定非线性阶段结构振型与线弹性阶段相同,且保持不变. 这一假定使得推覆荷载模式(式(16))仍近似适用于非线性阶段. 于是,第n阶振型在第i荷载步的刚度为
由式(20)可知,非线性体系第n阶振型的刚度仍与本文提出的振型刚度在数值上近似相等,则伪加速度增量ΔAn,i和振型位移增量ΔDn,i可表示为
综上,提出的振型刚度可以在考虑结构整体响应的基础上,较为全面地跟踪结构非线性力学行为,进而构建与振型相关的能力曲线. 此外,通过振型刚度能够观察结构刚度的退化过程,有助于判断结构抗震性能的变化特征与规律. 借助基于振型刚度给出的能力曲线,通过求解式(7),可得到Dn,将各阶振型位移组合即可得到总响应.
1.4. 等效线性化迭代求解性能点方法
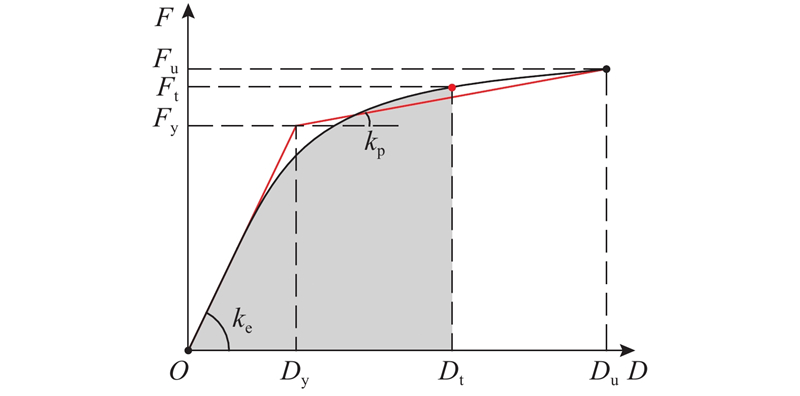
为便于求解性能点,通常需要对结构非线性能力曲线进行适当简化[12]. 基于等能量原则,能力曲线可按照下式等效为双线性模型:
式中:Fy和Dy分别为屈服荷载和屈服位移,Fu和Du分别为极限荷载和极限位移.
在弹性和弹塑性阶段,荷载和位移的关系为
式中:ke为弹性刚度,kp为屈服后刚度,Ft为目标荷载,Dt为目标位移. 据此,将非线性能力曲线简化为双线性曲线,如图1所示.
图 1
如前所述,由于上述简化模型在目标性能点处的耗能与实际不符,提出一种等效线性化迭代方法,用于快速准确地求解结构目标性能点. 基于等能量原则,将非线性体系等效为线性化体系,第i步迭代等效关系如下:
式中:ki和Di分别为第i迭代步等效线性刚度和目标位移.
对于初始迭代步,D1 = Du. 结合弹性位移反应谱,第i+1迭代步的目标位移Di+1为
式中:Ti为等效周期,
经过n次迭代后,Dn+1近似等于Dn,即满足:
此时,停止迭代,即迭代过程结束.
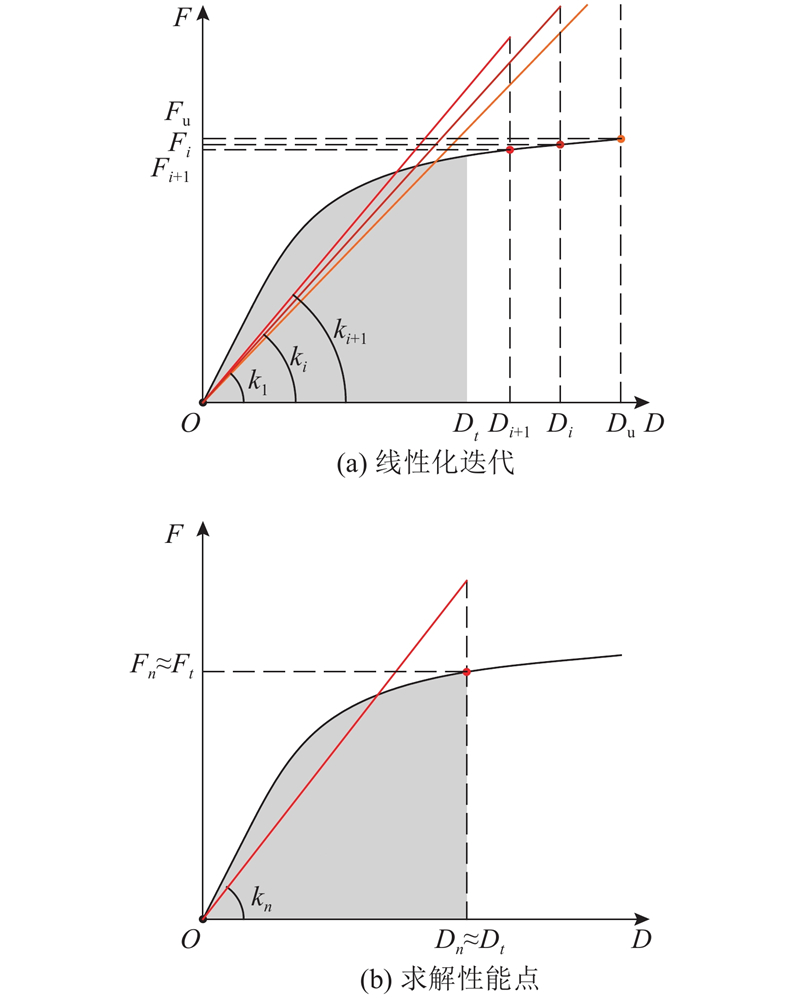
在等能量原则下,通过上述等效线性化迭代求解得到的目标位移Dn可逐渐逼近结构真实目标位移Dt,如图2所示. 实际计算结果表明,通常仅需要少数几次迭代求解即可收敛于Dn. 至此,通过等效线性化迭代方法,结合弹性反应谱,可计算得到更精确的结构目标位移.
图 2
图 2 能力曲线的等效线性化迭代模型
Fig.2 Equivalent linearized iteration model of capacity curve
1.5. 振型刚度法计算流程
本文提出的振型刚度法的计算步骤如下:
1) 建立结构有限元模型,并在进行数值分析时考虑材料和几何非线性;
2) 进行结构振型分析,遴选主振型,确定各阶主振型的荷载空间分布模式Mϕn;
3) 对结构进行非线性模态推覆分析,计算振型刚度并记录其变化过程;
4) 基于振型刚度,确定非线性能力曲线,建立对应各主振型的等效单自由度体系;
5) 借助于等效线性化迭代方法,将非线性能力曲线简化为等效模型,求解得到各单自由度体系的目标位移响应;
6) 采用CQC准则将各阶振型响应进行组合,从而得到结构总响应.
2. 算例分析
为分析振型刚度法的适用性及其计算效率,采用ANSYS和Matlab软件对2个典型网壳结构算例进行非线性推覆分析和时程分析,并以节点位移、单元最大应力、屈服杆件个数以及计算耗时作为对比参数,分析振型刚度法的误差和效率.
2.1. 网壳结构模型主要参数
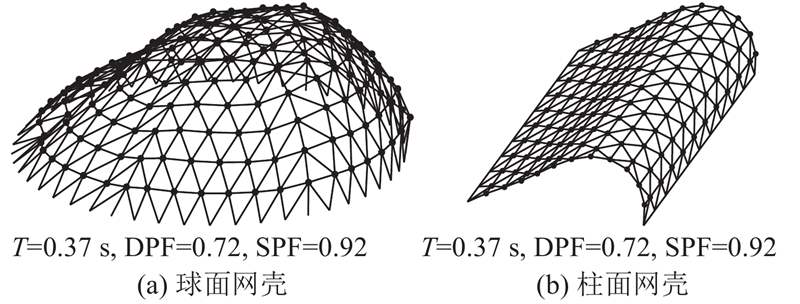
K6型单层球面网壳结构跨度为60 m,矢高为20 m,采用焊接球节点,底部为固定铰支座,如图3(a)所示. 三向型单层柱面网壳结构长度为30 m,跨度为15 m,矢高为5 m,采用焊接球节点,两纵边支承为固定铰支座,如图3(b)所示. 对网壳结构施加满跨均布荷载,其重力荷载代表值为1.5 kN/m2,并将其转化为节点集中质量以考虑其惯性力效应. 在满足静力设计要求下,结构构件均采用圆钢管,球面网壳主肋杆尺寸采用Φ140 mm × 5 mm,环杆和斜杆尺寸采用Φ121 mm × 4 mm,柱面网壳横杆、纵杆、斜杆尺寸分别采用Φ245 mm × 7 mm、Φ89 mm × 4 mm、Φ121 mm × 4 mm. 构件材料为Q235钢,采用双线性随动强化模型,弹性模量为206 GPa,屈服强度为235 MPa,屈服后弹性模量为0.8 GPa. 采用Rayleigh阻尼,阻尼比为0.02. 采用Beam189和Mass21模拟结构构件和节点集中质量. 为考虑杆件屈曲对结构抗震性能的影响,采用一杆两单元模型模拟杆件屈曲.
图 3
2.2. 主振型等效单自由度体系
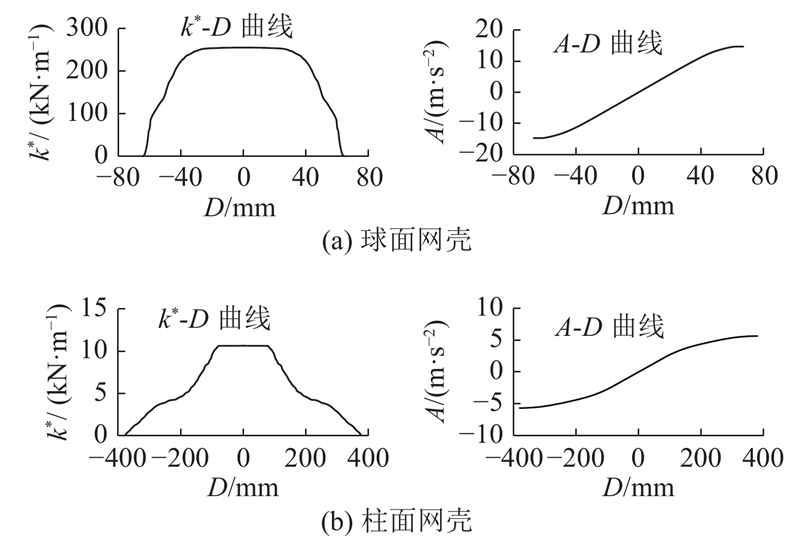
对网壳结构进行模态推覆分析,需要首先遴选结构主振型. 为兼顾主振型遴选的准确性和高效性,采用Luo等[13]提出的振型遴选阈值法识别主振型. 基于动力功参与系数(dynamic participation factor, DPF)和静力功参与系数(static participation factor, SPF),采用建议阈值δ = 0.10作为振型遴选标准,即参与系数大于0.10的振型为主振型. 如图4所示为基于阈值法遴选得到的主振型图. 对网壳结构按照主振型进行非线性模态推覆分析,得到等效单自由度体系振型刚度k*、伪加速度A和振型位移D的变化,进而可得各体系的能力曲线. 如图5所示为主振型等效单自由度体系的A-D曲线和k*-D曲线.
图 4
图 5
2.3. 地震动输入
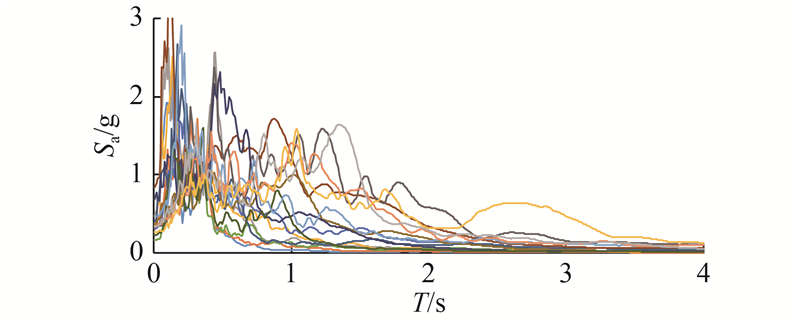
从日本K-NET强震数据库中选择过去15年来6次6.5级以上地震中共16条地震动记录的NS分量作为地震动输入,分别为硬土场地8条地震波(FS1~FS8)和软土场地8条地震波(SS1~SS8),其伪加速度反应谱如图6所示. Sa为谱加速度,T为周期, 为保证网壳结构在地震作用下进入弹塑性状态,在计算分析时,对于球面网壳,基本周期处的谱加速度调幅取为1.1 g;对于柱面网壳,其基本周期处的谱加速度调幅取为0.8 g.
图 6
2.4. 结构地震响应
2.4.1. 节点位移响应
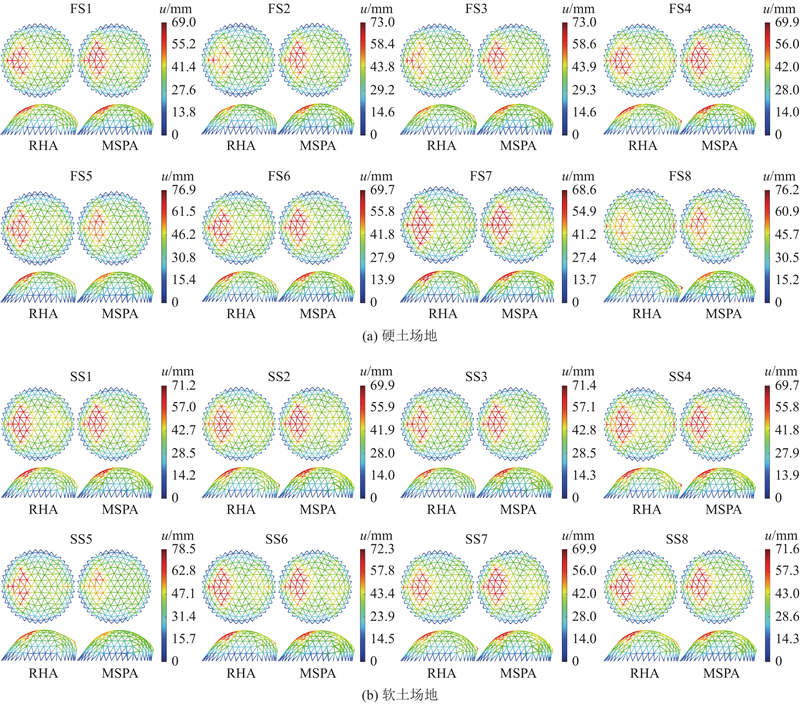
采用时程分析(response history analysis,RHA)法和振型刚度(MSPA)法计算得到网壳结构节点位移响应(u),如图7、8所示. 采用上述2种方法和传统模态推覆分析法(MPA)计算得到的节点位移的最大值计算结果如图9所示. 由图7、图8可见,结构位移响应与主振型形状相近,说明由阈值法遴选得到的主振型能够主导网壳结构地震响应. 对计算结果进行对比分析可知,采用振型刚度法计算得到的位移响应与时程分析法的计算结果比较接近且具有以下特征:1)两者计算结果变形模式基本一致,变形较大区域的分布位置相近,表明振型刚度法能有效预测结构变形及破坏趋势;2)与时程分析法的计算结果相比,振型刚度法在x方向位移计算值的平均误差δ为14.2%,绝大部分节点误差小于15%,z方向位移计算值的平均误差为18.5%,大部分节点误差小于20%,表明振型刚度法的位移计算精度满足工程要求.
图 7
图 7 球面网壳时程分析(RHA)法和振型刚度(MSPA)法的节点位移计算结果对比
Fig.7 Comparison of nodal displacements of spherical latticed shell calculated by response history analysis and (RHA) modal stiffness pushover analysis (MSPA) methods
图 8
图 8 柱面网壳时程分析法和振型刚度法节点位移计算结果对比
Fig.8 Comparison of nodal displacements of cylindrical latticed shell calculated by RHA and MSPA methods
图 9
图 9 网壳结构节点位移最大值计算结果对比
Fig.9 Comparison of maximum displacements of latticed shells
与传统模态推覆分析方法相比,本文方法具有如下优势:1)通过等效线性化迭代求解得到的结构目标性能点更为准确,且离散性较小;2) 振型刚度法在x和z方向位移的平均计算精度分别提高了17.1%和22.4%(传统方法大部分节点误差大于20%).
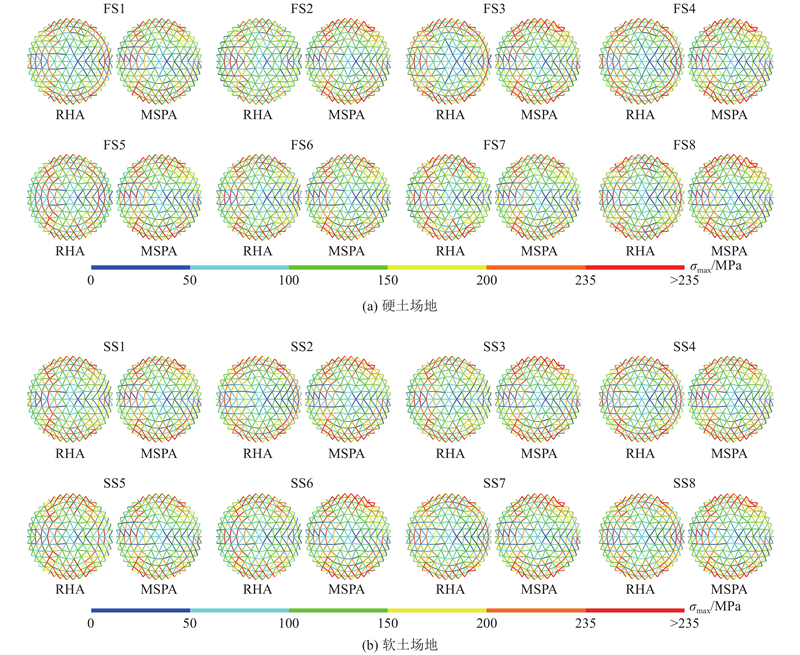
2.4.2. 单元应力响应
图 10
图 10 球面网壳时程分析法和振型刚度法单元应力计算结果对比
Fig.10 Comparison of element stresses of spherical latticed shell calculated by RHA and MSPA methods
图 11
图 11 柱面网壳时程分析法和振型刚度法单元应力计算结果对比
Fig.11 Comparison of element stresses of cylindrical latticed shell calculated by RHA and MSPA methods
2.4.3. 屈服杆件个数
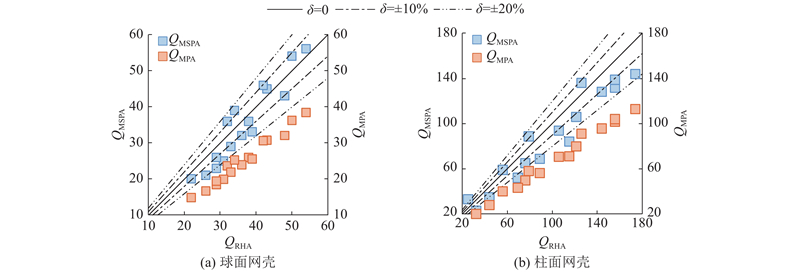
为进一步验证本文方法对于网壳结构塑性发展情况评估结果的准确性,提取网壳结构在16条地震动输入下的结构屈服杆件个数(Q),列于图12. 计算结果表明,虽然2种推覆分析方法得出的屈服杆件分布相近,但由于振型刚度法采用的非线性能力曲线更为合理,性能点计算更为准确,结构塑性发展更为充分,更接近真实情况,计算误差大部分控制在20%以内,表明振型刚度法能够有效预测结构屈服杆件分布与数量,可用于判断结构塑性发展情况. 而采用传统方法得到的能力曲线无法全面反映网壳结构的非线性效应,且性能点计算较为粗糙,低估了网壳结构塑性发展程度,计算误差普遍在20%以上,计算结果偏不安全. 本文仅考虑了一阶主振型,对屈服杆件个数的预测结果总体偏低;若考虑多阶振型,预测准确度可进一步提高.
图 12
图 12 网壳结构屈服杆件个数对比
Fig.12 Comparison for numbers of yielding members of latticed shells
2.5. 计算效率对比
3. 结 论
(1)振型刚度法物理意义明确,避免了传统推覆分析方法对特定节点和特征响应的依赖,能够考虑结构整体响应,从而合理描述结构非线性能力曲线;
(2)等效线性化迭代方法能够弥补现有等效模型实际耗能偏差大的缺点,进而提高了目标性能点的计算精度;
(3)研究结果表明,振型刚度法能够较好地预测网壳结构在地震作用下的结构形态和响应分布规律,且计算精度基本满足工程要求;
(4)与时程分析法相比,振型刚度法计算代价小,分析效率高,易于程序化.
参考文献
空间网格结构多维地震反应分析方法研究现状
[J].
State of the art of multi-dimensional seismic analysis techniques for spatial reticulated structures
[J].
A consecutive modal pushover procedure for estimating the seismic demands of tall buildings
[J].DOI:10.1016/j.engstruct.2008.10.009 [本文引用: 1]
An extended modal pushover procedure for estimating the in-plane seismic responses of latticed arches
[J].DOI:10.1016/j.soildyn.2016.12.005 [本文引用: 3]
空间结构弹塑性地震反应分析的简化模型与方法
[J].
Simplified model and procedure for elasto-plastic seismic response analysis of spatial structure
[J].
Prediction of inelastic seismic responses of arch-type long-span structures using a series of multimodal pushover analyses
[J].
Global stability analysis of spatial structures based on eigen-stiffness and structural eigen-curve
[J].DOI:10.1016/j.jcsr.2017.11.003 [本文引用: 1]
格构拱结构动力响应评估的改进模态推覆分析法
[J].
An improved modal pushover analysis procedure for estimating seismic responses of latticed arch
[J].
A modal pushover analysis procedure for estimating seismic demands for buildings
[J].
Evaluation of modal and FEMA pushover analyses: SAC buildings
[J].DOI:10.1193/1.1646390 [本文引用: 1]
Development and application of an advanced capacity spectrum method
[J].DOI:10.1016/j.engstruct.2008.05.008 [本文引用: 1]
能力曲线折线简化方法对比研究
[J].
Study on the comparison of different methods of simplifying capacity spectrum
[J].
A nonlinear analysis method for performance-based seismic design
[J].DOI:10.1193/1.1586128 [本文引用: 1]
Threshold value method and its application in dynamic analysis of spatial latticed structures
[J].DOI:10.1260/1369-4332.15.12.2215 [本文引用: 1]
基于设计反应谱的空间结构弹塑性地震反应分析方法
[J].
A procedure for elasto-plastic seismic response analysis of spatial structures based on design response spectra
[J].