采用影响线方法监测桥梁服役状态,可以基于少量传感器,最大程度反映结构刚度信息[6-7],如挠度或应力影响线[8-10]方法. 张延庆等[11]考虑转动弹性约束,建立铁路桥和曲线桥模型,采用位移影响线进行桥梁损伤诊断;Chen等[12]利用应力影响线对大跨桥梁进行损伤识别,通过算例验证所提方法的可行性. 此类方法均面临挠度、应变传感器不易布设与拆卸的问题,未考虑支座基础存在弹性变形或沉降的竖向弹性支承边界,也未考虑结构模型的不确定因素. Wang等[13]考虑抗弯刚度不确定性,采用跨中位移影响线进行主梁损伤识别,利用试验验证所提方法;Zhou等[14-15]认为转角影响线便于安装测试,并考虑初始模型不确定因素,提出基于转角影响线的桥梁损伤诊断方法,上述研究均未充分考虑桥梁模型非理想支承边界的影响.
针对上述问题,基于Euler-Bernoulli梁假定,考虑主梁截面参数的不确定性,建立带转动弹性约束与竖向弹性支承边界的主梁模型,推导模型的转角影响线解析式,提出考虑弹性约束支承与结构初始参数不确定性的主梁损伤诊断方法,结合解析证明与连续梁算例分析,研究测点位置、损伤位置与程度以及测试噪声对诊断结果的影响,开展边界等效子结构的室内试验,对所提方法进行试验验证.
1. 模型的建立
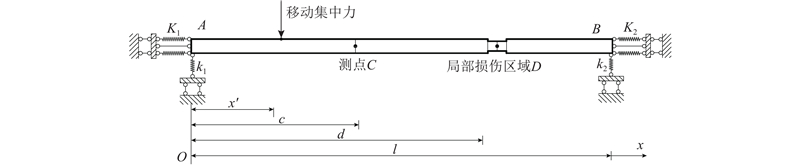
基于如图1所示的研究技术路线,建立弹性约束梁模型,如图2所示. 在梁端截面上、下缘设置一对水平平行弹簧实现弹性转动约束,其中刚度均为
图 1
图 1 基于弹性约束支承梁转角影响线的梁结构损伤诊断技术思路
Fig.1 Technical route of beam structure damage detection based on rotational-angle-influence-lines of elastic-constrained-support beam
图 2
图 2 含局部损伤的弹性约束反承梁模型
Fig.2 Elastic-constrained-support beam model with local damage
化简得到水平弹簧刚度与转动刚度关系:
在实测中,若A端为连续梁中支座,水平弹簧刚度
根据梁实际受拉区钢筋面积与实测受拉钢筋平均应变、实测受拉钢筋弹性模量可以计算梁A端转动约束刚度
对如图2所示的模型引入截面不确定性参数列
图 3
图 3 弹性约束支承梁的变形分解模型
Fig.3 Deformation analyze model of elastic-constrained-support beam
2. 转角影响线分析
在移动集中力影响线加载下,主梁刚体转角影响线即为
图 4
若竖向支承刚度无穷大,主梁刚体转动引起的
图 5
式中:
将式(7)~(11)代入式(6),求等效弯矩
由式(7)~(11)、(14)、(15)可知,
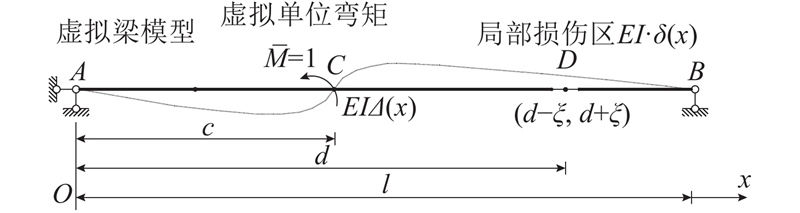
建立虚拟梁模型,如图6所示,图乘法求模型C截面转角.
图 6
式中:
建立虚拟梁模型各点弯矩表达式(式(17)). 将式(16)、(17)图乘,求截面C转角影响线表达式.
当
当
当
当
由于
3. 损伤诊断方法
分析损伤前、后
分析式(23)~(25)可知,损伤前、后的
提出基于弹性约束支承梁的转角影响线差曲率(rotational-angle influence lines difference curvature, RILDC)的损伤诊断指标:
根据式(28)~(29),当移动集中力位于损伤区外时,转角影响线差曲率为零;当移动集中力进入损伤区内时,转角影响线差曲率不为零,利用这一解析特征可以精确定位梁损伤位置. 当截面抗弯刚度确定时,即
4. 用于梁桥损伤的诊断实施方案
针对梁桥影响线测试中难以施加单轴集中荷载的问题,提出基于移动荷载叠减的3步加载方案,用于在短暂中断交通时快速诊断梁桥损伤.
1)选择2辆轴距相同且前后轴重比不同的两轴加载车. 每车前后、轴可以简化为相对位置相同、数值大小不同的集中力. 须注意,实际加载荷载效率既要考虑给与结构有效激励,又要考虑桥梁潜在损伤状况,限于本研究篇幅,在此不做深入研究.
2)利用两车分别对桥梁进行准静态影响线加载,要求2次影响线加载的桥梁虚拟加载节点相同,可以通过控制加载车辆移动速度一致实现,提取并记录2次转角响应数据.
3)求两车前轴等效集中力
5. 算例验证
5.1. 算例与损伤工况
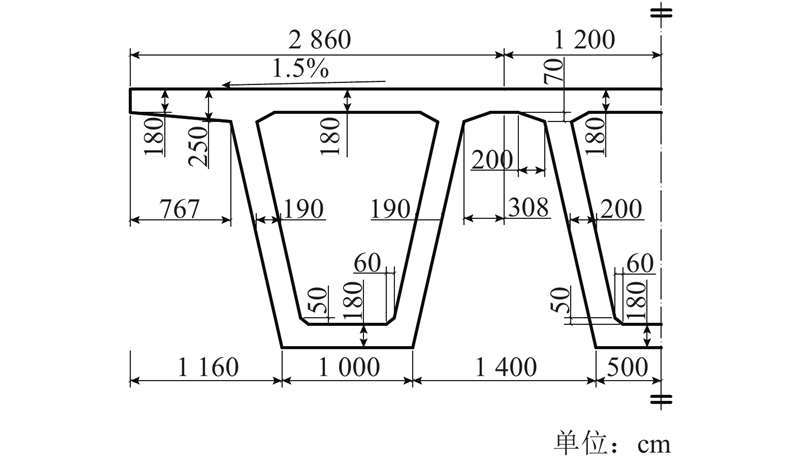
某三跨连续梁桥为3.0 m×40.0 m,设主梁单元长为0.5 m. 各跨每10.0 m布置一道横隔梁,支点处横隔梁截面为2.0 m×0.3 m,其余横隔梁截面为2.0 m×0.2 m,桥面铺装厚度为0.2 m. 主梁采用C50(E=3.45×107 kN/m2)混凝土,截面如图7所示,桥面板与横隔梁均采用C40(E=3.25×107 kN/m2)混凝土. 算例引入截面不确定性参数
图 7
表 1 算例损伤工况及测点布置
Tab.1
| 损伤工况 | 损伤位置 | DE | 测点位置 | 分析结果 |
| Ⅰ | G | 5%、10%、20%、30% | α | |
| Ⅱ | E | 5%、10%、20%、30% | α | |
| Ⅲ | F | 5%、10%、20%、30% | α | |
| Ⅳ | E、F | 5%、10%、20%、30% | α | |
| Ⅴ | E | 30% | α、α'、α'' | |
| Ⅵ | E | 30% | α、β、γ | |
| Ⅶ | E | 30%(噪声强度水平1%、3%、5%) | α’ | |
| Ⅷ | E | 5%、10%、20%(噪声强度水平5%) | α’ |
图 8
引入含噪声工况Ⅶ、Ⅷ检验RILDC的抗噪性,噪声以误差方式引入[15]:
式中:上标N表示含噪声信息,下标u表示损伤前,下标d表示损伤后,RAND (−1,1)为服从标准正态分布的随机数,μ为噪声强度水平.
5.2. 损伤诊断结果
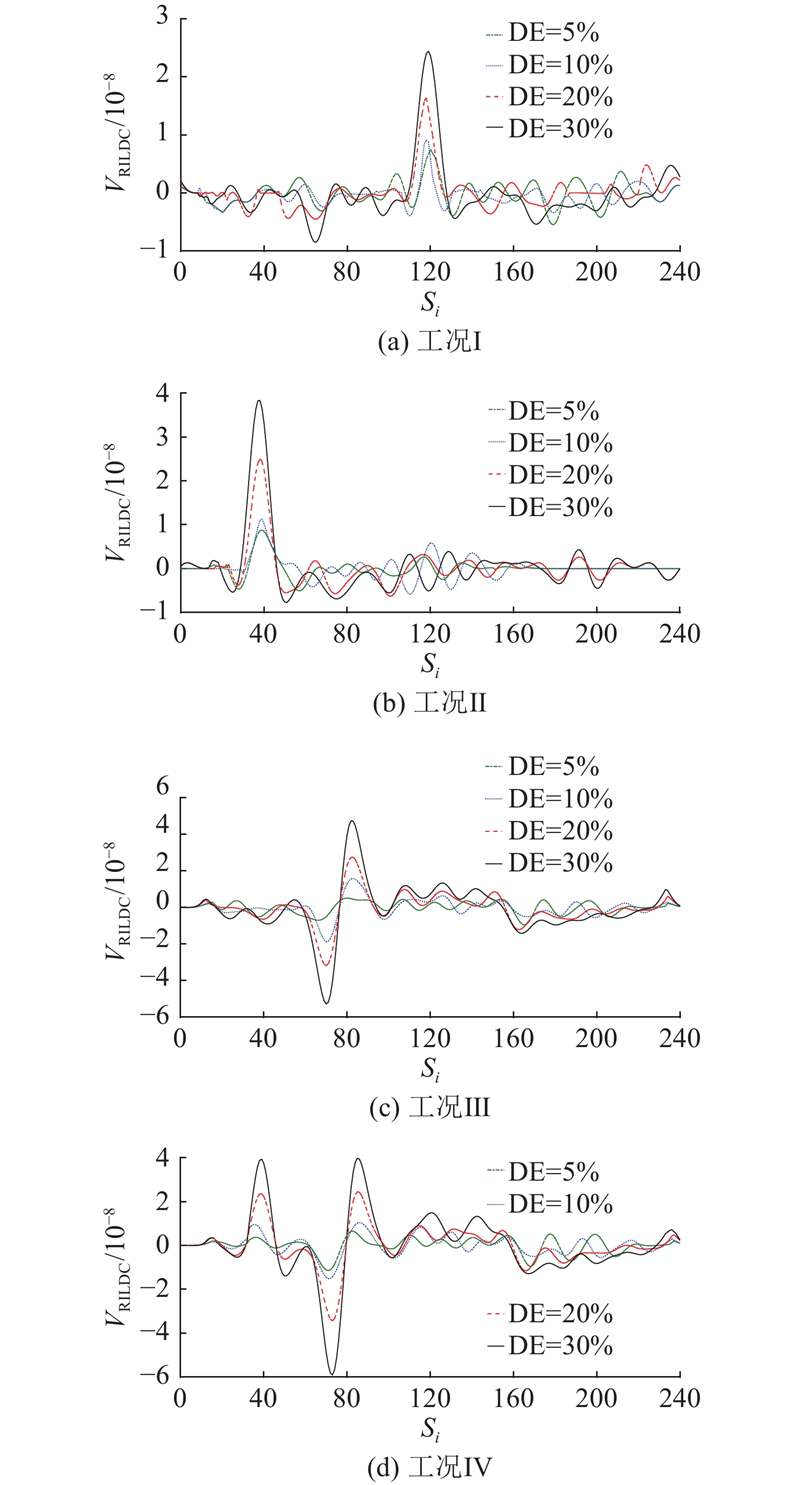
图 9
图 10
图 11
对比工况Ⅰ、Ⅱ诊断曲线,在相同程度损伤下,由于连续梁边支座转动约束刚度小于中跨,中跨损伤曲线幅值小于边跨. 可以看出,当梁端转动约束较弱时,RILDC的损伤诊断敏感性更好. 在截面初始抗弯刚度确定时,利用截面参数与工况Ⅰ中损伤30%的RILDC峰值,根据式(31)计算损伤程度,如表2所示. 损伤程度诊断相对误差为5.27%,表明根据RILDC计算损伤程度是可行的.
表 2 G点损伤程度的计算值
Tab.2
| RILDC | | | | | DE | ||
| 计算值/% | 模拟值/% | 相对误差/% | |||||
| 2.441 4×10−8 | 2. 392 3×1010 | 2 942 | 40 | 20 | 28.42 | 30.00 | 5.27 |
6. 试验验证
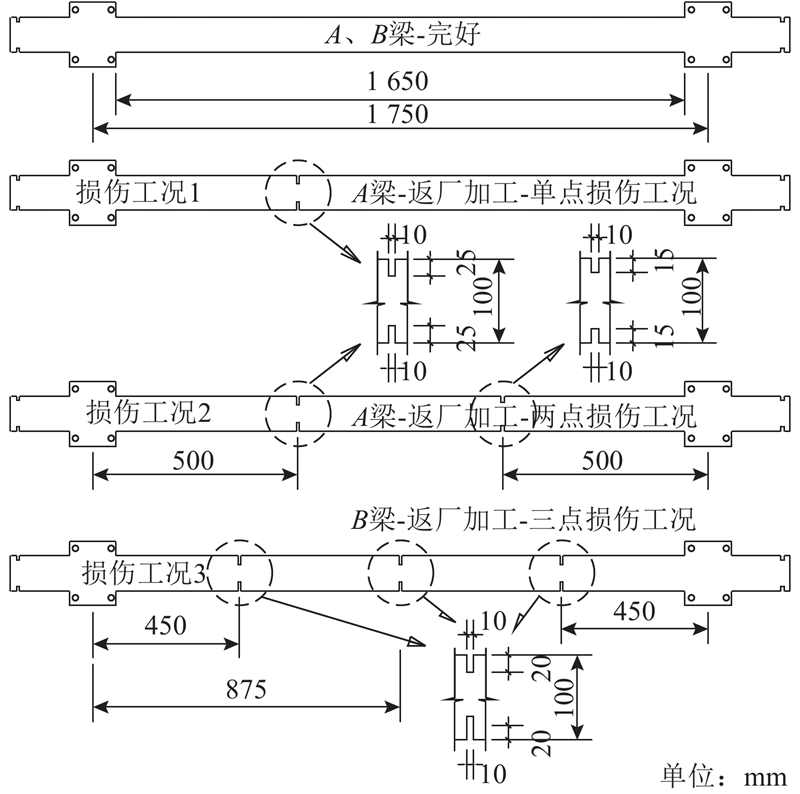
6.1. 试验准备及损伤工况
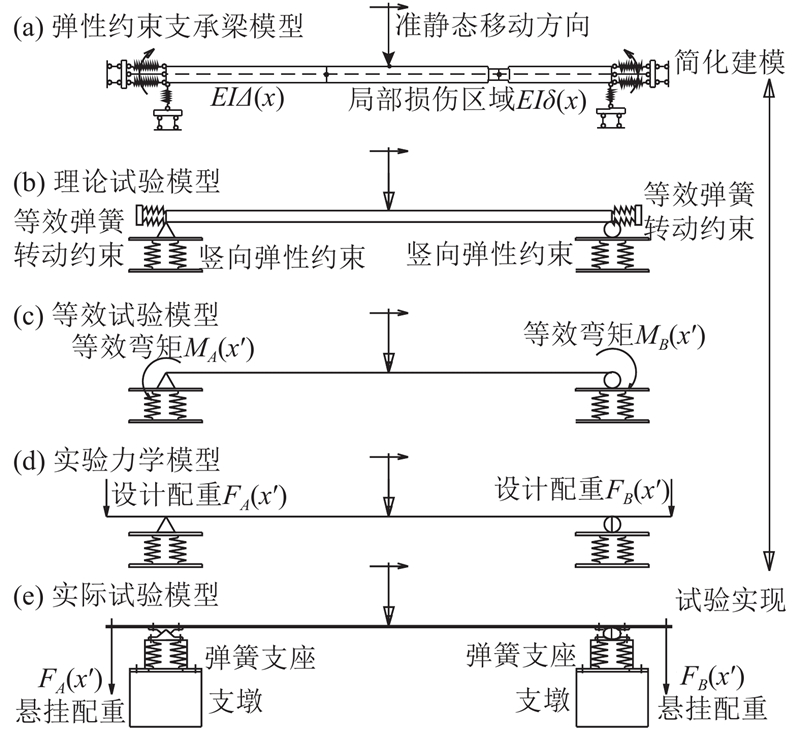
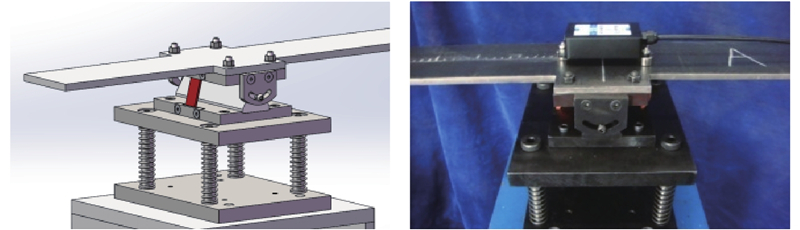
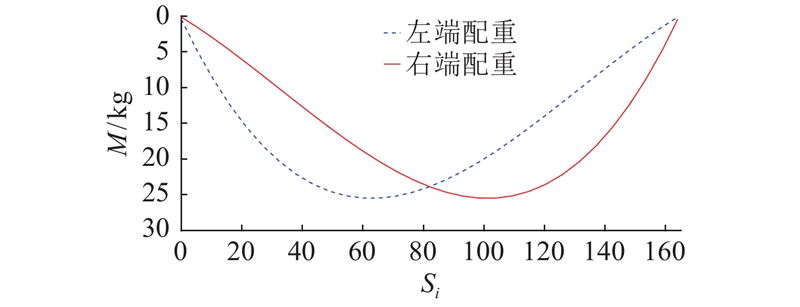
为了实现弹性约束支承,设计考虑边界等效子结构的试验模型,用于验证所提方法. 在梁悬臂外端进行等效配重,实现与三等跨连续梁中跨变形的等效状态. 配重悬挂用来等效连续梁中跨支座的负弯矩效应,模型实现思路如图12所示. 在简支支座下安装弹簧支承系统,如图13所示. 试件为2根钢扁梁:梁A、梁B. 试件梁因取材、加工引入的材料离散性与尺寸随机性,作为结构初始不确定性参数. 沿梁轴线绘制刻度以定位移动力,试验加载采用滚轴加载,集中力为299.8 N. 模型及安装如图14所示. 等效配重通过支座负弯矩影响线离散数据除以配重点与相邻支座支点间力臂距离得到,移动荷载每前进一加载步,梁两端进行一次配重调整,如此往复至加载完成. 配重影响线如图15所示. 图中,M为两端配重质量.
图 12
图 12 子结构试验模型的实现方法与建模思路
Fig.12 Implementation approach and modeling principle of substructure test model
图 13
图 13 竖向弹性支座设计图与倾角传感器安装
Fig.13 Vertical-elastic bearing design and sensor installation
图 14
图 15
图 16
图 17
6.2. 损伤诊断试验研究
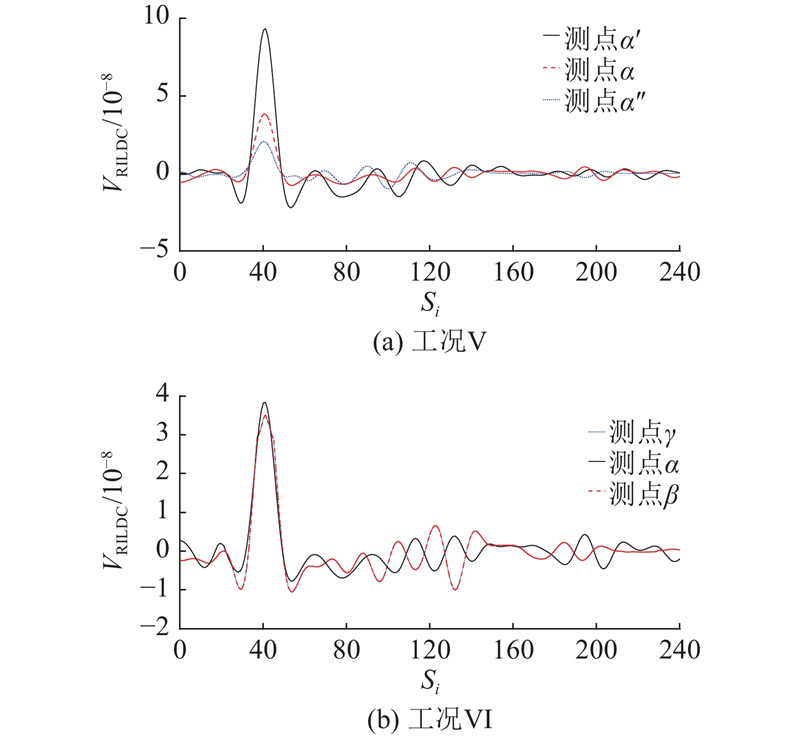
对3个损伤工况进行诊断试验研究. 试验提取无损A、B梁端的转角响应,经滑动平均后得到无损模型转角影响线基准曲线(baseline),如图18所示. 图中,θA、θB分别为梁A、B端的实测转角响应.
图 18
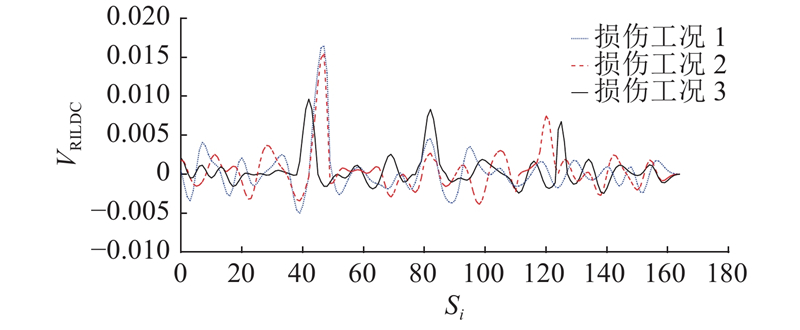
提取A、B试验梁转角影响线响应,经滑动平均得到平滑曲线,如图19所示,求解各损伤工况下RILDC. 受测试噪声影响,指标曲线存在波动,但不难发现,RILDC可以定位损伤,根据损伤工况2结果,RILDC可以定性损伤程度. 损伤工况3结果表明,RILDC对诊断测点附件局部损伤敏感性更高. 通过式(31)计算损伤工况1切口处损伤程度为37.5%,相对误差约为25%.
图 19
图 19 基于RILDC的损伤诊断试验结果
Fig.19 Experiment results of damage detection based on RILDC
7. 结 论
(1)提出弹性约束支承梁的力学模型,推导得到其转角影响线解析表达式,开展边界等效子结构的模型试验.
(2)基于弹性约束支承梁转角影响线可以有效定位、定量梁结构损伤,相比解析解,算例和试验的损伤程度诊断相对误差分别为5.27%、25.00%,指标的抗噪性较好;基于转角影响线指标,可以诊断连续梁桥得测点所在邻跨的损伤,且当梁端转动约束较弱时,损伤诊断敏感性较高.
(3)基于转角影响线的损伤诊断方法,可以解决基于挠度与应变影响线的损伤诊断应用中面临的传感器不易安装问题. 本研究所提出的诊断实施方案可以实现梁桥损伤的快速诊断,为既有梁桥的转角影响线分析与损伤快速诊断实施提供借鉴与参考.
(4)实际桥梁为多个单梁联合受力的复杂空间结构,所提方法在桥梁实际损伤识别中的应用效果有待进一步研究.
参考文献
Developmentsandprospects of long-span high-speed railway bridge technologies in China
[J].DOI:10.1016/j.eng.2017.11.001 [本文引用: 1]
Non-linear vibrations of a beam with non-ideal boundary conditions and uncertainties-modeling, numerical simulations and experiments
[J].DOI:10.1016/j.ymssp.2018.03.013
一类非理想杆端约束下的转角位移方程
[J].DOI:10.3969/j.issn.1000-4750.2004.03.037 [本文引用: 1]
Slope-deflection equation with a type of non-ideal constraints at end of beam
[J].DOI:10.3969/j.issn.1000-4750.2004.03.037 [本文引用: 1]
基于位移影响线曲率的小半径弯桥损伤识别
[J].
Damage identification of small-radius curved bridge based on curvature of displacement influence line
[J].
混凝土随机损伤力学研究进展
[J].
Recent developments on stochastic damage mechanics for concrete
[J].
Moving train loads identification on a continuous steel truss girder by using dynamic displacement influence line method
[J].DOI:10.1007/s13296-011-2001-7 [本文引用: 1]
Moving load-induced response of damaged beam and its application in damage localization
[J].DOI:10.1177/1077546314564587 [本文引用: 1]
Damage detection of beam structures using quasi-static moving load induced displacement response
[J].DOI:10.1016/j.engstruct.2017.05.009 [本文引用: 1]
考虑边界非理想的铁路桥梁挠度影响线分析与损伤识别
[J].
Influence line analysis and damage detection of railway bridge with non-ideal boundaries
[J].
Locate damage in long-span bridges based on stress influence lines and information fusion technique
[J].DOI:10.1260/1369-4332.17.8.1089 [本文引用: 1]
存在局部损伤时转动弹性支承铁路梁桥的位移影响线分析
[J].DOI:10.3969/j.issn.1001-8360.2016.02.016 [本文引用: 2]
Analysis of displacement influence line for railwaybridge with rotatable elastic support and local damage
[J].DOI:10.3969/j.issn.1001-8360.2016.02.016 [本文引用: 2]
Damage detection in long suspension bridges using stress influence lines
[J].DOI:10.1061/(ASCE)BE.1943-5592.0000681 [本文引用: 1]
Damage detection of bridges by using displacement data of two symmetrical points
[J].DOI:10.1061/(ASCE)CF.1943-5509.0000240 [本文引用: 1]
Damage identification of simply supported bridge based on rotational angle influence lines method
[J].DOI:10.1007/s12209-018-0135-9 [本文引用: 2]
Damage detection for simply supported bridge with bending stiffness fuzzy consideration
[J].DOI:10.1007/s12204-018-1939-4 [本文引用: 3]