浙江大学学报(工学版)

浙江大学学报(工学版), 2020, 54(5): 851-857 doi: 10.3785/j.issn.1008-973X.2020.05.002

土木工程、交通工程

超高韧性水泥基复合材料的波传播试验研究

李庆华,, 舒程岚青

Experimental study on stress wave propagation in ultra high toughness cementitious composites

LI Qing-hua,, SHU Cheng-lan-qing

收稿日期: 2019-04-22  

Received: 2019-04-22  

作者简介 About authors

李庆华（1981―），女，教授，从事新材料结构、防护力学研究.orcid.org/0000-0003-2694-1936.E-mail：liqinghua@zju.edu.cn , E-mail：liqinghua@zju.edu.cn

摘要

为了研究超高韧性水泥基复合材料（UHTCC）中应力波的传播特性，采用Hopkinson杆加载UHTCC试件，测得UHTCC在0.2、0.3、0.4、0.5 MPa冲击气压下的应力波信号. 通过对比入射杆波形，验证相同加载条件下加载波形的一致性. 分别采用两点法和峰值法计算每种冲击气压下UHTCC中应力波的波速，结果显示，两点法适用性较广，计算结果较稳定，利用峰值法测波速则需要入射杆和试件波阻抗相近. 计算结果显示，UHTCC中应力波波速、衰减系数随冲击气压均无明显变化，平均波速为3.060 km/s，平均衰减系数为2.777 m−1. 可以利用朱-王-唐本构模型参数表达材料中应力波的波速和衰减，也可以利用实测的波速和衰减系数将UHTCC的朱-王-唐冲击本构模型表示为只含单个准静态参数的方程，从而提供通过试验直接确定UHTCC动态本构的方法.

关键词： 应力波 ; 波速 ; 超高韧性水泥基复合材料（UHTCC） ; 衰减 ; 朱-王-唐本构模型

Abstract

The ultra high toughness cementitious composite (UHTCC) specimens were loaded with Hopkinson bar, and the stress wave signals in UHTCC under impact pressure of 0.2, 0.3, 0.4, 0.5 MPa were measured, in order to study the propagation characteristics of stress waves in UHTCC. The consistency of the loading waveforms under the same loading conditions was verified by comparing the incident bar waveforms. The stress wave speeds in UHTCC under different impact pressures were calculated by two methods, i.e. two point method and peak value method. Results show that the two point method is more applicable and the calculation results are relatively stable. However, the peak value method requires similar wave impedance of the incident bar and the specimen. Calculation results show that the stress wave speed and attenuation coefficient in UHTCC do not change significantly with the impact pressure, and the average wave speed is 3.060 km/s, as well as the average attenuation coefficient is 2.775 m−1. The wave speed and attenuation of stress waves in material can be expressed by parameters of Zhu-Wang-Tang constitutive model. Correspondingly, the measured wave speed and attenuation coefficient can represent the Zhu-Wang-Tang impact constitutive model of UHTCC as an equation with a single quasi-static parameter. An experimental method to determine the dynamic constitutive of UHTCC directly is provided.

Keywords： stress wave ; wave speed ; ultra high toughness cementitious composite (UHTCC) ; attenuation ; Zhu-Wang-Tang constitutive model

PDF (954KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李庆华, 舒程岚青. 超高韧性水泥基复合材料的波传播试验研究. 浙江大学学报(工学版)[J], 2020, 54(5): 851-857 doi:10.3785/j.issn.1008-973X.2020.05.002

LI Qing-hua, SHU Cheng-lan-qing. Experimental study on stress wave propagation in ultra high toughness cementitious composites. Journal of Zhejiang University(Engineering Science)[J], 2020, 54(5): 851-857 doi:10.3785/j.issn.1008-973X.2020.05.002

在冲击、爆炸等高速荷载作用下，材料受荷局部的应力、应变、质点速度等在短时间内发生剧烈变化，这种剧烈扰动向外扩散，就会形成应力波[1]. 应力波的传播导致材料中的应力、应变处于动态变化中，应力波反射叠加之后还可能使材料发生背面断裂[2]，与静态荷载下材料的破坏方式和破坏过程完全不同. 研究材料在高速荷载下的性能和破坏模式，首先须解决应力波在材料中如何传播的问题.

关于波传播的试验研究主要有2个方向：1）通过测量的波传播信号分析计算材料中的应力波传播参数，如波速、衰减系数、峰值等；2）通过波传播试验反推材料的动态本构.

在波传播参数方面，Bacon[3]定义复数形式的传播系数来描述黏弹性材料中应力波的衰减和弥散，并给出该传播系数的测定方法，但该方法计算过程较复杂. Siviour[4]利用Hopkinson压杆加载有机玻璃，计算波速和弹性模量，但实验采用间接测量方式，不能考虑试件中应力波的衰减. Ju等[5]采用活性粉末混凝土（reactive powder concrete，RPC）和聚乙烯纤维模拟天然砂岩，通过分离式Hopkinson压杆（split Hopkinson pressure bar，SHPB）研究不同孔隙体积分数对反射波峰值和耗能的影响，提出冲击荷载下孔隙的2种响应模式，但这种试验方法无法测得材料中的应力波信号. 胡时胜等[6]利用Hopkinson杆层裂试验装置，通过直接在试件表面黏贴应变片测得C30混凝土中应力波的波速和衰减系数. 赖建中等[7]采用与胡时胜等[6]相似的试验方法，测得RPC中的应力波传播信号，讨论冲击气压与衰减的关系. 综合以上研究可以发现，Hopkinson杆是波传播试验中常用的加载装置，因为这种加载装置通过波形加载，避免直接撞击和爆炸的加载方式带来的不确定性[8]. 此外，通过在试件表面黏贴应变片，可以获得材料中的应力波传播信号，进而分析材料中应力波的波速、衰减、峰值等.

在材料动态本构方面，学者们基于试验和模拟结果提出多种混凝土的本构模型[9-11]. 其中，国内学者提出的朱-王-唐（Z-W-T）本构模型[9]由于能够较好地描述材料在动、静态荷载下的非线性黏弹性行为，应用较广泛[12-13]. 目前获取材料的Z-W-T本构的主要方式是将实测应力应变曲线按Z-W-T本构方程直接拟合，通过这种方式可以直接得到材料的完整Z-W-T本构方程，且拟合效果通常较好，说明Z-W-T本构适用于描述混凝土[14]、超高性能水泥基材料（ultra-high performance cementitious composite，UHPCC）[15]、聚丙烯纤维增强混凝土（polypropylene fiber reinforced concrete，PFRC）[16]等水泥基材料，但这种方式得到的本构方程的适用范围有待考究.

超高韧性水泥基复合材料（ultra high toughness cementitious composite，UHTCC）[17-18]，也称工程水泥基复合材料（engineered cementitious composite，ECC）[19]、应变硬化水泥基材料（strain hardening cement-based composite，SHCC）[20]、高性能纤维增强水泥基材料（ultra high performance fiber reinforced cementitious composite，UHPFRCC）[21]等，通过掺入少量短纤维改善材料的微观结构[22]，使其具有独特的应变硬化和韧性特征[23-25]. 在掺入适量比例的纳米SiO2和钢纤维后，UHTCC在保持原有裂缝控制能力的基础上，抗压强度提升到50 MPa以上[26]，能够承受更高强度的荷载，适用于防护工程. 落锤冲击试验[27]和SHPB试验[28]都表明UHTCC具有较好的冲击韧性，冲击耗能较混凝土、钢纤维混凝土优势明显，因此，UHTCC具有可观的防护工程应用前景. 不过，作为防护工程的材料，UHTCC不仅须具备较高的抗压强度，其在冲击、爆炸、撞击等动态荷载下的响应更须明确，即须明确应力波在UHTCC材料中的传播特性.

本研究通过试验研究UHTCC的应力波传播特性. 采用Hopkinson杆加载，通过在试件表面黏贴多组应变片，获取试件上不同位置的应力波信号. 由实测信号推算UHTCC中应力波的传播参数，并对比2种波速计算方法的适用性. 探讨通过试验测试UHTCC材料的朱-王-唐冲击本构参数的方法.

1. 试验概况

1.1. 试件制备

本试验试件为细长圆柱体，试件长为1 000 mm、直径为76 mm. 采用精密机械加工的不锈钢模具浇筑而成. UHTCC的原材料包括：52.5水泥、粉煤灰、精细砂、纳米二氧化硅、钢纤维、聚乙烯醇（polyvinyl alcohol，PVA）纤维、高效减水剂、水. 试验材料配比如表1所示. 表中，ρB为质量浓度.

表 1   UHTCC材料配合比

Tab.1  Mix proportions of UHTCC

材料 ρB/(kg·m−3） 材料 ρB/(kg·m−3）
胶凝材料 1 265.0 微型钢纤维 78.0
水 448.0 PVA 28.7
砂 370.3 减水剂 7.3
纳米SiO2 40.0 − −

新窗口打开| 下载CSV


按表1的比例称量各种原材料，将所有干料加入搅拌机，干拌1 min；加入水和减水剂，搅拌至浆体提起成流状；在搅拌状态下，向浆体中撒入PVA纤维和钢纤维，搅拌至纤维完全分散. 将搅拌好的UHTCC浆体分3次装入模具，每次加入均振动1 min. 在浇筑完成后用塑料膜封口，在室温中放置24 h后拆模，置于标准养护室内养护28 d. 在养护结束后，将试件上、下两端面打磨平整. 测量并记录每根试件的长度和重量，试件密度取平均值为1 793.8 kg/m3. 另外，测量本试验材料56 d龄期的立方体抗压强度，为50.22 MPa.

1.2. 试验装置

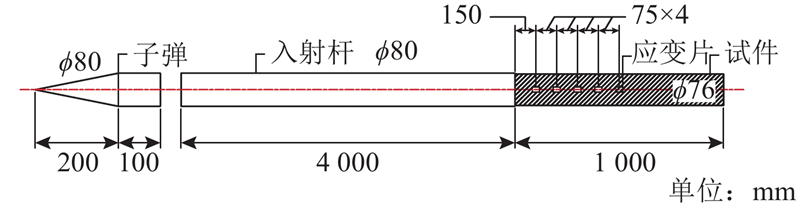
本试验采用直径为80 mm的Hopkinson杆作为加载装置，试验装置如图1所示. 撞击杆为变截面短杆，以产生短历时的三角形波. 入射杆和试件表面均布置应变片. 入射杆在固定位置处布置1组2个应变片，用于记录入射杆波形信号. 试件上应变片的位置与撞击端的距离L分别为150、225、300、375、450 mm. 试验采用冲击气压控制加载，选取0.2、0.3、0.4、0.5 MPa这4种冲击气压.

图 1

新窗口打开| 下载原图ZIP| 生成PPT

图 1   UHTCC应力波传播试验装置

Fig.1   Experimental device of stress wave propagation in UHTCC


2. 试验结果

2.1. 加载波形一致性验证

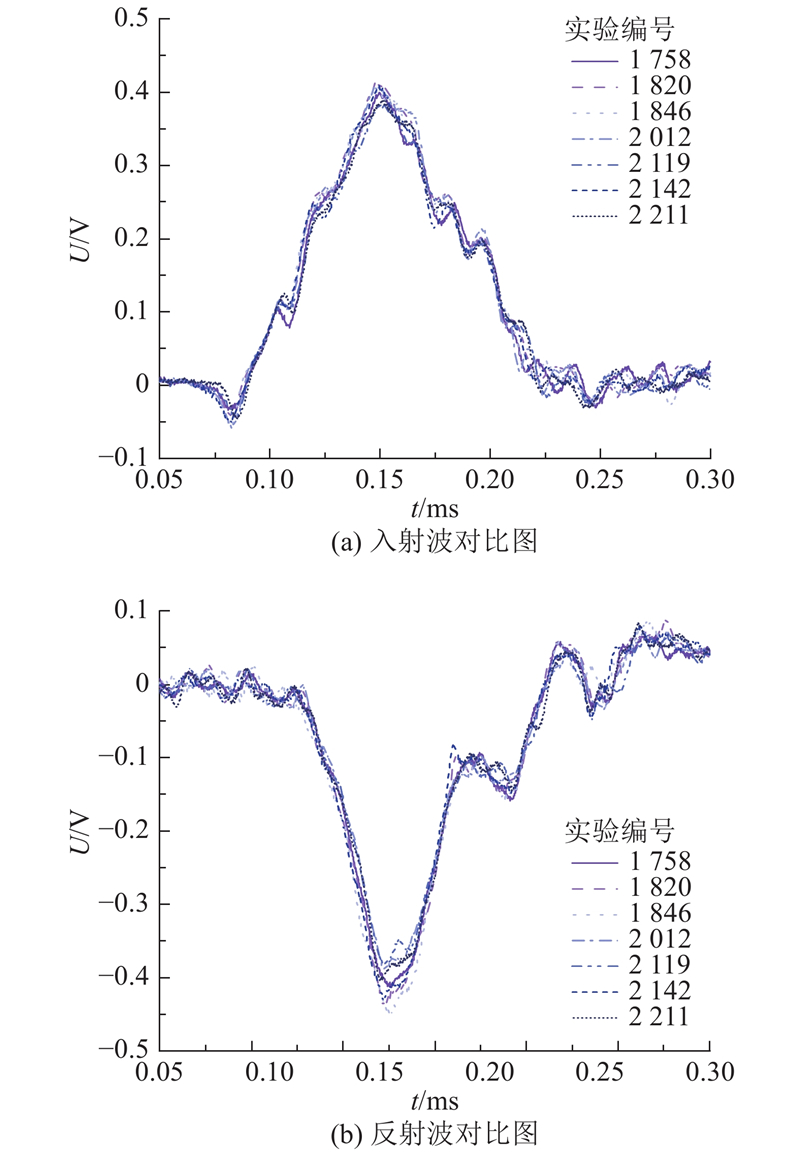
为了验证本试验装置加载波形的一致性，在相同冲击气压下，对比多次试验中入射杆上的入射波信号和反射波信号，如图2所示，图中， t为时间，U为电压. 图2列出在0.2 MPa冲击气压下，7次波传播试验的入射波和反射波信号，每次试验均为初次冲击，图例中数字为试验编号. 由图2（a）可以看出，7次试验的入射波波形起伏基本一致，没有明显偏差，峰值相差不超过0.03 V，波宽一致，可以认为本试验装置在子弹撞击入射杆时产生的入射波形一致性较高. 由图2（b）可以看出，入射杆上的反射波波形基本一致，峰值略有差异，最大峰值差约为0.06 V，占最大峰值的13%，反射波的一致性略差于入射波. 这与入射杆和试件接触面的微小差异有关，因为每次试验都须更换试件，试件表面的平整度、试件与入射杆的对中、试件与入射杆接触面真空脂的厚薄均会影响接触面的情况，从而导致入射杆上反射波峰值的差异. 反射波峰值差异扣除入射波峰值差异后余下部分才是入射杆和试件接触面情况引起的差异，因此，接触面引起的峰值差异约占最大峰值的6.5%，误差范围较小. 综上所述，本试验装置产生的加载波形一致性较好.

图 2

新窗口打开| 下载原图ZIP| 生成PPT

图 2   入射杆实测波形对比

Fig.2   Comparison of measured waveforms on incident bar


2.2. UHTCC中的实测波形图

在0.2、0.3、0.4、0.5 MPa冲击气压下，实测的典型波形曲线如图3所示. 各组气压下的实测波形均为近似三角形，且试件上不同位置的波形均保持完整，维持三角波形状. 随着冲击气压的增大，试件中应力波的峰值逐渐上升.

图 3

新窗口打开| 下载原图ZIP| 生成PPT

图 3   不同冲击气压下的典型波形图

Fig.3   Waveforms under different impact pressures


3. UHTCC中的应力波波速和峰值衰减

3.1. 试件上两点测波速

第1种测波速的方法是在试件上取2点进行测量，为了简化表达，称之为两点法. 两点法测波速的表达式为

$C = \Delta L/\Delta t .$

式中：C为材料中的应力波波速，∆L为2个测量点之间的距离，∆t为2个测量点之间应力波传播用时.

式（1）中∆t的取值对波速计算影响最大. 由于波峰相对于波的起始点更易精准判断，为了准确测量∆t，取波峰到达2个应变片的时间差作为∆t. 波速较快，若测量点间距过近，则∆t过小，微小的测量误差就可能引起较大的波速测量误差，因此，在测量波速时尽量选取相距较远的2个应变片作为测量点，具体波速计算数据如表2所示.表中，I为冲击气压，C0为平均波速. 除了编号为15的试件因5号应变片出现异常不能作为测点，其他试件均采用1号和5号应变片作为测量点. 按冲击气压分类，列出每一个档次的冲击气压下波速的平均值，可见波速随冲击气压的波动较小，考虑到试验中不可避免的测量误差，可以认为在本次试验中波速不变，平均波速为3.060 km/s.

表 2   两点法得到的波速计算表

Tab.2  Wave velocity calculation table calculated by two point method

I/MPa ∆L/mm ∆t/μs C/(km·s−1) C0/(km·s−1)
0.18 300 97.8 3.067 3.074
0.20 300 102.4 2.930
0.25 300 93.0 3.226
0.30 300 102.6 2.924 3.037
0.30 300 94.8 3.165
0.30 300 102.4 2.930
0.30 300 105.6 2.841
0.33 300 90.2 3.326
0.40 300 102.2 2.935 3.076
0.40 300 86.6 3.464
0.40 300 104.4 2.874
0.40 300 99.0 3.030
0.45 300 96.4 3.112 3.062
0.50 300 97.2 3.086
0.50 225 66.2 3.399
0.50 300 105.2 2.852
0.50 300 104.8 2.863

新窗口打开| 下载CSV


3.2. 入射杆波形测波速

由计算出的波速和测得的单个波的历时可以计算出加载应力波的波长约为480 mm，试件直径为76 mm，则试件直径与波长比值约为0.16，当试件直径远小于波长时，满足一维应力波假定[29]. 根据一维应力波理论可知，试验材料的波速还可以由入射杆上的应变信号计算. 应力波在不同波阻抗的介质中传播时，会在介质界面发生反射和透射. 反射波峰值可以由入射波峰值及2种介质的波阻抗表示：

${\sigma _{\rm{R}}}{\rm{ = }}\frac{{A_2 \rho_2 C_2 - A_1 \rho_1 C_1 }}{{A_2 \rho_2 C_2 + A_1 \rho_1 C_1 }}{\sigma _{\rm{I}}}.$

式中：σR为反射波应力；σI为入射波应力；A1ρ1C1为介质1的波阻抗，A1、ρ1、C1分别为入射杆横截面积、密度和波速；A2ρ2C2为介质2的波阻抗，A2、ρ2、C2分别为试件的横截面积、密度和波速.

根据式（2）可以将C2表示为

$C_2 {\rm{ = }}\frac{{A_1 \rho_1 C_1 ({\sigma _{\rm{I}}} + {\sigma _{\rm{R}}})}}{{A_2 \rho_2 ({\sigma _{\rm{I}}} - {\sigma _{\rm{R}}})}}.$

在本试验中，A1、ρ1、C1、 A2、ρ2均为已知量；σR、σI是待测值，可以取入射杆上入射波和反射波的应力峰值.

入射杆材料屈服强度高，在本试验气压下入射杆仍处于弹性状态，所以入射杆应力峰值等于相应的应变峰值乘以入射杆材料的弹性模量. 有

${\sigma _{\rm{I}}}/{\varepsilon _{\rm{I}}} = {\sigma _{\rm{R}}}/{\varepsilon _{\rm{R}}} = {E_1},$

则

$\frac{{{\sigma _{\rm{I}}} + {\sigma _{\rm{R}}}}}{{{\sigma _{\rm{I}}} - {\sigma _{\rm{R}}}}} = \frac{{{\varepsilon _{\rm{I}}} + {\varepsilon _{\rm{R}}}}}{{{\varepsilon _{\rm{I}}} - {\varepsilon _{\rm{R}}}}}.$

式中：εI为入射波应变峰值，εR为反射波应变峰值，E1为入射杆弹性模量.

由此，C2可以由入射杆上的应变表示：

${C_2} = \frac{{{A_1}{\rho _1}{C_1}}}{{{A_2}{\rho _2}}} \times \frac{{{\varepsilon _{\rm{I}}} + {\varepsilon _{\rm{R}}}}}{{{\varepsilon _{\rm{I}}} - {\varepsilon _{\rm{R}}}}}.$

试件中的波速可以通过在入射杆上黏贴一个应变片，取应变信号的最大值和最小值计算得出.

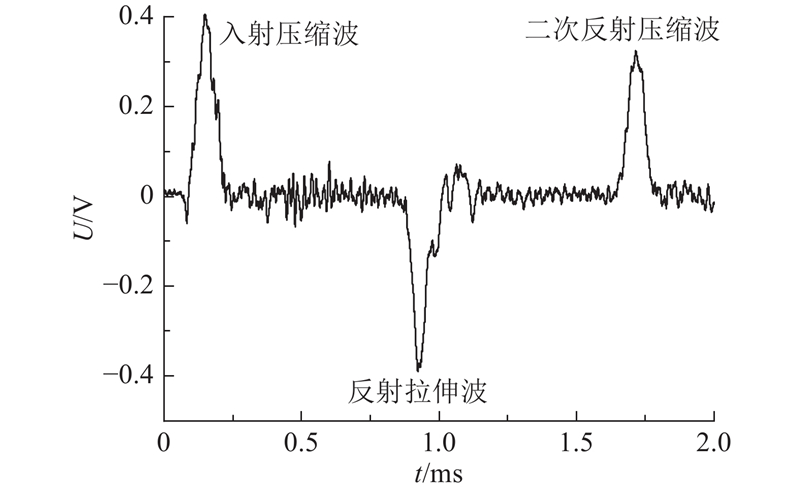
入射杆应变片测得的典型波形如图4所示. 图中，以压缩信号为正. 第1个压缩波为撞击杆撞击入射杆产生的入射波形，第2个波为入射波在入射杆与试件界面部分反射形成的拉伸波，第3个波为反射的拉伸波传播到入射杆靠近撞击杆的自由端时发生二次反射形成的压缩波. 在计算试件中波速时，只须取第1、2个波的峰值，保留正负号. 该方法通过测峰值得到波速，简称峰值法. 峰值法以一维应力波传播理论为基础，试验可行性高，只须在入射杆上布置一个应变片，排除了不同应变片间的测量差异. 经过实际验算，采用该方法计算得到的结果离散性较大，甚至有个别波形的拉伸波峰值绝对值大于压缩波峰值，从而计算出负波速，显然不合理，部分计算结果如表3所示. 表中，UI为入射波峰电压，UR为反射波峰电压，C2为计算波速. 产生如此大误差的原因，可能是UHTCC的波阻抗相较于入射杆材料的波阻抗较小，根据反射应力（式（2））可知，当介质2的波阻抗远小于介质1的波阻抗时，反射波的绝对值与入射波绝对值相近，差值相较于峰值比例较小，易受测量误差影响. 利用式（6）计算波速主要由实测的2个峰值之间的差值决定，因此在利用入射杆波形计算时会产生巨大误差.

表 3   峰值法得到的波速计算结果

Tab.3  Wave velocity calculation results obtained by peak value method

I/MPa UI/V UR/V C2/（km·s−1）
0.18 0.637 60 −0.574 7 1.263 8
0.18 0.127 30 −0.121 8 0.538 0
0.25 0.216 10 −0.191 8 1.449 5
0.30 2.538 40 −2.292 2 1.240 9
0.45 3.296 96 −2.782 0 2.063 1

新窗口打开| 下载CSV


图 4

新窗口打开| 下载原图ZIP| 生成PPT

图 4   入射杆上一点处的典型波形

Fig.4   Typical waveform at a point on incident bar


对比分析两点法和峰值法可以看出，两点法测波速适用性更广，测得结果直接可靠；峰值法测波速试验方法简便，但仅限于被测材料波阻抗与入射杆材料波阻抗在相近量级的情况，适用范围较小.

3.3. UHTCC中的应力波峰值衰减

波形图显示，在0.3、0.4、0.5 MPa冲击气压下，各截面峰值随着波的传播呈现较明显的下降趋势，符合黏弹性材料的衰减特性. 在0.2 MPa下的多次试验显示，波峰呈现出上下波动，没有统一的衰减趋势，可能是由于0.2 MPa冲击气压下冲击强度弱，材料尚未进入黏弹性状态，衰减趋势不明显. 根据黏弹性材料的应力波峰值呈指数衰减[6]，对0.3、0.4、0.5 MPa冲击气压下的峰值进行指数拟合，各组气压下的衰减系数平均值呈现出较小的波动，0.3、0.4、0.5 MPa对应的平均衰减系数分别为2.93、2.74、2.66 m−1. 衰减系数取平均值，为2.777 m−1.

4. UHTCC的朱-王-唐冲击本构参数

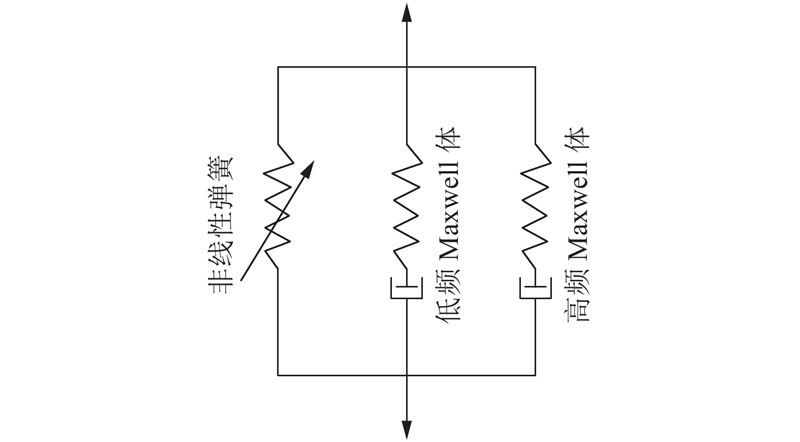
朱-王-唐本构模型由1个弹簧（非线性）和2个Maxwell体（一个低频，一个高频）并联组成，如图5所示. 朱-王-唐本构方程如下：

图 5

新窗口打开| 下载原图ZIP| 生成PPT

图 5   朱-王-唐本构物理模型

Fig.5   Zhu-Wang-Tang constitutive physical model


$\begin{split} \sigma = & {E_0}\varepsilon + \alpha {\varepsilon ^2} + \beta {\varepsilon ^3} + {E_1}\int_0^t {\dot \varepsilon (\tau ){{\rm exp}\;{\left( - \frac{{t - \tau }}{{{\theta _1}}}\right)}}}{\rm d}\tau + \\ & {E_2}\int_0^t {\dot \varepsilon (\tau ){{\rm exp}\;{\left( - \frac{{t - \tau }}{{{\theta _2}}}\right)}}}{\rm d}\tau . \end{split} $

式中：σ为应力；ε为应变； $\dot \varepsilon $为应变率；t为时间；等式右边前3项表征材料的非线性弹性响应，对应图5中的非线性弹簧，E0、α、β为材料的弹性参数；等式右边第1个积分项对应图5中的低频Maxwell体，用于描述低应变率下材料的黏弹性响应，E1、θ1为低频Maxwell体的弹性常数和松弛时间；等式右边第2个积分项对应高频Maxwell体，描述材料在高应变率下的黏弹性响应，E2、θ2为高频Maxwell体的相应参数.

根据文献[9]对朱-王-唐本构的总结，α、β远小于E0，因此只有当ε > 0.01时，才须考虑非线性. 在本试验中未出现大于0.01的应变，因此在应用朱-王-唐本构模型时可以不考虑非线性. 此外，在冲击荷载作用下，低频Maxwell体在加载结束前都不能恢复松弛，此时的低频Maxwell体将简化为一个线性弹簧，弹性常数为 E1. 朱-王-唐冲击本构方程可以简写为

$\sigma {\rm{ = }}{E_{\rm a}}\varepsilon + {E_2}\int_0^t {\dot \varepsilon (\tau ){{\rm exp}\;{\left( - \frac{{t - \tau }}{{{\theta _2}}}\right)}}}{\rm d}\tau. $

式中：Ea为2个弹簧的弹性常数之和，Ea=E0+E1.

结合应力波传播理论，将冲击荷载下的朱-王-唐本构代入波传播的控制方程组，求解这组偏微分控制方程组，可以得到特征波速：

${C_{\rm{v}}} = \sqrt {{{\left({E_{\rm{a}}} + {E_2}\right)}}/{{{\rho _2}}}}. $

应力波峰值随传播距离呈指数衰减：

$\sigma {\rm{ = }}{\sigma ^{\rm{*}}}{{\rm exp}\;{ (- {\alpha _{\rm a}}x)}}.$

式中：σ为一点的应力波峰值，σ*为初始应力，x为σ所在的点与初始应力点之间的距离，αa为衰减系数.

通过求解可以得到衰减系数公式：

${\alpha _{\rm a}} = {E_2}/(2{\theta _2}{\rho _2}C_{\rm v}^3).$

由式（9）、（11），可以用Cv、αa表示高频Maxwell体的参数E2、θ2：

${E_2} = {\rho _2}C_{\rm v}^2 - {E_{\rm a}},$

${\theta _2}{\rm{ = }}{E_2}/(2{\alpha _{\rm a}}{\rho _2}C_{\rm v}^3).$

将计算得到的Cv、αa、ρ2代入式（12）、（13），得出UHTCC材料中E2、θ2关于Ea的表达式：

${E_2} = 16.80 - {E_{\rm a}}\;,$

${\theta _2}{\rm{ = }}(16.80 - {E_{\rm a}})/0.285 \; .$

UHTCC的朱-王-唐冲击本构可以表示为

$\sigma={E_{\rm a}}\varepsilon + (16.8 - {E_{\rm a}})\int_0^t {\dot \varepsilon (\tau )}{\rm exp}\; {\left[ - \frac{{0.285(t - \tau )}}{{16.8 - {E_{\rm a}}}}\right]}{\rm d}\tau . $

式中：Ea可以通过准静态试验测出. UHTCC的冲击朱-王-唐本构转化为只含准静态材料参数的方程. 通过波传播试验和准静态试验共同测定材料的朱-王-唐本构参数，这种测量方法保留了参数的物理意义，得到的本构方程能够真实反映材料的非线性和黏弹性特性.

5. 结　论

（1）通过对比几次同等加载条件下入射杆上的入射波形和反射波形，验证本试验装置加载波形的一致性.

（2）在波速测试方法中，两点测量法结果较为稳定准确，入射杆波形法只适用于试件波阻抗与入射杆波阻抗量级相似的情况.

（3）UHTCC中的应力波波速、峰值衰减系数随冲击气压均没有明显变化，平均波速为3.060 km/s，平均峰值衰减系数为2.777 m−1.

（4）按照朱-王-唐本构模型的定义可以将高频参数E2、θ2用具有实际意义的材料参数表达. 在通过波传播试验确定波速和衰减后，朱-王-唐冲击本构可以表示为只含单个准静态参数的方程.

（5）接下来可以通过相应的准静态试验测出剩余的准静态参数，从而确定UHTCC的朱-王-唐本构方程，并进一步通过试验检验朱-王-唐本构对UHTCC的适用性.

参考文献

王礼立. 应力波基础[M]. 北京: 国防工业出版社, 1985.

[本文引用: 1]

王礼立, 胡时胜, 杨黎明, 等. 材料动力学[M]. 合肥: 中国科技大学出版社, 2017.

[本文引用: 1]

BACON C

An experimental method for considering dispersion and attenuation in a viscoelastic Hopkinson bar

[J]. Experimental Mechanics, 1998, 38 (4): 242- 249

DOI:10.1007/BF02410385      [本文引用: 1]

SIVIOUR C R

A measurement of wave propagation in the split Hopkinson pressure bar

[J]. Measurement Science and Technology, 2009, 20 (6): 1- 5

[本文引用: 1]

JU Y, YANG Y M, MAO Y Z, et al

Laboratory investigation on mechanisms of stress wave propagations in porous media

[J]. Science in China: Series E: Technological Sciences, 2009, 52 (5): 1374- 1389

DOI:10.1007/s11431-009-0128-y      [本文引用: 1]

胡时胜, 张磊, 武海军, 等

混凝土材料层裂强度的实验研究

[J]. 工程力学, 2004, 21 (4): 128- 132

DOI:10.3969/j.issn.1000-4750.2004.04.023      [本文引用: 3]

HU Shi-sheng, ZHANG Lei, WU Hai-jun, et al

Experimental study on spalling strength of concrete

[J]. Engineering Mechanics, 2004, 21 (4): 128- 132

DOI:10.3969/j.issn.1000-4750.2004.04.023      [本文引用: 3]

赖建中, 孙伟

活性粉末混凝土的层裂性能研究

[J]. 工程力学, 2009, 26 (1): 137- 141

[本文引用: 1]

LAI Jian-zhong, SUN Wei

The spalling behaviour of reactive powder concrete

[J]. Engineering Mechanics, 2009, 26 (1): 137- 141

[本文引用: 1]

KLEPACZKO J R, BRARA A

An experimental method for dynamic tensile testing of concrete by spalling

[J]. International Journal of Impact Engineering, 2001, 25 (4): 387- 409

DOI:10.1016/S0734-743X(00)00050-6      [本文引用: 1]

王礼立, PLUVINAGE G, LABIBES K

冲击载荷下高聚物动态本构关系对黏弹性波传播特性的影响

[J]. 宁波大学学报:理工版, 1995, 8 (3): 30- 57

[本文引用: 3]

WANG Li-li, PLUVINAGE G, LABIBES K

The influence of dynamic constitutive relations of polymers at impact loading on the viscoelastic wave propagation character

[J]. Journal of Ningbo University: Natural Science and Engineering Edition, 1995, 8 (3): 30- 57

[本文引用: 3]

FAN L F, WONG L N Y, MA G W

Experimental investigation and modeling of viscoelastic behavior of concrete

[J]. Construction and Building Materials, 2013, 48: 814- 821

DOI:10.1016/j.conbuildmat.2013.07.010     

GEORGIN J F, REYNOUARD J M

Modeling of structures subjected to impact: concrete behaviour under high strain rate

[J]. Cement and Concrete Composites, 2003, 25 (1): 131- 143

DOI:10.1016/S0958-9465(01)00060-9      [本文引用: 1]

WANG L L, ZHOU F H, SUN Z J, et al

Studies on rate-dependent macro-damage evolution of materials at high strain rates

[J]. International Journal of Damage Mechanics, 2010, 19 (7): 805- 820

DOI:10.1177/1056789509359654      [本文引用: 1]

ZHANG H, WANG B, XIE A Y, et al

Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete

[J]. Construction and Building Materials, 2017, 152: 154- 167

DOI:10.1016/j.conbuildmat.2017.06.177      [本文引用: 1]

胡时胜, 王道荣

冲击载荷下混凝土材料的动态本构关系

[J]. 爆炸与冲击, 2002, 22 (3): 242- 246

DOI:10.3321/j.issn:1001-1455.2002.03.009      [本文引用: 1]

HU Shi-sheng, WANG Dao-rong

Dynamic constitutive relation of concrete under impact

[J]. Explosion and Shock Waves, 2002, 22 (3): 242- 246

DOI:10.3321/j.issn:1001-1455.2002.03.009      [本文引用: 1]

LAI J Z, SUN W

Dynamic behaviour and visco-elastic damage model of ultra-high performance cementitious composite

[J]. Cement and Concrete Research, 2009, 39 (11): 1044- 1051

DOI:10.1016/j.cemconres.2009.07.012      [本文引用: 1]

ZHANG H, WANG L, ZHENG K, et al

Research on compressive impact dynamic behavior and constitutive model of polypropylene fiber reinforced concrete

[J]. Construction and Building Materials, 2018, 187: 584- 595

DOI:10.1016/j.conbuildmat.2018.07.164      [本文引用: 1]

XU S L, CAI X R

Experimental study and theoretical models on compressive properties of ultrahigh toughness cementitious composites

[J]. Journal of Materials in Civil Engineering, 2010, 22 (10): 1067- 1077

DOI:10.1061/(ASCE)MT.1943-5533.0000109      [本文引用: 1]

徐世烺, 李贺东

超高韧性水泥基复合材料研究进展及其工程应用

[J]. 土木工程学报, 2008, 41 (6): 45- 60

DOI:10.3321/j.issn:1000-131X.2008.06.008      [本文引用: 1]

XU Shi-lang, LI He-dong

A review on the development of research and application of ultra high toughness cementitious composites

[J]. China Civil Engineering Journal, 2008, 41 (6): 45- 60

DOI:10.3321/j.issn:1000-131X.2008.06.008      [本文引用: 1]

LI V C, WANG S X, WU C

Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC)

[J]. ACI Materials Journal, 2001, 98 (6): 483- 492

[本文引用: 1]

CUROSU I, MECHTCHERINE V, FORNI D, et al

Performance of various strain-hardening cement-based composites (SHCC) subject to uniaxial impact tensile loading

[J]. Cement and Concrete Research, 2017, 102: 16- 28

DOI:10.1016/j.cemconres.2017.08.008      [本文引用: 1]

KANG S, KIM J

The relation between fiber orientation and tensile behavior in an ultra high performance fiber reinforced cementitious composites (UHPFRCC)

[J]. Cement and Concrete Research, 2011, 41 (10): 1001- 1014

DOI:10.1016/j.cemconres.2011.05.009      [本文引用: 1]

LI V C, WU C, WANG S X, et al

Interface tailoring for strain-hardening polyvinyl alcohol engineered cementitious composite (PVA-ECC)

[J]. ACI Materials Journal, 2002, 99 (5): 463- 472

[本文引用: 1]

徐世烺, 李贺东

超高韧性水泥基复合材料直接拉伸试验研究

[J]. 土木工程学报, 2009, 42 (9): 32- 41

DOI:10.3321/j.issn:1000-131X.2009.09.005      [本文引用: 1]

XU Shi-lang, LI He-dong

Uniaxial tensile experiments of ultra-high toughness cementitious composite

[J]. China Civil Engineering Journal, 2009, 42 (9): 32- 41

DOI:10.3321/j.issn:1000-131X.2009.09.005      [本文引用: 1]

WILLE K, EL-TAWIL S, NAAMAN A E

Properties of strain hardening ultra high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading

[J]. Cement and Concrete Composites, 2014, 48: 53- 66

DOI:10.1016/j.cemconcomp.2013.12.015     

YU K Q, LI L Z, YU J T, et al

Direct tensile properties of engineered cementitious composites: a review

[J]. Construction and Building Materials, 2018, 165: 346- 362

DOI:10.1016/j.conbuildmat.2017.12.124      [本文引用: 1]

高翔. 纳米SiO2改性超高韧性水泥基复合材料试验研究[D]. 杭州: 浙江大学, 2016.

[本文引用: 1]

GAO Xiang. Experimental study on ultra high toughness cementitious composites with nano-SiO2 [D]. Hangzhou: Zhejiang University, 2016.

[本文引用: 1]

刘问. 超高韧性水泥基复合材料动态力学性能的试验研究[D]. 大连: 大连理工大学, 2012.

[本文引用: 1]

LIU Wen. Experimental study on dynamic mechanical properties of ultra-high toughness cementitious composites [D]. Dalian: Dalian University of Technology, 2012.

[本文引用: 1]

LI Q H, ZHAO X, XU S L, et al

Influence of steel fiber on dynamic compressive behavior of hybrid fiber ultra high toughness cementitious composites at different strain rates

[J]. Construction and Building Materials, 2016, 125: 490- 500

DOI:10.1016/j.conbuildmat.2016.08.066      [本文引用: 1]

王礼立, 王永刚

应力波在用SHPB研究材料动态本构特性中的重要作用

[J]. 爆炸与冲击, 2005, 25 (1): 17- 25

DOI:10.3321/j.issn:1001-1455.2005.01.004      [本文引用: 1]

WANG Li-li, WANG Yong-gang

The important role of stress waves in the study on dynamic constitutive behavior of materials by SHPB

[J]. Explosion and Shock Waves, 2005, 25 (1): 17- 25

DOI:10.3321/j.issn:1001-1455.2005.01.004      [本文引用: 1]

/

〈 〉